|
NVIDIA 2D Image And Signal Performance Primitives (NPP)
Version 10.2.*.*
|
|
NVIDIA 2D Image And Signal Performance Primitives (NPP)
Version 10.2.*.*
|
Primitives for computing the proximity measure between a source image and a template image. More...
Modules | |
| SqrDistanceFull_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with full mode. |
|
| SqrDistanceSame_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with same mode. |
|
| SqrDistanceValid_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with valid mode. |
|
| CrossCorrFull_Norm | |
| Primitives for computing the normalized cross correlation between two images with full mode. |
|
| CrossCorrSame_Norm | |
| Primitives for computing the normalized cross correlation between two images with same mode. |
|
| CrossCorrValid_Norm | |
| Primitives for computing the normalized cross correlation between two images with valid mode. |
|
| CrossCorrValid | |
| Primitives for computing the cross correlation between two images with valid mode. |
|
| CrossCorrFull_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with full mode. |
|
| CrossCorrSame_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with same mode. |
|
| CrossCorrValid_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with valid mode. |
|
Primitives for computing the proximity measure between a source image and a template image.
There are basically two approaches to compute the proximity measure for template matching, Euclidean distance and the cross correlation.
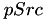 (
(  ) and a template image
) and a template image 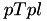 (
(  ), the Euclidean distance
), the Euclidean distance 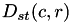 between two images at pixel in row
between two images at pixel in row 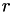 and column
and column 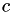 is computed as (
is computed as ( 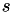 stands for source image and
stands for source image and 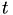 for template image for short):
for template image for short):
![\[D_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})]^2 \]](form_91.png)
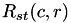 is calculated as:
is calculated as:
![\[R_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)\cdot pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})] \]](form_93.png)
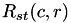 is affected by the brightness of the images which may vary due to the lighting and exposure conditions. Therefore, NPP computes the cross correlation coefficient to circumvent this dependence. This is typically done at every step by subtracting the mean from every pixel value, i.e.,
is affected by the brightness of the images which may vary due to the lighting and exposure conditions. Therefore, NPP computes the cross correlation coefficient to circumvent this dependence. This is typically done at every step by subtracting the mean from every pixel value, i.e.,
![\[\tilde{R}_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-Mean_t]\cdot [pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})-Mean_s] \]](form_94.png)
NPP computes the normalized values of Euclidean distance, cross correlation and the cross correlation coefficient.
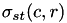 is defined as:
is defined as:
![\[\sigma_{st}(c,r) = \frac{D_{st}(c,r)}{\sqrt{R_{ss}(c,r)\cdot R_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_96.png)
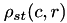 is defined as:
is defined as:
![\[\rho_{st}(c,r) = \frac{R_{st}(c,r)}{\sqrt{R_{ss}(c,r)\cdot R_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_98.png)
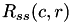 and
and 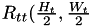 denote the auto correlation of the source image and the template image individually. They are defined as:
denote the auto correlation of the source image and the template image individually. They are defined as:
![\[R_{ss}(c,r)=\sum_{j=c-\frac{H_t}{2}}^{c+\frac{H_t}{2}}\sum_{i=r-\frac{W_t}{2}}^{r+\frac{W_t}{2}}pSrc(j, i) \]](form_101.png)
![\[R_{tt}(\frac{H_t}{2},\frac{W_t}{2})=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}pTpl(j,i) \]](form_102.png)
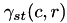 is calculated as:
is calculated as:
![\[\gamma_{st}(c,r) = \frac{\tilde{R}_{st}(c,r)}{\sqrt{\tilde{R}_{ss}(c,r)\cdot \tilde{R}_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_104.png)
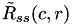 and
and 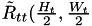 are defined as:
are defined as:
![\[\tilde{R}_{ss}(c,r)=\sum_{j=c-\frac{H_t}{2}}^{c+\frac{H_t}{2}}\sum_{i=r-\frac{W_t}{2}}^{r+\frac{W_t}{2}}[pSrc(j, i)-Mean_s] \]](form_107.png)
![\[\tilde{R}_{tt}(\frac{H_t}{2},\frac{W_t}{2})=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-Mean_t] \]](form_108.png)
The Euclidean distance and the cross correlation are categorized into three types, full, same, and valid.
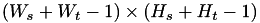 .
. .
.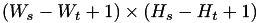 .
.