cuSPARSE Storage Formats

The cuSPARSE library supports dense and sparse vector, and dense and sparse matrix formats.

Index Base

The library supports zero- and one-based indexing to ensure the compatibility with C/C++ and Fortran languages respectively. The index base is selected through the cusparseIndexBase_t type.

Vector Formats

This section describes dense and sparse vector formats.

Dense Vector Format

Dense vectors are represented with a single data array that is stored linearly in memory, such as the following \(7 \times 1\) dense vector.

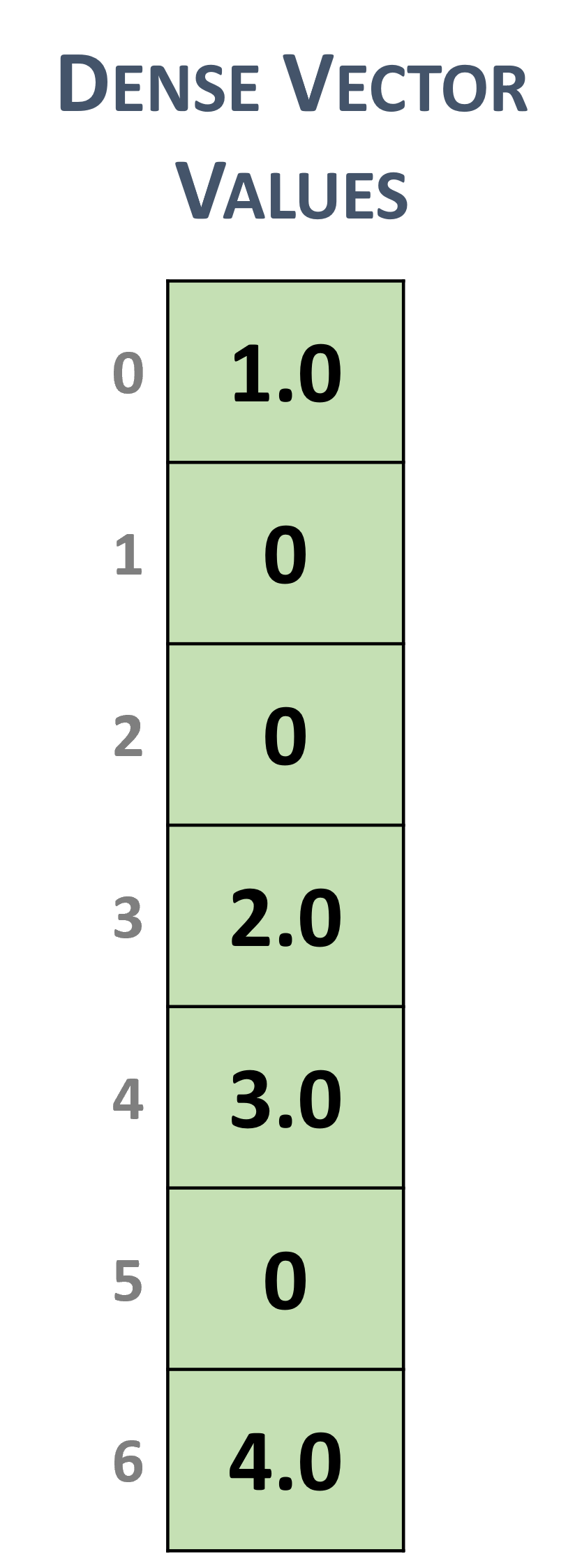
_images/dense_vector.png — Dense vector representation

Sparse Vector Format

Sparse vectors are represented with two arrays.

The values array stores the nonzero values from the equivalent array in dense format.
The indices array represent the positions of the corresponding nonzero values in the equivalent array in dense format.

For example, the dense vector in section 3.2.1 can be stored as a sparse vector with zero-based or one-based indexing.

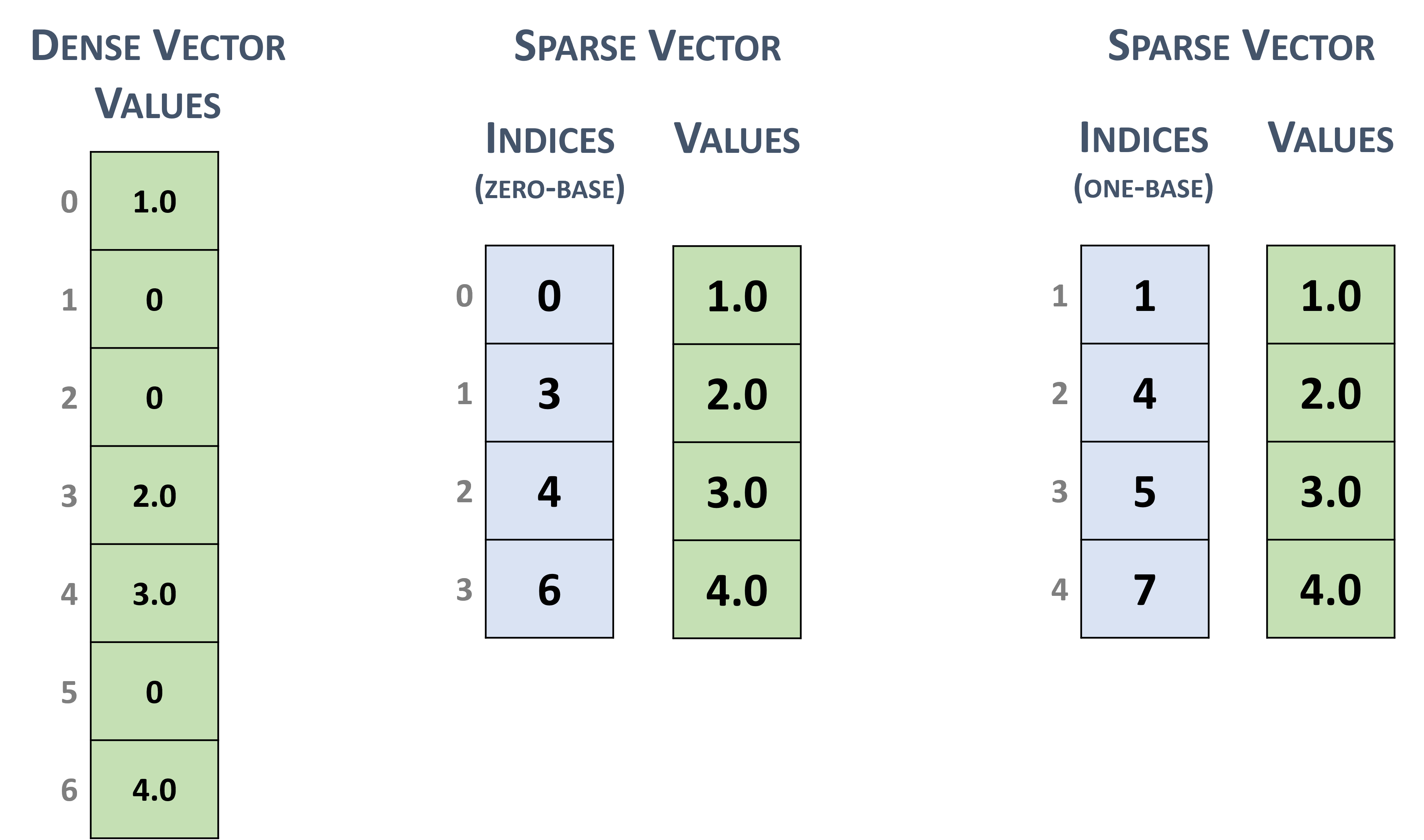
_images/sparse_vector.png — Sparse vector representation

Note

The cuSPARSE routines assume that the indices are provided in increasing order and that each index appears only once. In the opposite case, the correctness of the computation is not always ensured.

Matrix Formats

Dense and several sparse formats for matrices are discussed in this section.

Dense Matrix Format

A dense matrix can be stored in both row-major and column-major memory layout (ordering) and it is represented by the following parameters.

The number of rows in the matrix.
The number of columns in the matrix.
The leading dimension, which must be
- Greater than or equal to the number of columns in the row-major layout
- Greater than or equal to the number of rows in the column-major layout
The pointers to the values array of length
- \(rows \times leading\; dimension\) in the row-major layout
- \(columns \times leading\; dimension\) in the column-major layout

The following figure represents a \(5 \times 2\) dense matrix with both memory layouts

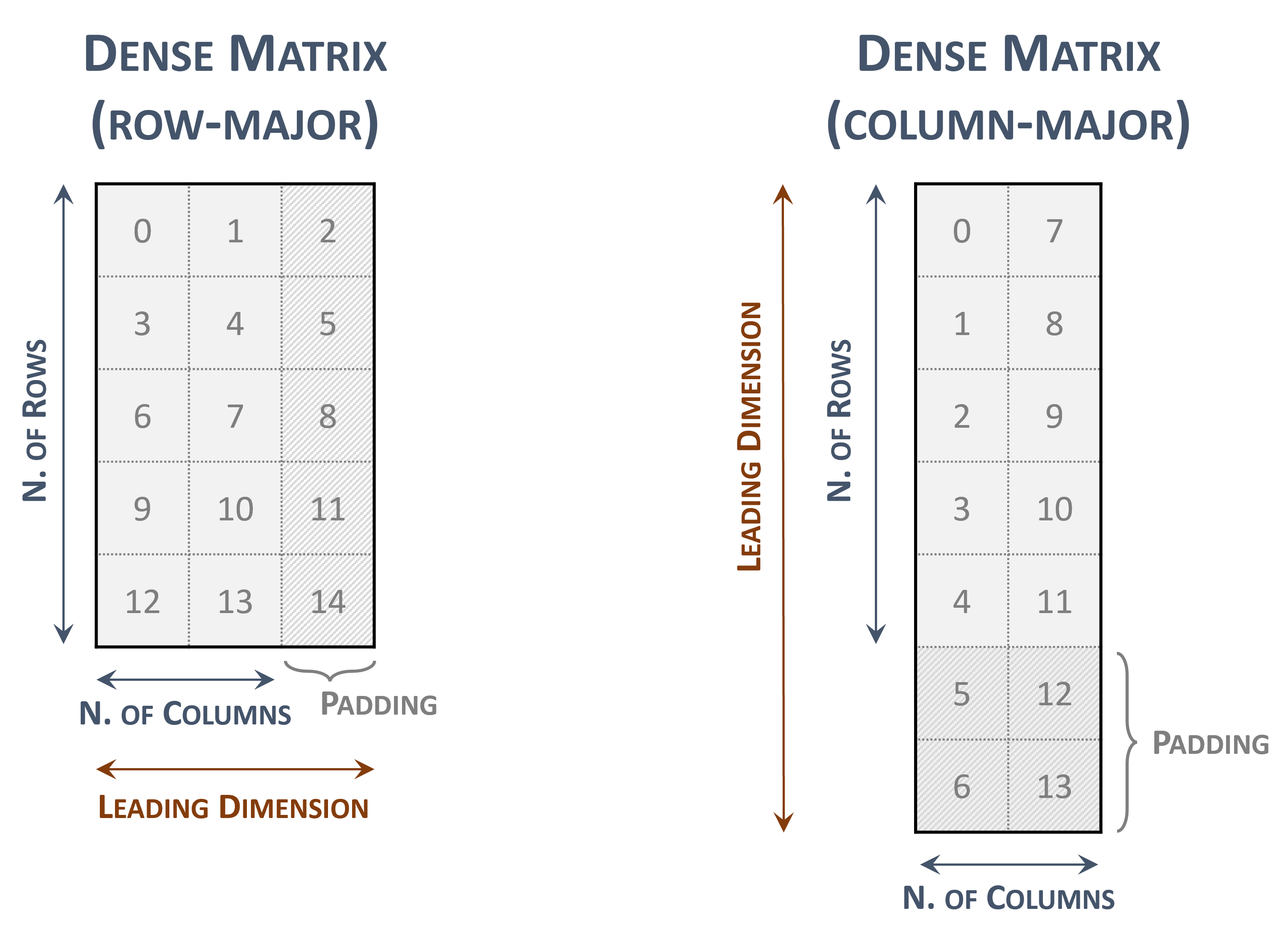
_images/dense_matrix.png — Dense matrix representations

The indices within the matrix represents the contiguous locations in memory.

The leading dimension is useful to represent a sub-matrix within the original one

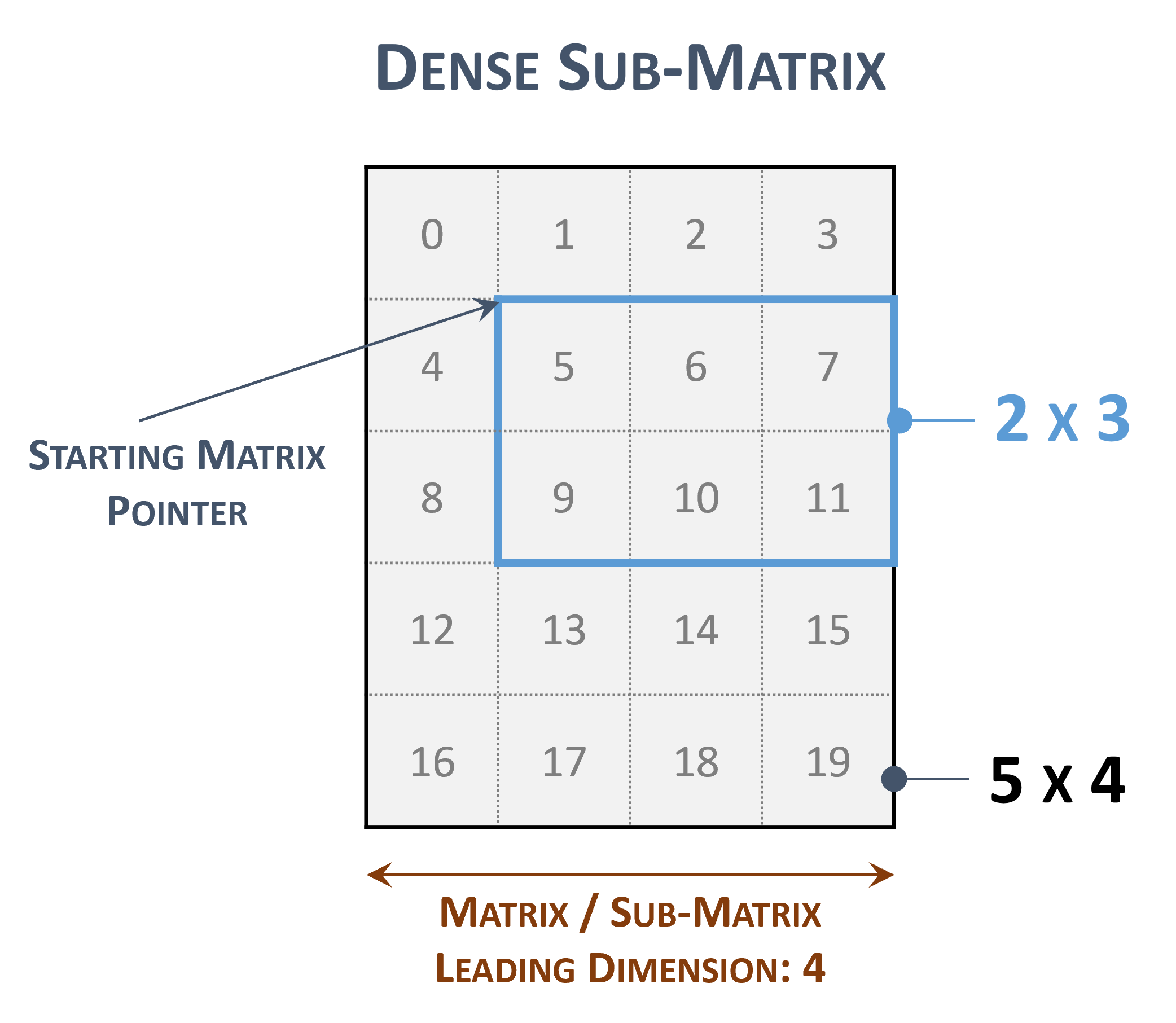
_images/sub_matrix.png — Sub-matrix representations

Coordinate (COO)

A sparse matrix stored in COO format is represented by the following parameters.

The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (nnz) in the matrix.
The pointers to the row indices array of length nnz that contains the row indices of the corresponding elements in the values array.
The pointers to the column indices array of length nnz that contains the column indices of the corresponding elements in the values array.
The pointers to the values array of length nnz that holds all nonzero values of the matrix in row-major ordering.
Each entry of the COO representation consists of a <row, column> pair.
The COO format is assumed to be sorted by row.

The following example shows a \(5 \times 4\) matrix represented in COO format.

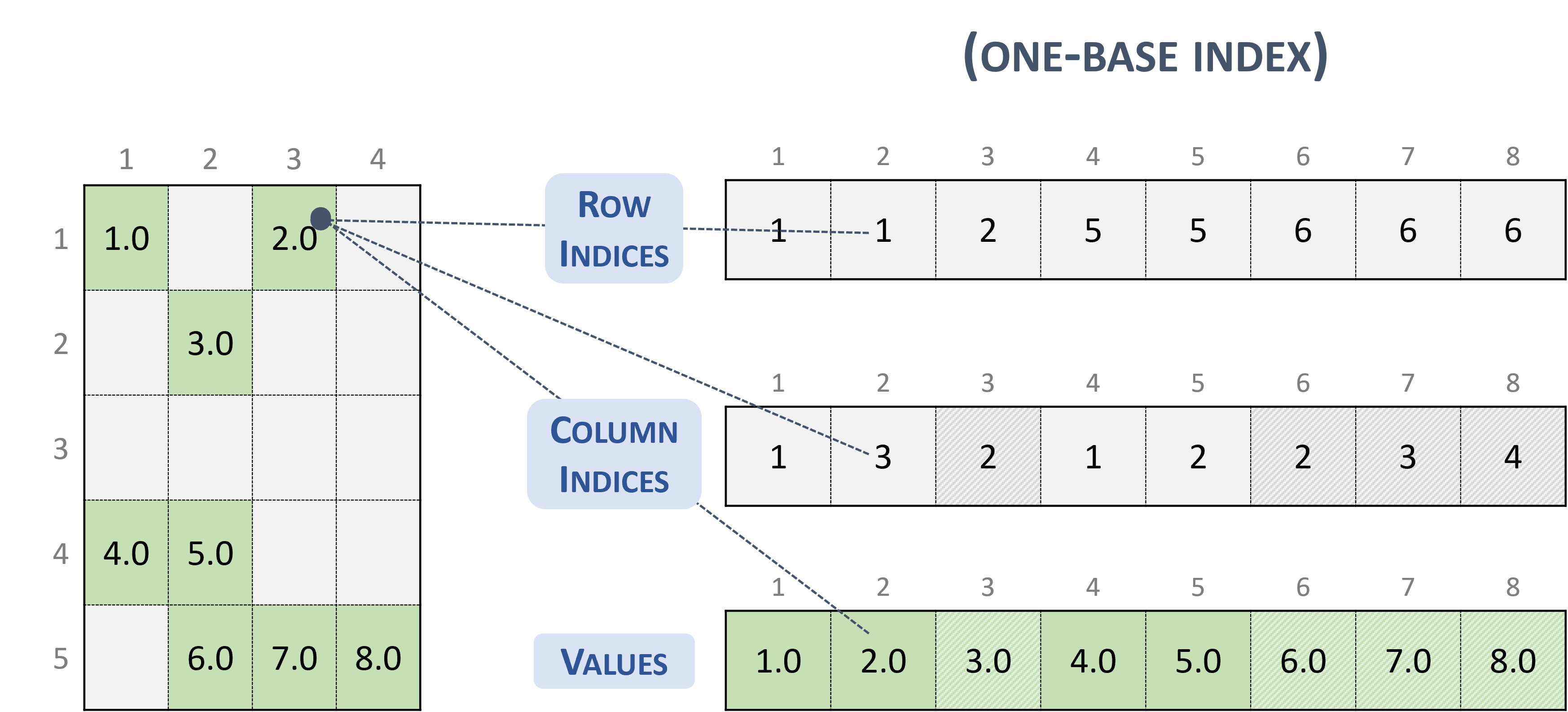
Note

cuSPARSE supports both sorted and unsorted column indices within a given row.

Note

If the column indices within a given row are unique, the correctness of the computation is not always ensured.

Given an entry in the COO format (zero-base), the corresponding position in the dense matrix is computed as:

// row-major
rows_indices[i] * leading_dimension + column_indices[i]

// column-major
column_indices[i] * leading_dimension + rows_indices[i]

Compressed Sparse Row (CSR)

The CSR format is similar to COO, where the row indices are compressed and replaced by an array of offsets.

A sparse matrix stored in CSR format is represented by the following parameters.

The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (nnz) in the matrix.
The pointers to the row offsets array of length number of rows + 1 that represents the starting position of each row in the columns and values arrays.
The pointers to the column indices array of length nnz that contains the column indices of the corresponding elements in the values array.
The pointers to the values array of length nnz that holds all nonzero values of the matrix in row-major ordering.

The following example shows a \(5 \times 4\) matrix represented in CSR format.

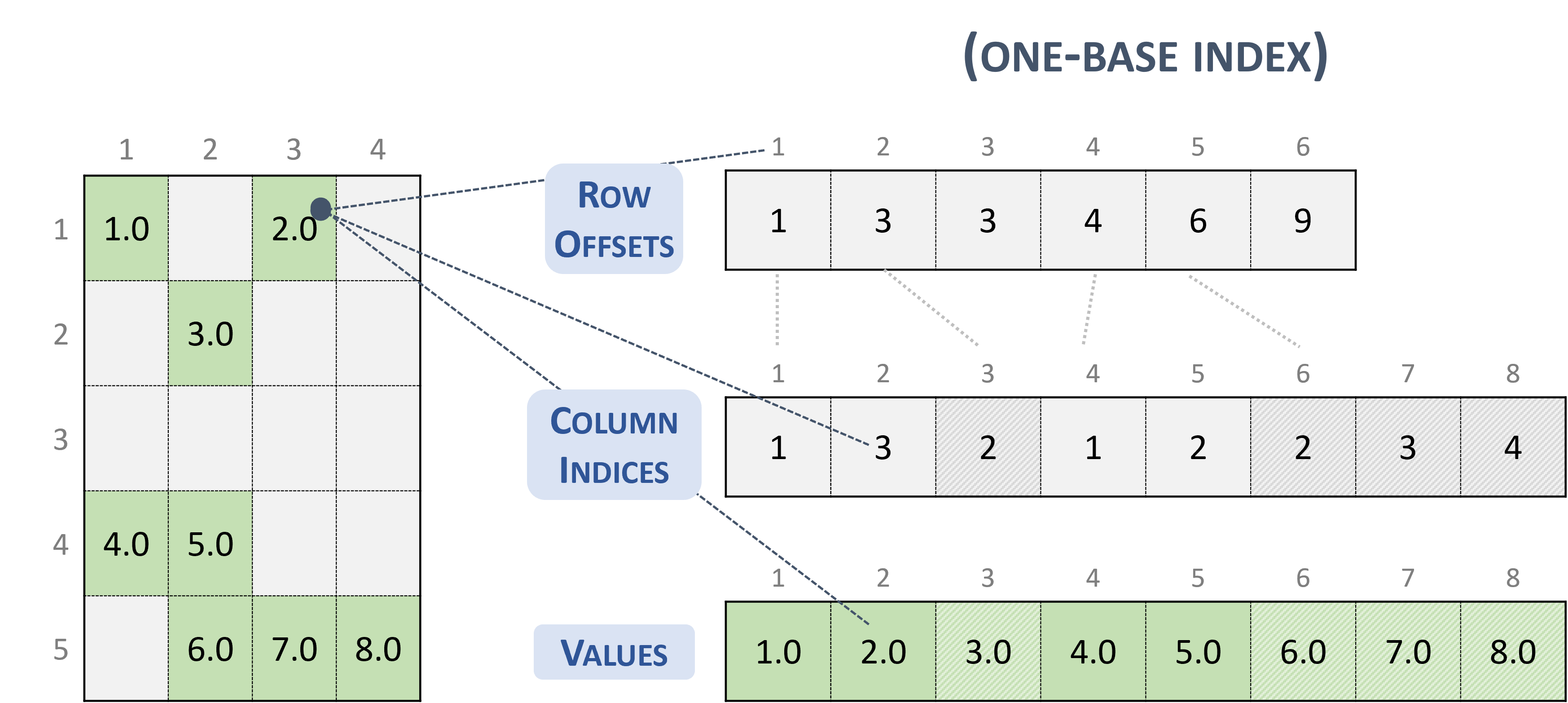
Note

cuSPARSE supports both sorted and unsorted column indices within a given row.

Note

If the column indices within a given row are not unique, the correctness of the computation is not always ensured.

Given an entry in the CSR format (zero-base), the corresponding position in the dense matrix is computed as:

// row-major
row * leading_dimension + column_indices[row_offsets[row] + k]

// column-major
column_indices[row_offsets[row] + k] * leading_dimension + row

Compressed Sparse Column (CSC)

The CSC format is similar to COO, where the column indices are compressed and replaced by an array of offsets.

A sparse matrix stored in CSC format is represented by the following parameters.

The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (nnz) in the matrix.
The pointers to the column offsets array of length number of column + 1 that represents the starting position of each column in the columns and values arrays.
The pointers to the row indices array of length nnz that contains row indices of the corresponding elements in the values array.
The pointers to the values array of length nnz that holds all nonzero values of the matrix in column-major ordering.

The following example shows a \(5 \times 4\) matrix represented in CSC format.

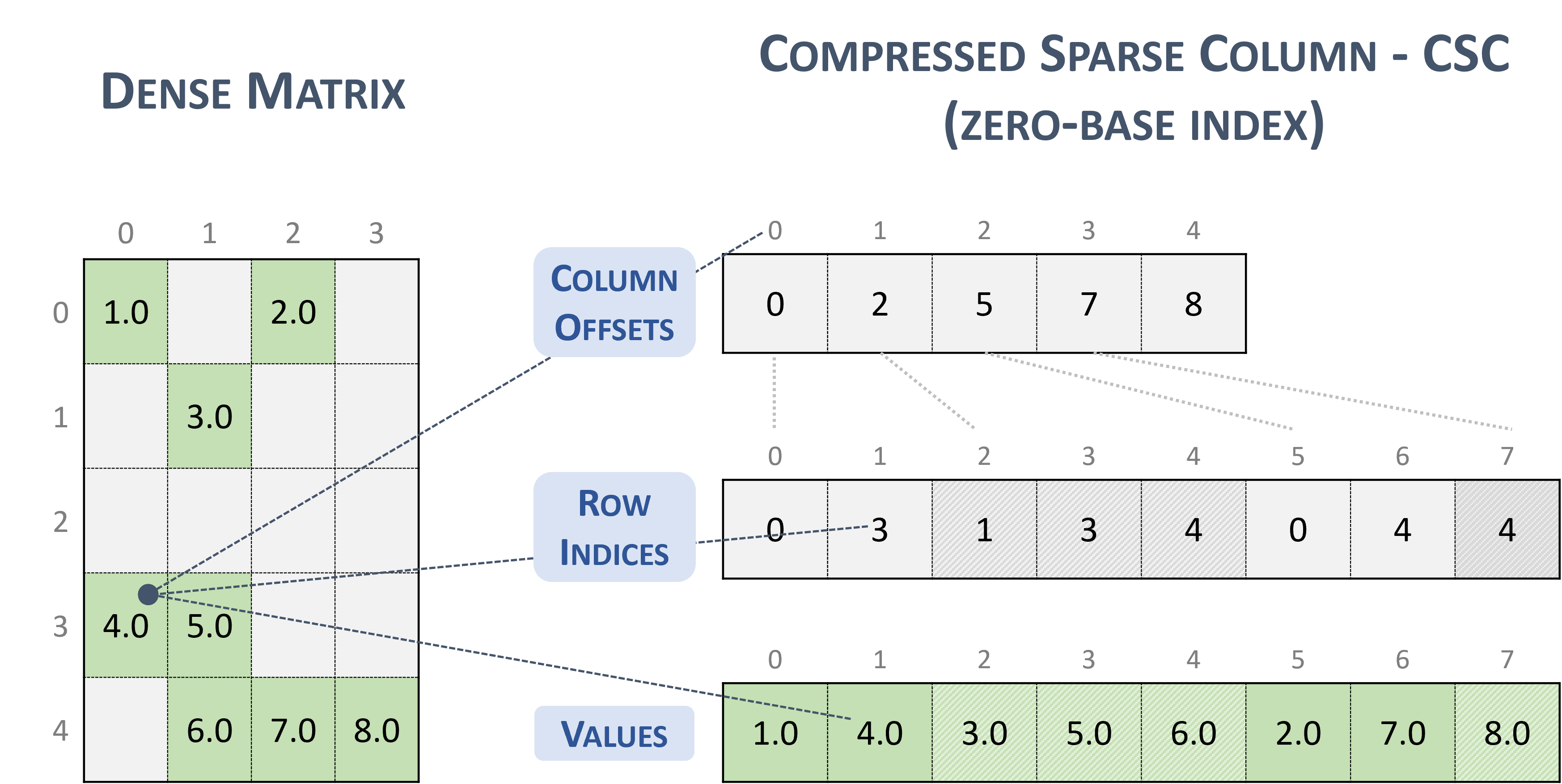
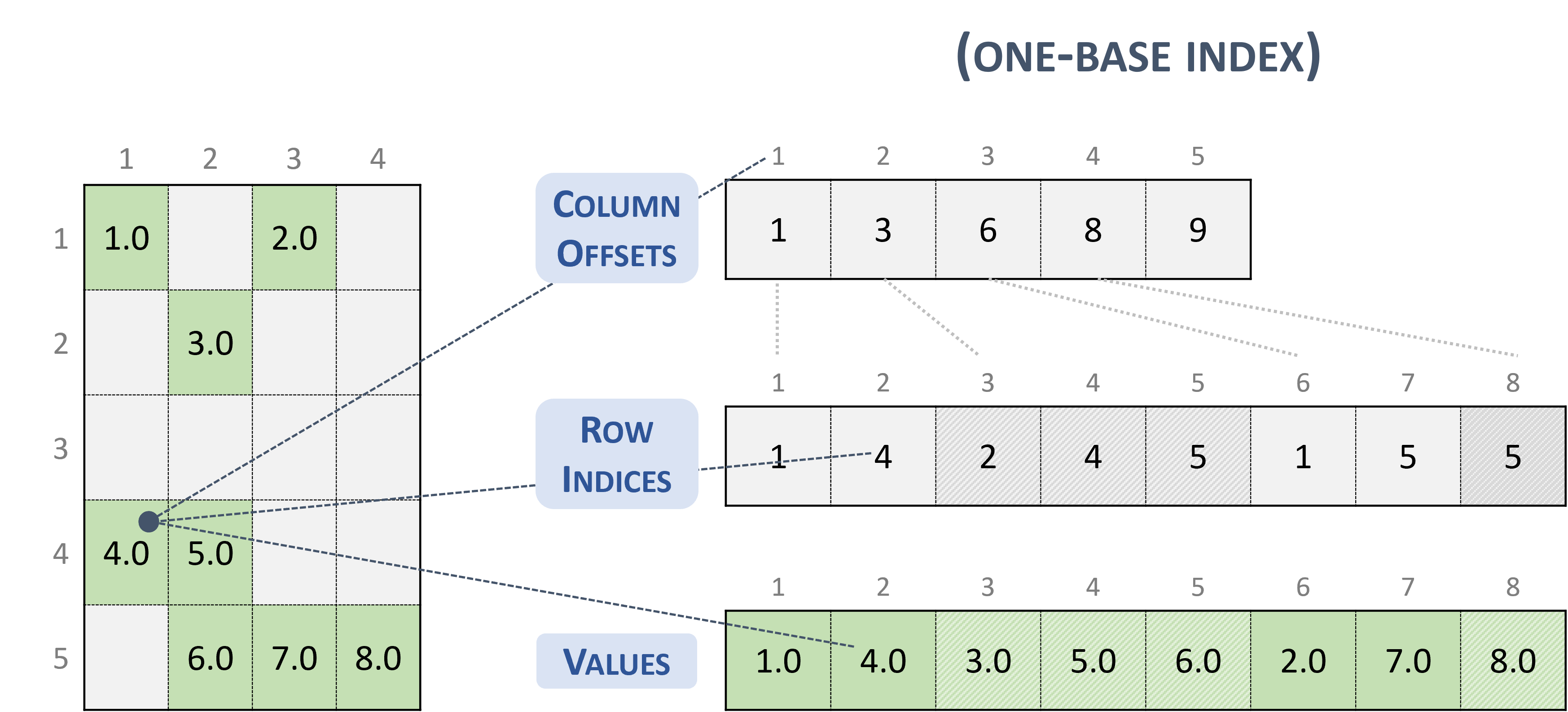
Note

The CSR format has exactly the same memory layout as its transpose in CSC format (and vice versa).

Note

cuSPARSE supports both sorted and unsorted row indices within a given column.

Note

If the row indices within a given column are not unique, the correctness of the computation is not always ensured.

Given an entry in the CSC format (zero-base), the corresponding position in the dense matrix is computed as:

// row-major
column * leading_dimension + row_indices[column_offsets[column] + k]

// column-major
row_indices[column_offsets[column] + k] * leading_dimension + column

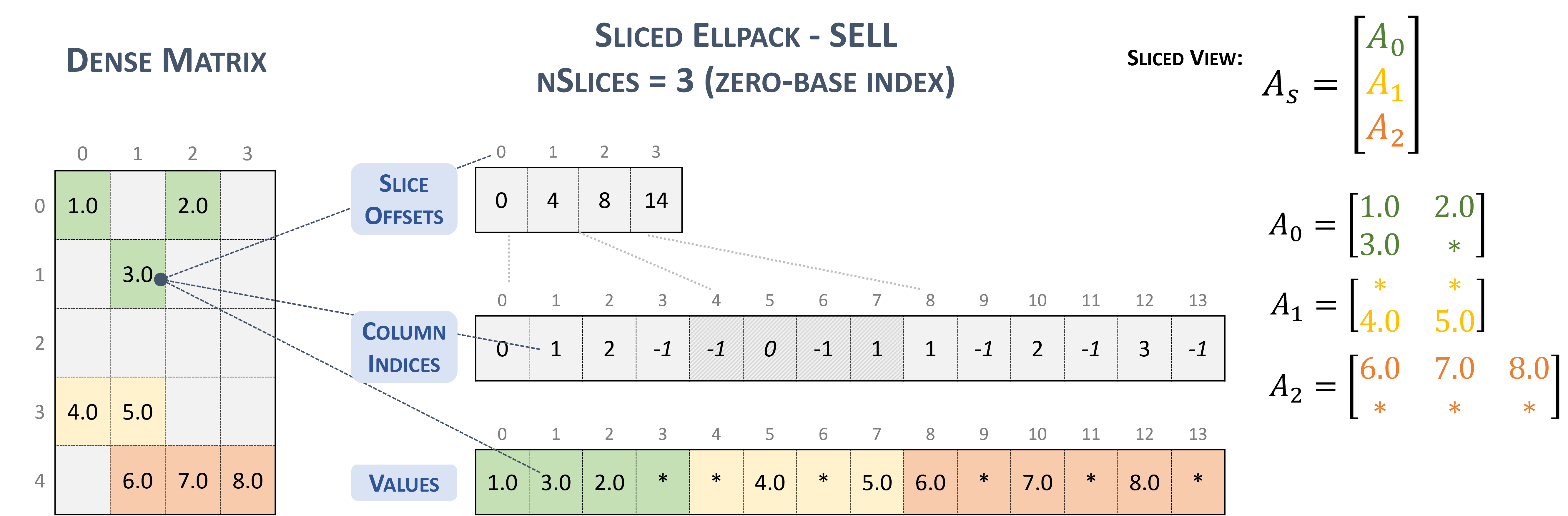
Sliced Ellpack (SELL)

The Sliced Ellpack format is standardized and well-known as the state of the art. This format allows to significantly improve the performance of all problems that involve low variability in the number of nonzero elements per row.

A matrix in the Sliced Ellpack format is divided into slices of an exact number of rows (\(sliceSize\)), defined by the user. The maximum row length (i.e., the maximum non-zeros per row) is found for each slice, and every row in the slice is padded to the maximum row length. The value -1 is used for padding.

A \(m \times n\) sparse matrix \(A\) is equivalent to a sliced sparse matrix \(A_{s}\) with \(nslices = \left \lceil{\frac{m}{sliceSize}}\right \rceil\) slice rows and \(n\) columns. To improve memory coalescing and memory utilization, each slice is stored in column-major order.

A sparse matrix stored in SELL format is represented by the following parameters.

The number of slices.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (nnz) in the matrix.
The total number elements (sellValuesSize), including non-zero values and padded elements.
The pointer to the slice offsets of length \(nslices + 1\) that holds offsets of the slides corresponding to the columns and values arrays.
The pointer to the column indices array of length sellValuesSize that contains column indices of the corresponding elements in the values array. The column indices are stored in column-major layout. Value -1 refers to padding.
The pointer to the values array of length sellValuesSize that holds all non-zero values and padding in column-major layout.

The following example shows a \(5 \times 4\) matrix represented in SELL format.

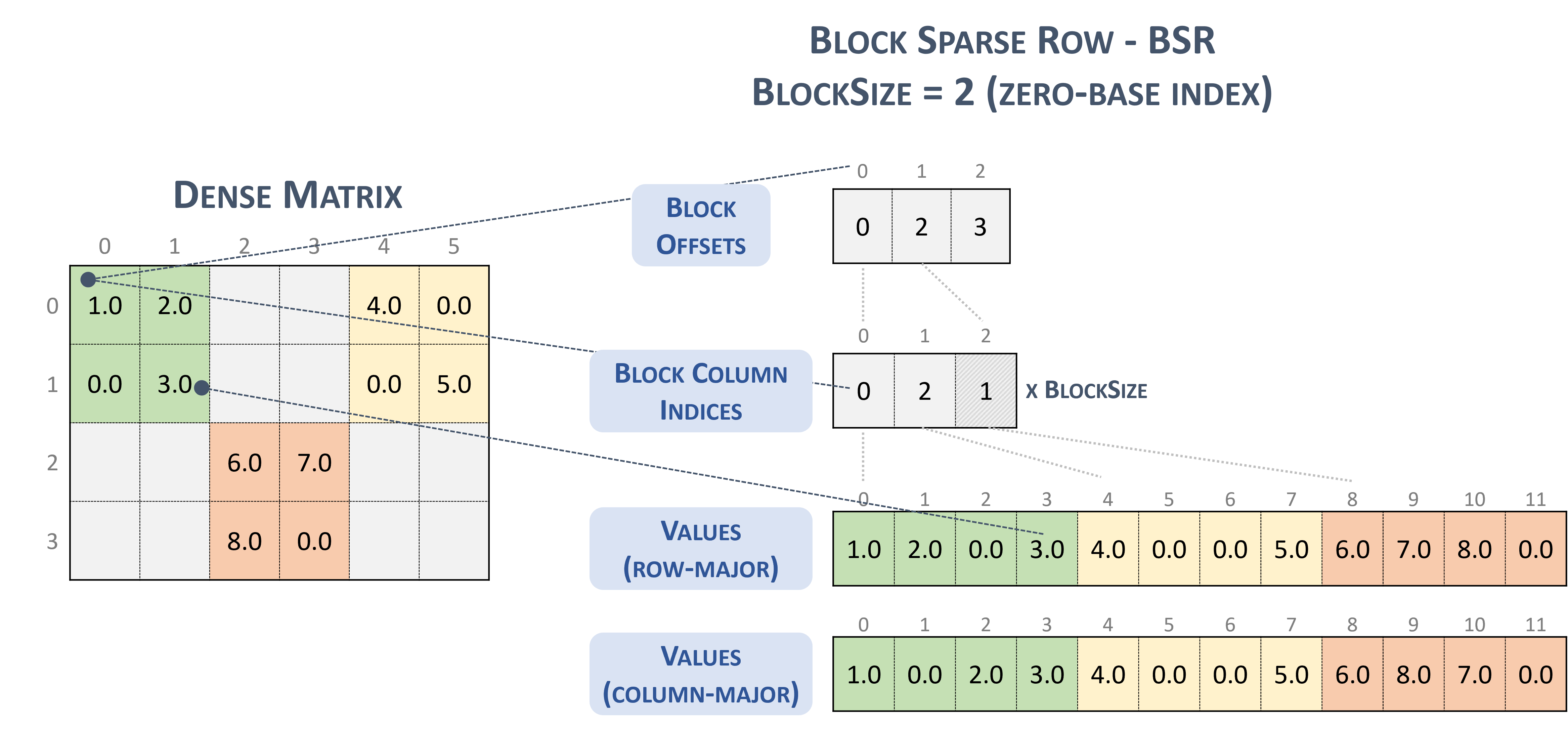
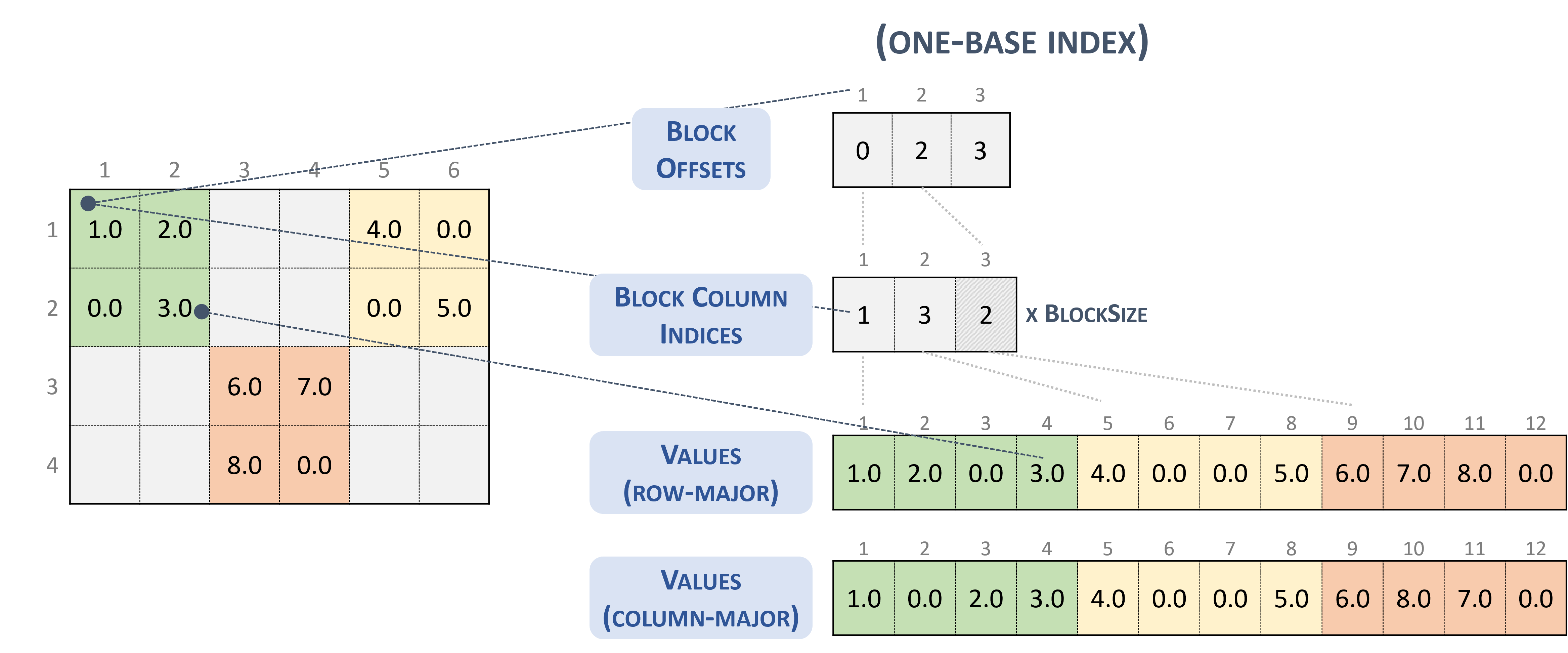
Block Sparse Row (BSR)

The BSR format is similar to CSR, where the column indices represent two-dimensional blocks instead of a single matrix entry.

A matrix in the Block Sparse Row format is organized into blocks of size \(blockSize\), defined by the user.

A \(m \times n\) sparse matrix \(A\) is equivalent to a block sparse matrix \(A_{B}\): \(mb \times nb\) with \(mb = \frac{m}{blockSize}\) block rows and \(nb = \frac{n}{blockSize}\) block columns. If \(m\) or \(n\) is not multiple of \(blockSize\), the user needs to pad the matrix with zeros.

Note

cuSPARSE currently supports only square blocks.

The BSR format stores the blocks in row-major ordering. However, the internal storage format of blocks can be column-major (cusparseDirection_t=CUSPARSE_DIRECTION_COLUMN) or row-major (cusparseDirection_t=CUSPARSE_DIRECTION_ROW), independently of the base index.

A sparse matrix stored in BSR format is represented by the following parameters.

The block size.
The number of row blocks in the matrix.
The number of column blocks in the matrix.
The number of non-zero blocks (nnzb) in the matrix.
The pointers to the row block offsets array of length number of row blocks + 1 that represents the starting position of each row block in the columns and values arrays.
The pointers to the column block indices array of length nnzb that contains the location of the corresponding elements in the values array.
The pointers to the values array of length nnzb that holds all nonzero values of the matrix.

The following example shows a \(4 \times 7\) matrix represented in BSR format.

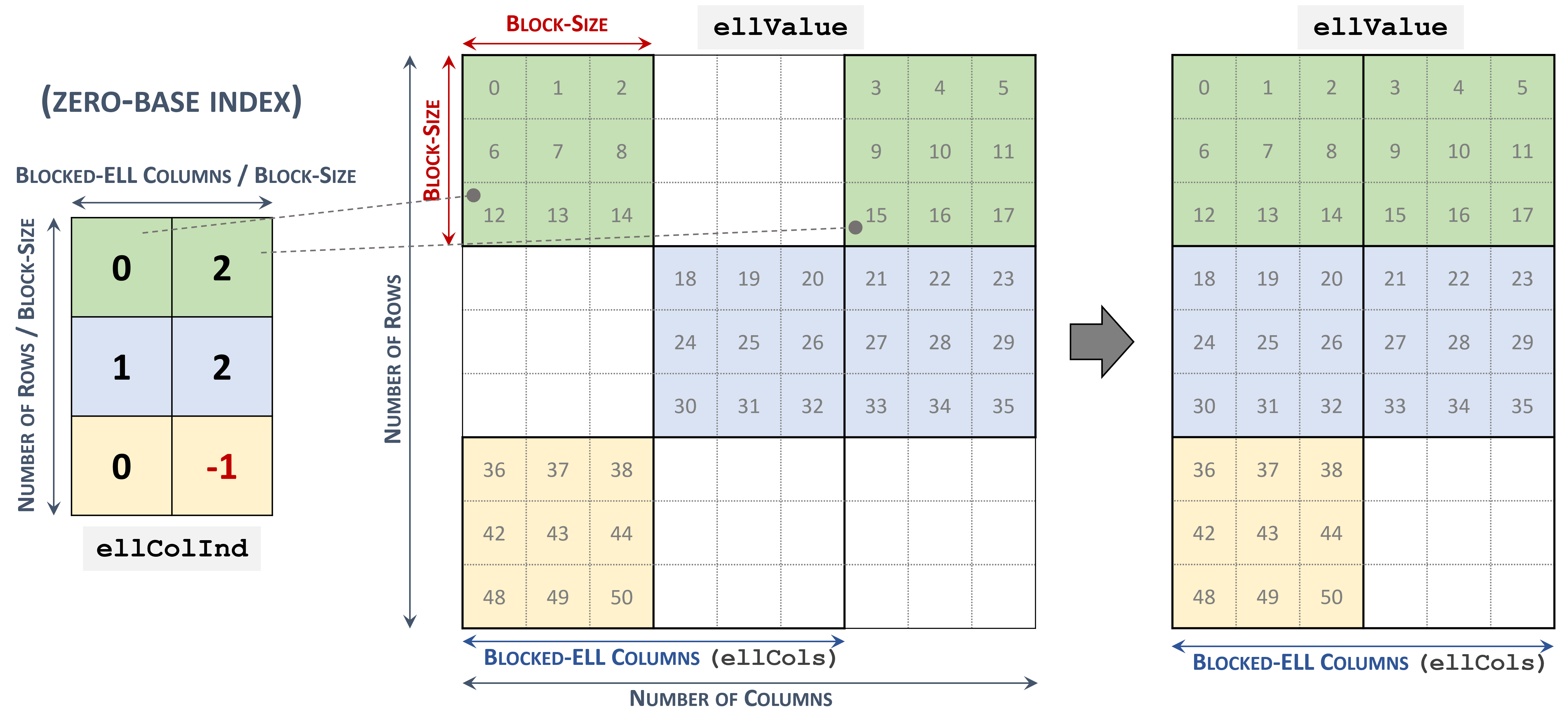
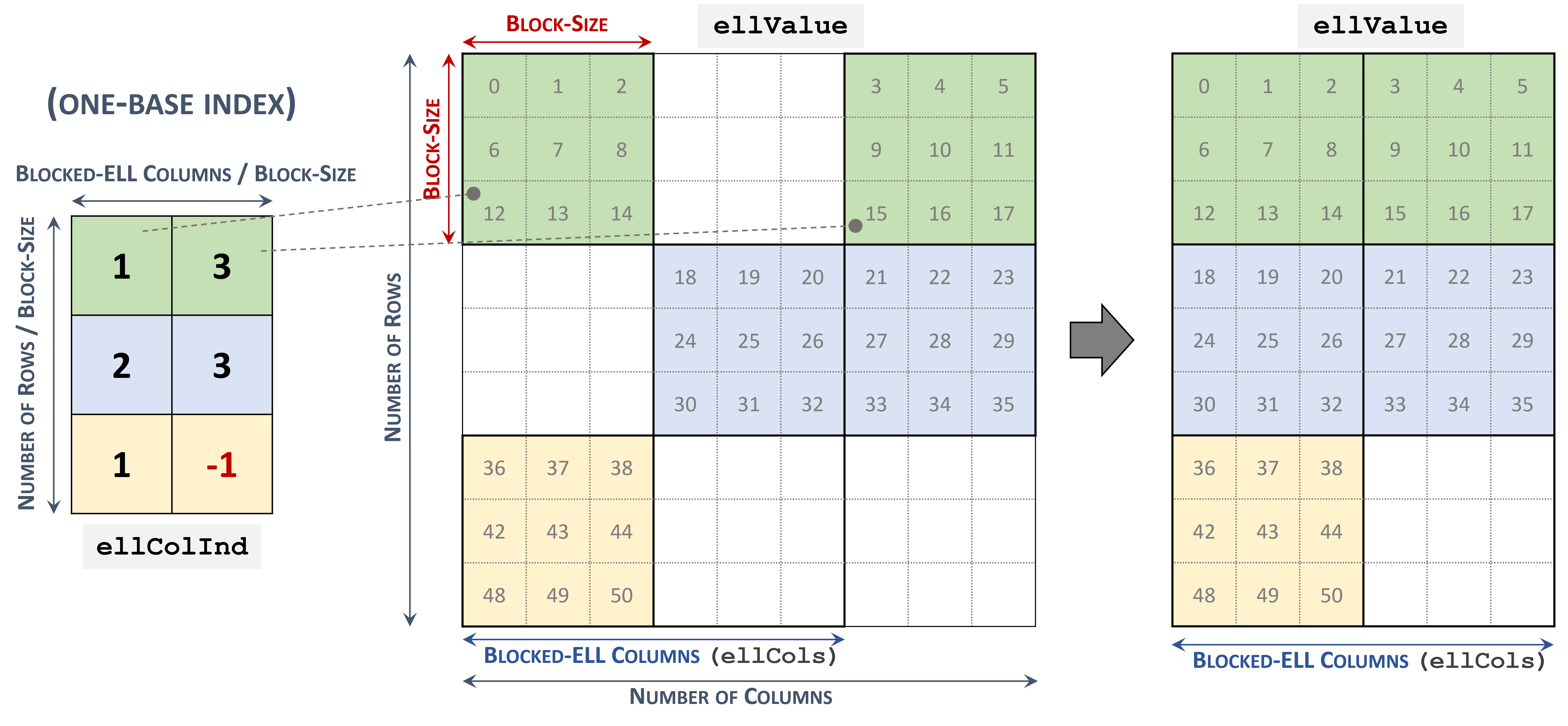
Blocked Ellpack (BLOCKED-ELL)

The Blocked Ellpack format is similar to the standard Ellpack, where the column indices represent two-dimensional blocks instead of a single matrix entry.

A matrix in the Blocked Ellpack format is organized into blocks of size \(blockSize\), defined by the user. The number of columns per row \(nEllCols\) is also defined by the user (\(nEllCols \le n\)).

A \(m \times n\) sparse matrix \(A\) is equivalent to a Blocked-ELL matrix \(A_{B}\): \(mb \times nb\) with \(mb = \left \lceil{\frac{m}{blockSize}}\right \rceil\) block rows, and \(nb = \left \lceil{\frac{nEllCols}{blockSize}}\right \rceil\) block columns. If \(m\) or \(n\) is not multiple of \(blockSize\), then the remaining elements are zero.

A sparse matrix stored in Blocked-ELL format is represented by the following parameters.

The block size.
The number of rows in the matrix.
The number of columns in the matrix.
The number of columns per row (nEllCols) in the matrix.
The pointers to the column block indices array of length \(mb \times nb\) that contains the location of the corresponding elements in the values array. Empty blocks can be represented with -1 index.
The pointers to the values array of length \(m \times nEllCols\) that holds all nonzero values of the matrix in row-major ordering.

The following example shows a \(9 \times 9\) matrix represented in Blocked-ELL format.

Extended BSR Format (BSRX) [DEPRECATED]

BSRX is the same as the BSR format, but the array bsrRowPtrA is separated into two parts. The first nonzero block of each row is still specified by the array bsrRowPtrA, which is the same as in BSR, but the position next to the last nonzero block of each row is specified by the array bsrEndPtrA. Briefly, BSRX format is simply like a 4-vector variant of BSR format.

Matrix A is represented in BSRX format by the following parameters.

`blockDim`	(integer)	Block dimension of matrix `A`.
`mb`	(integer)	The number of block rows of `A`.
`nb`	(integer)	The number of block columns of `A`.
`nnzb`	(integer)	number of nonzero blocks in the matrix `A`.
`bsrValA`	(pointer)	Points to the data array of length \(nnzb \ast blockDim^{2}\) that holds all the elements of the nonzero blocks of `A`. The block elements are stored in either column-major order or row-major order.
`bsrRowPtrA`	(pointer)	Points to the integer array of length `mb` that holds indices into the arrays `bsrColIndA` and `bsrValA`; `bsrRowPtrA(i)` is the position of the first nonzero block of the `i`th block row in `bsrColIndA` and `bsrValA`.
`bsrEndPtrA`	(pointer)	Points to the integer array of length `mb` that holds indices into the arrays `bsrColIndA` and `bsrValA`; `bsrRowPtrA(i)` is the position next to the last nonzero block of the `i`th block row in `bsrColIndA` and `bsrValA`.
`bsrColIndA`	(pointer)	Points to the integer array of length `nnzb` that contains the column indices of the corresponding blocks in array `bsrValA`.

A simple conversion between BSR and BSRX can be done as follows. Suppose the developer has a 2×3 block sparse matrix \(A_{b}\) represented as shown.

\(A_{b} = \begin{bmatrix} A_{00} & A_{01} & A_{02} \\ A_{10} & A_{11} & A_{12} \\ \end{bmatrix}\)

Assume it has this BSR format.

\(\begin{matrix} \text{bsrValA of BSR} & = & \begin{bmatrix} A_{00} & A_{01} & A_{10} & A_{11} & A_{12} \\ \end{bmatrix} \\ \text{bsrRowPtrA of BSR} & = & \begin{bmatrix} {0\phantom{.0}} & {2\phantom{.0}} & 5 \\ \end{bmatrix} \\ \text{bsrColIndA of BSR} & = & \begin{bmatrix} {0\phantom{.0}} & {1\phantom{.0}} & {0\phantom{.0}} & {1\phantom{.0}} & 2 \\ \end{bmatrix} \\ \end{matrix}\)

The bsrRowPtrA of the BSRX format is simply the first two elements of the bsrRowPtrA BSR format. The bsrEndPtrA of BSRX format is the last two elements of the bsrRowPtrA of BSR format.

\(\begin{matrix} \text{bsrRowPtrA of BSRX} & = & \begin{bmatrix} {0\phantom{.0}} & 2 \\ \end{bmatrix} \\ \text{bsrEndPtrA of BSRX} & = & \begin{bmatrix} {2\phantom{.0}} & 5 \\ \end{bmatrix} \\ \end{matrix}\)

The advantage of the BSRX format is that the developer can specify a submatrix in the original BSR format by modifying bsrRowPtrA and bsrEndPtrA while keeping bsrColIndA and bsrValA unchanged.

For example, to create another block matrix \(\widetilde{A} = \begin{bmatrix} O & O & O \\ O & A_{11} & O \\ \end{bmatrix}\) that is slightly different from \(A\) , the developer can keep bsrColIndA and bsrValA, but reconstruct \(\widetilde{A}\) by properly setting of bsrRowPtrA and bsrEndPtrA. The following 4-vector characterizes \(\widetilde{A}\) .

\(\begin{matrix} {\text{bsrValA of }\widetilde{A}} & = & \begin{bmatrix} A_{00} & A_{01} & A_{10} & A_{11} & A_{12} \\ \end{bmatrix} \\ {\text{bsrColIndA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & {1\phantom{.0}} & {0\phantom{.0}} & {1\phantom{.0}} & 2 \\ \end{bmatrix} \\ {\text{bsrRowPtrA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & 3 \\ \end{bmatrix} \\ {\text{bsrEndPtrA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & 4 \\ \end{bmatrix} \\ \end{matrix}\)