Using cuBLASMp for Tensor Parallelism in Distributed Machine Learning#

cuBLASMp is well-suited to perform some of the most commonly used GEMMs in distributed machine learning. cuBLASMp 0.3.0 release added two such popular variants: AllGather+GEMM (AG+GEMM) and GEMM+ReduceScatter (GEMM+RS) in the TN format, both implemented with communication-computation overlap achieved with the NVSHMEM backend. Version 0.4.0 added support for GEMM+AllReduce in the TN format and NN format support to AllGather+GEMM and GEMM+ReduceScatter.

cublasMpMatmul is the recommended API to perform those operations.

AllGather+GEMM and GEMM+ReduceScatter in terms of traditional PBLAS#

AllGather+GEMM and GEMM+ReduceScatter algorithms are both special cases of a traditional PBLAS GEMM operation, as used both in cuBLASMp and ScaLAPACK (P?GEMM).

Specifically, the data layout is a special case of 2D block-cyclic data layout, i.e., a 1D layout without the cyclic distribution:

For AG+GEMM, A and B are stored in column-major and distributed over processes column-wise (row-major), C and D are stored in column-major and distributed over processes row-wise (column-major). This translates to the process grid of A and B being 1 x nprocs (1 row of processes and nproc columns), and the output process grid of C and D being nprocs x 1. The number of rows of A and B is row block size, and the number of columns is column block size * nprocs. The number of rows of C and D is row block size * nprocs. This makes both layouts 1D and acyclic.
Respectively, for GEMM+RS, A and B are distributed row-wise (column-major), C and D - column-wise (row-major). The process grid of A and B is nprocs x 1 and the output process grid of C and D is 1 x nprocs.

On Python and cuBLASMp data ordering#

General considerations#

As primary users of tensor parallelism will be using cuBLASMp from Python, it is important to understand the data ordering conventions used by Python and cuBLASMp. Python uses C-ordered matrices, while cuBLASMp uses Fortran-ordered matrices:

C-ordered matrices store elements contiguously by rows. This convention is used by Python.
Fortran-ordered matrices store elements contiguously by columns. This convention is used by cuBLASMp and cuBLAS.
The transpose of a C-ordered (row-major) matrix is effectively a Fortran-ordered (column-major) matrix.
In a distributed setting, a row-wise distributed matrix A is equivalent to a column-wise distributed matrix A.T.

`output.T` (cuBLASMp) is `output` (Python)#

We cater to the torch.nn convention of storing transposed weights (weights_t).

If the objective is to calculate input * weights = output, we use cuBLASMp as follows:

Note

If input * weights = output, then weights_t * input.T = output.T. Fortran-ordered output.T, when viewed as a C-ordered array in Python, is equivalent to output.

Python calls a wrapper of a C function (TransformerEngine example) calling cublasMpMatmul requesting a TN GEMM of weights_t * input. (A = weights_t transposed, B = input not transposed). This is equivalent to weights_t.T * input.
Treating the given arrays as Fortran-ordered (see c.), cuBLASMp effectively sees the operation as a TN GEMM of weights_t.T * input.T (== weights_t.T.T * input.T == weights_t * input.T == output.T).
output.T, when viewed as a C-ordered array in Python, is equivalent to output.

Note

The approach used here is not specific to cuBLASMp and has been documented previously; see for example: How does PyTorch (row major) interact with cuBLAS (column major)?

AllGather+GEMM#

Problem definition#

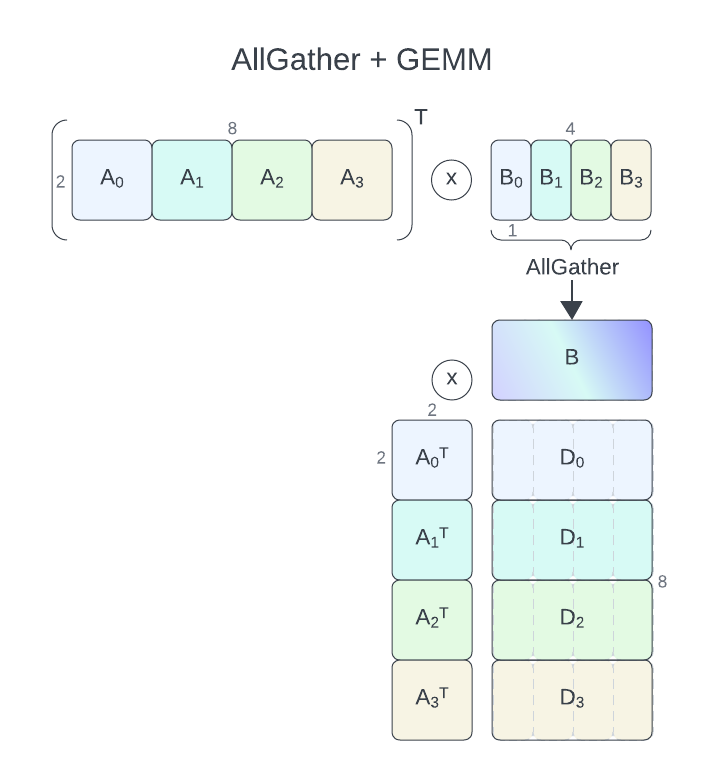
For AllGather+GEMM with communication-computation overlap, cuBLASMp currently requires its parameters, A and B to be distributed column-wise (row-major) over processes (process grid of 1 row and nproc columns). C and D matrices have to be distributed row-wise (column-major, process grid of nproc rows and 1 column). D = alpha * A.T * B + beta * C and D = alpha * A * B + beta * C operations (TN and NN format) are supported. B will be gathered using AllGather.

Note

This is equivalent to A.T (weights_t) and B.T (input) being distributed row-wise over processes and the D.T (output) being distributed column-wise over processes in C-ordering as viewed from Python.

Example#

Here, we will assume that the user is following the general setup as described in the CUDA Library Samples repository and focus on GEMM-specific parts. In this example, we will use 4 processes, with global A and B matrices of size 2 x 8 (each process 2 x 2) and 2 x 4 (each process 2 x 1), respectively. The output matrix D will be of size 8 x 4 (each process 2 x 4). We will assume an in-place matrix multiplication (C == D).

Once the CAL communicator has been created and the cuBLASMp handle initialized, we need to describe the grid and matrices using the appropriate descriptors. The following code snippet demonstrates the initialization of the grid descriptors describing the process grid layout.

cublasMpGrid_t grid_col_major = nullptr;
cublasMpGrid_t grid_row_major = nullptr;

cublasMpGridCreate(nranks, 1, CUBLASMP_GRID_LAYOUT_COL_MAJOR, cal_comm, &grid_col_major);
cublasMpGridCreate(1, nranks, CUBLASMP_GRID_LAYOUT_ROW_MAJOR, cal_comm, &grid_row_major);

grid_row_major, with its 1 row and nranks columns, will be used for A and B, while grid_col_major (nranks rows and 1 column), will be used for D.

Note

If NVSHMEM is not initialized by the user, cuBLASMp will initialize it as the first grid is created. If NVSHMEM has already been initialized, it will not be re-initialized. cuBLASMp will only call nvshmem_finalize if it was the one to initialize NVSHMEM.

Next, we need to describe the data stored in the matrices using the appropriate descriptors. The following code snippet demonstrates this:

cublasMpMatrixDescriptor_t descA = nullptr;
cublasMpMatrixDescriptor_t descB = nullptr;
cublasMpMatrixDescriptor_t descD = nullptr;

// Global sizes
const int64_t k = 2;  // Number of rows in A and B
const int64_t m = 8;  // Number of columns in A
const int64_t n = 4;  // Number of columns in B

// Local sizes on each process
const int64_t mbA = 2;   // Row block size of A (each process has 1 block, all the rows = k)
const int64_t nbA = 2;   // Col block size of A (each process has 1 block, m / nproc columns)
const int64_t mbB = 2;   // Row block size of B (each process has 1 block, all the rows = k)
const int64_t nbB = 1;   // Col block size of B (each process has 1 block, each process has n / nproc columns)
const int64_t mbD = nbA; // Row block size of D (has to match the layout of A, each process has 1 block = 4 rows)
const int64_t nbD = nbB; // Col block size of D (has to match the layout of B, each process has 4 blocks = 4x2 columns)

cublasMpMatrixDescriptorCreate(k, m, mbA, nbA, 0, 0, mbA, cuda_input_type,  grid_row_major, &descA);
cublasMpMatrixDescriptorCreate(k, n, mbB, nbB, 0, 0, mbB, cuda_input_type,  grid_row_major, &descB);
cublasMpMatrixDescriptorCreate(m, n, mbD, nbD, 0, 0, mbD, cuda_output_type, grid_col_major, &descD);

It should be noted here that the block sizes of D have to match the block sizes of A and B. That’s why each process logically splits its 4 columns of D into 4 blocks, each 1-column wide. This is only used to allow cuBLASMp to perform the tiled GEMM correctly and does not change how raw input or output data is laid out in the memory.

In the next step, we initialize cublasMpMatmulDescriptor_t to describe the matrix-matrix multiplication operation we want to perform:

cublasMpMatmulDescriptor_t matmulDesc = nullptr;
const cublasComputeType_t cublas_compute_type = CUBLAS_COMPUTE_32F;
const cublasOperation_t transA = CUBLAS_OP_T;
const cublasOperation_t transB = CUBLAS_OP_N;
const cublasMpMatmulAlgoType_t algoType = CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_P2P;

cublasMpMatmulDescriptorCreate(&matmulDesc, cublas_compute_type);
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSA, &transA, sizeof(transA));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSB, &transB, sizeof(transB));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_ALGO_TYPE, &algoType, sizeof(algoType));

With this, we can query for the required workspace sizes by calling cublasMpMatmul_bufferSize:

compute_t alpha = 1.0;
compute_t beta = 0.0;

size_t workspaceInBytesOnDevice = 0;
size_t workspaceInBytesOnHost = 0;

cublasMpMatmul_bufferSize(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1, // row index of the first element of A
    1, // col index of the first element of A
    descA,
    B,
    1, // row index of the first element of B
    1, // col index of the first element of B
    descB,
    &beta,
    D,
    1, // row index of the first element of C
    1, // col index of the first element of C
    descD,
    D,
    1, // row index of the first element of D
    1, // col index of the first element of D
    descD,
    &workspaceInBytesOnDevice,
    &workspaceInBytesOnHost);

With this, we are ready to allocate the required workspaces:

void* d_work = nvshmem_malloc(workspaceInBytesOnDevice);
std::vector<int8_t> h_work(workspaceInBytesOnHost);

Note

The workspace, d_work, has to be allocated using nvshmem_malloc to ensure that it is accessible by all processes. Allocating B with nvshmem_malloc will further improve performance as it allows to avoid an additional copy of part of B.

If possible, all the above steps should be executed as part of the initialization phase. The matrix-matrix multiplication is performed with a cublasMpMatmul call. Preferably, it should be the only function call on the performance-critical path. Its parameters mirror those of cublasMpMatmul_bufferSize almost exactly:

cublasMpMatmul(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1,
    1,
    descA,
    B,
    1,
    1,
    descB,
    &beta,
    D,
    1,
    1,
    descD,
    D,
    1,
    1,
    descD,
    d_work,
    workspaceInBytesOnDevice,
    h_work.data(),
    workspaceInBytesOnHost);

Resources should then be deallocated as shown in the example.

GEMM+ReduceScatter#

Problem definition#

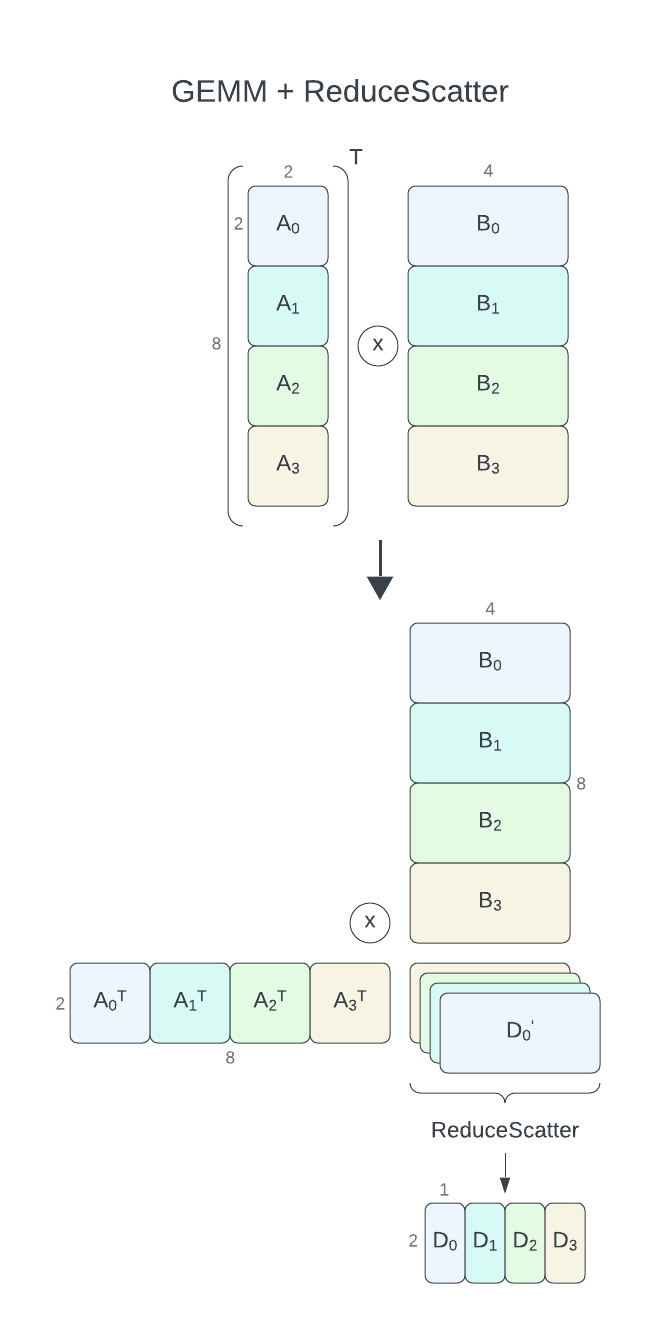
For GEMM+ReduceScatter with communication-computation overlap, cuBLASMp currently requires its parameters, A and B to be distributed row-wise (column-major) over processes (process grid of nproc rows and 1 column). C and D matrices have to be distributed column-wise (row-major, process grid of 1 row and nproc columns). D = alpha * A.T * B + beta * C and D = alpha * A * B + beta * C operations (TN and NN format) are supported. Each process will calculate a part of the output \({\alpha}A_i^T * B_i + {\beta}C_i = D_i'\) which will be then reduced and split among processes using the ReduceScatter operation resulting in \(D_i\). D is distributed column-wise (row-major) over processes.

Note

This is equivalent to A.T (weights_t) and B.T (input) being distributed column-wise over processes and D.T (output) being distributed row-wise over processes in C-ordering as viewed from Python.

Example#

As in the AllGather+GEMM example, we assume that the user is following the general setup as described in the CUDA Library Samples repository and focus on GEMM-specific parts. In this example, we will use 4 processes with matrices:

A of size 8 x 2 (each process 2 x 2)
B of size 8 x 4 (each process 2 x 4)
D of size 2 x 4 (each process 2 x 1)

We assume an in-place matrix multiplication (C == D).

We describe the grids as in the previous example:

cublasMpGrid_t grid_col_major = nullptr;
cublasMpGrid_t grid_row_major = nullptr;

cublasMpGridCreate(nranks, 1, CUBLASMP_GRID_LAYOUT_COL_MAJOR, cal_comm, &grid_col_major);
cublasMpGridCreate(1, nranks, CUBLASMP_GRID_LAYOUT_ROW_MAJOR, cal_comm, &grid_row_major);

Here, grid_col_major (nranks rows and 1 column), will be used for A and B, while grid_row_major (1 row and nranks columns) will be used for D.

Next, we create matrix descriptors:

cublasMpMatrixDescriptor_t descA = nullptr;
cublasMpMatrixDescriptor_t descB = nullptr;
cublasMpMatrixDescriptor_t descD = nullptr;

// Global sizes
const int64_t k = 8; // Number of rows in A and B
const int64_t m = 2; // Number of columns in A
const int64_t n = 4; // Number of columns in B

// Local sizes on each process
const int64_t mbA = 2;   // Row block size of A (each process has 1 block, k / nproc rows)
const int64_t nbA = 2;   // Col block size of A (each process has 1 block, all the columns = m)
const int64_t mbB = 2;   // Row block size of B (each process has 1 block, k / nproc rows)
const int64_t nbB = 1;   // Col block size of B (each process has 4 blocks, n / nproc columns = 4x1 = 4 columns)
const int64_t mbD = nbA; // Row block size of D (has to match the layout of A, each process has 1 block = 4 rows)
const int64_t nbD = 1;   // Col block size of D (each process has 1 block, 1 column)

cublasMpMatrixDescriptorCreate(k, m, mbA, nbA, 0, 0, mbA, cuda_input_type,  grid_col_major, &descA);
cublasMpMatrixDescriptorCreate(k, n, mbB, nbB, 0, 0, mbB, cuda_input_type,  grid_col_major, &descB);
cublasMpMatrixDescriptorCreate(m, n, mbD, nbD, 0, 0, mbD, cuda_output_type, grid_row_major, &descD);

As before, block sizes of D have to match the block sizes of A and B. This time, it is the column block size of D that is more constraining and forcing B to be logically split into 4 blocks, each 1-column wide. Again, it does not change the data layout and is only used to align GEMM tiles.

Next, we initialize cublasMpMatmulDescriptor_t to describe the matrix-matrix multiplication operation we want to perform:

cublasMpMatmulDescriptor_t matmulDesc = nullptr;
const cublasComputeType_t cublas_compute_type = CUBLAS_COMPUTE_32F;
const cublasOperation_t transA = CUBLAS_OP_T;
const cublasOperation_t transB = CUBLAS_OP_N;
const cublasMpMatmulAlgoType_t algoType = CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_P2P;

cublasMpMatmulDescriptorCreate(&matmulDesc, cublas_compute_type);
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSA, &transA, sizeof(transA));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSB, &transB, sizeof(transB));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_ALGO_TYPE, &algoType, sizeof(algoType));

Query for the required workspace sizes:

compute_t alpha = 1.0;
compute_t beta = 0.0;

size_t workspaceInBytesOnDevice = 0;
size_t workspaceInBytesOnHost = 0;

cublasMpMatmul_bufferSize(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1, // row index of the first element of A
    1, // col index of the first element of A
    descA,
    B,
    1, // row index of the first element of B
    1, // col index of the first element of B
    descB,
    &beta,
    D,
    1, // row index of the first element of C
    1, // col index of the first element of C
    descD,
    D,
    1, // row index of the first element of D
    1, // col index of the first element of D
    descD,
    &workspaceInBytesOnDevice,
    &workspaceInBytesOnHost);

With this, we are ready to allocate the required workspaces:

void* d_work = nvshmem_malloc(workspaceInBytesOnDevice);
std::vector<int8_t> h_work(workspaceInBytesOnHost);

And perform the matrix-matrix multiplication:

cublasMpMatmul(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1,
    1,
    descA,
    B,
    1,
    1,
    descB,
    &beta,
    D,
    1,
    1,
    descD,
    D,
    1,
    1,
    descD,
    d_work,
    workspaceInBytesOnDevice,
    h_work.data(),
    workspaceInBytesOnHost);

Resources should then be deallocated as shown in the example.

GEMM+AllReduce#

Problem definition#

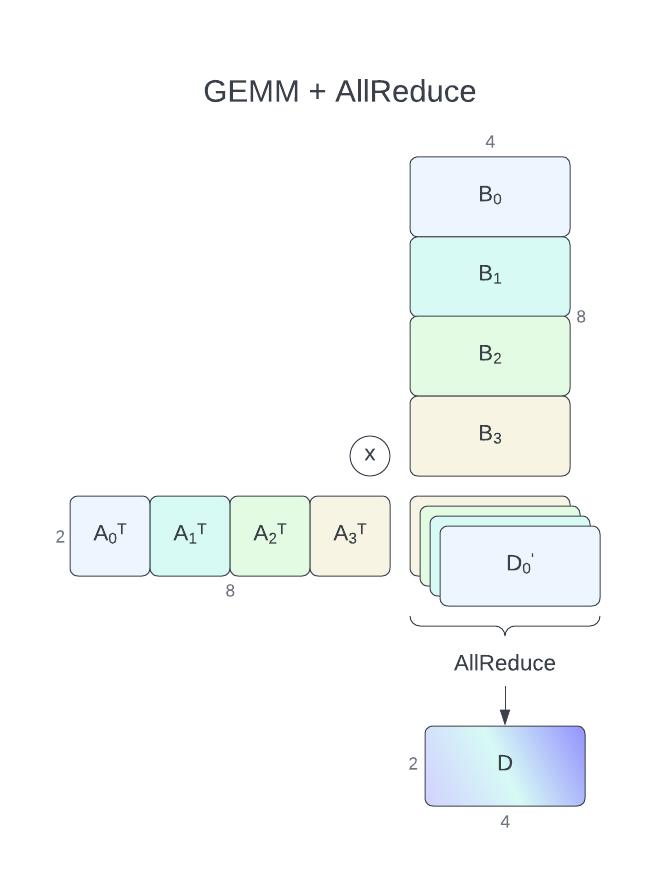
For GEMM+AllReduce with communication-computation overlap, cuBLASMp currently requires its parameters, A and B to be distributed row-wise (column-major) over processes (process grid of nproc rows and 1 column). C and D matrices have to be distributed column-wise (row-major, process grid of 1 row and nproc columns). Only D = alpha * A.T * B + beta * C operation (TN format) is supported. Each process will calculate a part of the output \({\alpha}A_i^T * B_i + {\beta}C_i = D_i'\) which will be then reduced (summed) using the AllReduce operation resulting in \(D\), which will be the same across all processes.

Note

GEMM+AllReduce requires Compute Capability 9.0 (Hopper) and newer GPUs as it relies on multicast communication.

Example#

As in the previous examples, we assume that the user is following the general setup as described in the CUDA Library Samples repository and focus on GEMM-specific parts. In this example, we will use 4 processes with matrices:

A of size 8 x 2 (each process 2 x 2)
B of size 8 x 4 (each process 2 x 4)
D of size 2 x 4 (each process 2 x 4)

We assume an in-place matrix multiplication (C == D).

We describe the grids as in the previous examples:

cublasMpGrid_t grid_col_major = nullptr;
cublasMpGrid_t grid_row_major = nullptr;

cublasMpGridCreate(nranks, 1, CUBLASMP_GRID_LAYOUT_COL_MAJOR, cal_comm, &grid_col_major);
cublasMpGridCreate(1, nranks, CUBLASMP_GRID_LAYOUT_ROW_MAJOR, cal_comm, &grid_row_major);

Here, grid_col_major (nranks rows and 1 column), will be used for A and B, while grid_row_major (1 row and nranks columns) will be used for D.

Next, we create matrix descriptors:

cublasMpMatrixDescriptor_t descA = nullptr;
cublasMpMatrixDescriptor_t descB = nullptr;
cublasMpMatrixDescriptor_t descD = nullptr;

// Global sizes
const int64_t k = 8;  // Number of rows in A and B
const int64_t m = 2;  // Number of columns in A
const int64_t n = 4;  // Number of columns in B

// Local sizes on each process
const int64_t mbA = 2;   // Row block size of A (each process has 1 block, k / nproc rows)
const int64_t nbA = 2;   // Col block size of A (each process has 1 block, all the columns = m)
const int64_t mbB = 2;   // Row block size of B (each process has 1 block, k / nproc rows)
const int64_t nbB = 4;   // Col block size of B (each process has 1 block, all the columns = n)
const int64_t mbD = nbA; // Row block size of D (has to match the layout of A, each process has 1 block = 2 rows)
const int64_t nbD = nbB; // Col block size of D (has to match the layout of B, each process has 1 block = 4 columns)

cublasMpMatrixDescriptorCreate(k, m,          mbA, nbA, 0, 0, mbA, cuda_input_type,  grid_col_major, &descA);
cublasMpMatrixDescriptorCreate(k, n,          mbB, nbB, 0, 0, mbB, cuda_input_type,  grid_col_major, &descB);
cublasMpMatrixDescriptorCreate(m, n * nranks, mbD, nbD, 0, 0, mbD, cuda_output_type, grid_row_major, &descD);

Note

Note that we declare D with the global size of m x n x nranks. While the output of the (m x k) * (k x n) matrix-matrix multiplication is m x n, the output matrix of those dimensions is not distributed over processes. Since the output of each process is (m x n), we need to declare D with the global size of m x n x nranks which is consistent with the 2D block-cyclic convention.

Next, we initialize cublasMpMatmulDescriptor_t to describe the matrix-matrix multiplication operation we want to perform:

cublasMpMatmulDescriptor_t matmulDesc = nullptr;
const cublasComputeType_t cublas_compute_type = CUBLAS_COMPUTE_32F;
const cublasOperation_t transA = CUBLAS_OP_T;
const cublasOperation_t transB = CUBLAS_OP_N;
const cublasMpMatmulAlgoType_t algoType = CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_MULTICAST;
const cublasMpMatmulEpilogue_t epilogue = CUBLASMP_MATMUL_EPILOGUE_ALLREDUCE;

cublasMpMatmulDescriptorCreate(&matmulDesc, cublas_compute_type);
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSA, &transA, sizeof(transA));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_TRANSB, &transB, sizeof(transB));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_ALGO_TYPE, &algoType, sizeof(algoType));
cublasMpMatmulDescriptorAttributeSet(matmulDesc, CUBLASMP_MATMUL_DESCRIPTOR_ATTRIBUTE_EPILOGUE, &epilogue, sizeof(epilogue));

Query for the required workspace sizes:

compute_t alpha = 1.0;
compute_t beta = 0.0;

size_t workspaceInBytesOnDevice = 0;
size_t workspaceInBytesOnHost = 0;

cublasMpMatmul_bufferSize(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1, // row index of the first element of A
    1, // col index of the first element of A
    descA,
    B,
    1, // row index of the first element of B
    1, // col index of the first element of B
    descB,
    &beta,
    D,
    1, // row index of the first element of C
    1, // col index of the first element of C
    descD,
    D,
    1, // row index of the first element of D
    1, // col index of the first element of D
    descD,
    &workspaceInBytesOnDevice,
    &workspaceInBytesOnHost);

With this, we are ready to allocate the required workspaces:

void* d_work = nvshmem_malloc(workspaceInBytesOnDevice);
std::vector<int8_t> h_work(workspaceInBytesOnHost);

And perform the matrix-matrix multiplication:

cublasMpMatmul(
    handle,
    matmulDesc,
    m,
    n,
    k,
    &alpha,
    A,
    1,
    1,
    descA,
    B,
    1,
    1,
    descB,
    &beta,
    D,
    1,
    1,
    descD,
    D,
    1,
    1,
    descD,
    d_work,
    workspaceInBytesOnDevice,
    h_work.data(),
    workspaceInBytesOnHost);

Resources should then be deallocated as shown in the example.

General assumptions and limitations#

GPUs have to be P2P-accessible or connected with an InfiniBand NIC.
Multicast-based algorithms, CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_MULTICAST and CUBLASMP_MATMUL_ALGO_TYPE_ATOMIC_MULTICAST (deprecated) require Compute Capability 9.0 (Hopper) and newer GPUs connected with an NVSwitch.
The output of CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_MULTICAST and CUBLASMP_MATMUL_ALGO_TYPE_ATOMIC_MULTICAST has to be 16-bit half precision, bfloat16 or 32-bit single precision.
CUBLASMP_MATMUL_ALGO_TYPE_SPLIT_MULTICAST algorithm is only supported for GEMM+ReduceScatter and GEMM+AllReduce.
FP8 support requires Compute Capability 9.0 (Hopper) and above.

Using cuBLASMp for Tensor Parallelism in Distributed Machine Learning#

AllGather+GEMM and GEMM+ReduceScatter in terms of traditional PBLAS#

On Python and cuBLASMp data ordering#

General considerations#

output.T (cuBLASMp) is output (Python)#

AllGather+GEMM#

Problem definition#

Example#

GEMM+ReduceScatter#

Problem definition#

Example#

GEMM+AllReduce#

Problem definition#

Example#

General assumptions and limitations#

`output.T` (cuBLASMp) is `output` (Python)#