|
NVIDIA 2D Image And Signal Performance Primitives (NPP)
Version 11.2.0.*
|
|
NVIDIA 2D Image And Signal Performance Primitives (NPP)
Version 11.2.0.*
|
The design of all the NPP functions follows the same guidelines as other NVIDIA CUDA libraries like cuFFT and cuBLAS. That is that all pointer arguments in those APIs are device pointers.
This convention enables the individual developer to make smart choices about memory management that minimize the number of memory transfers. It also allows the user the maximum flexibility regarding which of the various memory transfer mechanisms offered by the CUDA runtime is used, e.g. synchronous or asynchronous memory transfers, zero-copy and pinned memory, etc.
The most basic steps involved in using NPP for processing data is as follows:
Some primitives of NPP require additional device memory buffers (scratch buffers) for calculations, e.g. signal and image reductions (Sum, Max, Min, MinMax, etc.). In order to give the NPP user maximum control regarding memory allocations and performance, it is the user's responsibility to allocate and delete those temporary buffers. For one this has the benefit that the library will not allocate memory unbeknownst to the user. It also allows developers who invoke the same primitive repeatedly to allocate the scratch only once, improving performance and potential device-memory fragmentation.
Scratch-buffer memory is unstructured and may be passed to the primitive in uninitialized form. This allows for reuse of the same scratch buffers with any primitive require scratch memory, as long as it is sufficiently sized.
The minimum scratch-buffer size for a given primitive (e.g. nppsSum_32f()) can be obtained by a companion function (e.g. nppsSumGetBufferSize_32f()). The buffer size is returned via a host pointer as allocation of the scratch-buffer is performed via CUDA runtime host code.
An example to invoke signal sum primitive and allocate and free the necessary scratch memory:
Since NPP is a C API and therefore does not allow for function overloading for different data-types the NPP naming convention addresses the need to differentiate between different flavors of the same algorithm or primitive function but for various data types. This disambiguation of different flavors of a primitive is done via a suffix containing data type and other disambiguating information.
In addition to the flavor suffix, all NPP functions are prefixed with by the letters "npp". Primitives belonging to NPP's image-processing module add the letter "i" to the npp prefix, i.e. are prefixed by "nppi". Similarly signal-processing primitives are prefixed with "npps".
The general naming scheme is:
The data-type information uses the same names as the Basic NPP Data Types. For example the data-type information "8u" would imply that the primitive operates on Npp8u data.
If a primitive consumes different type data from what it produces, both types will be listed in the order of consumed to produced data type.
Details about the "additional flavor information" is provided for each of the NPP modules, since each problem domain uses different flavor information suffixes.
NPP signal processing and imaging primitives often operate on integer data. This integer data is usually a fixed point fractional representation of some physical magnitue (e.g. luminance). Because of this fixed-point nature of the representation many numerical operations (e.g. addition or multiplication) tend to produce results exceeding the original fixed-point range if treated as regular integers.
In cases where the results exceed the original range, these functions clamp the result values back to the valid range. E.g. the maximum positive value for a 16-bit unsigned integer is 32767. A multiplication operation of 4 * 10000 = 40000 would exceed this range. The result would be clamped to be 32767.
To avoid the level of lost information due to clamping most integer primitives allow for result scaling. Primitives with result scaling have the "Sfs" suffix in their name and provide a parameter "nScaleFactor" that controls the amount of scaling. Before the results of an operation are clamped to the valid output-data range by multiplying them with 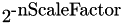 .
.
Example: The primitive nppsSqr_8u_Sfs() computes the square of 8-bit unsigned sample values in a signal (1D array of values). The maximum value of a 8-bit value is 255. The square of 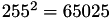 which would be clamped to 255 if no result scaling is performed. In order to map the maximum value of 255 to 255 in the result, one would specify an integer result scaling factor of 8, i.e. multiply each result with
which would be clamped to 255 if no result scaling is performed. In order to map the maximum value of 255 to 255 in the result, one would specify an integer result scaling factor of 8, i.e. multiply each result with 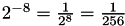 . The final result for a signal value of 255 being squared and scaled would be:
. The final result for a signal value of 255 being squared and scaled would be:
![\[255^2\cdot 2^{-8} = 254.00390625\]](form_131.png)
which would be rounded to a final result of 254.
A medium gray value of 128 would result in
![\[128^2 * 2^{-8} = 64\]](form_132.png)
Many NPP functions require converting floating-point values to integers. The NppRoundMode enum lists NPP's supported rounding modes. Not all primitives in NPP that perform rounding as part of their functionality allow the user to specify the round-mode used. Instead they use NPP's default rounding mode, which is NPP_RND_FINANCIAL.
A subset of NPP functions performing rounding as part of their functionality do allow the user to specify which rounding mode is used through a parameter of the NppRoundMode type.