cuSOLVER
The API reference guide for cuSOLVER, a GPU accelerated library for decompositions and linear system solutions for both dense and sparse matrices.
1. Introduction
- The cuSolver API on a single GPU
- The cuSolverMG API on a single node multiGPU
The intent of cuSolver is to provide useful LAPACK-like features, such as common matrix factorization and triangular solve routines for dense matrices, a sparse least-squares solver and an eigenvalue solver. In addition cuSolver provides a new refactorization library useful for solving sequences of matrices with a shared sparsity pattern.
cuSolver combines three separate components under a single umbrella. The first part of cuSolver is called cuSolverDN, and deals with dense matrix factorization and solve routines such as LU, QR, SVD and LDLT, as well as useful utilities such as matrix and vector permutations.
Next, cuSolverSP provides a new set of sparse routines based on a sparse QR factorization. Not all matrices have a good sparsity pattern for parallelism in factorization, so the cuSolverSP library also provides a CPU path to handle those sequential-like matrices. For those matrices with abundant parallelism, the GPU path will deliver higher performance. The library is designed to be called from C and C++.
The final part is cuSolverRF, a sparse re-factorization package that can provide very good performance when solving a sequence of matrices where only the coefficients are changed but the sparsity pattern remains the same.
The GPU path of the cuSolver library assumes data is already in the device memory. It is the responsibility of the developer to allocate memory and to copy data between GPU memory and CPU memory using standard CUDA runtime API routines, such as cudaMalloc(), cudaFree(), cudaMemcpy(), and cudaMemcpyAsync().
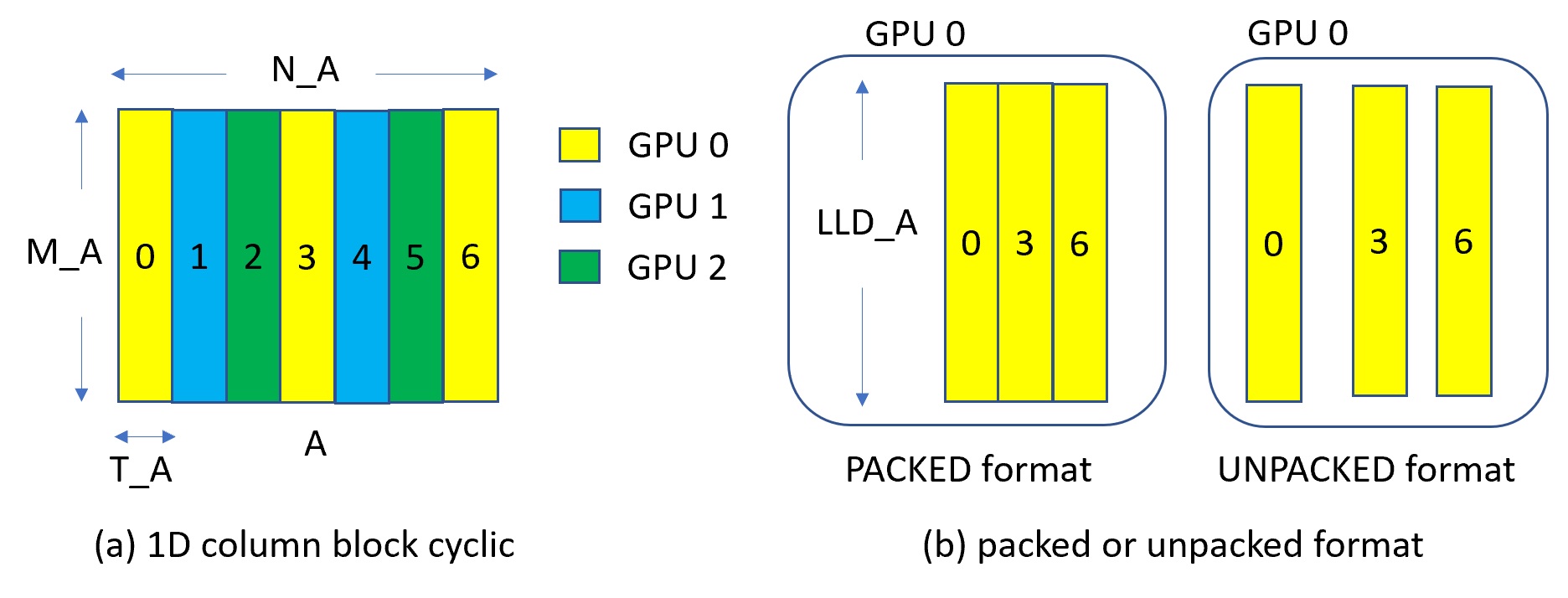
cuSolverMg is GPU-accelerated ScaLAPACK. By now, cuSolverMg supports 1-D column block cyclic layout and provides symmetric eigenvalue solver.
1.1. cuSolverDN: Dense LAPACK
The cuSolverDN library was designed to solve dense linear systems of the form
where the coefficient matrix , right-hand-side vector and solution vector
The cuSolverDN library provides QR factorization and LU with partial pivoting to handle a general matrix A, which may be non-symmetric. Cholesky factorization is also provided for symmetric/Hermitian matrices. For symmetric indefinite matrices, we provide Bunch-Kaufman (LDL) factorization.
The cuSolverDN library also provides a helpful bidiagonalization routine and singular value decomposition (SVD).
The cuSolverDN library targets computationally-intensive and popular routines in LAPACK, and provides an API compatible with LAPACK. The user can accelerate these time-consuming routines with cuSolverDN and keep others in LAPACK without a major change to existing code.
1.2. cuSolverSP: Sparse LAPACK
The cuSolverSP library was mainly designed to a solve sparse linear system
and the least-squares problem
where sparse matrix , right-hand-side vector and solution vector . For a linear system, we require m=n.
The core algorithm is based on sparse QR factorization. The matrix A is accepted in CSR format. If matrix A is symmetric/Hermitian, the user has to provide a full matrix, ie fill missing lower or upper part.
If matrix A is symmetric positive definite and the user only needs to solve , Cholesky factorization can work and the user only needs to provide the lower triangular part of A.
On top of the linear and least-squares solvers, the cuSolverSP library provides a simple eigenvalue solver based on shift-inverse power method, and a function to count the number of eigenvalues contained in a box in the complex plane.
1.3. cuSolverRF: Refactorization
The cuSolverRF library was designed to accelerate solution of sets of linear systems by fast re-factorization when given new coefficients in the same sparsity pattern
where a sequence of coefficient matrices , right-hand-sides and solutions are given for i=1,...,k.
The cuSolverRF library is applicable when the sparsity pattern of the coefficient matrices as well as the reordering to minimize fill-in and the pivoting used during the LU factorization remain the same across these linear systems. In that case, the first linear system (i=1) requires a full LU factorization, while the subsequent linear systems (i=2,...,k) require only the LU re-factorization. The later can be performed using the cuSolverRF library.
Notice that because the sparsity pattern of the coefficient matrices, the reordering and pivoting remain the same, the sparsity pattern of the resulting triangular factors and also remains the same. Therefore, the real difference between the full LU factorization and LU re-factorization is that the required memory is known ahead of time.
1.4. Naming Conventions
The cuSolverDN library provides two different APIs; legacy and generic.
The functions in the legacy API are available for data types float, double, cuComplex, and cuDoubleComplex. The naming convention for the legacy API is as follows:
| cusolverDn<t><operation> |
where <t> can be S, D, C, Z, or X, corresponding to the data types float, double, cuComplex, cuDoubleComplex, and the generic type, respectively. <operation> can be Cholesky factorization (potrf), LU with partial pivoting (getrf), QR factorization (geqrf) and Bunch-Kaufman factorization (sytrf).
The functions in the generic API provide a single entry point for each routine and support for 64-bit integers to define matrix and vector dimensions. The naming convention for the generic API is data-agnostic and is as follows:
| cusolverDn<operation> |
where <operation> can be Cholesky factorization (potrf), LU with partial pivoting (getrf) and QR factorization (geqrf).
The cuSolverSP library functions are available for data types float, double, cuComplex, and cuDoubleComplex. The naming convention is as follows:
| cusolverSp[Host]<t>[<matrix data format>]<operation>[<output matrix data format>]<based on> |
where cuSolverSp is the GPU path and cusolverSpHost is the corresponding CPU path. <t> can be S, D, C, Z, or X, corresponding to the data types float, double, cuComplex, cuDoubleComplex, and the generic type, respectively.
The <matrix data format> is csr, compressed sparse row format.
The <operation> can be ls, lsq, eig, eigs, corresponding to linear solver, least-square solver, eigenvalue solver and number of eigenvalues in a box, respectively.
The <output matrix data format> can be v or m, corresponding to a vector or a matrix.
<based on> describes which algorithm is used. For example, qr (sparse QR factorization) is used in linear solver and least-square solver.
All of the functions have the return type cusolverStatus_t and are explained in more detail in the chapters that follow.
| Routine | Data format | Operation | Output format | Based on |
|---|---|---|---|---|
| csrlsvlu | csr | linear solver (ls) | vector (v) | LU (lu) with partial pivoting |
| csrlsvqr | csr | linear solver (ls) | vector (v) | QR factorization (qr) |
| csrlsvchol | csr | linear solver (ls) | vector (v) | Cholesky factorization (chol) |
| csrlsqvqr | csr | least-square solver (lsq) | vector (v) | QR factorization (qr) |
| csreigvsi | csr | eigenvalue solver (eig) | vector (v) | shift-inverse |
| csreigs | csr | number of eigenvalues in a box (eigs) | ||
| csrsymrcm | csr | Symmetric Reverse Cuthill-McKee (symrcm) |
The cuSolverRF library routines are available for data type double. Most of the routines follow the naming convention:
| cusolverRf_<operation>_[[Host]](...) |
where the trailing optional Host qualifier indicates the data is accessed on the host versus on the device, which is the default. The <operation> can be Setup, Analyze, Refactor, Solve, ResetValues, AccessBundledFactors and ExtractSplitFactors.
Finally, the return type of the cuSolverRF library routines is cusolverStatus_t.
1.5. Asynchronous Execution
The cuSolver library functions prefer to keep asynchronous execution as much as possible. Developers can always use the cudaDeviceSynchronize() function to ensure that the execution of a particular cuSolver library routine has completed.
A developer can also use the cudaMemcpy() routine to copy data from the device to the host and vice versa, using the cudaMemcpyDeviceToHost and cudaMemcpyHostToDevice parameters, respectively. In this case there is no need to add a call to cudaDeviceSynchronize() because the call to cudaMemcpy() with the above parameters is blocking and completes only when the results are ready on the host.
1.6. Library Property
The libraryPropertyType data type is an enumeration of library property types. (ie. CUDA version X.Y.Z would yield MAJOR_VERSION=X, MINOR_VERSION=Y, PATCH_LEVEL=Z)
typedef enum libraryPropertyType_t { MAJOR_VERSION, MINOR_VERSION, PATCH_LEVEL } libraryPropertyType;
The following code can show the version of cusolver library.
int major=-1,minor=-1,patch=-1;
cusolverGetProperty(MAJOR_VERSION, &major);
cusolverGetProperty(MINOR_VERSION, &minor);
cusolverGetProperty(PATCH_LEVEL, &patch);
printf("CUSOLVER Version (Major,Minor,PatchLevel): %d.%d.%d\n", major,minor,patch);
1.7. High Precision Package
The cusolver library uses high precision for iterative refinement when necessary.
2. Using the CUSOLVER API
2.1.1. Thread Safety
The library is thread-safe, and its functions can be called from multiple host threads.
2.1.2. Scalar Parameters
In the cuSolver API, the scalar parameters can be passed by reference on the host.
2.1.3. Parallelism with Streams
If the application performs several small independent computations, or if it makes data transfers in parallel with the computation, then CUDA streams can be used to overlap these tasks.
- Create CUDA streams using the function cudaStreamCreate(), and
- Set the stream to be used by each individual cuSolver library routine by calling, for example, cusolverDnSetStream(), just prior to calling the actual cuSolverDN routine.
The computations performed in separate streams would then be overlapped automatically on the GPU, when possible. This approach is especially useful when the computation performed by a single task is relatively small, and is not enough to fill the GPU with work, or when there is a data transfer that can be performed in parallel with the computation.
2.1.4. How to Link cusolver Library
cusolver library provides dynamic library libcusolver.so and static library libcusolver_static.a. If the user links the application with libcusolver.so, libcublas.so and libcublasLt.so are also required. If the user links the application with libcusolver_static.a, the following libraries are also needed, libcudart_static.a, libculibos.aliblapack_static.a, libmetis_static.a, libcublas_static.a and libcusparse_static.a.
2.1.5. Link Third-party LAPACK Library
- If you use libcusolver_static.a, then you must link with liblapack_static.a explicitly, otherwise the linker will report missing symbols. No conflict of symbols between liblapack_static.a and other third-party LAPACK library, you are free to link the latter to your application.
- The liblapack_static.a is built inside libcusolver.so. Hence, if you use libcusolver.so, then you don't need to specify a LAPACK library. The libcusolver.so will not pick up any routines from the third-party LAPACK library even you link the application with it.
2.1.6. Convention of info
Each LAPACK routine returns an info which indicates the position of invalid parameter. If info = -i, then i-th parameter is invalid. To be consistent with base-1 in LAPACK, cusolver does not report invalid handle into info. Instead, cusolver returns CUSOLVER_STATUS_NOT_INITIALIZED for invalid handle.
2.1.7. Usage of _bufferSize
There is no cudaMalloc inside cuSolver library, the user must allocate the device workspace explicitly. The routine xyz_bufferSize is to query the size of workspace of the routine xyz, for example xyz = potrf. To make the API simple, xyz_bufferSize follows almost the same signature of xyz even it only depends on some parameters, for example, device pointer is not used to decide the size of workspace. In most cases, xyz_bufferSize is called in the beginning before actual device data (pointing by a device pointer) is prepared or before the device pointer is allocated. In such case, the user can pass null pointer to xyz_bufferSize without breaking the functionality.
2.2. cuSolver Types Reference
2.2.1. cuSolverDN Types
The float, double, cuComplex, and cuDoubleComplex data types are supported. The first two are standard C data types, while the last two are exported from cuComplex.h. In addition, cuSolverDN uses some familiar types from cuBLAS.
2.2.1.1. cusolverDnHandle_t
This is a pointer type to an opaque cuSolverDN context, which the user must initialize by calling cusolverDnCreate() prior to calling any other library function. An un-initialized Handle object will lead to unexpected behavior, including crashes of cuSolverDN. The handle created and returned by cusolverDnCreate() must be passed to every cuSolverDN function.
2.2.1.2. cublasFillMode_t
The type indicates which part (lower or upper) of the dense matrix was filled and consequently should be used by the function. Its values correspond to Fortran characters ‘L’ or ‘l’ (lower) and ‘U’ or ‘u’ (upper) that are often used as parameters to legacy BLAS implementations.
| Value | Meaning |
|---|---|
| CUBLAS_FILL_MODE_LOWER | The lower part of the matrix is filled. |
| CUBLAS_FILL_MODE_UPPER | The upper part of the matrix is filled. |
2.2.1.3. cublasOperation_t
The cublasOperation_t type indicates which operation needs to be performed with the dense matrix. Its values correspond to Fortran characters ‘N’ or ‘n’ (non-transpose), ‘T’ or ‘t’ (transpose) and ‘C’ or ‘c’ (conjugate transpose) that are often used as parameters to legacy BLAS implementations.
| Value | Meaning |
|---|---|
| CUBLAS_OP_N | The non-transpose operation is selected. |
| CUBLAS_OP_T | The transpose operation is selected. |
| CUBLAS_OP_C | The conjugate transpose operation is selected. |
2.2.1.4. cusolverEigType_t
The cusolverEigType_t type indicates which type of eigenvalue the solver is. Its values correspond to Fortran integer 1 (A*x = lambda*B*x), 2 (A*B*x = lambda*x), 3 (B*A*x = lambda*x), used as parameters to legacy LAPACK implementations.
| Value | Meaning |
|---|---|
| CUSOLVER_EIG_TYPE_1 | A*x = lambda*B*x |
| CUSOLVER_EIG_TYPE_2 | A*B*x = lambda*x |
| CUSOLVER_EIG_TYPE_3 | B*A*x = lambda*x |
2.2.1.5. cusolverEigMode_t
The cusolverEigMode_t type indicates whether or not eigenvectors are computed. Its values correspond to Fortran character 'N' (only eigenvalues are computed), 'V' (both eigenvalues and eigenvectors are computed) used as parameters to legacy LAPACK implementations.
| Value | Meaning |
|---|---|
| CUSOLVER_EIG_MODE_NOVECTOR | Only eigenvalues are computed. |
| CUSOLVER_EIG_MODE_VECTOR | Both eigenvalues and eigenvectors are computed. |
2.2.1.6. cusolverIRSRefinement_t
The cusolverIRSRefinement_t type indicates which solver type would be used for the specific cusolver function. Most of our experimentation shows that CUSOLVER_IRS_REFINE_GMRES is the best option.
More details about the refinement process can be found in Azzam Haidar, Stanimire Tomov, Jack Dongarra, and Nicholas J. Higham. 2018. Harnessing GPU tensor cores for fast FP16 arithmetic to speed up mixed-precision iterative refinement solvers. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis (SC '18). IEEE Press, Piscataway, NJ, USA, Article 47, 11 pages.
| Value | Meaning |
|---|---|
| CUSOLVER_IRS_REFINE_NOT_SET | Solver is not set; this value is what is set when creating the params structure. IRS solver will return an error. |
| CUSOLVER_IRS_REFINE_NONE | No refinement solver, the IRS solver performs a factorisation followed by a solve without any refinement. For example if the IRS solver was cusolverDnIRSXgesv(), this is equivalent to a Xgesv routine without refinement and where the factorisation is carried out in the lowest precision. If for example the main precision was CUSOLVER_R_64F and the lowest was CUSOLVER_R_64F as well, then this is equivalent to a call to cusolverDnDgesv(). |
| CUSOLVER_IRS_REFINE_CLASSICAL | Classical iterative refinement solver. Similar to the one used in LAPACK routines. |
| CUSOLVER_IRS_REFINE_GMRES | GMRES (Generalized Minimal Residual) based iterative refinement solver. In recent study, the GMRES method has drawn the scientific community attention for its ability to be used as refinement solver that outperforms the classical iterative refinement method. based on our experimentation, we recommend this setting. |
| CUSOLVER_IRS_REFINE_CLASSICAL_GMRES | Classical iterative refinement solver that uses the GMRES (Generalized Minimal Residual) internally to solve the correction equation at each iteration. We call the classical refinement iteration the outer iteration while the GMRES is called inner iteration. Note that if the tolerance of the inner GMRES is set very low, lets say to machine precision, then the outer classical refinement iteration will performs only one iteration and thus this option will behave like CUSOLVER_IRS_REFINE_GMRES. |
| CUSOLVER_IRS_REFINE_GMRES_GMRES | Similar to CUSOLVER_IRS_REFINE_CLASSICAL_GMRES which consists of classical refinement process that uses GMRES to solve the inner correction system; here it is a GMRES (Generalized Minimal Residual) based iterative refinement solver that uses another GMRES internally to solve the preconditioned system. |
2.2.1.7. cusolverDnIRSParams_t
This is a pointer type to an opaque cusolverDnIRSParams_t structure, which holds parameters for the iterative refinement linear solvers such as cusolverDnXgesv(). Use corresponding helper functions described below to either Create/Destroy this structure or Set/Get solver parameters.
2.2.1.8. cusolverDnIRSInfos_t
This is a pointer type to an opaque cusolverDnIRSInfos_t structure, which holds information about the performed call to an iterative refinement linear solver (e.g., cusolverDnXgesv()). Use corresponding helper functions described below to either Create/Destroy this structure or retrieve solve information.
2.2.1.9. cusolverDnFunction_t
The cusolverDnFunction_t type indicates which routine needs to be configured by cusolverDnSetAdvOptions(). The value CUSOLVERDN_GETRF corresponds to the routine Getrf.
| Value | Meaning |
|---|---|
| CUSOLVERDN_GETRF | Corresponds to Getrf. |
2.2.1.10. cusolverAlgMode_t
The cusolverAlgMode_t type indicates which algorithm is selected by cusolverDnSetAdvOptions(). The set of algorithms supported for each routine is described in detail along with the routine's documentation.
The default algorithm is CUSOLVER_ALG_0. The user can also provide NULL to use the default algorithm.
2.2.2. cuSolverSP Types
The float, double, cuComplex, and cuDoubleComplex data types are supported. The first two are standard C data types, while the last two are exported from cuComplex.h.
2.2.2.1. cusolverSpHandle_t
This is a pointer type to an opaque cuSolverSP context, which the user must initialize by calling cusolverSpCreate() prior to calling any other library function. An un-initialized Handle object will lead to unexpected behavior, including crashes of cuSolverSP. The handle created and returned by cusolverSpCreate() must be passed to every cuSolverSP function.
2.2.2.2. cusparseMatDescr_t
We have chosen to keep the same structure as exists in cuSparse to describe the shape and properties of a matrix. This enables calls to either cuSPARSE or cuSOLVER using the same matrix description.
typedef struct {
cusparseMatrixType_t MatrixType;
cusparseFillMode_t FillMode;
cusparseDiagType_t DiagType;
cusparseIndexBase_t IndexBase;
} cusparseMatDescr_t;
Please read documenation of the cuSPARSE Library to understand each field of cusparseMatDescr_t.
2.2.2.3. cusolverStatus_t
This is a status type returned by the library functions and it can have the following values.
| CUSOLVER_STATUS_SUCCESS |
The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED |
The cuSolver library was not initialized. This is usually caused by the lack of a prior call, an error in the CUDA Runtime API called by the cuSolver routine, or an error in the hardware setup. To correct: call cusolverCreate() prior to the function call; and check that the hardware, an appropriate version of the driver, and the cuSolver library are correctly installed. |
| CUSOLVER_STATUS_ALLOC_FAILED |
Resource allocation failed inside the cuSolver library. This is usually caused by a cudaMalloc() failure. To correct: prior to the function call, deallocate previously allocated memory as much as possible. |
| CUSOLVER_STATUS_INVALID_VALUE |
An unsupported value or parameter was passed to the function (a negative vector size, for example). To correct: ensure that all the parameters being passed have valid values. |
| CUSOLVER_STATUS_ARCH_MISMATCH |
The function requires a feature absent from the device architecture; usually caused by the lack of support for atomic operations or double precision. To correct: compile and run the application on a device with compute capability 2.0 or above. |
| CUSOLVER_STATUS_EXECUTION_FAILED |
The GPU program failed to execute. This is often caused by a launch failure of the kernel on the GPU, which can be caused by multiple reasons. To correct: check that the hardware, an appropriate version of the driver, and the cuSolver library are correctly installed. |
| CUSOLVER_STATUS_INTERNAL_ERROR |
An internal cuSolver operation failed. This error is usually caused by a cudaMemcpyAsync() failure. To correct: check that the hardware, an appropriate version of the driver, and the cuSolver library are correctly installed. Also, check that the memory passed as a parameter to the routine is not being deallocated prior to the routine’s completion. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED |
The matrix type is not supported by this function. This is usually caused by passing an invalid matrix descriptor to the function. To correct: check that the fields in descrA were set correctly. |
2.2.3. cuSolverRF Types
cuSolverRF only supports double.
2.2.3.1. cusolverRfHandle_t
The cusolverRfHandle_t is a pointer to an opaque data structure that contains the cuSolverRF library handle. The user must initialize the handle by calling cusolverRfCreate() prior to any other cuSolverRF library calls. The handle is passed to all other cuSolverRF library calls.
2.2.3.2. cusolverRfMatrixFormat_t
The cusolverRfMatrixFormat_t is an enum that indicates the input/output matrix format assumed by the cusolverRfSetupDevice(), cusolverRfSetupHost(), cusolverRfResetValues(), cusolveRfExtractBundledFactorsHost() and cusolverRfExtractSplitFactorsHost() routines.
| Value | Meaning |
|---|---|
| CUSOLVER_MATRIX_FORMAT_CSR | Matrix format CSR is assumed. (default) |
| CUSOLVER_MATRIX_FORMAT_CSC | Matrix format CSC is assumed. |
2.2.3.3. cusolverRfNumericBoostReport_t
The cusolverRfNumericBoostReport_t is an enum that indicates whether numeric boosting (of the pivot) was used during the cusolverRfRefactor() and cusolverRfSolve() routines. The numeric boosting is disabled by default.
| Value | Meaning |
|---|---|
| CUSOLVER_NUMERIC_BOOST_NOT_USED | Numeric boosting not used. (default) |
| CUSOLVER_NUMERIC_BOOST_USED | Numeric boosting used. |
2.2.3.4. cusolverRfResetValuesFastMode_t
The cusolverRfResetValuesFastMode_t is an enum that indicates the mode used for the cusolverRfResetValues() routine. The fast mode requires extra memory and is recommended only if very fast calls to cusolverRfResetValues() are needed.
| Value | Meaning |
|---|---|
| CUSOLVER_RESET_VALUES_FAST_MODE_OFF | Fast mode disabled. (default) |
| CUSOLVER_RESET_VALUES_FAST_MODE_ON | Ffast mode enabled. |
2.2.3.5. cusolverRfFactorization_t
The cusolverRfFactorization_t is an enum that indicates which (internal) algorithm is used for refactorization in the cusolverRfRefactor() routine.
| Value | Meaning |
|---|---|
| CUSOLVER_FACTORIZATION_ALG0 | Algorithm 0. (default) |
| CUSOLVER_FACTORIZATION_ALG1 | Algorithm 1. |
| CUSOLVER_FACTORIZATION_ALG2 | Algorithm 2. Domino-based scheme. |
2.2.3.6. cusolverRfTriangularSolve_t
The cusolverRfTriangularSolve_t is an enum that indicates which (internal) algorithm is used for triangular solve in the cusolverRfSolve() routine.
| Value | Meaning |
|---|---|
| CUSOLVER_TRIANGULAR_SOLVE_ALG1 | Algorithm 1. (default) |
| CUSOLVER_TRIANGULAR_SOLVE_ALG2 | Algorithm 2. Domino-based scheme. |
| CUSOLVER_TRIANGULAR_SOLVE_ALG3 | Aalgorithm 3. Domino-based scheme. |
2.2.3.7. cusolverRfUnitDiagonal_t
The cusolverRfUnitDiagonal_t is an enum that indicates whether and where the unit diagonal is stored in the input/output triangular factors in the cusolverRfSetupDevice(), cusolverRfSetupHost() and cusolverRfExtractSplitFactorsHost() routines.
| Value | Meaning |
|---|---|
| CUSOLVER_UNIT_DIAGONAL_STORED_L | Unit diagonal is stored in lower triangular factor. (default) |
| CUSOLVER_UNIT_DIAGONAL_STORED_U | Unit diagonal is stored in upper triangular factor. |
| CUSOLVER_UNIT_DIAGONAL_ASSUMED_L | Unit diagonal is assumed in lower triangular factor. |
| CUSOLVER_UNIT_DIAGONAL_ASSUMED_U | Unit diagonal is assumed in upper triangular factor. |
2.2.3.8. cusolverStatus_t
The cusolverStatus_t is an enum that indicates success or failure of the cuSolverRF library call. It is returned by all the cuSolver library routines, and it uses the same enumerated values as the sparse and dense Lapack routines.
2.3. cuSolver Formats Reference
2.3.1. Index Base Format
The CSR or CSC format requires either zero-based or one-based index for a sparse matrix A. The GLU library supports only zero-based indexing. Otherwise, both one-based and zero-based indexing are supported in cuSolver.
2.3.2. Vector (Dense) Format
The vectors are assumed to be stored linearly in memory. For example, the vector
|
|
is represented as
|
|
2.3.3. Matrix (Dense) Format
The dense matrices are assumed to be stored in column-major order in memory. The sub-matrix can be accessed using the leading dimension of the original matrix. For examle, the m*n (sub-)matrix
|
|
is represented as
|
|
with its elements arranged linearly in memory as
|
|
where lda ≥ m is the leading dimension of A.
2.3.4. Matrix (CSR) Format
In CSR format the matrix is represented by the following parameters:
| Parameter | Type | Size | Meaning |
|---|---|---|---|
| n | (int) | The number of rows (and columns) in the matrix. | |
| nnz | (int) | The number of non-zero elements in the matrix. | |
| csrRowPtr | (int *) | n+1 | The array of offsets corresponding to the start of each row in the arrays csrColInd and csrVal. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. |
| csrColInd | (int *) | nnz | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. |
| csrVal | (S|D|C|Z)* | nnz | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. |
Note that in our CSR format, sparse matrices are assumed to be stored in row-major order, in other words, the index arrays are first sorted by row indices and then within each row by column indices. Also it is assumed that each pair of row and column indices appears only once.
For example, the 4x4 matrix
|
|
is represented as
|
|
|
|
|
|
2.3.5. Matrix (CSC) Format
In CSC format the matrix is represented by the following parameters:
| Parameter | Type | Size | Meaning |
|---|---|---|---|
| n | (int) | The number of rows (and columns) in the matrix. | |
| nnz | (int) | The number of non-zero elements in the matrix. | |
| cscColPtr | (int *) | n+1 | The array of offsets corresponding to the start of each column in the arrays cscRowInd and cscVal. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. |
| cscRowInd | (int *) | nnz | The array of row indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by column and by row within each column. |
| cscVal | (S|D|C|Z)* | nnz | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by column and by row within each column. |
Note that in our CSC format, sparse matrices are assumed to be stored in column-major order, in other words, the index arrays are first sorted by column indices and then within each column by row indices. Also it is assumed that each pair of row and column indices appears only once.
For example, the 4x4 matrix
|
|
is represented as
|
|
|
|
|
|
2.4. cuSolverDN: dense LAPACK Function Reference
This section describes the API of cuSolverDN, which provides a subset of dense LAPACK functions.
2.4.1. cuSolverDN Helper Function Reference
The cuSolverDN helper functions are described in this section.
2.4.1.1. cusolverDnCreate()
cusolverStatus_t cusolverDnCreate(cusolverDnHandle_t *handle);
This function initializes the cuSolverDN library and creates a handle on the cuSolverDN context. It must be called before any other cuSolverDN API function is invoked. It allocates hardware resources necessary for accessing the GPU.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | output | The pointer to the handle to the cuSolverDN context. |
| CUSOLVER_STATUS_SUCCESS | The initialization succeeded. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The CUDA Runtime initialization failed. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
2.4.1.2. cusolverDnDestroy()
cusolverStatus_t cusolverDnDestroy(cusolverDnHandle_t handle);
This function releases CPU-side resources used by the cuSolverDN library.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| CUSOLVER_STATUS_SUCCESS | The shutdown succeeded. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.4.1.3. cusolverDnSetStream()
cusolverStatus_t cusolverDnSetStream(cusolverDnHandle_t handle, cudaStream_t streamId)
This function sets the stream to be used by the cuSolverDN library to execute its routines.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| streamId | host | input | The stream to be used by the library. |
| CUSOLVER_STATUS_SUCCESS | The stream was set successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.4.1.4. cusolverDnGetStream()
cusolverStatus_t cusolverDnGetStream(cusolverDnHandle_t handle, cudaStream_t *streamId)
This function sets the stream to be used by the cuSolverDN library to execute its routines.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| streamId | host | output | The stream to be used by the library. |
| CUSOLVER_STATUS_SUCCESS | The stream was set successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.4.1.5. cusolverDnCreateSyevjInfo()
cusolverStatus_t
cusolverDnCreateSyevjInfo(
syevjInfo_t *info);
This function creates and initializes the structure of syevj, syevjBatched and sygvj to default values.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | output | The pointer to the structure of syevj. |
| CUSOLVER_STATUS_SUCCESS | The structure was initialized successfully. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
2.4.1.6. cusolverDnDestroySyevjInfo()
cusolverStatus_t
cusolverDnDestroySyevjInfo(
syevjInfo_t info);
This function destroys and releases any memory required by the structure.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | input | The structure of syevj. |
| CUSOLVER_STATUS_SUCCESS | The resources are released successfully. |
2.4.1.7. cusolverDnXsyevjSetTolerance()
cusolverStatus_t
cusolverDnXsyevjSetTolerance(
syevjInfo_t info,
double tolerance)
This function configures tolerance of syevj.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of syevj. |
| tolerance | host | input | accuracy of numerical eigenvalues. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.8. cusolverDnXsyevjSetMaxSweeps()
cusolverStatus_t
cusolverDnXsyevjSetMaxSweeps(
syevjInfo_t info,
int max_sweeps)
This function configures maximum number of sweeps in syevj. The default value is 100.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of syevj. |
| max_sweeps | host | input | Maximum number of sweeps. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.9. cusolverDnXsyevjSetSortEig()
cusolverStatus_t
cusolverDnXsyevjSetSortEig(
syevjInfo_t info,
int sort_eig)
If sort_eig is zero, the eigenvalues are not sorted. This function only works for syevjBatched. syevj and sygvj always sort eigenvalues in ascending order. By default, eigenvalues are always sorted in ascending order.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of syevj. |
| sort_eig | host | input | If sort_eig is zero, the eigenvalues are not sorted. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.10. cusolverDnXsyevjGetResidual()
cusolverStatus_t
cusolverDnXsyevjGetResidual(
cusolverDnHandle_t handle,
syevjInfo_t info,
double *residual)
This function reports residual of syevj or sygvj. It does not support syevjBatched. If the user calls this function after syevjBatched, the error CUSOLVER_STATUS_NOT_SUPPORTED is returned.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| info | host | input | The pointer to the structure of syevj. |
| residual | host | output | Residual of syevj. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_SUPPORTED | Does not support batched version. |
2.4.1.11. cusolverDnXsyevjGetSweeps()
cusolverStatus_t
cusolverDnXsyevjGetSweeps(
cusolverDnHandle_t handle,
syevjInfo_t info,
int *executed_sweeps)
This function reports number of executed sweeps of syevj or sygvj. It does not support syevjBatched. If the user calls this function after syevjBatched, the error CUSOLVER_STATUS_NOT_SUPPORTED is returned.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| info | host | input | The pointer to the structure of syevj. |
| executed_sweeps | host | output | Number of executed sweeps. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_SUPPORTED | Does not support batched version. |
2.4.1.12. cusolverDnCreateGesvdjInfo()
cusolverStatus_t
cusolverDnCreateGesvdjInfo(
gesvdjInfo_t *info);
This function creates and initializes the structure of gesvdj and gesvdjBatched to default values.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | output | The pointer to the structure of gesvdj. |
| CUSOLVER_STATUS_SUCCESS | The structure was initialized successfully. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
2.4.1.13. cusolverDnDestroyGesvdjInfo()
cusolverStatus_t
cusolverDnDestroyGesvdjInfo(
gesvdjInfo_t info);
This function destroys and releases any memory required by the structure.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | input | The structure of gesvdj. |
| CUSOLVER_STATUS_SUCCESS | The resources are released successfully. |
2.4.1.14. cusolverDnXgesvdjSetTolerance()
cusolverStatus_t
cusolverDnXgesvdjSetTolerance(
gesvdjInfo_t info,
double tolerance)
This function configures tolerance of gesvdj.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of gesvdj. |
| tolerance | host | input | Accuracy of numerical singular values. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.15. cusolverDnXgesvdjSetMaxSweeps()
cusolverStatus_t
cusolverDnXgesvdjSetMaxSweeps(
gesvdjInfo_t info,
int max_sweeps)
This function configures the maximum number of sweeps in gesvdj. The default value is 100.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of gesvdj. |
| max_sweeps | host | input | Maximum number of sweeps. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.16. cusolverDnXgesvdjSetSortEig()
cusolverStatus_t
cusolverDnXgesvdjSetSortEig(
gesvdjInfo_t info,
int sort_svd)
If sort_svd is zero, the singular values are not sorted. This function only works for gesvdjBatched. gesvdj always sorts singular values in descending order. By default, singular values are always sorted in descending order.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The pointer to the structure of gesvdj. |
| sort_svd | host | input | If sort_svd is zero, the singular values are not sorted. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
2.4.1.17. cusolverDnXgesvdjGetResidual()
cusolverStatus_t
cusolverDnXgesvdjGetResidual(
cusolverDnHandle_t handle,
gesvdjInfo_t info,
double *residual)
This function reports residual of gesvdj. It does not support gesvdjBatched. If the user calls this function after gesvdjBatched, the error CUSOLVER_STATUS_NOT_SUPPORTED is returned.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| info | host | input | The pointer to the structure of gesvdj. |
| residual | host | output | Residual of gesvdj. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_SUPPORTED | Does not support batched version |
2.4.1.18. cusolverDnXgesvdjGetSweeps()
cusolverStatus_t
cusolverDnXgesvdjGetSweeps(
cusolverDnHandle_t handle,
gesvdjInfo_t info,
int *executed_sweeps)
This function reports number of executed sweeps of gesvdj. It does not support gesvdjBatched. If the user calls this function after gesvdjBatched, the error CUSOLVER_STATUS_NOT_SUPPORTED is returned.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| info | host | input | The pointer to the structure of gesvdj. |
| executed_sweeps | host | output | Number of executed sweeps. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_SUPPORTED | Does not support batched version |
2.4.1.19. cusolverDnIRSParamsCreate()
cusolverStatus_t cusolverDnIRSParamsCreate(cusolverDnIRSParams_t *params);
This function creates and initializes the structure of parameters for an IRS solver such as the cusolverDnIRSXgesv() or the cusolverDnIRSXgels() functions to default values. The params structure created by this function can be used by one or more call to the same or to a different IRS solver. Note that in CUDA 10.2, the behavior was different and a new params structure was needed to be created per each call to an IRS solver. Also note that the user can also change configurations of the params and then call a new IRS instance, but be careful that the previous call was done because any change to the configuration before the previous call was done could affect it.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | output | Pointer to the cusolverDnIRSParams_t Params structure |
| CUSOLVER_STATUS_SUCCESS | The structure was created and initialized successfully. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
2.4.1.20. cusolverDnIRSParamsDestroy()
cusolverStatus_t cusolverDnIRSParamsDestroy(cusolverDnIRSParams_t params);
This function destroys and releases any memory required by the Params structure.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | input | The cusolverDnIRSParams_t Params structure. |
| CUSOLVER_STATUS_SUCCESS | The resources are released successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_DESTROYED | Not all the Infos structure associated with this Params structure have been destroyed yet. |
2.4.1.21. cusolverDnIRSParamsSetSolverPrecisions()
cusolverStatus_t
cusolverDnIRSParamsSetSolverPrecisions(
cusolverDnIRSParams_t params,
cusolverPrecType_t solver_main_precision,
cusolverPrecType_t solver_lowest_precision );
This function sets both the main and the lowest precision for the Iterative Refinement Solver (IRS). By main precision, we mean the precision of the Input and Output datatype. By lowest precision, we mean the solver is allowed to use as lowest computational precision during the LU factorization process. Note that the user has to set both the main and lowest precision before the first call to the IRS solver because they are NOT set by default with the params structure creation, as it depends on the Input Output data type and user request. It is a wrapper to both cusolverDnIRSParamsSetSolverMainPrecision() and cusolverDnIRSParamsSetSolverLowestPrecision(). All possible combinations of main/lowest precision are described in the table below. Usually the lowest precision defines the speedup that can be achieved. The ratio of the performance of the lowest precision over the main precision (e.g., Inputs/Outputs datatype) define the upper bound of the speedup that could be obtained. More precisely, it depends on many factors, but for large matrices sizes, it is the ratio of the matrix-matrix rank-k product (e.g., GEMM where K is 256 and M=N=size of the matrix) that define the possible speedup. For instance, if the inout precision is real double precision CUSOLVER_R_64F and the lowest precision is CUSOLVER_R_32F, then we can expect a speedup of at most 2X for large problem sizes. If the lowest precision was CUSOLVER_R_16F, then we can expect 3X-4X. A reasonable strategy should take the number of right-hand sides, the size of the matrix as well as the convergence rate into account.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| solver_main_precision | host | input | Allowed Inputs/Outputs datatype (for example CUSOLVER_R_FP64 for a real double precision data). See the table below for the supported precisions. |
| solver_lowest_precision | host | input | Allowed lowest compute type (for example CUSOLVER_R_16F for half precision computation). See the table below for the supported precisions. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
| Inputs/Outputs Data Type (e.g., main precision) | Supported values for the lowest precision |
|---|---|
| CUSOLVER_C_64F | CUSOLVER_C_64F, CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_C_32F | CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_R_64F | CUSOLVER_R_64F, CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
| CUSOLVER_R_32F | CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
2.4.1.22. cusolverDnIRSParamsSetSolverMainPrecision()
cusolverStatus_t
cusolverDnIRSParamsSetSolverMainPrecision(
cusolverDnIRSParams_t params,
cusolverPrecType_t solver_main_precision);
This function sets the main precision for the Iterative Refinement Solver (IRS). By main precision, we mean, the type of the Input and Output data. Note that the user has to set both the main and lowest precision before a first call to the IRS solver because they are NOT set by default with the params structure creation, as it depends on the Input Output data type and user request. user can set it by either calling this function or by calling cusolverDnIRSParamsSetSolverPrecisions() which set both the main and the lowest precision together. All possible combinations of main/lowest precision are described in the table in the cusolverDnIRSParamsSetSolverPrecisions() section above.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| solver_main_precision | host | input | Allowed Inputs/Outputs datatype (for example CUSOLVER_R_FP64 for a real double precision data). See the table in the cusolverDnIRSParamsSetSolverPrecisions() section above for the supported precisions. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.23. cusolverDnIRSParamsSetSolverLowestPrecision()
cusolverStatus_t
cusolverDnIRSParamsSetSolverLowestPrecision(
cusolverDnIRSParams_t params,
cusolverPrecType_t lowest_precision_type);
This function sets the lowest precision that will be used by Iterative Refinement Solver. By lowest precision, we mean the solver is allowed to use as lowest computational precision during the LU factorization process. Note that the user has to set both the main and lowest precision before a first call to the IRS solver because they are NOT set by default with the params structure creation, as it depends on the Input Output data type and user request. Usually the lowest precision defines the speedup that can be achieved. The ratio of the performance of the lowest precision over the main precision (e.g., Inputs/Outputs datatype) define somehow the upper bound of the speedup that could be obtained. More precisely, it depends on many factors, but for large matrices sizes, it is the ratio of the matrix-matrix rank-k product (e.g., GEMM where K is 256 and M=N=size of the matrix) that define the possible speedup. For instance, if the inout precision is real double precision CUSOLVER_R_64F and the lowest precision is CUSOLVER_R_32F, then we can expect a speedup of at most 2X for large problem sizes. If the lowest precision was CUSOLVER_R_16F, then we can expect 3X-4X. A reasonable strategy should take the number of right-hand sides, the size of the matrix as well as the convergence rate into account.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| lowest_precision_type | host | input | Allowed lowest compute type (for example CUSOLVER_R_16F for half precision computation). See the table in the cusolverDnIRSParamsSetSolverPrecisions() section above for the supported precisions. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.24. cusolverDnIRSParamsSetRefinementSolver()
cusolverStatus_t
cusolverDnIRSParamsSetRefinementSolver(
cusolverDnIRSParams_t params,
cusolverIRSRefinement_t solver);
This function sets the refinement solver to be used in the Iterative Refinement Solver functions such as the cusolverDnIRSXgesv() or the cusolverDnIRSXgels() functions. Note that the user has to set the refinement algorithm before a first call to the IRS solver because it is NOT set by default with the creating of params. Details about values that can be set to and theirs meaning are described in the table below.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_tParams structure |
| solver | host | input | Type of the refinement solver to be used by the IRS solver such as cusolverDnIRSXgesv() or cusolverDnIRSXgels(). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
| CUSOLVER_IRS_REFINE_NOT_SET | Solver is not set, this value is what is set when creating the params structure. IRS solver will return an error. |
| CUSOLVER_IRS_REFINE_NONE | No refinement solver; the IRS solver performs a factorization followed by a solve without any refinement. For example, if the IRS solver was cusolverDnIRSXgesv(), this is equivalent to a Xgesv routine without refinement and where the factorization is carried out in the lowest precision. If for example the main precision was CUSOLVER_R_64F and the lowest was CUSOLVER_R_64F as well, then this is equivalent to a call to cusolverDnDgesv(). |
| CUSOLVER_IRS_REFINE_CLASSICAL | Classical iterative refinement solver. Similar to the one used in LAPACK routines. |
| CUSOLVER_IRS_REFINE_GMRES | GMRES (Generalized Minimal Residual) based iterative refinement solver. In recent study, the GMRES method has drawn the scientific community attention for its ability to be used as refinement solver that outperforms the classical iterative refinement method. Based on our experimentation, we recommend this setting. |
| CUSOLVER_IRS_REFINE_CLASSICAL_GMRES | Classical iterative refinement solver that uses the GMRES (Generalized Minimal Residual) internally to solve the correction equation at each iteration. We call the classical refinement iteration the outer iteration while the GMRES is called inner iteration. Note that if the tolerance of the inner GMRES is set very low, let say to machine precision, then the outer classical refinement iteration will performs only one iteration and thus this option will behaves like CUSOLVER_IRS_REFINE_GMRES. |
| CUSOLVER_IRS_REFINE_GMRES_GMRES | Similar to CUSOLVER_IRS_REFINE_CLASSICAL_GMRES which consists of classical refinement process that uses GMRES to solve the inner correction system, here it is a GMRES (Generalized Minimal Residual) based iterative refinement solver that uses another GMRES internally to solve the preconditioned system. |
2.4.1.25. cusolverDnIRSParamsSetTol()
cusolverStatus_t
cusolverDnIRSParamsSetTol(
cusolverDnIRSParams_t params,
double val );
This function sets the tolerance for the refinement solver. By default it is such that all the RHS satisfy:
- RNRM is the infinity-norm of the residual
- XNRM is the infinity-norm of the solution
- ANRM is the infinity-operator-norm of the matrix A
- EPS is the machine epsilon for the Inputs/Outputs datatype that matches LAPACK <X>LAMCH('Epsilon')
- BWDMAX, the value BWDMAX is fixed to 1.0
The user can use this function to change the tolerance to a lower or higher value. Our goal is to give the user more control such a way he can investigate and control every detail of the IRS solver. Note that the tolerance value is always in real double precision whatever the Inputs/Outputs datatype is.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| val | host | input | Double precision real value to which the refinement tolerance will be set. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.26. cusolverDnIRSParamsSetTolInner()
cusolverStatus_t
cusolverDnIRSParamsSetTolInner(
cusolverDnIRSParams_t params,
double val );
This function sets the tolerance for the inner refinement solver when the refinement solver consists of two-levels solver (e.g., CUSOLVER_IRS_REFINE_CLASSICAL_GMRES or CUSOLVER_IRS_REFINE_GMRES_GMRES cases). It is not referenced in case of one level refinement solver such as CUSOLVER_IRS_REFINE_CLASSICAL or CUSOLVER_IRS_REFINE_GMRES. It is set to 1e-4 by default. This function set the tolerance for the inner solver (e.g. the inner GMRES). For example, if the Refinement Solver was set to CUSOLVER_IRS_REFINE_CLASSICAL_GMRES, setting this tolerance mean that the inner GMRES solver will converge to that tolerance at each outer iteration of the classical refinement solver. Our goal is to give the user more control such a way he can investigate and control every detail of the IRS solver. Note the, the tolerance value is always in real double precision whatever the Inputs/Outputs datatype is.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| val | host | input | Double precision real value to which the tolerance of the inner refinement solver will be set. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.27. cusolverDnIRSParamsSetMaxIters()
cusolverStatus_t
cusolverDnIRSParamsSetMaxIters(
cusolverDnIRSParams_t params,
int max_iters);
This function sets the total number of allowed refinement iterations after which the solver will stop. Total means any iteration which means the sum of the outer and the inner iterations (inner is meaningful when two-levels refinement solver is set). Default value is set to 50. Our goal is to give the user more control such a way he can investigate and control every detail of the IRS solver.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure. |
| max_iters | host | input | Maximum total number of iterations allowed for the refinement solver. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.28. cusolverDnIRSParamsSetMaxItersInner()
cusolverStatus_t
cusolverDnIRSParamsSetMaxItersInner(
cusolverDnIRSParams_t params,
cusolver_int_t maxiters_inner );
This function sets the maximal number of iterations allowed for the inner refinement solver. It is not referenced in case of one level refinement solver such as CUSOLVER_IRS_REFINE_CLASSICAL or CUSOLVER_IRS_REFINE_GMRES. The inner refinement solver will stop after reaching either the inner tolerance or the MaxItersInner value. By default, it is set to 50. Note that this value could not be larger than the MaxIters since MaxIters is the total number of allowed iterations. Note that if the user calls cusolverDnIRSParamsSetMaxIters after calling this function, SetMaxIters has priority and will overwrite MaxItersInner to the minimum value of (MaxIters, MaxItersInner).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure |
| maxiters_inner | host | input | Maximum number of allowed inner iterations for the inner refinement solver. Meaningful when the refinement solver is a two-levels solver such as CUSOLVER_IRS_REFINE_CLASSICAL_GMRES or CUSOLVER_IRS_REFINE_GMRES_GMRES. Value should be less or equal to MaxIters. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID | If the value was larger than MaxIters. |
2.4.1.29. cusolverDnIRSParamsEnableFallback()
cusolverStatus_t
cusolverDnIRSParamsEnableFallback(
cusolverDnIRSParams_t params );
This function enable the fallback to the main precision in case the Iterative Refinement Solver (IRS) failed to converge. In other term, if the IRS solver failed to converge, the solver will return a no convergence code (e.g., niter < 0), but can either return the non-convergent solution as it is (e.g., disable fallback) or can fallback (e.g., enable fallback) to the main precision (which is the precision of the Inputs/Outputs data) and solve the problem from scratch returning the good solution. This is the behavior by default, and it will guarantee that the IRS solver always provide the good solution. This function is provided because we provided cusolverDnIRSParamsDisableFallback which allows the user to disable the fallback and thus this function allow the user to re-enable it.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.30. cusolverDnIRSParamsDisableFallback()
cusolverStatus_t
cusolverDnIRSParamsDisableFallback(
cusolverDnIRSParams_t params );
This function disables the fallback to the main precision in case the Iterative Refinement Solver (IRS) failed to converge. In other term, if the IRS solver failed to converge, the solver will return a no convergence code (e.g., niter < 0), but can either return the non-convergent solution as it is (e.g., disable fallback) or can fallback (e.g., enable fallback) to the main precision (which is the precision of the Inputs/Outputs data) and solve the problem from scratch returning the good solution. This function disables the fallback and the returned solution is whatever the refinement solver was able to reach before it returns. Disabling fallback does not guarantee that the solution is the good one. However, if users want to keep getting the solution of the lower precision in case the IRS did not converge after certain number of iterations, they need to disable the fallback. The user can re-enable it by calling cusolverDnIRSParamsEnableFallback.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The cusolverDnIRSParams_t Params structure |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.31. cusolverDnIRSParamsGetMaxIters()
cusolverStatus_t
cusolverDnIRSParamsGetMaxIters(
cusolverDnIRSParams_t params,
cusolver_int_t *maxiters );
This function returns the current setting in the params structure for the maximal allowed number of iterations (e.g., either the default MaxIters, or the one set by the user in case he set it using cusolverDnIRSParamsSetMaxIters). Note that this function returns the current setting in the params configuration and not to be confused with the cusolverDnIRSInfosGetMaxIters which return the maximal allowed number of iterations for a particular call to an IRS solver. To be clearer, the params structure can be used for many calls to an IRS solver. A user can change the allowed MaxIters between calls while the Infos structure in cusolverDnIRSInfosGetMaxIters contains information about a particular call and cannot be reused for different calls, and thus, cusolverDnIRSInfosGetMaxIters returns the allowed MaxIters for that call.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in | The cusolverDnIRSParams_t Params structure. |
| maxiters | host | output | The maximal number of iterations that is currently set. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The Params structure was not created. |
2.4.1.32. cusolverDnIRSInfosCreate()
cusolverStatus_t
cusolverDnIRSInfosCreate(
cusolverDnIRSInfos_t* infos )
This function creates and initializes the Infos structure that will hold the refinement information of an Iterative Refinement Solver (IRS) call. Such information includes the total number of iterations that was needed to converge (Niters), the outer number of iterations (meaningful when two-levels preconditioner such as CUSOLVER_IRS_REFINE_CLASSICAL_GMRES is used ), the maximal number of iterations that was allowed for that call, and a pointer to the matrix of the convergence history residual norms. The Infos structure needs to be created before a call to an IRS solver. The Infos structure is valid for only one call to an IRS solver, since it holds info about that solve and thus each solve will requires its own Infos structure.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | output | Pointer to the cusolverDnIRSInfos_t Infos structure. |
| CUSOLVER_STATUS_SUCCESS | The structure was initialized successfully. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
2.4.1.33. cusolverDnIRSInfosDestroy()
cusolverStatus_t
cusolverDnIRSInfosDestroy(
cusolverDnIRSInfos_t infos );
This function destroys and releases any memory required by the Infos structure. This function destroys all the information (e.g., Niters performed, OuterNiters performed, residual history etc.) about a solver call; thus, this function should only be called after the user is finished with the information.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| info | host | in/out | The cusolverDnIRSInfos_t Infos structure. |
| CUSOLVER_STATUS_SUCCESS | The resources are released successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
2.4.1.34. cusolverDnIRSInfosGetMaxIters()
cusolverStatus_t
cusolverDnIRSInfosGetMaxIters(
cusolverDnIRSInfos_t infos,
cusolver_int_t *maxiters );
This function returns the maximal allowed number of iterations that was set for the corresponding call to the IRS solver. Note that this function returns the setting that was set when that call happened and is not to be confused with the cusolverDnIRSParamsGetMaxIters which returns the current setting in the params configuration structure. To be clearer, the params structure can be used for many calls to an IRS solver. A user can change the allowed MaxIters between calls while the Infos structure in cusolverDnIRSInfosGetMaxIters contains information about a particular call and cannot be reused for different calls, thus cusolverDnIRSInfosGetMaxIters returns the allowed MaxIters for that call.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| infos | host | in | The cusolverDnIRSInfos_t Infos structure. |
| maxiters | host | output | The maximal number of iterations that is currently set. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
2.4.1.35. cusolverDnIRSInfosGetNiters()
cusolverStatus_t cusolverDnIRSInfosGetNiters(
cusolverDnIRSInfos_t infos,
cusolver_int_t *niters );
This function returns the total number of iterations performed by the IRS solver. If it was negative, it means that the IRS solver did not converge and if the user did not disable the fallback to full precision, then the fallback to a full precision solution happened and solution is good. Please refer to the description of negative niters values in the corresponding IRS linear solver functions such as cusolverDnXgesv() or cusolverDnXgels().
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| infos | host | in | The cusolverDnIRSInfos_t Infos structure. |
| niters | host | output | The total number of iterations performed by the IRS solver. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
2.4.1.36. cusolverDnIRSInfosGetOuterNiters()
cusolverStatus_t
cusolverDnIRSInfosGetOuterNiters(
cusolverDnIRSInfos_t infos,
cusolver_int_t *outer_niters );
This function returns the number of iterations performed by the outer refinement loop of the IRS solver. When the refinement solver consists of a one-level solver such as CUSOLVER_IRS_REFINE_CLASSICAL or CUSOLVER_IRS_REFINE_GMRES, it is the same as Niters. When the refinement solver consists of a two-levels solver such as CUSOLVER_IRS_REFINE_CLASSICAL_GMRES or CUSOLVER_IRS_REFINE_GMRES_GMRES, it is the number of iterations of the outer loop. Refer to the description of the cusolverIRSRefinement_t section for more details.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| infos | host | in | The cusolverDnIRSInfos_t Infos structure. |
| outer_niters | host | output | The number of iterations of the outer refinement loop of the IRS solver. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
2.4.1.37. cusolverDnIRSInfosRequestResidual()
cusolverStatus_t cusolverDnIRSInfosRequestResidual(
cusolverDnIRSInfos_t infos );
This function tells the IRS solver to store the convergence history (residual norms) of the refinement phase in a matrix that can be accessed via a pointer returned by the cusolverDnIRSInfosGetResidualHistory() function.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| infos | host | in | The cusolverDnIRSInfos_t Infos structure |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
2.4.1.38. cusolverDnIRSInfosGetResidualHistory()
cusolverStatus_t
cusolverDnIRSInfosGetResidualHistory(
cusolverDnIRSInfos_t infos,
void **residual_history );
If the user called cusolverDnIRSInfosRequestResidual() before the call to the IRS function, then the IRS solver will store the convergence history (residual norms) of the refinement phase in a matrix that can be accessed via a pointer returned by this function. The datatype of the residual norms depends on the input and output data type. If the Inputs/Outputs datatype is double precision real or complex (CUSOLVER_R_FP64 or CUSOLVER_C_FP64), this residual will be of type real double precision (FP64) double, otherwise if the Inputs/Outputs datatype is single precision real or complex (CUSOLVER_R_FP32 or CUSOLVER_C_FP32), this residual will be real single precision FP32 float.
The residual history matrix consists of two columns (even for the multiple right-hand side case NRHS) of MaxIters+1 row, thus a matrix of size (MaxIters+1,2). Only the first OuterNiters+1 rows contains the residual norms the other (e.g., OuterNiters+2:Maxiters+1) are garbage. On the first column, each row "i" specify the total number of iterations happened till this outer iteration "i" and on the second columns the residual norm corresponding to this outer iteration "i". Thus, the first row (e.g., outer iteration "0") consists of the initial residual (e.g., the residual before the refinement loop start) then the consecutive rows are the residual obtained at each outer iteration of the refinement loop. Note, it only consists of the history of the outer loop.
If the refinement solver was CUSOLVER_IRS_REFINE_CLASSICAL or CUSOLVER_IRS_REFINE_GMRES, then OuterNiters=Niters (Niters is the total number of iterations performed) and there is Niters+1 rows of norms that correspond to the Niters outer iterations.
If the refinement solver was CUSOLVER_IRS_REFINE_CLASSICAL_GMRES or CUSOLVER_IRS_REFINE_GMRES_GMRES, then OuterNiters <= Niters corresponds to the outer iterations performed by the outer refinement loop. Thus, there is OuterNiters+1 residual norms where row "i" correspond to the outer iteration "i" and the first column specify the total number of iterations (outer and inner) that were performed till this step the second columns correspond to the residual norm at this step.
For example, let's say the user specifies CUSOLVER_IRS_REFINE_CLASSICAL_GMRES as a refinement solver and say it needed 3 outer iterations to converge and 4,3,3 inner iterations at each outer, respectively. This consists of 10 total iterations. Row 0 corresponds to the first residual before the refinement start, so it has 0 in its first column. On row 1 which corresponds to the outer iteration 1, it will be 4 (4 is the total number of iterations that were performed till now), on row 2 it will be 7, and on row 3 it will be 10.
In summary, let's define ldh=Maxiters+1, the leading dimension of the residual matrix. then residual_history[i] shows the total number of iterations performed at the outer iteration "i" and residual_history[i+ldh] corresponds to the norm of the residual at this outer iteration.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| infos | host | in | The cusolverDnIRSInfos_t Infos structure. |
| residual_history | host | output | Returns a void pointer to the matrix of the convergence history residual norms. See the description above for the relation between the residual norm datatype and the inout datatype. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The Infos structure was not created. |
| CUSOLVER_STATUS_INVALID_VALUE | This function was called without calling cusolverDnIRSInfosRequestResidual() in advance. |
2.4.1.39. cusolverDnCreateParams()
cusolverStatus_t
cusolverDnCreateParams(
cusolverDnParams_t *params);
This function creates and initializes the structure of 64-bit API to default values.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | output | The pointer to the structure of 64-bit API. |
| CUSOLVER_STATUS_SUCCESS | The structure was initialized successfully. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
2.4.1.40. cusolverDnDestroyParams()
cusolverStatus_t
cusolverDnDestroyParams(
cusolverDnParams_t params);
This function destroys and releases any memory required by the structure.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | input | The structure of 64-bit API. |
| CUSOLVER_STATUS_SUCCESS | The resources were released successfully. |
2.4.1.41. cusolverDnSetAdvOptions()
cusolverStatus_t
cusolverDnSetAdvOptions (
cusolverDnParams_t params,
cusolverDnFunction_t function,
cusolverAlgMode_t algo );
This function configures algorithm algo of function, a 64-bit API routine.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| params | host | in/out | The pointer to the structure of 64-bit API. |
| function | host | input | The routine to be configured. |
| algo | host | input | The algorithm to be configured. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | Wrong combination of function and algo. |
2.4.2. Dense Linear Solver Reference (legacy)
This section describes linear solver API of cuSolverDN, including Cholesky factorization, LU with partial pivoting, QR factorization and Bunch-Kaufman (LDLT) factorization.
2.4.2.1. cusolverDn<t>potrf()
cusolverStatus_t
cusolverDnSpotrf_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnDpotrf_bufferSize(cusolveDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnCpotrf_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnZpotrf_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
int *Lwork);
cusolverStatus_t
cusolverDnSpotrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnDpotrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnCpotrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
cuComplex *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnZpotrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *Workspace,
int Lwork,
int *devInfo );
This function computes the Cholesky factorization of a Hermitian positive-definite matrix.
A is an n×n Hermitian matrix, only the lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other parts untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only the lower triangular part of A is processed, and replaced by the lower triangular Cholesky factor L.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular Cholesky factor U.
The user has to provide working space which is pointed by input parameter Workspace. The input parameter Lwork is size of the working space, and it is returned by potrf_bufferSize().
If Cholesky factorization failed, i.e. some leading minor of A is not positive definite, or equivalently some diagonal elements of L or U is not a real number. The output parameter devInfo would indicate smallest leading minor of A which is not positive definite.
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored; the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| Workspace | device | in/out | Working space, <type> array of size Lwork. |
| Lwork | host | input | Size of Workspace, returned by potrf_bufferSize. |
| devInfo | device | output | If devInfo = 0, the Cholesky factorization is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i, the leading minor of order i is not positive definite. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.2. cusolverDnPotrf()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXpotrf() instead. The routine will be removed in the next major release.
cusolverStatus_t
cusolverDnPotrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType computeType,
size_t *workspaceInBytes )
cusolverStatus_t
cusolverDnPotrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType computeType,
void *pBuffer,
size_t workspaceInBytes,
int *info )
Computes the Cholesky factorization of a Hermitian positive-definite matrix using the generic API interfacte.
A is an n×n Hermitian matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular Cholesky factor L.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular Cholesky factor U.
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytes of the working space, and it is returned by cusolverDnPotrf_bufferSize().
If Cholesky factorization failed, i.e. some leading minor of A is not positive definite, or equivalently some diagonal elements of L or U is not a real number. The output parameter info would indicate smallest leading minor of A which is not positive definite.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnPotrf supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnPotrf_bufferSize and cusolverDnPotrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | handle to the cuSolverDN library context. |
| params | host | input | structure with information collected by cusolverDnSetAdvOptions. |
| uplo | host | input | indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | number of rows and columns of matrix A. |
| dataTypeA | host | in | data type of array A. |
| A | device | in/out | array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | leading dimension of two-dimensional array used to store matrix A. |
| computeType | host | in | data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | size in bytes of pBuffer, returned by cusolverDnPotrf_bufferSize. |
| info | device | output | if info = 0, the Cholesky factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info = i, the leading minor of order i is not positive definite. |
The generic API has two different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation. cusolverDnPotrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
| CUDA_R_32F | CUDA_R_32F | SPOTRF |
| CUDA_R_64F | CUDA_R_64F | DPOTRF |
| CUDA_C_32F | CUDA_C_32F | CPOTRF |
| CUDA_C_64F | CUDA_C_64F | ZPOTRF |
| CUSOLVER_STATUS_SUCCESS | the operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | the library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | the device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | an internal operation failed. |
2.4.2.3. cusolverDn<t>potrs()
cusolverStatus_t
cusolverDnSpotrs(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
const float *A,
int lda,
float *B,
int ldb,
int *devInfo);
cusolverStatus_t
cusolverDnDpotrs(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
const double *A,
int lda,
double *B,
int ldb,
int *devInfo);
cusolverStatus_t
cusolverDnCpotrs(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
const cuComplex *A,
int lda,
cuComplex *B,
int ldb,
int *devInfo);
cusolverStatus_t
cusolverDnZpotrs(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
const cuDoubleComplex *A,
int lda,
cuDoubleComplex *B,
int ldb,
int *devInfo);
This function solves a system of linear equations
where A is an n×n Hermitian matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
The user has to call potrf first to factorize matrix A. If input parameter uplo is CUBLAS_FILL_MODE_LOWER, A is lower triangular Cholesky factor L correspoding to . If input parameter uplo is CUBLAS_FILL_MODE_UPPER, A is upper triangular Cholesky factor U corresponding to .
The operation is in-place, i.e. matrix X overwrites matrix B with the same leading dimension ldb.
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolveDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of columns of matrix X and B. |
| A | device | input | <type> array of dimension lda * n with lda is not less than max(1,n). A is either lower cholesky factor L or upper Cholesky factor U. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| B | device | in/out | <type> array of dimension ldb * nrhs. ldb is not less than max(1,n). As an input, B is right hand side matrix. As an output, B is the solution matrix. |
| devInfo | device | output | If devInfo = 0, the Cholesky factorization is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, nrhs<0, lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.4. cusolverDnPotrs()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXpotrs() instead. The routine will be removed in the next major release.
cusolverStatus_t
cusolverDnPotrs(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
int *info)
This function solves a system of linear equations
where A is a n×n Hermitian matrix, only lower or upper part is meaningful using the generic API interface. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
The user has to call cusolverDnPotrf first to factorize matrix A. If input parameter uplo is CUBLAS_FILL_MODE_LOWER, A is lower triangular Cholesky factor L correspoding to . If input parameter uplo is CUBLAS_FILL_MODE_UPPER, A is upper triangular Cholesky factor U corresponding to .
The operation is in-place, i.e. matrix X overwrites matrix B with the same leading dimension ldb.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnPotrs supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnPotrs:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolveDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of columns of matrix X and B. |
| dataTypeA | host | in | Data type of array A. |
| A | device | input | Array of dimension lda * n with lda is not less than max(1,n). A is either lower cholesky factor L or upper Cholesky factor U. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeB | host | in | Data type of array B. |
| B | device | in/out | Array of dimension ldb * nrhs. ldb is not less than max(1,n). As an input, B is right hand side matrix. As an output, B is the solution matrix. |
| info | device | output | If info = 0, the Cholesky factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types, dataTypeA is data type of the matrix A, dataTypeB is data type of the matrix B. cusolverDnPotrs only supports the following four combinations.
| dataTypeA | dataTypeB | Meaning |
| CUDA_R_32F | CUDA_R_32F | SPOTRS |
| CUDA_R_64F | CUDA_R_64F | DPOTRS |
| CUDA_C_32F | CUDA_C_32F | CPOTRS |
| CUDA_C_64F | CUDA_C_64F | ZPOTRS |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, nrhs<0, lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.5. cusolverDn<t>potri()
cusolverStatus_t
cusolverDnSpotri_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnDpotri_bufferSize(cusolveDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnCpotri_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnZpotri_bufferSize(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
int *Lwork);
cusolverStatus_t
cusolverDnSpotri(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnDpotri(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnCpotri(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
cuComplex *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnZpotri(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *Workspace,
int Lwork,
int *devInfo );
This function computes the inverse of a positive-definite matrix A using the Cholesky factorization
computed by potrf().
A is a n×n matrix containing the triangular factor L or U computed by the Cholesky factorization. Only lower or upper part is meaningful and the input parameter uplo indicates which part of the matrix is used. The function would leave the other part untouched.
If the input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced the by lower triangular part of the inverse of A.
If the input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by the upper triangular part of the inverse of A.
The user has to provide the working space which is pointed to by input parameter Workspace. The input parameter Lwork is the size of the working space, returned by potri_bufferSize().
If the computation of the inverse fails, i.e. some leading minor of L or U, is null, the output parameter devInfo would indicate the smallest leading minor of L or U which is not positive definite.
If the output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting the handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n where lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| Workspace | device | in/out | Working space, <type> array of size Lwork. |
| Lwork | host | input | Size of Workspace, returned by potri_bufferSize. |
| devInfo | device | output | If devInfo = 0, the computation of the inverse is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i, the leading minor of order i is zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.6. cusolverDn<t>getrf()
cusolverStatus_t
cusolverDnSgetrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
float *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnDgetrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
double *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnCgetrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
cuComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnZgetrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
cuDoubleComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnSgetrf(cusolverDnHandle_t handle,
int m,
int n,
float *A,
int lda,
float *Workspace,
int *devIpiv,
int *devInfo );
cusolverStatus_t
cusolverDnDgetrf(cusolverDnHandle_t handle,
int m,
int n,
double *A,
int lda,
double *Workspace,
int *devIpiv,
int *devInfo );
cusolverStatus_t
cusolverDnCgetrf(cusolverDnHandle_t handle,
int m,
int n,
cuComplex *A,
int lda,
cuComplex *Workspace,
int *devIpiv,
int *devInfo );
cusolverStatus_t
cusolverDnZgetrf(cusolverDnHandle_t handle,
int m,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *Workspace,
int *devIpiv,
int *devInfo );
This function computes the LU factorization of a m×n matrix
where A is a m×n matrix, P is a permutation matrix, L is a lower triangular matrix with unit diagonal, and U is an upper triangular matrix.
The user has to provide working space which is pointed by input parameter Workspace. The input parameter Lwork is size of the working space, and it is returned by getrf_bufferSize().
If LU factorization failed, i.e. matrix A (U) is singular, The output parameter devInfo=i indicates U(i,i) = 0.
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
If devIpiv is null, no pivoting is performed. The factorization is A=L*U, which is not numerically stable.
No matter LU factorization failed or not, the output parameter devIpiv contains pivoting sequence, row i is interchanged with row devIpiv(i).
The user can combine getrf and getrs to complete a linear solver. Please visit cuSOLVER Library Samples - getrf for a code example.
Remark: getrf uses fastest implementation with large workspace of size m*n. The user can choose the legacy implementation with minimal workspace by Getrf and cusolverDnSetAdvOptions(params, CUSOLVERDN_GETRF, CUSOLVER_ALG_1).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| Workspace | device | in/out | Working space, <type> array of size Lwork. |
| devIpiv | device | output | Array of size at least min(m,n), containing pivot indices. |
| devInfo | device | output | If devInfo = 0, the LU factorization is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i, the U(i,i) = 0. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.7. cusolverDnGetrf()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXgetrf() instead. The routine will be removed in the next major release.
cusolverStatus_t
cusolverDnGetrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType computeType,
size_t *workspaceInBytes )
cusolverStatus_t
cusolverDnGetrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
int64_t *ipiv,
cudaDataType computeType,
void *pBuffer,
size_t workspaceInBytes,
int *info )
computes the LU factorization of a m×n matrix
where A is an m×n matrix, P is a permutation matrix, L is a lower triangular matrix with unit diagonal, and U is an upper triangular matrix using the generic API interface.
If LU factorization failed, i.e. matrix A (U) is singular, The output parameter info=i indicates U(i,i) = 0.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
If ipiv is null, no pivoting is performed. The factorization is A=L*U, which is not numerically stable.
No matter LU factorization failed or not, the output parameter ipiv contains pivoting sequence, row i is interchanged with row ipiv(i).
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytes of the working space, and it is returned by cusolverDnGetrf_bufferSize().
The user can combine cusolverDnGetrf and cusolverDnGetrs to complete a linear solver.
Currently, cusolverDnGetrf supports two algorithms. To select legacy implementation, the user has to call cusolverDnSetAdvOptions.
| CUSOLVER_ALG_0 or NULL | Default algorithm. The fastest, requires a large workspace of m*n elements. |
| CUSOLVER_ALG_1 | Legacy implementation |
List of input arguments for cusolverDnGetrf_bufferSize and cusolverDnGetrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| m | host | input | number of rows of matrix A. |
| n | host | input | number of columns of matrix A. |
| dataTypeA | host | in | data type of array A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | output | array of size at least min(m,n), containing pivot indices. |
| computeType | host | in | data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | size in bytes of pBuffer, returned by cusolverDnGetrf_bufferSize. |
| info | device | output | if info = 0, the LU factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info = i, the U(i,i) = 0. |
The generic API has two different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation. cusolverDnGetrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
| CUDA_R_32F | CUDA_R_32F | SGETRF |
| CUDA_R_64F | CUDA_R_64F | DGETRF |
| CUDA_C_32F | CUDA_C_32F | CGETRF |
| CUDA_C_64F | CUDA_C_64F | ZGETRF |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.8. cusolverDn<t>getrs()
cusolverStatus_t
cusolverDnSgetrs(cusolverDnHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const float *A,
int lda,
const int *devIpiv,
float *B,
int ldb,
int *devInfo );
cusolverStatus_t
cusolverDnDgetrs(cusolverDnHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const double *A,
int lda,
const int *devIpiv,
double *B,
int ldb,
int *devInfo );
cusolverStatus_t
cusolverDnCgetrs(cusolverDnHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const cuComplex *A,
int lda,
const int *devIpiv,
cuComplex *B,
int ldb,
int *devInfo );
cusolverStatus_t
cusolverDnZgetrs(cusolverDnHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const cuDoubleComplex *A,
int lda,
const int *devIpiv,
cuDoubleComplex *B,
int ldb,
int *devInfo );
This function solves a linear system of multiple right-hand sides
where A is an n×n matrix, and was LU-factored by getrf, that is, lower trianular part of A is L, and upper triangular part (including diagonal elements) of A is U. B is a n×nrhs right-hand side matrix.
The input parameter trans is defined by
The input parameter devIpiv is an output of getrf. It contains pivot indices, which are used to permutate right-hand sides.
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user can combine getrf and getrs to complete a linear solver. Please visit cuSOLVER Library Samples - getrs for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| trans | host | input | Operation op(A) that is non- or (conj.) transpose. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of right-hand sides. |
| A | device | input | <type> array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| devIpiv | device | input | Array of size at least n, containing pivot indices. |
| B | device | output | <type> array of dimension ldb * nrhs with ldb is not less than max(1,n). |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.9. cusolverDnGetrs()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXgetrs() instead. The routine will be removed in the next major release.
cusolverStatus_t
cusolverDnGetrs(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasOperation_t trans,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
const int64_t *ipiv,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
int *info )
This function solves a linear system of multiple right-hand sides
where A is a n×n matrix, and was LU-factored by cusolverDnGetrf, that is, lower trianular part of A is L, and upper triangular part (including diagonal elements) of A is U. B is a n×nrhs right-hand side matrix using the generic API interface.
The input parameter trans is defined by
The input parameter ipiv is an output of cusolverDnGetrf. It contains pivot indices, which are used to permutate right-hand sides.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user can combine cusolverDnGetrf and cusolverDnGetrs to complete a linear solver.
Currently, cusolverDnGetrs supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnGetrss:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| trans | host | input | Operation op(A) that is non- or (conj.) transpose. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of right-hand sides. |
| dataTypeA | host | in | Data type of array A. |
| A | device | input | Array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | input | Array of size at least n, containing pivot indices. |
| dataTypeB | host | in | Data type of array B. |
| B | device | output | <type> array of dimension ldb * nrhs with ldb is not less than max(1,n). |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types, dataTypeA is data type of the matrix A and dataTypeB is data type of the matrix B. cusolverDnGetrs only supports the following four combinations.
| DataTypeA | dataTypeB | Meaning |
| CUDA_R_32F | CUDA_R_32F | SGETRS |
| CUDA_R_64F | CUDA_R_64F | DGETRS |
| CUDA_C_32F | CUDA_C_32F | CGETRS |
| CUDA_C_64F | CUDA_C_64F | ZGETRS |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.10. cusolverDn<t1><t2>gesv()
These functions are modelled after functions DSGESV and ZCGESV from LAPACK. They compute the solution of a system of linear equations with one or multiple right hand sides using mixed precision iterative refinement techniques based on the LU factorization Xgesv. These functions are similar in term of functionalities to the full precision LU solver (Xgesv, where X denotes Z,C,D,S) but it uses lower precision internally in order to provide faster time to solution, from here cames the name mixed precision. Mixed precision iterative refinement techniques means that the solver compute an LU factorization in lower precision and then iteratively refine the solution to achieve the accuracy of the Inputs/Outputs datatype precision. The <t1> corresponds to the Inputs/Outputs datatype precision while <t2> represent the internal lower precision at which the factorization will be carried on.
Where A is n-by-n matrix and X and B are n-by-nrhs matrices.
Functions API are designed to be as close as possible to LAPACK API to be considered as a quick and easy drop-in replacement. Parameters and behavior are mostly the same as LAPACK counterparts. Description of these functions and differences from LAPACK is given below. <t1><t2>gesv() functions are designated by two floating point precisions The <t1> corresponds to the main precision (e.g., Inputs/Outputs datatype precision) and the <t2> represent the internal lower precision at which the factorization will be carried on. cusolver<t1><t2>gesv() first attempts to factorize the matrix in lower precision and use this factorization within an iterative refinement procedure to obtain a solution with same normwise backward error as the main precision <t1>. If the approach fails to converge, then the method fallback to the main precision factorization and solve (Xgesv) such a way that there is always a good solution at the output of these functions. If <t2> is equal to <t1>, then it is not a mixed precision process but rather a full one precision factorisation, solve and refinement within the same main precision.
ITER > ITERMAX
or for all the RHS we have:
RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX
where
- ITER is the number of the current iteration in the iterative refinement process
- RNRM is the infinity-norm of the residual
- XNRM is the infinity-norm of the solution
- ANRM is the infinity-operator-norm of the matrix A
- EPS is the machine epsilon that matches LAPACK <t1>LAMCH('Epsilon')
The function returns value describes the results of the solving process. A CUSOLVER_STATUS_SUCCESS indicates that the function finished with success otherwise, it indicates if one of the API arguments is incorrect, or if the function did not finish with success. More details about the error will be in the niters and the dinfo API parameters. See their description below for more details. User should provide the required workspace allocated on device memory. The amount of bytes required can be queried by calling the respective function <t1><t2>gesv_bufferSize().
Note that in addition to the two mixed precision functions available in LAPACK (e.g., dsgesv and zcgesv), we provide a large set of mixed precision functions that include half, bfloat and tensorfloat as a lower precision as well as same precision functions (e.g., main and lowest precision are equal <t2> is equal to <t1>). The following table specifies which precisions will be used for which interface function.
Tensor Float (TF32), introduced with NVIDIA Ampere Architecture GPUs, is the most robust tensor core accelerated compute mode for the iterative refinement solver. It is able to solve the widest range of problems in HPC arising from different applications and provides up to 4X and 5X speedup for real and complex systems, respectively. On Volta and Turing architecture GPUs, half precision tensor core acceleration is recommended. In cases where the iterative refinement solver fails to converge to the desired accuracy (main precision, INOUT data precision), it is recommended to use main precision as internal lowest precision (i.e., cusolverDn[DD,ZZ]gesv for the FP64 case).
| Interface function | Main precision (matrix, rhs and solution datatype) | Lowest precision allowed to be used internally |
|---|---|---|
| cusolverDnZZgesv | cuDoubleComplex | double complex |
| cusolverDnZCgesv *has LAPACK counterparts | cuDoubleComplex | single complex |
| cusolverDnZKgesv | cuDoubleComplex | half complex |
| cusolverDnZEgesv | cuDoubleComplex | bfloat complex |
| cusolverDnZYgesv | cuDoubleComplex | tensorfloat complex |
| cusolverDnCCgesv | cuComplex | single complex |
| cusolverDnCKgesv | cuComplex | half complex |
| cusolverDnCEgesv | cuComplex | bfloat complex |
| cusolverDnCYgesv | cuComplex | tensorfloat complex |
| cusolverDnDDgesv | double | double |
| cusolverDnDSgesv *has LAPACK counterparts | double | single |
| cusolverDnDHgesv | double | half |
| cusolverDnDBgesv | double | bfloat |
| cusolverDnDXgesv | double | tensorfloat |
| cusolverDnSSgesv | float | single |
| cusolverDnSHgesv | float | half |
| cusolverDnSBgesv | float | bfloat |
| cusolverDnSXgesv | float | tensorfloat |
cusolverStatus_t
cusolverDnZZgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZCgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZKgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZEgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZYgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCCgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCKgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCEgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCYgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDDgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDSgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDHgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDBgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDXgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSSgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSHgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSBgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSXgesv_bufferSize(
cusolverHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDN library context. |
| n | host | input | Number of rows and columns of square matrix A. Should be non-negative. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. |
| dA | device | None | Matrix A with size n-by-n. Can be NULL. |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= n. |
| dipiv | device | None | Pivoting sequence. Not used and can be NULL. |
| dB | device | None | Set of right hand sides B of size n-by-nrhs. Can be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. ldb >= n. |
| dX | device | None | Set of soultion vectors X of size n-by-nrhs. Can be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. ldx >= n. |
| dwork | device | none | Pointer to device workspace. Not used and can be NULL. |
| lwork_bytes | host | output | Pointer to a variable where required size of temporary workspace in bytes will be stored. Can't be NULL. |
cusolverStatus_t cusolverDnZZgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZCgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZKgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZEgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZYgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
int * dipiv,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCCgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCKgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCEgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCYgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
cuComplex * dA,
int ldda,
int * dipiv,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDDgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDSgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDHgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDBgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDXgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
double * dA,
int ldda,
int * dipiv,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSSgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSHgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSBgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSXgesv(
cusolverDnHandle_t handle,
int n,
int nrhs,
float * dA,
int ldda,
int * dipiv,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDN library context. |
| n | host | input | Number of rows and columns of square matrix A. Should be non-negative. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. |
| dA | device | in/out | Matrix A with size n-by-n. Can't be NULL. On return - unchanged if the iterative refinement process converged. If not - will contains the factorization of the matrix A in the main precision <T1> (A = P * L * U, where P - permutation matrix defined by vector ipiv, L and U - lower and upper triangular matrices). |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= n. |
| dipiv | device | output | Vector that defines permutation for the factorization - row i was interchanged with row ipiv[i] |
| dB | device | input | Set of right hand sides B of size n-by-nrhs . Can't be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. ldb >= n. |
| dX | device | output | Set of soultion vectors X of size n-by-nrhs . Can't be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. ldx >= n. |
| dWorkspace | device | input | Pointer to an allocated workspace in device memory of size lwork_bytes. |
| lwork_bytes | host | input | Size of the allocated device workspace. Should be at least what was returned by cusolverDn<T1><T2>gesv_bufferSize() function. |
| niters | host | output | If iter is
|
| dinfo | device | output | Status of the IRS solver on the return. If 0 - solve was successful. If dinfo = -i then i-th argument is not valid. If dinfo = i, then U(i,i) computed in main precision is exactly zero. The factorization has been completed, but the factor U is exactly singular, so the solution could not be computed. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed, for example:
|
| CUSOLVER_STATUS_ARCH_MISMATCH | The IRS solver supports compute capability 7.0 and above. The lowest precision options CUSOLVER_[CR]_16BF and CUSOLVER_[CR]_TF32 are only available on compute capability 8.0 and above. |
| CUSOLVER_STATUS_INVALID_WORKSPACE | lwork_bytes is smaller than the required workspace. |
| CUSOLVER_STATUS_IRS_OUT_OF_RANGE | Numerical error related to niters <0, see niters description for more details. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal error occured, check the dinfo and the niters arguments for more details. |
2.4.2.11. cusolverDnIRSXgesv()
- the main precision (Inputs/Outputs precision) of the solver
- the lowest precision to be used internally by the solver
- the refinement solver type
- the maximum allowed number of iterations in the refinement phase
- the tolerance of the refinement solver
- the fallback to main precision
- and more
The function returns value describes the results of the solving process. A CUSOLVER_STATUS_SUCCESS indicates that the function finished with success otherwise, it indicates if one of the API arguments is incorrect, or if the configurations of params/infos structure is incorrect or if the function did not finish with success. More details about the error can be found by checking the niters and the dinfo API parameters. See their description below for further details. User should provide the required workspace allocated on device for the cusolverDnIRSXgesv() function. The amount of bytes required for the function can be queried by calling the respective function cusolverDnIRSXgesv_bufferSize(). Note that, if the user would like a praticular configuration to be set via the params structure, it should be set before the call to cusolverDnIRSXgesv_bufferSize() to get the size of the required workspace.
Tensor Float (TF32), introduced with NVIDIA Ampere Architecture GPUs, is the most robust tensor core accelerated compute mode for the iterative refinement solver. It is able to solve the widest range of problems in HPC arising from different applications and provides up to 4X and 5X speedup for real and complex systems, respectively. On Volta and Turing architecture GPUs, half precision tensor core acceleration is recommended. In cases where the iterative refinement solver fails to converge to the desired accuracy (main precision, INOUT data precision), it is recommended to use main precision as internal lowest precision.
The following table provides all possible combinations values for the lowest precision corresponding to the Inputs/Outputs data type. Note that if the lowest precision matches the Inputs/Outputs datatype, then the main precision factorization will be used.
| Inputs/Outputs Data Type (e.g., main precision) | Supported values for the lowest precision |
|---|---|
| CUSOLVER_C_64F | CUSOLVER_C_64F, CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_C_32F | CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_R_64F | CUSOLVER_R_64F, CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
| CUSOLVER_R_32F | CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
cusolverStatus_t
cusolverDnIRSXgesv_bufferSize(
cusolverDnHandle_t handle,
cusolverDnIRSParams_t gesv_irs_params,
cusolver_int_t n,
cusolver_int_t nrhs,
size_t * lwork_bytes);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDn library context. |
| params | host | input | Xgesv configuration parameters |
| n | host | input | Number of rows and columns of the square matrix A. Should be non-negative. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. Note that nrhs is limited to 1 if the selected IRS refinement solver is CUSOLVER_IRS_REFINE_GMRES, CUSOLVER_IRS_REFINE_GMRES_GMRES, CUSOLVER_IRS_REFINE_CLASSICAL_GMRES. |
| lwork_bytes | host | out | Pointer to a variable, where the required size in bytes, of the workspace will be stored after a call to cusolverDnIRSXgesv_bufferSize. Can't be NULL. |
cusolverStatus_t cusolverDnIRSXgesv(
cusolverDnHandle_t handle,
cusolverDnIRSParams_t gesv_irs_params,
cusolverDnIRSInfos_t gesv_irs_infos,
int n,
int nrhs,
void * dA,
int ldda,
void * dB,
int lddb,
void * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * dinfo);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDn library context. |
| gesv_irs_params | host | input | Configuration parameters structure, can serve one or more calls to any IRS solver |
| gesv_irs_infos | host | in/out | Info structure, where information about a particular solve will be stored. The gesv_irs_infos structure correspond to a particular call. Thus different calls requires different gesv_irs_infos structure otherwise, it will be overwritten. |
| n | host | input | Number of rows and columns of square matrix A. Should be non-negative. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. Note that, nrhs is limited to 1 if the selected IRS refinement solver is CUSOLVER_IRS_REFINE_GMRES, CUSOLVER_IRS_REFINE_GMRES_GMRES, CUSOLVER_IRS_REFINE_CLASSICAL_GMRES. |
| dA | device | in/out | Matrix A with size n-by-n. Can't be NULL. On return - will contain the factorization of the matrix A in the main precision (A = P * L * U, where P - permutation matrix defined by vector ipiv, L and U - lower and upper triangular matrices) if the iterative refinement solver was set to CUSOLVER_IRS_REFINE_NONE and the lowest precision is equal to the main precision (Inputs/Ouputs datatype), or if the iterative refinement solver did not converge and the fallback to main precision was enabled (fallback enabled is the default setting); unchanged otherwise. |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= n. |
| dB | device | input | Set of right hand sides B of size n-by-nrhs . Can't be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. ldb >= n. |
| dX | device | output | Set of soultion vectors X of size n-by-nrhs . Can't be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. ldx >= n. |
| dWorkspace | device | input | Pointer to an allocated workspace in device memory of size lwork_bytes. |
| lwork_bytes | host | input | Size of the allocated device workspace. Should be at least what was returned by cusolverDnIRSXgesv_bufferSize() function |
| niters | host | output | If iter is
|
| dinfo | device | output | Status of the IRS solver on the return. If 0 - solve was successful. If dinfo = -i then i-th argument is not valid. If dinfo = i, then U(i,i) computed in main precision is exactly zero. The factorization has been completed, but the factor U is exactly singular, so the solution could not be computed. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed, for example:
|
| CUSOLVER_STATUS_ARCH_MISMATCH | The IRS solver supports compute capability 7.0 and above. The lowest precision options CUSOLVER_[CR]_16BF and CUSOLVER_[CR]_TF32 are only available on compute capability 8.0 and above. |
| CUSOLVER_STATUS_INVALID_WORKSPACE | lwork_bytes is smaller than the required workspace. Could happen if the users called cusolverDnIRSXgesv_bufferSize() function, then changed some of the configurations setting such as the lowest precision. |
| CUSOLVER_STATUS_IRS_OUT_OF_RANGE | Numerical error related to niters <0, see niters description for more details. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal error occured, check the dinfo and the niters arguments for more details. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The configuration parameter gesv_irs_params structure was not created. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID | One of the configuration parameter in the gesv_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_PREC | The main and/or the lowest precision configuration parameter in the gesv_irs_params structure is not valid, check the table above for the supported combinations. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_MAXITER | The maxiter configuration parameter in the gesv_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_REFINE | The refinement solver configuration parameter in the gesv_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_NOT_SUPPORTED | One of the configuration parameter in the gesv_irs_params structure is not supported. For example if nrhs >1, and refinement solver was set to CUSOLVER_IRS_REFINE_GMRES. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The information structure gesv_irs_infos was not created. |
| CUSOLVER_STATUS_ALLOC_FAILED | CPU memory allocation failed, most likely during the allocation of the residual array that store the residual norms. |
2.4.2.12. cusolverDn<t>geqrf()
cusolverStatus_t
cusolverDnSgeqrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
float *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnDgeqrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
double *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnCgeqrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
cuComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnZgeqrf_bufferSize(cusolverDnHandle_t handle,
int m,
int n,
cuDoubleComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnSgeqrf(cusolverDnHandle_t handle,
int m,
int n,
float *A,
int lda,
float *TAU,
float *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnDgeqrf(cusolverDnHandle_t handle,
int m,
int n,
double *A,
int lda,
double *TAU,
double *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnCgeqrf(cusolverDnHandle_t handle,
int m,
int n,
cuComplex *A,
int lda,
cuComplex *TAU,
cuComplex *Workspace,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnZgeqrf(cusolverDnHandle_t handle,
int m,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *TAU,
cuDoubleComplex *Workspace,
int Lwork,
int *devInfo );
This function computes the QR factorization of a m×n matrix
where A is an m×n matrix, Q is an m×n matrix, and R is a n×n upper triangular matrix.
The user has to provide working space which is pointed by input parameter Workspace. The input parameter Lwork is size of the working space, and it is returned by geqrf_bufferSize().
The matrix R is overwritten in upper triangular part of A, including diagonal elements.
The matrix Q is not formed explicitly, instead, a sequence of householder vectors are stored in lower triangular part of A. The leading nonzero element of householder vector is assumed to be 1 such that output parameter TAU contains the scaling factor τ. If v is original householder vector, q is the new householder vector corresponding to τ, satisying the following relation
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| TAU | device | output | <type> array of dimension at least min(m,n). |
| Workspace | device | in/out | Working space, <type> array of size Lwork. |
| Lwork | host | input | Size of working array Workspace. |
| devInfo | device | output | If devInfo = 0, the LU factorization is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.13. cusolverDnGeqrf()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXgeqrf() instead. The routine will be removed in the next major release.
cusolverStatus_t
cusolverDnGeqrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeTau,
const void *tau,
cudaDataType computeType,
size_t *workspaceInBytes )
cusolverStatus_t
cusolverDnGeqrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeTau,
void *tau,
cudaDataType computeType,
void *pBuffer,
size_t workspaceInBytes,
int *info )
computes the QR factorization of an m×n matrix
where A is a m×n matrix, Q is an m×n matrix, and R is an n×n upper triangular matrix using the generic API interface.
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytes of the working space, and it is returned by cusolverDnGeqrf_bufferSize().
The matrix R is overwritten in upper triangular part of A, including diagonal elements.
The matrix Q is not formed explicitly, instead, a sequence of householder vectors are stored in lower triangular part of A. The leading nonzero element of householder vector is assumed to be 1 such that output parameter TAU contains the scaling factor τ. If v is original householder vector, q is the new householder vector corresponding to τ, satisying the following relation
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnGeqrf supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnGeqrf_bufferSize and cusolverDnGeqrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| TAU | device | output | Array of dimension at least min(m,n). |
| computeType | host | in | Data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | Size in bytes of working array pBuffer. |
| info | device | output | If info = 0, the LU factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types, dataTypeA is data type of the matrix A and array tau and computeType is compute type of the operation. cusolverDnGeqrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
| CUDA_R_32F | CUDA_R_32F | SGEQRF |
| CUDA_R_64F | CUDA_R_64F | DGEQRF |
| CUDA_C_32F | CUDA_C_32F | CGEQRF |
| CUDA_C_64F | CUDA_C_64F | ZGEQRF |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.14. cusolverDn<t1><t2>gels()
These functions compute the solution of a system of linear equations with one or multiple right hand sides using mixed precision iterative refinement techniques based on the QR factorization Xgels. These functions are similar in term of functionalities to the full precision LAPACK QR (least squares) solver (Xgels, where X denotes Z,C,D,S) but it uses lower precision internally in order to provide faster time to solution, from here cames the name mixed precision. Mixed precision iterative refinement techniques means that the solver compute an QR factorization in lower precision and then iteratively refine the solution to achieve the accuracy of the Inputs/Outputs datatype precision. The <t1> corresponds to the Inputs/Outputs datatype precision while <t2> represent the internal lower precision at which the factorization will be carried on.
Where A is m-by-n matrix and X is n-by-nrhs and B is m-by-nrhs matrices.
Functions API are designed to be as close as possible to LAPACK API to be considered as a quick and easy drop-in replacement. Description of these functions is given below. <t1><t2>gels() functions are designated by two floating point precisions The <t1> corresponds to the main precision (e.g., Inputs/Outputs datatype precision) and the <t2> represent the internal lower precision at which the factorization will be carried on. cusolver<t1><t2>gels() first attempts to factorize the matrix in lower precision and use this factorization within an iterative refinement procedure to obtain a solution with same normwise backward error as the main precision <t1>. If the approach fails to converge, then the method fallback to the main precision factorization and solve (Xgels) such a way that there is always a good solution at the output of these functions. If <t2> is equal to <t1>, then it is not a mixed precision process but rather a full one precision factorisation, solve and refinement within the same main precision.
ITER > ITERMAX
or for all the RHS we have:
RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX
where
- ITER is the number of the current iteration in the iterative refinement process
- RNRM is the infinity-norm of the residual
- XNRM is the infinity-norm of the solution
- ANRM is the infinity-operator-norm of the matrix A
- EPS is the machine epsilon that matches LAPACK <t1>LAMCH('Epsilon')
The function returns value describes the results of the solving process. A CUSOLVER_STATUS_SUCCESS indicates that the function finished with success otherwise, it indicates if one of the API arguments is incorrect, or if the function did not finish with success. More details about the error will be in the niters and the dinfo API parameters. See their description below for more details. User should provide the required workspace allocated on device memory. The amount of bytes required can be queried by calling the respective function <t1><t2>gels_bufferSize().
We provide a large set of mixed precision functions that include half, bfloat and tensorfloat as a lower precision as well as same precision functions (e.g., main and lowest precision are equal <t2> is equal to <t1>). The following table specifies which precisions will be used for which interface function:
Tensor Float (TF32), introduced with NVIDIA Ampere Architecture GPUs, is the most robust tensor core accelerated compute mode for the iterative refinement solver. It is able to solve the widest range of problems in HPC arising from different applications and provides up to 4X and 5X speedup for real and complex systems, respectively. On Volta and Turing architecture GPUs, half precision tensor core acceleration is recommended. In cases where the iterative refinement solver fails to converge to the desired accuracy (main precision, INOUT data precision), it is recommended to use main precision as internal lowest precision (i.e., cusolverDn[DD,ZZ]gels for the FP64 case).
| Interface function | Main precision (matrix, rhs and solution datatype) | Lowest precision allowed to be used internally |
|---|---|---|
| cusolverDnZZgels | cuDoubleComplex | double complex |
| cusolverDnZCgels | cuDoubleComplex | single complex |
| cusolverDnZKgels | cuDoubleComplex | half complex |
| cusolverDnZEgels | cuDoubleComplex | bfloat complex |
| cusolverDnZYgels | cuDoubleComplex | tensorfloat complex |
| cusolverDnCCgels | cuComplex | single complex |
| cusolverDnCKgels | cuComplex | half complex |
| cusolverDnCEgels | cuComplex | bfloat complex |
| cusolverDnCYgels | cuComplex | tensorfloat complex |
| cusolverDnDDgels | double | double |
| cusolverDnDSgels | double | single |
| cusolverDnDHgels | double | half |
| cusolverDnDBgels | double | bfloat |
| cusolverDnDXgels | double | tensorfloat |
| cusolverDnSSgels | float | single |
| cusolverDnSHgels | float | half |
| cusolverDnSBgels | float | bfloat |
| cusolverDnSXgels | float | tensorfloat |
cusolverStatus_t
cusolverDnZZgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZCgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZKgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZEgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnZYgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCCgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCKgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCEgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnCYgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDDgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDSgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDHgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDBgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnDXgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSSgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSHgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSBgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
cusolverStatus_t
cusolverDnSXgels_bufferSize(
cusolverHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dwork,
size_t * lwork_bytes);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDN library context. |
| m | host | input | Number of rows of the matrix A. Should be non-negative and n<=m |
| n | host | input | Number of columns of the matrix A. Should be non-negative and n<=m. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. |
| dA | device | None | Matrix A with size m-by-n. Can be NULL. |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. ldda >= m. |
| dB | device | None | Set of right hand sides B of size m-by-nrhs. Can be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. lddb >= max(1,m). |
| dX | device | None | Set of soultion vectors X of size n-by-nrhs. Can be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. lddx >= max(1,n). |
| dwork | device | none | Pointer to device workspace. Not used and can be NULL. |
| lwork_bytes | host | output | Pointer to a variable where required size of temporary workspace in bytes will be stored. Can't be NULL. |
cusolverStatus_t cusolverDnZZgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZCgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZKgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZEgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnZYgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuDoubleComplex * dA,
int ldda,
cuDoubleComplex * dB,
int lddb,
cuDoubleComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCCgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCKgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCEgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnCYgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
cuComplex * dA,
int ldda,
cuComplex * dB,
int lddb,
cuComplex * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDDgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDSgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDHgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDBgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnDXgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
double * dA,
int ldda,
double * dB,
int lddb,
double * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSSgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSHgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSBgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
cusolverStatus_t cusolverDnSXgels(
cusolverDnHandle_t handle,
int m,
int n,
int nrhs,
float * dA,
int ldda,
float * dB,
int lddb,
float * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * niter,
int * dinfo);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDN library context. |
| m | host | input | Number of rows of the matrix A. Should be non-negative and n<=m |
| n | host | input | Number of columns of the matrix A. Should be non-negative and n<=m. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. |
| dA | device | in/out | Matrix A with size m-by-n. Can't be NULL. On return - unchanged if the lowest precision is not equal to the main precision and the iterative refinement solver converged, - garbage otherwise. |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. ldda >= m. |
| dB | device | input | Set of right hand sides B of size m-by-nrhs . Can't be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. lddb >= max(1,m). |
| dX | device | output | Set of soultion vectors X of size n-by-nrhs . Can't be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. lddx >= max(1,n). |
| dWorkspace | device | input | Pointer to an allocated workspace in device memory of size lwork_bytes. |
| lwork_bytes | host | input | Size of the allocated device workspace. Should be at least what was returned by cusolverDn<T1><T2>gels_bufferSize() function |
| niters | host | output | If iter is
|
| dinfo | device | output | Status of the IRS solver on the return. If 0 - solve was successful. If dinfo = -i then i-th argument is not valid. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed, for example:
|
| CUSOLVER_STATUS_ARCH_MISMATCH | The IRS solver supports compute capability 7.0 and above. The lowest precision options CUSOLVER_[CR]_16BF and CUSOLVER_[CR]_TF32 are only available on compute capability 8.0 and above. |
| CUSOLVER_STATUS_INVALID_WORKSPACE | lwork_bytes is smaller than the required workspace. |
| CUSOLVER_STATUS_IRS_OUT_OF_RANGE | Numerical error related to niters <0, see niters description for more details. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal error occurred; check the dinfo and the niters arguments for more details. |
2.4.2.15. cusolverDnIRSXgels()
- the main precision (Inputs/Outputs precision) of the solver,
- the lowest precision to be used internally by the solver,
- the refinement solver type
- the maximum allowed number of iterations in the refinement phase
- the tolerance of the refinement solver
- the fallback to main precision
- and others
The function returns value describes the results of the solving process. A CUSOLVER_STATUS_SUCCESS indicates that the function finished with success otherwise, it indicates if one of the API arguments is incorrect, or if the configurations of params/infos structure is incorrect or if the function did not finish with success. More details about the error can be found by checking the niters and the dinfo API parameters. See their description below for further details. Users should provide the required workspace allocated on device for the cusolverDnIRSXgels() function. The amount of bytes required for the function can be queried by calling the respective function cusolverDnIRSXgels_bufferSize(). Note that, if the user would like a praticular configuration to be set via the params structure, it should be set before the call to cusolverDnIRSXgels_bufferSize() to get the size of the required workspace.
The following table provides all possible combinations values for the lowest precision corresponding to the Inputs/Outputs data type. Note that if the lowest precision matches the Inputs/Outputs datatype, then main precision factorization will be used
Tensor Float (TF32), introduced with NVIDIA Ampere Architecture GPUs, is the most robust tensor core accelerated compute mode for the iterative refinement solver. It is able to solve the widest range of problems in HPC arising from different applications and provides up to 4X and 5X speedup for real and complex systems, respectively. On Volta and Turing architecture GPUs, half precision tensor core acceleration is recommended. In cases where the iterative refinement solver fails to converge to the desired accuracy (main precision, INOUT data precision), it is recommended to use main precision as internal lowest precision.
| Inputs/Outputs Data Type (e.g., main precision) | Supported values for the lowest precision |
|---|---|
| CUSOLVER_C_64F | CUSOLVER_C_64F, CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_C_32F | CUSOLVER_C_32F, CUSOLVER_C_16F, CUSOLVER_C_16BF, CUSOLVER_C_TF32 |
| CUSOLVER_R_64F | CUSOLVER_R_64F, CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
| CUSOLVER_R_32F | CUSOLVER_R_32F, CUSOLVER_R_16F, CUSOLVER_R_16BF, CUSOLVER_R_TF32 |
cusolverStatus_t
cusolverDnIRSXgels_bufferSize(
cusolverDnHandle_t handle,
cusolverDnIRSParams_t gels_irs_params,
cusolver_int_t m,
cusolver_int_t n,
cusolver_int_t nrhs,
size_t * lwork_bytes);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDn library context. |
| params | host | input | Xgels configuration parameters |
| m | host | input | Number of rows of the matrix A. Should be non-negative and n<=m |
| n | host | input | Number of columns of the matrix A. Should be non-negative and n<=m. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. Note that, nrhs is limited to 1 if the selected IRS refinement solver is CUSOLVER_IRS_REFINE_GMRES, CUSOLVER_IRS_REFINE_GMRES_GMRES, CUSOLVER_IRS_REFINE_CLASSICAL_GMRES. |
| lwork_bytes | host | out | Pointer to a variable, where the required size in bytes, of the workspace will be stored after a call to cusolverDnIRSXgels_bufferSize. Can't be NULL. |
cusolverStatus_t cusolverDnIRSXgels(
cusolverDnHandle_t handle,
cusolverDnIRSParams_t gels_irs_params,
cusolverDnIRSInfos_t gels_irs_infos,
int m,
int n,
int nrhs,
void * dA,
int ldda,
void * dB,
int lddb,
void * dX,
int lddx,
void * dWorkspace,
size_t lwork_bytes,
int * dinfo);
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cusolverDn library context. |
| gels_irs_params | host | input | Configuration parameters structure, can serve one or more calls to any IRS solver |
| gels_irs_infos | host | in/out | Info structure, where information about a particular solve will be stored. The gels_irs_infos struture correspond to a particular call. Thus different calls requires different gels_irs_infos structure otherwise, it will be overwritten. |
| m | host | input | Number of rows of the matrix A. Should be non-negative and n<=m |
| n | host | input | Number of columns of the matrix A. Should be non-negative and n<=m. |
| nrhs | host | input | Number of right hand sides to solve. Should be non-negative. Note that, nrhs is limited to 1 if the selected IRS refinement solver is CUSOLVER_IRS_REFINE_GMRES, CUSOLVER_IRS_REFINE_GMRES_GMRES, CUSOLVER_IRS_REFINE_CLASSICAL_GMRES. |
| dA | device | in/out | Matrix A with size m-by-n. Can't be NULL. On return - unchanged if the lowest precision is not equal to the main precision and the iterative refinement solver converged, - garbage otherwise. |
| ldda | host | input | Leading dimension of two-dimensional array used to store matrix A. ldda >= m. |
| dB | device | input | Set of right hand sides B of size m-by-nrhs . Can't be NULL. |
| lddb | host | input | Leading dimension of two-dimensional array used to store matrix of right hand sides B. lddb >= max(1,m). |
| dX | device | output | Set of soultion vectors X of size n-by-nrhs . Can't be NULL. |
| lddx | host | input | Leading dimension of two-dimensional array used to store matrix of solution vectors X. lddx >= max(1,n). |
| dWorkspace | device | input | Pointer to an allocated workspace in device memory of size lwork_bytes. |
| lwork_bytes | host | input | Size of the allocated device workspace. Should be at least what was returned by cusolverDnIRSXgels_bufferSize() function. |
| niters | host | output | If iter is
|
| dinfo | device | output | Status of the IRS solver on the return. If 0 - solve was successful. If dinfo = -i then i-th argument is not valid. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed, for example:
|
| CUSOLVER_STATUS_ARCH_MISMATCH | The IRS solver supports compute capability 7.0 and above. The lowest precision options CUSOLVER_[CR]_16BF and CUSOLVER_[CR]_TF32 are only available on compute capability 8.0 and above. |
| CUSOLVER_STATUS_INVALID_WORKSPACE | lwork_bytes is smaller than the required workspace. Could happen if the users called cusolverDnIRSXgels_bufferSize() function, then changed some of the configurations setting such as the lowest precision. |
| CUSOLVER_STATUS_IRS_OUT_OF_RANGE | Numerical error related to niters <0; see niters description for more details. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal error occured, check the dinfo and the niters arguments for more details. |
| CUSOLVER_STATUS_IRS_PARAMS_NOT_INITIALIZED | The configuration parameter gels_irs_params structure was not created. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID | One of the configuration parameter in the gels_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_PREC | The main and/or the lowest precision configuration parameter in the gels_irs_params structure is not valid, check the table above for the supported combinations. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_MAXITER | The maxiter configuration parameter in the gels_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_PARAMS_INVALID_REFINE | The refinement solver configuration parameter in the gels_irs_params structure is not valid. |
| CUSOLVER_STATUS_IRS_NOT_SUPPORTED | One of the configuration parameter in the gels_irs_params structure is not supported. For example if nrhs >1, and refinement solver was set to CUSOLVER_IRS_REFINE_GMRES. |
| CUSOLVER_STATUS_IRS_INFOS_NOT_INITIALIZED | The information structure gels_irs_infos was not created. |
| CUSOLVER_STATUS_ALLOC_FAILED | CPU memory allocation failed, most likely during the allocation of the residual array that store the residual norms. |
2.4.2.16. cusolverDn<t>ormqr()
cusolverStatus_t
cusolverDnSormqr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const float *A,
int lda,
const float *tau,
const float *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnDormqr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const double *A,
int lda,
const double *tau,
const double *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnCunmqr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const cuComplex *A,
int lda,
const cuComplex *tau,
const cuComplex *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnZunmqr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
const cuDoubleComplex *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnSormqr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const float *A,
int lda,
const float *tau,
float *C,
int ldc,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDormqr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const double *A,
int lda,
const double *tau,
double *C,
int ldc,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCunmqr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const cuComplex *A,
int lda,
const cuComplex *tau,
cuComplex *C,
int ldc,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZunmqr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasOperation_t trans,
int m,
int n,
int k,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
cuDoubleComplex *C,
int ldc,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function overwrites m×n matrix C by
The operation of Q is defined by
Q is a unitary matrix formed by a sequence of elementary reflection vectors from QR factorization (geqrf) of A.
Q=H(1)H(2) ... H(k)
Q is of order m if side = CUBLAS_SIDE_LEFT and of order n if side = CUBLAS_SIDE_RIGHT.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by geqrf_bufferSize() or ormqr_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user can combine geqrf, ormqr and trsm to complete a linear solver or a least-square solver. Please visit cuSOLVER Library Samples - ormqr for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDn library context. |
| side | host | input | Indicates if matrix Q is on the left or right of C. |
| trans | host | input | Operation op(Q) that is non- or (conj.) transpose. |
| m | host | input | Number of rows of matrix C. |
| n | host | input | Number of columns of matrix C. |
| k | host | input | Number of elementary relfections whose product defines the matrix Q. |
| A | device | in/out | <type> array of dimension lda * k with lda is not less than max(1,m). The matrix A is from geqrf, so i-th column contains elementary reflection vector. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. if side is CUBLAS_SIDE_LEFT, lda >= max(1,m); if side is CUBLAS_SIDE_RIGHT, lda >= max(1,n). |
| tau | device | output | <type> array of dimension at least min(m,n). The vector tau is from geqrf, so tau(i) is the scalar of i-th elementary reflection vector. |
| C | device | in/out | <type> array of size ldc * n. On exit, C is overwritten by op(Q)*C. |
| ldc | host | input | Leading dimension of two-dimensional array of matrix C. ldc >= max(1,m). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working array work. |
| devInfo | device | output | If devInfo = 0, the ormqr is successful. If devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or wrong lda or ldc). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.17. cusolverDn<t>orgqr()
cusolverStatus_t
cusolverDnSorgqr_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int k,
const float *A,
int lda,
const float *tau,
int *lwork);
cusolverStatus_t
cusolverDnDorgqr_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int k,
const double *A,
int lda,
const double *tau,
int *lwork);
cusolverStatus_t
cusolverDnCungqr_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int k,
const cuComplex *A,
int lda,
const cuComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnZungqr_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int k,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnSorgqr(
cusolverDnHandle_t handle,
int m,
int n,
int k,
float *A,
int lda,
const float *tau,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDorgqr(
cusolverDnHandle_t handle,
int m,
int n,
int k,
double *A,
int lda,
const double *tau,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCungqr(
cusolverDnHandle_t handle,
int m,
int n,
int k,
cuComplex *A,
int lda,
const cuComplex *tau,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZungqr(
cusolverDnHandle_t handle,
int m,
int n,
int k,
cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function overwrites m×n matrix A by
where Q is a unitary matrix formed by a sequence of elementary reflection vectors stored in A.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by orgqr_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user can combine geqrf, orgqr to complete orthogonalization. Please visit cuSOLVER Library Samples - orgqr for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| m | host | input | Number of rows of matrix Q. m >= 0; |
| n | host | input | Number of columns of matrix Q. m >= n >= 0; |
| k | host | input | Number of elementary relfections whose product defines the matrix Q. n >= k >= 0; |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). i-th column of A contains elementary reflection vector. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= max(1,m). |
| tau | device | output | <type> array of dimension k. tau(i) is the scalar of i-th elementary reflection vector. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working array work. |
| devInfo | device | output | If info = 0, the orgqr is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n,k<0, n>m, k>n or lda<m). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.18. cusolverDn<t>sytrf()
cusolverStatus_t
cusolverDnSsytrf_bufferSize(cusolverDnHandle_t handle,
int n,
float *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnDsytrf_bufferSize(cusolverDnHandle_t handle,
int n,
double *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnCsytrf_bufferSize(cusolverDnHandle_t handle,
int n,
cuComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnZsytrf_bufferSize(cusolverDnHandle_t handle,
int n,
cuDoubleComplex *A,
int lda,
int *Lwork );
cusolverStatus_t
cusolverDnSsytrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
int *ipiv,
float *work,
int lwork,
int *devInfo );
cusolverStatus_t
cusolverDnDsytrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
int *ipiv,
double *work,
int lwork,
int *devInfo );
cusolverStatus_t
cusolverDnCsytrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
int *ipiv,
cuComplex *work,
int lwork,
int *devInfo );
cusolverStatus_t
cusolverDnZsytrf(cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
int *ipiv,
cuDoubleComplex *work,
int lwork,
int *devInfo );
This function computes the Bunch-Kaufman factorization of a n×n symmetric indefinite matrix
A is a n×n symmetric matrix, only lower or upper part is meaningful. The input parameter uplo which part of the matrix is used. The function would leave other part untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular factor L and block diagonal matrix D. Each block of D is either 1x1 or 2x2 block, depending on pivoting.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular factor U and block diagonal matrix D.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by sytrf_bufferSize().
If Bunch-Kaufman factorization failed, i.e. A is singular. The output parameter devInfo = i would indicate D(i,i)=0.
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
The output parameter devIpiv contains pivoting sequence. If devIpiv(i) = k > 0, D(i,i) is 1x1 block, and i-th row/column of A is interchanged with k-th row/column of A. If uplo is CUBLAS_FILL_MODE_UPPER and devIpiv(i-1) = devIpiv(i) = -m < 0, D(i-1:i,i-1:i) is a 2x2 block, and (i-1)-th row/column is interchanged with m-th row/column. If uplo is CUBLAS_FILL_MODE_LOWER and devIpiv(i+1) = devIpiv(i) = -m < 0, D(i:i+1,i:i+1) is a 2x2 block, and (i+1)-th row/column is interchanged with m-th row/column.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | output | Array of size at least n, containing pivot indices. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working space work. |
| devInfo | device | output | if devInfo = 0, the LU factorization is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i, the D(i,i) = 0. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.19. cusolverDn<t>potrfBatched()
cusolverStatus_t
cusolverDnSpotrfBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *Aarray[],
int lda,
int *infoArray,
int batchSize);
cusolverStatus_t
cusolverDnDpotrfBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *Aarray[],
int lda,
int *infoArray,
int batchSize);
cusolverStatus_t
cusolverDnCpotrfBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *Aarray[],
int lda,
int *infoArray,
int batchSize);
cusolverStatus_t
cusolverDnZpotrfBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *Aarray[],
int lda,
int *infoArray,
int batchSize);
This function computes the Cholesky factorization of a squence of Hermitian positive-definite matrices.
Each Aarray[i] for i=0,1,..., batchSize-1 is a n×n Hermitian matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular Cholesky factor L.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular Cholesky factor U.
If Cholesky factorization failed, i.e. some leading minor of A is not positive definite, or equivalently some diagonal elements of L or U is not a real number. The output parameter infoArray would indicate smallest leading minor of A which is not positive definite.
infoArray is an integer array of size batchsize. If potrfBatched returns CUSOLVER_STATUS_INVALID_VALUE, infoArray[0] = -i (less than zero), meaning that the i-th parameter is wrong (not counting handle). If potrfBatched returns CUSOLVER_STATUS_SUCCESS but infoArray[i] = k is positive, then i-th matrix is not positive definite and the Cholesky factorization failed at row k.
Remark: the other part of A is used as a workspace. For example, if uplo is CUBLAS_FILL_MODE_UPPER, upper triangle of A contains cholesky factor U and lower triangle of A is destroyed after potrfBatched.
Please visit cuSOLVER Library Samples - potrfBatched for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if lower or upper part is stored; the other part is used as a workspace. |
| n | host | input | Number of rows and columns of matrix A. |
| Aarray | device | in/out | Array of pointers to <type> array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store each matrix Aarray[i]. |
| infoArray | device | output | Array of size batchSize. infoArray[i] contains information of factorization of Aarray[i]. if potrfBatched returns CUSOLVER_STATUS_INVALID_VALUE, infoArray[0] = -i (less than zero) means the i-th parameter is wrong (not counting handle). if potrfBatched returns CUSOLVER_STATUS_SUCCESS, infoArray[i] = 0 means the Cholesky factorization of i-th matrix is successful, and infoArray[i] = k means the leading submatrix of order k of i-th matrix is not positive definite. |
| batchSize | host | input | Number of pointers in Aarray. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n) or batchSize<1). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.2.20. cusolverDn<t>potrsBatched()
cusolverStatus_t
cusolverDnSpotrsBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
float *Aarray[],
int lda,
float *Barray[],
int ldb,
int *info,
int batchSize);
cusolverStatus_t
cusolverDnDpotrsBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
double *Aarray[],
int lda,
double *Barray[],
int ldb,
int *info,
int batchSize);
cusolverStatus_t
cusolverDnCpotrsBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
cuComplex *Aarray[],
int lda,
cuComplex *Barray[],
int ldb,
int *info,
int batchSize);
cusolverStatus_t
cusolverDnZpotrsBatched(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
int nrhs,
cuDoubleComplex *Aarray[],
int lda,
cuDoubleComplex *Barray[],
int ldb,
int *info,
int batchSize);
This function solves a squence of linear systems
where each Aarray[i] for i=0,1,..., batchSize-1 is a n×n Hermitian matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used.
The user has to call potrfBatched first to factorize matrix Aarray[i]. If input parameter uplo is CUBLAS_FILL_MODE_LOWER, A is lower triangular Cholesky factor L correspoding to . If input parameter uplo is CUBLAS_FILL_MODE_UPPER, A is upper triangular Cholesky factor U corresponding to .
The operation is in-place, i.e. matrix X overwrites matrix B with the same leading dimension ldb.
The output parameter info is a scalar. If info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Remark 1: only nrhs=1 is supported.
Remark 2: infoArray from potrfBatched indicates if the matrix is positive definite. info from potrsBatched only shows which input parameter is wrong (not counting handle).
Remark 3: the other part of A is used as a workspace. For example, if uplo is CUBLAS_FILL_MODE_UPPER, upper triangle of A contains cholesky factor U and lower triangle of A is destroyed after potrsBatched.
Please visit cuSOLVER Library Samples - potrfBatched for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolveDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of columns of matrix X and B. |
| Aarray | device | in/out | Array of pointers to <type> array of dimension lda * n with lda is not less than max(1,n). Aarray[i] is either lower cholesky factor L or upper Cholesky factor U. |
| lda | host | input | Leading dimension of two-dimensional array used to store each matrix Aarray[i]. |
| Barray | device | in/out | Array of pointers to <type> array of dimension ldb * nrhs. ldb is not less than max(1,n). As an input, Barray[i] is right hand side matrix. As an output, Barray[i] is the solution matrix. |
| ldb | host | input | Leading dimension of two-dimensional array used to store each matrix Barray[i]. |
| info | device | output | If info = 0, all parameters are correct. if info = -i, the i-th parameter is wrong (not counting handle). |
| batchSize | host | input | Number of pointers in Aarray. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, nrhs<0, lda<max(1,n), ldb<max(1,n) or batchSize<0). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3. Dense Eigenvalue Solver Reference (legacy)
This chapter describes eigenvalue solver API of cuSolverDN, including bidiagonalization and SVD.
2.4.3.1. cusolverDn<t>gebrd()
cusolverStatus_t
cusolverDnSgebrd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *Lwork );
cusolverStatus_t
cusolverDnDgebrd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *Lwork );
cusolverStatus_t
cusolverDnCgebrd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *Lwork );
cusolverStatus_t
cusolverDnZgebrd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *Lwork );
cusolverStatus_t
cusolverDnSgebrd(cusolverDnHandle_t handle,
int m,
int n,
float *A,
int lda,
float *D,
float *E,
float *TAUQ,
float *TAUP,
float *Work,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnDgebrd(cusolverDnHandle_t handle,
int m,
int n,
double *A,
int lda,
double *D,
double *E,
double *TAUQ,
double *TAUP,
double *Work,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnCgebrd(cusolverDnHandle_t handle,
int m,
int n,
cuComplex *A,
int lda,
float *D,
float *E,
cuComplex *TAUQ,
cuComplex *TAUP,
cuComplex *Work,
int Lwork,
int *devInfo );
cusolverStatus_t
cusolverDnZgebrd(cusolverDnHandle_t handle,
int m,
int n,
cuDoubleComplex *A,
int lda,
double *D,
double *E,
cuDoubleComplex *TAUQ,
cuDoubleComplex *TAUP,
cuDoubleComplex *Work,
int Lwork,
int *devInfo );
This function reduces a general m×n matrix A to a real upper or lower bidiagonal form B by an orthogonal transformation:
If m>=n, B is upper bidiagonal; if m<n, B is lower bidiagonal.
The matrix Q and P are overwritten into matrix A in the following sense:
- if m>=n, the diagonal and the first superdiagonal are overwritten with the upper bidiagonal matrix B; the elements below the diagonal, with the array TAUQ, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the first superdiagonal, with the array TAUP, represent the orthogonal matrix P as a product of elementary reflectors.
- if m<n, the diagonal and the first subdiagonal are overwritten with the lower bidiagonal matrix B; the elements below the first subdiagonal, with the array TAUQ, represent the orthogonal matrix Q as a product of elementary reflectors, and the elements above the diagonal, with the array TAUP, represent the orthogonal matrix P as a product of elementary reflectors.
The user has to provide working space which is pointed by input parameter Work. The input parameter Lwork is size of the working space, and it is returned by gebrd_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
Remark: gebrd only supports m>=n.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| D | device | output | Real array of dimension min(m,n). The diagonal elements of the bidiagonal matrix B: D(i) = A(i,i). |
| E | device | output | Real array of dimension min(m,n). The off-diagonal elements of the bidiagonal matrix B: if m>=n, E(i) = A(i,i+1) for i = 1,2,...,n-1; if m<n, E(i) = A(i+1,i) for i = 1,2,...,m-1. |
| TAUQ | device | output | <type> array of dimension min(m,n). The scalar factors of the elementary reflectors which represent the orthogonal matrix Q. |
| TAUP | device | output | <type> array of dimension min(m,n). The scalar factors of the elementary reflectors which represent the orthogonal matrix P. |
| Work | device | in/out | Working space, <type> array of size Lwork. |
| Lwork | host | input | Size of Work, returned by gebrd_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0, or lda<max(1,m)). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.2. cusolverDn<t>orgbr()
cusolverStatus_t
cusolverDnSorgbr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
const float *A,
int lda,
const float *tau,
int *lwork);
cusolverStatus_t
cusolverDnDorgbr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
const double *A,
int lda,
const double *tau,
int *lwork);
cusolverStatus_t
cusolverDnCungbr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
const cuComplex *A,
int lda,
const cuComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnZungbr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnSorgbr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
float *A,
int lda,
const float *tau,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDorgbr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
double *A,
int lda,
const double *tau,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCungbr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
cuComplex *A,
int lda,
const cuComplex *tau,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZungbr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
int m,
int n,
int k,
cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function generates one of the unitary matrices Q or P**H determined by gebrd when reducing a matrix A to bidiagonal form:
Q and P**H are defined as products of elementary reflectors H(i) or G(i) respectively.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by orgbr_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| side | host | input | If side = CUBLAS_SIDE_LEFT, generate Q. if side = CUBLAS_SIDE_RIGHT, generate P**T. |
| m | host | input | Number of rows of matrix Q or P**T. |
| n | host | input | If side = CUBLAS_SIDE_LEFT, m>= n>= min(m,k). if side = CUBLAS_SIDE_RIGHT, n>= m>= min(n,k). |
| k | host | input | If side = CUBLAS_SIDE_LEFT, the number of columns in the original m-by-k matrix reduced by gebrd. if side = CUBLAS_SIDE_RIGHT, the number of rows in the original k-by-n matrix reduced by gebrd. |
| A | device | in/out | <type> array of dimension lda * n On entry, the vectors which define the elementary reflectors, as returned by gebrd. On exit, the m-by-n matrix Q or P**T. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= max(1,m); |
| tau | device | output | <type> array of dimension min(m,k) if side is CUBLAS_SIDE_LEFT; of dimension min(n,k) if side is CUBLAS_SIDE_RIGHT; tau(i) must contain the scalar factor of the elementary reflector H(i) or G(i), which determines Q or P**T, as returned by gebrd in its array argument TAUQ or TAUP. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working array work. |
| devInfo | device | output | If info = 0, the ormqr is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | the operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | the library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | invalid parameters were passed (m,n<0 or wrong lda ). |
| CUSOLVER_STATUS_ARCH_MISMATCH | the device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | an internal operation failed. |
2.4.3.3. cusolverDn<t>sytrd()
cusolverStatus_t
cusolverDnSsytrd_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *d,
const float *e,
const float *tau,
int *lwork);
cusolverStatus_t
cusolverDnDsytrd_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *d,
const double *e,
const double *tau,
int *lwork);
cusolverStatus_t
cusolverDnChetrd_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const float *d,
const float *e,
const cuComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnZhetrd_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const double *d,
const double *e,
const cuDoubleComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnSsytrd(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *d,
float *e,
float *tau,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDsytrd(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *d,
double *e,
double *tau,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnChetrd(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
float *d,
float *e,
cuComplex *tau,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t CUDENSEAPI cusolverDnZhetrd(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
double *d,
double *e,
cuDoubleComplex *tau,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function reduces a general symmetric (Hermitian) n×n matrix A to real symmetric tridiagonal form T by an orthogonal transformation:
As an output, A contains T and householder reflection vectors. If uplo = CUBLAS_FILL_MODE_UPPER, the diagonal and first superdiagonal of A are overwritten by the corresponding elements of the tridiagonal matrix T, and the elements above the first superdiagonal, with the array tau, represent the orthogonal matrix Q as a product of elementary reflectors; If uplo = CUBLAS_FILL_MODE_LOWER, the diagonal and first subdiagonal of A are overwritten by the corresponding elements of the tridiagonal matrix T, and the elements below the first subdiagonal, with the array tau, represent the orthogonal matrix Q as a product of elementary reflectors.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by sytrd_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (columns) of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A, and the strictly lower triangular part of A is not referenced. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A, and the strictly upper triangular part of A is not referenced. On exit, A is overwritten by T and householder reflection vectors. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= max(1,n). |
| D | device | output | Real array of dimension n. The diagonal elements of the tridiagonal matrix T: D(i) = A(i,i). |
| E | device | output | Real array of dimension (n-1). The off-diagonal elements of the tridiagonal matrix T: if uplo = CUBLAS_FILL_MODE_UPPER, E(i) = A(i,i+1). if uplo = CUBLAS_FILL_MODE_LOWERE(i) = A(i+1,i). |
| tau | device | output | <type> array of dimension (n-1). The scalar factors of the elementary reflectors which represent the orthogonal matrix Q. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by sytrd_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.4. cusolverDn<t>ormtr()
cusolverStatus_t
cusolverDnSormtr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
const float *A,
int lda,
const float *tau,
const float *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnDormtr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
const double *A,
int lda,
const double *tau,
const double *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnCunmtr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
const cuComplex *A,
int lda,
const cuComplex *tau,
const cuComplex *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnZunmtr_bufferSize(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
const cuDoubleComplex *C,
int ldc,
int *lwork);
cusolverStatus_t
cusolverDnSormtr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
float *A,
int lda,
float *tau,
float *C,
int ldc,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDormtr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
double *A,
int lda,
double *tau,
double *C,
int ldc,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCunmtr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
cuComplex *A,
int lda,
cuComplex *tau,
cuComplex *C,
int ldc,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZunmtr(
cusolverDnHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
int m,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *tau,
cuDoubleComplex *C,
int ldc,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function overwrites m×n matrix C by
where Q is a unitary matrix formed by a sequence of elementary reflection vectors from sytrd.
The operation on Q is defined by
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by ormtr_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| side | host | input | side = CUBLAS_SIDE_LEFT, apply Q or Q**T from the Left; side = CUBLAS_SIDE_RIGHT, apply Q or Q**T from the Right. |
| uplo | host | input | uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A contains elementary reflectors from sytrd. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A contains elementary reflectors from sytrd. |
| trans | host | input | Operation op(Q) that is non- or (conj.) transpose. |
| m | host | input | Number of rows of matrix C. |
| n | host | input | Number of columns of matrix C. |
| A | device | in/out | <type> array of dimension lda * m if side = CUBLAS_SIDE_LEFT; lda * n if side = CUBLAS_SIDE_RIGHT. The matrix A from sytrd contains the elementary reflectors. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. if side is CUBLAS_SIDE_LEFT, lda >= max(1,m); if side is CUBLAS_SIDE_RIGHT, lda >= max(1,n). |
| tau | device | output | <type> array of dimension (m-1) if side is CUBLAS_SIDE_LEFT; of dimension (n-1) if side is CUBLAS_SIDE_RIGHT; The vector tau is from sytrd, so tau(i) is the scalar of i-th elementary reflection vector. |
| C | device | in/out | <type> array of size ldc * n. On exit, C is overwritten by op(Q)*C or C*op(Q). |
| ldc | host | input | Leading dimension of two-dimensional array of matrix C. ldc >= max(1,m). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working array work. |
| devInfo | device | output | If devInfo = 0, the ormqr is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or wrong lda or ldc). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.5. cusolverDn<t>orgtr()
cusolverStatus_t
cusolverDnSorgtr_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *tau,
int *lwork);
cusolverStatus_t
cusolverDnDorgtr_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *tau,
int *lwork);
cusolverStatus_t
cusolverDnCungtr_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const cuComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnZungtr_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
int *lwork);
cusolverStatus_t
cusolverDnSorgtr(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
const float *tau,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDorgtr(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
const double *tau,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCungtr(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
const cuComplex *tau,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZungtr(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
const cuDoubleComplex *tau,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function generates a unitary matrix Q which is defined as the product of n-1 elementary reflectors of order n, as returned by sytrd:
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by orgtr_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle).
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A contains elementary reflectors from sytrd. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A contains elementary reflectors from sytrd. |
| n | host | input | Number of rows (columns) of matrix Q. |
| A | device | in/out | <type> array of dimension lda * n On entry, matrix A from sytrd contains the elementary reflectors. On exit, matrix A contains the n-by-n orthogonal matrix Q. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda >= max(1,n). |
| tau | device | output | <type> array of dimension (n-1)tau(i) is the scalar of i-th elementary reflection vector. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of working array work. |
| devInfo | device | output | If devInfo = 0, the orgtr is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or wrong lda ). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.6. cusolverDn<t>gesvd()
cusolverStatus_t
cusolverDnSgesvd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *lwork );
cusolverStatus_t
cusolverDnDgesvd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *lwork );
cusolverStatus_t
cusolverDnCgesvd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *lwork );
cusolverStatus_t
cusolverDnZgesvd_bufferSize(
cusolverDnHandle_t handle,
int m,
int n,
int *lwork );
cusolverStatus_t
cusolverDnSgesvd (
cusolverDnHandle_t handle,
signed char jobu,
signed char jobvt,
int m,
int n,
float *A,
int lda,
float *S,
float *U,
int ldu,
float *VT,
int ldvt,
float *work,
int lwork,
float *rwork,
int *devInfo);
cusolverStatus_t
cusolverDnDgesvd (
cusolverDnHandle_t handle,
signed char jobu,
signed char jobvt,
int m,
int n,
double *A,
int lda,
double *S,
double *U,
int ldu,
double *VT,
int ldvt,
double *work,
int lwork,
double *rwork,
int *devInfo);
cusolverStatus_t
cusolverDnCgesvd (
cusolverDnHandle_t handle,
signed char jobu,
signed char jobvt,
int m,
int n,
cuComplex *A,
int lda,
float *S,
cuComplex *U,
int ldu,
cuComplex *VT,
int ldvt,
cuComplex *work,
int lwork,
float *rwork,
int *devInfo);
cusolverStatus_t
cusolverDnZgesvd (
cusolverDnHandle_t handle,
signed char jobu,
signed char jobvt,
int m,
int n,
cuDoubleComplex *A,
int lda,
double *S,
cuDoubleComplex *U,
int ldu,
cuDoubleComplex *VT,
int ldvt,
cuDoubleComplex *work,
int lwork,
double *rwork,
int *devInfo);
This function computes the singular value decomposition (SVD) of a m×n matrix A and corresponding the left and/or right singular vectors. The SVD is written
where Σ is an m×n matrix which is zero except for its min(m,n) diagonal elements, U is an m×m unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by gesvd_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle). if bdsqr did not converge, devInfo specifies how many superdiagonals of an intermediate bidiagonal form did not converge to zero.
The rwork is real array of dimension (min(m,n)-1). If devInfo>0 and rwork is not nil, rwork contains the unconverged superdiagonal elements of an upper bidiagonal matrix. This is slightly different from LAPACK which puts unconverged superdiagonal elements in work if type is real; in rwork if type is complex. rwork can be a NULL pointer if the user does not want the information from supperdiagonal.
Please visit cuSOLVER Library Samples - gesvd for a code example.
Remark 1: gesvd only supports m>=n.
Remark 2: the routine returns , not V.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobu | host | input | Specifies options for computing all or part of the matrix U: = 'A': all m columns of U are returned in array U: = 'S': the first min(m,n) columns of U (the left singular vectors) are returned in the array U; = 'O': the first min(m,n) columns of U (the left singular vectors) are overwritten on the array A; = 'N': no columns of U (no left singular vectors) are computed. |
| jobvt | host | input | Specifies options for computing all or part of the matrix V**T: = 'A': all N rows of V**T are returned in the array VT; = 'S': the first min(m,n) rows of V**T (the right singular vectors) are returned in the array VT; = 'O': the first min(m,n) rows of V**T (the right singular vectors) are overwritten on the array A; = 'N': no rows of V**T (no right singular vectors) are computed. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| S | device | output | Real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| U | device | output | <type> array of dimension ldu * m with ldu is not less than max(1,m). U contains the m×m unitary matrix U. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix U. |
| VT | device | output | <type> array of dimension ldvt * n with ldvt is not less than max(1,n). VT contains the n×n unitary matrix V**T. |
| ldvt | host | input | Leading dimension of two-dimensional array used to store matrix Vt. |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by gesvd_bufferSize. |
| rwork | device | input | Real array of dimension min(m,n)-1. It contains the unconverged superdiagonal elements of an upper bidiagonal matrix if devInfo > 0. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). If devInfo > 0, devInfo indicates how many superdiagonals of an intermediate bidiagonal form did not converge to zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldvt<max(1,n) ). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.7. cusolverDnGesvd()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXgesvd() instead. The routine will be removed in the next major release.
cusolverStatus_t cusolverDnGesvd_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
signed char jobu,
signed char jobvt,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeS,
const void *S,
cudaDataType dataTypeU,
const void *U,
int64_t ldu,
cudaDataType dataTypeVT,
const void *VT,
int64_t ldvt,
cudaDataType computeType,
size_t *workspaceInBytes);
cusolverStatus_t CUSOLVERAPI cusolverDnGesvd(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
signed char jobu,
signed char jobvt,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeS,
void *S,
cudaDataType dataTypeU,
void *U,
int64_t ldu,
cudaDataType dataTypeVT,
void *VT,
int64_t ldvt,
cudaDataType computeType,
void *pBuffer,
size_t workspaceInBytes,
int *info);
This function computes the singular value decomposition (SVD) of a m×n matrix A and corresponding the left and/or right singular vectors. The SVD is written
where Σ is an m×n matrix which is zero except for its min(m,n) diagonal elements, U is an m×m unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytes of the working space, and it is returned by cusolverDnGesvd_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). if bdsqr did not converge, info specifies how many superdiagonals of an intermediate bidiagonal form did not converge to zero.
Currently, cusolverDnGesvd supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
Appendix G.5 provides a simple example of cusolverDnGesvd.
Remark 1: gesvd only supports m>=n.
Remark 2: the routine returns , not V.
List of input arguments for cusolverDnGesvd_bufferSize and cusolverDnGesvd:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | handle to the cuSolverDN library context. |
| params | host | input | structure with information collected by cusolverDnSetAdvOptions. |
| jobu | host | input | specifies options for computing all or part of the matrix U: = 'A': all m columns of U are returned in array U: = 'S': the first min(m,n) columns of U (the left singular vectors) are returned in the array U; = 'O': the first min(m,n) columns of U (the left singular vectors) are overwritten on the array A; = 'N': no columns of U (no left singular vectors) are computed. |
| jobvt | host | input | specifies options for computing all or part of the matrix V**T: = 'A': all N rows of V**T are returned in the array VT; = 'S': the first min(m,n) rows of V**T (the right singular vectors) are returned in the array VT; = 'O': the first min(m,n) rows of V**T (the right singular vectors) are overwritten on the array A; = 'N': no rows of V**T (no right singular vectors) are computed. |
| m | host | input | number of rows of matrix A. |
| n | host | input | number of columns of matrix A. |
| dataTypeA | host | input | data type of array A. |
| A | device | in/out | array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | leading dimension of two-dimensional array used to store matrix A. |
| dataTypeS | host | input | data type of array S. |
| S | device | output | real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| dataTypeU | host | input | data type of array U. |
| U | device | output | array of dimension ldu * m with ldu is not less than max(1,m). U contains the m×m unitary matrix U. |
| ldu | host | input | leading dimension of two-dimensional array used to store matrix U. |
| dataTypeVT | host | input | data type of array VT. |
| VT | device | output | array of dimension ldvt * n with ldvt is not less than max(1,n). VT contains the n×n unitary matrix V**T. |
| ldvt | host | input | leading dimension of two-dimensional array used to store matrix Vt. |
| computeType | host | input | data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | Size in bytes of pBuffer, returned by cusolverDnGesvd_bufferSize. |
| info | device | output | if info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info > 0, info indicates how many superdiagonals of an intermediate bidiagonal form did not converge to zero. |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeS is data type of the vector S and dataTypeU is data type of the matrix U, dataTypeVT is data type of the matrix VT, computeType is compute type of the operation. cusolverDnGesvd only supports the following four combinations.
| DataTypeA | DataTypeS | DataTypeU | DataTypeVT | ComputeType | Meaning |
|---|---|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SGESVD |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DGESVD |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CGESVD |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZGESVD |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldvt<max(1,n) ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.8. cusolverDn<t>gesvdj()
cusolverStatus_t
cusolverDnSgesvdj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
const float *A,
int lda,
const float *S,
const float *U,
int ldu,
const float *V,
int ldv,
int *lwork,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnDgesvdj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
const double *A,
int lda,
const double *S,
const double *U,
int ldu,
const double *V,
int ldv,
int *lwork,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnCgesvdj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
const cuComplex *A,
int lda,
const float *S,
const cuComplex *U,
int ldu,
const cuComplex *V,
int ldv,
int *lwork,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnZgesvdj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
const cuDoubleComplex *A,
int lda,
const double *S,
const cuDoubleComplex *U,
int ldu,
const cuDoubleComplex *V,
int ldv,
int *lwork,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnSgesvdj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
float *A,
int lda,
float *S,
float *U,
int ldu,
float *V,
int ldv,
float *work,
int lwork,
int *info,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnDgesvdj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
double *A,
int lda,
double *S,
double *U,
int ldu,
double *V,
int ldv,
double *work,
int lwork,
int *info,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnCgesvdj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
cuComplex *A,
int lda,
float *S,
cuComplex *U,
int ldu,
cuComplex *V,
int ldv,
cuComplex *work,
int lwork,
int *info,
gesvdjInfo_t params);
cusolverStatus_t
cusolverDnZgesvdj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int econ,
int m,
int n,
cuDoubleComplex *A,
int lda,
double *S,
cuDoubleComplex *U,
int ldu,
cuDoubleComplex *V,
int ldv,
cuDoubleComplex *work,
int lwork,
int *info,
gesvdjInfo_t params);
This function computes the singular value decomposition (SVD) of a m×n matrix A and corresponding the left and/or right singular vectors. The SVD is written:
where Σ is an m×n matrix which is zero except for its min(m,n) diagonal elements, U is an m×m unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
gesvdj has the same functionality as gesvd. The difference is that gesvd uses QR algorithm and gesvdj uses Jacobi method. The parallelism of Jacobi method gives GPU better performance on small and medium size matrices. Moreover the user can configure gesvdj to perform approximation up to certain accuracy.
gesvdj iteratively generates a sequence of unitary matrices to transform matrix A to the following form
where S is diagonal and diagonal of E is zero.
During the iterations, the Frobenius norm of E decreases monotonically. As E goes down to zero, S is the set of singular values. In practice, Jacobi method stops if
where eps is given tolerance.
gesvdj has two parameters to control the accuracy. First parameter is tolerance (eps). The default value is machine accuracy but The user can use function cusolverDnXgesvdjSetTolerance to set a priori tolerance. The second parameter is maximum number of sweeps which controls number of iterations of Jacobi method. The default value is 100 but the user can use function cusolverDnXgesvdjSetMaxSweeps to set a proper bound. The experimentis show 15 sweeps are good enough to converge to machine accuracy. gesvdj stops either tolerance is met or maximum number of sweeps is met.
Jacobi method has quadratic convergence, so the accuracy is not proportional to number of sweeps. To guarantee certain accuracy, the user should configure tolerance only.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by gesvdj_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = min(m,n)+1, gesvdj does not converge under given tolerance and maximum sweeps.
If the user sets an improper tolerance, gesvdj may not converge. For example, tolerance should not be smaller than machine accuracy.
Please visit cuSOLVER Library Samples - gesvdj for a code example.
Remark 1: gesvdj supports any combination of m and n.
Remark 2: the routine returns V, not . This is different from gesvd.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute singular value only or singular vectors as well: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute singular values only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute singular values and singular vectors. |
| econ | host | input | econ = 1 for economy size for U and V. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| S | device | output | Real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| U | device | output | <type> array of dimension ldu * m if econ is zero. If econ is nonzero, the dimension is ldu * min(m,n). U contains the left singular vectors. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix U. ldu is not less than max(1,m). |
| V | device | output | <type> array of dimension ldv * n if econ is zero. If econ is nonzero, the dimension is ldv * min(m,n). V contains the right singular vectors. |
| ldv | host | input | Leading dimension of two-dimensional array used to store matrix V. ldv is not less than max(1,n). |
| work | device | in/out | <type> array of size lwork, working space. |
| lwork | host | input | Size of work, returned by gesvdj_bufferSize. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info = min(m,n)+1, gesvdj dose not converge under given tolerance and maximum sweeps. |
| params | host | in/out | Structure filled with parameters of Jacobi algorithm and results of gesvdj. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldv<max(1,n) or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.9. cusolverDn<t>gesvdjBatched()
cusolverStatus_t
cusolverDnSgesvdjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
const float *A,
int lda,
const float *S,
const float *U,
int ldu,
const float *V,
int ldv,
int *lwork,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnDgesvdjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
const double *A,
int lda,
const double *S,
const double *U,
int ldu,
const double *V,
int ldv,
int *lwork,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnCgesvdjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
const cuComplex *A,
int lda,
const float *S,
const cuComplex *U,
int ldu,
const cuComplex *V,
int ldv,
int *lwork,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnZgesvdjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
const cuDoubleComplex *A,
int lda,
const double *S,
const cuDoubleComplex *U,
int ldu,
const cuDoubleComplex *V,
int ldv,
int *lwork,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnSgesvdjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
float *A,
int lda,
float *S,
float *U,
int ldu,
float *V,
int ldv,
float *work,
int lwork,
int *info,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnDgesvdjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
double *A,
int lda,
double *S,
double *U,
int ldu,
double *V,
int ldv,
double *work,
int lwork,
int *info,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnCgesvdjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
cuComplex *A,
int lda,
float *S,
cuComplex *U,
int ldu,
cuComplex *V,
int ldv,
cuComplex *work,
int lwork,
int *info,
gesvdjInfo_t params,
int batchSize);
cusolverStatus_t
cusolverDnZgesvdjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int m,
int n,
cuDoubleComplex *A,
int lda,
double *S,
cuDoubleComplex *U,
int ldu,
cuDoubleComplex *V,
int ldv,
cuDoubleComplex *work,
int lwork,
int *info,
gesvdjInfo_t params,
int batchSize);
This function computes singular values and singular vectors of a squence of general m×n matrices
where is a real m×n diagonal matrix which is zero except for its min(m,n) diagonal elements. (left singular vectors) is a m×m unitary matrix and (right singular vectors) is a n×n unitary matrix. The diagonal elements of are the singular values of in either descending order or non-sorting order.
gesvdjBatched performs gesvdj on each matrix. It requires that all matrices are of the same size m,n no greater than 32 and are packed in contiguous way,
|
|
Each matrix is column-major with leading dimension lda, so the formula for random access is .
The parameter S also contains singular values of each matrix in contiguous way,
|
|
The formula for random access of S is .
Except for tolerance and maximum sweeps, gesvdjBatched can either sort the singular values in descending order (default) or chose as-is (without sorting) by the function cusolverDnXgesvdjSetSortEig. If the user packs several tiny matrices into diagonal blocks of one matrix, non-sorting option can separate singular values of those tiny matrices.
gesvdjBatched cannot report residual and executed sweeps by function cusolverDnXgesvdjGetResidual and cusolverDnXgesvdjGetSweeps. Any call of the above two returns CUSOLVER_STATUS_NOT_SUPPORTED. The user needs to compute residual explicitly.
The user has to provide working space pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by gesvdjBatched_bufferSize().
The output parameter info is an integer array of size batchSize. If the function returns CUSOLVER_STATUS_INVALID_VALUE, the first element info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = min(m,n)+1, gesvdjBatched does not converge on i-th matrix under given tolerance and maximum sweeps.
Please visit cuSOLVER Library Samples - gesvdjBatched for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute singular value only or singular vectors as well: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute singular values only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute singular values and singular vectors. |
| m | host | input | Number of rows of matrix Aj. m is no greater than 32. |
| n | host | input | Number of columns of matrix Aj. n is no greater than 32. |
| A | device | in/out | <type> array of dimension lda * n * batchSize with lda is not less than max(1,n). on Exit: the contents of Aj are destroyed. |
| lda | host | input | Lading dimension of two-dimensional array used to store matrix Aj. |
| S | device | output | Areal array of dimension min(m,n)*batchSize. It stores the singular values of Aj in descending order or non-sorting order. |
| U | device | output | <type> array of dimension ldu * m * batchSize. Uj contains the left singular vectors of Aj. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix Uj. ldu is not less than max(1,m). |
| V | device | output | <type> array of dimension ldv * n * batchSize. Vj contains the right singular vectors of Aj. |
| ldv | host | input | Leading dimension of two-dimensional array used to store matrix Vj. ldv is not less than max(1,n). |
| work | device | in/out | <type> array of size lwork, working space. |
| lwork | host | input | Size of work, returned by gesvdjBatched_bufferSize. |
| info | device | output | An integer array of dimension batchSize. If CUSOLVER_STATUS_INVALID_VALUE is returned, info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = 0, the operation is successful. if info[i] = min(m,n)+1, gesvdjBatched dose not converge on i-th matrix under given tolerance and maximum sweeps. |
| params | host | in/out | Structure filled with parameters of Jacobi algorithm. |
| batchSize | host | input | Number of matrices. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldv<max(1,n) or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR , or batchSize<0 ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.10. cusolverDn<t>gesvdaStridedBatched()
cusolverStatus_t
cusolverDnSgesvdaStridedBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const float *A,
int lda,
long long int strideA,
const float *S,
long long int strideS,
const float *U,
int ldu,
long long int strideU,
const float *V,
int ldv,
long long int strideV,
int *lwork,
int batchSize);
cusolverStatus_t
cusolverDnDgesvdaStridedBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const double *A,
int lda,
long long int strideA,
const double *S,
long long int strideS,
const double *U,
int ldu,
long long int strideU,
const double *V,
int ldv,
long long int strideV,
int *lwork,
int batchSize);
cusolverStatus_t
cusolverDnCgesvdaStridedBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const cuComplex *A,
int lda,
long long int strideA,
const float *S,
long long int strideS,
const cuComplex *U,
int ldu,
long long int strideU,
const cuComplex *V,
int ldv,
long long int strideV,
int *lwork,
int batchSize);
cusolverStatus_t
cusolverDnZgesvdaStridedBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const cuDoubleComplex *A,
int lda,
long long int strideA,
const double *S,
long long int strideS,
const cuDoubleComplex *U,
int ldu,
long long int strideU,
const cuDoubleComplex *V,
int ldv,
long long int strideV,
int *lwork,
int batchSize);
cusolverStatus_t
cusolverDnSgesvdaStridedBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const float *A,
int lda,
long long int strideA,
float *S,
long long int strideS,
float *U,
int ldu,
long long int strideU,
float *V,
int ldv,
long long int strideV,
float *work,
int lwork,
int *info,
double *h_R_nrmF,
int batchSize);
cusolverStatus_t
cusolverDnDgesvdaStridedBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const double *A,
int lda,
long long int strideA,
double *S,
long long int strideS,
double *U,
int ldu,
long long int strideU,
double *V,
int ldv,
long long int strideV,
double *work,
int lwork,
int *info,
double *h_R_nrmF,
int batchSize);
cusolverStatus_t
cusolverDnCgesvdaStridedBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const cuComplex *A,
int lda,
long long int strideA,
float *S,
long long int strideS,
cuComplex *U,
int ldu,
long long int strideU,
cuComplex *V,
int ldv,
long long int strideV,
cuComplex *work,
int lwork,
int *info,
double *h_R_nrmF,
int batchSize);
cusolverStatus_t
cusolverDnZgesvdaStridedBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
int rank,
int m,
int n,
const cuDoubleComplex *A,
int lda,
long long int strideA,
double *S,
long long int strideS,
cuDoubleComplex *U,
int ldu,
long long int strideU,
cuDoubleComplex *V,
int ldv,
long long int strideV,
cuDoubleComplex *work,
int lwork,
int *info,
double *h_R_nrmF,
int batchSize);
This function gesvda (a stands for approximate) approximates the singular value decomposition of a tall skinny m×n matrix A and corresponding the left and right singular vectors. The economy form of SVD is written by
where Σ is an n×n matrix. U is an m×n unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. U and V are the left and right singular vectors of A.
gesvda computes eigenvalues of A**T*A to approximate singular values and singular vectors. It generates matrices U and V and transforms the matrix A to the following form
where S is diagonal and E depends on rounding errors. To certain conditions, U, V and S approximate singular values and singular vectors up to machine zero of single precision. In general, V is unitary, S is more accurate than U. If singular value is far from zero, then left singular vector U is accurate. In other words, the accuracy of singular values and left singular vectors depend on the distance between singular value and zero.
The input parameter rank decides the number of singualr values and singular vectors are computed in parameter S, U and V.
The output parameter h_RnrmF computes Frobenius norm of residual.
if the parameter rank is equal n. Otherwise, h_RnrmF reports
in Frobenius norm sense, that is, how far U is from unitary.
gesvdaStridedBatched performs gesvda on each matrix. It requires that all matrices are of the same size m,n and are packed in a contiguous way,
|
|
Each matrix is column-major with leading dimension lda, so the formula for random access is . Similarly, the formula for random access of S is , the formula for random access of U is and the formula for random access of V is .
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by gesvdaStridedBatched_bufferSize().
The output parameter info is an integer array of size batchSize. If the function returns CUSOLVER_STATUS_INVALID_VALUE, the first element info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = min(m,n)+1, gesvdaStridedBatched does not converge on i-th matrix under given tolerance.
Please visit cuSOLVER Library Samples - gesvdaStridedBatched for a code example.
Remark 1: the routine returns V, not . This is different from gesvd.
Remark 2: if the user is confident on the accuracy of singular values and singular vectors, for example, certain conditions hold (required singular value is far from zero), then the performance can be improved by passing a null pointer to h_RnrmF, i.e. no computation of residual norm.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute singular value only or singular vectors as well: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute singular values only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute singular values and singular vectors. |
| rank | host | input | Number of singular values (from largest to smallest). |
| m | host | input | Number of rows of matrix Aj. |
| n | host | input | Number of columns of matrix Aj. |
| A | device | input | <type> array of dimension strideA * batchSize with lda is not less than max(1,m). Aj is of dimension m * n. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix Aj. |
| strideA | host | input | Value of type long long int that gives the address offset between A[i] and A[i+1]. strideA is not less than lda*n. |
| S | device | output | A real array of dimension strideS*batchSize. It stores the singular values of Aj in descending order. Sj is of dimension rank * 1 |
| strideS | host | input | Value of type long long int that gives the address offset between S[i] and S[i+1]. strideS is not less than rank. |
| U | device | output | <type> array of dimension strideU * batchSize. Uj contains the left singular vectors of Aj. Uj is of dimension m * rank. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix Uj. ldu is not less than max(1,m). |
| strideU | host | input | Value of type long long int that gives the address offset between U[i] and U[i+1]. strideU is not less than ldu*rank. |
| V | device | output | <type> array of dimension strideV * batchSize. Vj contains the right singular vectors of Aj. Vj is of dimension n * rank. |
| ldv | host | input | Leading dimension of two-dimensional array used to store matrix Vj. ldv is not less than max(1,n). |
| strideV | host | input | Value of type long long int that gives the address offset between V[i] and V[i+1]. strideV is not less than ldv*rank. |
| work | device | in/out | <type> array of size lwork, working space. |
| lwork | host | input | Size of work, returned by gesvdaStridedBatched_bufferSize. |
| info | device | output | An integer array of dimension batchSize. If CUSOLVER_STATUS_INVALID_VALUE is returned, info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = 0, the operation is successful. if info[i] = min(m,n)+1, gesvdaStridedBatched dose not converge on i-th matrix. |
| h_RnrmF | host | output | <double> array of size batchSize. h_RnrmF[i] is norm of residual of i-th matrix. |
| batchSize | host | input | Number of matrices. batchSize is not less than 1. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldv<max(1,n) or strideA<lda*n or strideS<rank or strideU<ldu*rank or strideV<ldv*rank or batchSize<1 or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.11. cusolverDn<t>syevd()
cusolverStatus_t
cusolverDnSsyevd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnDsyevd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnCheevd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnZheevd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnSsyevd(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *W,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDsyevd(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *W,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCheevd(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
float *W,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZheevd(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
double *W,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix A. The standard symmetric eigenvalue problem is
where Λ is a real n×n diagonal matrix. V is an n×n unitary matrix. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by syevd_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle). If devInfo = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Please visit cuSOLVER Library Samples - syevd for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (or columns) of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and devInfo = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, in ascending order ie, sorted so that W(i) <= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| Lwork | host | input | Size of work, returned by syevd_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i (> 0), devInfo indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero; |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.12. cusolverDnSyevd()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXsyevd() instead. The routine will be removed in the next major release.
cusolverStatus_t cusolverDnSyevd_bufferSize( cusolverDnHandle_t handle, cusolverParams_t params, cusolverEigMode_t jobz, cublasFillMode_t uplo, int n, cudaDataType dataTypeA, const void *A, int64_t lda, cudaDataType dataTypeW, const void *W, cudaDataType computeType, size_t *workspaceInBytes);
cusolverStatus_t cusolverDnSyevd( cusolverDnHandle_t handle, cusolverParams_t params, cusolverEigMode_t jobz, cublasFillMode_t uplo, int n, cudaDataType dataTypeA, const void *A, int64_t lda, cudaDataType dataTypeW, const void *W, cudaDataType computeType, void *pBuffer, size_t workspaceInBytes, int *info);
computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix A using the generic API interface. The standard symmetric eigenvalue problem is
where Λ is a real n×n diagonal matrix. V is an n×n unitary matrix. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytes of the working space, and it is returned by cusolverDnSyevd_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
if jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Currently, cusolverDnSyevd supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnSyevd_bufferSize and cusolverDnSyevd:
| parameter | Memory | In/out | Meaning |
| handle | host | input | handle to the cuSolverDN library context. |
| params | host | input | structure with information collected by cusolverDnSetAdvOptions. |
| jobz | host | input | specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | number of rows (or columns) of matrix A. |
| dataTypeA | host | in | data type of array A. |
| A | device | in/out | array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | leading dimension of two-dimensional array used to store matrix A. |
| dataTypeW | host | in | data type of array W. |
| W | device | output | a real array of dimension n. The eigenvalue values of A, in ascending order ie, sorted so that W(i) <= W(i+1). |
| computeType | host | in | data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | Size in bytes of pBuffer, returned by cusolverDnSyevd_bufferSize. |
| info | device | output | if info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info = i (> 0), info indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero; |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeW is data type of the matrix W and computeType is compute type of the operation. cusolverDnSyevd only supports the following four combinations.
| DataTypeA | DataTypeW | ComputeType | Meaning |
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SSYEVD |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DSYEVD |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CHEEVD |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | ZHEEVD |
| CUSOLVER_STATUS_SUCCESS | the operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | the library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | the device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | an internal operation failed. |
2.4.3.13. cusolverDn<t>syevdx()
cusolverStatus_t
cusolverDnSsyevdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
float vl,
float vu,
int il,
int iu,
int *h_meig,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnDsyevdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
double vl,
double vu,
int il,
int iu,
int *h_meig,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnCheevdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
float vl,
float vu,
int il,
int iu,
int *h_meig,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnZheevdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
double vl,
double vu,
int il,
int iu,
int *h_meig,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnSsyevdx(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float vl,
float vu,
int il,
int iu,
int *h_meig,
float *W,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDsyevdx(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double vl,
double vu,
int il,
int iu,
int *h_meig,
double *W,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnCheevdx(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
float vl,
float vu,
int il,
int iu,
int *h_meig,
float *W,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZheevdx(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
double vl,
double vu,
int il,
int iu,
int *h_meig,
double *W,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function computes all or selection of the eigenvalues and optionally eigenvectors of a symmetric (Hermitian) n×n matrix A. The standard symmetric eigenvalue problem is:
where Λ is a real n×h_meig diagonal matrix. V is an n×h_meig unitary matrix. h_meig is the number of eigenvalues/eigenvectors computed by the routine, h_meig is equal to n when the whole spectrum (e.g., range = CUSOLVER_EIG_RANGE_ALL) is requested. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by syevdx_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle). If devInfo = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Please visit cuSOLVER Library Samples - syevdx for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| range | host | input | Specifies options to which selection of eigenvalues and optionally eigenvectors that need to be computed: range = CUSOLVER_EIG_RANGE_ALL : all eigenvalues/eigenvectors will be found, will becomes the classical syevd/heevd routine; range = CUSOLVER_EIG_RANGE_V : all eigenvalues/eigenvectors in the half-open interval (vl,vu] will be found; range = CUSOLVER_EIG_RANGE_I : the il-th through iu-th eigenvalues/eigenvectors will be found; |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (or columns) of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and devInfo = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A.lda is not less than max(1,n). |
| vl,vu | host | input | Real values float or double for (C, S) or (Z, D) precision respectively. If range = CUSOLVER_EIG_RANGE_V, the lower and upper bounds of the interval to be searched for eigenvalues. vl > vu. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_I. Note that, if eigenvalues are very close to each other, it is well known that two different eigenvalues routines might find slightly different number of eigenvalues inside the same interval. This is due to the fact that different eigenvalue algorithms, or even same algorithm but different run might find eigenvalues within some rounding error close to the machine precision. Thus, if the user wants to be sure not to miss any eigenvalue within the interval bound, we suggest that the user substract/add epsilon (machine precision) to the interval bound such as (vl=vl-eps, vu=vu+eps]. This suggestion is valid for any selective routine from cuSolver or LAPACK. |
| il,iu | host | input | Integer. If range = CUSOLVER_EIG_RANGE_I, the indices (in ascending order) of the smallest and largest eigenvalues to be returned. 1 <= il <= iu <= n, if n > 0; il = 1 and iu = 0 if n = 0. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_V. |
| h_meig | host | output | Integer. The total number of eigenvalues found. 0 <= h_meig <= n. If range = CUSOLVER_EIG_RANGE_ALL, h_meig = n, and if range = CUSOLVER_EIG_RANGE_I, h_meig = iu-il+1. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, in ascending order ie, sorted so that W(i) <= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by syevdx_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). if devInfo = i (> 0), devInfo indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or range is not CUSOLVER_EIG_RANGE_ALL or CUSOLVER_EIG_RANGE_V or CUSOLVER_EIG_RANGE_I, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.14. cusolverDnSyevdx()[DEPRECATED]
[[DEPRECATED]] use cusolverDnXsyevdx() instead. The routine will be removed in the next major release.
cusolverStatus_t cusolverDnSyevdx_bufferSize( cusolverDnHandle_t handle, cusolverParams_t params, cusolverEigMode_t jobz, cusolverEigRange_t range, cublasFillMode_t uplo, int n, cudaDataType dataTypeA, const void *A, int64_t lda, void *vl, void *vu, int64_t il, int64_t iu, int64_t *h_meig, cudaDataType dataTypeW, const void *W, cudaDataType computeType, size_t *workspaceInBytes);
cusolverStatus_t cusolverDnSyevdx ( cusolverDnHandle_t handle, cusolverParams_t params, cusolverEigMode_t jobz, cusolverEigRange_t range, cublasFillMode_t uplo, int n, cudaDataType dataTypeA, const void *A, int64_t lda, void *vl, void *vu, int64_t il, int64_t iu, int64_t *h_meig, cudaDataType dataTypeW, const void *W, cudaDataType computeType, void *pBuffer, size_t workspaceInBytes, int *info);
computes all or selection of the eigenvalues and optionally eigenvectors of a symmetric (Hermitian) n×n matrix A using the generic API interface. The standard symmetric eigenvalue problem is
where Λ is a real n×h_meig diagonal matrix. V is an n×h_meig unitary matrix. h_meig is the number of eigenvalues/eigenvectors computed by the routine, h_meig is equal to n when the whole spectrum (e.g., range = CUSOLVER_EIG_RANGE_ALL) is requested. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide working space which is pointed by input parameter pBuffer. The input parameter workspaceInBytes is size in bytesr of the working space, and it is returned by cusolverDnSyevdx_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
if jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Currently, cusolverDnSyevdx supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnSyevdx_bufferSize and cusolverDnSyevdx:
| parameter | Memory | In/out | Meaning |
| handle | host | input | handle to the cuSolverDN library context. |
| params | host | input | structure with information collected by cusolverDnSetAdvOptions. |
| jobz | host | input | specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| range | host | input | specifies options to which selection of eigenvalues and optionally eigenvectors that need to be computed: range = CUSOLVER_EIG_RANGE_ALL : all eigenvalues/eigenvectors will be found, will becomes the classical syevd/heevd routine; range = CUSOLVER_EIG_RANGE_V : all eigenvalues/eigenvectors in the half-open interval (vl,vu] will be found; range = CUSOLVER_EIG_RANGE_I : the il-th through iu-th eigenvalues/eigenvectors will be found; |
| uplo | host | input | specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | number of rows (or columns) of matrix A. |
| dataTypeA | host | in | data type of array A. |
| A | device | in/out | array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | leading dimension of two-dimensional array used to store matrix A.lda is not less than max(1,n). |
| vl,vu | host | input | If range = CUSOLVER_EIG_RANGE_V, the lower and upper bounds of the interval to be searched for eigenvalues. vl > vu. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_I. Note that, if eigenvalues are very close to each other, it is well known that two different eigenvalues routines might find slightly different number of eigenvalues inside the same interval. This is due to the fact that different eigenvalue algorithms, or even same algorithm but different run might find eigenvalues within some rounding error close to the machine precision. Thus, if the user want to be sure not to miss any eigenvalue within the interval bound, we suggest that, the user substract/add epsilon (machine precision) to the interval bound such as (vl=vl-eps, vu=vu+eps]. this suggestion is valid for any selective routine from cuSolver or LAPACK. |
| il,iu | host | input | integer. If range = CUSOLVER_EIG_RANGE_I, the indices (in ascending order) of the smallest and largest eigenvalues to be returned. 1 <= il <= iu <= n, if n > 0; il = 1 and iu = 0 if n = 0. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_V. |
| h_meig | host | output | integer. The total number of eigenvalues found. 0 <= h_meig <= n. If range = CUSOLVER_EIG_RANGE_ALL, h_meig = n, and if range = CUSOLVER_EIG_RANGE_I, h_meig = iu-il+1. |
| dataTypeW | host | in | data type of array W. |
| W | device | output | a real array of dimension n. The eigenvalue values of A, in ascending order ie, sorted so that W(i) <= W(i+1). |
| computeType | host | in | data type of computation. |
| pBuffer | device | in/out | Working space. Array of type void of size workspaceInBytes bytes. |
| workspaceInBytes | host | input | Size in bytes of pBuffer, returned by cusolverDnSyevdx_bufferSize. |
| info | device | output | if info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info = i (> 0), info indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero; |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeW is data type of the matrix W and computeType is compute type of the operation. cusolverDnSyevdx only supports the following four combinations.
| DataTypeA | DataTypeW | ComputeType | Meaning |
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SSYEVDX |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DSYEVDX |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CHEEVDX |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | ZHEEVDX |
| CUSOLVER_STATUS_SUCCESS | the operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | the library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or range is not CUSOLVER_EIG_RANGE_ALL or CUSOLVER_EIG_RANGE_V or CUSOLVER_EIG_RANGE_I, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | the device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | an internal operation failed. |
2.4.3.15. cusolverDn<t>sygvd()
cusolverStatus_t
cusolverDnSsygvd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *B,
int ldb,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnDsygvd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *B,
int ldb,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnChegvd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const cuComplex *B,
int ldb,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnZhegvd_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *B,
int ldb,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnSsygvd(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *B,
int ldb,
float *W,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDsygvd(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *B,
int ldb,
double *W,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnChegvd(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
cuComplex *B,
int ldb,
float *W,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZhegvd(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *B,
int ldb,
double *W,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix-pair (A,B). The generalized symmetric-definite eigenvalue problem is
where the matrix B is positive definite. Λ is a real n×n diagonal matrix. The diagonal elements of Λ are the eigenvalues of (A, B) in ascending order. V is an n×n orthogonal matrix. The eigenvectors are normalized as follows:
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by sygvd_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle). If devInfo = i (i > 0 and i<=n) and jobz = CUSOLVER_EIG_MODE_NOVECTOR, i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. If devInfo = N + i (i > 0), then the leading minor of order i of B is not positive definite. The factorization of B could not be completed and no eigenvalues or eigenvectors were computed.
if jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthogonal eigenvectors of the matrix A. The eigenvectors are computed by divide and conquer algorithm.
Please visit cuSOLVER Library Samples - sygvd for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| itype | host | input | Specifies the problem type to be solved:
|
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of A and B are stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A and B are stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A and B are stored. |
| n | host | input | Number of rows (or columns) of matrix A and B. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and devInfo = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda is not less than max(1,n). |
| B | device | in/out | <type> array of dimension ldb * n. If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of B contains the upper triangular part of the matrix B. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of B contains the lower triangular part of the matrix B. On exit, if devInfo is less than n, B is overwritten by triangular factor U or L from the Cholesky factorization of B. |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. ldb is not less than max(1,n). |
| W | device | output | A real array of dimension n. The eigenvalue values of A, sorted so that W(i) >= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| Lwork | host | input | Size of work, returned by sygvd_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). If devInfo = i (> 0), devInfo indicates either potrf or syevd is wrong. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or ldb<max(1,n), or itype is not 1, 2 or 3, or jobz is not 'N' or 'V', or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.16. cusolverDn<t>sygvdx()
cusolverStatus_t
cusolverDnSsygvdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *B,
int ldb,
float vl,
float vu,
int il,
int iu,
int *h_meig,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnDsygvdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *B,
int ldb,
double vl,
double vu,
int il,
int iu,
int *h_meig,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnChegvdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const cuComplex *B,
int ldb,
float vl,
float vu,
int il,
int iu,
int *h_meig,
const float *W,
int *lwork);
cusolverStatus_t
cusolverDnZhegvdx_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *B,
int ldb,
double vl,
double vu,
int il,
int iu,
int *h_meig,
const double *W,
int *lwork);
cusolverStatus_t
cusolverDnSsygvdx(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *B,
int ldb,
float vl,
float vu,
int il,
int iu,
int *h_meig,
float *W,
float *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnDsygvdx(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *B,
int ldb,
double vl,
double vu,
int il,
int iu,
int *h_meig,
double *W,
double *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnChegvdx(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
cuComplex *B,
int ldb,
float vl,
float vu,
int il,
int iu,
int *h_meig,
float *W,
cuComplex *work,
int lwork,
int *devInfo);
cusolverStatus_t
cusolverDnZhegvdx(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *B,
int ldb,
double vl,
double vu,
int il,
int iu,
int *h_meig,
double *W,
cuDoubleComplex *work,
int lwork,
int *devInfo);
This function computes all or selection of the eigenvalues and optionally eigenvectors of a symmetric (Hermitian) n×n matrix-pair (A,B). The generalized symmetric-definite eigenvalue problem is
where the matrix B is positive definite. Λ is a real n×h_meig diagonal matrix. The diagonal elements of Λ are the eigenvalues of (A, B) in ascending order. V is an n×h_meig orthogonal matrix. h_meig is the number of eigenvalues/eigenvectors computed by the routine, h_meig is equal to n when the whole spectrum (e.g., range = CUSOLVER_EIG_RANGE_ALL) is requested. The eigenvectors are normalized as follows:
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is size of the working space, and it is returned by sygvdx_bufferSize().
If output parameter devInfo = -i (less than zero), the i-th parameter is wrong (not counting handle). If devInfo = i (i > 0 and i<=n) and jobz = CUSOLVER_EIG_MODE_NOVECTOR, i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. If devInfo = n + i (i > 0), then the leading minor of order i of B is not positive definite. The factorization of B could not be completed and no eigenvalues or eigenvectors were computed.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthogonal eigenvectors of the matrix A. The eigenvectors are computed by divide and conquer algorithm.
Please visit cuSOLVER Library Samples - sygvdx for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| itype | host | input | Specifies the problem type to be solved:
|
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| range | host | input | Specifies options to which selection of eigenvalues and optionally eigenvectors that need to be computed: range = CUSOLVER_EIG_RANGE_ALL : all eigenvalues/eigenvectors will be found, will becomes the classical syevd/heevd routine; range = CUSOLVER_EIG_RANGE_V : all eigenvalues/eigenvectors in the half-open interval (vl,vu] will be found; range = CUSOLVER_EIG_RANGE_I : the il-th through iu-th eigenvalues/eigenvectors will be found; |
| uplo | host | input | Specifies which part of A and B are stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A and B are stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A and B are stored. |
| n | host | input | Number of rows (or columns) of matrix A and B. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and devInfo = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda is not less than max(1,n). |
| B | device | in/out | <type> array of dimension ldb * n. If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of B contains the upper triangular part of the matrix B. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of B contains the lower triangular part of the matrix B. On exit, if devInfo is less than n, B is overwritten by triangular factor U or L from the Cholesky factorization of B. |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. ldb is not less than max(1,n). |
| vl,vu | host | input | Real values float or double for (C, S) or (Z, D) precision respectively. If range = CUSOLVER_EIG_RANGE_V, the lower and upper bounds of the interval to be searched for eigenvalues. vl > vu. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_I. Note that, if eigenvalues are very close to each other, it is well known that two different eigenvalues routines might find slightly different number of eigenvalues inside the same interval. This is due to the fact that different eigenvalue algorithms, or even same algorithm but different run might find eigenvalues within some rounding error close to the machine precision. Thus, if the user want to be sure not to miss any eigenvalue within the interval bound, we suggest that, the user substract/add epsilon (machine precision) to the interval bound such as (vl=vl-eps, vu=vu+eps]. this suggestion is valid for any selective routine from cuSolver or LAPACK. |
| il,iu | host | input | Integer. If range = CUSOLVER_EIG_RANGE_I, the indices (in ascending order) of the smallest and largest eigenvalues to be returned. 1 <= il <= iu <= n, if n > 0; il = 1 and iu = 0 if n = 0. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_V. |
| h_meig | host | output | Integer. The total number of eigenvalues found. 0 <= h_meig <= n. If range = CUSOLVER_EIG_RANGE_ALL, h_meig = n, and if range = CUSOLVER_EIG_RANGE_I, h_meig = iu-il+1. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, sorted so that W(i) >= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by sygvdx_bufferSize. |
| devInfo | device | output | If devInfo = 0, the operation is successful. if devInfo = -i, the i-th parameter is wrong (not counting handle). If devInfo = i (> 0), devInfo indicates either potrf or syevd is wrong. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or ldb<max(1,n), or itype is not CUSOLVER_EIG_TYPE_1 or CUSOLVER_EIG_TYPE_2 or CUSOLVER_EIG_TYPE_3 or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTORL, or range is not CUSOLVER_EIG_RANGE_ALL or CUSOLVER_EIG_RANGE_V or CUSOLVER_EIG_RANGE_I, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.17. cusolverDn<t>syevj()
cusolverStatus_t
cusolverDnSsyevj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnDsyevj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnCheevj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const float *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnZheevj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const double *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnSsyevj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *W,
float *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnDsyevj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *W,
double *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnCheevj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
float *W,
cuComplex *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnZheevj(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
double *W,
cuDoubleComplex *work,
int lwork,
int *info,
syevjInfo_t params);
This function computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix A. The standard symmetric eigenvalue problem is
where Λ is a real n×n diagonal matrix. Q is an n×n unitary matrix. The diagonal elements of Λ are the eigenvalues of A in ascending order.
syevj has the same functionality as syevd. The difference is that syevd uses QR algorithm and syevj uses Jacobi method. The parallelism of Jacobi method gives GPU better performance on small and medium size matrices. Moreover the user can configure syevj to perform approximation up to certain accuracy.
How does it work?
syevj iteratively generates a sequence of unitary matrices to transform matrix A to the following form
where W is diagonal and E is symmetric without diagonal.
During the iterations, the Frobenius norm of E decreases monotonically. As E goes down to zero, W is the set of eigenvalues. In practice, Jacobi method stops if
where eps is the given tolerance.
syevj has two parameters to control the accuracy. First parameter is tolerance (eps). The default value is machine accuracy but The user can use function cusolverDnXsyevjSetTolerance to set a priori tolerance. The second parameter is maximum number of sweeps which controls number of iterations of Jacobi method. The default value is 100 but the user can use function cusolverDnXsyevjSetMaxSweeps to set a proper bound. The experimentis show 15 sweeps are good enough to converge to machine accuracy. syevj stops either tolerance is met or maximum number of sweeps is met.
The Jacobi method has quadratic convergence, so the accuracy is not proportional to number of sweeps. To guarantee certain accuracy, the user should configure tolerance only.
After syevj, the user can query residual by function cusolverDnXsyevjGetResidual and number of executed sweeps by function cusolverDnXsyevjGetSweeps. However the user needs to be aware that residual is the Frobenius norm of E, not accuracy of individual eigenvalue, i.e.
The same as syevd, the user has to provide working space pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by syevj_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = n+1, syevj does not converge under given tolerance and maximum sweeps.
If the user sets an improper tolerance, syevj may not converge. For example, tolerance should not be smaller than machine accuracy.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors V.
Please visit cuSOLVER Library Samples - syevj for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (or columns) of matrix A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, in ascending order ie, sorted so that W(i) <= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by syevj_bufferSize. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). If info = n+1, syevj does not converge under given tolerance and maximum sweeps. |
| params | host | in/out | Structure filled with parameters of Jacobi algorithm and results of syevj. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.18. cusolverDn<t>sygvj()
cusolverStatus_t
cusolverDnSsygvj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *B,
int ldb,
const float *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnDsygvj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *B,
int ldb,
const double *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnChegvj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const cuComplex *B,
int ldb,
const float *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnZhegvj_bufferSize(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const cuDoubleComplex *B,
int ldb,
const double *W,
int *lwork,
syevjInfo_t params);
cusolverStatus_t
cusolverDnSsygvj(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *B,
int ldb,
float *W,
float *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnDsygvj(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *B,
int ldb,
double *W,
double *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnChegvj(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
cuComplex *B,
int ldb,
float *W,
cuComplex *work,
int lwork,
int *info,
syevjInfo_t params);
cusolverStatus_t
cusolverDnZhegvj(
cusolverDnHandle_t handle,
cusolverEigType_t itype,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
cuDoubleComplex *B,
int ldb,
double *W,
cuDoubleComplex *work,
int lwork,
int *info,
syevjInfo_t params);
This function computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix-pair (A,B). The generalized symmetric-definite eigenvalue problem is
where the matrix B is positive definite. Λ is a real n×n diagonal matrix. The diagonal elements of Λ are the eigenvalues of (A, B) in ascending order. V is an n×n orthogonal matrix. The eigenvectors are normalized as follows:
This function has the same functionality as sygvd except that syevd in sygvd is replaced by syevj in sygvj. Therefore, sygvj inherits properties of syevj, the user can use cusolverDnXsyevjSetTolerance and cusolverDnXsyevjSetMaxSweeps to configure tolerance and maximum sweeps.
However the meaning of residual is different from syevj. sygvj first computes Cholesky factorization of matrix B,
transform the problem to standard eigenvalue problem, then calls syevj.
For example, the standard eigenvalue problem of type I is
where matrix M is symmtric
The residual is the result of syevj on matrix M, not A.
The user has to provide working space which is pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by sygvj_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (i > 0 and i<=n), B is not positive definite, the factorization of B could not be completed and no eigenvalues or eigenvectors were computed. If info = n+1, syevj does not converge under given tolerance and maximum sweeps. In this case, the eigenvalues and eigenvectors are still computed because non-convergence comes from improper tolerance of maximum sweeps.
if jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthogonal eigenvectors V.
Please visit cuSOLVER Library Samples - sygvj for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| itype | host | input | Specifies the problem type to be solved: itype=CUSOLVER_EIG_TYPE_1: A*x = (lambda)*B*x. itype=CUSOLVER_EIG_TYPE_2: A*B*x = (lambda)*x. itype=CUSOLVER_EIG_TYPE_3: B*A*x = (lambda)*x. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of A and B are stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A and B are stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A and B are stored. |
| n | host | input | Number of rows (or columns) of matrix A and B. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. lda is not less than max(1,n). |
| B | device | in/out | <type> array of dimension ldb * n. If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of B contains the upper triangular part of the matrix B. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of B contains the lower triangular part of the matrix B. On exit, if info is less than n, B is overwritten by triangular factor U or L from the Cholesky factorization of B. |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. ldb is not less than max(1,n). |
| W | device | output | A real array of dimension n. The eigenvalue values of A, sorted so that W(i) >= W(i+1). |
| work | device | in/out | Working space, <type> array of size lwork. |
| lwork | host | input | Size of work, returned by sygvj_bufferSize. |
| info | device | output | if info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). If info = i (> 0), info indicates either B is not positive definite or syevj (called by sygvj) does not converge. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or ldb<max(1,n), or itype is not 1, 2 or 3, or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.3.19. cusolverDn<t>syevjBatched()
cusolverStatus_t
cusolverDnSsyevjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
const float *W,
int *lwork,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnDsyevjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
const double *W,
int *lwork,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnCheevjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
const float *W,
int *lwork,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnZheevjBatched_bufferSize(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
const double *W,
int *lwork,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnSsyevjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
float *A,
int lda,
float *W,
float *work,
int lwork,
int *info,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnDsyevjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
double *A,
int lda,
double *W,
double *work,
int lwork,
int *info,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnCheevjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuComplex *A,
int lda,
float *W,
cuComplex *work,
int lwork,
int *info,
syevjInfo_t params,
int batchSize
);
cusolverStatus_t
cusolverDnZheevjBatched(
cusolverDnHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int n,
cuDoubleComplex *A,
int lda,
double *W,
cuDoubleComplex *work,
int lwork,
int *info,
syevjInfo_t params,
int batchSize
);
This function computes eigenvalues and eigenvectors of a squence of symmetric (Hermitian) n×n matrices
where is a real n×n diagonal matrix. is an n×n unitary matrix. The diagonal elements of are the eigenvalues of in either ascending order or non-sorting order.
syevjBatched performs syevj on each matrix. It requires that all matrices are of the same size n and are packed in contiguous way,
|
|
Each matrix is column-major with leading dimension lda, so the formula for random access is .
The parameter W also contains eigenvalues of each matrix in contiguous way,
|
|
The formula for random access of W is .
Except for tolerance and maximum sweeps, syevjBatched can either sort the eigenvalues in ascending order (default) or chose as-is (without sorting) by the function cusolverDnXsyevjSetSortEig. If the user packs several tiny matrices into diagonal blocks of one matrix, non-sorting option can separate spectrum of those tiny matrices.
syevjBatched cannot report residual and executed sweeps by function cusolverDnXsyevjGetResidual and cusolverDnXsyevjGetSweeps. Any call of the above two returns CUSOLVER_STATUS_NOT_SUPPORTED. The user needs to compute residual explicitly.
The user has to provide working space pointed by input parameter work. The input parameter lwork is the size of the working space, and it is returned by syevjBatched_bufferSize().
The output parameter info is an integer array of size batchSize. If the function returns CUSOLVER_STATUS_INVALID_VALUE, the first element info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = n+1, syevjBatched does not converge on i-th matrix under given tolerance and maximum sweeps.
If jobz = CUSOLVER_EIG_MODE_VECTOR, contains the orthonormal eigenvectors .
Please visit cuSOLVER Library Samples - syevjBatched for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of Aj is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of Aj is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of Aj is stored. |
| n | host | input | Number of rows (or columns) of matrix each Aj. |
| A | device | in/out | <type> array of dimension lda * n * batchSize with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of Aj contains the upper triangular part of the matrix Aj. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of Aj contains the lower triangular part of the matrix Aj. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info[j] = 0, Aj contains the orthonormal eigenvectors of the matrix Aj. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of Aj are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix Aj. |
| W | device | output | A real array of dimension n*batchSize. It stores the eigenvalues of Aj in ascending order or non-sorting order. |
| work | device | in/out | <type> array of size lwork, workspace. |
| lwork | host | input | Size of work, returned by syevjBatched_bufferSize. |
| info | device | output | An integer array of dimension batchSize. If CUSOLVER_STATUS_INVALID_VALUE is returned, info[0] = -i (less than zero) indicates i-th parameter is wrong (not counting handle). Otherwise, if info[i] = 0, the operation is successful. If info[i] = n+1, syevjBatched does not converge on i-th matrix under given tolerance and maximum sweeps. |
| params | host | in/out | Structure filled with parameters of Jacobi algorithm. |
| batchSize | host | input | Number of matrices. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER), or batchSize<0. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4. Dense Linear Solver Reference (64-bit API)
This section describes linear solver 64-bit API of cuSolverDN, including Cholesky factorization, LU with partial pivoting and QR factorization.
2.4.4.1. cusolverDnXpotrf()
cusolverStatus_t
cusolverDnXpotrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t
cusolverDnXpotrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info )
computes the Cholesky factorization of a Hermitian positive-definite matrix using the generic API interfacte.
A is a n×n Hermitian matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular Cholesky factor L.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular Cholesky factor U.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXpotrf_bufferSize().
If Cholesky factorization failed, i.e. some leading minor of A is not positive definite, or equivalently some diagonal elements of L or U is not a real number. The output parameter info would indicate smallest leading minor of A which is not positive definite.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnXpotrf supports only the default algorithm.
Please visit cuSOLVER Library Samples - Xpotrf for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXpotrf_bufferSize and cusolverDnXpotrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| computeType | host | in | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the Cholesky factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, the leading minor of order i is not positive definite. |
The generic API has two different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation. cusolverDnXpotrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SPOTRF |
| CUDA_R_64F | CUDA_R_64F | DPOTRF |
| CUDA_C_32F | CUDA_C_32F | CPOTRF |
| CUDA_C_64F | CUDA_C_64F | ZPOTRF |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.2. cusolverDnXpotrs()
cusolverStatus_t
cusolverDnXpotrs(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasFillMode_t uplo,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
int *info)
This function solves a system of linear equations
where A is a n×n Hermitian matrix, only lower or upper part is meaningful using the generic API interface. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
The user has to call cusolverDnXpotrf first to factorize matrix A. If input parameter uplo is CUBLAS_FILL_MODE_LOWER, A is lower triangular Cholesky factor L correspoding to . If input parameter uplo is CUBLAS_FILL_MODE_UPPER, A is upper triangular Cholesky factor U corresponding to .
The operation is in-place, i.e. matrix X overwrites matrix B with the same leading dimension ldb.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnXpotrs supports only the default algorithm.
Please visit cuSOLVER Library Samples - Xpotrf for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXpotrs:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolveDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of columns of matrix X and B. |
| dataTypeA | host | in | Data type of array A. |
| A | device | input | Array of dimension lda * n with lda is not less than max(1,n). A is either lower cholesky factor L or upper Cholesky factor U. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeB | host | in | Data type of array B. |
| B | device | in/out | Array of dimension ldb * nrhs. ldb is not less than max(1,n). As an input, B is right hand side matrix. As an output, B is the solution matrix. |
| info | device | output | If info = 0, the Cholesky factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types, dataTypeA is data type of the matrix A, dataTypeB is data type of the matrix B. cusolverDnXpotrs only supports the following four combinations.
| dataTypeA | dataTypeB | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SPOTRS |
| CUDA_R_64F | CUDA_R_64F | DPOTRS |
| CUDA_C_32F | CUDA_C_32F | CPOTRS |
| CUDA_C_64F | CUDA_C_64F | ZPOTRS |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, nrhs<0, lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.3. cusolverDnXgetrf()
cusolverStatus_t cusolverDnXgetrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t
cusolverDnXgetrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
int64_t *ipiv,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info )
computes the LU factorization of a m×n matrix
where A is a m×n matrix, P is a permutation matrix, L is a lower triangular matrix with unit diagonal, and U is an upper triangular matrix using the generic API interface.
If LU factorization failed, i.e. matrix A (U) is singular, The output parameter info=i indicates U(i,i) = 0.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
If ipiv is null, no pivoting is performed. The factorization is A=L*U, which is not numerically stable.
No matter LU factorization failed or not, the output parameter ipiv contains pivoting sequence, row i is interchanged with row ipiv(i).
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXgetrf_bufferSize().
The user can combine cusolverDnXgetrf and cusolverDnGetrs to complete a linear solver.
Currently, cusolverDnXgetrf supports two algorithms. To select legacy implementation, the user has to call cusolverDnSetAdvOptions.
Please visit cuSOLVER Library Samples - Xgetrf for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. The fastest, requires a large workspace of m*n elements. |
| CUSOLVER_ALG_1 | Legacy implementation |
List of input arguments for cusolverDnXgetrf_bufferSize and cusolverDnXgetrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | <type> array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | output | Array of size at least min(m,n), containing pivot indices. |
| computeType | host | in | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the LU factorization is successful. if info = -i, the i-th parameter is wrong (not counting handle). If info = i, the U(i,i) = 0. |
The generic API has two different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation. cusolverDnXgetrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SGETRF |
| CUDA_R_64F | CUDA_R_64F | DGETRF |
| CUDA_C_32F | CUDA_C_32F | CGETRF |
| CUDA_C_64F | CUDA_C_64F | ZGETRF |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.4. cusolverDnXgetrs()
cusolverStatus_t
cusolverDnXgetrs(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cublasOperation_t trans,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
const int64_t *ipiv,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
int *info )
This function solves a linear system of multiple right-hand sides
where A is a n×n matrix, and was LU-factored by cusolverDnXgetrf, that is, lower trianular part of A is L, and upper triangular part (including diagonal elements) of A is U. B is a n×nrhs right-hand side matrix using the generic API interface.
The input parameter trans is defined by
The input parameter ipiv is an output of cusolverDnXgetrf. It contains pivot indices, which are used to permutate right-hand sides.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user can combine cusolverDnXgetrf and cusolverDnXgetrs to complete a linear solver.
Currently, cusolverDnXgetrs supports only the default algorithm.
Please visit cuSOLVER Library Samples - Xgetrf for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXgetrss:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| trans | host | input | Operation op(A) that is non- or (conj.) transpose. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of right-hand sides. |
| dataTypeA | host | in | Data type of array A. |
| A | device | input | Array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | input | Array of size at least n, containing pivot indices. |
| dataTypeB | host | in | Data type of array B. |
| B | device | output | <type> array of dimension ldb * nrhs with ldb is not less than max(1,n). |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types: dataTypeA is data type of the matrix A and dataTypeB is data type of the matrix B. cusolverDnXgetrs only supports the following four combinations:
| DataTypeA | dataTypeB | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SGETRS |
| CUDA_R_64F | CUDA_R_64F | DGETRS |
| CUDA_C_32F | CUDA_C_32F | CGETRS |
| CUDA_C_64F | CUDA_C_64F | ZGETRS |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n) or ldb<max(1,n)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.5. cusolverDnXgeqrf()
cusolverStatus_t
cusolverDnXgeqrf_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeTau,
const void *tau,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t cusolverDnXgeqrf(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeTau,
void *tau,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info )
computes the QR factorization of a m×n matrix
where A is an m×n matrix, Q is a m×n matrix, and R is an n×n upper triangular matrix using the generic API interface.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXgeqrf_bufferSize().
The matrix R is overwritten in upper triangular part of A, including diagonal elements.
The matrix Q is not formed explicitly, instead, a sequence of householder vectors are stored in lower triangular part of A. The leading nonzero element of householder vector is assumed to be 1 such that output parameter TAU contains the scaling factor τ. If v is original householder vector, q is the new householder vector corresponding to τ, satisying the following relation
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnXgeqrf supports only the default algorithm.
Please visit cuSOLVER Library Samples - Xgeqrf for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXgeqrf_bufferSize and cusolverDnXgeqrf:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,m). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| TAU | device | output | Array of dimension at least min(m,n). |
| computeType | host | in | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the LU factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has two different types, dataTypeA is data type of the matrix A and array tau and computeType is compute type of the operation. cusolverDnXgeqrf only supports the following four combinations.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SGEQRF |
| CUDA_R_64F | CUDA_R_64F | DGEQRF |
| CUDA_C_32F | CUDA_C_32F | CGEQRF |
| CUDA_C_64F | CUDA_C_64F | ZGEQRF |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.6. cusolverDnXsytrs()
cusolverStatus_t
cusolverDnXsytrs_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
const int64_t *ipiv,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost);
cusolverStatus_t CUSOLVERAPI cusolverDnXsytrs(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
int64_t n,
int64_t nrhs,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
const int64_t *ipiv,
cudaDataType dataTypeB,
void *B,
int64_t ldb,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info);
solves a system of linear equations using the generic API interfacte.
A contains the factorization from cusolverDnXsytrf(), only lower or upper part is meaningful, the other part is not touched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, the details of the factorization are stores as:
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, the details of the factorization are stores as:
The user has to provide the pivot indices that can be otained by cusolverDnXsytrf() as well as device and host work spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice and workspaceInBytesOnHost are sizes in bytes of the device and host work spaces, and they are returned by cusolverDnXsytrs_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
List of input arguments for cusolverDnXsytrs_bufferSize and cusolverDnXsytrs:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| n | host | input | Number of rows and columns of matrix A. |
| nrhs | host | input | Number of right-hand sides. |
| dataTypeA | host | in | Data type of array A. |
| A | device | input | Array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| ipiv | device | input | Array of size at least n, containing pivot indices. |
| dataTypeB | host | in | Data type of array B. |
| B | device | in/out | Array of dimension ldb * nrhs with ldb is not less than max(1,nrhs). |
| ldb | host | input | Leading dimension of two-dimensional array used to store matrix B. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXsytrs_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXsytrs_bufferSize. |
| info | device | output | If info = 0, the Cholesky factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, the leading minor of order i is not positive definite. |
The generic API has two different types: dataTypeA is data type of the matrix A, dataTypeB is data type of the matrix A. cusolverDnXsytrs only supports the following four combinations:
| DataTypeA | DataTypeB | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SSYTRS |
| CUDA_R_64F | CUDA_R_64F | DSYTRS |
| CUDA_C_32F | CUDA_C_32F | CSYTRS |
| CUDA_C_64F | CUDA_C_64F | ZSYTRS |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | Data type is not supported. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.4.7. cusolverDnXtrtri()
cusolverStatus_t
cusolverDnXtrtri_bufferSize(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
cublasDiagType_t diag,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost);
The following routine:
cusolverStatus_t
cusolverDnXtrtri(
cusolverDnHandle_t handle,
cublasFillMode_t uplo,
cublasDiagType_t diag,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info);
computes the inverse of a triangular matrix using the generic API interfacte.
A is an n×n triangular matrix, only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other part untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular inverse.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular inverse.
The user has to provide device and host work spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice and workspaceInBytesOnHost are sizes in bytes of the device and host work spaces, and they are returned by cusolverDnXtrtri_bufferSize().
If matrix inversion fails, the output parameter info = i shows A(i,i) = 0.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Please visit cuSOLVER Library Samples - Xtrtri for a code example.
List of input arguments for cusolverDnXtrtri_bufferSize and cusolverDnXtrtri:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. |
| diag | host | input | The enumerated unit diagonal type. |
| n | host | input | Number of rows and columns of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,n). |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXtrtri_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXtrtri_bufferSize. |
| info | device | output | If info = 0, the matrix inversion succeeded. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, A(i,i) = 0. |
| DataTypeA | Meaning |
| CUDA_R_32F | STRTRI |
| CUDA_R_64F | DTRTRI |
| CUDA_C_32F | CTRTRI |
| CUDA_C_64F | ZTRTRI |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_NOT_SUPPORTED | Data type is not supported. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0 or lda<max(1,n)). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.5. Dense Eigenvalue Solver Reference (64-bit API)
This section describes eigenvalue solver API of cuSolverDN, including bidiagonalization and SVD.
2.4.5.1. cusolverDnXgesvd()
cusolverStatus_t
cusolverDnXgesvd_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
signed char jobu,
signed char jobvt,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeS,
const void *S,
cudaDataType dataTypeU,
const void *U,
int64_t ldu,
cudaDataType dataTypeVT,
const void *VT,
int64_t ldvt,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t
cusolverDnXgesvd(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
signed char jobu,
signed char jobvt,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeS,
void *S,
cudaDataType dataTypeU,
void *U,
int64_t ldu,
cudaDataType dataTypeVT,
void *VT,
int64_t ldvt,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info)
This function computes the singular value decomposition (SVD) of a m×n matrix A and corresponding the left and/or right singular vectors. The SVD is written
where Σ is an m×n matrix which is zero except for its min(m,n) diagonal elements, U is an m×m unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXgesvd_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). if bdsqr did not converge, info specifies how many superdiagonals of an intermediate bidiagonal form did not converge to zero.
Currently, cusolverDnXgesvd supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
Please visit cuSOLVER Library Samples - Xgesvd for a code example.
Remark 1: gesvd only supports m>=n.
Remark 2: the routine returns , not V.
List of input arguments for cusolverDnXgesvd_bufferSize and cusolverDnXgesvd:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| jobu | host | input | Specifies options for computing all or part of the matrix U: = 'A': all m columns of U are returned in array U: = 'S': the first min(m,n) columns of U (the left singular vectors) are returned in the array U; = 'O': the first min(m,n) columns of U (the left singular vectors) are overwritten on the array A; = 'N': no columns of U (no left singular vectors) are computed. |
| jobvt | host | input | Specifies options for computing all or part of the matrix V**T: = 'A': all N rows of V**T are returned in the array VT; = 'S': the first min(m,n) rows of V**T (the right singular vectors) are returned in the array VT; = 'O': the first min(m,n) rows of V**T (the right singular vectors) are overwritten on the array A; = 'N': no rows of V**T (no right singular vectors) are computed. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| dataTypeA | host | input | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeS | host | input | Data type of array S. |
| S | device | output | Real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| dataTypeU | host | input | Data type of array U. |
| U | device | output | Array of dimension ldu * m with ldu is not less than max(1,m). U contains the m×m unitary matrix U. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix U. |
| dataTypeVT | host | input | Data type of array VT. |
| VT | device | output | Array of dimension ldvt * n with ldvt is not less than max(1,n). VT contains the n×n unitary matrix V**T. |
| ldvt | host | input | Leading dimension of two-dimensional array used to store matrix Vt. |
| computeType | host | input | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Dize in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). if info > 0, info indicates how many superdiagonals of an intermediate bidiagonal form did not converge to zero. |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeS is data type of the vector S and dataTypeU is data type of the matrix U, dataTypeVT is data type of the matrix VT, computeType is compute type of the operation. cusolverDnXgesvd only supports the following four combinations.
| DataTypeA | DataTypeS | DataTypeU | DataTypeVT | ComputeType | Meaning |
|---|---|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SGESVD |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DGESVD |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CGESVD |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZGESVD |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldvt<max(1,n) ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.5.2. cusolverDnXgesvdp()
cusolverStatus_t
cusolverDnXgesvdp_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
int econ,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeS,
const void *S,
cudaDataType dataTypeU,
const void *U,
int64_t ldu,
cudaDataType dataTypeV,
const void *V,
int64_t ldv,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t
cusolverDnXgesvdp(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
int econ,
int64_t m,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeS,
void *S,
cudaDataType dataTypeU,
void *U,
int64_t ldu,
cudaDataType dataTypeV,
void *V,
int64_t ldv,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *d_info,
double *h_err_sigma)
This function computes the singular value decomposition (SVD) of a m×n matrix A and corresponding the left and/or right singular vectors. The SVD is written
where Σ is an m×n matrix which is zero except for its min(m,n) diagonal elements, U is an m×m unitary matrix, and V is an n×n unitary matrix. The diagonal elements of Σ are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
cusolverDnXgesvdp combines polar decomposition in [14] and cusolverDnXsyevd to compute SVD. It is much faster than cusolverDnXgesvd which is based on QR algorithm. However polar decomposition in [14] may not deliver a full unitary matrix when the matrix A has a singular value close to zero. To workaround the issue when the singular value is close to zero, we add a small perturbation so polar decomposition can deliver the correct result. The consequence is inaccurate singular values shifted by this perturbation. The output parameter h_err_sigma is the magnitude of this perturbation. In other words, h_err_sigma shows the accuracy of SVD.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXgesvdp_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnXgesvdp supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
Please visit cuSOLVER Library Samples - Xgesvdp for a code example.
Remark 1: gesvdp supports n>=m as well.
Remark 2: the routine returns V, not
List of input arguments for cusolverDnXgesvdp_bufferSize and cusolverDnXgesvdp:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| jobz | host | input |
Specifies options to either compute singular values only or compute singular vectors as well: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute singular values only. jobz = CUSOLVER_EIG_MODE_VECTOR : Compute singular values and singular vectors. |
| econ | host | input | econ = 1 for economy size for U and V. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| dataTypeA | host | input | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeS | host | input | Data type of array S. |
| S | device | output | Real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| dataTypeU | host | input | Data type of array U. |
| U | device | output | Array of dimension ldu * m with ldu is not less than max(1,m). U contains the m×m unitary matrix U. If econ=1, only reports first min(m,n) columns of U. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix U. |
| dataTypeV | host | input | Data type of array V. |
| V | device | output | Array of dimension ldv * n with ldv is not less than max(1,n). V contains the n×n unitary matrix V. if econ=1, only reports first min(m,n) columns of V. |
| ldv | host | input | Leading dimension of two-dimensional array used to store matrix V. |
| computeType | host | input | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). |
| h_err_sigma | host | output | Magnitude of the perturbation, showing the accuracy of SVD. |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeS is data type of the vector S and dataTypeU is data type of the matrix U, dataTypeV is data type of the matrix V, computeType is compute type of the operation. cusolverDnXgesvdp only supports the following four combinations:
| DataTypeA | DataTypeS | DataTypeU | DataTypeV | ComputeType | Meaning |
|---|---|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SGESVDP |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DGESVDP |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CGESVDP |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZGESVDP |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldv<max(1,n) ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.5.3. cusolverDnXgesvdr()
cusolverStatus_t cusolverDnXgesvdr_bufferSize ( cusolverDnHandle_t handle, cusolverDnParams_t params, signed char jobu, signed char jobv, int64_t m, int64_t n, int64_t k, int64_t p, int64_t niters, cudaDataType dataTypeA, const void *A, int64_t lda, cudaDataType dataTypeSrand, const void *Srand, cudaDataType dataTypeUrand, const void *Urand, int64_t ldUrand, cudaDataType dataTypeVrand, const void *Vrand, int64_t ldVrand, cudaDataType computeType, size_t *workspaceInBytesOnDevice, size_t *workspaceInBytesOnHost )
cusolverStatus_t cusolverDnXgesvdr( cusolverDnHandle_t handle, cusolverDnParams_t params, signed char jobu, signed char jobv, int64_t m, int64_t n, int64_t k, int64_t p, int64_t niters, cudaDataType dataTypeA, void *A, int64_t lda, cudaDataType dataTypeSrand, void *Srand, cudaDataType dataTypeUrand, void *Urand, int64_t ldUrand, cudaDataType dataTypeVrand, void *Vrand, int64_t ldVrand, cudaDataType computeType, void *bufferOnDevice, size_t workspaceInBytesOnDevice, void *bufferOnHost, size_t workspaceInBytesOnHost, int *d_info)
This function computes the approximated rank-k singular value decomposition (k-SVD) of an m×n matrix A and the corresponding left and/or right singular vectors. The k-SVD is written as
where Σ is a k×k matrix which is zero except for its diagonal elements, U is an m×k orthonormal matrix, and V is an k×n orthonormal matrix. The diagonal elements of Σ are the approximated singular values of A; they are real and non-negative, and are returned in descending order. The columns of U and V are the top-k left and right singular vectors of A.
cusolverDnXgesvdr implements randomized methods described in [15] to compute k-SVD that is accurate with high probablity if the conditions described in [15] hold. cusolverDnXgesvdr is intended to compute a very small portion of the spectrum (meaning that k is very small compared to min(m,n)). of A fast and with good quality, specially when the dimenions of the matrix are large.
The accuracy of the method depends on the spectrum of A, the number of power iterations niters, the oversampling parameter p and the ratio between p and the dimensions of the matrix A. Larger values of oversampling p or larger number of iterations niters might produce more accurate approximations, but it will also increase the run time of cusolverDnXgesvdr.
Our recommendation is to use two iterations and set the oversampling to at least 2k. Once the solver provides enough accuracy, adjust the values of k and niters for better performance.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXgesvdr_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
Currently, cusolverDnXgesvdr supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
Please visit cuSOLVER Library Samples - Xgesvdr for a code example.
Remark 1: gesvdr supports n>=m as well.
Remark 2: the routine returns V, not
List of input arguments for cusolverDnXgesvdr_bufferSize and cusolverDnXgesvdr:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| jobu | host | input | Specifies options for computing all or part of the matrix U: = 'S': the first k columns of U (the left singular vectors) are returned in the array U; = 'N': no columns of U (no left singular vectors) are computed. |
| jobv | host | input | Specifies options for computing all or part of the matrix V: = 'S': the first k rows of V (the right singular vectors) are returned in the array V; = 'N': no rows of V (no right singular vectors) are computed. |
| m | host | input | Number of rows of matrix A. |
| n | host | input | Number of columns of matrix A. |
| k | host | input | Rank of the k-SVD decomposition of matrix A. rank is less than min(m,n). |
| p | host | input | Oversampling. The size of the subspace will be (k + p). (k+p) is less than min(m,n). |
| niters | host | input | Number of iteration of power method. |
| dataTypeA | host | input | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,m). On exit, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeS | host | input | Data type of array S. |
| S | device | output | Real array of dimension min(m,n). The singular values of A, sorted so that S(i) >= S(i+1). |
| dataTypeU | host | input | Data type of array U. |
| U | device | output | Array of dimension ldu * m with ldu is not less than max(1,m). U contains the m×m unitary matrix U. if jobu=S, only reports first min(m,n) columns of U. |
| ldu | host | input | Leading dimension of two-dimensional array used to store matrix U. |
| dataTypeV | host | input | Data type of array V. |
| V | device | output | Array of dimension ldv * n with ldv is not less than max(1,n). V contains the n×n unitary matrix V. If jobv=S, only reports first min(m,n) columns of V. |
| ldv | host | input | Leading dimension of two-dimensional array used to store matrix V. |
| computeType | host | input | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXgesvdr_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXgesvdr_bufferSize. |
| d_info | device | output | If info = 0, the operation is successful. If info = -i, the i-th parameter is wrong (not counting handle). |
The generic API has five different types, dataTypeA is data type of the matrix A, dataTypeS is data type of the vector S and dataTypeU is data type of the matrix U, dataTypeV is data type of the matrix V, computeType is compute type of the operation. cusolverDnXgesvdr only supports the following four combinations.
| DataTypeA | DataTypeS | DataTypeU | DataTypeV | ComputeType | Meaning |
|---|---|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SGESVDR |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DGESVDR |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CGESVDR |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZGESVDR |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n<0 or lda<max(1,m) or ldu<max(1,m) or ldv<max(1,n) ). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.5.4. cusolverDnXsyevd()
cusolverStatus_t
cusolverDnXsyevd_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
cudaDataType dataTypeW,
const void *W,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t
cusolverDnXsyevd(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
cudaDataType dataTypeW,
void *W,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info)
computes eigenvalues and eigenvectors of a symmetric (Hermitian) n×n matrix A using the generic API interface. The standard symmetric eigenvalue problem is
where Λ is a real n×n diagonal matrix. V is an n×n unitary matrix. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXsyevd_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Please visit cuSOLVER Library Samples - Xsyevd for a code example.
Currently, cusolverDnXsyevd supports only the default algorithm.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXsyevd_bufferSize and cusolverDnXsyevd:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (or columns) of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A. |
| dataTypeW | host | in | Data type of array W. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, in ascending order, i.e., sorted so that W(i) <= W(i+1). |
| computeType | host | in | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the operation is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i (> 0), info indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeW is data type of the matrix W and computeType is compute type of the operation. cusolverDnXsyevd only supports the following four combinations.
| DataTypeA | DataTypeW | ComputeType | Meaning |
|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SSYEVD |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DSYEVD |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CHEEVD |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | ZHEEVD |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.4.5.5. cusolverDnXsyevdx()
cusolverStatus_t
cusolverDnXsyevdx_bufferSize(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
const void *A,
int64_t lda,
void *vl,
void *vu,
int64_t il,
int64_t iu,
int64_t *h_meig,
cudaDataType dataTypeW,
const void *W,
cudaDataType computeType,
size_t *workspaceInBytesOnDevice,
size_t *workspaceInBytesOnHost)
cusolverStatus_t CUSOLVERAPI cusolverDnXsyevdx(
cusolverDnHandle_t handle,
cusolverDnParams_t params,
cusolverEigMode_t jobz,
cusolverEigRange_t range,
cublasFillMode_t uplo,
int64_t n,
cudaDataType dataTypeA,
void *A,
int64_t lda,
void * vl,
void * vu,
int64_t il,
int64_t iu,
int64_t *meig64,
cudaDataType dataTypeW,
void *W,
cudaDataType computeType,
void *bufferOnDevice,
size_t workspaceInBytesOnDevice,
void *bufferOnHost,
size_t workspaceInBytesOnHost,
int *info)
computes all or selection of the eigenvalues and optionally eigenvectors of a symmetric (Hermitian) n×n matrix A using the generic API interface. The standard symmetric eigenvalue problem is
where Λ is a real n×h_meig diagonal matrix. V is an n×h_meig unitary matrix. h_meig is the number of eigenvalues/eigenvectors computed by the routine, h_meig is equal to n when the whole spectrum (e.g., range = CUSOLVER_EIG_RANGE_ALL) is requested. The diagonal elements of Λ are the eigenvalues of A in ascending order.
The user has to provide device and host working spaces which are pointed by input parameters bufferOnDevice and bufferOnHost. The input parameters workspaceInBytesOnDevice (and workspaceInBytesOnHost) is size in bytes of the device (and host) working space, and it is returned by cusolverDnXsyevdx_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
if jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Currently, cusolverDnXsyevdx supports only the default algorithm.
Please visit cuSOLVER Library Samples - Xsyevdx for a code example.
| CUSOLVER_ALG_0 or NULL | Default algorithm. |
List of input arguments for cusolverDnXsyevdx_bufferSize and cusolverDnXsyevdx:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverDN library context. |
| params | host | input | Structure with information collected by cusolverDnSetAdvOptions. |
| jobz | host | input | Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only; jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors. |
| range | host | input | Specifies options to which selection of eigenvalues and optionally eigenvectors that need to be computed: range = CUSOLVER_EIG_RANGE_ALL : all eigenvalues/eigenvectors will be found, will becomes the classical syevd/heevd routine; range = CUSOLVER_EIG_RANGE_V : all eigenvalues/eigenvectors in the half-open interval (vl,vu] will be found; range = CUSOLVER_EIG_RANGE_I : the il-th through iu-th eigenvalues/eigenvectors will be found; |
| uplo | host | input | Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. |
| n | host | input | Number of rows (or columns) of matrix A. |
| dataTypeA | host | in | Data type of array A. |
| A | device | in/out | Array of dimension lda * n with lda is not less than max(1,n). If uplo = CUBLAS_FILL_MODE_UPPER, the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A. If uplo = CUBLAS_FILL_MODE_LOWER, the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A. On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, A contains the orthonormal eigenvectors of the matrix A. If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| lda | host | input | Leading dimension of two-dimensional array used to store matrix A.lda is not less than max(1,n). |
| vl,vu | host | input | If range = CUSOLVER_EIG_RANGE_V, the lower and upper bounds of the interval to be searched for eigenvalues. vl > vu. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_I. Note that, if eigenvalues are very close to each other, it is well known that two different eigenvalues routines might find slightly different number of eigenvalues inside the same interval. This is due to the fact that different eigenvalue algorithms, or even same algorithm but different run might find eigenvalues within some rounding error close to the machine precision. Thus, if the user want to be sure not to miss any eigenvalue within the interval bound, we suggest that, the user substract/add epsilon (machine precision) to the interval bound such as (vl=vl-eps, vu=vu+eps]. this suggestion is valid for any selective routine from cuSolver or LAPACK. |
| il,iu | host | input | Integer. If range = CUSOLVER_EIG_RANGE_I, the indices (in ascending order) of the smallest and largest eigenvalues to be returned. 1 <= il <= iu <= n, if n > 0; il = 1 and iu = 0 if n = 0. Not referenced if range = CUSOLVER_EIG_RANGE_ALL or range = CUSOLVER_EIG_RANGE_V. |
| h_meig | host | output | Integer. The total number of eigenvalues found. 0 <= h_meig <= n. If range = CUSOLVER_EIG_RANGE_ALL, h_meig = n, and if range = CUSOLVER_EIG_RANGE_I, h_meig = iu-il+1. |
| dataTypeW | host | in | Data type of array W. |
| W | device | output | A real array of dimension n. The eigenvalue values of A, in ascending order, i.e., sorted so that W(i) <= W(i+1). |
| computeType | host | in | Data type of computation. |
| bufferOnDevice | device | in/out | Device workspace. Array of type void of size workspaceInBytesOnDevice bytes. |
| workspaceInBytesOnDevice | host | input | Size in bytes of bufferOnDevice, returned by cusolverDnXpotrf_bufferSize. |
| bufferOnHost | host | in/out | Host workspace. Array of type void of size workspaceInBytesOnHost bytes. |
| workspaceInBytesOnHost | host | input | Size in bytes of bufferOnHost, returned by cusolverDnXpotrf_bufferSize. |
| info | device | output | If info = 0, the operation is successful. if info = -i, the i-th parameter is wrong (not counting handle). If info = i (> 0), info indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. |
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeW is data type of the matrix W and computeType is compute type of the operation. cusolverDnXsyevdx only supports the following four combinations:
| DataTypeA | DataTypeW | ComputeType | Meaning |
|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SSYEVDX |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DSYEVDX |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CHEEVDX |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | ZHEEVDX |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n<0, or lda<max(1,n), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or range is not CUSOLVER_EIG_RANGE_ALL or CUSOLVER_EIG_RANGE_V or CUSOLVER_EIG_RANGE_I, or uplo is not CUBLAS_FILL_MODE_LOWER or CUBLAS_FILL_MODE_UPPER). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.5. cuSolverSP: sparse LAPACK Function Reference
This section describes the API of cuSolverSP, which provides a subset of LAPACK funtions for sparse matrices in CSR or CSC format.
2.5.1. Helper Function Reference
2.5.1.1. cusolverSpCreate()
cusolverStatus_t cusolverSpCreate(cusolverSpHandle_t *handle)
This function initializes the cuSolverSP library and creates a handle on the cuSolver context. It must be called before any other cuSolverSP API function is invoked. It allocates hardware resources necessary for accessing the GPU.
| handle | The pointer to the handle to the cuSolverSP context. |
| CUSOLVER_STATUS_SUCCESS | The initialization succeeded. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The CUDA Runtime initialization failed. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
2.5.1.2. cusolverSpDestroy()
cusolverStatus_t cusolverSpDestroy(cusolverSpHandle_t handle)
This function releases CPU-side resources used by the cuSolverSP library.
| handle | The handle to the cuSolverSP context. |
| CUSOLVER_STATUS_SUCCESS | The shutdown succeeded. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.5.1.3. cusolverSpSetStream()
cusolverStatus_t cusolverSpSetStream(cusolverSpHandle_t handle, cudaStream_t streamId)
This function sets the stream to be used by the cuSolverSP library to execute its routines.
| handle | The handle to the cuSolverSP context. |
| streamId | The stream to be used by the library. |
| CUSOLVER_STATUS_SUCCESS | The stream was set successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.5.1.4. cusolverSpXcsrissym()
cusolverStatus_t
cusolverSpXcsrissymHost(cusolverSpHandle_t handle,
int m,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrEndPtrA,
const int *csrColIndA,
int *issym);
This function checks if A has symmetric pattern or not. The output parameter issym reports 1 if A is symmetric; otherwise, it reports 0.
The matrix A is an m×m sparse matrix that is defined in CSR storage format by the four arrays csrValA, csrRowPtrA, csrEndPtrA and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL.
The csrlsvlu and csrlsvqr do not accept non-general matrix. the user has to extend the matrix into its missing upper/lower part, otherwise the result is not expected. The user can use csrissym to check if the matrix has symmetric pattern or not.
Remark 1: only CPU path is provided.
Remark 2: the user has to check returned status to get valid information. The function converts A to CSC format and compare CSR and CSC format. If the CSC failed because of insufficient resources, issym is undefined, and this state can only be detected by the return status code.
| Parameter | MemorySpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| m | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of m elements that contains the start of every row. |
| csrEndPtrA | host | Integer array of m elements that contains the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| Parameter | MemorySpace | Description |
|---|---|---|
| issym | host | 1 if A is symmetric; 0 otherwise. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2. High Level Function Reference
This section describes high level API of cuSolverSP, including linear solver, least-square solver and eigenvalue solver. The high-level API is designed for ease-of-use, so it allocates any required memory under the hood automatically. If the host or GPU system memory is not enough, an error is returned.
2.5.2.1. cusolverSp<t>csrlsvlu()
cusolverStatus_t
cusolverSpScsrlsvlu[Host](cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const float *b,
float tol,
int reorder,
float *x,
int *singularity);
cusolverStatus_t
cusolverSpDcsrlsvlu[Host](cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const double *b,
double tol,
int reorder,
double *x,
int *singularity);
cusolverStatus_t
cusolverSpCcsrlsvlu[Host](cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuComplex *b,
float tol,
int reorder,
cuComplex *x,
int *singularity);
cusolverStatus_t
cusolverSpZcsrlsvlu[Host](cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuDoubleComplex *b,
double tol,
int reorder,
cuDoubleComplex *x,
int *singularity);
This function solves the linear system
where A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. b is the right-hand-side vector of size n, and x is the solution vector of size n.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If matrix A is symmetric/Hermitian and only lower/upper part is used or meaningful, the user has to extend the matrix into its missing upper/lower part, otherwise the result would be wrong.
The linear system is solved by sparse LU with partial pivoting:
cusolver library provides three reordering schemes, symrcmsymamd, and csrmetisnd to reduce zero fill-in which dramactically affects the performance of LU factorization. The input parameter reorder can enable symrcm (symamd or csrmetisnd) if reorder is 1 (2, or 3), otherwise, no reordering is performed.
If reorder is nonzero, csrlsvlu does
where .
If A is singular under given tolerance (max(tol,0)), then some diagonal elements of U is zero, i.e.
The output parameter singularity is the smallest index of such j. If A is non-singular, singularity is -1. The index is base-0, independent of base index of A. For example, if 2nd column of A is the same as first column, then A is singular and singularity = 1 which means U(1,1)≈0.
Remark 1: csrlsvlu performs traditional LU with partial pivoting, the pivot of k-th column is determined dynamically based on the k-th column of intermediate matrix. csrlsvlu follows Gilbert and Peierls's algorithm [4] which uses depth-first-search and topological ordering to solve triangular system (Davis also describes this algorithm in detail in his book [1]). since cuda 10.1, csrlsvlu will incrementally reallocate the memory to store L and U. This feature can avoid over-estimate size from QR factorization. In some cases, zero fill-in of QR can be order of magnitude higher than LU.
Remark 2: only CPU (Host) path is provided.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolverSP library context. |
| n | host | host | Number of rows and columns of matrix A. |
| nnzA | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzAcsrRowPtrA(n)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of n elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzAcsrRowPtrA(n)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| b | device | host | Right hand side vector of size n. |
| tol | host | host | Tolerance to decide if singular or not. |
| reorder | host | host | No ordering if reorder=0. Otherwise, symrcm, symamd, or csrmetisnd is used to reduce zero fill-in. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| x | device | host | Solution vector of size n, x = inv(A)*b. |
| singularity | host | host | -1 if A is invertible. Otherwise, first index j such that U(j,j)≈0 |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0, base index is not 0 or 1, reorder is not 0,1,2,3) |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2.2. cusolverSp<t>csrlsvqr()
cusolverStatus_t
cusolverSpScsrlsvqr[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const float *b,
float tol,
int reorder,
float *x,
int *singularity);
cusolverStatus_t
cusolverSpDcsrlsvqr[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const double *b,
double tol,
int reorder,
double *x,
int *singularity);
cusolverStatus_t
cusolverSpCcsrlsvqr[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuComplex *b,
float tol,
int reorder,
cuComplex *x,
int *singularity);
cusolverStatus_t
cusolverSpZcsrlsvqr[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuDoubleComplex *b,
double tol,
int reorder,
cuDoubleComplex *x,
int *singularity);
This function solves the linear system
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. b is the right-hand-side vector of size m, and x is the solution vector of size m.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If matrix A is symmetric/Hermitian and only lower/upper part is used or meaningful, the user has to extend the matrix into its missing upper/lower part, otherwise the result would be wrong.
The linear system is solved by sparse QR factorization,
If A is singular under given tolerance (max(tol,0)), then some diagonal elements of R is zero, i.e.
The output parameter singularity is the smallest index of such j. If A is non-singular, singularity is -1. The singularity is base-0, independent of base index of A. For example, if 2nd column of A is the same as first column, then A is singular and singularity = 1 which means R(1,1)≈0.
cusolver library provides three reordering schemes, symrcmsymamd, and csrmetisnd to reduce zero fill-in which dramactically affects the performance of QR factorization. The input parameter reorder can enable symrcm (symamd or csrmetisnd) if reorder is 1 (2, or 3), otherwise, no reordering is performed.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolverSP library context. |
| m | host | host | Number of rows and columns of matrix A. |
| nnz | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of m elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzcsrRowPtrA(m)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| b | device | host | Right hand side vector of size m. |
| tol | host | host | Tolerance to decide if singular or not. |
| reorder | host | host | No ordering if reorder=0. Otherwise, symrcm, symamd, or csrmetisnd is used to reduce zero fill-in. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| x | device | host | solution vector of size m, x = inv(A)*b. |
| singularity | host | host | -1 if A is invertible. Otherwise, first index j such that R(j,j)≈0 |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,nnz<=0, base index is not 0 or 1, reorder is not 0,1,2,3) |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2.3. cusolverSp<t>csrlsvchol()
cusolverStatus_t
cusolverSpScsrlsvchol[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float *csrVal,
const int *csrRowPtr,
const int *csrColInd,
const float *b,
float tol,
int reorder,
float *x,
int *singularity);
cusolverStatus_t
cusolverSpDcsrlsvchol[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrVal,
const int *csrRowPtr,
const int *csrColInd,
const double *b,
double tol,
int reorder,
double *x,
int *singularity);
cusolverStatus_t
cusolverSpCcsrlsvchol[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex *csrVal,
const int *csrRowPtr,
const int *csrColInd,
const cuComplex *b,
float tol,
int reorder,
cuComplex *x,
int *singularity);
cusolverStatus_t
cusolverSpZcsrlsvchol[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrVal,
const int *csrRowPtr,
const int *csrColInd,
const cuDoubleComplex *b,
double tol,
int reorder,
cuDoubleComplex *x,
int *singularity);
This function solves the linear system
A is an m×m symmetric postive definite sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. b is the right-hand-side vector of size m, and x is the solution vector of size m.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL and upper triangular part of A is ignored (if parameter reorder is zero). In other words, suppose input matrix A is decomposed as , where L is lower triangular, D is diagonal and U is upper triangular. The function would ignore U and regard A as a symmetric matrix with the formula . If parameter reorder is nonzero, the user has to extend A to a full matrix, otherwise the solution would be wrong.
The linear system is solved by sparse Cholesky factorization,
where G is the Cholesky factor, a lower triangular matrix.
The output parameter singularity has two meanings:
- If A is not postive definite, there exists some integer k such that A(0:k, 0:k) is not positive definite. singularity is the minimum of such k.
- If A is postive definite but near singular under tolerance (max(tol,0)), i.e. there exists some integer k such that . singularity is the minimum of such k.
singularity is base-0. If A is positive definite and not near singular under tolerance, singularity is -1. If the user wants to know if A is postive definite or not, tol=0 is enough.
cusolver library provides three reordering schemes, symrcmsymamd, and csrmetisnd to reduce zero fill-in which dramactically affects the performance of Cholesky factorization. The input parameter reorder can enable symrcm (symamd or csrmetisnd) if reorder is 1 (2, or 3), otherwise, no reordering is performed.
Remark 1: the function works for in-place (x and b point to the same memory block) and out-of-place.
Remark 2: the function only works on 32-bit index, if matrix G has large zero fill-in such that number of nonzeros is bigger than , then CUSOLVER_STATUS_ALLOC_FAILED is returned.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolverSP library context. |
| m | host | host | Number of rows and columns of matrix A. |
| nnz | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of m elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzcsrRowPtrA(m)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| b | device | host | Right hand side vector of size m. |
| tol | host | host | Tolerance to decide singularity. |
| reorder | host | host | No ordering if reorder=0. Otherwise, symrcm, symamd, or csrmetisnd is used to reduce zero fill-in. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| x | device | host | solution vector of size m, x = inv(A)*b. |
| singularity | host | host | -1 if A is symmetric postive definite. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,nnz<=0, base index is not 0 or 1, reorder is not 0,1,2,3) |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2.4. cusolverSp<t>csrlsqvqr()
cusolverStatus_t
cusolverSpScsrlsqvqr[Host](cusolverSpHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const float *b,
float tol,
int *rankA,
float *x,
int *p,
float *min_norm);
cusolverStatus_t
cusolverSpDcsrlsqvqr[Host](cusolverSpHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const double *b,
double tol,
int *rankA,
double *x,
int *p,
double *min_norm);
cusolverStatus_t
cusolverSpCcsrlsqvqr[Host](cusolverSpHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuComplex *b,
float tol,
int *rankA,
cuComplex *x,
int *p,
float *min_norm);
cusolverStatus_t
cusolverSpZcsrlsqvqr[Host](cusolverSpHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuDoubleComplex *b,
double tol,
int *rankA,
cuDoubleComplex *x,
int *p,
double *min_norm);
This function solves the following least-square problem:
A is an m×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. b is the right-hand-side vector of size m, and x is the least-square solution vector of size n.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If A is square, symmetric/Hermitian and only lower/upper part is used or meaningful, the user has to extend the matrix into its missing upper/lower part, otherwise the result is wrong.
This function only works if m is greater or equal to n, in other words, A is a tall matrix.
The least-square problem is solved by sparse QR factorization with column pivoting,
If A is of full rank (i.e. all columns of A are linear independent), then matrix P is an identity. Suppose rank of A is k, less than n, the permutation matrix P reorders columns of A in the following sense:
|
|
where and A have the same rank, but is almost zero, i.e. every column of is linear combination of .
The input parameter tol decides numerical rank. The absolute value of every entry in is less than or equal to tolerance=max(tol,0).
The output parameter rankA denotes numerical rank of A.
Suppose and , the least square problem can be reformed by
|
|
or in matrix form
|
|
The output parameter min_norm is , which is minimum value of least-square problem.
If A is not of full rank, above equation does not have a unique solution. The least-square problem is equivalent to
|
|
Or equivalently another least-square problem
|
|
The output parameter x is , the solution of least-square problem.
The output parameter p is a vector of size n. It corresponds to a permutation matrix P. p(i)=j means (P*x)(i) = x(j). If A is of full rank, p=0:n-1.
Remark 1: p is always base 0, independent of base index of A.
Remark 2: only CPU (Host) path is provided.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolver library context. |
| m | host | host | Number of rows of matrix A. |
| n | host | host | Number of columns of matrix A. |
| nnz | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of m elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzcsrRowPtrA(m)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| b | device | host | Right hand side vector of size m. |
| tol | host | host | Tolerance to decide rank of A. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| rankA | host | host | Numerical rank of A. |
| x | device | host | Solution vector of size n, x=pinv(A)*b. |
| p | device | host | A vector of size n, which represents the permuation matrix P satisfying A*P^T=Q*R. |
| min_norm | host | host | ||A*x-b||, x=pinv(A)*b. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n,nnz<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2.5. cusolverSp<t>csreigvsi()
cusolverStatus_t
cusolverSpScsreigvsi[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
float mu0,
const float *x0,
int maxite,
float tol,
float *mu,
float *x);
cusolverStatus_t
cusolverSpDcsreigvsi[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
double mu0,
const double *x0,
int maxite,
double tol,
double *mu,
double *x);
cusolverStatus_t
cusolverSpCcsreigvsi[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuComplex mu0,
const cuComplex *x0,
int maxite,
float tol,
cuComplex *mu,
cuComplex *x);
cusolverStatus_t
cusolverSpZcsreigvsi(cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuDoubleComplex mu0,
const cuDoubleComplex *x0,
int maxite,
double tol,
cuDoubleComplex *mu,
cuDoubleComplex *x);
This function solves the simple eigenvalue problem by shift-inverse method.
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. The output paramter x is the approximated eigenvector of size m,
The following shift-inverse method corrects eigenpair step-by-step until convergence.
It accepts several parameters:
mu0 is an initial guess of eigenvalue. The shift-inverse method will converge to the eigenvalue mu nearest mu0 if mu is a singleton. Otherwise, the shift-inverse method may not converge.
x0 is an initial eigenvector. If the user has no preference, just chose x0 randomly. x0 must be nonzero. It can be non-unit length.
tol is the tolerance to decide convergence. If tol is less than zero, it would be treated as zero.
maxite is maximum number of iterations. It is useful when shift-inverse method does not converge because the tolerance is too small or the desired eigenvalue is not a singleton.
|
|
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If A is symmetric/Hermitian and only lower/upper part is used or meaningful, the user has to extend the matrix into its missing upper/lower part, otherwise the result is wrong.
Remark 1: [cu|h]solver[S|D]csreigvsi only allows mu0 as a real number. This works if A is symmetric. Otherwise, the non-real eigenvalue has a conjugate counterpart on the complex plan, and shift-inverse method would not converge to such eigevalue even the eigenvalue is a singleton. The user has to extend A to complex numbre and call [cu|h]solver[C|Z]csreigvsi with mu0 not on real axis.
Remark 2: the tolerance tol should not be smaller than |mu0|*eps, where eps is machine zero. Otherwise, shift-inverse may not converge because of small tolerance.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolver library context. |
| m | host | host | Number of rows and columns of matrix A. |
| nnz | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of m elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzcsrRowPtrA(m)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| mu0 | host | host | Initial guess of eigenvalue. |
| x0 | device | host | Initial guess of eigenvector, a vecotr of size m. |
| maxite | host | host | Maximum iterations in shift-inverse method. |
| tol | host | host | Tolerance for convergence. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| mu | device | host | Approximated eigenvalue nearest mu0 under tolerance. |
| x | device | host | Approximated eigenvector of size m. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,nnz<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.2.6. cusolverSp<t>csreigs()
cusolverStatus_t
solverspScsreigs[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuComplex left_bottom_corner,
cuComplex right_upper_corner,
int *num_eigs);
cusolverStatus_t
cusolverSpDcsreigs[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuDoubleComplex left_bottom_corner,
cuDoubleComplex right_upper_corner,
int *num_eigs);
cusolverStatus_t
cusolverSpCcsreigs[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuComplex left_bottom_corner,
cuComplex right_upper_corner,
int *num_eigs);
cusolverStatus_t
cusolverSpZcsreigs[Host](cusolverSpHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
cuDoubleComplex left_bottom_corner,
cuDoubleComplex right_upper_corner,
int *num_eigs);
This function computes number of algebraic eigenvalues in a given box B by contour integral
where closed line C is boundary of the box B which is a rectangle specified by two points, one is left bottom corner (input parameter left_botoom_corner) and the other is right upper corner (input parameter right_upper_corner). P(z)=det(A - z*I) is the characteristic polynomial of A.
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The output parameter num_eigs is number of algebraic eigenvalues in the box B. This number may not be accurate due to several reasons:
- The contour C is close to some eigenvalues or even passes through some eigenvalues.
- The numerical integration is not accurate due to coarse grid size. The default resolution is 1200 grids along contour C uniformly.
Even though csreigs may not be accurate, it still can give the user some idea how many eigenvalues in a region where the resolution of disk theorem is bad. For example, standard 3-point stencil of finite difference of Laplacian operator is a tridiagonal matrix, and disk theorem would show "all eigenvalues are in the interval [0, 4*N^2]" where N is number of grids. In this case, csreigs is useful for any interval inside [0, 4*N^2].
Remark 1: if A is symmetric in real or hermitian in complex, all eigenvalues are real. The user still needs to specify a box, not an interval. The height of the box can be much smaller than the width.
Remark 2: only CPU (Host) path is provided.
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| handle | host | host | Handle to the cuSolverSP library context. |
| m | host | host | Number of rows and columns of matrix A. |
| nnz | host | host | Number of nonzeros of matrix A. |
| descrA | host | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | host | <type> array of nnzcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | device | host | Integer array of m elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | host | Integer array of nnzcsrRowPtrA(m)csrRowPtrA(0) column indices of the nonzero elements of matrix A. |
| left_bottom_corner | host | host | Left bottom corner of the box. |
| right_upper_corner | host | host | Right upper corner of the box. |
| Parameter | cusolverSp MemSpace | *Host MemSpace | Description |
|---|---|---|---|
| num_eigs | host | host | Number of algebraic eigenvalues in a box. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,nnz<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3. Low Level Function Reference
This section describes low level API of cuSolverSP, including symrcm and batched QR.
2.5.3.1. cusolverSpXcsrsymrcm()
cusolverStatus_t
cusolverSpXcsrsymrcmHost(cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrColIndA,
int *p);
This function implements Symmetric Reverse Cuthill-McKee permutation. It returns a permutation vector p such that A(p,p) would concentrate nonzeros to diagonal. This is equivalent to symrcm in MATLAB, however the result may not be the same because of different heuristics in the pseudoperipheral finder. The cuSolverSP library implements symrcm based on the following two papers:
E. Chuthill and J. McKee, reducing the bandwidth of sparse symmetric matrices, ACM '69 Proceedings of the 1969 24th national conference, Pages 157-172
Alan George, Joseph W. H. Liu, An Implementation of a Pseudoperipheral Node Finder, ACM Transactions on Mathematical Software (TOMS) Volume 5 Issue 3, Sept. 1979, Pages 284-295
The output parameter p is an integer array of n elements. It represents a permutation array and it indexed using the base-0 convention. The permutation array p corresponds to a permutation matrix P, and satisfies the following relation:
A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Internally rcm works on , the user does not need to extend the matrix if the matrix is not symmetric.
Remark 1: only CPU (Host) path is provided.
| Parameter | *Host MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| n | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of n+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| Parameter | hsolver | Description |
|---|---|---|
| p | host | Permutation vector of size n. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3.2. cusolverSpXcsrsymmdq()
cusolverStatus_t
cusolverSpXcsrsymmdqHost(cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrColIndA,
int *p);
This function implements Symmetric Minimum Degree Algorithm based on Quotient Graph. It returns a permutation vector p such that A(p,p) would have less zero fill-in during Cholesky factorization. The cuSolverSP library implements symmdq based on the following two papers:
Patrick R. Amestoy, Timothy A. Davis, Iain S. Duff, An Approximate Minimum Degree Ordering Algorithm, SIAM J. Matrix Analysis Applic. Vol 17, no 4, pp. 886-905, Dec. 1996.
Alan George, Joseph W. Liu, A Fast Implementation of the Minimum Degree Algorithm Using Quotient Graphs, ACM Transactions on Mathematical Software, Vol 6, No. 3, September 1980, page 337-358.
The output parameter p is an integer array of n elements. It represents a permutation array with base-0 index. The permutation array p corresponds to a permutation matrix P, and satisfies the following relation:
A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Internally mdq works on , the user does not need to extend the matrix if the matrix is not symmetric.
Remark 1: only CPU (Host) path is provided.
| Parameter | *Host MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| n | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of n+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| Parameter | hsolver | Description |
|---|---|---|
| p | host | Permutation vector of size n. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3.3. cusolverSpXcsrsymamd()
cusolverStatus_t
cusolverSpXcsrsymamdHost(cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrColIndA,
int *p);
This function implements Symmetric Approximate Minimum Degree Algorithm based on Quotient Graph. It returns a permutation vector p such that A(p,p) would have less zero fill-in during Cholesky factorization. The cuSolverSP library implements symamd based on the following paper:
Patrick R. Amestoy, Timothy A. Davis, Iain S. Duff, An Approximate Minimum Degree Ordering Algorithm, SIAM J. Matrix Analysis Applic. Vol 17, no 4, pp. 886-905, Dec. 1996.
The output parameter p is an integer array of n elements. It represents a permutation array with base-0 index. The permutation array p corresponds to a permutation matrix P, and satisfies the following relation:
A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Internally amd works on , the user does not need to extend the matrix if the matrix is not symmetric.
Remark 1: only CPU (Host) path is provided.
| Parameter | *Host MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| n | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of n+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| Parameter | hsolver | Description |
|---|---|---|
| p | host | Permutation vector of size n. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | the matrix type is not supported. |
2.5.3.4. cusolverSpXcsrmetisnd()
cusolverStatus_t
cusolverSpXcsrmetisndHost(
cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrColIndA,
const int64_t *options,
int *p);
This function is a wrapper of METIS_NodeND. It returns a permutation vector p such that A(p,p) would have less zero fill-in during nested dissection. The cuSolverSP library links libmetis_static.a which is 64-bit metis-5.1.0 .
The parameter options is the configuration of metis. For those who do not have experiences of metis, set options = NULL for default setting.
The output parameter p is an integer array of n elements. It represents a permutation array with base-0 index. The permutation array p corresponds to a permutation matrix P, and satisfies the following relation:
A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Internally csrmetisnd works on , the user does not need to extend the matrix if the matrix is not symmetric.
Remark 1: only CPU (Host) path is provided.
| Parameter | *Host MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| n | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of n+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| options | host | Integer array to configure metis. |
| Parameter | *Host MemSpace | Description |
|---|---|---|
| p | host | Permutation vector of size n. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3.5. cusolverSpXcsrzfd()
cusolverStatus_t
cusolverSpScsrzfdHost(
cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int *P,
int *numnz)
cusolverStatus_t
cusolverSpDcsrzfdHost(
cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int *P,
int *numnz)
cusolverStatus_t
cusolverSpCcsrzfdHost(
cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int *P,
int *numnz)
cusolverStatus_t
cusolverSpZcsrzfdHost(
cusolverSpHandle_t handle,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int *P,
int *numnz)
This function implements MC21, zero-free diagonal algorithm. It returns a permutation vector p such that A(p,:) has no zero diagonal.
A is an n×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL.
The output parameter p is an integer array of n elements. It represents a permutation array with base-0 index. The permutation array p corresponds to a permutation matrix P, and satisfies the following relation:
The output parameter numnz describes number of nonzero diagonal in permutated matrix A(p,:). If numnz is less than n, matrix A has structural singularity.
Remark 1: only CPU (Host) path is provided.
Remark 2: this routine does not maximize diagonal value of permuted matrix. The user cannot expect this routine can make "LU without pivoting" stable.
| Parameter | *Host MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| n | host | Number of rows and columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | host | <type> array of nnzAcsrRowPtrA(m)csrRowPtrA(0) nonzero elements of matrix A. |
| csrRowPtrA | host | Integer array of n+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| Parameter | *Host MemSpace | Description |
|---|---|---|
| p | host | Permutation vector of size n. |
| numnz | host | Number of nonzeros on diagonal of permuted matrix. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3.6. cusolverSpXcsrperm()
cusolverStatus_t
cusolverSpXcsrperm_bufferSizeHost(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
int *csrRowPtrA,
int *csrColIndA,
const int *p,
const int *q,
size_t *bufferSizeInBytes);
cusolverStatus_t
cusolverSpXcsrpermHost(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
int *csrRowPtrA,
int *csrColIndA,
const int *p,
const int *q,
int *map,
void *pBuffer);
Given a left permutation vector p which corresponds to permutation matrix P and a right permutation vector q which corresponds to permutation matrix Q, this function computes permutation of matrix A by
A is an m×n sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA and csrColIndA.
The operation is in-place, i.e. the matrix A is overwritten by B.
The permutation vector p and q are base 0. p performs row permutation while q performs column permutation. One can also use MATLAB command to permutate matrix A.
This function only computes sparsity pattern of B. The user can use parameter map to get csrValB as well. The parameter map is an input/output. If the user sets map=0:1:(nnzA-1) before calling csrperm, csrValB=csrValA(map).
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If A is symmetric and only lower/upper part is provided, the user has to pass into this function.
This function requires a buffer size returned by csrperm_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If it is not, CUSOLVER_STATUS_INVALID_VALUE is returned.
For example, if matrix A is
|
|
and left permutation vector p=(0,2,1), right permutation vector q=(2,1,0), then is
|
|
Remark 1: only CPU (Host) path is provided.
Remark 2: the user can combine csrsymrcm and csrperm to get which has less zero fill-in during QR factorization.
| Parameter | cusolverSp MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolver library context. |
| m | host | Number of rows of matrix A. |
| n | host | Number of columns of matrix A. |
| nnzA | host | Number of nonzeros of matrix A. It is the size of csrValA and csrColIndA. |
| descrA | host | The descriptor of matrix A. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrRowPtrA | host | Integer array of m+1 elements that contains the start of every row and end of last row plus one of matrix A. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix A. |
| p | host | Left permutation vector of size m. |
| q | host | Right permutation vector of size n. |
| map | host | Integer array of nnzA indices. If the user wants to get relationship between A and B, map must be set 0:1:(nnzA-1). |
| pBuffer | host | Buffer allocated by the user, the size is returned by csrperm_bufferSize(). |
| Parameter | hsolver | Description |
|---|---|---|
| csrRowPtrA | host | Integer array of m+1 elements that contains the start of every row and end of last row plus one of matrix B. |
| csrColIndA | host | Integer array of nnzAcolumn indices of the nonzero elements of matrix B. |
| map | host | Integer array of nnzA indices that maps matrix A to matrix B. |
| pBufferSizeInBytes | host | Number of bytes of the buffer. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.5.3.7. cusolverSpXcsrqrBatched()
cusolverStatus_t cusolverSpCreateCsrqrInfo(csrqrInfo_t *info); cusolverStatus_t cusolverSpDestroyCsrqrInfo(csrqrInfo_t info);
cusolverStatus_t
cusolverSpXcsrqrAnalysisBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const int *csrRowPtrA,
const int *csrColIndA,
csrqrInfo_t info);
cusolverStatus_t
cusolverSpScsrqrBufferInfoBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int batchSize,
csrqrInfo_t info,
size_t *internalDataInBytes,
size_t *workspaceInBytes);
cusolverStatus_t
cusolverSpDcsrqrBufferInfoBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int batchSize,
csrqrInfo_t info,
size_t *internalDataInBytes,
size_t *workspaceInBytes);
cusolverStatus_t
cusolverSpCcsrqrBufferInfoBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int batchSize,
csrqrInfo_t info,
size_t *internalDataInBytes,
size_t *workspaceInBytes);
cusolverStatus_t
cusolverSpZcsrqrBufferInfoBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
int batchSize,
csrqrInfo_t info,
size_t *internalDataInBytes,
size_t *workspaceInBytes);
cusolverStatus_t
cusolverSpScsrqrsvBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const float *b,
float *x,
int batchSize,
csrqrInfo_t info,
void *pBuffer);
cusolverStatus_t
cusolverSpDcsrqrsvBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const double *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const double *b,
double *x,
int batchSize,
csrqrInfo_t info,
void *pBuffer);
cusolverStatus_t
cusolverSpCcsrqrsvBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuComplex *b,
cuComplex *x,
int batchSize,
csrqrInfo_t info,
void *pBuffer);
cusolverStatus_t
cusolverSpZcsrqrsvBatched(cusolverSpHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const cuDoubleComplex *csrValA,
const int *csrRowPtrA,
const int *csrColIndA,
const cuDoubleComplex *b,
cuDoubleComplex *x,
int batchSize,
csrqrInfo_t info,
void *pBuffer);
The batched sparse QR factorization is used to solve either a set of least-squares problems
or a set of linear systems
where each is a m×n sparse matrix that is defined in CSR storage format by the four arrays csrValA, csrRowPtrA and csrColIndA.
The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. If A is symmetric and only lower/upper part is prvided, the user has to pass into this function.
The prerequisite to use batched sparse QR has two-folds. First all matrices must have the same sparsity pattern. Second, no column pivoting is used in least-square problem, so the solution is valid only if is of full rank for all j = 1,2,..., batchSize . All matrices have the same sparity pattern, so only one copy of csrRowPtrA and csrColIndA is used. But the array csrValA stores coefficients of one after another. In other words, csrValA[k*nnzA : (k+1)*nnzA] is the value of .
The batched QR uses opaque data structure csrqrInfo to keep intermediate data, for example, matrix Q and matrix R of QR factorization. The user needs to create csrqrInfo first by cusolverSpCreateCsrqrInfo before any function in batched QR operation. The csrqrInfo would not release internal data until cusolverSpDestroyCsrqrInfo is called.
There are three routines in batched sparse QR, cusolverSpXcsrqrAnalysisBatched, cusolverSp[S|D|C|Z]csrqrBufferInfoBatched and cusolverSp[S|D|C|Z]csrqrsvBatched.
First, cusolverSpXcsrqrAnalysisBatched is the analysis phase, used to analyze sparsity pattern of matrix Q and matrix R of QR factorization. Also parallelism is extracted during analysis phase. Once analysis phase is done, the size of working space to perform QR is known. However cusolverSpXcsrqrAnalysisBatched uses CPU to analyze the structure of matrix A, and this may consume a lot of memory. If host memory is not sufficient to finish the analysis, CUSOLVER_STATUS_ALLOC_FAILED is returned. The required memory for analysis is proportional to zero fill-in in QR factorization. The user may need to perform some kind of reordering to minimize zero fill-in, for example, colamd or symrcm in MATLAB. cuSolverSP library provides symrcm (cusolverSpXcsrsymrcm).
Second, the user needs to choose proper batchSize and to prepare working space for sparse QR. There are two memory blocks used in batched sparse QR. One is internal memory block used to store matrix Q and matrix R. The other is working space used to perform numerical factorization. The size of the former is proportional to batchSize, and the size is specified by returned parameter internalDataInBytes of cusolverSp[S|D|C|Z]csrqrBufferInfoBatched. while the size of the latter is almost independent of batchSize, and the size is specified by returned parameter workspaceInBytes of cusolverSp[S|D|C|Z]csrqrBufferInfoBatched. The internal memory block is allocated implicitly during first call of cusolverSp[S|D|C|Z]csrqrsvBatched. The user only needs to allocate working space for cusolverSp[S|D|C|Z]csrqrsvBatched.
Instead of trying all batched matrices, the user can find maximum batchSize by querying cusolverSp[S|D|C|Z]csrqrBufferInfoBatched. For example, the user can increase batchSize till summation of internalDataInBytes and workspaceInBytes is greater than size of available device memory.
Suppose that the user needs to perform 253 linear solvers and available device memory is 2GB. if cusolverSp[S|D|C|Z]csrqrsvBatched can only afford batchSize 100, the user has to call cusolverSp[S|D|C|Z]csrqrsvBatched three times to finish all. The user calls cusolverSp[S|D|C|Z]csrqrBufferInfoBatched with batchSize 100. The opaque info would remember this batchSize and any subsequent call of cusolverSp[S|D|C|Z]csrqrsvBatched cannot exceed this value. In this example, the first two calls of cusolverSp[S|D|C|Z]csrqrsvBatched will use batchSize 100, and last call of cusolverSp[S|D|C|Z]csrqrsvBatched will use batchSize 53.
Example: suppose that A0, A1, .., A9 have the same sparsity pattern, the following code solves 10 linear systems by batched sparse QR.
// Suppose that A0, A1, .., A9 are m x m sparse matrix represented by CSR format, // Each matrix Aj has nonzero nnzA, and shares the same csrRowPtrA and csrColIndA. // csrValA is aggregation of A0, A1, ..., A9. int m ; // number of rows and columns of each Aj int nnzA ; // number of nonzeros of each Aj int *csrRowPtrA ; // each Aj has the same csrRowPtrA int *csrColIndA ; // each Aj has the same csrColIndA double *csrValA ; // aggregation of A0,A1,...,A9 cont int batchSize = 10; // 10 linear systems cusolverSpHandle_t handle; // handle to cusolver library csrqrInfo_t info = NULL; cusparseMatDescr_t descrA = NULL; void *pBuffer = NULL; // working space for numerical factorization // step 1: create a descriptor cusparseCreateMatDescr(&descrA); cusparseSetMatIndexBase(descrA, CUSPARSE_INDEX_BASE_ONE); // A is base-1 cusparseSetMatType(descrA, CUSPARSE_MATRIX_TYPE_GENERAL); // A is a general matrix // step 2: create empty info structure cusolverSpCreateCsrqrInfo(&info); // step 3: symbolic analysis cusolverSpXcsrqrAnalysisBatched( handle, m, m, nnzA, descrA, csrRowPtrA, csrColIndA, info);
// step 4: allocate working space for Aj*xj=bj cusolverSpDcsrqrBufferInfoBatched( handle, m, m, nnzA, descrA, csrValA, csrRowPtrA, csrColIndA, batchSize, info, &internalDataInBytes, &workspaceInBytes); cudaMalloc(&pBuffer, workspaceInBytes); // step 5: solve Aj*xj = bj cusolverSpDcsrqrsvBatched( handle, m, m, nnzA, descrA, csrValA, csrRowPtrA, csrColIndA, b, x, batchSize, info, pBuffer); // step 7: destroy info cusolverSpDestroyCsrqrInfo(info);
Please refer to cuSOLVER Library Samples - csrqr for a code example.
Remark 1: only GPU (device) path is provided.
| Parameter | cusolverSp MemSpace | Description |
|---|---|---|
| handle | host | Handle to the cuSolverSP library context. |
| m | host | Number of rows of each matrix Aj. |
| n | host | Number of columns of each matrix Aj. |
| nnzA | host | Number of nonzeros of each matrix Aj. It is the size csrColIndA. |
| descrA | host | The descriptor of each matrix Aj. The supported matrix type is CUSPARSE_MATRIX_TYPE_GENERAL. Also, the supported index bases are CUSPARSE_INDEX_BASE_ZERO and CUSPARSE_INDEX_BASE_ONE. |
| csrValA | device | <type> array of nnzA*batchSize nonzero elements of matrices A0, A1, .... All matrices are aggregated one after another. |
| csrRowPtrA | device | Integer array of m+1 elements that contains the start of every row and the end of the last row plus one. |
| csrColIndA | device | Integer array of nnzAcolumn indices of the nonzero elements of each matrix Aj. |
| b | device | <type> array of m*batchSize of right-hand-side vectors b0, b1, .... All vectors are aggregated one after another. |
| batchSize | host | Number of systems to be solved. |
| info | host | Opaque structure for QR factorization. |
| pBuffer | device | Buffer allocated by the user, the size is returned by cusolverSpXcsrqrBufferInfoBatched(). |
| Parameter | cusolverSp MemSpace | Description |
|---|---|---|
| x | device | <type> array of m*batchSize of solution vectors x0, x1, .... All vectors are aggregated one after another. |
| internalDataInBytes | host | Number of bytes of the internal data. |
| workspaceInBytes | host | Number of bytes of the buffer in numerical factorization. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (m,n,nnzA<=0), base index is not 0 or 1. |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
| CUSOLVER_STATUS_MATRIX_TYPE_NOT_SUPPORTED | The matrix type is not supported. |
2.6. cuSolverRF: Refactorization Reference
This section describes API of cuSolverRF, a library for fast refactorization.
2.6.1. cusolverRfAccessBundledFactors()
cusolverStatus_t cusolverRfAccessBundledFactors(/* Input */ cusolverRfHandle_t handle, /* Output (in the host memory) */ int* nnzM, /* Output (in the device memory) */ int** Mp, int** Mi, double** Mx);
This routine allows direct access to the lower L and upper U triangular factors stored in the cuSolverRF library handle. The factors are compressed into a single matrix M=(L-I)+U, where the unitary diagonal of L is not stored. It is assumed that a prior call to the cusolverRfRefactor() was done in order to generate these triangular factors.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| nnzM | host | output | The number of non-zero elements of matrix M. |
| Mp | device | output | The array of offsets corresponding to the start of each row in the arrays Mi and Mx. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix $M$. The array size is n+1. |
| Mi | device | output | The array of column indices corresponding to the non-zero elements in the matrix M. It is assumed that this array is sorted by row and by column within each row. The array size is nnzM. |
| Mx | device | output | The array of values corresponding to the non-zero elements in the matrix M. It is assumed that this array is sorted by row and by column within each row. The array size is nnzM. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.2. cusolverRfAnalyze()
cusolverStatus_t cusolverRfAnalyze(cusolverRfHandle_t handle);
This routine performs the appropriate analysis of parallelism available in the LU re-factorization depending upon the algorithm chosen by the user.
It is assumed that a prior call to the cusolverRfSetup[Host|Device]() was done in order to create internal data structures needed for the analysis.
This routine needs to be called only once for a single linear system
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | in/out | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.3. cusolverRfSetupDevice()
cusolverStatus_t cusolverRfSetupDevice(/* Input (in the device memory) */ int n, int nnzA, int* csrRowPtrA, int* csrColIndA, double* csrValA, int nnzL, int* csrRowPtrL, int* csrColIndL, double* csrValL, int nnzU, int* csrRowPtrU, int* csrColIndU, double* csrValU, int* P, int* Q, /* Output */ cusolverRfHandle_t handle);
This routine assembles the internal data structures of the cuSolverRF library. It is often the first routine to be called after the call to the cusolverRfCreate() routine.
This routine accepts as input (on the device) the original matrix A, the lower (L) and upper (U) triangular factors, as well as the left (P) and the right (Q) permutations resulting from the full LU factorization of the first (i=1) linear system
The permutations P and Q represent the final composition of all the left and right reorderings applied to the original matrix A, respectively. However, these permutations are often associated with partial pivoting and reordering to minimize fill-in, respectively.
This routine needs to be called only once for a single linear system
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| n | host | input | The number of rows (and columns) of matrix A. |
| nnzA | host | input | The number of non-zero elements of matrix A. |
| csrRowPtrA | device | input | The array of offsets corresponding to the start of each row in the arrays csrColIndA and csrValA. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. The array size is n+1. |
| csrColIndA | device | input | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| csrValA | device | input | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| nnzL | host | input | The number of non-zero elements of matrix L. |
| csrRowPtrL | device | input | The array of offsets corresponding to the start of each row in the arrays csrColIndL and csrValL. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix L. The array size is n+1. |
| csrColIndL | device | input | The array of column indices corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| csrValL | device | input | The array of values corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| nnzU | host | input | the number of non-zero elements of matrix U. |
| csrRowPtrU | device | input | The array of offsets corresponding to the start of each row in the arrays csrColIndU and csrValU. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix U. The array size is n+1. |
| csrColIndU | device | input | The array of column indices corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| csrValU | device | input | The array of values corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| P | device | input | The left permutation (often associated with pivoting). The array size in n. |
| Q | device | input | The right permutation (often associated with reordering). The array size in n. |
| handle | host | output | The handle to the GLU library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.4. cusolverRfSetupHost()
cusolverStatus_t cusolverRfSetupHost(/* Input (in the host memory) */ int n, int nnzA, int* h_csrRowPtrA, int* h_csrColIndA, double* h_csrValA, int nnzL, int* h_csrRowPtrL, int* h_csrColIndL, double* h_csrValL, int nnzU, int* h_csrRowPtrU, int* h_csrColIndU, double* h_csrValU, int* h_P, int* h_Q, /* Output */ cusolverRfHandle_t handle);
This routine assembles the internal data structures of the cuSolverRF library. It is often the first routine to be called after the call to the cusolverRfCreate() routine.
This routine accepts as input (on the host) the original matrix A, the lower (L) and upper (U) triangular factors, as well as the left (P) and the right (Q) permutations resulting from the full LU factorization of the first (i=1) linear system
The permutations P and Q represent the final composition of all the left and right reorderings applied to the original matrix A, respectively. However, these permutations are often associated with partial pivoting and reordering to minimize fill-in, respectively.
This routine needs to be called only once for a single linear system
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| n | host | input | The number of rows (and columns) of matrix A. |
| nnzA | host | input | The number of non-zero elements of matrix A. |
| h_csrRowPtrA | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndA and h_csrValA. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. The array size is n+1. |
| h_csrColIndA | host | input | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| h_csrValA | host | input | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| nnzL | host | input | The number of non-zero elements of matrix L. |
| h_csrRowPtrL | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndL and h_csrValL. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix L. The array size is n+1. |
| h_csrColIndL | host | input | The array of column indices corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| h_csrValL | host | input | The array of values corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| nnzU | host | input | The number of non-zero elements of matrix U. |
| h_csrRowPtrU | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndU and h_csrValU. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix U. The array size is n+1. |
| h_csrColIndU | host | input | The array of column indices corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| h_csrValU | host | input | The array of values corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| h_P | host | input | The left permutation (often associated with pivoting). The array size in n. |
| h_Q | host | input | The right permutation (often associated with reordering). The array size in n. |
| handle | host | output | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.5. cusolverRfCreate()
cusolverStatus_t cusolverRfCreate(cusolverRfHandle_t *handle);
This routine initializes the cuSolverRF library. It allocates required resources and must be called prior to any other cuSolverRF library routine.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | output | The pointer to the cuSolverRF library handle. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.6. cusolverRfExtractBundledFactorsHost()
cusolverStatus_t cusolverRfExtractBundledFactorsHost(/* Input */ cusolverRfHandle_t handle, /* Output (in the host memory) */ int* h_nnzM, int** h_Mp, int** h_Mi, double** h_Mx);
This routine extracts lower (L) and upper (U) triangular factors from the cuSolverRF library handle into the host memory. The factors are compressed into a single matrix M=(L-I)+U, where the unitary diagonal of (L) is not stored. It is assumed that a prior call to the cusolverRfRefactor() was done in order to generate these triangular factors.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| h_nnzM | host | output | The number of non-zero elements of matrix M. |
| h_Mp | host | output | The array of offsets corresponding to the start of each row in the arrays h_Mi and h_Mx. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix M. The array size is n+1. |
| h_Mi | host | output | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzM. |
| h_Mx | host | output | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzM. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.7. cusolverRfExtractSplitFactorsHost()
cusolverStatus_t cusolverRfExtractSplitFactorsHost(/* Input */ cusolverRfHandle_t handle, /* Output (in the host memory) */ int* h_nnzL, int** h_Lp, int** h_Li, double** h_Lx, int* h_nnzU, int** h_Up, int** h_Ui, double** h_Ux);
This routine extracts lower (L) and upper (U) triangular factors from the cuSolverRF library handle into the host memory. It is assumed that a prior call to the cusolverRfRefactor() was done in order to generate these triangular factors.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| h_nnzL | host | output | The number of non-zero elements of matrix L. |
| h_Lp | host | output | The array of offsets corresponding to the start of each row in the arrays h_Li and h_Lx. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix L. The array size is n+1. |
| h_Li | host | output | The array of column indices corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzL. |
| h_Lx | host | output | The array of values corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzL. |
| h_nnzU | host | output | The number of non-zero elements of matrix U. |
| h_Up | host | output | The array of offsets corresponding to the start of each row in the arrays h_Ui and h_Ux. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix U. The array size is n+1. |
| h_Ui | host | output | The array of column indices corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzU. |
| h_Ux | host | output | The array of values corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is h_nnzU. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.8. cusolverRfDestroy()
cusolverStatus_t cusolverRfDestroy(cusolverRfHandle_t handle);
This routine shuts down the cuSolverRF library. It releases acquired resources and must be called after all the cuSolverRF library routines.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The cuSolverRF library handle. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.9. cusolverRfGetMatrixFormat()
cusolverStatus_t
cusolverRfGetMatrixFormat(cusolverRfHandle_t handle,
cusolverRfMatrixFormat_t *format,
cusolverRfUnitDiagonal_t *diag);
This routine gets the matrix format used in the cusolverRfSetupDevice(), cusolverRfSetupHost(), cusolverRfResetValues(), cusolverRfExtractBundledFactorsHost() and cusolverRfExtractSplitFactorsHost() routines.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| format | host | output | The enumerated matrix format type. |
| diag | host | output | The enumerated unit diagonal type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.10. cusolverRfGetNumericProperties()
cusolverStatus_t
cusolverRfGetNumericProperties(cusolverRfHandle_t handle,
double *zero,
double *boost);
This routine gets the numeric values used for checking for ''zero'' pivot and for boosting it in the cusolverRfRefactor() and cusolverRfSolve() routines. The numeric boosting will be used only if boost > 0.0.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| zero | host | output | The value below which zero pivot is flagged. |
| boost | host | output | The value which is substituted for zero pivot (if the later is flagged). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.11. cusolverRfGetNumericBoostReport()
cusolverStatus_t
cusolverRfGetNumericBoostReport(cusolverRfHandle_t handle,
cusolverRfNumericBoostReport_t *report);
This routine gets the report whether numeric boosting was used in the cusolverRfRefactor() and cusolverRfSolve() routines.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| report | host | output | The enumerated boosting report type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.12. cusolverRfGetResetValuesFastMode()
cusolverStatus_t
cusolverRfGetResetValuesFastMode(cusolverRfHandle_t handle,
rfResetValuesFastMode_t *fastMode);
This routine gets the mode used in the cusolverRfResetValues routine.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| fastMode | host | output | The enumerated mode type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.13. cusolverRfGet_Algs()
cusolverStatus_t
cusolverRfGet_Algs(cusolverRfHandle_t handle,
cusolverRfFactorization_t* fact_alg,
cusolverRfTriangularSolve_t* solve_alg);
This routine gets the algorithm used for the refactorization in cusolverRfRefactor() and the triangular solve in cusolverRfSolve().
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| alg | host | output | The enumerated algorithm type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.14. cusolverRfRefactor()
cusolverStatus_t cusolverRfRefactor(cusolverRfHandle_t handle);
This routine performs the LU re-factorization:
exploring the available parallelism on the GPU. It is assumed that a prior call to the glu_analyze() was done in order to find the available paralellism.
This routine may be called multiple times, once for each of the linear systems:
There are some constraints to the combination of algorithms used for refactorization and solving routines, cusolverRfRefactor() and cusolverRfSolve(). The wrong combination generates the error code CUSOLVER_STATUS_INVALID_VALUE. The table bellow summarizes the supported combinations of algorithms:
| Factorization | Solving |
|---|---|
| CUSOLVERRF_FACTORIZATION_ALG0 | TRIANGULAR_SOLVE_ALG1 |
| CUSOLVERRF_FACTORIZATION_ALG1 | TRIANGULAR_SOLVE_ALG2, TRIANGULAR_SOLVE_ALG3 |
| CUSOLVERRF_FACTORIZATION_ALG2 | TRIANGULAR_SOLVE_ALG2, TRIANGULAR_SOLVE_ALG3 |
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | in/out | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_ZERO_PIVOT | A zero pivot was encountered during the computation. |
2.6.15. cusolverRfResetValues()
cusolverStatus_t cusolverRfResetValues(/* Input (in the device memory) */ int n, int nnzA, int* csrRowPtrA, int* csrColIndA, double* csrValA, int* P, int* Q, /* Output */ cusolverRfHandle_t handle);
This routine updates internal data structures with the values of the new coefficient matrix. It is assumed that the arrays csrRowPtrA, csrColIndA, P and Q have not changed since the last call to the cusolverRfSetup[Host|Device] routine. This assumption reflects the fact that the sparsity pattern of coefficient matrices as well as reordering to minimize fill-in and pivoting remain the same in the set of linear systems:
This routine may be called multiple times, once for each of the linear systems:
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| n | host | input | The number of rows (and columns) of matrix A. |
| nnzA | host | input | The number of non-zero elements of matrix A. |
| csrRowPtrA | device | input | The array of offsets corresponding to the start of each row in the arrays csrColIndA and csrValA. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. The array size is n+1. |
| csrColIndA | device | input | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| csrValA | device | input | The array of values corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| P | device | input | The left permutation (often associated with pivoting). The array size in n. |
| Q | device | input | The right permutation (often associated with reordering). The array size in n. |
| handle | host | output | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.16. cusolverRfSetMatrixFormat()
cusolverStatus_t
cusolverRfSetMatrixFormat(cusolverRfHandle_t handle,
gluMatrixFormat_t format,
gluUnitDiagonal_t diag);
This routine sets the matrix format used in the cusolverRfSetupDevice(), cusolverRfSetupHost(), cusolverRfResetValues(), cusolverRfExtractBundledFactorsHost() and cusolverRfExtractSplitFactorsHost() routines. It may be called once prior to cusolverRfSetupDevice() and cusolverRfSetupHost() routines.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| format | host | input | The enumerated matrix format type. |
| diag | host | input | The enumerated unit diagonal type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An enumerated mode parameter is wrong. |
2.6.17. cusolverRfSetNumericProperties()
cusolverStatus_t
cusolverRfSetNumericProperties(cusolverRfHandle_t handle,
double zero,
double boost);
This routine sets the numeric values used for checking for ''zero'' pivot and for boosting it in the cusolverRfRefactor() and cusolverRfSolve() routines. It may be called multiple times prior to cusolverRfRefactor() and cusolverRfSolve() routines. The numeric boosting will be used only if boost > 0.0.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| zero | host | input | The value below which zero pivot is flagged. |
| boost | host | input | The value which is substituted for zero pivot (if the later is flagged). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.18. cusolverRfSetResetValuesFastMode()
cusolverStatus_t
cusolverRfSetResetValuesFastMode(cusolverRfHandle_t handle,
gluResetValuesFastMode_t fastMode);
This routine sets the mode used in the cusolverRfResetValues routine. The fast mode requires extra memory and is recommended only if very fast calls to cusolverRfResetValues() are needed. It may be called once prior to cusolverRfAnalyze() routine.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| fastMode | host | input | The enumerated mode type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An enumerated mode parameter is wrong. |
2.6.19. cusolverRfSetAlgs()
cusolverStatus_t
cusolverRfSetAlgs(cusolverRfHandle_t handle,
gluFactorization_t fact_alg,
gluTriangularSolve_t alg);
This routine sets the algorithm used for the refactorization in cusolverRfRefactor() and the triangular solve in cusolverRfSolve(). It may be called once prior to cusolverRfAnalyze() routine.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| alg | host | input | The enumerated algorithm type. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
2.6.20. cusolverRfSolve()
cusolverStatus_t cusolverRfSolve(/* Input (in the device memory) */ cusolverRfHandle_t handle, int *P, int *Q, int nrhs, double *Temp, int ldt, /* Input/Output (in the device memory) */ double *XF, /* Input */ int ldxf);
This routine performs the forward and backward solve with the lower and upper triangular factors resulting from the LU re-factorization:
which is assumed to have been computed by a prior call to the cusolverRfRefactor() routine.
The routine can solve linear systems with multiple right-hand-sides (RHS):
even though currently only a single RHS is supported.
This routine may be called multiple times, once for each of the linear systems:
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | output | The handle to the cuSolverRF library. |
| P | device | input | The left permutation (often associated with pivoting). The array size in n. |
| Q | device | input | The right permutation (often associated with reordering). The array size in n. |
| nrhs | host | input | The number right-hand-sides to be solved. |
| Temp | host | input | The dense matrix that contains temporary workspace (of size ldt*nrhs). |
| ldt | host | input | The leading dimension of dense matrix Temp (ldt >= n). |
| XF | host | in/out | The dense matrix that contains the right-hand-sides F and solutions X (of size ldxf*nrhs). |
| ldxf | host | input | The leading dimension of dense matrix XF (ldxf >= n). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.21. cusolverRfBatchSetupHost()
cusolverStatus_t cusolverRfBatchSetupHost(/* Input (in the host memory) */ int batchSize, int n, int nnzA, int* h_csrRowPtrA, int* h_csrColIndA, double *h_csrValA_array[], int nnzL, int* h_csrRowPtrL, int* h_csrColIndL, double *h_csrValL, int nnzU, int* h_csrRowPtrU, int* h_csrColIndU, double *h_csrValU, int* h_P, int* h_Q, /* Output */ cusolverRfHandle_t handle);
This routine assembles the internal data structures of the cuSolverRF library for batched operation. It is called after the call to the cusolverRfCreate() routine, and before any other batched routines.
The batched operation assumes that the user has the following linear systems:
where each matrix in the set: has the same sparsity pattern, and quite similar such that factorization can be done by the same permutation P and Q. In other words, is a small perturbation of .
This routine accepts as input (on the host) the original matrix A (sparsity pattern and batched values), the lower (L) and upper (U) triangular factors, as well as the left (P) and the right (Q) permutations resulting from the full LU factorization of the first (i=1) linear system:
The permutations P and Q represent the final composition of all the left and right reorderings applied to the original matrix A, respectively. However, these permutations are often associated with partial pivoting and reordering to minimize fill-in, respectively.
Remark 1: the matrices A, L and U must be CSR format and base-0.
Remark 2: to get best performance, batchSize should be multiple of 32 and greater or equal to 32. The algorithm is memory-bound, once bandwidth limit is reached, there is no room to improve performance by large batchSize. In practice, batchSize of 32 - 128 is often enough to obtain good performance, but in some cases larger batchSize might be beneficial.
The following routine needs to be called only once for a single linear system:
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| batchSize | host | input | The number of matrices in the batched mode. |
| n | host | input | The number of rows (and columns) of matrix A. |
| nnzA | host | input | The number of non-zero elements of matrix A. |
| h_csrRowPtrA | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndA and h_csrValA. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. The array size is n+1. |
| h_csrColIndA | host | input | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| h_csrValA_array | host | input | Array of pointers of size batchSize, each pointer points to the array of values corresponding to the non-zero elements in the matrix. |
| nnzL | host | input | The number of non-zero elements of matrix L. |
| h_csrRowPtrL | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndL and h_csrValL. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix L. The array size is n+1. |
| h_csrColIndL | host | input | The array of column indices corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| h_csrValL | host | input | The array of values corresponding to the non-zero elements in the matrix L. It is assumed that this array is sorted by row and by column within each row. The array size is nnzL. |
| nnzU | host | input | The number of non-zero elements of matrix U. |
| h_csrRowPtrU | host | input | The array of offsets corresponding to the start of each row in the arrays h_csrColIndU and h_csrValU. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix U. The array size is n+1. |
| h_csrColIndU | host | input | The array of column indices corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| h_csrValU | host | input | The array of values corresponding to the non-zero elements in the matrix U. It is assumed that this array is sorted by row and by column within each row. The array size is nnzU. |
| h_P | host | input | The left permutation (often associated with pivoting). The array size in n. |
| h_Q | host | input | The right permutation (often associated with reordering). The array size in n. |
| handle | host | output | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.22. cusolverRfBatchAnalyze()
cusolverStatus_t cusolverRfBatchAnalyze(cusolverRfHandle_t handle);
This routine performs the appropriate analysis of parallelism available in the batched LU re-factorization.
It is assumed that a prior call to the cusolverRfBatchSetup[Host]() was done in order to create internal data structures needed for the analysis.
The following routine needs to be called only once for a single linear system:
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | in/out | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_ALLOC_FAILED | An allocation of memory failed. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.23. cusolverRfBatchResetValues()
cusolverStatus_t cusolverRfBatchResetValues(/* Input (in the device memory) */ int batchSize, int n, int nnzA, int* csrRowPtrA, int* csrColIndA, double* csrValA_array[], int *P, int *Q, /* Output */ cusolverRfHandle_t handle);
This routine updates internal data structures with the values of the new coefficient matrix. It is assumed that the arrays csrRowPtrA, csrColIndA, P and Q have not changed since the last call to the cusolverRfbatch_setup_host routine.
This assumption reflects the fact that the sparsity pattern of coefficient matrices as well as reordering to minimize fill-in and pivoting remain the same in the set of linear systems:
The input parameter csrValA_array is an array of pointers on device memory. csrValA_array(j) points to matrix: which is also on device memory.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| batchSize | host | input | The number of matrices in batched mode. |
| n | host | input | The number of rows (and columns) of matrix A. |
| nnzA | host | input | The number of non-zero elements of matrix A. |
| csrRowPtrA | device | input | The array of offsets corresponding to the start of each row in the arrays csrColIndA and csrValA. This array has also an extra entry at the end that stores the number of non-zero elements in the matrix. The array size is n+1. |
| csrColIndA | device | input | The array of column indices corresponding to the non-zero elements in the matrix. It is assumed that this array is sorted by row and by column within each row. The array size is nnzA. |
| csrValA_array | device | input | Array of pointers of size batchSize, each pointer points to the array of values corresponding to the non-zero elements in the matrix. |
| P | device | input | The left permutation (often associated with pivoting). The array size in n. |
| Q | device | input | The right permutation (often associated with reordering). The array size in n. |
| handle | host | output | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.24. cusolverRfBatchRefactor()
cusolverStatus_t cusolverRfBatchRefactor(cusolverRfHandle_t handle);
This routine performs the LU re-factorization:
exploring the available parallelism on the GPU. It is assumed that a prior call to the cusolverRfBatchAnalyze() was done in order to find the available paralellism.
Remark: cusolverRfBatchRefactor() would not report any failure of LU refactorization. The user has to call cusolverRfBatchZeroPivot() to know which matrix failed the LU refactorization.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | in/out | The handle to the cuSolverRF library. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
2.6.25. cusolverRfBatchSolve()
cusolverStatus_t cusolverRfBatchSolve(/* Input (in the device memory) */ cusolverRfHandle_t handle, int *P, int *Q, int nrhs, double *Temp, int ldt, /* Input/Output (in the device memory) */ double *XF_array[], /* Input */ int ldxf);
To solve , first we reform the equation by where . Then do refactorization by cusolverRfBatch_Refactor(). Further cusolverRfBatch_Solve() takes over the remaining steps, including:
The input parameter XF_array is an array of pointers on device memory. XF_array(j) points to matrix which is also on device memory.
Remark 1: only a single rhs is supported.
Remark 2: no singularity is reported during backward solve. If some matrix failed the refactorization and has some zero diagonal, backward solve would compute NAN. The user has to call cusolverRfBatch_Zero_Pivot to check if refactorization is successful or not.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | output | The handle to the cuSolverRF library. |
| P | device | input | The left permutation (often associated with pivoting). The array size in n. |
| Q | device | input | The right permutation (often associated with reordering). The array size in n. |
| nrhs | host | input | The number right-hand-sides to be solved. |
| Temp | device | input | The dense matrix that contains temporary workspace (of size ldt*nrhs). |
| ldt | host | input | The leading dimension of dense matrix Temp (ldt >= n). |
| XF_array | device | in/out | Array of pointers of size batchSize, each pointer points to the dense matrix that contains the right-hand-sides F and solutions X (of size ldxf*nrhs). |
| ldxf | host | input | The leading dimension of dense matrix XF (ldxf >= n). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | An unsupported value or parameter was passed. |
| CUSOLVER_STATUS_EXECUTION_FAILED | A kernel failed to launch on the GPU. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
2.6.26. cusolverRfBatchZeroPivot()
cusolverStatus_t cusolverRfBatchZeroPivot(/* Input */ cusolverRfHandle_t handle /* Output (in the host memory) */ int *position);
Although is close to each other, it does not mean exists for every j. The user can query which matrix failed LU refactorization by checking corresponding value in position array. The input parameter position is an integer array of size batchSize.
The j-th component denotes the refactorization result of matrix . If position(j) is -1, the LU refactorization of matrix is successful. If position(j) is k >= 0, matrix is not LU factorizable and its matrix is zero.
The return value of cusolverRfBatch_Zero_Pivot is CUSOLVER_STATUS_ZERO_PIVOT if there exists one which failed LU refactorization. The user can redo LU factorization to get new permutation P and Q if error code CUSOLVER_STATUS_ZERO_PIVOT is returned.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| handle | host | input | The handle to the cuSolverRF library. |
| position | host | output | Integer array of size batchSize. The value of position(j) reports singularity of matrix Aj, -1 if no structural/numerical zero, k >= 0 if Aj(k,k) is either structural zero or numerical zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_ZERO_PIVOT | A zero pivot was encountered during the computation. |
3. Using the CUSOLVERMG API
3.1. General Description
This section describes how to use the cuSolverMG library API. It is not a reference for the cuSolverMG API data types and functions; that is provided in subsequent chapters.
3.1.2. Determinism
Currently all cuSolverMG API routines from a given toolkit version generate the same bit-wise results when the following conditions are respected :
- all GPUs particating to the computation have the same compute-capabilities and the same number of SMs.
- the tiles size is kept the same between run.
- number of logical GPUs is kept the same. The order of GPUs are not important because all have the same compute-capabilities.
3.1.3. Tile Strategy
The tiling strategy of cuSolverMG is compatible with ScaLAPACK. The current release only supports 1-D column block cyclic, column-major PACKED format.
Figure 1.a shows a partition of the matrix A of dimension M_A by N_A. Each column tile has T_A columns. There are seven columns of tiles, labeled as 0,1,2,3,4,5,6, distributed into three GPUs in a cyclic way, i.e. each GPU takes one column tile in turn. For example, GPU 0 has column tile 0, 3, 6 (yellow tiles) and GPU 1 takes column tiles next to GPU 0 (blue tiles). Not all GPUs have the same number of tiles; in this example, GPU 0 has three tiles, others have only two tiles.
Figure 1.b shows two possilbe formats to store those column tiles locally in each GPU. Left side is called PACKED format and right side is UNPACKED format. PACKED format aggregates three column tiles in a contiguous memory block while UNPACKED format distributes these three column tiles into different memory blocks. The only difference between them is that PACKED format can have a big GEMM call instead of three GEMM calls in UNPACKED format. So theoretically speaking, PACKED format can deliver better performance than UNPACKED format. cusolveMG only supports PACKED format in the API. In order to achieve maximal performance, the user just needs to choose the proper tile size T_A to partition the matrix, not too small, for example 256 or above is enough.
There is another parameter, called LLD_A, to control the leading dimension of the local matrix in each GPU. LLD_A must be greater or equal to M_A. The purpose of LLD_A is for better performance of GEMM. For small problems, GEMM is faster if LLD_A is power of 2. However for big problems, LLD_A does not show significant improvement. cuSolverMG only supports LLD_A=M_A.
The processing grid in cuSolverMG is a list of GPU IDs, similar to the process ID in ScaLAPACK. cuSolverMG only supports 1D column block cyclic, so only 1D grid is supported as well. Suppose deviceId is a list of GPU IDs, both deviceId=1,1,1 and deviceId=2,1,0 are valid. The former describes three logical devices that are selected to run cuSolverMG routines, and all have the same physical ID, 0. The latter still uses three logical devices, but each has a different physical ID. The current design only accepts 32 logical devices, that is, the length of deviceId is less or equal to 32. Figure 1 uses deviceId=0,1,2.
In practice, the matrix A is distributed into GPUs listed in deviceId. If the user chooses deviceId=1,1,1, all columns tile are located in GPU 1, this will limit the size of the problem because of memory capacity of one GPU. Besides, multiGPU routine adds extra overhead on data communication through the off-chip bus, which has a big performance impact if NVLINK is not supported or used. It would be faster to run on a single GPU instead of runing multiGPU version with devices of the same GPU ID.
3.1.4. Global Matrix Versus Local Matrix
Operating a submatrix of the matrix A is simple in dense linear algebra, just shift the pointer to the starting point of the submatrix relative to A. For example, gesvd(10,10, A) is SVD of A(0:9,0:9). gesvd(10,10, A + 5 + 2*lda ) is SVD of 10-by-10 submatrix starting at A(5,2).
However it is not simple to operate on a submatrix of a distributed matrix because different starting point of the submatrix changes the distribution of the layout of that submatrix. ScaLAPACK introduces two parameters, IA and JA, to locate the submatrix. Figure 2 shows (global) matrix A of dimension M_A by N_A. The sub(A) is a M by N submatrix of A, starting at IA and JA. Please be aware that IA and JA are base-1.
Given a distributed matrix A, the user can compute eigenvalues of the submatrix sub(A) by either calling syevd(A, IA, JA) or gathering sub(A) to another distributed matrix B and calling syevd(B, IB=1, JB=1).
3.1.5. Usage of _bufferSize
There is no cudaMalloc inside cuSolverMG library, so the user must allocate the device workspace explicitly. The routine xyz_bufferSize is to query the size of workspace of the routine xyz, for example xyz = syevd. To make the API simple, xyz_bufferSize follows almost the same signature of xyz even it only depends on some parameters, for example, the device pointer is not used to decide the size of workspace. In most cases, xyz_bufferSize is called in the beginning before actual device data (pointing by a device pointer) is prepared or before the device pointer is allocated. In such cases, the user can pass a null pointer to xyz_bufferSize without breaking the functionality.
xyz_bufferSize returns bufferSize for each device. The size is number of elements, not number of bytes.
3.1.6. Synchronization
All routines are in synchronous (blocking call) manner. The data is ready after the routine. However the user has to prepare the distributed data before calling the routine. For example, if the user has multiple streams to set up the matrix, stream synchronization or device synchronization is necessary to guarantee the distributed matrix is ready.
3.1.7. Context Switch
The user does not need to restore the device by cudaSetDevice() after each cuSolverMG call. All routines set the device back to what the caller has.
3.1.8. NVLINK
The peer-to-peer communication via NVLINK can dramatically reduce the overhead of data exchange among GPUs. cuSolverMG does not enable NVLINK implicitly, instead, it gives this option back to the user, not to interfere with other libraries. The example code H.1 shows how to enable peer-to-peer communication.
3.2. cuSolverMG Types Reference
3.2.1. cuSolverMG Types
The float, double, cuComplex, and cuDoubleComplex data types are supported. The first two are standard C data types, while the last two are exported from cuComplex.h. In addition, cuSolverMG uses some familiar types from cuBLAS.
3.2.2. cusolverMgHandle_t
This is a pointer type to an opaque cuSolverMG context, which the user must initialize by calling cusolverMgCreate() prior to calling any other library function. An un-initialized handle object will lead to unexpected behavior, including crashes of cuSolverMG. The handle created and returned by cusolverMgCreate() must be passed to every cuSolverMG function.
3.2.3. cusolverMgGridMapping_t
The type indicates layout of grids.
| Value | Meaning |
|---|---|
| CUDALIBMG_GRID_MAPPING_ROW_MAJOR | Row-major ordering. |
| CUDALIBMG_GRID_MAPPING_COL_MAJOR | Column-major ordering. |
3.3. Helper Function Reference
3.3.1. cusolverMgCreate()
cusolverStatus_t cusolverMgCreate(cusolverMgHandle_t *handle)
This function initializes the cuSolverMG library and creates a handle on the cuSolverMG context. It must be called before any other cuSolverMG API function is invoked. It allocates hardware resources necessary for accessing the GPU.
| handle | The pointer to the handle to the cuSolverMG context. |
| CUSOLVER_STATUS_SUCCESS | The initialization succeeded. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
3.3.2. cusolverMgDestroy()
cusolverStatus_t cusolverMgDestroy( cusolverMgHandle_t handle)
This function releases CPU-side resources used by the cuSolverMG library.
| handle | The handle to the cuSolverMG context. |
| CUSOLVER_STATUS_SUCCESS | The shutdown succeeded. |
3.3.3. cusolverMgDeviceSelect()
cusolverStatus_t
cusolverMgDeviceSelect(
cusolverMgHandle_t handle,
int nbDevices,
int deviceId[] )
This function registers a subset of devices (GPUs) to cuSolverMG handle. Such subset of devices is used in subsequent API calls. The array deviceId contains a list of logical device ID. The term logical means repeated device ID are permitted. For example, suppose the user has only one GPU in the system, say device 0. If the user sets deviceId=0,0,0, then cuSolverMG treats them as three independent GPUs, one stream each, so concurrent kernel launches still hold. The current design only supports up to 32 logical devices.
| handle | The pointer to the handle to the cuSolverMG context. |
| nbDevices | The number of logical devices. |
| deviceId | An integer array of size nbDevices. |
| CUSOLVER_STATUS_SUCCESS | The initialization succeeded. |
| CUSOLVER_STATUS_INVALID_VALUE | nbDevices must be greater than zero, and less or equal to 32. |
| CUSOLVER_STATUS_ALLOC_FAILED | The resources could not be allocated. |
| CUSOLVER_STATUS_INTERNAL_ERROR | Internal error occurred when setting internal streams and events. |
3.3.4. cusolverMgCreateDeviceGrid()
cusolverStatus_t
cusolverMgCreateDeviceGrid(
cusolverMgGrid_t* grid,
int32_t numRowDevices,
int32_t numColDevices,
const int32_t deviceId[],
cusolverMgGridMapping_t mapping)
This function sets up a grid of devices.
Only 1-D column block cyclic is supported, so numRowDevices must be equal to 1.
WARNING: cusolverMgCreateDeviceGrid() must be consistent with cusolverMgDeviceSelect(), i.e. numColDevices must be equal to nbDevices in cusolverMgDeviceSelect().
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| grid | host | output | The pointer to the opaque structure. |
| numRowDevices | host | input | Number of devices in the row. |
| numColDevices | host | input | Number of devices in the column. |
| deviceId | host | input | Integer array of size numColDevices, containing device IDs. |
| mapping | host | input | Row-major or column-major ordering. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | numColDevices is not greater than 0. numRowDevices is not 1. |
3.3.5. cusolverMgDestroyGrid()
cusolverStatus_t
cusolverMgDestroyGrid(
cusolverMgGrid_t grid)
This function releases resources of a grid.
| Parameter | MemSpace | In/out | Meaning |
|---|---|---|---|
| grid | host | input/output | The pointer to the opaque structure. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
3.3.6. cusolverMgCreateMatDescr()
cusolverStatus_t
cusolverMgCreateMatrixDesc(
cusolverMgMatrixDesc_t * desc,
int64_t numRows,
int64_t numCols,
int64_t rowBlockSize,
int64_t colBlockSize,
cudaDataType_t dataType,
const cusolverMgGrid_t grid)
This function sets up the matrix descriptor desc.
Only 1-D column block cyclic is supported, so numRows must be equal to rowBlockSize.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| desc | host | output | The matrix descriptor. |
| numRows | host | input | The number of rows of global A. |
| numCols | host | input | The number of columns of global A. |
| rowBlockSize | host | input | The number of rows per tile. |
| colBlockSize | host | input | The number of columns per tile. |
| dataType | host | input | Data type of the matrix. |
| grid | host | input | The pointer to structure of grid. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | numRows, numCols, or rowBlockSize or colBlockSize is less than 0. numRows is not equal to rowBlockSize. |
3.3.7. cusolverMgDestroyMatrixDesc()
cusolverStatus_t
cusolverMgDestroyMatrixDesc(
cusolverMgMatrixDesc_t desc)
This function releases the matrix descriptor desc.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| desc | host | input/output | The matrix descriptor. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
3.4. Dense Linear Solver Reference
This section describes the linear solver API of cuSolverMG.
3.4.1. cusolverMgPotrf()
cusolverStatus_t
cusolverMgPotrf_bufferSize(
cusolverMgHandle_t handle,
cublasFillMode_t uplo,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
cudaDataType computeType,
int64_t *lwork)
cusolverStatus_t
cusolverMgPotrf(
cusolverMgHandle_t handle,
cublasFillMode_t uplo,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
cudaDataType computeType,
void *array_d_work[],
int64_t lwork,
int *info)
computes the Cholesky factorization of a Hermitian positive-definite matrix using the generic API interface.
A is an n×n Hermitian matrix; only lower or upper part is meaningful. The input parameter uplo indicates which part of the matrix is used. The function would leave other parts untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, only lower triangular part of A is processed, and replaced by lower triangular Cholesky factor L:
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, only upper triangular part of A is processed, and replaced by upper triangular Cholesky factor U:
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is number of devices. array_d_work[j] is a device pointer pointing to a device memory in j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is the number of elements per device, returned by cusolverMgPotrf_bufferSize().
If Cholesky factorization failed, i.e. some leading minor of A is not positive definite, or equivalently some diagonal elements of L or U is not a real number. The output parameter info would indicate smallest leading minor of A which is not positive definite.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The generic API has two different types, dataTypeA is data type of the matrix A, andcomputeType is compute type of the operation and data type of the workspace (array_d_work) descrA contains dataTypeA, so there is no explicit parameter of dataTypeA. cusolverMgPotrf only supports the following four combinations.
Please visit cuSOLVER Library Samples - MgPotrf for a code example.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SPOTRF |
| CUDA_R_64F | CUDA_R_64F | DPOTRF |
| CUDA_C_32F | CUDA_C_32F | CPOTRF |
| CUDA_C_64F | CUDA_C_64F | ZPOTRF |
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMg library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. Only CUBLAS_FILL_MODE_LOWER is supported. |
| N | host | input | Number of rows and columns of matrix sub(A). |
| array_d_A | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension N * N. On exit, sub(A) contains the factors L or U. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Sze of array_d_work[j], returned by cusolverMgPotrf_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the Cholesky factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, the leading minor of order i is not positive definite. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (M,N<0). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
3.4.2. cusolverMgPotrs()
cusolverStatus_t cusolverMgPotrs_bufferSize( cusolverMgHandle_t handle, cublasFillMode_t uplo, int n, int nrhs, void *array_d_A[], int IA, int JA, cudaLibMgMatrixDesc_t descrA, void *array_d_B[], int IB, int JB, cudaLibMgMatrixDesc_t descrB, cudaDataType computeType, int64_t *lwork )
cusolverStatus_t cusolverMgPotrs( cusolverMgHandle_t handle, cublasFillMode_t uplo, int n, int nrhs, void *array_d_A[], int IA, int JA, cudaLibMgMatrixDesc_t descrA, void *array_d_B[], int IB, int JB, cudaLibMgMatrixDesc_t descrB, cudaDataType computeType, void *array_d_work[], int64_t lwork, int *info)
This function solves a system of linear equations:
where A is a n×n Hermitian matrix, only lower or upper part is meaningful using the generic API interface. The input parameter uplo indicates which part of the matrix is used. The function would leave other parts untouched.
If input parameter uplo is CUBLAS_FILL_MODE_LOWER, the matrix should A contain the lower triangular factor for Cholesky decomposition previously computed by cusolverMgPotrf routine.
If input parameter uplo is CUBLAS_FILL_MODE_UPPER, the matrix should A contain the upper triangular factor for Cholesky decomposition previously computed by the cusolverMgPotrf routine.
The operation is in-place, i.e. matrix B contains the solution of the linear system on exit.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is the number of devices. array_d_work[j] is a device pointer pointing to a device memory in the j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is number of elements per device, returned by cusolverMgPotrs_bufferSize().
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The generic API has four different types: dataTypeA is data type of the matrix A, dataTypeB is data type of the matrix B, computeType is compute type of the operation and data type of the workspace (array_d_work) descrA contains dataTypeA and descrB contains dataTypeB and so there is no explicit parameter of dataTypeA and dataTypeB. cusolverMgPotrs only supports the following four combinations.
Please visit cuSOLVER Library Samples - MgPotrf for a code example.
| DataTypeA | DataTypeB | ComputeType | Meaning |
|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SPOTRS |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DPOTRS |
| CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CPOTRS |
| CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZPOTRS |
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMg library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. Only CUBLAS_FILL_MODE_LOWER is supported. |
| N | host | input | Number of rows and columns of matrix sub(A). |
| NRHS | host | input | Number of columns of matrix sub(A) and sub(B). |
| array_d_A | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension M * N. On exit, sub(A) contains the factors L and U. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| array_d_B | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(B) of dimension N * NRHS. On exit, sub(A) contains the solution to the linear system. |
| IB | host | input | The row index in the global array B indicating the first row of sub(B). |
| JB | host | input | The column index in the global array B indicating the first column of sub(B). |
| descrB | host | input | Matrix descriptor for the distributed matrix B. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Size of array_d_work[j], returned by cusolverMgPotrs_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the routine successful. If info = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (M,N<0). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
3.4.3. cusolverMgPotri()
cusolverStatus_t cusolverMgPotri_bufferSize( cusolverMgHandle_t handle, cublasFillMode_t uplo, int N, void *array_d_A[], int IA, int JA, cudaLibMgMatrixDesc_t descrA, cudaDataType computeType, int64_t *lwork)
cusolverStatus_t cusolverMgPotri( cusolverMgHandle_t handle, cublasFillMode_t uplo, int N, void *array_d_A[], int IA, int JA, cudaLibMgMatrixDesc_t descrA, cudaDataType computeType, void *array_d_work[], int64_t lwork, int *info)
This function computes the inverse of a Hermitian positive-definite matrix A using the Cholesky factorization
computed by cusolverMgPotrf().
If the input parameter uplo is CUBLAS_FILL_MODE_LOWER, on input, matrix A contains the lower triangular factor of A computed by cusolverMgPotrf. Only lower triangular part of A is processed, and replaced the by lower triangular part of the inverse of A.
If the input parameter uplo is CUBLAS_FILL_MODE_UPPER, on input, matrix A contains the upper triangular factor of A computed by cusolverMgPotrf. Only upper triangular part of A is processed, and replaced the by upper triangular part of the inverse of A.
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is number of devices. array_d_work[j] is a device pointer pointing to a device memory in the j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is number of elements per device, returned by cusolverMgPotri_bufferSize().
If the computation of the inverse fails, i.e. some leading minor of L or U, is null, the output parameter info would indicate the smallest leading minor of L or U which is not positive definite.
If the output parameter info = -i (less than zero), the i-th parameter is wrong (not counting the handle).
The generic API has two different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation and data type of the workspace (array_d_work) descrA contains dataTypeA, so there is no explicit parameter of dataTypeA. cusolverMgPotri only supports the following four combinations.
Please visit cuSOLVER Library Samples - MgPotrf for a code example.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SPOTRI |
| CUDA_R_64F | CUDA_R_64F | DPOTRI |
| CUDA_C_32F | CUDA_C_32F | CPOTRI |
| CUDA_C_64F | CUDA_C_64F | ZPOTRI |
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMg library context. |
| uplo | host | input | Indicates if matrix A lower or upper part is stored, the other part is not referenced. Only CUBLAS_FILL_MODE_LOWER is supported. |
| N | host | input | Number of rows and columns of matrix sub(A). |
| array_d_A | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension N * N. On exit, sub(A) contains the upper or lower triangular part of the inverse of A depeding on the value of uplo argument. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Size of array_d_work[j], returned by cusolverMgPotri_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the Cholesky factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, the leading minor of order i is zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_NOT_INITIALIZED | The library was not initialized. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (M,N<0). |
| CUSOLVER_STATUS_ARCH_MISMATCH | The device only supports compute capability 2.0 and above. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
3.4.4. cusolverMgGetrf()
cusolverStatus_t
cusolverMgGetrf_bufferSize(
cusolverMgHandle_t handle,
int M,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
int *array_d_IPIV[],
cudaDataType_t computeType,
int64_t *lwork);
cusolverStatus_t
cusolverMgGetrf(
cusolverMgHandle_t handle,
int M,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
int *array_d_IPIV[],
cudaDataType_t computeType,
void *array_d_work[],
int64_t lwork,
int *info );
This function computes the LU factorization of a M×N matrix
where A is a M×N matrix, P is a permutation matrix, L is a lower triangular matrix with unit diagonal, and U is an upper triangular matrix.
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is number of devices. array_d_work[j] is a device pointer pointing to a device memory in j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is number of elements per device, returned by cusolverMgGetrf_bufferSize().
If LU factorization failed, i.e. matrix A (U) is singular, The output parameter info=i indicates U(i,i) = 0.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
If array_d_IPIV is null, no pivoting is performed. The factorization is A=L*U, which is not numerically stable.
array_d_IPIV must be consistent with array_d_A, i.e. JA is the first column of sub(A), also the first column of sub(IPIV).
No matter LU factorization failed or not, the output parameter array_d_IPIV contains pivoting sequence, row i is interchanged with row array_d_IPIV(i).
The generic API has three different types, dataTypeA is data type of the matrix A, computeType is compute type of the operation and data type of the workspace (array_d_work) descrA conatins dataTypeA, so there is no explicit parameter of dataTypeA. cusolverMgGetrf only supports the following four combinations.
Please visit cuSOLVER Library Samples - MgGetrf for a code example.
| DataTypeA | ComputeType | Meaning |
|---|---|---|
| CUDA_R_32F | CUDA_R_32F | SGETRF |
| CUDA_R_64F | CUDA_R_64F | DGETRF |
| CUDA_C_32F | CUDA_C_32F | CGETRF |
| CUDA_C_64F | CUDA_C_64F | ZGETRF |
Remark 1: tile size TA must be less or equal to 512.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMg library context. |
| M | host | input | Number of rows of matrix sub(A). |
| N | host | input | Number of columns of matrix sub(A). |
| array_d_A | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension M * N. On exit, sub(A) contains the factors L and U. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| array_d_IPIV | host | output | A host pointer array of dimension G. it contains a distributed integer array containing sub(IPIV) of size min(M,N). sub(IPIV) contains pivot indices. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Size of array_d_work[j], returned by cusolverMgGetrf_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the LU factorization is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i, the U(i,i) = 0. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (M,N<0). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
3.4.5. cusolverMgGetrs()
cusolverStatus_t
cusolverMgGetrs_bufferSize(
cusolverMgHandle_t handle,
cublasOperation_t TRANS,
int N,
int NRHS,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
int *array_d_IPIV[],
void *array_d_B[],
int IB,
int JB,
cudaLibMgMatrixDesc_t descrB,
cudaDataType_t computeType,
int64_t *lwork);
cusolverStatus_t
cusolverMgGetrs(
cusolverMgHandle_t handle,
cublasOperation_t TRANS,
int N,
int NRHS,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
int *array_d_IPIV[],
void *array_d_B[],
int IB,
int JB,
cudaLibMgMatrixDesc_t descrB,
cudaDataType_t computeType,
void *array_d_work[],
int64_t lwork,
int *info );
This function solves a linear system of multiple right-hand sides
where A is a N×N matrix, and was LU-factored by getrf, that is, lower trianular part of A is L, and upper triangular part (including diagonal elements) of A is U. B is a N×NRHS right-hand side matrix. The solution matirx X overwrites the right-hand-side matrix B.
The input parameter TRANS is defined by
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is number of devices. array_d_work[j] is a device pointer pointing to a device memory in j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is number of elements per device, returned by cusolverMgGetrs_bufferSize().
If array_d_IPIV is null, no pivoting is performed. Otherwise, array_d_IPIV is an output of getrf. It contains pivot indices, which are used to permutate right-hand sides.
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle).
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeB is data type of the matrix B, and computeType is compute type of the operation and data type of the workspace (array_d_work) descrA conatins dataTypeA, so there is no explicit parameter of dataTypeA. descrB conatins dataTypeB, so there is no explicit parameter of dataTypeB. cusolverMgGetrs only supports the following four combinations.
| DataTypeA | DataTypeB | ComputeType | Meaning |
|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SGETRS |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DGETRS |
| CUDA_C_32F | CUDA_C_32F | CUDA_C_32F | CGETRS |
| CUDA_C_64F | CUDA_C_64F | CUDA_C_64F | ZGETRS |
Remark 1: tile size TA must be less or equal to 512.
Remark 2: only support TRANS=CUBLAS_OP_N.
Please visit cuSOLVER Library Samples - MgGetrf for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMG library context. |
| TRANS | host | input | Operation op(A) that is non- or (conj.) transpose. |
| N | host | input | Number of rows and columns of matrix sub(A). |
| NRHS | host | input | Number of columns of matrix sub(B). |
| array_d_A | host | input | A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension M * N. sub(A) contains the factors L and U. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| array_d_IPIV | host | input | A host pointer array of dimension G. it contains a distributed integer array containing sub(IPIV) of dimension min(M,N). sub(IPIV) contains pivot indices. |
| array_d_B | host | in/out | A host pointer array of dimension G. It contains a distributed <type> array containing sub(B) of dimension N * NRHS. |
| IB | host | input | The row index in the global array B indicating the first row of sub(B). |
| JB | host | input | The column index in the global array B indicating the first column of sub(B). |
| descrB | host | input | Matrix descriptor for the distributed matrix B. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Size of array_d_work[j], returned by cusolverMgGetrs_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the operation is successful. If info = -i, the i-th parameter is wrong (not counting handle). |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (N<0 or NRHS<0). |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
3.5. Dense Eigenvalue Solver Reference
This section describes the eigenvalue solver API of cuSolverMG.
3.5.1. cusolverMgSyevd()
cusolverStatus_t
cusolverMgSyevd_bufferSize(
cusolverMgHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
void *W,
cudaDataType_t dataTypeW,
cudaDataType_t computeType,
int64_t *lwork
);
cusolverStatus_t
cusolverMgSyevd(
cusolverMgHandle_t handle,
cusolverEigMode_t jobz,
cublasFillMode_t uplo,
int N,
void *array_d_A[],
int IA,
int JA,
cudaLibMgMatrixDesc_t descrA,
void *W,
cudaDataType_t dataTypeW,
cudaDataType_t computeType,
void *array_d_work[],
int64_t lwork,
int *info );
This function computes eigenvalues and eigenvectors of a symmetric (Hermitian) N×N matrix A. The standard symmetric eigenvalue problem is:
where Λ is a real N×N diagonal matrix. V is an N×N unitary matrix. The diagonal elements of Λ are the eigenvalues of A in ascending order.
cusolverMgSyevd returns the eigenvalues in W and overwrites the eigenvectors in A. W is a host 1×N vector.
The generic API has three different types, dataTypeA is data type of the matrix A, dataTypeW is data type of the vector W, and computeType is compute type of the operation and data type of the workspace (array_d_work) descrA conatins dataTypeA, so there is no explicit parameter of dataTypeA. cusolverMgSyevd only supports the following four combinations.
| DataTypeA | DataTypeW | ComputeType | Meaning |
|---|---|---|---|
| CUDA_R_32F | CUDA_R_32F | CUDA_R_32F | SSYEVD |
| CUDA_R_64F | CUDA_R_64F | CUDA_R_64F | DSYEVD |
| CUDA_C_32F | CUDA_R_32F | CUDA_C_32F | CHEEVD |
| CUDA_C_64F | CUDA_R_64F | CUDA_C_64F | ZHEEVD |
The user has to provide device working space in array_d_work. array_d_work is a host pointer array of dimension G, where G is number of devices. array_d_work[j] is a device pointer pointing to a device memory in j-th device. The data type of array_d_work[j] is computeType. The size of array_d_work[j] is lwork which is number of elements per device, returned by cusolverMgSyevd_bufferSize().
array_d_A is also a host pointer array of dimension G. array_d_A[j] is a device pointer pointing to a device memory in j-th device. The data type of array_d_A[j] is dataTypeA. The size of array_d_A[j] is about N*TA*(blocks per device). The user has to prepare array_d_A manually (seecuSOLVER Library Samples - MgSyevd for a code example.).
If output parameter info = -i (less than zero), the i-th parameter is wrong (not counting handle). If info = i (greater than zero), i off-diagonal elements of an intermediate tridiagonal form did not converge to zero.
If jobz = CUSOLVER_EIG_MODE_VECTOR, A contains the orthonormal eigenvectors of the matrix A. The eigenvectors are computed by a divide and conquer algorithm.
Remark 1: only CUBLAS_FILL_MODE_LOWER is supported, so the user has to prepare lower triangle of A.
Remark 2: only IA=1 and JA=1 are supported.
Remark 3: tile size TA must be less or equal to 1024. To achieve best performance, TA should be 256 or 512.
Please visit cuSOLVER Library Samples - MgSyevd for a code example.
| Parameter | Memory | In/out | Meaning |
|---|---|---|---|
| handle | host | input | Handle to the cuSolverMG library context. |
| jobz | host | input |
Specifies options to either compute eigenvalue only or compute eigen-pair: jobz = CUSOLVER_EIG_MODE_NOVECTOR : Compute eigenvalues only jobz = CUSOLVER_EIG_MODE_VECTOR : Compute eigenvalues and eigenvectors |
| uplo | host | input |
Specifies which part of A is stored. uplo = CUBLAS_FILL_MODE_LOWER: Lower triangle of A is stored. uplo = CUBLAS_FILL_MODE_UPPER: Upper triangle of A is stored. Only CUBLAS_FILL_MODE_LOWER is supported. |
| N | host | input | Number of rows (or columns) of matrix sub(A). |
| array_d_A | host | in/out |
A host pointer array of dimension G. It contains a distributed <type> array containing sub(A) of dimension N * N. If uplo = CUBLAS_FILL_MODE_UPPER, the leading N-by-N upper triangular part of sub(A) contains the upper triangular part of the matrix sub(A). If uplo = CUBLAS_FILL_MODE_LOWER, the leading N-by-N lower triangular part of sub(A) contains the lower triangular part of the matrix sub(A). On exit, if jobz = CUSOLVER_EIG_MODE_VECTOR, and info = 0, sub(A) contains the orthonormal eigenvectors of the matrix sub(A). If jobz = CUSOLVER_EIG_MODE_NOVECTOR, the contents of A are destroyed. |
| IA | host | input | The row index in the global array A indicating the first row of sub(A). |
| JA | host | input | The column index in the global array A indicating the first column of sub(A). |
| descrA | host | input | Matrix descriptor for the distributed matrix A. |
| W | host | output | A real array of dimension N. The eigenvalue values of sub(A), in ascending order ie, sorted so that W(i) <= W(i+1). |
| dataTypeW | host | input | Data type of the vector W. |
| computeType | host | input | Data type used for computation. |
| array_d_work | host | in/out | A host pointer array of dimension G. array_d_work[j] points to a device working space in j-th device, <type> array of size lwork. |
| lwork | host | input | Size of array_d_work[j], returned by cusolverMgSyevd_bufferSize. lwork denotes number of elements, not number of bytes. |
| info | host | output |
If info = 0, the operation is successful. If info = -i, the i-th parameter is wrong (not counting handle). If info = i (> 0), info indicates i off-diagonal elements of an intermediate tridiagonal form did not converge to zero. |
| CUSOLVER_STATUS_SUCCESS | The operation completed successfully. |
| CUSOLVER_STATUS_INVALID_VALUE | Invalid parameters were passed (N<0, or lda<max(1,N), or jobz is not CUSOLVER_EIG_MODE_NOVECTOR or CUSOLVER_EIG_MODE_VECTOR, or uplo is not CUBLAS_FILL_MODE_LOWER, or IA and JA are not 1, or N is bigger than dimension of global A, or the combination of dataType and computeType is not valid. |
| CUSOLVER_STATUS_INTERNAL_ERROR | An internal operation failed. |
A. cuSolverRF Examples
A.1. cuSolverRF In-memory Example
#include <stdio.h> #include <stdlib.h> #include <cuda_runtime.h> #include "cusolverRf.h" #define TEST_PASSED 0 #define TEST_FAILED 1 int main (void){ /* matrix A */ int n; int nnzA; int *Ap=NULL; int *Ai=NULL; double *Ax=NULL; int *d_Ap=NULL; int *d_Ai=NULL; double *d_rAx=NULL; /* matrices L and U */ int nnzL, nnzU; int *Lp=NULL; int *Li=NULL; double* Lx=NULL; int *Up=NULL; int *Ui=NULL; double* Ux=NULL; /* reordering matrices */ int *P=NULL; int *Q=NULL; int * d_P=NULL; int * d_Q=NULL; /* solution and rhs */ int nrhs; //# of rhs for each system (currently only =1 is supported) double *d_X=NULL; double *d_T=NULL; /* cuda */ cudaError_t cudaStatus; /* cuolverRf */ cusolverRfHandle_t gH=NULL; cusolverStatus_t status; /* host sparse direct solver */ /* ... */ /* other variables */ int tnnzL, tnnzU; int *tLp=NULL; int *tLi=NULL; double *tLx=NULL; int *tUp=NULL; int *tUi=NULL; double *tUx=NULL; double t1, t2;
/* ASSUMPTION: recall that we are solving a set of linear systems
A_{i} x_{i} = f_{i} for i=0,...,k-1
where the sparsity pattern of the coefficient matrices A_{i}
as well as the reordering to minimize fill-in and the pivoting
used during the LU factorization remain the same. */
/* Step 1: solve the first linear system (i=0) on the host,
using host sparse direct solver, which involves
full LU factorization and solve. */
/* ... */
/* Step 2: interface to the library by extracting the following
information from the first solve:
a) triangular factors L and U
b) pivoting and reordering permutations P and Q
c) also, allocate all the necessary memory */
/* ... */
/* Step 3: use the library to solve subsequent (i=1,...,k-1) linear systems
a) the library setup (called only once) */
//create handle
status = cusolverRfCreate(&gH);
if (status != CUSOLVER_STATUS_SUCCESS){
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
//set fast mode
status = cusolverRfSetResetValuesFastMode(gH,GLU_RESET_VALUES_FAST_MODE_ON);
if (status != CUSOLVER_STATUS_SUCCESS){
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
//assemble internal data structures (you should use the coeffcient matrix A
//corresponding to the second (i=1) linear system in this call)
t1 = cusolver_test_seconds();
status = cusolverRfSetupHost(n, nnzA, Ap, Ai, Ax,
nnzL, Lp, Li, Lx, nnzU, Up, Ui, Ux, P, Q, gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfSetupHost time = \%f (s)\n", t2-t1);
//analyze available parallelism
t1 = cusolver_test_seconds();
status = cusolverRfAnalyze(gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfAnalyze time = \%f (s)\n", t2-t1);
/* b) The library subsequent (i=1,...,k-1) LU re-factorization
and solve (called multiple times). */
for (i=1; i<k; i++){
//LU re-factorization
t1 = cusolver_test_seconds();
status = cusolverRfRefactor(gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRF status \%d]\n",status);
return TEST_FAILED;
}
printf("cuSolverReRefactor time = \%f (s)\n", t2-t1);
//forward and backward solve
t1 = cusolver_test_seconds();
status = cusolverRfSolve(gH, d_P, d_Q, nrhs, d_T, n, d_X, n);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfSolve time = \%f (s)\n", t2-t1);
// extract the factors (if needed)
status = cusolverRfExtractSplitFactorsHost(gH, &tnnzL, &tLp, &tLi, &tLx,
&tnnzU, &tUp, &tUi, &tUx);
if(status != CUSOLVER_STATUS_SUCCESS){
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
/*
//print
int row, j;
printf("printing L\n");
for (row=0; row<n; row++){
for (j=tLp[row]; j<tLp[row+1]; j++){
printf("\%d,\%d,\%f\n",row,tLi[j],tLx[j]);
}
}
printf("printing U\n");
for (row=0; row<n; row++){
for (j=tUp[row]; j<tUp[row+1]; j++){
printf("\%d,\%d,\%f\n",row,tUi[j],tUx[j]);
}
}
*/
/* perform any other operations based on the solution */
/* ... */
/* check if done */
/* ... */
/* proceed to solve the next linear system */
// update the coefficient matrix using reset values
// (assuming that the new linear system, in other words,
// new values are already on the GPU in the array d_rAx)
t1 = cusolver_test_seconds();
status = cusolverRfResetValues(n,nnzA,d_Ap,d_Ai,d_rAx,d_P,d_Q,gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status \%d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfResetValues time = \%f (s)\n", t2-t1);
}
/* free memory and exit */
/* ... */
return TEST_PASSED;
}
A.2. cuSolverRF-batch Example
This chapter provides an example in the C programming language of how to use the batched routines in the cuSolverRF library. We focus on solving the set of linear systems
#include <stdio.h> #include <stdlib.h> #include <cuda_runtime.h> #include "cusolverRf.h" #define TEST_PASSED 0 #define TEST_FAILED 1 int main (void){ /* matrix A */ int batchSize; int n; int nnzA; int *Ap=NULL; int *Ai=NULL; //array of pointers to the values of each matrix in the batch (of size //batchSize) on the host double **Ax_array=NULL; //For example, if Ax_batch is the array (of size batchSize*nnzA) containing //the values of each matrix in the batch written contiguosly one matrix //after another on the host, then Ax_array[j] = &Ax_batch[nnzA*j]; //for j=0,...,batchSize-1. double *Ax_batch=NULL; int *d_Ap=NULL; int *d_Ai=NULL; //array of pointers to the values of each matrix in the batch (of size //batchSize) on the device double **d_Ax_array=NULL; //For example, if d_Ax_batch is the array (of size batchSize*nnzA) containing //the values of each matrix in the batch written contiguosly one matrix //after another on the device, then d_Ax_array[j] = &d_Ax_batch[nnzA*j]; //for j=0,...,batchSize-1. double *d_Ax_batch=NULL; /* matrices L and U */ int nnzL, nnzU; int *Lp=NULL; int *Li=NULL; double* Lx=NULL; int *Up=NULL; int *Ui=NULL; double* Ux=NULL; /* reordering matrices */ int *P=NULL; int *Q=NULL; int *d_P=NULL; int *d_Q=NULL;
/* solution and rhs */
int nrhs; //# of rhs for each system (currently only =1 is supported)
//temporary storage (of size 2*batchSize*n*nrhs)
double *d_T=NULL;
//array (of size batchSize*n*nrhs) containing the values of each rhs in
//the batch written contiguously one rhs after another on the device
double **d_X_array=NULL;
//array (of size batchSize*n*nrhs) containing the values of each rhs in
//the batch written contiguously one rhs after another on the host
double **X_array=NULL;
/* cuda */
cudaError_t cudaStatus;
/* cusolverRf */
cusolverRfHandle_t gH=NULL;
cusolverStatus_t status;
/* host sparse direct solver */
...
/* other variables */
double t1, t2;
/* ASSUMPTION:
recall that we are solving a batch of linear systems
A_{j} x_{j} = f_{j} for j=0,...,batchSize-1
where the sparsity pattern of the coefficient matrices A_{j}
as well as the reordering to minimize fill-in and the pivoting
used during the LU factorization remain the same. */
/* Step 1: solve the first linear system (j=0) on the host,
using host sparse direct solver, which involves
full LU factorization and solve. */
/* ... */
/* Step 2: interface to the library by extracting the following
information from the first solve:
a) triangular factors L and U
b) pivoting and reordering permutations P and Q
c) also, allocate all the necessary memory */
/* ... */
/* Step 3: use the library to solve the remaining (j=1,...,batchSize-1)
linear systems.
a) the library setup (called only once) */
//create handle
status = cusolverRfcreate(&gH);
if (status != CUSOLVER_STATUS_SUCCESS){
printf ("[cusolverRf status %d]\n",status);
return TEST_FAILED;
}
//assemble internal data structures
t1 = cusolver_test_seconds();
status = cusolverRfBatchSetupHost(batchSize, n, nnzA, Ap, Ai, Ax_array,
nnzL, Lp, Li, Lx, nnzU, Up, Ui, Ux, P, Q, gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status %d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfBatchSetupHost time = %f (s)\n", t2-t1);
//analyze available parallelism
t1 = cusolver_test_seconds();
status = cusolverRfBatchAnalyze(gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status %d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfBatchAnalyze time = %f (s)\n", t2-t1);
/* b) The library subsequent (j=1,...,batchSize-1) LU re-factorization
and solve (may be called multiple times). For the subsequent batches
the values can be reset using cusolverRfBatch_reset_values_routine. */
//LU re-factorization
t1 = cusolver_test_seconds();
status = cusolverRfBatchRefactor(gH);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status %d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfBatchRefactor time = %f (s)\n", t2-t1);
//forward and backward solve
t1 = cusolver_test_seconds();
status = cusolverRfBatchSolve(gH, d_P, d_Q, nrhs, d_T, n, d_X_array, n);
cudaStatus = cudaDeviceSynchronize();
t2 = cusolver_test_seconds();
if ((status != CUSOLVER_STATUS_SUCCESS) || (cudaStatus != cudaSuccess)) {
printf ("[cusolverRf status %d]\n",status);
return TEST_FAILED;
}
printf("cusolverRfBatchSolve time = %f (s)\n", t2-t1);
/* free memory and exit */
/* ... */
return TEST_PASSED;
}
B. Acknowledgements
NVIDIA would like to thank the following individuals and institutions for their contributions:
- CPU LAPACK routines from netlib, CLAPACK-3.2.1 (http://www.netlib.org/clapack/)
The following is license of CLAPACK-3.2.1.
Copyright (c) 1992-2008 The University of Tennessee. All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
- Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
- Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer listed in this license in the documentation and/or other materials provided with the distribution.
- Neither the name of the copyright holders nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
- METIS-5.1.0 (http://glaros.dtc.umn.edu/gkhome/metis/metis/overview)
The following is license of METIS (Apache 2.0 license).
Copyright 1995-2013, Regents of the University of Minnesota
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
- QD (A C++/fortran-90 double-double and quad-double package) (http://crd-legacy.lbl.gov/~dhbailey/mpdist/)
The following is license of QD (modified BSD license).
Copyright (c) 2003-2009, The Regents of the University of California, through Lawrence Berkeley National Laboratory (subject to receipt of any required approvals from U.S. Dept. of Energy) All rights reserved.
1. Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
(1) Redistributions of source code must retain the copyright notice, this list of conditions and the following disclaimer.
(2) Redistributions in binary form must reproduce the copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
(3) Neither the name of the University of California, Lawrence Berkeley National Laboratory, U.S. Dept. of Energy nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
2. THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
3. You are under no obligation whatsoever to provide any bug fixes, patches, or upgrades to the features, functionality or performance of the source code ("Enhancements") to anyone; however, if you choose to make your Enhancements available either publicly, or directly to Lawrence Berkeley National Laboratory, without imposing a separate written license agreement for such Enhancements, then you hereby grant the following license: a non-exclusive, royalty-free perpetual license to install, use, modify, prepare derivative works, incorporate into other computer software, distribute, and sublicense such enhancements or derivative works thereof, in binary and source code form.
C. Bibliography
[1] Timothy A. Davis, Direct Methods for sparse Linear Systems, siam 2006.
[2] E. Chuthill and J. McKee, reducing the bandwidth of sparse symmetric matrices, ACM '69 Proceedings of the 1969 24th national conference, Pages 157-172.
[3] Alan George, Joseph W. H. Liu, An Implementation of a Pseudoperipheral Node Finder, ACM Transactions on Mathematical Software (TOMS) Volume 5 Issue 3, Sept. 1979 Pages 284-295.
[4] J. R. Gilbert and T. Peierls, Sparse partial pivoting in time proportional to arithmetic operations, SIAM J. Sci. Statist. Comput., 9 (1988), pp. 862-874.
[5] Alan George and Esmond Ng, An Implementation of Gaussian Elimination with Partial Pivoting for Sparse Systems, SIAM J. Sci. and Stat. Comput., 6(2), 390-409.
[6] Alan George and Esmond Ng, Symbolic Factorization for Sparse Gaussian Elimination with Paritial Pivoting, SIAM J. Sci. and Stat. Comput., 8(6), 877-898.
[7] John R. Gilbert, Xiaoye S. Li, Esmond G. Ng, Barry W. Peyton, Computing Row and Column Counts for Sparse QR and LU Factorization, BIT 2001, Vol. 41, No. 4, pp. 693-711.
[8] Patrick R. Amestoy, Timothy A. Davis, Iain S. Duff, An Approximate Minimum Degree Ordering Algorithm, SIAM J. Matrix Analysis Applic. Vol 17, no 4, pp. 886-905, Dec. 1996.
[9] Alan George, Joseph W. Liu, A Fast Implementation of the Minimum Degree Algorithm Using Quotient Graphs, ACM Transactions on Mathematical Software, Vol 6, No. 3, September 1980, page 337-358.
[10] Alan George, Joseph W. Liu, Computer Solution of Large Sparse Positive Definite Systems, Englewood Cliffs, New Jersey: Prentice-Hall, 1981.
[11] Iain S. Duff, ALGORITHM 575 Permutations for a Zero-Free Diagonal, ACM Transactions on Mathematical Software, Vol 7, No 3, September 1981, Page 387-390
[12] Iain S. Duff and Jacko Koster, On algorithms for permuting large entries to the diagonal of a sparse matrix, SIAM Journal on Matrix Analysis and Applications, 2001, Vol. 22, No. 4 : pp. 973-996
[13] "A Fast and Highly Quality Multilevel Scheme for Partitioning Irregular Graphs". George Karypis and Vipin Kumar. SIAM Journal on Scientific Computing, Vol. 20, No. 1, pp. 359-392, 1999.
[14] YUJI NAKATSUKASA, ZHAOJUN BAI, AND FRANC¸OIS GYGI, OPTIMIZING HALLEY’S ITERATION FOR COMPUTING THE MATRIX POLAR DECOMPOSITION, SIAM J. Matrix Anal. Appl., 31 (5): 2700-2720,2010
[15] Halko, Nathan, Per-Gunnar Martinsson, and Joel A. Tropp. "Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions." SIAM review 53.2 (2011): 217-288.
Notices
Notice
This document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.
NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice.
Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.
NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgement, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.
NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk.
NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.
No license, either expressed or implied, is granted under any NVIDIA patent right, copyright, or other NVIDIA intellectual property right under this document. Information published by NVIDIA regarding third-party products or services does not constitute a license from NVIDIA to use such products or services or a warranty or endorsement thereof. Use of such information may require a license from a third party under the patents or other intellectual property rights of the third party, or a license from NVIDIA under the patents or other intellectual property rights of NVIDIA.
Reproduction of information in this document is permissible only if approved in advance by NVIDIA in writing, reproduced without alteration and in full compliance with all applicable export laws and regulations, and accompanied by all associated conditions, limitations, and notices.
THIS DOCUMENT AND ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, “MATERIALS”) ARE BEING PROVIDED “AS IS.” NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE. TO THE EXTENT NOT PROHIBITED BY LAW, IN NO EVENT WILL NVIDIA BE LIABLE FOR ANY DAMAGES, INCLUDING WITHOUT LIMITATION ANY DIRECT, INDIRECT, SPECIAL, INCIDENTAL, PUNITIVE, OR CONSEQUENTIAL DAMAGES, HOWEVER CAUSED AND REGARDLESS OF THE THEORY OF LIABILITY, ARISING OUT OF ANY USE OF THIS DOCUMENT, EVEN IF NVIDIA HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. Notwithstanding any damages that customer might incur for any reason whatsoever, NVIDIA’s aggregate and cumulative liability towards customer for the products described herein shall be limited in accordance with the Terms of Sale for the product.