cuSPARSE
The API reference guide for cuSPARSE, the CUDA sparse matrix library.
1. Introduction
cuSPARSE Release Notes: cuda-toolkit-release-notes
cuSPARSE GitHub Samples: CUDALibrarySamples
Nvidia Developer Forum: GPU-Accelerated Libraries
Provide Feedback: Math-Libs-Feedback@nvidia.com
Recent cuSPARSE/cuSPARSELt Blog Posts and GTC presentations:
Exploiting NVIDIA Ampere Structured Sparsity with cuSPARSELt
Accelerating Matrix Multiplication with Block Sparse Format and NVIDIA Tensor Cores
Just-In-Time Link-Time Optimization Adoption in cuSPARSE/cuFFT: Use Case Overview
Structured Sparsity in the NVIDIA Ampere Architecture and Applications in Search Engines
Making the Most of Structured Sparsity in the NVIDIA Ampere Architecture
The library routines provide the following functionalities:
Operations between a sparse vector and a dense vector: sum, dot product, scatter, gather
Operations between a dense matrix and a sparse vector: multiplication
Operations between a sparse matrix and a dense vector: multiplication, triangular solver, tridiagonal solver, pentadiagonal solver
Operations between a sparse matrix and a dense matrix: multiplication, triangular solver, tridiagonal solver, pentadiagonal solver
Operations between a sparse matrix and a sparse matrix: sum, multiplication
Operations between dense matrices with output a sparse matrix: multiplication
Sparse matrix preconditioners: Incomplete Cholesky Factorization (level 0), Incomplete LU Factorization (level 0)
Reordering and Conversion operations between different sparse matrix storage formats
1.1. Library Organization and Features
The cuSPARSE library is organized in two set of APIs:
The Legacy APIs, inspired by the Sparse BLAS standard, provide a limited set of functionalities and will not be improved in future releases, even if standard maintenance is still ensured. Some routines in this category could be deprecated and removed in the short-term. A replacement will be provided for the most important of them during the deprecation process.
The Generic APIs provide the standard interface layer of cuSPARSE. They allow computing the most common sparse linear algebra operations, such as sparse matrix-vector (SpMV) and sparse matrix-matrix multiplication (SpMM), in a flexible way. The new APIs have the following capabilities and features:
Set matrix data layouts, number of batches, and storage formats (for example, CSR, COO, and so on).
Set input/output/compute data types. This also allows mixed data-type computation.
Set types of sparse vector/matrix indices (e.g. 32-bit, 64-bit).
Choose the algorithm for the computation.
Guarantee external device memory for internal operations.
Provide extensive consistency checks across input matrices and vectors. This includes the validation of sizes, data types, layout, allowed operations, etc.
Provide constant descriptors for vector and matrix inputs to support const-safe interface and guarantee that the APIs do not modify their inputs.
1.2. Static Library Support
Starting with CUDA 6.5, the cuSPARSE library is also delivered in a static form as libcusparse_static.a on Linux.
For example, to compile a small application using cuSPARSE against the dynamic library, the following command can be used:
nvcc my_cusparse_app.cu -lcusparse -o my_cusparse_app
Whereas to compile against the static library, the following command has to be used:
nvcc my_cusparse_app.cu -lcusparse_static -o my_cusparse_app
It is also possible to use the native Host C++ compiler. Depending on the Host Operating system, some additional libraries like pthread or dl might be needed on the linking line. The following command on Linux is suggested:
gcc my_cusparse_app.c -lcusparse_static -lcudart_static -lpthread -ldl -I <cuda-toolkit-path>/include -L <cuda-toolkit-path>/lib64 -o my_cusparse_app
Note that in the latter case, the library cuda is not needed. The CUDA Runtime will try to open explicitly the cuda library if needed. In the case of a system which does not have the CUDA driver installed, this allows the application to gracefully manage this issue and potentially run if a CPU-only path is available.
1.3. Library Dependencies
Starting with CUDA 12.0, cuSPARSE will depend on nvJitLink library for JIT (Just-In-Time) LTO (Link-Time-Optimization) capabilities; refer to the cusparseSpMMOp APIs for more information.
If the user links to the dynamic library, the environment variables for loading the libraries at run-time (such as LD_LIBRARY_PATH on Linux and PATH on Windows) must include the path where libnvjitlink.so is located. If it is in the same directory as cuSPARSE, the user doesn’t need to take any action.
If linking to the static library, the user needs to link with -lnvjitlink and set the environment variables for loading the libraries at compile-time LIBRARY_PATH/PATH accordingly.
2. Using the cuSPARSE API
This chapter describes how to use the cuSPARSE library API. It is not a reference for the cuSPARSE API data types and functions; that is provided in subsequent chapters.
2.1. APIs Usage Notes
The cuSPARSE library allows developers to access the computational resources of the NVIDIA graphics processing unit (GPU).
The cuSPARSE APIs assume that input and output data (vectors and matrices) reside in GPU (device) memory.
The input and output scalars (e.g. \(\alpha\) and \(\beta\)) can be passed by reference on the host or the device, instead of only being allowed to be passed by value on the host. This allows library functions to execute asynchronously using streams even when they are generated by a previous kernel resulting in maximum parallelism.
The handle to the cuSPARSE library context is initialized using the function and is explicitly passed to every subsequent library function call. This allows the user to have more control over the library setup when using multiple host threads and multiple GPUs.
The error status
cusparseStatus_tis returned by all cuSPARSE library function calls.
It is the responsibility of the developer to allocate memory and to copy data between GPU memory and CPU memory using standard CUDA runtime API routines, such as cudaMalloc(), cudaFree(), cudaMemcpy(), and cudaMemcpyAsync().
The cuSPARSE library functions are executed asynchronously with respect to the host and may return control to the application on the host before the result is ready. Developers can use the cudaDeviceSynchronize() function to ensure that the execution of a particular cuSPARSE library routine has completed.
A developer can also use the cudaMemcpy() routine to copy data from the device to the host and vice versa, using the cudaMemcpyDeviceToHost and cudaMemcpyHostToDevice parameters, respectively. In this case there is no need to add a call to cudaDeviceSynchronize() because the call to cudaMemcpy() with the above parameters is blocking and completes only when the results are ready on the host.
2.2. Deprecated APIs
The cuSPARSE library documentation explicitly indicates the set of APIs/enumerators/data structures that are deprecated. The library policy for deprecated APIs is the following:
An API is marked
[[DEPRECATED]]on a release X.Y (e.g. 11.2)The documentation indices a replacement if available
Otherwise, the functionality will not be maintained in the future
The API will be removed in the release X+1.0 (e.g. 12.0)
Correctness bugs are still addressed even for deprecated APIs, while performance issues are not always ensured.
In addition to the documentation, deprecated APIs generate a compile-time warning for most platforms when used. Deprecation warnings can be disabled by defining the macro DISABLE_CUSPARSE_DEPRECATED before including cusparse.h or by passing the flag -DDISABLE_CUSPARSE_DEPRECATED to the compiler.
2.3. Thread Safety
The library is thread safe and its functions can be called from multiple host threads. However, simultaneous read/writes of the same objects (or of the same handle) are not safe. Hence the handle must be private per thread, i.e., only one handle per thread is safe.
2.4. Parallelism with Streams
If the application performs several small independent computations, or if it makes data transfers in parallel with the computation, CUDA streams can be used to overlap these tasks.
The application can conceptually associate a stream with each task. To achieve the overlap of computation between the tasks, the developer should create CUDA streams using the function cudaStreamCreate() and set the stream to be used by each individual cuSPARSE library routine by calling cusparseSetStream() just before calling the actual cuSPARSE routine. Then, computations performed in separate streams would be overlapped automatically on the GPU, when possible. This approach is especially useful when the computation performed by a single task is relatively small and is not enough to fill the GPU with work, or when there is a data transfer that can be performed in parallel with the computation.
When streams are used, we recommend using the new cuSPARSE API with scalar parameters and results passed by reference in the device memory to achieve maximum computational overlap.
Although a developer can create many streams, in practice it is not possible to have more than 16 concurrent kernels executing at the same time.
2.5. Compatibility and Versioning
The cuSPARSE APIs are intended to be backward compatible at the source level with future releases (unless stated otherwise in the release notes of a specific future release). In other words, if a program uses cuSPARSE, it should continue to compile and work correctly with newer versions of cuSPARSE without source code changes. cuSPARSE is not guaranteed to be backward compatible at the binary level. Using different versions of the cusparse.h header file and shared library is not supported. Using different versions of cuSPARSE and the CUDA runtime is not supported.
The library uses the standard version semantic convention for identify different releases.
The version takes the form of four fields joined by periods: MAJOR.MINOR.PATCH.BUILD
These version fields are incremented based on the following rules:
MAJOR: API breaking changes or new CUDA major version (breaking changes at lower level, e.g. drivers, compilers, libraries)MINOR: new APIs and functionalitiesPATCH: Bug fixes or performance improvements (or * new CUDA release)BUILD: Internal build number
* Different CUDA toolkit releases ensure distinct library versions even if there are no changes at library level.
2.6. Optimization Notes
Most of the cuSPARSE routines can be optimized by exploiting CUDA Graphs capture and Hardware Memory Compression features.
More in details, a single cuSPARSE call or a sequence of calls can be captured by a CUDA Graph and executed in a second moment. This minimizes kernels launch overhead and allows the CUDA runtime to optimize the whole workflow. A full example of CUDA graphs capture applied to a cuSPARSE routine can be found in cuSPARSE Library Samples - CUDA Graph.
Secondly, the data types and functionalities involved in cuSPARSE are suitable for Hardware Memory Compression available in Ampere GPU devices (compute capability 8.0) or above. The feature allows memory compression for data with enough zero bytes without no loss of information. The device memory must be allocation with the CUDA driver APIs. A full example of Hardware Memory Compression applied to a cuSPARSE routine can be found in cuSPARSE Library Samples - Memory Compression.
3. cuSPARSE Storage Formats
The cuSPARSE library supports dense and sparse vector, and dense and sparse matrix formats.
3.1. Index Base
The library supports zero- and one-based indexing to ensure the compatibility with C/C++ and Fortran languages respectively. The index base is selected through the cusparseIndexBase_t type.
3.2. Vector Formats
This section describes dense and sparse vector formats.
3.2.1. Dense Vector Format
Dense vectors are represented with a single data array that is stored linearly in memory, such as the following \(7 \times 1\) dense vector.
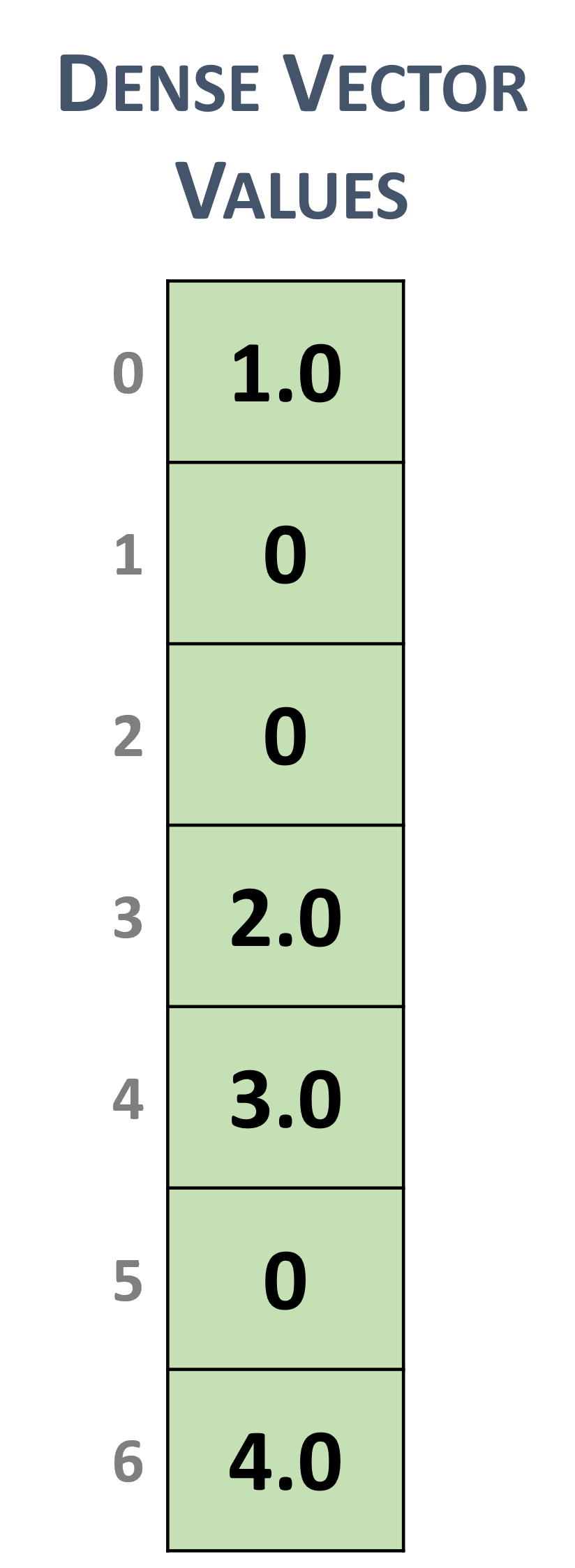
Dense vector representation
3.2.2. Sparse Vector Format
Sparse vectors are represented with two arrays.
The values array stores the nonzero values from the equivalent array in dense format.
The indices array represent the positions of the corresponding nonzero values in the equivalent array in dense format.
For example, the dense vector in section 3.2.1 can be stored as a sparse vector with zero-based or one-based indexing.
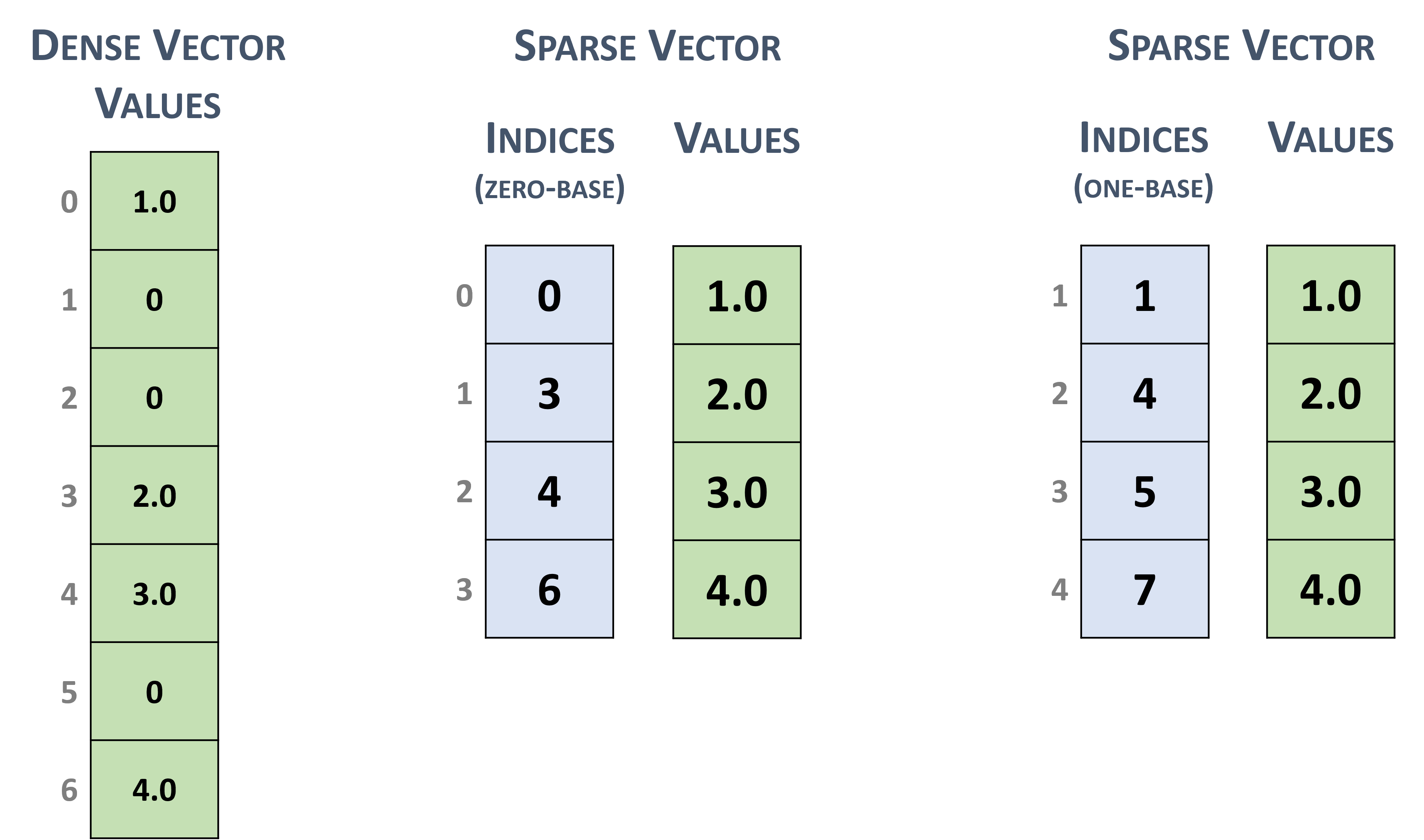
Sparse vector representation
Note
The cuSPARSE routines assume that the indices are provided in increasing order and that each index appears only once. In the opposite case, the correctness of the computation is not always ensured.
3.3. Matrix Formats
Dense and several sparse formats for matrices are discussed in this section.
3.3.1. Dense Matrix Format
A dense matrix can be stored in both row-major and column-major memory layout (ordering) and it is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The leading dimension, which must be
Greater than or equal to the number of columns in the row-major layout
Greater than or equal to the number of rows in the column-major layout
The pointers to the values array of length
\(rows \times leading\; dimension\) in the row-major layout
\(columns \times leading\; dimension\) in the column-major layout
The following figure represents a \(5 \times 2\) dense matrix with both memory layouts
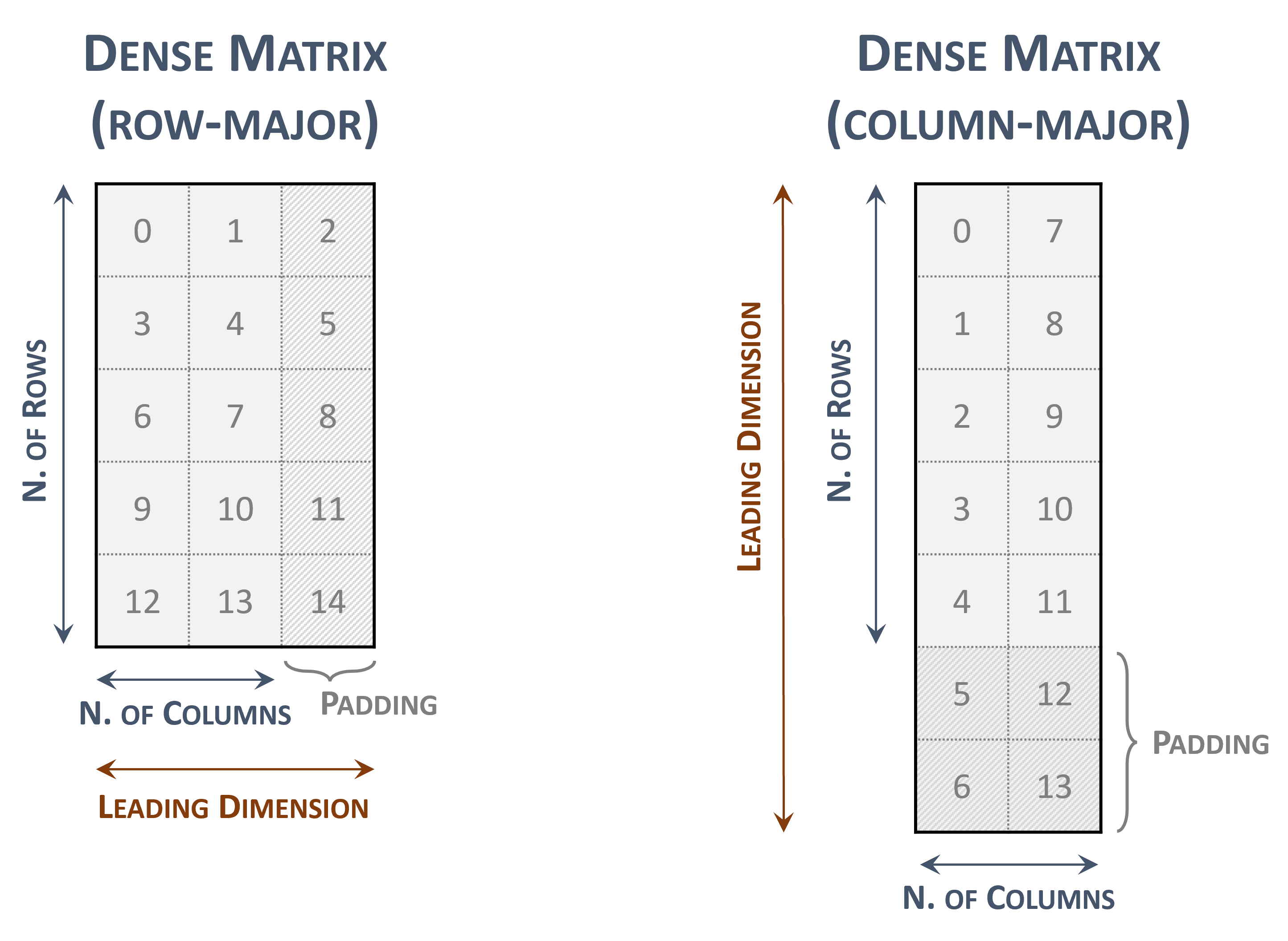
Dense matrix representations
The indices within the matrix represents the contiguous locations in memory.
The leading dimension is useful to represent a sub-matrix within the original one
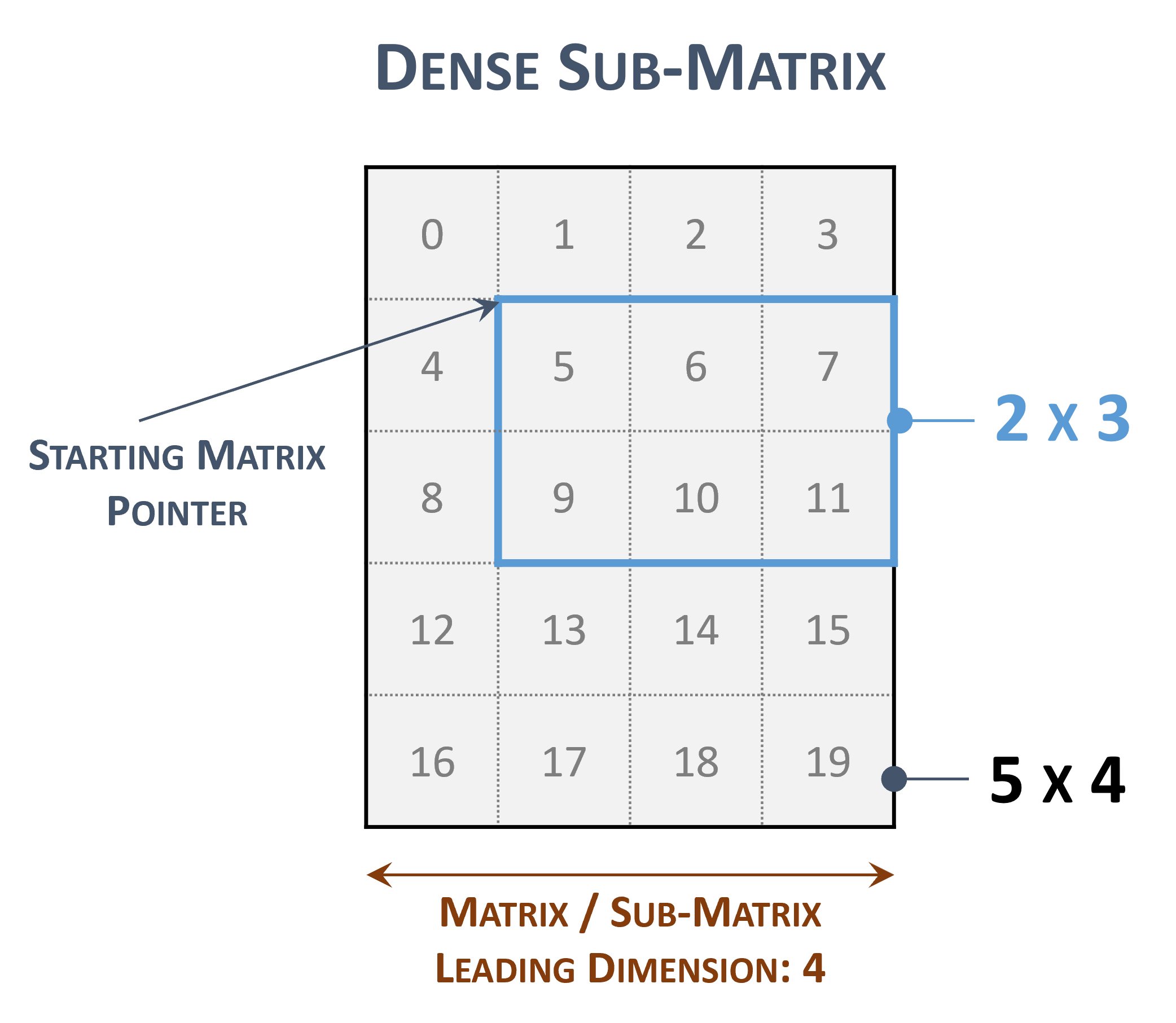
Sub-matrix representations
3.3.2. Coordinate (COO)
A sparse matrix stored in COO format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the row indices array of length
nnzthat contains the row indices of the corresponding elements in the values array.The pointers to the column indices array of length
nnzthat contains the column indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in row-major ordering.Each entry of the COO representation consists of a
<row, column>pair.The COO format is assumed to be sorted by row.
The following example shows a \(5 \times 4\) matrix represented in COO format.

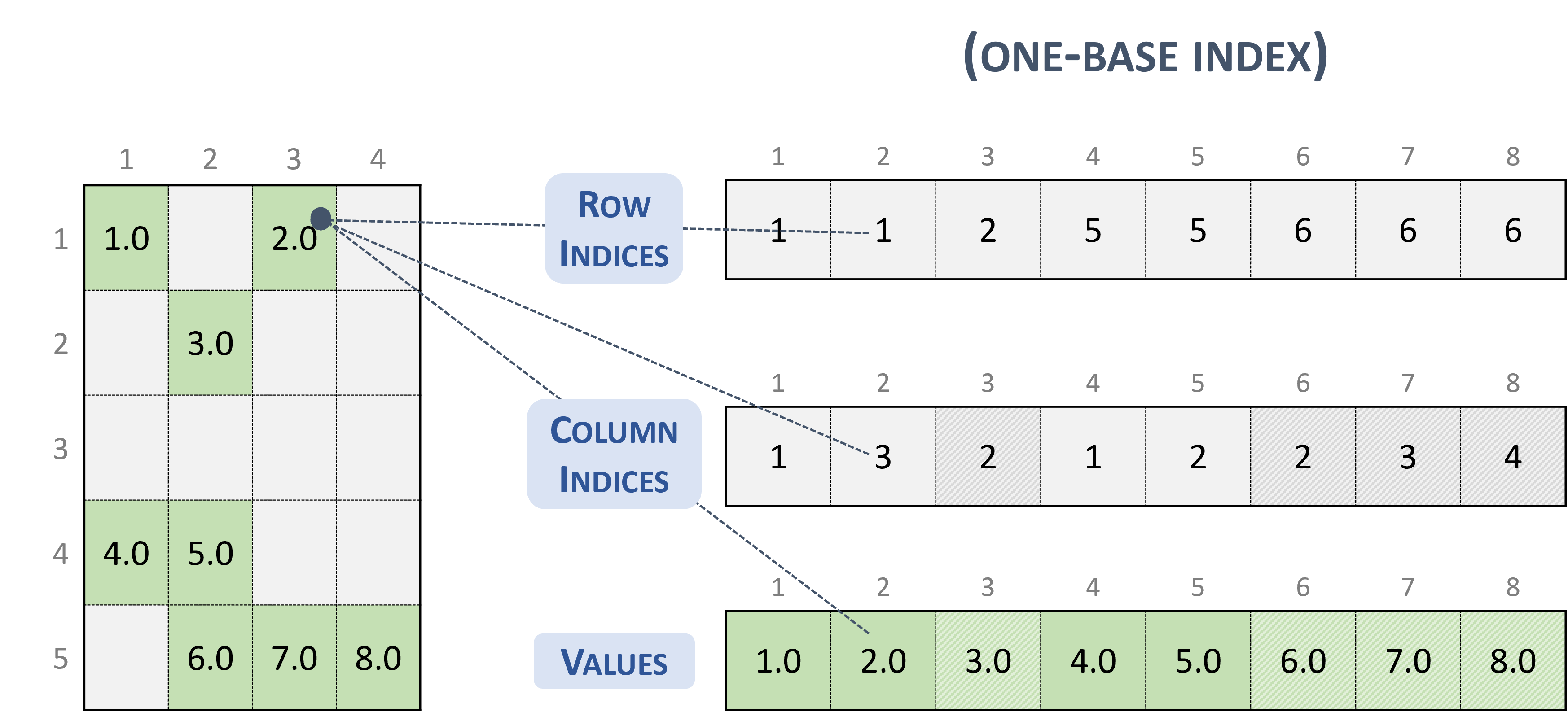
Note
cuSPARSE supports both sorted and unsorted column indices within a given row.
Note
If the column indices within a given row are unique, the correctness of the computation is not always ensured.
Given an entry in the COO format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
rows_indices[i] * leading_dimension + column_indices[i]
// column-major
column_indices[i] * leading_dimension + rows_indices[i]
3.3.3. Compressed Sparse Row (CSR)
The CSR format is similar to COO, where the row indices are compressed and replaced by an array of offsets.
A sparse matrix stored in CSR format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the row offsets array of length number of rows + 1 that represents the starting position of each row in the columns and values arrays.
The pointers to the column indices array of length
nnzthat contains the column indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in row-major ordering.
The following example shows a \(5 \times 4\) matrix represented in CSR format.

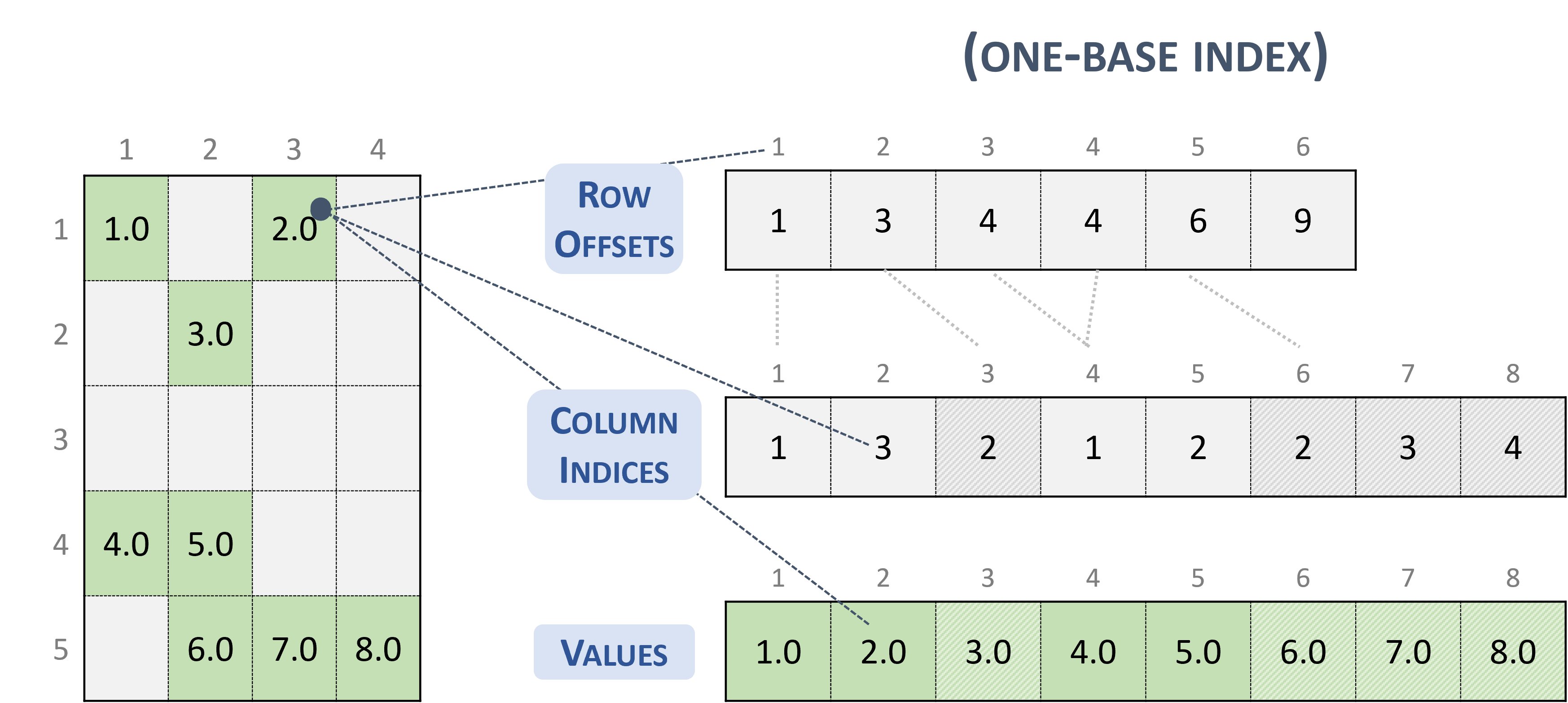
Note
cuSPARSE supports both sorted and unsorted column indices within a given row.
Note
If the column indices within a given row are not unique, the correctness of the computation is not always ensured.
Given an entry in the CSR format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
row * leading_dimension + column_indices[row_offsets[row] + k]
// column-major
column_indices[row_offsets[row] + k] * leading_dimension + row
3.3.4. Compressed Sparse Column (CSC)
The CSC format is similar to COO, where the column indices are compressed and replaced by an array of offsets.
A sparse matrix stored in CSC format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the column offsets array of length number of column + 1 that represents the starting position of each column in the columns and values arrays.
The pointers to the row indices array of length
nnzthat contains row indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in column-major ordering.
The following example shows a \(5 \times 4\) matrix represented in CSC format.
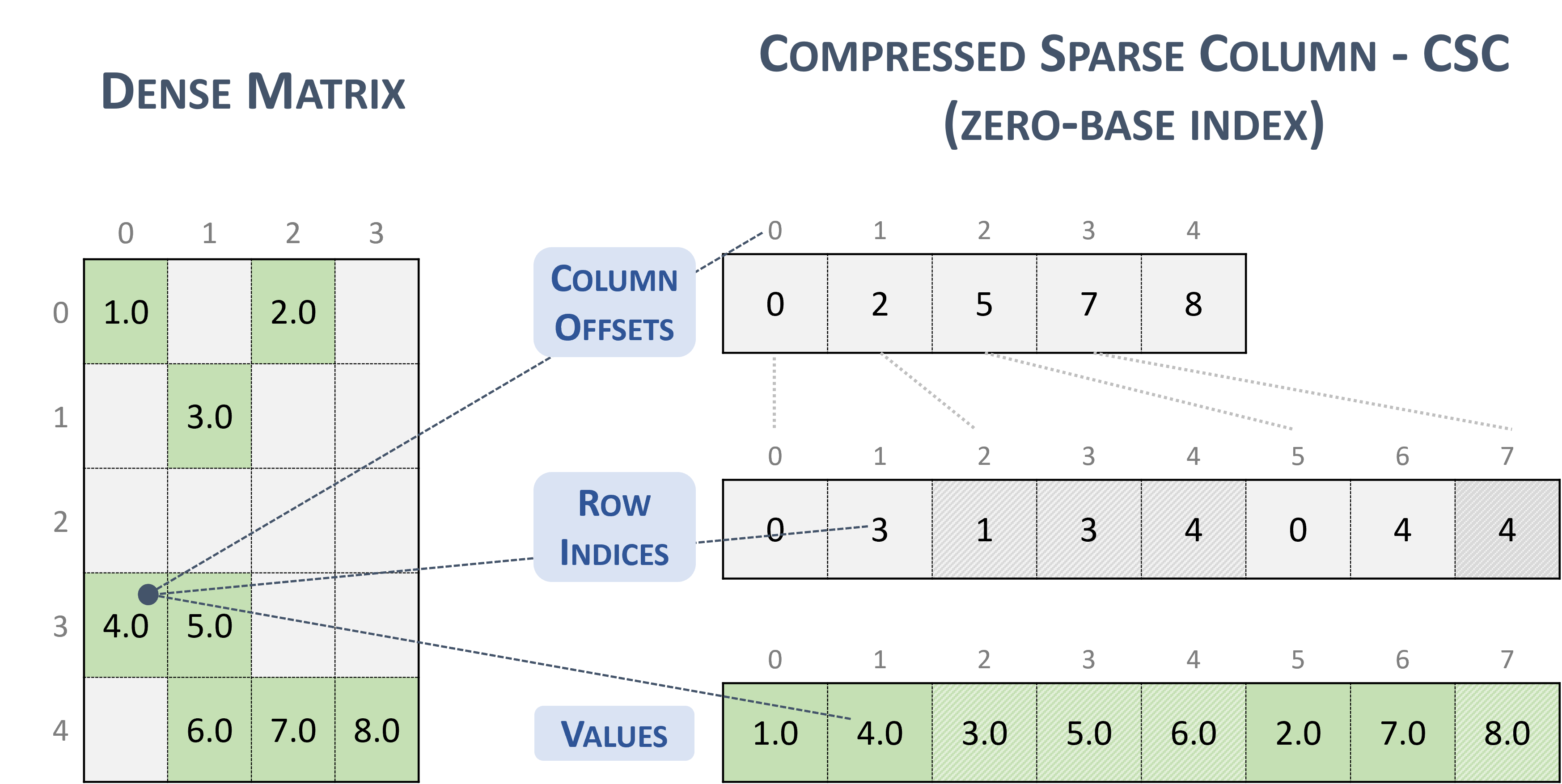
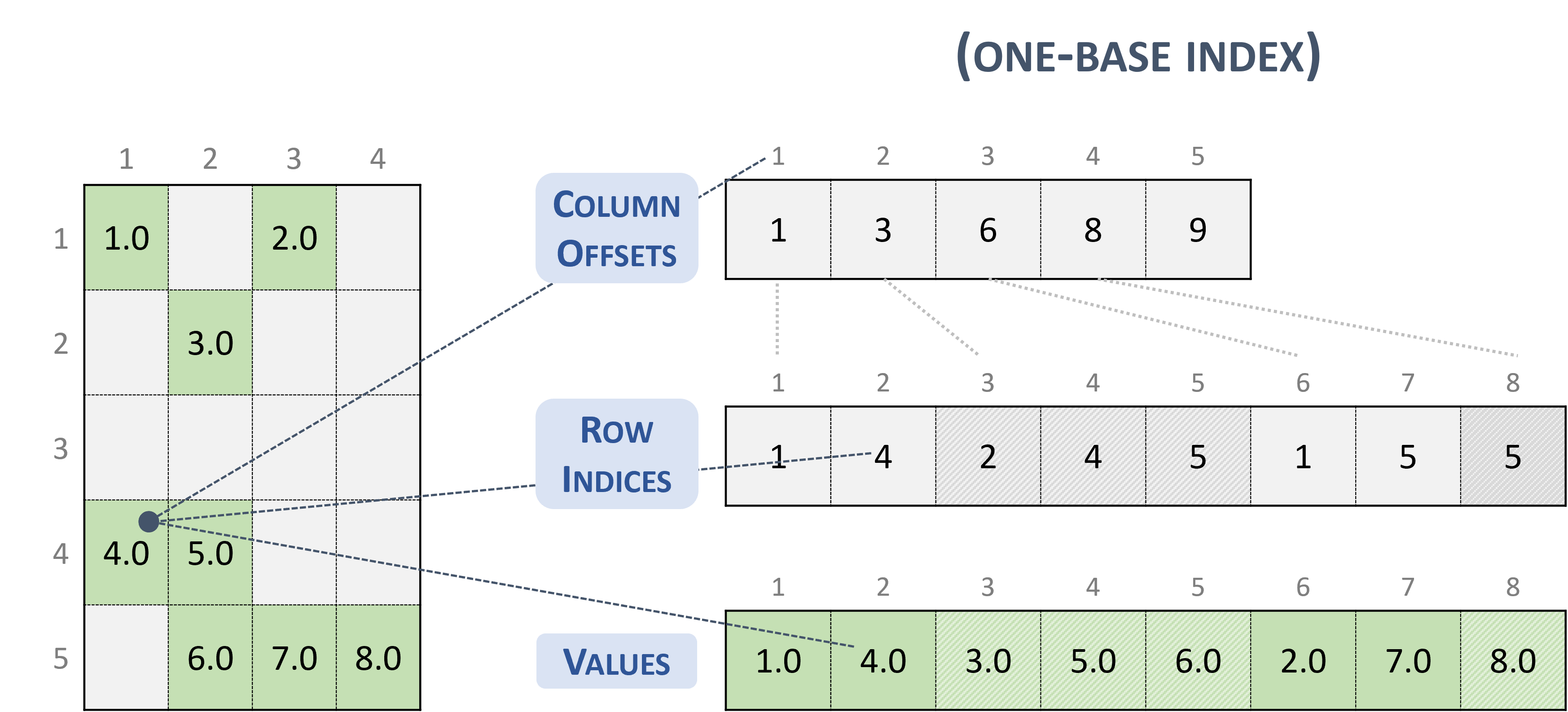
Note
The CSR format has exactly the same memory layout as its transpose in CSC format (and vice versa).
Note
cuSPARSE supports both sorted and unsorted row indices within a given column.
Note
If the row indices within a given column are not unique, the correctness of the computation is not always ensured.
Given an entry in the CSC format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
column * leading_dimension + row_indices[column_offsets[column] + k]
// column-major
row_indices[column_offsets[column] + k] * leading_dimension + column
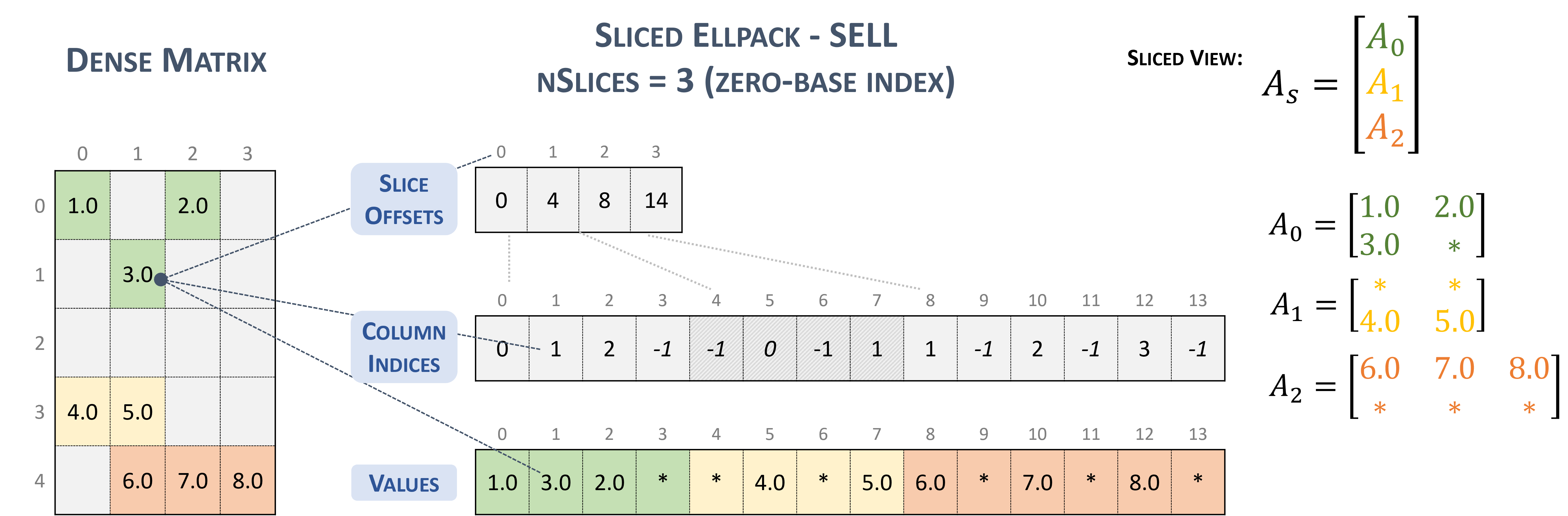
3.3.5. Sliced Ellpack (SELL)
The Sliced Ellpack format is standardized and well-known as the state of the art. This format allows to significantly improve the performance of all problems that involve low variability in the number of nonzero elements per row.
A matrix in the Sliced Ellpack format is divided into slices of an exact number of rows (\(sliceSize\)), defined by the user.
The maximum row length (i.e., the maximum non-zeros per row) is found for each slice, and every row in the slice is padded to the maximum row length.
The value -1 is used for padding.
A \(m \times n\) sparse matrix \(A\) is equivalent to a sliced sparse matrix \(A_{s}\) with \(nslices = \left \lceil{\frac{m}{sliceSize}}\right \rceil\) slice rows and \(n\) columns. To improve memory coalescing and memory utilization, each slice is stored in column-major order.
A sparse matrix stored in SELL format is represented by the following parameters.
The number of slices.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The total number elements (
sellValuesSize), including non-zero values and padded elements.The pointer to the slice offsets of length \(nslices + 1\) that holds offsets of the slides corresponding to the columns and values arrays.
The pointer to the column indices array of length
sellValuesSizethat contains column indices of the corresponding elements in the values array. The column indices are stored in column-major layout. Value-1refers to padding.The pointer to the values array of length
sellValuesSizethat holds all non-zero values and padding in column-major layout.
The following example shows a \(5 \times 4\) matrix represented in SELL format.

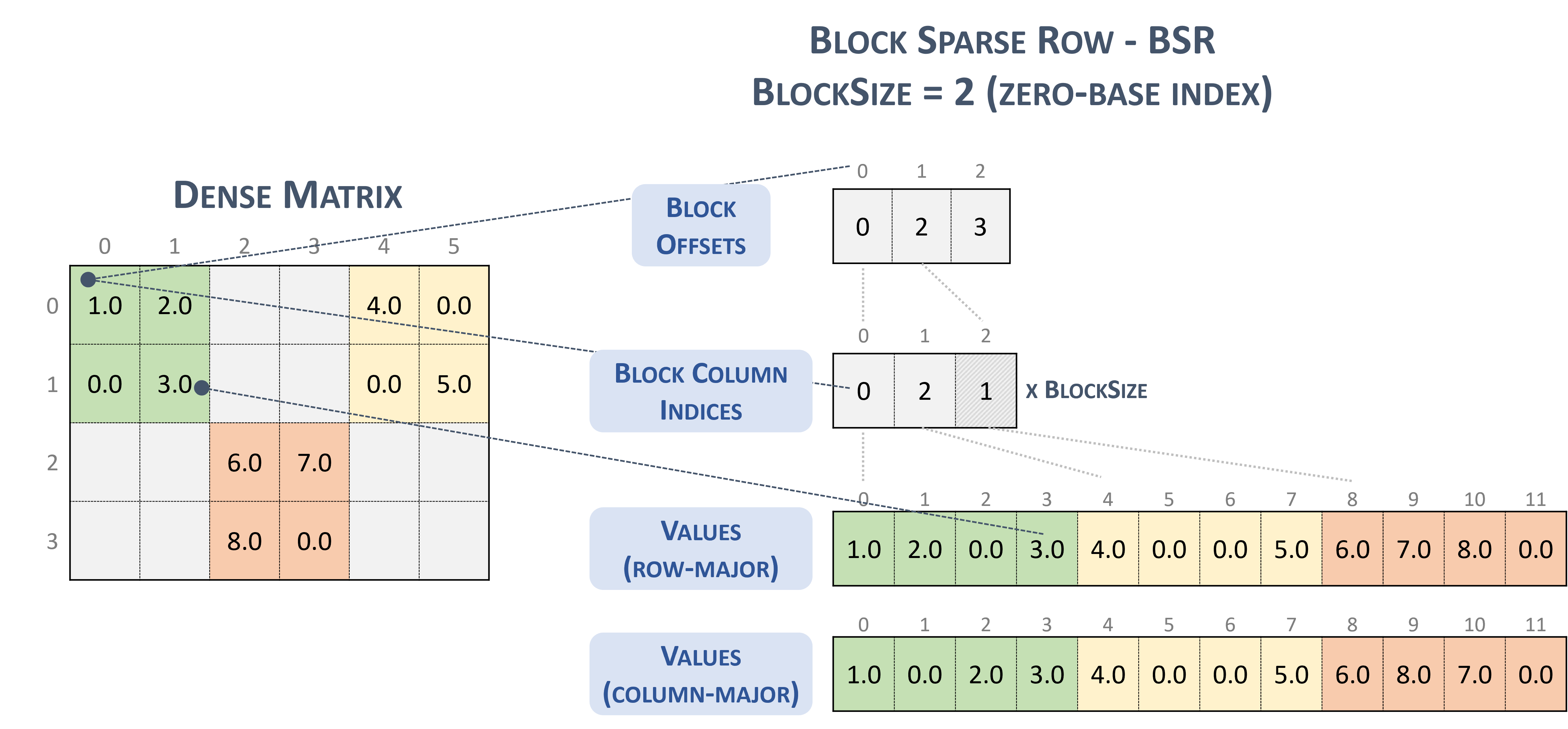
3.3.6. Block Sparse Row (BSR)
The BSR format is similar to CSR, where the column indices represent two-dimensional blocks instead of a single matrix entry.
A matrix in the Block Sparse Row format is organized into blocks of size \(blockSize\), defined by the user.
A \(m \times n\) sparse matrix \(A\) is equivalent to a block sparse matrix \(A_{B}\): \(mb \times nb\) with \(mb = \frac{m}{blockSize}\) block rows and \(nb = \frac{n}{blockSize}\) block columns. If \(m\) or \(n\) is not multiple of \(blockSize\), the user needs to pad the matrix with zeros.
Note
cuSPARSE currently supports only square blocks.
The BSR format stores the blocks in row-major ordering. However, the internal storage format of blocks can be column-major (cusparseDirection_t=CUSPARSE_DIRECTION_COLUMN) or row-major (cusparseDirection_t=CUSPARSE_DIRECTION_ROW), independently of the base index.
A sparse matrix stored in BSR format is represented by the following parameters.
The block size.
The number of row blocks in the matrix.
The number of column blocks in the matrix.
The number of non-zero blocks (
nnzb) in the matrix.The pointers to the row block offsets array of length number of row blocks + 1 that represents the starting position of each row block in the columns and values arrays.
The pointers to the column block indices array of length
nnzbthat contains the location of the corresponding elements in the values array.The pointers to the values array of length
nnzbthat holds all nonzero values of the matrix.
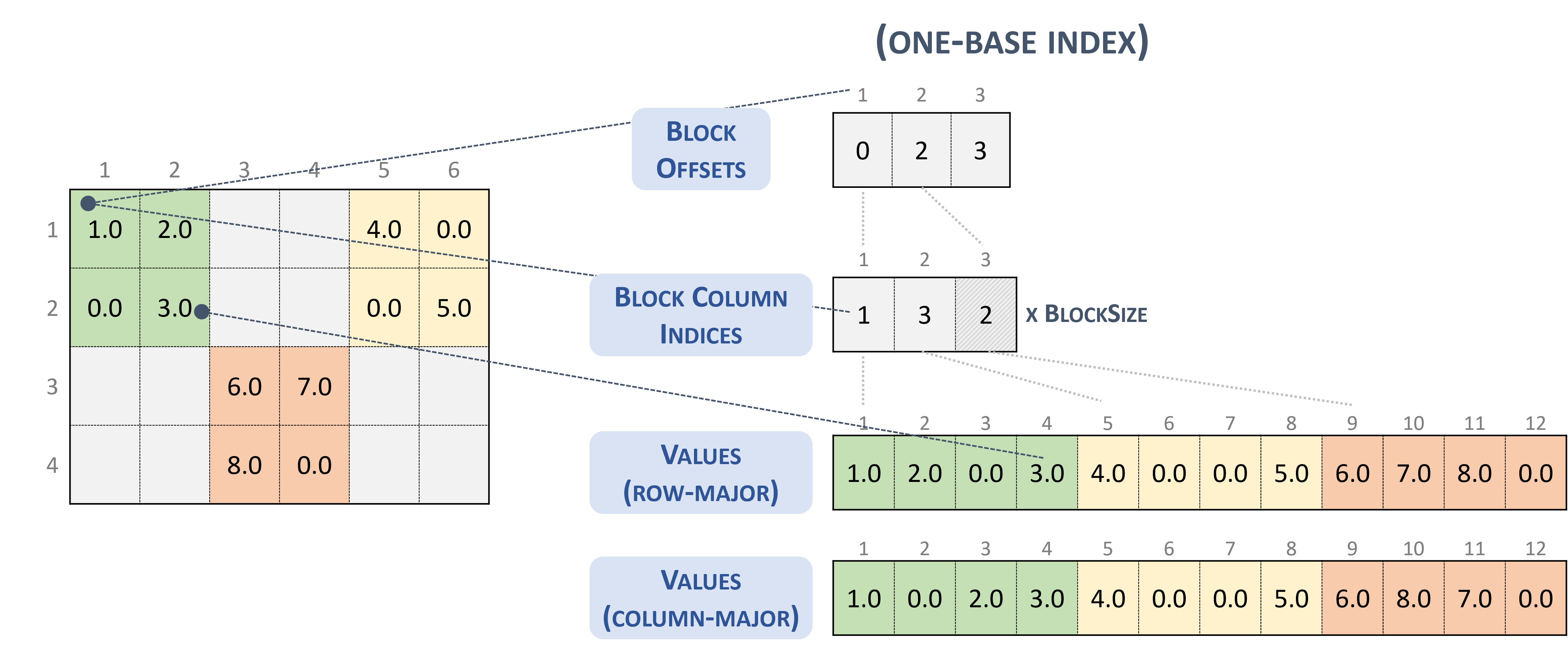
The following example shows a \(4 \times 7\) matrix represented in BSR format.
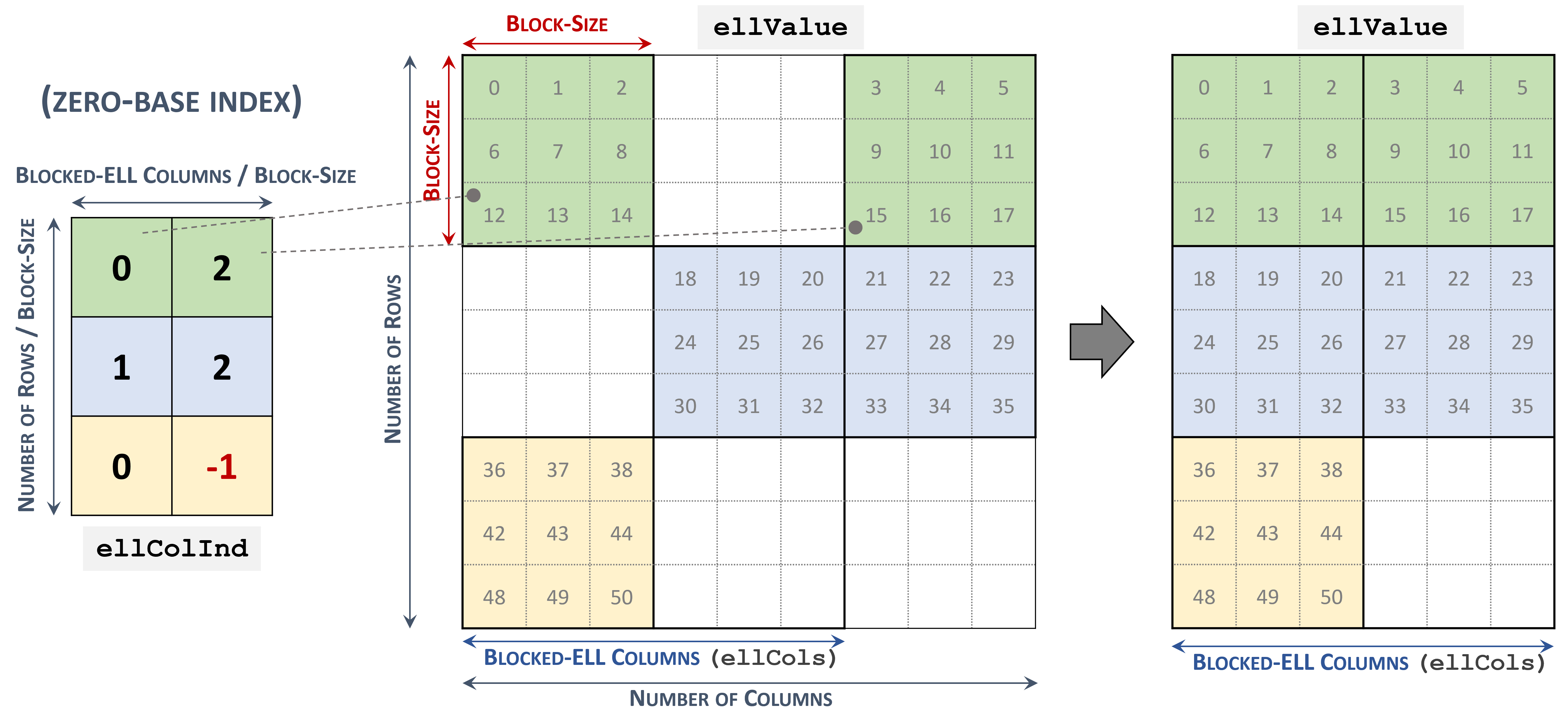
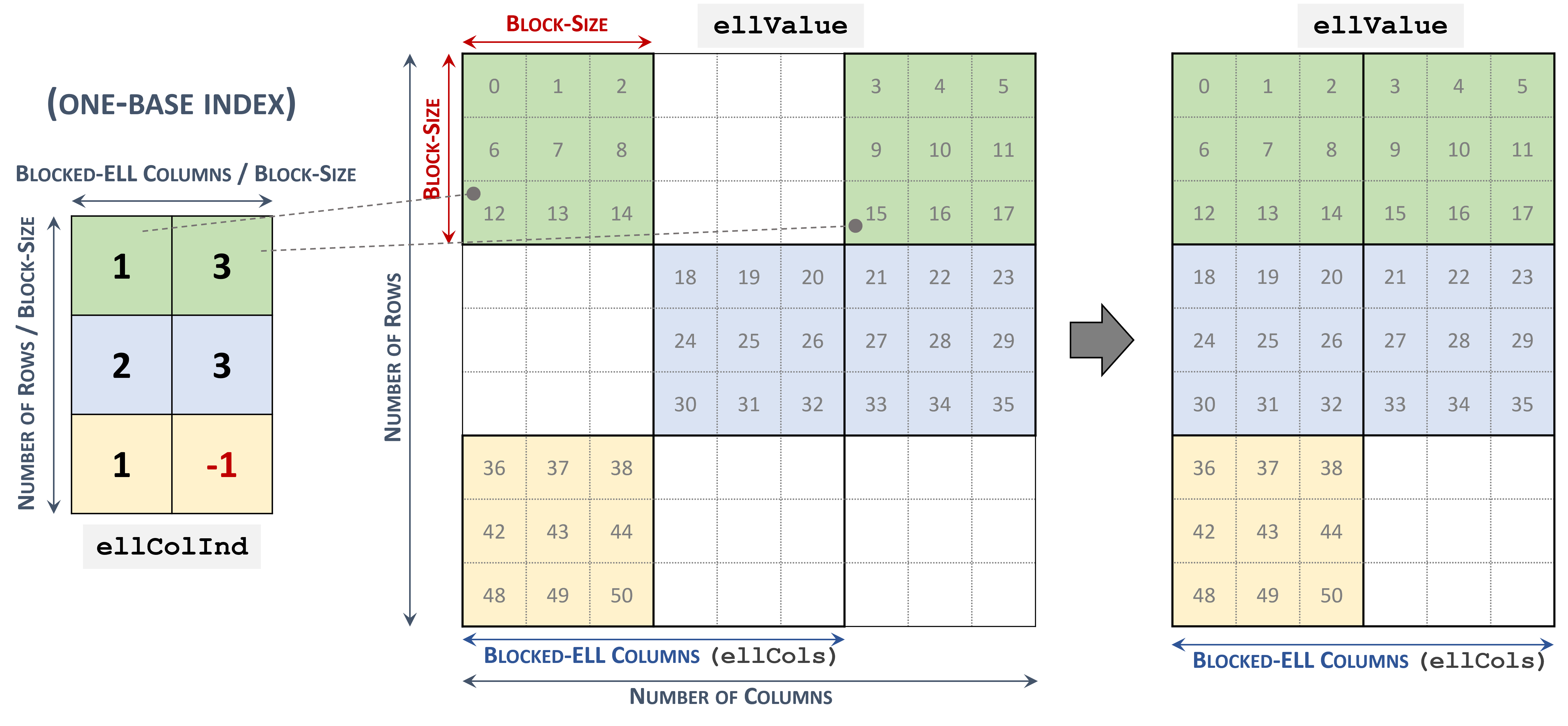
3.3.7. Blocked Ellpack (BLOCKED-ELL)
The Blocked Ellpack format is similar to the standard Ellpack, where the column indices represent two-dimensional blocks instead of a single matrix entry.
A matrix in the Blocked Ellpack format is organized into blocks of size \(blockSize\), defined by the user. The number of columns per row \(nEllCols\) is also defined by the user (\(nEllCols \le n\)).
A \(m \times n\) sparse matrix \(A\) is equivalent to a Blocked-ELL matrix \(A_{B}\): \(mb \times nb\) with \(mb = \left \lceil{\frac{m}{blockSize}}\right \rceil\) block rows, and \(nb = \left \lceil{\frac{nEllCols}{blockSize}}\right \rceil\) block columns. If \(m\) or \(n\) is not multiple of \(blockSize\), then the remaining elements are zero.
A sparse matrix stored in Blocked-ELL format is represented by the following parameters.
The block size.
The number of rows in the matrix.
The number of columns in the matrix.
The number of columns per row (
nEllCols) in the matrix.The pointers to the column block indices array of length \(mb \times nb\) that contains the location of the corresponding elements in the values array. Empty blocks can be represented with
-1index.The pointers to the values array of length \(m \times nEllCols\) that holds all nonzero values of the matrix in row-major ordering.
The following example shows a \(9 \times 9\) matrix represented in Blocked-ELL format.
3.3.8. Extended BSR Format (BSRX) [DEPRECATED]
BSRX is the same as the BSR format, but the array bsrRowPtrA is separated into two parts. The first nonzero block of each row is still specified by the array bsrRowPtrA, which is the same as in BSR, but the position next to the last nonzero block of each row is specified by the array bsrEndPtrA. Briefly, BSRX format is simply like a 4-vector variant of BSR format.
Matrix A is represented in BSRX format by the following parameters.
|
(integer) |
Block dimension of matrix |
|
(integer) |
The number of block rows of |
|
(integer) |
The number of block columns of |
|
(integer) |
number of nonzero blocks in the matrix |
|
(pointer) |
Points to the data array of length \(nnzb \ast blockDim^{2}\) that holds all the elements of the nonzero blocks of |
|
(pointer) |
Points to the integer array of length |
|
(pointer) |
Points to the integer array of length |
|
(pointer) |
Points to the integer array of length |
A simple conversion between BSR and BSRX can be done as follows. Suppose the developer has a 2×3 block sparse matrix \(A_{b}\) represented as shown.
\(A_{b} = \begin{bmatrix} A_{00} & A_{01} & A_{02} \\ A_{10} & A_{11} & A_{12} \\ \end{bmatrix}\) |
Assume it has this BSR format.
\(\begin{matrix} \text{bsrValA of BSR} & = & \begin{bmatrix} A_{00} & A_{01} & A_{10} & A_{11} & A_{12} \\ \end{bmatrix} \\ \text{bsrRowPtrA of BSR} & = & \begin{bmatrix} {0\phantom{.0}} & {2\phantom{.0}} & 5 \\ \end{bmatrix} \\ \text{bsrColIndA of BSR} & = & \begin{bmatrix} {0\phantom{.0}} & {1\phantom{.0}} & {0\phantom{.0}} & {1\phantom{.0}} & 2 \\ \end{bmatrix} \\ \end{matrix}\) |
The bsrRowPtrA of the BSRX format is simply the first two elements of the bsrRowPtrA BSR format. The bsrEndPtrA of BSRX format is the last two elements of the bsrRowPtrA of BSR format.
\(\begin{matrix} \text{bsrRowPtrA of BSRX} & = & \begin{bmatrix} {0\phantom{.0}} & 2 \\ \end{bmatrix} \\ \text{bsrEndPtrA of BSRX} & = & \begin{bmatrix} {2\phantom{.0}} & 5 \\ \end{bmatrix} \\ \end{matrix}\) |
The advantage of the BSRX format is that the developer can specify a submatrix in the original BSR format by modifying bsrRowPtrA and bsrEndPtrA while keeping bsrColIndA and bsrValA unchanged.
For example, to create another block matrix \(\widetilde{A} = \begin{bmatrix}
O & O & O \\
O & A_{11} & O \\
\end{bmatrix}\) that is slightly different from \(A\) , the developer can keep bsrColIndA and bsrValA, but reconstruct \(\widetilde{A}\) by properly setting of bsrRowPtrA and bsrEndPtrA. The following 4-vector characterizes \(\widetilde{A}\) .
\(\begin{matrix} {\text{bsrValA of }\widetilde{A}} & = & \begin{bmatrix} A_{00} & A_{01} & A_{10} & A_{11} & A_{12} \\ \end{bmatrix} \\ {\text{bsrColIndA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & {1\phantom{.0}} & {0\phantom{.0}} & {1\phantom{.0}} & 2 \\ \end{bmatrix} \\ {\text{bsrRowPtrA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & 3 \\ \end{bmatrix} \\ {\text{bsrEndPtrA of }\widetilde{A}} & = & \begin{bmatrix} {0\phantom{.0}} & 4 \\ \end{bmatrix} \\ \end{matrix}\) |
4. cuSPARSE Basic APIs
4.1. cuSPARSE Types Reference
4.1.1. cudaDataType_t
The section describes the types shared by multiple CUDA Libraries and defined in the header file library_types.h. The cudaDataType type is an enumerator to specify the data precision. It is used when the data reference does not carry the type itself (e.g. void*). For example, it is used in the routine cusparseSpMM().
Value |
Meaning |
Data Type |
Header |
|
|---|---|---|---|---|
|
The data type is 16-bit IEEE-754 floating-point |
|
cuda_fp16.h |
|
|
The data type is 16-bit complex IEEE-754 floating-point |
|
cuda_fp16.h |
[DEPRECATED] |
|
The data type is 16-bit bfloat floating-point |
|
cuda_bf16.h |
|
|
The data type is 16-bit complex bfloat floating-point |
|
cuda_bf16.h |
[DEPRECATED] |
|
The data type is 32-bit IEEE-754 floating-point |
|
||
|
The data type is 32-bit complex IEEE-754 floating-point |
|
cuComplex.h |
|
|
The data type is 64-bit IEEE-754 floating-point |
|
||
|
The data type is 64-bit complex IEEE-754 floating-point |
|
cuComplex.h |
|
|
The data type is 8-bit integer |
|
stdint.h |
|
|
The data type is 32-bit integer |
|
stdint.h |
IMPORTANT: The Generic API routines allow all data types reported in the respective section of the documentation only on GPU architectures with native support for them. If a specific GPU model does not provide native support for a given data type, the routine returns CUSPARSE_STATUS_ARCH_MISMATCH error.
Unsupported data types and Compute Capability (CC):
__halfon GPUs withCC < 53(e.g. Kepler)__nv_bfloat16on GPUs withCC < 80(e.g. Kepler, Maxwell, Pascal, Volta, Turing)
see https://developer.nvidia.com/cuda-gpus
4.1.2. cusparseStatus_t
This data type represents the status returned by the library functions and it can have the following values
Value |
Description |
|---|---|
|
The operation completed successfully |
|
The cuSPARSE library was not initialized. This is usually caused by the lack of a prior call, an error in the CUDA Runtime API called by the cuSPARSE routine, or an error in the hardware setup To correct: call The error also applies to generic APIs ( Generic APIs reference) for indicating a matrix/vector descriptor not initialized |
|
Resource allocation failed inside the cuSPARSE library. This is usually caused by a device memory allocation ( To correct: prior to the function call, deallocate previously allocated memory as much as possible |
|
An unsupported value or parameter was passed to the function (a negative vector size, for example) To correct: ensure that all the parameters being passed have valid values |
|
The function requires a feature absent from the device architecture To correct: compile and run the application on a device with appropriate compute capability |
|
The GPU program failed to execute. This is often caused by a launch failure of the kernel on the GPU, which can be caused by multiple reasons To correct: check that the hardware, an appropriate version of the driver, and the cuSPARSE library are correctly installed |
|
An internal cuSPARSE operation failed To correct: check that the hardware, an appropriate version of the driver, and the cuSPARSE library are correctly installed. Also, check that the memory passed as a parameter to the routine is not being deallocated prior to the routine completion |
|
The matrix type is not supported by this function. This is usually caused by passing an invalid matrix descriptor to the function To correct: check that the fields in |
|
The operation or data type combination is currently not supported by the function |
|
The resources for the computation, such as GPU global or shared memory, are not sufficient to complete the operation. The error can also indicate that the current computation mode (e.g. bit size of sparse matrix indices) does not allow to handle the given input |
4.1.3. cusparseHandle_t
This is a pointer type to an opaque cuSPARSE context, which the user must initialize by calling prior to calling cusparseCreate() any other library function. The handle created and returned by cusparseCreate() must be passed to every cuSPARSE function.
4.1.4. cusparsePointerMode_t
This type indicates whether the scalar values are passed by reference on the host or device. It is important to point out that if several scalar values are passed by reference in the function call, all of them will conform to the same single pointer mode. The pointer mode can be set and retrieved using cusparseSetPointerMode() and cusparseGetPointerMode() routines, respectively.
Value |
Meaning |
|---|---|
|
The scalars are passed by reference on the host. |
|
The scalars are passed by reference on the device. |
4.1.5. cusparseOperation_t
This type indicates which operations is applied to the related input (e.g. sparse matrix, or vector).
Value |
Meaning |
|---|---|
|
The non-transpose operation is selected. |
|
The transpose operation is selected. |
|
The conjugate transpose operation is selected. |
4.1.6. cusparseDiagType_t
This type indicates if the matrix diagonal entries are unity. The diagonal elements are always assumed to be present, but if CUSPARSE_DIAG_TYPE_UNIT is passed to an API routine, then the routine assumes that all diagonal entries are unity and will not read or modify those entries. Note that in this case the routine assumes the diagonal entries are equal to one, regardless of what those entries are actually set to in memory.
Value |
Meaning |
|---|---|
|
The matrix diagonal has non-unit elements. |
|
The matrix diagonal has unit elements. |
4.1.7. cusparseFillMode_t
This type indicates if the lower or upper part of a matrix is stored in sparse storage.
Value |
Meaning |
|---|---|
|
The lower triangular part is stored. |
|
The upper triangular part is stored. |
4.1.8. cusparseIndexBase_t
This type indicates if the base of the matrix indices is zero or one.
Value |
Meaning |
|---|---|
|
The base index is zero (C compatibility). |
|
The base index is one (Fortran compatibility). |
4.1.9. cusparseDirection_t
This type indicates whether the elements of a dense matrix should be parsed by rows or by columns (assuming column-major storage in memory of the dense matrix) in function cusparse[S|D|C|Z]nnz. Besides storage format of blocks in BSR format is also controlled by this type.
Value |
Meaning |
|---|---|
|
The matrix should be parsed by rows. |
|
The matrix should be parsed by columns. |
4.2. cuSPARSE Management API
The cuSPARSE functions for managing the library are described in this section.
4.2.1. cusparseCreate()
cusparseStatus_t
cusparseCreate(cusparseHandle_t *handle)
This function initializes the cuSPARSE library and creates a handle on the cuSPARSE context. It must be called before any other cuSPARSE API function is invoked. It allocates hardware resources necessary for accessing the GPU.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The pointer to the handle to the cuSPARSE context |
See cusparseStatus_t for the description of the return status
4.2.2. cusparseDestroy()
cusparseStatus_t
cusparseDestroy(cusparseHandle_t handle)
This function releases CPU-side resources used by the cuSPARSE library. The release of GPU-side resources may be deferred until the application shuts down.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The handle to the cuSPARSE context |
See cusparseStatus_t for the description of the return status
4.2.3. cusparseGetErrorName()
const char*
cusparseGetErrorString(cusparseStatus_t status)
The function returns the string representation of an error code enum name. If the error code is not recognized, “unrecognized error code” is returned.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Error code to convert to string |
|
OUT |
Pointer to a NULL-terminated string |
4.2.4. cusparseGetErrorString()
const char*
cusparseGetErrorString(cusparseStatus_t status)
Returns the description string for an error code. If the error code is not recognized, “unrecognized error code” is returned.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Error code to convert to string |
|
OUT |
Pointer to a NULL-terminated string |
4.2.5. cusparseGetProperty()
cusparseStatus_t
cusparseGetProperty(libraryPropertyType type,
int* value)
The function returns the value of the requested property. Refer to libraryPropertyType for supported types.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Requested property |
|
OUT |
Value of the requested property |
libraryPropertyType (defined in library_types.h):
Value |
Meaning |
|---|---|
|
Enumerator to query the major version |
|
Enumerator to query the minor version |
|
Number to identify the patch level |
See cusparseStatus_t for the description of the return status
4.2.6. cusparseGetVersion()
cusparseStatus_t
cusparseGetVersion(cusparseHandle_t handle,
int* version)
This function returns the version number of the cuSPARSE library.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
cuSPARSE handle |
|
OUT |
The version number of the library |
See cusparseStatus_t for the description of the return status
4.2.7. cusparseGetPointerMode()
cusparseStatus_t
cusparseGetPointerMode(cusparseHandlet handle,
cusparsePointerMode_t *mode)
This function obtains the pointer mode used by the cuSPARSE library. Please see the section on the cusparsePointerMode_t type for more details.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The handle to the cuSPARSE context |
|
OUT |
One of the enumerated pointer mode types |
See cusparseStatus_t for the description of the return status
4.2.8. cusparseSetPointerMode()
cusparseStatus_t
cusparseSetPointerMode(cusparseHandle_t handle,
cusparsePointerMode_t mode)
This function sets the pointer mode used by the cuSPARSE library. The default is for the values to be passed by reference on the host. Please see the section on the cublasPointerMode_t type for more details.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The handle to the cuSPARSE context |
|
IN |
One of the enumerated pointer mode types |
See cusparseStatus_t for the description of the return status
4.2.9. cusparseGetStream()
cusparseStatus_t
cusparseGetStream(cusparseHandle_t handle, cudaStream_t *streamId)
This function gets the cuSPARSE library stream, which is being used to to execute all calls to the cuSPARSE library functions. If the cuSPARSE library stream is not set, all kernels use the default NULL stream.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The handle to the cuSPARSE context |
|
OUT |
The stream used by the library |
See cusparseStatus_t for the description of the return status
4.2.10. cusparseSetStream()
cusparseStatus_t
cusparseSetStream(cusparseHandle_t handle, cudaStream_t streamId)
This function sets the stream to be used by the cuSPARSE library to execute its routines.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
The handle to the cuSPARSE context |
|
IN |
The stream to be used by the library |
See cusparseStatus_t for the description of the return status
4.3. cuSPARSE Logging API
cuSPARSE logging mechanism can be enabled by setting the following environment variables before launching the target application:
CUSPARSE_LOG_LEVEL=<level> - while level is one of the following levels:
0- Off - logging is disabled (default)1- Error - only errors will be logged2- Trace - API calls that launch CUDA kernels will log their parameters and important information3- Hints - hints that can potentially improve the application’s performance4- Info - provides general information about the library execution, may contain details about heuristic status5- API Trace - API calls will log their parameter and important information
CUSPARSE_LOG_MASK=<mask> - while mask is a combination of the following masks:
0- Off1- Error2- Trace4- Hints8- Info16- API Trace
CUSPARSE_LOG_FILE=<file_name> - while file name is a path to a logging file. File name may contain %i, that will be replaced with the process id. E.g <file_name>_%i.log.
If CUSPARSE_LOG_FILE is not defined, the log messages are printed to stdout.
Starting from CUDA 12.3, it is also possible to dump sparse matrices (CSR, CSC, COO, SELL, BSR) in binary files during the creation by setting the environment variable CUSPARSE_STORE_INPUT_MATRIX. Later on, the binary files can be send to Math-Libs-Feedback@nvidia.com for debugging and reproducibility purposes of a specific correctness/performance issue.
Another option is to use the experimental cuSPARSE logging API. See:
Note
The logging mechanism is not available for the legacy APIs.
4.3.1. cusparseLoggerSetCallback()
cusparseStatus_t
cusparseLoggerSetCallback(cusparseLoggerCallback_t callback)
Experimental: The function sets the logging callback function.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Pointer to a callback function |
where cusparseLoggerCallback_t has the following signature:
void (*cusparseLoggerCallback_t)(int logLevel,
const char* functionName,
const char* message)
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Selected log level |
|
IN |
The name of the API that logged this message |
|
IN |
The log message |
See cusparseStatus_t for the description of the return status
4.3.2. cusparseLoggerSetFile()
cusparseStatus_t
cusparseLoggerSetFile(FILE* file)
Experimental: The function sets the logging output file. Note: once registered using this function call, the provided file handle must not be closed unless the function is called again to switch to a different file handle.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Pointer to an open file. File should have write permission |
See cusparseStatus_t for the description of the return status
4.3.3. cusparseLoggerOpenFile()
cusparseStatus_t
cusparseLoggerOpenFile(const char* logFile)
Experimental: The function opens a logging output file in the given path.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Path of the logging output file |
See cusparseStatus_t for the description of the return status
4.3.4. cusparseLoggerSetLevel()
cusparseStatus_t
cusparseLoggerSetLevel(int level)
Experimental: The function sets the value of the logging level. path.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Value of the logging level |
See cusparseStatus_t for the description of the return status
4.3.5. cusparseLoggerSetMask()
cusparseStatus_t
cusparseLoggerSetMask(int mask)
Experimental: The function sets the value of the logging mask.
Param. |
In/out |
Meaning |
|---|---|---|
|
IN |
Value of the logging mask |
See cusparseStatus_t for the description of the return status
5. cuSPARSE Legacy APIs
5.1. Naming Conventions
The cuSPARSE legacy functions are available for data types float, double, cuComplex, and cuDoubleComplex. The sparse Level 2, and Level 3 functions follow this naming convention:
cusparse<t>[<matrix data format>]<operation>[<output matrix data format>]
where <t> can be S, D, C, Z, or X, corresponding to the data types float, double, cuComplex, cuDoubleComplex, and the generic type, respectively.
The <matrix data format> can be dense, coo, csr, or csc, corresponding to the dense, coordinate, compressed sparse row, and compressed sparse column formats, respectively.
5.2. cuSPARSE Legacy Types Reference
5.2.1. cusparseAction_t
This type indicates whether the operation is performed only on indices or on data and indices.
Value |
Meaning |
|---|---|
|
the operation is performed only on indices. |
|
the operation is performed on data and indices. |
5.2.2. cusparseMatDescr_t
This structure is used to describe the shape and properties of a matrix.
typedef struct {
cusparseMatrixType_t MatrixType;
cusparseFillMode_t FillMode;
cusparseDiagType_t DiagType;
cusparseIndexBase_t IndexBase;
} cusparseMatDescr_t;
5.2.3. cusparseMatrixType_t
This type indicates the type of matrix stored in sparse storage. Notice that for symmetric, Hermitian and triangular matrices only their lower or upper part is assumed to be stored.
The whole idea of matrix type and fill mode is to keep minimum storage for symmetric/Hermitian matrix, and also to take advantage of symmetric property on SpMV (Sparse Matrix Vector multiplication). To compute y=A*x when A is symmetric and only lower triangular part is stored, two steps are needed. First step is to compute y=(L+D)*x and second step is to compute y=L^T*x + y. Given the fact that the transpose operation y=L^T*x is 10x slower than non-transpose version y=L*x, the symmetric property does not show up any performance gain. It is better for the user to extend the symmetric matrix to a general matrix and apply y=A*x with matrix type CUSPARSE_MATRIX_TYPE_GENERAL.
In general, SpMV, preconditioners (incomplete Cholesky or incomplete LU) and triangular solver are combined together in iterative solvers, for example PCG and GMRES. If the user always uses general matrix (instead of symmetric matrix), there is no need to support other than general matrix in preconditioners. Therefore the new routines, [bsr|csr]sv2 (triangular solver), [bsr|csr]ilu02 (incomplete LU) and [bsr|csr]ic02 (incomplete Cholesky), only support matrix type CUSPARSE_MATRIX_TYPE_GENERAL.
Value |
Meaning |
|---|---|
|
the matrix is general. |
|
the matrix is symmetric. |
|
the matrix is Hermitian. |
|
the matrix is triangular. |
5.2.4. cusparseColorInfo_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in csrcolor().
5.2.5. cusparseSolvePolicy_t [DEPRECATED]
This type indicates whether level information is generated and used in csrsv2, csric02, csrilu02, bsrsv2, bsric02 and bsrilu02.
Value |
Meaning |
|---|---|
|
no level information is generated and used. |
|
generate and use level information. |
5.2.6. bsric02Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in bsric02_bufferSize(), bsric02_analysis(), and bsric02().
5.2.7. bsrilu02Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in bsrilu02_bufferSize(), bsrilu02_analysis(), and bsrilu02().
5.2.8. bsrsm2Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in bsrsm2_bufferSize(), bsrsm2_analysis(), and bsrsm2_solve().
5.2.9. bsrsv2Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in bsrsv2_bufferSize(), bsrsv2_analysis(), and bsrsv2_solve().
5.2.10. csric02Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in csric02_bufferSize(), csric02_analysis(), and csric02().
5.2.11. csrilu02Info_t [DEPRECATED]
This is a pointer type to an opaque structure holding the information used in csrilu02_bufferSize(), csrilu02_analysis(), and csrilu02().
5.3. cuSPARSE Helper Function Reference
The cuSPARSE helper functions are described in this section.
5.3.1. cusparseCreateColorInfo() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateColorInfo(cusparseColorInfo_t* info)
This function creates and initializes the cusparseColorInfo_t structure to default values.
Input
|
the pointer to the |
See cusparseStatus_t for the description of the return status
5.3.2. cusparseCreateMatDescr()
cusparseStatus_t
cusparseCreateMatDescr(cusparseMatDescr_t *descrA)
This function initializes the matrix descriptor. It sets the fields MatrixType and IndexBase to the default values CUSPARSE_MATRIX_TYPE_GENERAL and CUSPARSE_INDEX_BASE_ZERO , respectively, while leaving other fields uninitialized.
Input
|
the pointer to the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.3. cusparseDestroyColorInfo() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyColorInfo(cusparseColorInfo_t info)
This function destroys and releases any memory required by the structure.
Input
|
the pointer to the structure of |
See cusparseStatus_t for the description of the return status
5.3.4. cusparseDestroyMatDescr()
cusparseStatus_t
cusparseDestroyMatDescr(cusparseMatDescr_t descrA)
This function releases the memory allocated for the matrix descriptor.
Input
|
the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.5. cusparseGetMatDiagType()
cusparseDiagType_t
cusparseGetMatDiagType(const cusparseMatDescr_t descrA)
This function returns the DiagType field of the matrix descriptor descrA.
Input
|
the matrix descriptor. |
Returned
|
One of the enumerated diagType types. |
5.3.6. cusparseGetMatFillMode()
cusparseFillMode_t
cusparseGetMatFillMode(const cusparseMatDescr_t descrA)
This function returns the FillMode field of the matrix descriptor descrA.
Input
|
the matrix descriptor. |
Returned
|
One of the enumerated fillMode types. |
5.3.7. cusparseGetMatIndexBase()
cusparseIndexBase_t
cusparseGetMatIndexBase(const cusparseMatDescr_t descrA)
This function returns the IndexBase field of the matrix descriptor descrA.
Input
|
the matrix descriptor. |
Returned
|
One of the enumerated indexBase types. |
5.3.8. cusparseGetMatType()
cusparseMatrixType_t
cusparseGetMatType(const cusparseMatDescr_t descrA)
This function returns the MatrixType field of the matrix descriptor descrA.
Input
|
the matrix descriptor. |
Returned
|
One of the enumerated matrix types. |
5.3.9. cusparseSetMatDiagType()
cusparseStatus_t
cusparseSetMatDiagType(cusparseMatDescr_t descrA,
cusparseDiagType_t diagType)
This function sets the DiagType field of the matrix descriptor descrA.
Input
|
One of the enumerated diagType types. |
Output
|
the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.10. cusparseSetMatFillMode()
cusparseStatus_t
cusparseSetMatFillMode(cusparseMatDescr_t descrA,
cusparseFillMode_t fillMode)
This function sets the FillMode field of the matrix descriptor descrA.
Input
|
One of the enumerated fillMode types. |
Output
|
the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.11. cusparseSetMatIndexBase()
cusparseStatus_t
cusparseSetMatIndexBase(cusparseMatDescr_t descrA,
cusparseIndexBase_t base)
This function sets the IndexBase field of the matrix descriptor descrA.
Input
|
One of the enumerated indexBase types. |
Output
|
the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.12. cusparseSetMatType()
cusparseStatus_t
cusparseSetMatType(cusparseMatDescr_t descrA, cusparseMatrixType_t type)
This function sets the MatrixType field of the matrix descriptor descrA.
Input
|
One of the enumerated matrix types. |
Output
|
the matrix descriptor. |
See cusparseStatus_t for the description of the return status
5.3.13. cusparseCreateCsric02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateCsric02Info(csric02Info_t *info);
This function creates and initializes the solve and analysis structure of incomplete Cholesky to default values.
Input
|
the pointer to the solve and analysis structure of incomplete Cholesky. |
See cusparseStatus_t for the description of the return status
5.3.14. cusparseDestroyCsric02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyCsric02Info(csric02Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.15. cusparseCreateCsrilu02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateCsrilu02Info(csrilu02Info_t *info);
This function creates and initializes the solve and analysis structure of incomplete LU to default values.
Input
|
the pointer to the solve and analysis structure of incomplete LU. |
See cusparseStatus_t for the description of the return status
5.3.16. cusparseDestroyCsrilu02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyCsrilu02Info(csrilu02Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.17. cusparseCreateBsrsv2Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateBsrsv2Info(bsrsv2Info_t *info);
This function creates and initializes the solve and analysis structure of bsrsv2 to default values.
Input
|
the pointer to the solve and analysis structure of bsrsv2. |
See cusparseStatus_t for the description of the return status
5.3.18. cusparseDestroyBsrsv2Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyBsrsv2Info(bsrsv2Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.19. cusparseCreateBsrsm2Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateBsrsm2Info(bsrsm2Info_t *info);
This function creates and initializes the solve and analysis structure of bsrsm2 to default values.
Input
|
the pointer to the solve and analysis structure of bsrsm2. |
See cusparseStatus_t for the description of the return status
5.3.20. cusparseDestroyBsrsm2Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyBsrsm2Info(bsrsm2Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.21. cusparseCreateBsric02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateBsric02Info(bsric02Info_t *info);
This function creates and initializes the solve and analysis structure of block incomplete Cholesky to default values.
Input
|
the pointer to the solve and analysis structure of block incomplete Cholesky. |
See cusparseStatus_t for the description of the return status
5.3.22. cusparseDestroyBsric02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyBsric02Info(bsric02Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.23. cusparseCreateBsrilu02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateBsrilu02Info(bsrilu02Info_t *info);
This function creates and initializes the solve and analysis structure of block incomplete LU to default values.
Input
|
the pointer to the solve and analysis structure of block incomplete LU. |
See cusparseStatus_t for the description of the return status
5.3.24. cusparseDestroyBsrilu02Info() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyBsrilu02Info(bsrilu02Info_t info);
This function destroys and releases any memory required by the structure.
Input
|
the solve |
See cusparseStatus_t for the description of the return status
5.3.25. cusparseCreatePruneInfo() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreatePruneInfo(pruneInfo_t *info);
This function creates and initializes structure of prune to default values.
Input
|
the pointer to the structure of |
See cusparseStatus_t for the description of the return status
5.3.26. cusparseDestroyPruneInfo() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseDestroyPruneInfo(pruneInfo_t info);
This function destroys and releases any memory required by the structure.
Input
|
the structure of |
See cusparseStatus_t for the description of the return status
5.4. cuSPARSE Level 2 Function Reference
This chapter describes the sparse linear algebra functions that perform operations between sparse matrices and dense vectors.
5.4.1. cusparse<t>bsrmv()
cusparseStatus_t
cusparseSbsrmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int mb,
int nb,
int nnzb,
const float* alpha,
const cusparseMatDescr_t descr,
const float* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int blockDim,
const float* x,
const float* beta,
float* y)
cusparseStatus_t
cusparseDbsrmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int mb,
int nb,
int nnzb,
const double* alpha,
const cusparseMatDescr_t descr,
const double* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int blockDim,
const double* x,
const double* beta,
double* y)
cusparseStatus_t
cusparseCbsrmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int mb,
int nb,
int nnzb,
const cuComplex* alpha,
const cusparseMatDescr_t descr,
const cuComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int blockDim,
const cuComplex* x,
const cuComplex* beta,
cuComplex* y)
cusparseStatus_t
cusparseZbsrmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int mb,
int nb,
int nnzb,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descr,
const cuDoubleComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int blockDim,
const cuDoubleComplex* x,
const cuDoubleComplex* beta,
cuDoubleComplex* y)
This function performs the matrix-vector operation
\(\text{y} = \alpha \ast \text{op}(A) \ast \text{x} + \beta \ast \text{y}\) |
where \(A\text{ is an }(mb \ast blockDim) \times (nb \ast blockDim)\) sparse matrix that is defined in BSR storage format by the three arrays bsrVal, bsrRowPtr, and bsrColInd); x and y are vectors; \(\alpha\text{ and }\beta\) are scalars; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if trans == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
bsrmv() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Several comments on bsrmv():
Only
blockDim > 1is supportedOnly
CUSPARSE_OPERATION_NON_TRANSPOSEis supported, that is
\(\text{y} = \alpha \ast A \ast \text{x} + \beta{} \ast \text{y}\) |
Only
CUSPARSE_MATRIX_TYPE_GENERALis supported.The size of vector
xshould be \((nb \ast blockDim)\) at least, and the size of vectoryshould be \((mb \ast blockDim)\) at least; otherwise, the kernel may returnCUSPARSE_STATUS_EXECUTION_FAILEDbecause of an out-of-bounds array.
For example, suppose the user has a CSR format and wants to try bsrmv(), the following code demonstrates how to use csr2bsr() conversion and bsrmv() multiplication in single precision.
// Suppose that A is m x n sparse matrix represented by CSR format,
// hx is a host vector of size n, and hy is also a host vector of size m.
// m and n are not multiple of blockDim.
// step 1: transform CSR to BSR with column-major order
int base, nnz;
int nnzb;
cusparseDirection_t dirA = CUSPARSE_DIRECTION_COLUMN;
int mb = (m + blockDim-1)/blockDim;
int nb = (n + blockDim-1)/blockDim;
cudaMalloc((void**)&bsrRowPtrC, sizeof(int) *(mb+1));
cusparseXcsr2bsrNnz(handle, dirA, m, n,
descrA, csrRowPtrA, csrColIndA, blockDim,
descrC, bsrRowPtrC, &nnzb);
cudaMalloc((void**)&bsrColIndC, sizeof(int)*nnzb);
cudaMalloc((void**)&bsrValC, sizeof(float)*(blockDim*blockDim)*nnzb);
cusparseScsr2bsr(handle, dirA, m, n,
descrA, csrValA, csrRowPtrA, csrColIndA, blockDim,
descrC, bsrValC, bsrRowPtrC, bsrColIndC);
// step 2: allocate vector x and vector y large enough for bsrmv
cudaMalloc((void**)&x, sizeof(float)*(nb*blockDim));
cudaMalloc((void**)&y, sizeof(float)*(mb*blockDim));
cudaMemcpy(x, hx, sizeof(float)*n, cudaMemcpyHostToDevice);
cudaMemcpy(y, hy, sizeof(float)*m, cudaMemcpyHostToDevice);
// step 3: perform bsrmv
cusparseSbsrmv(handle, dirA, transA, mb, nb, nnzb, &alpha,
descrC, bsrValC, bsrRowPtrC, bsrColIndC, blockDim, x, &beta, y);
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation \(\text{op}(A)\) . Only |
|
number of block rows of matrix \(A\). |
|
number of block columns of matrix \(A\). |
|
number of nonzero blocks of matrix \(A\). |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix \(A\). The supported matrix type is |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix \(A\), larger than zero. |
|
<type> vector of \(nb \ast blockDim\) elements. |
|
<type> scalar used for multiplication. If |
|
<type> vector of \(mb \ast blockDim\) elements. |
Output
|
<type> updated vector. |
See cusparseStatus_t for the description of the return status.
5.4.2. cusparse<t>bsrxmv() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrxmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int sizeOfMask,
int mb,
int nb,
int nnzb,
const float* alpha,
const cusparseMatDescr_t descr,
const float* bsrVal,
const int* bsrMaskPtr,
const int* bsrRowPtr,
const int* bsrEndPtr,
const int* bsrColInd,
int blockDim,
const float* x,
const float* beta,
float* y)
cusparseStatus_t
cusparseDbsrxmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int sizeOfMask,
int mb,
int nb,
int nnzb,
const double* alpha,
const cusparseMatDescr_t descr,
const double* bsrVal,
const int* bsrMaskPtr,
const int* bsrRowPtr,
const int* bsrEndPtr,
const int* bsrColInd,
int blockDim,
const double* x,
const double* beta,
double* y)
cusparseStatus_t
cusparseCbsrxmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int sizeOfMask,
int mb,
int nb,
int nnzb,
const cuComplex* alpha,
const cusparseMatDescr_t descr,
const cuComplex* bsrVal,
const int* bsrMaskPtr,
const int* bsrRowPtr,
const int* bsrEndPtr,
const int* bsrColInd,
int blockDim,
const cuComplex* x,
const cuComplex* beta,
cuComplex* y)
cusparseStatus_t
cusparseZbsrxmv(cusparseHandle_t handle,
cusparseDirection_t dir,
cusparseOperation_t trans,
int sizeOfMask,
int mb,
int nb,
int nnzb,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descr,
const cuDoubleComplex* bsrVal,
const int* bsrMaskPtr,
const int* bsrRowPtr,
const int* bsrEndPtr,
const int* bsrColInd,
int blockDim,
const cuDoubleComplex* x,
const cuDoubleComplex* beta,
cuDoubleComplex* y)
This function performs a bsrmv and a mask operation
\(\text{y(mask)} = (\alpha \ast \text{op}(A) \ast \text{x} + \beta \ast \text{y})\text{(mask)}\) |
where \(A\text{ is an }(mb \ast blockDim) \times (nb \ast blockDim)\) sparse matrix that is defined in BSRX storage format by the four arrays bsrVal, bsrRowPtr, bsrEndPtr, and bsrColInd); x and y are vectors; \(\alpha\text{~and~}\beta\) are scalars; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if trans == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The mask operation is defined by array bsrMaskPtr which contains updated block row indices of \(y\) . If row \(i\) is not specified in bsrMaskPtr, then bsrxmv() does not touch row block \(i\) of \(A\) and \(y\) .
For example, consider the \(2 \times 3\) block matrix \(A\):
\(\begin{matrix} {A = \begin{bmatrix} A_{11} & A_{12} & O \\ A_{21} & A_{22} & A_{23} \\ \end{bmatrix}} \\ \end{matrix}\) |
and its one-based BSR format (three vector form) is
\(\begin{matrix} \text{bsrVal} & = & \begin{bmatrix} A_{11} & A_{12} & A_{21} & A_{22} & A_{23} \\ \end{bmatrix} \\ \text{bsrRowPtr} & = & \begin{bmatrix} {1\phantom{.0}} & {3\phantom{.0}} & 6 \\ \end{bmatrix} \\ \text{bsrColInd} & = & \begin{bmatrix} {1\phantom{.0}} & {2\phantom{.0}} & {1\phantom{.0}} & {2\phantom{.0}} & 3 \\ \end{bmatrix} \\ \end{matrix}\) |
Suppose we want to do the following bsrmv operation on a matrix \(\overset{¯}{A}\) which is slightly different from \(A\) .
\(\begin{bmatrix} y_{1} \\ y_{2} \\ \end{bmatrix}:=alpha \ast (\widetilde{A} = \begin{bmatrix} O & O & O \\ O & A_{22} & O \\ \end{bmatrix}) \ast \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} + \begin{bmatrix} y_{1} \\ {beta \ast y_{2}} \\ \end{bmatrix}\) |
We don’t need to create another BSR format for the new matrix \(\overset{¯}{A}\) , all that we should do is to keep bsrVal and bsrColInd unchanged, but modify bsrRowPtr and add an additional array bsrEndPtr which points to the last nonzero elements per row of \(\overset{¯}{A}\) plus 1.
For example, the following bsrRowPtr and bsrEndPtr can represent matrix \(\overset{¯}{A}\) :
\(\begin{matrix} \text{bsrRowPtr} & = & \begin{bmatrix} {1\phantom{.0}} & 4 \\ \end{bmatrix} \\ \text{bsrEndPtr} & = & \begin{bmatrix} {1\phantom{.0}} & 5 \\ \end{bmatrix} \\ \end{matrix}\) |
Further we can use a mask operator (specified by array bsrMaskPtr) to update particular block row indices of \(y\) only because \(y_{1}\) is never changed. In this case, bsrMaskPtr\(=\) [2] and sizeOfMask=1.
The mask operator is equivalent to the following operation:
\(\begin{bmatrix} ? \\ y_{2} \\ \end{bmatrix}:=alpha \ast \begin{bmatrix} ? & ? & ? \\ O & A_{22} & O \\ \end{bmatrix} \ast \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} + beta \ast \begin{bmatrix} ? \\ y_{2} \\ \end{bmatrix}\) |
If a block row is not present in the bsrMaskPtr, then no calculation is performed on that row, and the corresponding value in y is unmodified. The question mark “?” is used to inidcate row blocks not in bsrMaskPtr.
In this case, first row block is not present in bsrMaskPtr, so bsrRowPtr[0] and bsrEndPtr[0] are not touched also.
\(\begin{matrix} \text{bsrRowPtr} & = & \begin{bmatrix} {?\phantom{.0}} & 4 \\ \end{bmatrix} \\ \text{bsrEndPtr} & = & \begin{bmatrix} {?\phantom{.0}} & 5 \\ \end{bmatrix} \\ \end{matrix}\) |
bsrxmv() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
A couple of comments on bsrxmv():
Only
blockDim > 1is supportedOnly
CUSPARSE_OPERATION_NON_TRANSPOSEandCUSPARSE_MATRIX_TYPE_GENERALare supported.Parameters
bsrMaskPtr,bsrRowPtr,bsrEndPtrandbsrColIndare consistent with base index, either one-based or zero-based. The above example is one-based.
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation \(\text{op}(A)\) . Only |
|
number of updated block rows of \(y\). |
|
number of block rows of matrix \(A\). |
|
number of block columns of matrix \(A\). |
|
number of nonzero blocks of matrix \(A\). |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix \(A\). The supported matrix type is |
|
<type> array of |
|
integer array of |
|
integer array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix \(A\), larger than zero. |
|
<type> vector of \(nb \ast blockDim\) elements. |
|
<type> scalar used for multiplication. If |
|
<type> vector of \(mb \ast blockDim\) elements. |
See cusparseStatus_t for the description of the return status.
5.4.3. cusparse<t>bsrsv2_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsv2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseDbsrsv2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseCbsrsv2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseZbsrsv2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
int* pBufferSizeInBytes)
This function returns size of the buffer used in bsrsv2, a new sparse triangular linear system op(A)*y =\(\alpha\)x.
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); x and y are the right-hand-side and the solution vectors; \(\alpha\) is a scalar; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if trans == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
Although there are six combinations in terms of parameter trans and the upper (lower) triangular part of A, bsrsv2_bufferSize() returns the maximum size buffer among these combinations. The buffer size depends on the dimensions mb, blockDim, and the number of nonzero blocks of the matrix nnzb. If the user changes the matrix, it is necessary to call bsrsv2_bufferSize() again to have the correct buffer size; otherwise a segmentation fault may occur.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation \(\text{op}(A)\) . |
|
number of block rows of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A; must be larger than zero. |
Output
|
record of internal states based on different algorithms. |
|
number of bytes of the buffer used in the |
See cusparseStatus_t for the description of the return status.
5.4.4. cusparse<t>bsrsv2_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsv2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrsv2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrsv2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrsv2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of bsrsv2, a new sparse triangular linear system op(A)*y =\(\alpha\)x.
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); x and y are the right-hand side and the solution vectors; \(\alpha\) is a scalar; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if trans == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The block of BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored.
It is expected that this function will be executed only once for a given matrix and a particular operation type.
This function requires a buffer size returned by bsrsv2_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsrsv2_analysis() reports a structural zero and computes level information, which stored in the opaque structure info. The level information can extract more parallelism for a triangular solver. However bsrsv2_solve() can be done without level information. To disable level information, the user needs to specify the policy of the triangular solver as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
Function bsrsv2_analysis() always reports the first structural zero, even when parameter policy is CUSPARSE_SOLVE_POLICY_NO_LEVEL. No structural zero is reported if CUSPARSE_DIAG_TYPE_UNIT is specified, even if block A(j,j) is missing for some j. The user needs to call cusparseXbsrsv2_zeroPivot() to know where the structural zero is.
It is the user’s choice whether to call bsrsv2_solve() if bsrsv2_analysis() reports a structural zero. In this case, the user can still call bsrsv2_solve(), which will return a numerical zero at the same position as a structural zero. However the result x is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation \(\text{op}(A)\) . |
|
number of block rows of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A, larger than zero. |
|
structure initialized using |
|
the supported policies are |
|
buffer allocated by the user, the size is return by |
Output
|
structure filled with information collected during the analysis phase (that should be passed to the solve phase unchanged). |
See cusparseStatus_t for the description of the return status.
5.4.5. cusparse<t>bsrsv2_solve() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsv2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const float* alpha,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
const float* x,
float* y,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrsv2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const double* alpha,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
const double* x,
double* y,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsrsv2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cuComplex* alpha,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
const cuComplex* x,
cuComplex* y,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrsv2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
int mb,
int nnzb,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrsv2Info_t info,
const cuDoubleComplex* x,
cuDoubleComplex* y,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of bsrsv2, a new sparse triangular linear system op(A)*y =\(\alpha\)x.
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); x and y are the right-hand-side and the solution vectors; \(\alpha\) is a scalar; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if trans == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The block in BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored. Function bsrsv02_solve() can support an arbitrary blockDim.
This function may be executed multiple times for a given matrix and a particular operation type.
This function requires a buffer size returned by bsrsv2_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Although bsrsv2_solve() can be done without level information, the user still needs to be aware of consistency. If bsrsv2_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, bsrsv2_solve() can be run with or without levels. On the other hand, if bsrsv2_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, bsrsv2_solve() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
The level information may not improve the performance, but may spend extra time doing analysis. For example, a tridiagonal matrix has no parallelism. In this case, CUSPARSE_SOLVE_POLICY_NO_LEVEL performs better than CUSPARSE_SOLVE_POLICY_USE_LEVEL. If the user has an iterative solver, the best approach is to do bsrsv2_analysis() with CUSPARSE_SOLVE_POLICY_USE_LEVEL once. Then do bsrsv2_solve() with CUSPARSE_SOLVE_POLICY_NO_LEVEL in the first run, and with CUSPARSE_SOLVE_POLICY_USE_LEVEL in the second run, and pick the fastest one to perform the remaining iterations.
Function bsrsv02_solve() has the same behavior as csrsv02_solve(). That is, bsr2csr(bsrsv02(A)) = csrsv02(bsr2csr(A)). The numerical zero of csrsv02_solve() means there exists some zero A(j,j). The numerical zero of bsrsv02_solve() means there exists some block A(j,j) that is not invertible.
Function bsrsv2_solve() reports the first numerical zero, including a structural zero. No numerical zero is reported if CUSPARSE_DIAG_TYPE_UNIT is specified, even if A(j,j) is not invertible for some j. The user needs to call cusparseXbsrsv2_zeroPivot() to know where the numerical zero is.
The function supports the following properties if pBuffer != NULL
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
For example, suppose L is a lower triangular matrix with unit diagonal, then the following code solves L*y=x by level information.
// Suppose that L is m x m sparse matrix represented by BSR format,
// The number of block rows/columns is mb, and
// the number of nonzero blocks is nnzb.
// L is lower triangular with unit diagonal.
// Assumption:
// - dimension of matrix L is m(=mb*blockDim),
// - matrix L has nnz(=nnzb*blockDim*blockDim) nonzero elements,
// - handle is already created by cusparseCreate(),
// - (d_bsrRowPtr, d_bsrColInd, d_bsrVal) is BSR of L on device memory,
// - d_x is right hand side vector on device memory.
// - d_y is solution vector on device memory.
// - d_x and d_y are of size m.
cusparseMatDescr_t descr = 0;
bsrsv2Info_t info = 0;
int pBufferSize;
void *pBuffer = 0;
int structural_zero;
int numerical_zero;
const double alpha = 1.;
const cusparseSolvePolicy_t policy = CUSPARSE_SOLVE_POLICY_USE_LEVEL;
const cusparseOperation_t trans = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
// step 1: create a descriptor which contains
// - matrix L is base-1
// - matrix L is lower triangular
// - matrix L has unit diagonal, specified by parameter CUSPARSE_DIAG_TYPE_UNIT
// (L may not have all diagonal elements.)
cusparseCreateMatDescr(&descr);
cusparseSetMatIndexBase(descr, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatFillMode(descr, CUSPARSE_FILL_MODE_LOWER);
cusparseSetMatDiagType(descr, CUSPARSE_DIAG_TYPE_UNIT);
// step 2: create a empty info structure
cusparseCreateBsrsv2Info(&info);
// step 3: query how much memory used in bsrsv2, and allocate the buffer
cusparseDbsrsv2_bufferSize(handle, dir, trans, mb, nnzb, descr,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, &pBufferSize);
// pBuffer returned by cudaMalloc is automatically aligned to 128 bytes.
cudaMalloc((void**)&pBuffer, pBufferSize);
// step 4: perform analysis
cusparseDbsrsv2_analysis(handle, dir, trans, mb, nnzb, descr,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim,
info, policy, pBuffer);
// L has unit diagonal, so no structural zero is reported.
status = cusparseXbsrsv2_zeroPivot(handle, info, &structural_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("L(%d,%d) is missing\n", structural_zero, structural_zero);
}
// step 5: solve L*y = x
cusparseDbsrsv2_solve(handle, dir, trans, mb, nnzb, &alpha, descr,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info,
d_x, d_y, policy, pBuffer);
// L has unit diagonal, so no numerical zero is reported.
status = cusparseXbsrsv2_zeroPivot(handle, info, &numerical_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("L(%d,%d) is zero\n", numerical_zero, numerical_zero);
}
// step 6: free resources
cudaFree(pBuffer);
cusparseDestroyBsrsv2Info(info);
cusparseDestroyMatDescr(descr);
cusparseDestroy(handle);
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation \(\text{op}(A)\). |
|
number of block rows and block columns of matrix |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
|
structure with information collected during the analysis phase (that should have been passed to the solve phase unchanged). |
|
<type> right-hand-side vector of size |
|
the supported policies are |
|
buffer allocated by the user, the size is returned by |
Output
|
<type> solution vector of size |
See cusparseStatus_t for the description of the return status.
5.4.6. cusparseXbsrsv2_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXbsrsv2_zeroPivot(cusparseHandle_t handle,
bsrsv2Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) is either structural zero or numerical zero (singular block). Otherwise position=-1.
The position can be 0-based or 1-based, the same as the matrix.
Function cusparseXbsrsv2_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set the proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
|
Output
|
if no structural or numerical zero, |
See cusparseStatus_t for the description of the return status
5.4.7. cusparse<t>gemvi()
cusparseStatus_t
cusparseSgemvi_bufferSize(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
int nnz,
int* pBufferSize)
cusparseStatus_t
cusparseDgemvi_bufferSize(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
int nnz,
int* pBufferSize)
cusparseStatus_t
cusparseCgemvi_bufferSize(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
int nnz,
int* pBufferSize)
cusparseStatus_t
cusparseZgemvi_bufferSize(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
int nnz,
int* pBufferSize)
cusparseStatus_t
cusparseSgemvi(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
const float* alpha,
const float* A,
int lda,
int nnz,
const float* x,
const int* xInd,
const float* beta,
float* y,
cusparseIndexBase_t idxBase,
void* pBuffer)
cusparseStatus_t
cusparseDgemvi(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
const double* alpha,
const double* A,
int lda,
int nnz,
const double* x,
const int* xInd,
const double* beta,
double* y,
cusparseIndexBase_t idxBase,
void* pBuffer)
cusparseStatus_t
cusparseCgemvi(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
const cuComplex* alpha,
const cuComplex* A,
int lda,
int nnz,
const cuComplex* x,
const int* xInd,
const cuComplex* beta,
cuComplex* y,
cusparseIndexBase_t idxBase,
void* pBuffer)
cusparseStatus_t
cusparseZgemvi(cusparseHandle_t handle,
cusparseOperation_t transA,
int m,
int n,
const cuDoubleComplex* alpha,
const cuDoubleComplex* A,
int lda,
int nnz,
const cuDoubleComplex* x,
const int* xInd,
const cuDoubleComplex* beta,
cuDoubleComplex* y,
cusparseIndexBase_t idxBase,
void* pBuffer)
This function performs the matrix-vector operation
\(\text{y} = \alpha \ast \text{op}(A) \ast \text{x} + \beta \ast \text{y}\) |
A is an m×n dense matrix and a sparse vector x that is defined in a sparse storage format by the two arrays xVal, xInd of length nnz, and y is a dense vector; \(\alpha\)and \(\beta\)are scalars; and
\(\text{op}(A) = \begin{cases} A & \text{if trans == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if trans == CUSPARSE_OPERATION_TRANSPOSE} \\ \end{cases}\)
To simplify the implementation, we have not (yet) optimized the transpose multiple case. We recommend the following for users interested in this case.
Convert the matrix from CSR to CSC format using one of the
csr2csc()functions. Notice that by interchanging the rows and columns of the result you are implicitly transposing the matrix.Call the
gemvi()function with thecusparseOperation_tparameter set toCUSPARSE_OPERATION_NON_TRANSPOSEand with the interchanged rows and columns of the matrix stored in CSC format. This (implicitly) multiplies the vector by the transpose of the matrix in the original CSR format.The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
The function cusparse<t>gemvi_bufferSize() returns the size of buffer used in cusparse<t>gemvi().
Input
|
Handle to the cuSPARSE library context. |
|
The operation \(\text{op}(A)\). |
|
Number of rows of matrix |
|
Number of columns of matrix |
|
<type> scalar used for multiplication. |
|
The pointer to dense matrix |
|
Size of the leading dimension of |
|
Number of nonzero elements of vector |
|
<type> sparse vector of |
|
Indices of non-zero values in |
|
<type> scalar used for multiplication. If |
|
<type> dense vector of |
|
0 or 1, for 0 based or 1 based indexing, respectively. |
|
Number of elements needed the buffer used in |
|
Working space buffer. |
Output
|
<type> updated dense vector. |
See cusparseStatus_t for the description of the return status.
5.5. cuSPARSE Level 3 Function Reference
This chapter describes sparse linear algebra functions that perform operations between sparse and (usually tall) dense matrices.
5.5.1. cusparse<t>bsrmm()
cusparseStatus_t
cusparseSbsrmm(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transB,
int mb,
int n,
int kb,
int nnzb,
const float* alpha,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const float* B,
int ldb,
const float* beta,
float* C,
int ldc)
cusparseStatus_t
cusparseDbsrmm(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transB,
int mb,
int n,
int kb,
int nnzb,
const double* alpha,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const double* B,
int ldb,
const double* beta,
double* C,
int ldc)
cusparseStatus_t
cusparseCbsrmm(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transB,
int mb,
int n,
int kb,
int nnzb,
const cuComplex* alpha,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cuComplex* B,
int ldb,
const cuComplex* beta,
cuComplex* C,
int ldc)
cusparseStatus_t
cusparseZbsrmm(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transB,
int mb,
int n,
int kb,
int nnzb,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cuDoubleComplex* B,
int ldb,
const cuDoubleComplex* beta,
cuDoubleComplex* C,
int ldc)
This function performs one of the following matrix-matrix operations:
\(C = \alpha \ast \text{op}(A) \ast \text{op}(B) + \beta \ast C\) |
A is an mb×kb sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA; B and C are dense matrices; \(\alpha\text{~and~}\beta\) are scalars; and
\(\text{op}(A) = \begin{cases} A & \text{if transA == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if transA == CUSPARSE_OPERATION_TRANSPOSE (not\ supported)} \\ A^{H} & \text{if transA == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE (not supported)} \\ \end{cases}\)
and
\(\text{op}(B) = \begin{cases} B & \text{if transB == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ B^{T} & \text{if transB == CUSPARSE_OPERATION_TRANSPOSE} \\ B^{H} & \text{if transB == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE (not supported)} \\ \end{cases}\)
The function has the following limitations:
Only
CUSPARSE_MATRIX_TYPE_GENERALmatrix type is supportedOnly
blockDim > 1is supportedif
blockDim≤ 4, then max(mb)/max(n) = 524,272if 4 <
blockDim≤ 8, then max(mb) = 524,272, max(n) = 262,136if
blockDim> 8, then m < 65,535 and max(n) = 262,136
The motivation of transpose(B) is to improve memory access of matrix B. The computational pattern of A*transpose(B) with matrix B in column-major order is equivalent to A*B with matrix B in row-major order.
In practice, no operation in an iterative solver or eigenvalue solver uses A*transpose(B). However, we can perform A*transpose(transpose(B)) which is the same as A*B. For example, suppose A is mb*kb, B is k*n and C is m*n, the following code shows usage of cusparseDbsrmm().
// A is mb*kb, B is k*n and C is m*n
const int m = mb*blockSize;
const int k = kb*blockSize;
const int ldb_B = k; // leading dimension of B
const int ldc = m; // leading dimension of C
// perform C:=alpha*A*B + beta*C
cusparseSetMatType(descrA, CUSPARSE_MATRIX_TYPE_GENERAL );
cusparseDbsrmm(cusparse_handle,
CUSPARSE_DIRECTION_COLUMN,
CUSPARSE_OPERATION_NON_TRANSPOSE,
CUSPARSE_OPERATION_NON_TRANSPOSE,
mb, n, kb, nnzb, alpha,
descrA, bsrValA, bsrRowPtrA, bsrColIndA, blockSize,
B, ldb_B,
beta, C, ldc);
Instead of using A*B, our proposal is to transpose B to Bt by first calling cublas<t>geam(), and then to perform A*transpose(Bt).
// step 1: Bt := transpose(B)
const int m = mb*blockSize;
const int k = kb*blockSize;
double *Bt;
const int ldb_Bt = n; // leading dimension of Bt
cudaMalloc((void**)&Bt, sizeof(double)*ldb_Bt*k);
double one = 1.0;
double zero = 0.0;
cublasSetPointerMode(cublas_handle, CUBLAS_POINTER_MODE_HOST);
cublasDgeam(cublas_handle, CUBLAS_OP_T, CUBLAS_OP_T,
n, k, &one, B, int ldb_B, &zero, B, int ldb_B, Bt, ldb_Bt);
// step 2: perform C:=alpha*A*transpose(Bt) + beta*C
cusparseDbsrmm(cusparse_handle,
CUSPARSE_DIRECTION_COLUMN,
CUSPARSE_OPERATION_NON_TRANSPOSE,
CUSPARSE_OPERATION_TRANSPOSE,
mb, n, kb, nnzb, alpha,
descrA, bsrValA, bsrRowPtrA, bsrColIndA, blockSize,
Bt, ldb_Bt,
beta, C, ldc);
bsrmm() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation |
|
the operation |
|
number of block rows of sparse matrix |
|
number of columns of dense matrix |
|
number of block columns of sparse matrix |
|
number of non-zero blocks of sparse matrix |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
|
array of dimensions |
|
leading dimension of |
|
<type> scalar used for multiplication. If |
|
array of dimensions |
|
leading dimension of |
Output
|
<type> updated array of dimensions |
See cusparseStatus_t for the description of the return status
5.5.2. cusparse<t>bsrsm2_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsm2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
float* bsrSortedValA,
const int* bsrSortedRowPtrA,
const int* bsrSortedColIndA,
int blockDim,
bsrsm2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseDbsrsm2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
double* bsrSortedValA,
const int* bsrSortedRowPtrA,
const int* bsrSortedColIndA,
int blockDim,
bsrsm2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseCbsrsm2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex* bsrSortedValA,
const int* bsrSortedRowPtrA,
const int* bsrSortedColIndA,
int blockDim,
bsrsm2Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseZbsrsm2_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex* bsrSortedValA,
const int* bsrSortedRowPtrA,
const int* bsrSortedColIndA,
int blockDim,
bsrsm2Info_t info,
int* pBufferSizeInBytes)
This function returns size of buffer used in bsrsm2(), a new sparse triangular linear system op(A)*op(X)=\(\alpha\)op(B).
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); B and X are the right-hand-side and the solution matrices; \(\alpha\) is a scalar; and
\(\text{op}(A) == \text{CUSPARSE_OPERATION_NON_TRANSPOSE}\)
Although there are six combinations in terms of parameter trans and the upper (and lower) triangular part of A, bsrsm2_bufferSize() returns the maximum size of the buffer among these combinations. The buffer size depends on dimension mb,blockDim and the number of nonzeros of the matrix, nnzb. If the user changes the matrix, it is necessary to call bsrsm2_bufferSize() again to get the correct buffer size, otherwise a segmentation fault may occur.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation |
|
the operation |
|
number of block rows of matrix |
|
number of columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
Output
|
record internal states based on different algorithms. |
|
number of bytes of the buffer used in |
See cusparseStatus_t for the description of the return status
5.5.3. cusparse<t>bsrsm2_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsm2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
const float* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrsm2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
const double* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsrsm2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrsm2_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of bsrsm2(), a new sparse triangular linear system op(A)*op(X) =\(\alpha\)op(B).
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); B and X are the right-hand-side and the solution matrices; \(\alpha\) is a scalar; and
\(\text{op}(A) == \text{CUSPARSE_OPERATION_NON_TRANSPOSE}\)
and
\(\text{op}(X) = \begin{cases} X & \text{if transX == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ X^{T} & \text{if transX == CUSPARSE_OPERATION_TRANSPOSE} \\ X^{H} & \text{if transX == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE (not supported)} \\ \end{cases}\)
and op(B) and op(X) are equal.
The block of BSR format is of size blockDim*blockDim, stored in column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_ROW or CUSPARSE_DIRECTION_COLUMN. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored.
It is expected that this function will be executed only once for a given matrix and a particular operation type.
This function requires the buffer size returned by bsrsm2_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsrsm2_analysis() reports a structural zero and computes the level information stored in opaque structure info. The level information can extract more parallelism during a triangular solver. However bsrsm2_solve() can be done without level information. To disable level information, the user needs to specify the policy of the triangular solver as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
Function bsrsm2_analysis() always reports the first structural zero, even if the parameter policy is CUSPARSE_SOLVE_POLICY_NO_LEVEL. Besides, no structural zero is reported if CUSPARSE_DIAG_TYPE_UNIT is specified, even if block A(j,j) is missing for some j. The user must call cusparseXbsrsm2_query_zero_pivot() to know where the structural zero is.
If bsrsm2_analysis() reports a structural zero, the solve will return a numerical zero in the same position as the structural zero but this result X is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation |
|
the operation |
|
number of block rows of matrix |
|
number of columns of matrix |
|
number of non-zero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
|
structure initialized using |
|
The supported policies are |
|
buffer allocated by the user; the size is return by |
Output
|
structure filled with information collected during the analysis phase (that should be passed to the solve phase unchanged). |
See cusparseStatus_t for the description of the return status
5.5.4. cusparse<t>bsrsm2_solve() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrsm2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const float* alpha,
const cusparseMatDescr_t descrA,
const float* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
const float* B,
int ldb,
float* X,
int ldx,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrsm2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const double* alpha,
const cusparseMatDescr_t descrA,
const double* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
const double* B,
int ldb,
double* X,
int ldx,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsrsm2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cuComplex* alpha,
const cusparseMatDescr_t descrA,
const cuComplex* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
const cuComplex* B,
int ldb,
cuComplex* X,
int ldx,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrsm2_solve(cusparseHandle_t handle,
cusparseDirection_t dirA,
cusparseOperation_t transA,
cusparseOperation_t transX,
int mb,
int n,
int nnzb,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrSortedVal,
const int* bsrSortedRowPtr,
const int* bsrSortedColInd,
int blockDim,
bsrsm2Info_t info,
const cuDoubleComplex* B,
int ldb,
cuDoubleComplex* X,
int ldx,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of the solution of a sparse triangular linear system:
\(\text{op}(A) \ast \text{op(X)} = \alpha \ast \text{op(B)}\) |
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA); B and X are the right-hand-side and the solution matrices; \(\alpha\) is a scalar, and
\(\text{op}(A) == \text{CUSPARSE_OPERATION_NON_TRANSPOSE}\)
and
\(\text{op}(X) = \begin{cases} X & \text{if transX == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ X^{T} & \text{if transX == CUSPARSE_OPERATION_TRANSPOSE} \\ X^{H} & \text{not supported} \\ \end{cases}\)
Only op(A)=A is supported.
op(B) and op(X) must be performed in the same way. In other words, if op(B)=B, op(X)=X.
The block of BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_ROW or CUSPARSE_DIRECTION_COLUMN. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored. Function bsrsm02_solve() can support an arbitrary blockDim.
This function may be executed multiple times for a given matrix and a particular operation type.
This function requires the buffer size returned by bsrsm2_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Although bsrsm2_solve() can be done without level information, the user still needs to be aware of consistency. If bsrsm2_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, bsrsm2_solve() can be run with or without levels. On the other hand, if bsrsm2_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, bsrsm2_solve() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsrsm02_solve() has the same behavior as bsrsv02_solve(), reporting the first numerical zero, including a structural zero. The user must call cusparseXbsrsm2_query_zero_pivot() to know where the numerical zero is.
The motivation of transpose(X) is to improve the memory access of matrix X. The computational pattern of transpose(X) with matrix X in column-major order is equivalent to X with matrix X in row-major order.
In-place is supported and requires that B and X point to the same memory block, and ldb=ldx.
The function supports the following properties if pBuffer != NULL:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
the operation |
|
the operation |
|
number of block rows of matrix |
|
number of columns of matrix |
|
number of non-zero blocks of matrix |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
|
structure initialized using |
|
<type> right-hand-side array. |
|
leading dimension of |
|
leading dimension of |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
<type> solution array with leading dimensions |
See cusparseStatus_t for the description of the return status.
5.5.5. cusparseXbsrsm2_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXbsrsm2_zeroPivot(cusparseHandle_t handle,
bsrsm2Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) is either a structural zero or a numerical zero (singular block). Otherwise position=-1.
The position can be 0-base or 1-base, the same as the matrix.
Function cusparseXbsrsm2_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set the proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
|
Output
|
if no structural or numerical zero, |
See cusparseStatus_t for the description of the return status.
5.6. cuSPARSE Extra Function Reference
This chapter describes the extra routines used to manipulate sparse matrices.
5.6.1. cusparse<t>csrgeam2()
cusparseStatus_t
cusparseScsrgeam2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const float* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const float* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const float* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const float* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
const float* csrSortedValC,
const int* csrSortedRowPtrC,
const int* csrSortedColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDcsrgeam2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const double* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const double* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const double* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const double* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
const double* csrSortedValC,
const int* csrSortedRowPtrC,
const int* csrSortedColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseCcsrgeam2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuComplex* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const cuComplex* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const cuComplex* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const cuComplex* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
const cuComplex* csrSortedValC,
const int* csrSortedRowPtrC,
const int* csrSortedColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseZcsrgeam2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const cuDoubleComplex* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const cuDoubleComplex* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const cuDoubleComplex* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
const cuDoubleComplex* csrSortedValC,
const int* csrSortedRowPtrC,
const int* csrSortedColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseXcsrgeam2Nnz(cusparseHandle_t handle,
int m,
int n,
const cusparseMatDescr_t descrA,
int nnzA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const cusparseMatDescr_t descrB,
int nnzB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
int* csrSortedRowPtrC,
int* nnzTotalDevHostPtr,
void* workspace)
cusparseStatus_t
cusparseScsrgeam2(cusparseHandle_t handle,
int m,
int n,
const float* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const float* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const float* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const float* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
float* csrSortedValC,
int* csrSortedRowPtrC,
int* csrSortedColIndC,
void* pBuffer)
cusparseStatus_t
cusparseDcsrgeam2(cusparseHandle_t handle,
int m,
int n,
const double* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const double* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const double* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const double* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
double* csrSortedValC,
int* csrSortedRowPtrC,
int* csrSortedColIndC,
void* pBuffer)
cusparseStatus_t
cusparseCcsrgeam2(cusparseHandle_t handle,
int m,
int n,
const cuComplex* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const cuComplex* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const cuComplex* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const cuComplex* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
cuComplex* csrSortedValC,
int* csrSortedRowPtrC,
int* csrSortedColIndC,
void* pBuffer)
cusparseStatus_t
cusparseZcsrgeam2(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* alpha,
const cusparseMatDescr_t descrA,
int nnzA,
const cuDoubleComplex* csrSortedValA,
const int* csrSortedRowPtrA,
const int* csrSortedColIndA,
const cuDoubleComplex* beta,
const cusparseMatDescr_t descrB,
int nnzB,
const cuDoubleComplex* csrSortedValB,
const int* csrSortedRowPtrB,
const int* csrSortedColIndB,
const cusparseMatDescr_t descrC,
cuDoubleComplex* csrSortedValC,
int* csrSortedRowPtrC,
int* csrSortedColIndC,
void* pBuffer)
This function performs following matrix-matrix operation
\(C = \alpha \ast A + \beta \ast B\) |
where A, B, and C are m×n sparse matrices (defined in CSR storage format by the three arrays csrValA|csrValB|csrValC, csrRowPtrA|csrRowPtrB|csrRowPtrC, and csrColIndA|csrColIndB|csrcolIndC respectively), and \(\alpha\text{~and~}\beta\) are scalars. Since A and B have different sparsity patterns, cuSPARSE adopts a two-step approach to complete sparse matrix C. In the first step, the user allocates csrRowPtrC of m+1elements and uses function cusparseXcsrgeam2Nnz() to determine csrRowPtrC and the total number of nonzero elements. In the second step, the user gathers nnzC (number of nonzero elements of matrix C) from either (nnzC=*nnzTotalDevHostPtr) or (nnzC=csrRowPtrC(m)-csrRowPtrC(0)) and allocates csrValC, csrColIndC of nnzC elements respectively, then finally calls function cusparse[S|D|C|Z]csrgeam2() to complete matrix C.
The general procedure is as follows:
int baseC, nnzC;
/* alpha, nnzTotalDevHostPtr points to host memory */
size_t BufferSizeInBytes;
char *buffer = NULL;
int *nnzTotalDevHostPtr = &nnzC;
cusparseSetPointerMode(handle, CUSPARSE_POINTER_MODE_HOST);
cudaMalloc((void**)&csrRowPtrC, sizeof(int)*(m+1));
/* prepare buffer */
cusparseScsrgeam2_bufferSizeExt(handle, m, n,
alpha,
descrA, nnzA,
csrValA, csrRowPtrA, csrColIndA,
beta,
descrB, nnzB,
csrValB, csrRowPtrB, csrColIndB,
descrC,
csrValC, csrRowPtrC, csrColIndC
&bufferSizeInBytes
);
cudaMalloc((void**)&buffer, sizeof(char)*bufferSizeInBytes);
cusparseXcsrgeam2Nnz(handle, m, n,
descrA, nnzA, csrRowPtrA, csrColIndA,
descrB, nnzB, csrRowPtrB, csrColIndB,
descrC, csrRowPtrC, nnzTotalDevHostPtr,
buffer);
if (NULL != nnzTotalDevHostPtr){
nnzC = *nnzTotalDevHostPtr;
}else{
cudaMemcpy(&nnzC, csrRowPtrC+m, sizeof(int), cudaMemcpyDeviceToHost);
cudaMemcpy(&baseC, csrRowPtrC, sizeof(int), cudaMemcpyDeviceToHost);
nnzC -= baseC;
}
cudaMalloc((void**)&csrColIndC, sizeof(int)*nnzC);
cudaMalloc((void**)&csrValC, sizeof(float)*nnzC);
cusparseScsrgeam2(handle, m, n,
alpha,
descrA, nnzA,
csrValA, csrRowPtrA, csrColIndA,
beta,
descrB, nnzB,
csrValB, csrRowPtrB, csrColIndB,
descrC,
csrValC, csrRowPtrC, csrColIndC
buffer);
Several comments on csrgeam2():
The other three combinations, NT, TN, and TT, are not supported by cuSPARSE. In order to do any one of the three, the user should use the routine
csr2csc()to convert \(A\) | \(B\) to \(A^{T}\) | \(B^{T}\) .Only
CUSPARSE_MATRIX_TYPE_GENERALis supported. If eitherAorBis symmetric or Hermitian, then the user must extend the matrix to a full one and reconfigure theMatrixTypefield of the descriptor toCUSPARSE_MATRIX_TYPE_GENERAL.If the sparsity pattern of matrix
Cis known, the user can skip the call to functioncusparseXcsrgeam2Nnz(). For example, suppose that the user has an iterative algorithm which would updateAandBiteratively but keep the sparsity patterns. The user can call functioncusparseXcsrgeam2Nnz()once to set up the sparsity pattern ofC, then call functioncusparse[S|D|C|Z]geam()only for each iteration.The pointers
alphaandbetamust be valid.When
alphaorbetais zero, it is not considered a special case by cuSPARSE. The sparsity pattern ofCis independent of the value ofalphaandbeta. If the user wants \(C = 0 \times A + 1 \times B^{T}\) , thencsr2csc()is better thancsrgeam2().csrgeam2()is the same ascsrgeam()exceptcsrgeam2()needs explicit buffer wherecsrgeam()allocates the buffer internally.This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows of sparse matrix |
|
number of columns of sparse matrix |
|
<type> scalar used for multiplication. |
|
the descriptor of matrix |
|
number of nonzero elements of sparse matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
<type> scalar used for multiplication. If |
|
the descriptor of matrix |
|
number of nonzero elements of sparse matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
the descriptor of matrix |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
|
total number of nonzero elements in device or host memory. It is equal to |
See cusparseStatus_t for the description of the return status
5.7. cuSPARSE Preconditioners Reference
This chapter describes the routines that implement different preconditioners.
5.7.1. Incomplete Cholesky Factorization: level 0 [DEPRECATED]
Different algorithms for ic0 are discussed in this section.
5.7.1.1. cusparse<t>csric02_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsric02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseDcsric02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseCcsric02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseZcsric02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
int* pBufferSizeInBytes)
This function returns size of buffer used in computing the incomplete-Cholesky factorization with \(0\) fill-in and no pivoting:
\(A \approx LL^{H}\) |
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The buffer size depends on dimension m and nnz, the number of nonzeros of the matrix. If the user changes the matrix, it is necessary to call csric02_bufferSize() again to have the correct buffer size; otherwise, a segmentation fault may occur.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
Output
|
record internal states based on different algorithms |
|
number of bytes of the buffer used in |
See cusparseStatus_t for the description of the return status.
5.7.1.2. cusparse<t>csric02_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsric02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDcsric02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCcsric02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZcsric02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of the incomplete-Cholesky factorization with \(0\) fill-in and no pivoting:
\(A \approx LL^{H}\) |
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
This function requires a buffer size returned by csric02_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function csric02_analysis() reports a structural zero and computes level information stored in the opaque structure info. The level information can extract more parallelism during incomplete Cholesky factorization. However csric02() can be done without level information. To disable level information, the user must specify the policy of csric02_analysis() and csric02() as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
Function csric02_analysis() always reports the first structural zero, even if the policy is CUSPARSE_SOLVE_POLICY_NO_LEVEL. The user needs to call cusparseXcsric02_zeroPivot() to know where the structural zero is.
It is the user’s choice whether to call csric02() if csric02_analysis() reports a structural zero. In this case, the user can still call csric02(), which will return a numerical zero at the same position as the structural zero. However the result is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
structure initialized using |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
number of bytes of the buffer used in |
See cusparseStatus_t for the description of the return status.
5.7.1.3. cusparse<t>csric02() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsric02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
float* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDcsric02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
double* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCcsric02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZcsric02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of the computing the incomplete-Cholesky factorization with \(0\) fill-in and no pivoting:
\(A \approx LL^{H}\) |
This function requires a buffer size returned by csric02_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Although csric02() can be done without level information, the user still needs to be aware of consistency. If csric02_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, csric02() can be run with or without levels. On the other hand, if csric02_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, csric02() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function csric02() reports the first numerical zero, including a structural zero. The user must call cusparseXcsric02_zeroPivot() to know where the numerical zero is.
Function csric02() only takes the lower triangular part of matrix A to perform factorization. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, the fill mode and diagonal type are ignored, and the strictly upper triangular part is ignored and never touched. It does not matter if A is Hermitian or not. In other words, from the point of view of csric02()A is Hermitian and only the lower triangular part is provided.
Note
In practice, a positive definite matrix may not have incomplete cholesky factorization. To the best of our knowledge, only matrix M can guarantee the existence of incomplete cholesky factorization. If csric02() failed cholesky factorization and reported a numerical zero, it is possible that incomplete cholesky factorization does not exist.
For example, suppose A is a real m × m matrix, the following code solves the precondition system M*y = x where M is the product of Cholesky factorization L and its transpose.
\(M = LL^{H}\) |
// Suppose that A is m x m sparse matrix represented by CSR format,
// Assumption:
// - handle is already created by cusparseCreate(),
// - (d_csrRowPtr, d_csrColInd, d_csrVal) is CSR of A on device memory,
// - d_x is right hand side vector on device memory,
// - d_y is solution vector on device memory.
// - d_z is intermediate result on device memory.
cusparseMatDescr_t descr_M = 0;
cusparseMatDescr_t descr_L = 0;
csric02Info_t info_M = 0;
csrsv2Info_t info_L = 0;
csrsv2Info_t info_Lt = 0;
int pBufferSize_M;
int pBufferSize_L;
int pBufferSize_Lt;
int pBufferSize;
void *pBuffer = 0;
int structural_zero;
int numerical_zero;
const double alpha = 1.;
const cusparseSolvePolicy_t policy_M = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_L = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_Lt = CUSPARSE_SOLVE_POLICY_USE_LEVEL;
const cusparseOperation_t trans_L = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseOperation_t trans_Lt = CUSPARSE_OPERATION_TRANSPOSE;
// step 1: create a descriptor which contains
// - matrix M is base-1
// - matrix L is base-1
// - matrix L is lower triangular
// - matrix L has non-unit diagonal
cusparseCreateMatDescr(&descr_M);
cusparseSetMatIndexBase(descr_M, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_M, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseCreateMatDescr(&descr_L);
cusparseSetMatIndexBase(descr_L, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_L, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_L, CUSPARSE_FILL_MODE_LOWER);
cusparseSetMatDiagType(descr_L, CUSPARSE_DIAG_TYPE_NON_UNIT);
// step 2: create a empty info structure
// we need one info for csric02 and two info's for csrsv2
cusparseCreateCsric02Info(&info_M);
cusparseCreateCsrsv2Info(&info_L);
cusparseCreateCsrsv2Info(&info_Lt);
// step 3: query how much memory used in csric02 and csrsv2, and allocate the buffer
cusparseDcsric02_bufferSize(handle, m, nnz,
descr_M, d_csrVal, d_csrRowPtr, d_csrColInd, info_M, &bufferSize_M);
cusparseDcsrsv2_bufferSize(handle, trans_L, m, nnz,
descr_L, d_csrVal, d_csrRowPtr, d_csrColInd, info_L, &pBufferSize_L);
cusparseDcsrsv2_bufferSize(handle, trans_Lt, m, nnz,
descr_L, d_csrVal, d_csrRowPtr, d_csrColInd, info_Lt,&pBufferSize_Lt);
pBufferSize = max(bufferSize_M, max(pBufferSize_L, pBufferSize_Lt));
// pBuffer returned by cudaMalloc is automatically aligned to 128 bytes.
cudaMalloc((void**)&pBuffer, pBufferSize);
// step 4: perform analysis of incomplete Cholesky on M
// perform analysis of triangular solve on L
// perform analysis of triangular solve on L'
// The lower triangular part of M has the same sparsity pattern as L, so
// we can do analysis of csric02 and csrsv2 simultaneously.
cusparseDcsric02_analysis(handle, m, nnz, descr_M,
d_csrVal, d_csrRowPtr, d_csrColInd, info_M,
policy_M, pBuffer);
status = cusparseXcsric02_zeroPivot(handle, info_M, &structural_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("A(%d,%d) is missing\n", structural_zero, structural_zero);
}
cusparseDcsrsv2_analysis(handle, trans_L, m, nnz, descr_L,
d_csrVal, d_csrRowPtr, d_csrColInd,
info_L, policy_L, pBuffer);
cusparseDcsrsv2_analysis(handle, trans_Lt, m, nnz, descr_L,
d_csrVal, d_csrRowPtr, d_csrColInd,
info_Lt, policy_Lt, pBuffer);
// step 5: M = L * L'
cusparseDcsric02(handle, m, nnz, descr_M,
d_csrVal, d_csrRowPtr, d_csrColInd, info_M, policy_M, pBuffer);
status = cusparseXcsric02_zeroPivot(handle, info_M, &numerical_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("L(%d,%d) is zero\n", numerical_zero, numerical_zero);
}
// step 6: solve L*z = x
cusparseDcsrsv2_solve(handle, trans_L, m, nnz, &alpha, descr_L, // replace with cusparseSpSV
d_csrVal, d_csrRowPtr, d_csrColInd, info_L,
d_x, d_z, policy_L, pBuffer);
// step 7: solve L'*y = z
cusparseDcsrsv2_solve(handle, trans_Lt, m, nnz, &alpha, descr_L, // replace with cusparseSpSV
d_csrVal, d_csrRowPtr, d_csrColInd, info_Lt,
d_z, d_y, policy_Lt, pBuffer);
// step 6: free resources
cudaFree(pBuffer);
cusparseDestroyMatDescr(descr_M);
cusparseDestroyMatDescr(descr_L);
cusparseDestroyCsric02Info(info_M);
cusparseDestroyCsrsv2Info(info_L);
cusparseDestroyCsrsv2Info(info_Lt);
cusparseDestroy(handle);
The function supports the following properties if pBuffer != NULL
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
structure with information collected during the analysis phase (that should have been passed to the solve phase unchanged). |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
<type> matrix containing the incomplete-Cholesky lower triangular factor. |
See cusparseStatus_t for the description of the return status.
5.7.1.4. cusparseXcsric02_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXcsric02_zeroPivot(cusparseHandle_t handle,
csric02Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) has either a structural zero or a numerical zero; otherwise, position=-1.
The position can be 0-based or 1-based, the same as the matrix.
Function cusparseXcsric02_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
|
Output
|
if no structural or numerical zero, |
See cusparseStatus_t for the description of the return status.
5.7.1.5. cusparse<t>bsric02_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsric02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseDbsric02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseCbsric02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseZbsric02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
int* pBufferSizeInBytes)
This function returns the size of a buffer used in computing the incomplete-Cholesky factorization with 0 fill-in and no pivoting
\(A \approx LL^{H}\) |
A is an (mb*blockDim)*(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA.
The buffer size depends on the dimensions of mb, blockDim, and the number of nonzero blocks of the matrix nnzb. If the user changes the matrix, it is necessary to call bsric02_bufferSize() again to have the correct buffer size; otherwise, a segmentation fault may occur.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows and block columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A, larger than zero. |
Output
|
record internal states based on different algorithms. |
|
number of bytes of the buffer used in |
See cusparseStatus_t for the description of the return status.
5.7.1.6. cusparse<t>bsric02_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsric02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsric02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsric02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsric02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of the incomplete-Cholesky factorization with 0 fill-in and no pivoting
\(A \approx LL^{H}\) |
A is an (mb*blockDim)x(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA. The block in BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored.
This function requires a buffer size returned by bsric02_bufferSize90. The address of pBuffer must be a multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Functionbsric02_analysis() reports structural zero and computes level information stored in the opaque structure info. The level information can extract more parallelism during incomplete Cholesky factorization. However bsric02() can be done without level information. To disable level information, the user needs to specify the parameter policy of bsric02[_analysis| ] as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
Function bsric02_analysis always reports the first structural zero, even when parameter policy is CUSPARSE_SOLVE_POLICY_NO_LEVEL. The user must call cusparseXbsric02_zeroPivot() to know where the structural zero is.
It is the user’s choice whether to call bsric02() if bsric02_analysis() reports a structural zero. In this case, the user can still call bsric02(), which returns a numerical zero in the same position as the structural zero. However the result is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows and block columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A; must be larger than zero. |
|
structure initialized using |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
Structure filled with information collected during the analysis phase (that should be passed to the solve phase unchanged). |
See cusparseStatus_t for the description of the return status.
5.7.1.7. cusparse<t>bsric02() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsric02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsric02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsric02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsric02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsric02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of the incomplete-Cholesky factorization with 0 fill-in and no pivoting
\(A \approx LL^{H}\) |
A is an (mb*blockDim)×(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA. The block in BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored.
This function requires a buffer size returned by bsric02_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Although bsric02() can be done without level information, the user must be aware of consistency. If bsric02_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, bsric02() can be run with or without levels. On the other hand, if bsric02_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, bsric02() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsric02() has the same behavior as csric02(). That is, bsr2csr(bsric02(A)) = csric02(bsr2csr(A)). The numerical zero of csric02() means there exists some zero L(j,j). The numerical zero of bsric02() means there exists some block Lj,j) that is not invertible.
Function bsric02 reports the first numerical zero, including a structural zero. The user must call cusparseXbsric02_zeroPivot() to know where the numerical zero is.
The bsric02() function only takes the lower triangular part of matrix A to perform factorization. The strictly upper triangular part is ignored and never touched. It does not matter if A is Hermitian or not. In other words, from the point of view of bsric02(), A is Hermitian and only the lower triangular part is provided. Moreover, the imaginary part of diagonal elements of diagonal blocks is ignored.
For example, suppose A is a real m-by-m matrix, where m=mb*blockDim. The following code solves precondition system M*y = x, where M is the product of Cholesky factorization L and its transpose.
\(M = LL^{H}\) |
// Suppose that A is m x m sparse matrix represented by BSR format,
// The number of block rows/columns is mb, and
// the number of nonzero blocks is nnzb.
// Assumption:
// - handle is already created by cusparseCreate(),
// - (d_bsrRowPtr, d_bsrColInd, d_bsrVal) is BSR of A on device memory,
// - d_x is right hand side vector on device memory,
// - d_y is solution vector on device memory.
// - d_z is intermediate result on device memory.
// - d_x, d_y and d_z are of size m.
cusparseMatDescr_t descr_M = 0;
cusparseMatDescr_t descr_L = 0;
bsric02Info_t info_M = 0;
bsrsv2Info_t info_L = 0;
bsrsv2Info_t info_Lt = 0;
int pBufferSize_M;
int pBufferSize_L;
int pBufferSize_Lt;
int pBufferSize;
void *pBuffer = 0;
int structural_zero;
int numerical_zero;
const double alpha = 1.;
const cusparseSolvePolicy_t policy_M = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_L = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_Lt = CUSPARSE_SOLVE_POLICY_USE_LEVEL;
const cusparseOperation_t trans_L = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseOperation_t trans_Lt = CUSPARSE_OPERATION_TRANSPOSE;
const cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
// step 1: create a descriptor which contains
// - matrix M is base-1
// - matrix L is base-1
// - matrix L is lower triangular
// - matrix L has non-unit diagonal
cusparseCreateMatDescr(&descr_M);
cusparseSetMatIndexBase(descr_M, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_M, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseCreateMatDescr(&descr_L);
cusparseSetMatIndexBase(descr_L, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_L, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_L, CUSPARSE_FILL_MODE_LOWER);
cusparseSetMatDiagType(descr_L, CUSPARSE_DIAG_TYPE_NON_UNIT);
// step 2: create a empty info structure
// we need one info for bsric02 and two info's for bsrsv2
cusparseCreateBsric02Info(&info_M);
cusparseCreateBsrsv2Info(&info_L);
cusparseCreateBsrsv2Info(&info_Lt);
// step 3: query how much memory used in bsric02 and bsrsv2, and allocate the buffer
cusparseDbsric02_bufferSize(handle, dir, mb, nnzb,
descr_M, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M, &bufferSize_M);
cusparseDbsrsv2_bufferSize(handle, dir, trans_L, mb, nnzb,
descr_L, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_L, &pBufferSize_L);
cusparseDbsrsv2_bufferSize(handle, dir, trans_Lt, mb, nnzb,
descr_L, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_Lt, &pBufferSize_Lt);
pBufferSize = max(bufferSize_M, max(pBufferSize_L, pBufferSize_Lt));
// pBuffer returned by cudaMalloc is automatically aligned to 128 bytes.
cudaMalloc((void**)&pBuffer, pBufferSize);
// step 4: perform analysis of incomplete Cholesky on M
// perform analysis of triangular solve on L
// perform analysis of triangular solve on L'
// The lower triangular part of M has the same sparsity pattern as L, so
// we can do analysis of bsric02 and bsrsv2 simultaneously.
cusparseDbsric02_analysis(handle, dir, mb, nnzb, descr_M,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M,
policy_M, pBuffer);
status = cusparseXbsric02_zeroPivot(handle, info_M, &structural_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("A(%d,%d) is missing\n", structural_zero, structural_zero);
}
cusparseDbsrsv2_analysis(handle, dir, trans_L, mb, nnzb, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim,
info_L, policy_L, pBuffer);
cusparseDbsrsv2_analysis(handle, dir, trans_Lt, mb, nnzb, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim,
info_Lt, policy_Lt, pBuffer);
// step 5: M = L * L'
cusparseDbsric02_solve(handle, dir, mb, nnzb, descr_M,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M, policy_M, pBuffer);
status = cusparseXbsric02_zeroPivot(handle, info_M, &numerical_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("L(%d,%d) is not positive definite\n", numerical_zero, numerical_zero);
}
// step 6: solve L*z = x
cusparseDbsrsv2_solve(handle, dir, trans_L, mb, nnzb, &alpha, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_L,
d_x, d_z, policy_L, pBuffer);
// step 7: solve L'*y = z
cusparseDbsrsv2_solve(handle, dir, trans_Lt, mb, nnzb, &alpha, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_Lt,
d_z, d_y, policy_Lt, pBuffer);
// step 6: free resources
cudaFree(pBuffer);
cusparseDestroyMatDescr(descr_M);
cusparseDestroyMatDescr(descr_L);
cusparseDestroyBsric02Info(info_M);
cusparseDestroyBsrsv2Info(info_L);
cusparseDestroyBsrsv2Info(info_Lt);
cusparseDestroy(handle);
The function supports the following properties if pBuffer != NULL
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows and block columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A, larger than zero. |
|
structure with information collected during the analysis phase (that should have been passed to the solve phase unchanged). |
|
the supported policies are |
|
buffer allocated by the user, the size is returned by |
Output
|
<type> matrix containing the incomplete-Cholesky lower triangular factor. |
See cusparseStatus_t for the description of the return status.
5.7.1.8. cusparseXbsric02_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXbsric02_zeroPivot(cusparseHandle_t handle,
bsric02Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) has either a structural zero or a numerical zero (the block is not positive definite). Otherwise position=-1.
The position can be 0-based or 1-based, the same as the matrix.
Function cusparseXbsric02_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set the proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
|
Output
|
If no structural or numerical zero, |
See cusparseStatus_t for the description of the return status.
5.7.2. Incomplete LU Factorization: level 0 [DEPRECATED]
Different algorithms for ilu0 are discussed in this section.
5.7.2.1. cusparse<t>csrilu02_numericBoost() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsrilu02_numericBoost(cusparseHandle_t handle,
csrilu02Info_t info,
int enable_boost,
double* tol,
float* boost_val)
cusparseStatus_t
cusparseDcsrilu02_numericBoost(cusparseHandle_t handle,
csrilu02Info_t info,
int enable_boost,
double* tol,
double* boost_val)
cusparseStatus_t
cusparseCcsrilu02_numericBoost(cusparseHandle_t handle,
csrilu02Info_t info,
int enable_boost,
double* tol,
cuComplex* boost_val)
cusparseStatus_t
cusparseZcsrilu02_numericBoost(cusparseHandle_t handle,
csrilu02Info_t info,
int enable_boost,
double* tol,
cuDoubleComplex* boost_val)
The user can use a boost value to replace a numerical value in incomplete LU factorization. The tol is used to determine a numerical zero, and the boost_val is used to replace a numerical zero. The behavior is
if tol >= fabs(A(j,j)), then A(j,j)=boost_val.
To enable a boost value, the user has to set parameter enable_boost to 1 before calling csrilu02(). To disable a boost value, the user can call csrilu02_numericBoost() again with parameter enable_boost=0.
If enable_boost=0, tol and boost_val are ignored.
Both tol and boost_val can be in the host memory or device memory. The user can set the proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context |
|
structure initialized using |
|
disable boost by |
|
tolerance to determine a numerical zero |
|
boost value to replace a numerical zero |
See cusparseStatus_t for the description of the return status.
5.7.2.2. cusparse<t>csrilu02_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsrilu02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseDcsrilu02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseCcsrilu02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
int* pBufferSizeInBytes)
cusparseStatus_t
cusparseZcsrilu02_bufferSize(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
int* pBufferSizeInBytes)
This function returns size of the buffer used in computing the incomplete-LU factorization with \(0\) fill-in and no pivoting:
\(A \approx LU\) |
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
The buffer size depends on the dimension m and nnz, the number of nonzeros of the matrix. If the user changes the matrix, it is necessary to call csrilu02_bufferSize() again to have the correct buffer size; otherwise, a segmentation fault may occur.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
Output
|
record internal states based on different algorithms |
|
number of bytes of the buffer used in |
See cusparseStatus_t for the description of the return status.
5.7.2.3. cusparse<t>csrilu02_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsrilu02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDcsrilu02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCcsrilu02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZcsrilu02_analysis(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of the incomplete-LU factorization with \(0\) fill-in and no pivoting:
\(A \approx LU\) |
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA, csrRowPtrA, and csrColIndA.
This function requires the buffer size returned by csrilu02_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function csrilu02_analysis() reports a structural zero and computes level information stored in the opaque structure info. The level information can extract more parallelism during incomplete LU factorization; however csrilu02() can be done without level information. To disable level information, the user must specify the policy of csrilu02() as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
It is the user’s choice whether to call csrilu02() if csrilu02_analysis() reports a structural zero. In this case, the user can still call csrilu02(), which will return a numerical zero at the same position as the structural zero. However the result is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
structure initialized using |
|
the supported policies are |
|
buffer allocated by the user, the size is returned by |
Output
|
Structure filled with information collected during the analysis phase (that should be passed to the solve phase unchanged). |
See cusparseStatus_t for the description of the return status.
5.7.2.4. cusparse<t>csrilu02() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsrilu02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
float* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDcsrilu02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
double* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCcsrilu02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZcsrilu02(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrValA_valM,
const int* csrRowPtrA,
const int* csrColIndA,
csrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of the incomplete-LU factorization with \(0\) fill-in and no pivoting:
\(A \approx LU\) |
A is an m×m sparse matrix that is defined in CSR storage format by the three arrays csrValA_valM, csrRowPtrA, and csrColIndA.
This function requires a buffer size returned by csrilu02_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL. The fill mode and diagonal type are ignored.
Although csrilu02() can be done without level information, the user still needs to be aware of consistency. If csrilu02_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, csrilu02() can be run with or without levels. On the other hand, if csrilu02_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, csrilu02() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function csrilu02() reports the first numerical zero, including a structural zero. The user must call cusparseXcsrilu02_zeroPivot() to know where the numerical zero is.
For example, suppose A is a real m × m matrix, the following code solves precondition system M*y = x where M is the product of LU factors L and U.
// Suppose that A is m x m sparse matrix represented by CSR format,
// Assumption:
// - handle is already created by cusparseCreate(),
// - (d_csrRowPtr, d_csrColInd, d_csrVal) is CSR of A on device memory,
// - d_x is right hand side vector on device memory,
// - d_y is solution vector on device memory.
// - d_z is intermediate result on device memory.
cusparseMatDescr_t descr_M = 0;
cusparseMatDescr_t descr_L = 0;
cusparseMatDescr_t descr_U = 0;
csrilu02Info_t info_M = 0;
csrsv2Info_t info_L = 0;
csrsv2Info_t info_U = 0;
int pBufferSize_M;
int pBufferSize_L;
int pBufferSize_U;
int pBufferSize;
void *pBuffer = 0;
int structural_zero;
int numerical_zero;
const double alpha = 1.;
const cusparseSolvePolicy_t policy_M = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_L = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_U = CUSPARSE_SOLVE_POLICY_USE_LEVEL;
const cusparseOperation_t trans_L = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseOperation_t trans_U = CUSPARSE_OPERATION_NON_TRANSPOSE;
// step 1: create a descriptor which contains
// - matrix M is base-1
// - matrix L is base-1
// - matrix L is lower triangular
// - matrix L has unit diagonal
// - matrix U is base-1
// - matrix U is upper triangular
// - matrix U has non-unit diagonal
cusparseCreateMatDescr(&descr_M);
cusparseSetMatIndexBase(descr_M, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_M, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseCreateMatDescr(&descr_L);
cusparseSetMatIndexBase(descr_L, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_L, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_L, CUSPARSE_FILL_MODE_LOWER);
cusparseSetMatDiagType(descr_L, CUSPARSE_DIAG_TYPE_UNIT);
cusparseCreateMatDescr(&descr_U);
cusparseSetMatIndexBase(descr_U, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_U, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_U, CUSPARSE_FILL_MODE_UPPER);
cusparseSetMatDiagType(descr_U, CUSPARSE_DIAG_TYPE_NON_UNIT);
// step 2: create a empty info structure
// we need one info for csrilu02 and two info's for csrsv2
cusparseCreateCsrilu02Info(&info_M);
cusparseCreateCsrsv2Info(&info_L);
cusparseCreateCsrsv2Info(&info_U);
// step 3: query how much memory used in csrilu02 and csrsv2, and allocate the buffer
cusparseDcsrilu02_bufferSize(handle, m, nnz,
descr_M, d_csrVal, d_csrRowPtr, d_csrColInd, info_M, &pBufferSize_M);
cusparseDcsrsv2_bufferSize(handle, trans_L, m, nnz,
descr_L, d_csrVal, d_csrRowPtr, d_csrColInd, info_L, &pBufferSize_L);
cusparseDcsrsv2_bufferSize(handle, trans_U, m, nnz,
descr_U, d_csrVal, d_csrRowPtr, d_csrColInd, info_U, &pBufferSize_U);
pBufferSize = max(pBufferSize_M, max(pBufferSize_L, pBufferSize_U));
// pBuffer returned by cudaMalloc is automatically aligned to 128 bytes.
cudaMalloc((void**)&pBuffer, pBufferSize);
// step 4: perform analysis of incomplete Cholesky on M
// perform analysis of triangular solve on L
// perform analysis of triangular solve on U
// The lower(upper) triangular part of M has the same sparsity pattern as L(U),
// we can do analysis of csrilu0 and csrsv2 simultaneously.
cusparseDcsrilu02_analysis(handle, m, nnz, descr_M,
d_csrVal, d_csrRowPtr, d_csrColInd, info_M,
policy_M, pBuffer);
status = cusparseXcsrilu02_zeroPivot(handle, info_M, &structural_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("A(%d,%d) is missing\n", structural_zero, structural_zero);
}
cusparseDcsrsv2_analysis(handle, trans_L, m, nnz, descr_L,
d_csrVal, d_csrRowPtr, d_csrColInd,
info_L, policy_L, pBuffer);
cusparseDcsrsv2_analysis(handle, trans_U, m, nnz, descr_U,
d_csrVal, d_csrRowPtr, d_csrColInd,
info_U, policy_U, pBuffer);
// step 5: M = L * U
cusparseDcsrilu02(handle, m, nnz, descr_M,
d_csrVal, d_csrRowPtr, d_csrColInd, info_M, policy_M, pBuffer);
status = cusparseXcsrilu02_zeroPivot(handle, info_M, &numerical_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == status){
printf("U(%d,%d) is zero\n", numerical_zero, numerical_zero);
}
// step 6: solve L*z = x
cusparseDcsrsv2_solve(handle, trans_L, m, nnz, &alpha, descr_L, // replace with cusparseSpSV
d_csrVal, d_csrRowPtr, d_csrColInd, info_L,
d_x, d_z, policy_L, pBuffer);
// step 7: solve U*y = z
cusparseDcsrsv2_solve(handle, trans_U, m, nnz, &alpha, descr_U, // replace with cusparseSpSV
d_csrVal, d_csrRowPtr, d_csrColInd, info_U,
d_z, d_y, policy_U, pBuffer);
// step 6: free resources
cudaFree(pBuffer);
cusparseDestroyMatDescr(descr_M);
cusparseDestroyMatDescr(descr_L);
cusparseDestroyMatDescr(descr_U);
cusparseDestroyCsrilu02Info(info_M);
cusparseDestroyCsrsv2Info(info_L);
cusparseDestroyCsrsv2Info(info_U);
cusparseDestroy(handle);
The function supports the following properties if pBuffer != NULL
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
number of rows and columns of matrix |
|
number of nonzeros of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
structure with information collected during the analysis phase (that should have been passed to the solve phase unchanged). |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
<type> matrix containing the incomplete-LU lower and upper triangular factors. |
See cusparseStatus_t for the description of the return status.
5.7.2.5. cusparseXcsrilu02_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXcsrilu02_zeroPivot(cusparseHandle_t handle,
csrilu02Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) has either a structural zero or a numerical zero; otherwise, position=-1.
The position can be 0-based or 1-based, the same as the matrix.
Function cusparseXcsrilu02_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
Handle to the cuSPARSE library context. |
|
|
Output
|
If no structural or numerical zero, |
See cusparseStatus_t for the description of the return status.
5.7.2.6. cusparse<t>bsrilu02_numericBoost() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrilu02_numericBoost(cusparseHandle_t handle,
bsrilu02Info_t info,
int enable_boost,
double* tol,
float* boost_val)
cusparseStatus_t
cusparseDbsrilu02_numericBoost(cusparseHandle_t handle,
bsrilu02Info_t info,
int enable_boost,
double* tol,
double* boost_val)
cusparseStatus_t
cusparseCbsrilu02_numericBoost(cusparseHandle_t handle,
bsrilu02Info_t info,
int enable_boost,
double* tol,
cuComplex* boost_val)
cusparseStatus_t
cusparseZbsrilu02_numericBoost(cusparseHandle_t handle,
bsrilu02Info_t info,
int enable_boost,
double* tol,
cuDoubleComplex* boost_val)
The user can use a boost value to replace a numerical value in incomplete LU factorization. Parameter tol is used to determine a numerical zero, and boost_val is used to replace a numerical zero. The behavior is as follows:
if tol >= fabs(A(j,j)), then reset each diagonal element of block A(j,j) by boost_val.
To enable a boost value, the user sets parameter enable_boost to 1 before calling bsrilu02(). To disable the boost value, the user can call bsrilu02_numericBoost() with parameter enable_boost=0.
If enable_boost=0, tol and boost_val are ignored.
Both tol and boost_val can be in host memory or device memory. The user can set the proper mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
structure initialized using |
|
disable boost by setting |
|
tolerance to determine a numerical zero. |
|
boost value to replace a numerical zero. |
See cusparseStatus_t for the description of the return status.
5.7.2.7. cusparse<t>bsrilu02_bufferSize() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrilu02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
float *bsrValA,
const int *bsrRowPtrA,
const int *bsrColIndA,
int blockDim,
bsrilu02Info_t info,
int *pBufferSizeInBytes);
cusparseStatus_t
cusparseDbsrilu02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
double *bsrValA,
const int *bsrRowPtrA,
const int *bsrColIndA,
int blockDim,
bsrilu02Info_t info,
int *pBufferSizeInBytes);
cusparseStatus_t
cusparseCbsrilu02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex *bsrValA,
const int *bsrRowPtrA,
const int *bsrColIndA,
int blockDim,
bsrilu02Info_t info,
int *pBufferSizeInBytes);
cusparseStatus_t
cusparseZbsrilu02_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex *bsrValA,
const int *bsrRowPtrA,
const int *bsrColIndA,
int blockDim,
bsrilu02Info_t info,
int *pBufferSizeInBytes);
This function returns the size of the buffer used in computing the incomplete-LU factorization with 0 fill-in and no pivoting.
\(A \approx LU\) |
A is an (mb*blockDim)*(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA.
The buffer size depends on the dimensions of mb, blockDim, and the number of nonzero blocks of the matrix nnzb. If the user changes the matrix, it is necessary to call bsrilu02_bufferSize() again to have the correct buffer size; otherwise, a segmentation fault may occur.
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows and columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A, larger than zero. |
Output
|
record internal states based on different algorithms. |
|
number of bytes of the buffer used in |
Status Returned
|
the operation completed successfully. |
|
the library was not initialized. |
|
the resources could not be allocated. |
|
invalid parameters were passed ( |
|
the device only supports compute capability 2.0 and above. |
|
an internal operation failed. |
|
the matrix type is not supported. |
5.7.2.8. cusparse<t>bsrilu02_analysis() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrilu02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrilu02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsrilu02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrilu02_analysis(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descrA,
cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the analysis phase of the incomplete-LU factorization with 0 fill-in and no pivoting.
\(A \approx LU\) |
A is an (mb*blockDim)×(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA. The block in BSR format is of size blockDim*blockDim, stored as column-major or row-major as determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored.
This function requires a buffer size returned by bsrilu02_bufferSize(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsrilu02_analysis() reports a structural zero and computes level information stored in the opaque structure info. The level information can extract more parallelism during incomplete LU factorization. However bsrilu02() can be done without level information. To disable level information, the user needs to specify the parameter policy of bsrilu02[_analysis| ] as CUSPARSE_SOLVE_POLICY_NO_LEVEL.
Function bsrilu02_analysis() always reports the first structural zero, even with parameter policy is CUSPARSE_SOLVE_POLICY_NO_LEVEL. The user must call cusparseXbsrilu02_zeroPivot() to know where the structural zero is.
It is the user’s choice whether to call bsrilu02() if bsrilu02_analysis() reports a structural zero. In this case, the user can still call bsrilu02(), which will return a numerical zero at the same position as the structural zero. However the result is meaningless.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows and block columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A, larger than zero. |
|
structure initialized using |
|
the supported policies are |
|
buffer allocated by the user, the size is returned by |
Output
|
structure filled with information collected during the analysis phase (that should be passed to the solve phase unchanged) |
See cusparseStatus_t for the description of the return status.
5.7.2.9. cusparse<t>bsrilu02() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSbsrilu02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descry,
float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseDbsrilu02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descry,
double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseCbsrilu02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descry,
cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
cusparseStatus_t
cusparseZbsrilu02(cusparseHandle_t handle,
cusparseDirection_t dirA,
int mb,
int nnzb,
const cusparseMatDescr_t descry,
cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
bsrilu02Info_t info,
cusparseSolvePolicy_t policy,
void* pBuffer)
This function performs the solve phase of the incomplete-LU factorization with 0 fill-in and no pivoting.
\(A \approx LU\) |
A is an (mb*blockDim)×(mb*blockDim) sparse matrix that is defined in BSR storage format by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA. The block in BSR format is of size blockDim*blockDim, stored as column-major or row-major determined by parameter dirA, which is either CUSPARSE_DIRECTION_COLUMN or CUSPARSE_DIRECTION_ROW. The matrix type must be CUSPARSE_MATRIX_TYPE_GENERAL, and the fill mode and diagonal type are ignored. Function bsrilu02() supports an arbitrary blockDim.
This function requires a buffer size returned by bsrilu02_bufferSize(). The address of pBuffer must be a multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
Although bsrilu02() can be used without level information, the user must be aware of consistency. If bsrilu02_analysis() is called with policy CUSPARSE_SOLVE_POLICY_USE_LEVEL, bsrilu02() can be run with or without levels. On the other hand, if bsrilu02_analysis() is called with CUSPARSE_SOLVE_POLICY_NO_LEVEL, bsrilu02() can only accept CUSPARSE_SOLVE_POLICY_NO_LEVEL; otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Function bsrilu02() has the same behavior as csrilu02(). That is, bsr2csr(bsrilu02(A)) = csrilu02(bsr2csr(A)). The numerical zero of csrilu02() means there exists some zero U(j,j). The numerical zero of bsrilu02() means there exists some block U(j,j) that is not invertible.
Function bsrilu02 reports the first numerical zero, including a structural zero. The user must call cusparseXbsrilu02_zeroPivot() to know where the numerical zero is.
For example, suppose A is a real m-by-m matrix where m=mb*blockDim. The following code solves precondition system M*y = x, where M is the product of LU factors L and U.
// Suppose that A is m x m sparse matrix represented by BSR format,
// The number of block rows/columns is mb, and
// the number of nonzero blocks is nnzb.
// Assumption:
// - handle is already created by cusparseCreate(),
// - (d_bsrRowPtr, d_bsrColInd, d_bsrVal) is BSR of A on device memory,
// - d_x is right hand side vector on device memory.
// - d_y is solution vector on device memory.
// - d_z is intermediate result on device memory.
// - d_x, d_y and d_z are of size m.
cusparseMatDescr_t descr_M = 0;
cusparseMatDescr_t descr_L = 0;
cusparseMatDescr_t descr_U = 0;
bsrilu02Info_t info_M = 0;
bsrsv2Info_t info_L = 0;
bsrsv2Info_t info_U = 0;
int pBufferSize_M;
int pBufferSize_L;
int pBufferSize_U;
int pBufferSize;
void *pBuffer = 0;
int structural_zero;
int numerical_zero;
const double alpha = 1.;
const cusparseSolvePolicy_t policy_M = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_L = CUSPARSE_SOLVE_POLICY_NO_LEVEL;
const cusparseSolvePolicy_t policy_U = CUSPARSE_SOLVE_POLICY_USE_LEVEL;
const cusparseOperation_t trans_L = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseOperation_t trans_U = CUSPARSE_OPERATION_NON_TRANSPOSE;
const cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
// step 1: create a descriptor which contains
// - matrix M is base-1
// - matrix L is base-1
// - matrix L is lower triangular
// - matrix L has unit diagonal
// - matrix U is base-1
// - matrix U is upper triangular
// - matrix U has non-unit diagonal
cusparseCreateMatDescr(&descr_M);
cusparseSetMatIndexBase(descr_M, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_M, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseCreateMatDescr(&descr_L);
cusparseSetMatIndexBase(descr_L, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_L, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_L, CUSPARSE_FILL_MODE_LOWER);
cusparseSetMatDiagType(descr_L, CUSPARSE_DIAG_TYPE_UNIT);
cusparseCreateMatDescr(&descr_U);
cusparseSetMatIndexBase(descr_U, CUSPARSE_INDEX_BASE_ONE);
cusparseSetMatType(descr_U, CUSPARSE_MATRIX_TYPE_GENERAL);
cusparseSetMatFillMode(descr_U, CUSPARSE_FILL_MODE_UPPER);
cusparseSetMatDiagType(descr_U, CUSPARSE_DIAG_TYPE_NON_UNIT);
// step 2: create a empty info structure
// we need one info for bsrilu02 and two info's for bsrsv2
cusparseCreateBsrilu02Info(&info_M);
cusparseCreateBsrsv2Info(&info_L);
cusparseCreateBsrsv2Info(&info_U);
// step 3: query how much memory used in bsrilu02 and bsrsv2, and allocate the buffer
cusparseDbsrilu02_bufferSize(handle, dir, mb, nnzb,
descr_M, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M, &pBufferSize_M);
cusparseDbsrsv2_bufferSize(handle, dir, trans_L, mb, nnzb,
descr_L, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_L, &pBufferSize_L);
cusparseDbsrsv2_bufferSize(handle, dir, trans_U, mb, nnzb,
descr_U, d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_U, &pBufferSize_U);
pBufferSize = max(pBufferSize_M, max(pBufferSize_L, pBufferSize_U));
// pBuffer returned by cudaMalloc is automatically aligned to 128 bytes.
cudaMalloc((void**)&pBuffer, pBufferSize);
// step 4: perform analysis of incomplete LU factorization on M
// perform analysis of triangular solve on L
// perform analysis of triangular solve on U
// The lower(upper) triangular part of M has the same sparsity pattern as L(U),
// we can do analysis of bsrilu0 and bsrsv2 simultaneously.
cusparseDbsrilu02_analysis(handle, dir, mb, nnzb, descr_M,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M,
policy_M, pBuffer);
status = cusparseXbsrilu02_zeroPivot(handle, info_M, &structural_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == statuss){
printf("A(%d,%d) is missing\n", structural_zero, structural_zero);
}
cusparseDbsrsv2_analysis(handle, dir, trans_L, mb, nnzb, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim,
info_L, policy_L, pBuffer);
cusparseDbsrsv2_analysis(handle, dir, trans_U, mb, nnzb, descr_U,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim,
info_U, policy_U, pBuffer);
// step 5: M = L * U
cusparseDbsrilu02(handle, dir, mb, nnzb, descr_M,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_M, policy_M, pBuffer);
status = cusparseXbsrilu02_zeroPivot(handle, info_M, &numerical_zero);
if (CUSPARSE_STATUS_ZERO_PIVOT == statuss){
printf("block U(%d,%d) is not invertible\n", numerical_zero, numerical_zero);
}
// step 6: solve L*z = x
cusparseDbsrsv2_solve(handle, dir, trans_L, mb, nnzb, &alpha, descr_L,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_L,
d_x, d_z, policy_L, pBuffer);
// step 7: solve U*y = z
cusparseDbsrsv2_solve(handle, dir, trans_U, mb, nnzb, &alpha, descr_U,
d_bsrVal, d_bsrRowPtr, d_bsrColInd, blockDim, info_U,
d_z, d_y, policy_U, pBuffer);
// step 6: free resources
cudaFree(pBuffer);
cusparseDestroyMatDescr(descr_M);
cusparseDestroyMatDescr(descr_L);
cusparseDestroyMatDescr(descr_U);
cusparseDestroyBsrilu02Info(info_M);
cusparseDestroyBsrsv2Info(info_L);
cusparseDestroyBsrsv2Info(info_U);
cusparseDestroy(handle);
The function supports the following properties if pBuffer != NULL
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks: either |
|
number of block rows and block columns of matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix A; must be larger than zero. |
|
structure with information collected during the analysis phase (that should have been passed to the solve phase unchanged). |
|
the supported policies are |
|
buffer allocated by the user; the size is returned by |
Output
|
<type> matrix containing the incomplete-LU lower and upper triangular factors |
See cusparseStatus_t for the description of the return status.
5.7.2.10. cusparseXbsrilu02_zeroPivot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseXbsrilu02_zeroPivot(cusparseHandle_t handle,
bsrilu02Info_t info,
int* position)
If the returned error code is CUSPARSE_STATUS_ZERO_PIVOT, position=j means A(j,j) has either a structural zero or a numerical zero (the block is not invertible). Otherwise position=-1.
The position can be 0-based or 1-based, the same as the matrix.
Function cusparseXbsrilu02_zeroPivot() is a blocking call. It calls cudaDeviceSynchronize() to make sure all previous kernels are done.
The position can be in the host memory or device memory. The user can set proper the mode with cusparseSetPointerMode().
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
|
Output
|
if no structural or numerical zero, |
See cusparseStatus_t for the description of the return status.
5.7.3. Tridiagonal Solve
Different algorithms for tridiagonal solve are discussed in this section.
5.7.3.1. cusparse<t>gtsv2_buffSizeExt()
cusparseStatus_t
cusparseSgtsv2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const float* dl,
const float* d,
const float* du,
const float* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseDgtsv2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const double* dl,
const double* d,
const double* du,
const double* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseCgtsv2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
const cuComplex* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseZgtsv2_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
const cuDoubleComplex* B,
int ldb,
size_t* bufferSizeInBytes)
This function returns the size of the buffer used in gtsv2 which computes the solution of a tridiagonal linear system with multiple right-hand sides.
\(A \ast X = B\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
number of right-hand sides, columns of matrix |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The first element of each lower diagonal must be zero. |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The last element of each upper diagonal must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
leading dimension of |
Output
|
number of bytes of the buffer used in the |
See cusparseStatus_t for the description of the return status.
5.7.3.2. cusparse<t>gtsv2()
cusparseStatus_t
cusparseSgtsv2(cusparseHandle_t handle,
int m,
int n,
const float* dl,
const float* d,
const float* du,
float* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseDgtsv2(cusparseHandle_t handle,
int m,
int n,
const double* dl,
const double* d,
const double* du,
double* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseCgtsv2(cusparseHandle_t handle,
int m,
int n,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
cuComplex* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseZgtsv2(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
cuDoubleComplex* B,
int ldb,
void* pBuffer)
This function computes the solution of a tridiagonal linear system with multiple right-hand sides:
\(A \ast X = B\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
Assuming A is of size m and base-1, dl, d and du are defined by the following formula:
dl(i) := A(i, i-1) for i=1,2,...,m
The first element of dl is out-of-bound (dl(1) := A(1,0)), so dl(1) = 0.
d(i) = A(i,i) for i=1,2,...,m
du(i) = A(i,i+1) for i=1,2,...,m
The last element of du is out-of-bound (du(m) := A(m,m+1)), so du(m) = 0.
The routine does perform pivoting, which usually results in more accurate and more stable results than cusparse<t>gtsv_nopivot() or cusparse<t>gtsv2_nopivot() at the expense of some execution time.
This function requires a buffer size returned by gtsv2_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
number of right-hand sides, columns of matrix |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The first element of each lower diagonal must be zero. |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The last element of each upper diagonal must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
leading dimension of |
|
buffer allocated by the user, the size is return by |
Output
|
<type> dense solution array of dimensions |
See cusparseStatus_t for the description of the return status.
5.7.3.3. cusparse<t>gtsv2_nopivot_bufferSizeExt()
cusparseStatus_t
cusparseSgtsv2_nopivot_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const float* dl,
const float* d,
const float* du,
const float* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseDgtsv2_nopivot_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const double* dl,
const double* d,
const double* du,
const double* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseCgtsv2_nopivot_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
const cuComplex* B,
int ldb,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseZgtsv2_nopivot_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
const cuDoubleComplex* B,
int ldb,
size_t* bufferSizeInBytes)
This function returns the size of the buffer used in gtsv2_nopivot which computes the solution of a tridiagonal linear system with multiple right-hand sides.
\(A \ast X = B\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
number of right-hand sides, columns of matrix |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The first element of each lower diagonal must be zero. |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The last element of each upper diagonal must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
leading dimension of |
Output
|
number of bytes of the buffer used in the |
See cusparseStatus_t for the description of the return status.
5.7.3.4. cusparse<t>gtsv2_nopivot()
cusparseStatus_t
cusparseSgtsv2_nopivot(cusparseHandle_t handle,
int m,
int n,
const float* dl,
const float* d,
const float* du,
float* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseDgtsv2_nopivot(cusparseHandle_t handle,
int m,
int n,
const double* dl,
const double* d,
const double* du,
double* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseCgtsv2_nopivot(cusparseHandle_t handle,
int m,
int n,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
cuComplex* B,
int ldb,
void* pBuffer)
cusparseStatus_t
cusparseZgtsv2_nopivot(cusparseHandle_t handle,
int m,
int n,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
cuDoubleComplex* B,
int ldb,
void* pBuffer)
This function computes the solution of a tridiagonal linear system with multiple right-hand sides:
\(A \ast X = B\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
The routine does not perform any pivoting and uses a combination of the Cyclic Reduction (CR) and the Parallel Cyclic Reduction (PCR) algorithms to find the solution. It achieves better performance when m is a power of 2.
This function requires a buffer size returned by gtsv2_nopivot_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
number of right-hand sides, columns of matrix |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The first element of each lower diagonal must be zero. |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The last element of each upper diagonal must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
leading dimension of |
|
buffer allocated by the user, the size is return by |
Output
|
<type> dense solution array of dimensions |
See cusparseStatus_t for the description of the return status.
5.7.4. Batched Tridiagonal Solve
Different algorithms for batched tridiagonal solve are discussed in this section.
5.7.4.1. cusparse<t>gtsv2StridedBatch_bufferSizeExt()
cusparseStatus_t
cusparseSgtsv2StridedBatch_bufferSizeExt(cusparseHandle_t handle,
int m,
const float* dl,
const float* d,
const float* du,
const float* x,
int batchCount,
int batchStride,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseDgtsv2StridedBatch_bufferSizeExt(cusparseHandle_t handle,
int m,
const double* dl,
const double* d,
const double* du,
const double* x,
int batchCount,
int batchStride,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseCgtsv2StridedBatch_bufferSizeExt(cusparseHandle_t handle,
int m,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
const cuComplex* x,
int batchCount,
int batchStride,
size_t* bufferSizeInBytes)
cusparseStatus_t
cusparseZgtsv2StridedBatch_bufferSizeExt(cusparseHandle_t handle,
int m,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
const cuDoubleComplex* x,
int batchCount,
int batchStride,
size_t* bufferSizeInBytes)
This function returns the size of the buffer used in gtsv2StridedBatch which computes the solution of multiple tridiagonal linear systems for i=0,…,batchCount:
\(A^{(i)} \ast \text{y}^{(i)} = \text{x}^{(i)}\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix X. Notice that solution Y overwrites right-hand-side matrix X on exit. The different matrices are assumed to be of the same size and are stored with a fixed batchStride in memory.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The lower diagonal \(dl^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. The main diagonal \(d^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The upper diagonal \(du^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array that contains the right-hand-side of the tri-diagonal linear system. The right-hand-side \(x^{(i)}\) that corresponds to the ith linear system starts at location |
|
number of systems to solve. |
|
stride (number of elements) that separates the vectors of every system (must be at least |
Output
|
number of bytes of the buffer used in the |
See cusparseStatus_t for the description of the return status.
5.7.4.2. cusparse<t>gtsv2StridedBatch()
cusparseStatus_t
cusparseSgtsv2StridedBatch(cusparseHandle_t handle,
int m,
const float* dl,
const float* d,
const float* du,
float* x,
int batchCount,
int batchStride,
void* pBuffer)
cusparseStatus_t
cusparseDgtsv2StridedBatch(cusparseHandle_t handle,
int m,
const double* dl,
const double* d,
const double* du,
double* x,
int batchCount,
int batchStride,
void* pBuffer)
cusparseStatus_t
cusparseCgtsv2StridedBatch(cusparseHandle_t handle,
int m,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
cuComplex* x,
int batchCount,
int batchStride,
void* pBuffer)
cusparseStatus_t
cusparseZgtsv2StridedBatch(cusparseHandle_t handle,
int m,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
cuDoubleComplex* x,
int batchCount,
int batchStride,
void* pBuffer)
This function computes the solution of multiple tridiagonal linear systems for i=0,…,batchCount:
\(A^{(i)} \ast \text{y}^{(i)} = \text{x}^{(i)}\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix X. Notice that solution Y overwrites right-hand-side matrix X on exit. The different matrices are assumed to be of the same size and are stored with a fixed batchStride in memory.
The routine does not perform any pivoting and uses a combination of the Cyclic Reduction (CR) and the Parallel Cyclic Reduction (PCR) algorithms to find the solution. It achieves better performance when m is a power of 2.
This function requires a buffer size returned by gtsv2StridedBatch_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
the size of the linear system (must be ≥ 3). |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The lower diagonal \(dl^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. The main diagonal \(d^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The upper diagonal \(du^{(i)}\) that corresponds to the ith linear system starts at location |
|
<type> dense array that contains the right-hand-side of the tri-diagonal linear system. The right-hand-side \(x^{(i)}\) that corresponds to the ith linear system starts at location |
|
number of systems to solve. |
|
stride (number of elements) that separates the vectors of every system (must be at least |
|
buffer allocated by the user, the size is return by |
Output
|
<type> dense array that contains the solution of the tri-diagonal linear system. The solution \(x^{(i)}\) that corresponds to the ith linear system starts at location |
See cusparseStatus_t for the description of the return status.
5.7.4.3. cusparse<t>gtsvInterleavedBatch()
cusparseStatus_t
cusparseSgtsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const float* dl,
const float* d,
const float* du,
const float* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDgtsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const double* dl,
const double* d,
const double* du,
const double* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseCgtsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
const cuComplex* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseZgtsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
const cuDoubleComplex* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSgtsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
float* dl,
float* d,
float* du,
float* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseDgtsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
double* dl,
double* d,
double* du,
double* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseCgtsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
cuComplex* dl,
cuComplex* d,
cuComplex* du,
cuComplex* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseZgtsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
cuDoubleComplex* dl,
cuDoubleComplex* d,
cuDoubleComplex* du,
cuDoubleComplex* x,
int batchCount,
void* pBuffer)
This function computes the solution of multiple tridiagonal linear systems for i=0,…,batchCount:
\(A^{(i)} \ast \text{x}^{(i)} = \text{b}^{(i)}\) |
The coefficient matrix A of each of these tri-diagonal linear system is defined with three vectors corresponding to its lower (dl), main (d), and upper (du) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
Assuming A is of size m and base-1, dl, d and du are defined by the following formula:
dl(i) := A(i, i-1) for i=1,2,...,m
The first element of dl is out-of-bound (dl(1) := A(1,0)), so dl(1) = 0.
d(i) = A(i,i) for i=1,2,...,m
du(i) = A(i,i+1) for i=1,2,...,m
The last element of du is out-of-bound (du(m) := A(m,m+1)), so du(m) = 0.
The data layout is different from gtsvStridedBatch which aggregates all matrices one after another. Instead, gtsvInterleavedBatch gathers different matrices of the same element in a continous manner. If dl is regarded as a 2-D array of size m-by-batchCount, dl(:,j) to store j-th matrix. gtsvStridedBatch uses column-major while gtsvInterleavedBatch uses row-major.
The routine provides three different algorithms, selected by parameter algo. The first algorithm is cuThomas provided by Barcelona Supercomputing Center. The second algorithm is LU with partial pivoting and last algorithm is QR. From stability perspective, cuThomas is not numerically stable because it does not have pivoting. LU with partial pivoting and QR are stable. From performance perspective, LU with partial pivoting and QR is about 10% to 20% slower than cuThomas.
This function requires a buffer size returned by gtsvInterleavedBatch_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
If the user prepares aggregate format, one can use cublasXgeam to get interleaved format. However such transformation takes time comparable to solver itself. To reach best performance, the user must prepare interleaved format explicitly.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
algo = 0: cuThomas (unstable algorithm); algo = 1: LU with pivoting (stable algorithm); algo = 2: QR (stable algorithm) |
|
the size of the linear system. |
|
<type> dense array containing the lower diagonal of the tri-diagonal linear system. The first element of each lower diagonal must be zero. |
|
<type> dense array containing the main diagonal of the tri-diagonal linear system. |
|
<type> dense array containing the upper diagonal of the tri-diagonal linear system. The last element of each upper diagonal must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
buffer allocated by the user, the size is return by |
Output
|
<type> dense solution array of dimensions |
See cusparseStatus_t for the description of the return status.
5.7.5. Batched Pentadiagonal Solve
Different algorithms for batched pentadiagonal solve are discussed in this section.
5.7.5.1. cusparse<t>gpsvInterleavedBatch()
cusparseStatus_t
cusparseSgpsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const float* ds,
const float* dl,
const float* d,
const float* du,
const float* dw,
const float* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDgpsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const double* ds,
const double* dl,
const double* d,
const double* du,
const double* dw,
const double* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseCgpsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const cuComplex* ds,
const cuComplex* dl,
const cuComplex* d,
const cuComplex* du,
const cuComplex* dw,
const cuComplex* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseZgpsvInterleavedBatch_bufferSizeExt(cusparseHandle_t handle,
int algo,
int m,
const cuDoubleComplex* ds,
const cuDoubleComplex* dl,
const cuDoubleComplex* d,
const cuDoubleComplex* du,
const cuDoubleComplex* dw,
const cuDoubleComplex* x,
int batchCount,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSgpsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
float* ds,
float* dl,
float* d,
float* du,
float* dw,
float* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseDgpsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
double* ds,
double* dl,
double* d,
double* du,
double* dw,
double* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseCgpsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
cuComplex* ds,
cuComplex* dl,
cuComplex* d,
cuComplex* du,
cuComplex* dw,
cuComplex* x,
int batchCount,
void* pBuffer)
cusparseStatus_t
cusparseZgpsvInterleavedBatch(cusparseHandle_t handle,
int algo,
int m,
cuDoubleComplex* ds,
cuDoubleComplex* dl,
cuDoubleComplex* d,
cuDoubleComplex* du,
cuDoubleComplex* dw,
cuDoubleComplex* x,
int batchCount,
void* pBuffer)
This function computes the solution of multiple penta-diagonal linear systems for i=0,…,batchCount:
\(A^{(i)} \ast \text{x}^{(i)} = \text{b}^{(i)}\) |
The coefficient matrix A of each of these penta-diagonal linear system is defined with five vectors corresponding to its lower (ds, dl), main (d), and upper (du, dw) matrix diagonals; the right-hand sides are stored in the dense matrix B. Notice that solution X overwrites right-hand-side matrix B on exit.
Assuming A is of size m and base-1, ds, dl, d, du and dw are defined by the following formula:
ds(i) := A(i, i-2) for i=1,2,...,m
The first two elements of ds is out-of-bound (ds(1) := A(1,-1), ds(2) := A(2,0)), so ds(1) = 0 and ds(2) = 0.
dl(i) := A(i, i-1) for i=1,2,...,m
The first element of dl is out-of-bound (dl(1) := A(1,0)), so dl(1) = 0.
d(i) = A(i,i) for i=1,2,...,m
du(i) = A(i,i+1) for i=1,2,...,m
The last element of du is out-of-bound (du(m) := A(m,m+1)), so du(m) = 0.
dw(i) = A(i,i+2) for i=1,2,...,m
The last two elements of dw is out-of-bound (dw(m-1) := A(m-1,m+1), dw(m) := A(m,m+2)), so dw(m-1) = 0 and dw(m) = 0.
The data layout is the same as gtsvStridedBatch.
The routine is numerically stable because it uses QR to solve the linear system.
This function requires a buffer size returned by gpsvInterleavedBatch_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If it is not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The function supports the following properties if pBuffer != NULL
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
only support algo = 0 (QR) |
|
the size of the linear system. |
|
<type> dense array containing the lower diagonal (distance 2 to the diagonal) of the penta-diagonal linear system. The first two elements must be zero. |
|
<type> dense array containing the lower diagonal (distance 1 to the diagonal) of the penta-diagonal linear system. The first element must be zero. |
|
<type> dense array containing the main diagonal of the penta-diagonal linear system. |
|
<type> dense array containing the upper diagonal (distance 1 to the diagonal) of the penta-diagonal linear system. The last element must be zero. |
|
<type> dense array containing the upper diagonal (distance 2 to the diagonal) of the penta-diagonal linear system. The last two elements must be zero. |
|
<type> dense right-hand-side array of dimensions |
|
buffer allocated by the user, the size is return by |
Output
|
<type> dense solution array of dimensions |
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSgpsvInterleavedBatch for a code example.
5.8. cuSPARSE Reorderings Reference
This chapter describes the reordering routines used to manipulate sparse matrices.
5.8.1. cusparse<t>csrcolor() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseScsrcolor(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const float* fractionToColor,
int* ncolors,
int* coloring,
int* reordering,
cusparseColorInfo_t info)
cusparseStatus_t
cusparseDcsrcolor(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const double* fractionToColor,
int* ncolors,
int* coloring,
int* reordering,
cusparseColorInfo_t info)
cusparseStatus_t
cusparseCcsrcolor(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cuComplex* fractionToColor,
int* ncolors,
int* coloring,
int* reordering,
cusparseColorInfo_t info)
cusparseStatus_t
cusparseZcsrcolor(cusparseHandle_t handle,
int m,
int nnz,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cuDoubleComplex* fractionToColor,
int* ncolors,
int* coloring,
int* reordering,
cusparseColorInfo_t info)
This function performs the coloring of the adjacency graph associated with the matrix A stored in CSR format. The coloring is an assignment of colors (integer numbers) to nodes, such that neighboring nodes have distinct colors. An approximate coloring algorithm is used in this routine, and is stopped when a certain percentage of nodes has been colored. The rest of the nodes are assigned distinct colors (an increasing sequence of integers numbers, starting from the last integer used previously). The last two auxiliary routines can be used to extract the resulting number of colors, their assignment and the associated reordering. The reordering is such that nodes that have been assigned the same color are reordered to be next to each other.
The matrix A passed to this routine, must be stored as a general matrix and have a symmetric sparsity pattern. If the matrix is nonsymmetric the user should pass A+A^T as a parameter to this routine.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows of matrix |
|
number of nonzero elements of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
fraction of nodes to be colored, which should be in the interval [0.0,1.0], for example 0.8 implies that 80 percent of nodes will be colored. |
|
structure with information to be passed to the coloring. |
Output
|
The number of distinct colors used (at most the size of the matrix, but likely much smaller). |
|
The resulting coloring permutation |
|
The resulting reordering permutation (untouched if NULL) |
See cusparseStatus_t for the description of the return status.
5.9. cuSPARSE Format Conversion Reference
This chapter describes the conversion routines between different sparse and dense storage formats.
coosort, csrsort, cscsort, and csru2csr are sorting routines without malloc inside, the following table estimates the buffer size.
|
|
|
|
|
125M |
|
|
100M |
|
|
71M for ‘d’ and 55M for ‘z’ |
5.9.1. cusparse<t>bsr2csr()
cusparseStatus_t
cusparseSbsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cusparseMatDescr_t descrC,
float* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseDbsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cusparseMatDescr_t descrC,
double* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseCbsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cusparseMatDescr_t descrC,
cuComplex* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseZbsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int blockDim,
const cusparseMatDescr_t descrC,
cuDoubleComplex* csrValC,
int* csrRowPtrC,
int* csrColIndC)
This function converts a sparse matrix in BSR format that is defined by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA) into a sparse matrix in CSR format that is defined by arrays csrValC, csrRowPtrC, and csrColIndC.
Let m(=mb*blockDim) be the number of rows of A and n(=nb*blockDim) be number of columns of A, then A and C are m*n sparse matrices. The BSR format of A contains nnzb(=bsrRowPtrA[mb] - bsrRowPtrA[0]) nonzero blocks, whereas the sparse matrix A contains nnz(=nnzb*blockDim*blockDim) elements. The user must allocate enough space for arrays csrRowPtrC, csrColIndC, and csrValC. The requirements are as follows:
csrRowPtrC of m+1 elements
csrValC of nnz elements
csrColIndC of nnz elements
The general procedure is as follows:
// Given BSR format (bsrRowPtrA, bsrcolIndA, bsrValA) and
// blocks of BSR format are stored in column-major order.
cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
int m = mb*blockDim;
int nnzb = bsrRowPtrA[mb] - bsrRowPtrA[0]; // number of blocks
int nnz = nnzb * blockDim * blockDim; // number of elements
cudaMalloc((void**)&csrRowPtrC, sizeof(int)*(m+1));
cudaMalloc((void**)&csrColIndC, sizeof(int)*nnz);
cudaMalloc((void**)&csrValC, sizeof(float)*nnz);
cusparseSbsr2csr(handle, dir, mb, nb,
descrA,
bsrValA, bsrRowPtrA, bsrColIndA,
blockDim,
descrC,
csrValC, csrRowPtrC, csrColIndC);
The routine requires no extra storage
The routine supports asynchronous execution if
blockDim != 1or the Stream Ordered Memory Allocator is availableThe routine supports CUDA graph capture if
blockDim != 1or the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows of sparse matrix |
|
number of block columns of sparse matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
block dimension of sparse matrix |
|
the descriptor of matrix |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
See cusparseStatus_t for the description of the return status.
5.9.2. cusparse<t>gebsr2gebsc()
cusparseStatus_t
cusparseSgebsr2gebsc_bufferSize(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const float* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseDgebsr2gebsc_bufferSize(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const double* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseCgebsr2gebsc_bufferSize(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const cuComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseZgebsr2gebsc_bufferSize(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const cuDoubleComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseSgebsr2gebsc(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const float* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
float* bscVal,
int* bscRowInd,
int* bscColPtr,
cusparseAction_t copyValues,
cusparseIndexBase_t baseIdx,
void* pBuffer)
cusparseStatus_t
cusparseDgebsr2gebsc(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const double* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
double* bscVal,
int* bscRowInd,
int* bscColPtr,
cusparseAction_t copyValues,
cusparseIndexBase_t baseIdx,
void* pBuffer)
cusparseStatus_t
cusparseCgebsr2gebsc(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const cuComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
cuComplex* bscVal,
int* bscRowInd,
int* bscColPtr,
cusparseAction_t copyValues,
cusparseIndexBase_t baseIdx,
void* pBuffer)
cusparseStatus_t
cusparseZgebsr2gebsc(cusparseHandle_t handle,
int mb,
int nb,
int nnzb,
const cuDoubleComplex* bsrVal,
const int* bsrRowPtr,
const int* bsrColInd,
int rowBlockDim,
int colBlockDim,
cuDoubleComplex* bscVal,
int* bscRowInd,
int* bscColPtr,
cusparseAction_t copyValues,
cusparseIndexBase_t baseIdx,
void* pBuffer)
This function can be seen as the same as csr2csc() when each block of size rowBlockDim*colBlockDim is regarded as a scalar.
This sparsity pattern of the result matrix can also be seen as the transpose of the original sparse matrix, but the memory layout of a block does not change.
The user must call gebsr2gebsc_bufferSize() to determine the size of the buffer required by gebsr2gebsc(), allocate the buffer, and pass the buffer pointer to gebsr2gebsc().
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of block rows of sparse matrix |
|
number of block columns of sparse matrix |
|
number of nonzero blocks of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
number of rows within a block of |
|
number of columns within a block of |
|
|
|
|
|
host pointer containing number of bytes of the buffer used in |
|
buffer allocated by the user; the size is return by |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
See cusparseStatus_t for the description of the return status.
5.9.3. cusparse<t>gebsr2gebsr()
cusparseStatus_t
cusparseSgebsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
int rowBlockDimC,
int colBlockDimC,
int* pBufferSize)
cusparseStatus_t
cusparseDgebsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
int rowBlockDimC,
int colBlockDimC,
int* pBufferSize)
cusparseStatus_t
cusparseCgebsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
int rowBlockDimC,
int colBlockDimC,
int* pBufferSize)
cusparseStatus_t
cusparseZgebsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
int rowBlockDimC,
int colBlockDimC,
int* pBufferSize)
cusparseStatus_t
cusparseXgebsr2gebsrNnz(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
const cusparseMatDescr_t descrC,
int* bsrRowPtrC,
int rowBlockDimC,
int colBlockDimC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseSgebsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
const cusparseMatDescr_t descrC,
float* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDimC,
int colBlockDimC,
void* pBuffer)
cusparseStatus_t
cusparseDgebsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
const cusparseMatDescr_t descrC,
double* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDimC,
int colBlockDimC,
void* pBuffer)
cusparseStatus_t
cusparseCgebsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
const cusparseMatDescr_t descrC,
cuComplex* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDimC,
int colBlockDimC,
void* pBuffer)
cusparseStatus_t
cusparseZgebsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
int nnzb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDimA,
int colBlockDimA,
const cusparseMatDescr_t descrC,
cuDoubleComplex* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDimC,
int colBlockDimC,
void* pBuffer)
This function converts a sparse matrix in general BSR format that is defined by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA into a sparse matrix in another general BSR format that is defined by arrays bsrValC, bsrRowPtrC, and bsrColIndC.
If rowBlockDimA=1 and colBlockDimA=1, cusparse[S|D|C|Z]gebsr2gebsr() is the same as cusparse[S|D|C|Z]csr2gebsr().
If rowBlockDimC=1 and colBlockDimC=1, cusparse[S|D|C|Z]gebsr2gebsr() is the same as cusparse[S|D|C|Z]gebsr2csr().
A is an m*n sparse matrix where m(=mb*rowBlockDim) is the number of rows of A, and n(=nb*colBlockDim) is the number of columns of A. The general BSR format of A contains nnzb(=bsrRowPtrA[mb] - bsrRowPtrA[0]) nonzero blocks. The matrix C is also general BSR format with a different block size, rowBlockDimC*colBlockDimC. If m is not a multiple of rowBlockDimC, or n is not a multiple of colBlockDimC, zeros are filled in. The number of block rows of C is mc(=(m+rowBlockDimC-1)/rowBlockDimC). The number of block rows of C is nc(=(n+colBlockDimC-1)/colBlockDimC). The number of nonzero blocks of C is nnzc.
The implementation adopts a two-step approach to do the conversion. First, the user allocates bsrRowPtrC of mc+1 elements and uses function cusparseXgebsr2gebsrNnz() to determine the number of nonzero block columns per block row of matrix C. Second, the user gathers nnzc (number of non-zero block columns of matrix C) from either (nnzc=*nnzTotalDevHostPtr) or (nnzc=bsrRowPtrC[mc]-bsrRowPtrC[0]) and allocates bsrValC of nnzc*rowBlockDimC*colBlockDimC elements and bsrColIndC of nnzc integers. Finally the function cusparse[S|D|C|Z]gebsr2gebsr() is called to complete the conversion.
The user must call gebsr2gebsr_bufferSize() to know the size of the buffer required by gebsr2gebsr(), allocate the buffer, and pass the buffer pointer to gebsr2gebsr().
The general procedure is as follows:
// Given general BSR format (bsrRowPtrA, bsrColIndA, bsrValA) and
// blocks of BSR format are stored in column-major order.
cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
int base, nnzc;
int m = mb*rowBlockDimA;
int n = nb*colBlockDimA;
int mc = (m+rowBlockDimC-1)/rowBlockDimC;
int nc = (n+colBlockDimC-1)/colBlockDimC;
int bufferSize;
void *pBuffer;
cusparseSgebsr2gebsr_bufferSize(handle, dir, mb, nb, nnzb,
descrA, bsrValA, bsrRowPtrA, bsrColIndA,
rowBlockDimA, colBlockDimA,
rowBlockDimC, colBlockDimC,
&bufferSize);
cudaMalloc((void**)&pBuffer, bufferSize);
cudaMalloc((void**)&bsrRowPtrC, sizeof(int)*(mc+1));
// nnzTotalDevHostPtr points to host memory
int *nnzTotalDevHostPtr = &nnzc;
cusparseXgebsr2gebsrNnz(handle, dir, mb, nb, nnzb,
descrA, bsrRowPtrA, bsrColIndA,
rowBlockDimA, colBlockDimA,
descrC, bsrRowPtrC,
rowBlockDimC, colBlockDimC,
nnzTotalDevHostPtr,
pBuffer);
if (NULL != nnzTotalDevHostPtr){
nnzc = *nnzTotalDevHostPtr;
}else{
cudaMemcpy(&nnzc, bsrRowPtrC+mc, sizeof(int), cudaMemcpyDeviceToHost);
cudaMemcpy(&base, bsrRowPtrC, sizeof(int), cudaMemcpyDeviceToHost);
nnzc -= base;
}
cudaMalloc((void**)&bsrColIndC, sizeof(int)*nnzc);
cudaMalloc((void**)&bsrValC, sizeof(float)*(rowBlockDimC*colBlockDimC)*nnzc);
cusparseSgebsr2gebsr(handle, dir, mb, nb, nnzb,
descrA, bsrValA, bsrRowPtrA, bsrColIndA,
rowBlockDimA, colBlockDimA,
descrC, bsrValC, bsrRowPtrC, bsrColIndC,
rowBlockDimC, colBlockDimC,
pBuffer);
The routines require no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routines do not support CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows of sparse matrix |
|
number of block columns of sparse matrix |
|
number of nonzero blocks of matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
number of rows within a block of |
|
number of columns within a block of |
|
the descriptor of matrix |
|
number of rows within a block of |
|
number of columns within a block of |
|
host pointer containing number of bytes of the buffer used in |
|
buffer allocated by the user; the size is return by |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
|
total number of nonzero blocks of |
See cusparseStatus_t for the description of the return status.
5.9.4. cusparse<t>gebsr2csr()
cusparseStatus_t
cusparseSgebsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const float* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDim,
int colBlockDim,
const cusparseMatDescr_t descrC,
float* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseDgebsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const double* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDim,
int colBlockDim,
const cusparseMatDescr_t descrC,
double* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseCgebsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const cuComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDim,
int colBlockDim,
const cusparseMatDescr_t descrC,
cuComplex* csrValC,
int* csrRowPtrC,
int* csrColIndC)
cusparseStatus_t
cusparseZgebsr2csr(cusparseHandle_t handle,
cusparseDirection_t dir,
int mb,
int nb,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* bsrValA,
const int* bsrRowPtrA,
const int* bsrColIndA,
int rowBlockDim,
int colBlockDim,
const cusparseMatDescr_t descrC,
cuDoubleComplex* csrValC,
int* csrRowPtrC,
int* csrColIndC)
This function converts a sparse matrix in general BSR format that is defined by the three arrays bsrValA, bsrRowPtrA, and bsrColIndA into a sparse matrix in CSR format that is defined by arrays csrValC, csrRowPtrC, and csrColIndC.
Let m(=mb*rowBlockDim) be number of rows of A and n(=nb*colBlockDim) be number of columns of A, then A and C are m*n sparse matrices. The general BSR format of A contains nnzb(=bsrRowPtrA[mb] - bsrRowPtrA[0]) non-zero blocks, whereas sparse matrix A contains nnz(=nnzb*rowBlockDim*colBlockDim) elements. The user must allocate enough space for arrays csrRowPtrC, csrColIndC, and csrValC. The requirements are as follows:
csrRowPtrC of m+1 elements
csrValC of nnz elements
csrColIndC of nnz elements
The general procedure is as follows:
// Given general BSR format (bsrRowPtrA, bsrColIndA, bsrValA) and
// blocks of BSR format are stored in column-major order.
cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
int m = mb*rowBlockDim;
int n = nb*colBlockDim;
int nnzb = bsrRowPtrA[mb] - bsrRowPtrA[0]; // number of blocks
int nnz = nnzb * rowBlockDim * colBlockDim; // number of elements
cudaMalloc((void**)&csrRowPtrC, sizeof(int)*(m+1));
cudaMalloc((void**)&csrColIndC, sizeof(int)*nnz);
cudaMalloc((void**)&csrValC, sizeof(float)*nnz);
cusparseSgebsr2csr(handle, dir, mb, nb,
descrA,
bsrValA, bsrRowPtrA, bsrColIndA,
rowBlockDim, colBlockDim,
descrC,
csrValC, csrRowPtrC, csrColIndC);
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of block rows of sparse matrix |
|
number of block columns of sparse matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
number of rows within a block of |
|
number of columns within a block of |
|
the descriptor of matrix |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
See cusparseStatus_t for the description of the return status.
5.9.5. cusparse<t>csr2gebsr()
cusparseStatus_t
cusparseScsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseDcsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseCcsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseZcsr2gebsr_bufferSize(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
int rowBlockDim,
int colBlockDim,
int* pBufferSize)
cusparseStatus_t
cusparseXcsr2gebsrNnz(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const int* csrRowPtrA,
const int* csrColIndA,
const cusparseMatDescr_t descrC,
int* bsrRowPtrC,
int rowBlockDim,
int colBlockDim,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseScsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cusparseMatDescr_t descrC,
float* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDim,
int colBlockDim,
void* pBuffer)
cusparseStatus_t
cusparseDcsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cusparseMatDescr_t descrC,
double* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDim,
int colBlockDim,
void* pBuffer)
cusparseStatus_t
cusparseCcsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cusparseMatDescr_t descrC,
cuComplex* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDim,
int colBlockDim,
void* pBuffer)
cusparseStatus_t
cusparseZcsr2gebsr(cusparseHandle_t handle,
cusparseDirection_t dir,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const cusparseMatDescr_t descrC,
cuDoubleComplex* bsrValC,
int* bsrRowPtrC,
int* bsrColIndC,
int rowBlockDim,
int colBlockDim,
void* pBuffer)
This function converts a sparse matrix A in CSR format (that is defined by arrays csrValA, csrRowPtrA, and csrColIndA) into a sparse matrix C in general BSR format (that is defined by the three arrays bsrValC, bsrRowPtrC, and bsrColIndC).
The matrix A is a m*n sparse matrix and matrix C is a (mb*rowBlockDim)*(nb*colBlockDim) sparse matrix, where mb(=(m+rowBlockDim-1)/rowBlockDim) is the number of block rows of C, and nb(=(n+colBlockDim-1)/colBlockDim) is the number of block columns of C.
The block of C is of size rowBlockDim*colBlockDim. If m is not multiple of rowBlockDim or n is not multiple of colBlockDim, zeros are filled in.
The implementation adopts a two-step approach to do the conversion. First, the user allocates bsrRowPtrC of mb+1 elements and uses function cusparseXcsr2gebsrNnz() to determine the number of nonzero block columns per block row. Second, the user gathers nnzb (number of nonzero block columns of matrix C) from either (nnzb=*nnzTotalDevHostPtr) or (nnzb=bsrRowPtrC[mb]-bsrRowPtrC[0]) and allocates bsrValC of nnzb*rowBlockDim*colBlockDim elements and bsrColIndC of nnzb integers. Finally function cusparse[S|D|C|Z]csr2gebsr() is called to complete the conversion.
The user must obtain the size of the buffer required by csr2gebsr() by calling csr2gebsr_bufferSize(), allocate the buffer, and pass the buffer pointer to csr2gebsr().
The general procedure is as follows:
// Given CSR format (csrRowPtrA, csrColIndA, csrValA) and
// blocks of BSR format are stored in column-major order.
cusparseDirection_t dir = CUSPARSE_DIRECTION_COLUMN;
int base, nnzb;
int mb = (m + rowBlockDim-1)/rowBlockDim;
int nb = (n + colBlockDim-1)/colBlockDim;
int bufferSize;
void *pBuffer;
cusparseScsr2gebsr_bufferSize(handle, dir, m, n,
descrA, csrValA, csrRowPtrA, csrColIndA,
rowBlockDim, colBlockDim,
&bufferSize);
cudaMalloc((void**)&pBuffer, bufferSize);
cudaMalloc((void**)&bsrRowPtrC, sizeof(int) *(mb+1));
// nnzTotalDevHostPtr points to host memory
int *nnzTotalDevHostPtr = &nnzb;
cusparseXcsr2gebsrNnz(handle, dir, m, n,
descrA, csrRowPtrA, csrColIndA,
descrC, bsrRowPtrC, rowBlockDim, colBlockDim,
nnzTotalDevHostPtr,
pBuffer);
if (NULL != nnzTotalDevHostPtr){
nnzb = *nnzTotalDevHostPtr;
}else{
cudaMemcpy(&nnzb, bsrRowPtrC+mb, sizeof(int), cudaMemcpyDeviceToHost);
cudaMemcpy(&base, bsrRowPtrC, sizeof(int), cudaMemcpyDeviceToHost);
nnzb -= base;
}
cudaMalloc((void**)&bsrColIndC, sizeof(int)*nnzb);
cudaMalloc((void**)&bsrValC, sizeof(float)*(rowBlockDim*colBlockDim)*nnzb);
cusparseScsr2gebsr(handle, dir, m, n,
descrA,
csrValA, csrRowPtrA, csrColIndA,
descrC,
bsrValC, bsrRowPtrC, bsrColIndC,
rowBlockDim, colBlockDim,
pBuffer);
The routine cusparseXcsr2gebsrNnz() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>csr2gebsr() has the following properties:
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
storage format of blocks, either |
|
number of rows of sparse matrix |
|
number of columns of sparse matrix |
|
the descriptor of matrix |
|
<type> array of |
|
integer array of |
|
integer array of |
|
the descriptor of matrix |
|
number of rows within a block of |
|
number of columns within a block of |
|
buffer allocated by the user, the size is return by |
Output
|
<type> array of |
|
integer array of |
|
integer array of |
|
total number of nonzero blocks of matrix |
See cusparseStatus_t for the description of the return status.
5.9.6. cusparse<t>coo2csr()
cusparseStatus_t
cusparseXcoo2csr(cusparseHandle_t handle,
const int* cooRowInd,
int nnz,
int m,
int* csrRowPtr,
cusparseIndexBase_t idxBase)
This function converts the array containing the uncompressed row indices (corresponding to COO format) into an array of compressed row pointers (corresponding to CSR format).
It can also be used to convert the array containing the uncompressed column indices (corresponding to COO format) into an array of column pointers (corresponding to CSC format).
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
integer array of |
|
number of non-zeros of the sparse matrix (that is also the length of array |
|
number of rows of matrix |
|
|
Output
|
integer array of |
See cusparseStatus_t for the description of the return status.
5.9.7. cusparse<t>csr2coo()
cusparseStatus_t
cusparseXcsr2coo(cusparseHandle_t handle,
const int* csrRowPtr,
int nnz,
int m,
int* cooRowInd,
cusparseIndexBase_t idxBase)
This function converts the array containing the compressed row pointers (corresponding to CSR format) into an array of uncompressed row indices (corresponding to COO format).
It can also be used to convert the array containing the compressed column indices (corresponding to CSC format) into an array of uncompressed column indices (corresponding to COO format).
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
handle to the cuSPARSE library context. |
|
integer array of |
|
number of nonzeros of the sparse matrix (that is also the length of array |
|
number of rows of matrix |
|
|
Output
|
integer array of |
See cusparseStatus_t for the description of the return status.
5.9.8. cusparseCsr2cscEx2()
cusparseStatus_t
cusparseCsr2cscEx2_bufferSize(cusparseHandle_t handle,
int m,
int n,
int nnz,
const void* csrVal,
const int* csrRowPtr,
const int* csrColInd,
void* cscVal,
int* cscColPtr,
int* cscRowInd,
cudaDataType valType,
cusparseAction_t copyValues,
cusparseIndexBase_t idxBase,
cusparseCsr2CscAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseCsr2cscEx2(cusparseHandle_t handle,
int m,
int n,
int nnz,
const void* csrVal,
const int* csrRowPtr,
const int* csrColInd,
void* cscVal,
int* cscColPtr,
int* cscRowInd,
cudaDataType valType,
cusparseAction_t copyValues,
cusparseIndexBase_t idxBase,
cusparseCsr2CscAlg_t alg,
void* buffer)
This function converts a sparse matrix in CSR format (that is defined by the three arrays csrVal, csrRowPtr, and csrColInd) into a sparse matrix in CSC format (that is defined by arrays cscVal, cscRowInd, and cscColPtr). The resulting matrix can also be seen as the transpose of the original sparse matrix. Notice that this routine can also be used to convert a matrix in CSC format into a matrix in CSR format.
The routine requires extra storage proportional to the number of nonzero values nnz. It provides in output always the same matrix.
It is executed asynchronously with respect to the host, and it may return control to the application on the host before the result is ready.
The function cusparseCsr2cscEx2_bufferSize() returns the size of the workspace needed by cusparseCsr2cscEx2(). User needs to allocate a buffer of this size and give that buffer to cusparseCsr2cscEx2() as an argument.
If nnz == 0, then csrColInd, csrVal, cscVal, and cscRowInd could have NULL value. In this case, cscColPtr is set to idxBase for all values.
If m == 0 or n == 0, the pointers are not checked and the routine returns CUSPARSE_STATUS_SUCCESS.
Input
|
Handle to the cuSPARSE library context |
|
Number of rows of the CSR input matrix; number of columns of the CSC ouput matrix |
|
Number of columns of the CSR input matrix; number of rows of the CSC ouput matrix |
|
Number of nonzero elements of the CSR and CSC matrices |
|
Value array of size |
|
Integer array of size |
|
Integer array of size |
|
Value array of size |
|
Integer array of size |
|
Integer array of size |
|
Value type for both CSR and CSC matrices |
|
|
|
Index base |
|
Algorithm implementation. see |
|
Number of bytes of workspace needed by |
|
Pointer to workspace buffer |
cusparseCsr2cscEx2() supports the following data types:
|
|---|
|
|
|
|
|
|
|
|
|
cusparseCsr2cscEx2() supports the following algorithms (cusparseCsr2CscAlg_t):
Algorithm |
Notes |
|---|---|
|
Default algorithm |
Action |
Notes |
|---|---|
|
Compute the “structure” of the CSC output matrix (offset, row indices) |
|
Compute the “structure” of the CSC output matrix and copy the values |
cusparseCsr2cscEx2() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
cusparseCsr2cscEx2() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
5.9.9. cusparse<t>nnz()
cusparseStatus_t
cusparseSnnz(cusparseHandle_t handle,
cusparseDirection_t dirA,
int m,
int n,
const cusparseMatDescr_t descrA,
const float* A,
int lda,
int* nnzPerRowColumn,
int* nnzTotalDevHostPtr)
cusparseStatus_t
cusparseDnnz(cusparseHandle_t handle,
cusparseDirection_t dirA,
int m,
int n,
const cusparseMatDescr_t descrA,
const double* A,
int lda,
int* nnzPerRowColumn,
int* nnzTotalDevHostPtr)
cusparseStatus_t
cusparseCnnz(cusparseHandle_t handle,
cusparseDirection_t dirA,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuComplex* A,
int lda,
int* nnzPerRowColumn,
int* nnzTotalDevHostPtr)
cusparseStatus_t
cusparseZnnz(cusparseHandle_t handle,
cusparseDirection_t dirA,
int m,
int n,
const cusparseMatDescr_t descrA,
const cuDoubleComplex* A,
int lda,
int* nnzPerRowColumn,
int* nnzTotalDevHostPtr)
This function computes the number of nonzero elements per row or column and the total number of nonzero elements in a dense matrix.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
direction that specifies whether to count nonzero elements by |
|
number of rows of matrix |
|
number of columns of matrix |
|
the descriptor of matrix |
|
array of dimensions |
|
leading dimension of dense array |
Output
|
array of size |
|
total number of nonzero elements in device or host memory. |
See cusparseStatus_t for the description of the return status.
5.9.10. cusparseCreateIdentityPermutation() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateIdentityPermutation(cusparseHandle_t handle,
int n,
int* p);
This function creates an identity map. The output parameter p represents such map by p = 0:1:(n-1).
This function is typically used with coosort, csrsort, cscsort.
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
size of the map. |
Output
|
|
|
|
|
integer array of dimensions |
See cusparseStatus_t for the description of the return status.
5.9.11. cusparseXcoosort()
cusparseStatus_t
cusparseXcoosort_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
const int* cooRows,
const int* cooCols,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseXcoosortByRow(cusparseHandle_t handle,
int m,
int n,
int nnz,
int* cooRows,
int* cooCols,
int* P,
void* pBuffer)
cusparseStatus_t
cusparseXcoosortByColumn(cusparseHandle_t handle,
int m,
int n,
int nnz,
int* cooRows,
int* cooCols,
int* P,
void* pBuffer);
This function sorts COO format. The sorting is in-place. Also the user can sort by row or sort by column.
A is an m×n sparse matrix that is defined in COO storage format by the three arrays cooVals, cooRows, and cooCols.
There is no assumption for the base index of the matrix. coosort uses stable sort on signed integer, so the value of cooRows or cooCols can be negative.
This function coosort() requires buffer size returned by coosort_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The parameter P is both input and output. If the user wants to compute sorted cooVal, P must be set as 0:1:(nnz-1) before coosort(), and after coosort(), new sorted value array satisfies cooVal_sorted = cooVal(P).
Remark: the dimension m and n are not used. If the user does not know the value of m or n, just passes a value positive. This usually happens if the user only reads a COO array first and needs to decide the dimension m or n later.
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzero elements of matrix |
|
|
integer array of |
|
|
integer array of |
|
|
integer array of |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
integer array of |
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status
Please visit cuSPARSE Library Samples - cusparseXcoosortByRow for a code example.
5.9.12. cusparseXcsrsort()
cusparseStatus_t
cusparseXcsrsort_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
const int* csrRowPtr,
const int* csrColInd,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseXcsrsort(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const int* csrRowPtr,
int* csrColInd,
int* P,
void* pBuffer)
This function sorts CSR format. The stable sorting is in-place.
The matrix type is regarded as CUSPARSE_MATRIX_TYPE_GENERAL implicitly. In other words, any symmetric property is ignored.
This function csrsort() requires buffer size returned by csrsort_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The parameter P is both input and output. If the user wants to compute sorted csrVal, P must be set as 0:1:(nnz-1) before csrsort(), and after csrsort(), new sorted value array satisfies csrVal_sorted = csrVal(P).
The general procedure is as follows:
// A is a 3x3 sparse matrix, base-0
// | 1 2 3 |
// A = | 4 5 6 |
// | 7 8 9 |
const int m = 3;
const int n = 3;
const int nnz = 9;
csrRowPtr[m+1] = { 0, 3, 6, 9}; // on device
csrColInd[nnz] = { 2, 1, 0, 0, 2,1, 1, 2, 0}; // on device
csrVal[nnz] = { 3, 2, 1, 4, 6, 5, 8, 9, 7}; // on device
size_t pBufferSizeInBytes = 0;
void *pBuffer = NULL;
int *P = NULL;
// step 1: allocate buffer
cusparseXcsrsort_bufferSizeExt(handle, m, n, nnz, csrRowPtr, csrColInd, &pBufferSizeInBytes);
cudaMalloc( &pBuffer, sizeof(char)* pBufferSizeInBytes);
// step 2: setup permutation vector P to identity
cudaMalloc( (void**)&P, sizeof(int)*nnz);
cusparseCreateIdentityPermutation(handle, nnz, P);
// step 3: sort CSR format
cusparseXcsrsort(handle, m, n, nnz, descrA, csrRowPtr, csrColInd, P, pBuffer);
// step 4: gather sorted csrVal
cusparseDgthr(handle, nnz, csrVal, csrVal_sorted, P, CUSPARSE_INDEX_BASE_ZERO);
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzero elements of matrix |
|
|
integer array of |
|
|
integer array of |
|
|
integer array of |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.13. cusparseXcscsort()
cusparseStatus_t
cusparseXcscsort_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
const int* cscColPtr,
const int* cscRowInd,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseXcscsort(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
const int* cscColPtr,
int* cscRowInd,
int* P,
void* pBuffer)
This function sorts CSC format. The stable sorting is in-place.
The matrix type is regarded as CUSPARSE_MATRIX_TYPE_GENERAL implicitly. In other words, any symmetric property is ignored.
This function cscsort() requires buffer size returned by cscsort_bufferSizeExt(). The address of pBuffer must be multiple of 128 bytes. If not, CUSPARSE_STATUS_INVALID_VALUE is returned.
The parameter P is both input and output. If the user wants to compute sorted cscVal, P must be set as 0:1:(nnz-1) before cscsort(), and after cscsort(), new sorted value array satisfies cscVal_sorted = cscVal(P).
The general procedure is as follows:
// A is a 3x3 sparse matrix, base-0
// | 1 2 |
// A = | 4 0 |
// | 0 8 |
const int m = 3;
const int n = 2;
const int nnz = 4;
cscColPtr[n+1] = { 0, 2, 4}; // on device
cscRowInd[nnz] = { 1, 0, 2, 0}; // on device
cscVal[nnz] = { 4.0, 1.0, 8.0, 2.0 }; // on device
size_t pBufferSizeInBytes = 0;
void *pBuffer = NULL;
int *P = NULL;
// step 1: allocate buffer
cusparseXcscsort_bufferSizeExt(handle, m, n, nnz, cscColPtr, cscRowInd, &pBufferSizeInBytes);
cudaMalloc( &pBuffer, sizeof(char)* pBufferSizeInBytes);
// step 2: setup permutation vector P to identity
cudaMalloc( (void**)&P, sizeof(int)*nnz);
cusparseCreateIdentityPermutation(handle, nnz, P);
// step 3: sort CSC format
cusparseXcscsort(handle, m, n, nnz, descrA, cscColPtr, cscRowInd, P, pBuffer);
// step 4: gather sorted cscVal
cusparseDgthr(handle, nnz, cscVal, cscVal_sorted, P, CUSPARSE_INDEX_BASE_ZERO);
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzero elements of matrix |
|
|
integer array of |
|
|
integer array of |
|
|
integer array of |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.14. cusparseXcsru2csr() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseCreateCsru2csrInfo(csru2csrInfo_t *info);
cusparseStatus_t
cusparseDestroyCsru2csrInfo(csru2csrInfo_t info);
cusparseStatus_t
cusparseScsru2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
float* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDcsru2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
double* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseCcsru2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
cuComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseZcsru2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnz,
cuDoubleComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseScsru2csr(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
float* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDcsru2csr(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
double* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseCcsru2csr(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseZcsru2csr(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseScsr2csru(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
float* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDcsr2csru(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
double* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseCcsr2csru(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
cuComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseZcsr2csru(cusparseHandle_t handle,
int m,
int n,
int nnz,
const cusparseMatDescr_t descrA,
cuDoubleComplex* csrVal,
const int* csrRowPtr,
int* csrColInd,
csru2csrInfo_t info,
void* pBuffer)
This function transfers unsorted CSR format to CSR format, and vice versa. The operation is in-place.
This function is a wrapper of csrsort and gthr. The usecase is the following scenario.
If the user has a matrix A of CSR format which is unsorted, and implements his own code (which can be CPU or GPU kernel) based on this special order (for example, diagonal first, then lower triangle, then upper triangle), and wants to convert it to CSR format when calling CUSPARSE library, and then convert it back when doing something else on his/her kernel. For example, suppose the user wants to solve a linear system Ax=b by the following iterative scheme
\(x^{(k+1)} = x^{(k)} + L^{(-1)}*(b - Ax^{(k)})\) |
The code heavily uses SpMV and triangular solve. Assume that the user has an in-house design of SpMV (Sparse Matrix-Vector multiplication) based on special order of A. However the user wants to use the cuSPARSE library for triangular solver. Then the following code can work.
do step 1: compute residual vector r = b - A x (k) by in-house SpMV step 2: B := sort(A), and L is lower triangular part of B (only sort A once and keep the permutation vector) step 3: solve z = L (-1) * ( b - A x (k) ) by cusparseXcsrsv step 4: add correction x (k+1) = x (k) + z step 5: A := unsort(B) (use permutation vector to get back the unsorted CSR) until convergence |
The requirements of step 2 and step 5 are
In-place operation.
The permutation vector
Pis hidden in an opaque structure.No
cudaMallocinside the conversion routine. Instead, the user has to provide the buffer explicitly.The conversion between unsorted CSR and sorted CSR may needs several times, but the function only generates the permutation vector
Ponce.The function is based on
csrsort,gatherandscatteroperations.
The operation is called csru2csr, which means unsorted CSR to sorted CSR. Also we provide the inverse operation, called csr2csru.
In order to keep the permutation vector invisible, we need an opaque structure called csru2csrInfo. Then two functions (cusparseCreateCsru2csrInfo, cusparseDestroyCsru2csrInfo) are used to initialize and to destroy the opaque structure.
cusparse[S|D|C|Z]csru2csr_bufferSizeExt returns the size of the buffer. The permutation vector P is also allcated inside csru2csrInfo. The lifetime of the permutation vector is the same as the lifetime of csru2csrInfo.
cusparse[S|D|C|Z]csru2csr performs forward transformation from unsorted CSR to sorted CSR. First call uses csrsort to generate the permutation vector P, and subsequent call uses P to do transformation.
cusparse[S|D|C|Z]csr2csru performs backward transformation from sorted CSR to unsorted CSR. P is used to get unsorted form back.
The routine cusparse<t>csru2csr() has the following properties:
The routine requires no extra storage if
pBuffer != NULLThe routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>csr2csru() has the following properties if pBuffer != NULL:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
The following tables describe parameters of csr2csru_bufferSizeExt and csr2csru.
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzero elements of matrix |
|
|
the descriptor of matrix |
|
|
<type> array of nnz unsorted nonzero elements of matrix |
|
|
integer array of |
|
|
integer array of |
|
|
opaque structure initialized using |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
<type> array of nnz sorted nonzero elements of matrix |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.15. cusparseXpruneDense2csr() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseHpruneDense2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
const __half* threshold,
const cusparseMatDescr_t descrC,
const __half* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSpruneDense2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
const float* threshold,
const cusparseMatDescr_t descrC,
const float* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDpruneDense2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
const double* threshold,
const cusparseMatDescr_t descrC,
const double* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseHpruneDense2csrNnz(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
const __half* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseSpruneDense2csrNnz(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
const float* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseDpruneDense2csrNnz(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
const double* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseHpruneDense2csr(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
const __half* threshold,
const cusparseMatDescr_t descrC,
__half* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
cusparseStatus_t
cusparseSpruneDense2csr(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
const float* threshold,
const cusparseMatDescr_t descrC,
float* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
cusparseStatus_t
cusparseDpruneDense2csr(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
const double* threshold,
const cusparseMatDescr_t descrC,
double* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
This function prunes a dense matrix to a sparse matrix with CSR format.
Given a dense matrix A and a non-negative value threshold, the function returns a sparse matrix C, defined by
\(\begin{matrix} {{C(i,j)} = {A(i,j)}} & \text{if\ |A(i,j)|\ >\ threshold} \\ \end{matrix}\) |
The implementation adopts a two-step approach to do the conversion. First, the user allocates csrRowPtrC of m+1 elements and uses function pruneDense2csrNnz() to determine the number of nonzeros columns per row. Second, the user gathers nnzC (number of nonzeros of matrix C) from either (nnzC=*nnzTotalDevHostPtr) or (nnzC=csrRowPtrC[m]-csrRowPtrC[0]) and allocates csrValC of nnzC elements and csrColIndC of nnzC integers. Finally function pruneDense2csr() is called to complete the conversion.
The user must obtain the size of the buffer required by pruneDense2csr() by calling pruneDense2csr_bufferSizeExt(), allocate the buffer, and pass the buffer pointer to pruneDense2csr().
Examples of prune chapter provides a simple example of pruneDense2csr().
The routine cusparse<t>pruneDense2csrNnz() has the following properties:
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>DpruneDense2csr() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
array of dimension (lda, n). |
|
|
leading dimension of |
|
|
a value to drop the entries of A. |
|
|
the descriptor of matrix |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
total number of nonzero of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.16. cusparseXpruneCsr2csr() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseHpruneCsr2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const __half* threshold,
const cusparseMatDescr_t descrC,
const __half* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSpruneCsr2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const float* threshold,
const cusparseMatDescr_t descrC,
const float* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDpruneCsr2csr_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const double* threshold,
const cusparseMatDescr_t descrC,
const double* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseHpruneCsr2csrNnz(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const __half* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseSpruneCsr2csrNnz(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const float* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseDpruneCsr2csrNnz(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const double* threshold,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
void* pBuffer)
cusparseStatus_t
cusparseHpruneCsr2csr(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const __half* threshold,
const cusparseMatDescr_t descrC,
__half* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
cusparseStatus_t
cusparseSpruneCsr2csr(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const float* threshold,
const cusparseMatDescr_t descrC,
float* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
cusparseStatus_t
cusparseDpruneCsr2csr(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
const double* threshold,
const cusparseMatDescr_t descrC,
double* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
void* pBuffer)
This function prunes a sparse matrix to a sparse matrix with CSR format.
Given a sparse matrix A and a non-negative value threshold, the function returns a sparse matrix C, defined by
\(\begin{matrix} {{C(i,j)} = {A(i,j)}} & \text{if\ |A(i,j)|\ >\ threshold} \\ \end{matrix}\) |
The implementation adopts a two-step approach to do the conversion. First, the user allocates csrRowPtrC of m+1 elements and uses function pruneCsr2csrNnz() to determine the number of nonzeros columns per row. Second, the user gathers nnzC (number of nonzeros of matrix C) from either (nnzC=*nnzTotalDevHostPtr) or (nnzC=csrRowPtrC[m]-csrRowPtrC[0]) and allocates csrValC of nnzC elements and csrColIndC of nnzC integers. Finally function pruneCsr2csr() is called to complete the conversion.
The user must obtain the size of the buffer required by pruneCsr2csr() by calling pruneCsr2csr_bufferSizeExt(), allocate the buffer, and pass the buffer pointer to pruneCsr2csr().
Examples of prune chapter provides a simple example of pruneCsr2csr().
The routine cusparse<t>pruneCsr2csrNnz() has the following properties:
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>pruneCsr2csr() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzeros of matrix |
|
|
the descriptor of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
a value to drop the entries of A. |
|
|
the descriptor of matrix |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
total number of nonzero of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.17. cusparseXpruneDense2csrPercentage() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseHpruneDense2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
const __half* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSpruneDense2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
const float* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDpruneDense2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
const double* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseHpruneDense2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseSpruneDense2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDpruneDense2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseHpruneDense2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
const __half* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
__half* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseSpruneDense2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
const float* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
float* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDpruneDense2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
const double* A,
int lda,
float percentage,
const cusparseMatDescr_t descrC,
double* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
This function prunes a dense matrix to a sparse matrix by percentage.
Given a dense matrix A and a non-negative value percentage, the function computes sparse matrix C by the following three steps:
Step 1: sort absolute value of A in ascending order.
\(\begin{matrix} {key\ :=\ sort(\ |A|\ )} \\ \end{matrix}\) |
Step 2: choose threshold by the parameter percentage
\(\begin{matrix} {pos\ =\ ceil(m*n*(percentage/100))\ -\ 1} \\ {pos\ =\ min(pos,\ m*n-1)} \\ {pos\ =\ max(pos,\ 0)} \\ {threshold\ =\ key\lbrack pos\rbrack} \\ \end{matrix}\) |
Step 3: call pruneDense2csr() by with the parameter threshold.
The implementation adopts a two-step approach to do the conversion. First, the user allocates csrRowPtrC of m+1 elements and uses function pruneDense2csrNnzByPercentage() to determine the number of nonzeros columns per row. Second, the user gathers nnzC (number of nonzeros of matrix C) from either (nnzC=*nnzTotalDevHostPtr) or (nnzC=csrRowPtrC[m]-csrRowPtrC[0]) and allocates csrValC of nnzC elements and csrColIndC of nnzC integers. Finally function pruneDense2csrByPercentage() is called to complete the conversion.
The user must obtain the size of the buffer required by pruneDense2csrByPercentage() by calling pruneDense2csrByPercentage_bufferSizeExt(), allocate the buffer, and pass the buffer pointer to pruneDense2csrByPercentage().
Remark 1: the value of percentage must be not greater than 100. Otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Remark 2: the zeros of A are not ignored. All entries are sorted, including zeros. This is different from pruneCsr2csrByPercentage()
Examples of prune chapter provides a simple example of pruneDense2csrNnzByPercentage().
The routine cusparse<t>pruneDense2csrNnzByPercentage() has the following properties:
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>pruneDense2csrByPercentage() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
array of dimension (lda, n). |
|
|
leading dimension of |
|
|
percentage <=100 and percentage >= 0 |
|
|
the descriptor of matrix |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
total number of nonzero of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.18. cusparseXpruneCsr2csrByPercentage() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseHpruneCsr2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
const __half* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseSpruneCsr2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
const float* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseDpruneCsr2csrByPercentage_bufferSizeExt(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
const double* csrValC,
const int* csrRowPtrC,
const int* csrColIndC,
pruneInfo_t info,
size_t* pBufferSizeInBytes)
cusparseStatus_t
cusparseHpruneCsr2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseSpruneCsr2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDpruneCsr2csrNnzByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
int* csrRowPtrC,
int* nnzTotalDevHostPtr,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseHpruneCsr2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const __half* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
__half* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseSpruneCsr2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const float* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
float* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
cusparseStatus_t
cusparseDpruneCsr2csrByPercentage(cusparseHandle_t handle,
int m,
int n,
int nnzA,
const cusparseMatDescr_t descrA,
const double* csrValA,
const int* csrRowPtrA,
const int* csrColIndA,
float percentage,
const cusparseMatDescr_t descrC,
double* csrValC,
const int* csrRowPtrC,
int* csrColIndC,
pruneInfo_t info,
void* pBuffer)
This function prunes a sparse matrix to a sparse matrix by percentage.
Given a sparse matrix A and a non-negative value percentage, the function computes sparse matrix C by the following three steps:
Step 1: sort absolute value of A in ascending order.
\(\begin{matrix} {key\ :=\ sort(\ |csrValA|\ )} \\ \end{matrix}\) |
Step 2: choose threshold by the parameter percentage
\(\begin{matrix} {pos\ =\ ceil(nnzA*(percentage/100))\ -\ 1} \\ {pos\ =\ min(pos,\ nnzA-1)} \\ {pos\ =\ max(pos,\ 0)} \\ {threshold\ =\ key\lbrack pos\rbrack} \\ \end{matrix}\) |
Step 3: call pruneCsr2csr() by with the parameter threshold.
The implementation adopts a two-step approach to do the conversion. First, the user allocates csrRowPtrC of m+1 elements and uses function pruneCsr2csrNnzByPercentage() to determine the number of nonzeros columns per row. Second, the user gathers nnzC (number of nonzeros of matrix C) from either (nnzC=*nnzTotalDevHostPtr) or (nnzC=csrRowPtrC[m]-csrRowPtrC[0]) and allocates csrValC of nnzC elements and csrColIndC of nnzC integers. Finally function pruneCsr2csrByPercentage() is called to complete the conversion.
The user must obtain the size of the buffer required by pruneCsr2csrByPercentage() by calling pruneCsr2csrByPercentage_bufferSizeExt(), allocate the buffer, and pass the buffer pointer to pruneCsr2csrByPercentage().
Remark 1: the value of percentage must be not greater than 100. Otherwise, CUSPARSE_STATUS_INVALID_VALUE is returned.
Examples of prune chapter provides a simple example of pruneCsr2csrByPercentage().
The routine cusparse<t>pruneCsr2csrNnzByPercentage() has the following properties:
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
The routine cusparse<t>pruneCsr2csrByPercentage() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine supports CUDA graph capture
Input
|
|
|
|
|
handle to the cuSPARSE library context. |
|
|
number of rows of matrix |
|
|
number of columns of matrix |
|
|
number of nonzeros of matrix |
|
|
the descriptor of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
percentage <=100 and percentage >= 0 |
|
|
the descriptor of matrix |
|
|
buffer allocated by the user; the size is returned by |
Output
|
|
|
|
|
total number of nonzero of matrix |
|
|
<type> array of |
|
|
integer array of |
|
|
integer array of |
|
|
number of bytes of the buffer. |
See cusparseStatus_t for the description of the return status.
5.9.19. cusparse<t>nnz_compress() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseSnnz_compress(cusparseHandle_t handle,
int m,
const cusparseMatDescr_t descr,
const float* csrValA,
const int* csrRowPtrA,
int* nnzPerRow,
int* nnzC,
float tol)
cusparseStatus_t
cusparseDnnz_compress(cusparseHandle_t handle,
int m,
const cusparseMatDescr_t descr,
const double* csrValA,
const int* csrRowPtrA,
int* nnzPerRow,
int* nnzC,
double tol)
cusparseStatus_t
cusparseCnnz_compress(cusparseHandle_t handle,
int m,
const cusparseMatDescr_t descr,
const cuComplex* csrValA,
const int* csrRowPtrA,
int* nnzPerRow,
int* nnzC,
cuComplex tol)
cusparseStatus_t
cusparseZnnz_compress(cusparseHandle_t handle,
int m,
const cusparseMatDescr_t descr,
const cuDoubleComplex* csrValA,
const int* csrRowPtrA,
int* nnzPerRow,
int* nnzC,
cuDoubleComplex tol)
This function is the step one to convert from csr format to compressed csr format.
Given a sparse matrix A and a non-negative value threshold, the function returns nnzPerRow(the number of nonzeros columns per row) and nnzC(the total number of nonzeros) of a sparse matrix C, defined by
\(\begin{matrix} {{C(i,j)} = {A(i,j)}} & \text{if\ |A(i,j)|\ >\ threshold} \\ \end{matrix}\) |
A key assumption for the cuComplex and cuDoubleComplex case is that this tolerance is given as the real part. For example tol = 1e-8 + 0*i and we extract cureal, that is the x component of this struct.
This function requires temporary extra storage that is allocated internally
The routine supports asynchronous execution if the Stream Ordered Memory Allocator is available
The routine supports CUDA graph capture if the Stream Ordered Memory Allocator is available
Input
|
handle to the cuSPARSE library context. |
|
number of rows of matrix |
|
the descriptor of matrix |
|
csr noncompressed values array |
|
the corresponding input noncompressed row pointer. |
|
non-negative tolerance to determine if a number less than or equal to it. |
Output
|
this array contains the number of elements whose absolute values are greater than tol per row. |
|
host/device pointer of the total number of elements whose absolute values are greater than tol. |
See cusparseStatus_t for the description of the return status.
6. cuSPARSE Generic APIs
The cuSPARSE Generic APIs allow computing the most common sparse linear algebra operations, such as sparse matrix-vector (SpMV) and sparse matrix-matrix multiplication (SpMM), in a flexible way. The new APIs have the following capabilities and features:
Set matrix data layouts, number of batches, and storage formats (for example, CSR, COO, and so on).
Set input/output/compute data types. This also allows mixed data-type computation.
Set types of sparse vector/matrix indices (e.g. 32-bit, 64-bit).
Choose the algorithm for the computation.
Guarantee external device memory for internal operations.
Provide extensive consistency checks across input matrices and vectors. This includes the validation of sizes, data types, layout, allowed operations, etc.
Provide constant descriptors for vector and matrix inputs to support const-safe interface and guarantee that the APIs do not modify their inputs.
6.1. Generic Types Reference
The cuSPARSE generic type references are described in this section.
6.1.1. cusparseFormat_t
This type indicates the format of the sparse matrix. See cuSPARSE Storage Format for their description.
Value |
Meaning |
|---|---|
|
The matrix is stored in Coordinate (COO) format organized in Structure of Arrays (SoA) layout |
|
The matrix is stored in Compressed Sparse Row (CSR) format |
|
The matrix is stored in Compressed Sparse Column (CSC) format |
|
The matrix is stored in Blocked-Ellpack (Blocked-ELL) format |
|
The matrix is stored in Sliced-Ellpack (Sliced-ELL) format |
|
The matrix is stored in Block Sparse Row (BSR) format |
6.1.2. cusparseOrder_t
This type indicates the memory layout of a dense matrix.
Value |
Meaning |
|---|---|
|
The matrix is stored in row-major |
|
The matrix is stored in column-major |
6.1.3. cusparseIndexType_t
This type indicates the index type for representing the sparse matrix indices.
Value |
Meaning |
|---|---|
|
32-bit signed integer [1, 2^31 - 1] |
|
64-bit signed integer [1, 2^63 - 1] |
6.2. Dense Vector APIs
The cuSPARSE helper functions for dense vector descriptor are described in this section.
See the Dense Vector Format section for the detailed description of the storage format.
6.2.1. cusparseCreateDnVec()
cusparseStatus_t
cusparseCreateDnVec(cusparseDnVecDescr_t* dnVecDescr,
int64_t size,
void* values,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstDnVec(cusparseConstDnVecDescr_t* dnVecDescr,
int64_t size,
const void* values,
cudaDataType valueType)
This function initializes the dense vector descriptor dnVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Dense vector descriptor |
|
HOST |
IN |
Size of the dense vector |
|
DEVICE |
IN |
Values of the dense vector. Array with |
|
HOST |
IN |
Enumerator specifying the datatype of |
cusparseCreateDnVec() has the following constraints:
valuesmust be aligned to the size of the datatype specified byvalueType. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.2.2. cusparseDestroyDnVec()
cusparseStatus_t
cusparseDestroyDnVec(cusparseConstDnVecDescr_t dnVecDescr) // non-const descriptor supported
This function releases the host memory allocated for the dense vector descriptor dnVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense vector descriptor |
See cusparseStatus_t for the description of the return status.
6.2.3. cusparseDnVecGet()
cusparseStatus_t
cusparseDnVecGet(cusparseDnVecDescr_t dnVecDescr,
int64_t* size,
void** values,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstDnVecGet(cusparseConstDnVecDescr_t dnVecDescr,
int64_t* size,
const void** values,
cudaDataType* valueType)
This function returns the fields of the dense vector descriptor dnVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense vector descriptor |
|
HOST |
OUT |
Size of the dense vector |
|
DEVICE |
OUT |
Values of the dense vector. Array with |
|
HOST |
OUT |
Enumerator specifying the datatype of |
See cusparseStatus_t for the description of the return status.
6.2.4. cusparseDnVecGetValues()
cusparseStatus_t
cusparseDnVecGetValues(cusparseDnVecDescr_t dnVecDescr,
void** values)
cusparseStatus_t
cusparseConstDnVecGetValues(cusparseConstDnVecDescr_t dnVecDescr,
const void** values)
This function returns the values field of the dense vector descriptor dnVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense vector descriptor |
|
DEVICE |
OUT |
Values of the dense vector |
See cusparseStatus_t for the description of the return status.
6.2.5. cusparseDnVecSetValues()
cusparseStatus_t
cusparseDnVecSetValues(cusparseDnVecDescr_t dnVecDescr,
void* values)
This function set the values field of the dense vector descriptor dnVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense vector descriptor |
|
DEVICE |
IN |
Values of the dense vector. Array with |
cusparseDnVecSetValues() has the following constraints:
valuesmust be aligned to the size of the datatype specified indnVecDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.3. Sparse Vector APIs
The cuSPARSE helper functions for sparse vector descriptor are described in this section.
See the Sparse Vector Format section for the detailed description of the storage format.
6.3.1. cusparseCreateSpVec()
cusparseStatus_t
cusparseCreateSpVec(cusparseSpVecDescr_t* spVecDescr,
int64_t size,
int64_t nnz,
void* indices,
void* values,
cusparseIndexType_t idxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstSpVec(cusparseConstSpVecDescr_t* spVecDescr,
int64_t size,
int64_t nnz,
const void* indices,
const void* values,
cusparseIndexType_t idxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse vector descriptor |
|
HOST |
IN |
Size of the sparse vector |
|
HOST |
IN |
Number of non-zero entries of the sparse vector |
|
DEVICE |
IN |
Indices of the sparse vector. Array with |
|
DEVICE |
IN |
Values of the sparse vector. Array with |
|
HOST |
IN |
Enumerator specifying the data type of |
|
HOST |
IN |
Enumerator specifying the the index base of |
|
HOST |
IN |
Enumerator specifying the datatype of |
cusparseCreateSpVec() has the following constraints:
indicesandvaluesmust be aligned to the size of the datatypes specified byidxTypeandvalueType, respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.3.2. cusparseDestroySpVec()
cusparseStatus_t
cusparseDestroySpVec(cusparseConstSpVecDescr_t spVecDescr) // non-const descriptor supported
This function releases the host memory allocated for the sparse vector descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse vector descriptor |
See cusparseStatus_t for the description of the return status.
6.3.3. cusparseSpVecGet()
cusparseStatus_t
cusparseSpVecGet(cusparseSpVecDescr_t spVecDescr,
int64_t* size,
int64_t* nnz,
void** indices,
void** values,
cusparseIndexType_t* idxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstSpVecGet(cusparseConstSpVecDescr_t spVecDescr,
int64_t* size,
int64_t* nnz,
const void** indices,
const void** values,
cusparseIndexType_t* idxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
This function returns the fields of the sparse vector descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse vector descriptor |
|
HOST |
OUT |
Size of the sparse vector |
|
HOST |
OUT |
Number of non-zero entries of the sparse vector |
|
DEVICE |
OUT |
Indices of the sparse vector. Array with |
|
DEVICE |
OUT |
Values of the sparse vector. Array with |
|
HOST |
OUT |
Enumerator specifying the data type of |
|
HOST |
OUT |
Enumerator specifying the the index base of |
|
HOST |
OUT |
Enumerator specifying the datatype of |
See cusparseStatus_t for the description of the return status.
6.3.4. cusparseSpVecGetIndexBase()
cusparseStatus_t
cusparseSpVecGetIndexBase(cusparseConstSpVecDescr_t spVecDescr, // non-const descriptor supported
cusparseIndexBase_t* idxBase)
This function returns the idxBase field of the sparse vector descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse vector descriptor |
|
HOST |
OUT |
Enumerator specifying the the index base of |
See cusparseStatus_t for the description of the return status.
6.3.5. cusparseSpVecGetValues()
cusparseStatus_t
cusparseSpVecGetValues(cusparseSpVecDescr_t spVecDescr,
void** values)
cusparseStatus_t
cusparseConstSpVecGetValues(cusparseConstSpVecDescr_t spVecDescr,
const void** values)
This function returns the values field of the sparse vector descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse vector descriptor |
|
DEVICE |
OUT |
Values of the sparse vector. Array with |
See cusparseStatus_t for the description of the return status.
6.3.6. cusparseSpVecSetValues()
cusparseStatus_t
cusparseSpVecSetValues(cusparseSpVecDescr_t spVecDescr,
void* values)
This function set the values field of the sparse vector descriptor spVecDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse vector descriptor |
|
DEVICE |
IN |
Values of the sparse vector. Array with |
cusparseDnVecSetValues() has the following constraints:
valuesmust be aligned to the size of the datatype specified inspVecDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.4. Dense Matrix APIs
The cuSPARSE helper functions for dense matrix descriptor are described in this section.
See the Dense Matrix Format section for the detailed description of the storage format.
6.4.1. cusparseCreateDnMat()
cusparseStatus_t
cusparseCreateDnMat(cusparseDnMatDescr_t* dnMatDescr,
int64_t rows,
int64_t cols,
int64_t ld,
void* values,
cudaDataType valueType,
cusparseOrder_t order)
cusparseStatus_t
cusparseCreateConstDnMat(cusparseConstDnMatDescr_t* dnMatDescr,
int64_t rows,
int64_t cols,
int64_t ld,
const void* values,
cudaDataType valueType,
cusparseOrder_t order)
The function initializes the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Dense matrix descriptor |
|
HOST |
IN |
Number of rows of the dense matrix |
|
HOST |
IN |
Number of columns of the dense matrix |
|
HOST |
IN |
Leading dimension of the dense matrix |
|
DEVICE |
IN |
Values of the dense matrix. Array with |
|
HOST |
IN |
Enumerator specifying the datatype of |
|
HOST |
IN |
Enumerator specifying the memory layout of the dense matrix |
cusparseCreateDnMat() has the following constraints:
valuesmust be aligned to the size of the datatype specified byvalueType. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.4.2. cusparseDestroyDnMat()
cusparseStatus_t
cusparseDestroyDnMat(cusparseConstDnMatDescr_t dnMatDescr) // non-const descriptor supported
This function releases the host memory allocated for the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
See cusparseStatus_t for the description of the return status.
6.4.3. cusparseDnMatGet()
cusparseStatus_t
cusparseDnMatGet(cusparseDnMatDescr_t dnMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* ld,
void** values,
cudaDataType* type,
cusparseOrder_t* order)
cusparseStatus_t
cusparseConstDnMatGet(cusparseConstDnMatDescr_t dnMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* ld,
const void** values,
cudaDataType* type,
cusparseOrder_t* order)
This function returns the fields of the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
|
HOST |
OUT |
Number of rows of the dense matrix |
|
HOST |
OUT |
Number of columns of the dense matrix |
|
HOST |
OUT |
Leading dimension of the dense matrix |
|
DEVICE |
OUT |
Values of the dense matrix. Array with |
|
HOST |
OUT |
Enumerator specifying the datatype of |
|
HOST |
OUT |
Enumerator specifying the memory layout of the dense matrix |
See cusparseStatus_t for the description of the return status.
6.4.4. cusparseDnMatGetValues()
cusparseStatus_t
cusparseDnMatGetValues(cusparseDnMatDescr_t dnMatDescr,
void** values)
cusparseStatus_t
cusparseConstDnMatGetValues(cusparseConstDnMatDescr_t dnMatDescr,
const void** values)
This function returns the values field of the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
|
DEVICE |
OUT |
Values of the dense matrix. Array with |
See cusparseStatus_t for the description of the return status.
6.4.5. cusparseDnMatSetValues()
cusparseStatus_t
cusparseDnMatSetValues(cusparseDnMatDescr_t dnMatDescr,
void* values)
This function sets the values field of the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
|
DEVICE |
IN |
Values of the dense matrix. Array with |
cusparseDnMatSetValues() has the following constraints:
valuesmust be aligned to the size of the datatype specified indnMatDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.4.6. cusparseDnMatGetStridedBatch()
cusparseStatus_t
cusparseDnMatGetStridedBatch(cusparseConstDnMatDescr_t dnMatDescr, // non-const descriptor supported
int* batchCount,
int64_t* batchStride)
The function returns the number of batches and the batch stride of the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
|
HOST |
OUT |
Number of batches of the dense matrix |
|
HOST |
OUT |
Address offset between a matrix and the next one in the batch |
See cusparseStatus_t for the description of the return status.
6.4.7. cusparseDnMatSetStridedBatch()
cusparseStatus_t
cusparseDnMatSetStridedBatch(cusparseDnMatDescr_t dnMatDescr,
int batchCount,
int64_t batchStride)
The function sets the number of batches and the batch stride of the dense matrix descriptor dnMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Dense matrix descriptor |
|
HOST |
IN |
Number of batches of the dense matrix |
|
HOST |
IN |
Address offset between a matrix and the next one in the batch. |
See cusparseStatus_t for the description of the return status.
6.5. Sparse Matrix APIs
The cuSPARSE helper functions for sparse matrix descriptor are described in this section.
See the COO, CSR , CSC , SELL , BSR, Blocked-Ell sections for the detailed description of the storage formats.
6.5.1. Coordinate (COO)
6.5.1.1. cusparseCreateCoo()
cusparseStatus_t
cusparseCreateCoo(cusparseSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
void* cooRowInd,
void* cooColInd,
void* cooValues,
cusparseIndexType_t cooIdxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstCoo(cusparseConstSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
const void* cooRowInd,
const void* cooColInd,
const void* cooValues,
cusparseIndexType_t cooIdxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spMatDescr in the COO format (Structure of Arrays layout).
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of rows of the sparse matrix |
|
HOST |
IN |
Number of columns of the sparse matrix |
|
HOST |
IN |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
IN |
Row indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Column indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Index base of |
|
HOST |
IN |
Datatype of |
cusparseCreateCoo() has the following constraints:
cooRowInd,cooColInd, andcooValuesmust be aligned to the size of the datatypes specified bycooIdxType,cooIdxType, andvalueType. respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.1.2. cusparseCooGet()
cusparseStatus_t
cusparseCooGet(cusparseSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
void** cooRowInd,
void** cooColInd,
void** cooValues,
cusparseIndexType_t* idxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstCooGet(cusparseConstSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
const void** cooRowInd,
const void** cooColInd,
const void** cooValues,
cusparseIndexType_t* idxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
This function returns the fields of the sparse matrix descriptor spMatDescr stored in COO format (Array of Structures layout).
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of rows of the sparse matrix |
|
HOST |
OUT |
Number of columns of the sparse matrix |
|
HOST |
OUT |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
OUT |
Row indices of the sparse matrix. Array |
|
DEVICE |
OUT |
Column indices of the sparse matrix. Array |
|
DEVICE |
OUT |
Values of the sparse matrix. Array |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Index base of |
|
HOST |
OUT |
Datatype of |
See cusparseStatus_t for the description of the return status.
6.5.1.3. cusparseCooSetPointers()
cusparseStatus_t
cusparseCooSetPointers(cusparseSpMatDescr_t spMatDescr,
void* cooRows,
void* cooColumns,
void* cooValues)
This function sets the pointers of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
DEVICE |
IN |
Row indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Column indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
cusparseCooSetPointers() has the following constraints:
cooRows,cooColumns, andcooValuesmust be aligned to the size of their corresponding datatypes specified inspMatDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.1.4. cusparseCooSetStridedBatch()
cusparseStatus_t
cusparseCooSetStridedBatch(cusparseSpMatDescr_t spMatDescr,
int batchCount,
int64_t batchStride)
This function sets the batchCount and the batchStride fields of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
IN |
Number of batches of the sparse matrix |
|
HOST |
IN |
address offset between consecutive batches |
See cusparseStatus_t for the description of the return status.
6.5.2. Compressed Sparse Row (CSR)
6.5.2.1. cusparseCreateCsr()
cusparseStatus_t
cusparseCreateCsr(cusparseSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
void* csrRowOffsets,
void* csrColInd,
void* csrValues,
cusparseIndexType_t csrRowOffsetsType,
cusparseIndexType_t csrColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstCsr(cusparseConstSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
const void* csrRowOffsets,
const void* csrColInd,
const void* csrValues,
cusparseIndexType_t csrRowOffsetsType,
cusparseIndexType_t csrColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spMatDescr in the CSR format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of rows of the sparse matrix |
|
HOST |
IN |
Number of columns of the sparse matrix |
|
HOST |
IN |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
IN |
Row offsets of the sparse matrix. Array with |
|
DEVICE |
IN |
Column indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Index base of |
|
HOST |
IN |
Datatype of |
cusparseCreateCsr() has the following constraints:
csrRowOffsets,csrColInd, andcsrValuesmust be aligned to the size of the datatypes specified bycsrRowOffsetsType,csrColIndType, andvalueType, respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.2.2. cusparseCsrGet()
cusparseStatus_t
cusparseCsrGet(cusparseSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
void** csrRowOffsets,
void** csrColInd,
void** csrValues,
cusparseIndexType_t* csrRowOffsetsType,
cusparseIndexType_t* csrColIndType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstCsrGet(cusparseConstSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
const void** csrRowOffsets,
const void** csrColInd,
const void** csrValues,
cusparseIndexType_t* csrRowOffsetsType,
cusparseIndexType_t* csrColIndType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
This function returns the fields of the sparse matrix descriptor spMatDescr stored in CSR format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of rows of the sparse matrix |
|
HOST |
OUT |
Number of columns of the sparse matrix |
|
HOST |
OUT |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
OUT |
Row offsets of the sparse matrix. Array with |
|
DEVICE |
OUT |
Column indices of the sparse matrix. Array with |
|
DEVICE |
OUT |
Values of the sparse matrix. Array with |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Index base of |
|
HOST |
OUT |
Datatype of |
See cusparseStatus_t for the description of the return status.
6.5.2.3. cusparseCsrSetPointers()
cusparseStatus_t
cusparseCsrSetPointers(cusparseSpMatDescr_t spMatDescr,
void* csrRowOffsets,
void* csrColInd,
void* csrValues)
This function sets the pointers of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
DEVICE |
IN |
Row offsets of the sparse matrix. Array with |
|
DEVICE |
IN |
Column indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
cusparseCsrSetPointers() has the following constraints:
csrRowOffsets,csrColInd, andcsrValuesmust be aligned to the size of their corresponding datatypes specified inspMatDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.2.4. cusparseCsrSetStridedBatch()
cusparseStatus_t
cusparseCsrSetStridedBatch(cusparseSpMatDescr_t spMatDescr,
int batchCount,
int64_t offsetsBatchStride,
int64_t columnsValuesBatchStride)
This function sets the batchCount and the batchStride fields of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
IN |
Number of batches of the sparse matrix |
|
HOST |
IN |
Address offset between consecutive batches for the row offset array |
|
HOST |
IN |
Address offset between consecutive batches for the column and value arrays |
See cusparseStatus_t for the description of the return status.
6.5.3. Compressed Sparse Column (CSC)
6.5.3.1. cusparseCreateCsc()
cusparseStatus_t
cusparseCreateCsc(cusparseSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
void* cscColOffsets,
void* cscRowInd,
void* cscValues,
cusparseIndexType_t cscColOffsetsType,
cusparseIndexType_t cscRowIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstCsc(cusparseConstSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
const void* cscColOffsets,
const void* cscRowInd,
const void* cscValues,
cusparseIndexType_t cscColOffsetsType,
cusparseIndexType_t cscRowIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spMatDescr in the CSC format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of rows of the sparse matrix |
|
HOST |
IN |
Number of columns of the sparse matrix |
|
HOST |
IN |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
IN |
Column offsets of the sparse matrix. Array with |
|
DEVICE |
IN |
Row indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Index base of |
|
HOST |
IN |
Datatype of |
cusparseCreateCsc() has the following constraints:
cscColOffsets,cscRowInd, andcscValuesmust be aligned to the size of the datatypes specified bycscColOffsetsType,cscRowIndType, andvalueType, respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.3.2. cusparseCscGet()
cusparseStatus_t
cusparseCscGet(cusparseSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
void** cscColOffsets,
void** cscRowInd,
void** cscValues,
cusparseIndexType_t* cscColOffsetsType,
cusparseIndexType_t* cscRowIndType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstCscGet(cusparseConstSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* nnz,
const void** cscColOffsets,
const void** cscRowInd,
const void** cscValues,
cusparseIndexType_t* cscColOffsetsType,
cusparseIndexType_t* cscRowIndType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
This function returns the fields of the sparse matrix descriptor spMatDescr stored in CSC format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of rows of the sparse matrix |
|
HOST |
OUT |
Number of columns of the sparse matrix |
|
HOST |
OUT |
Number of non-zero entries of the sparse matrix |
|
DEVICE |
OUT |
Row offsets of the sparse matrix. Array with |
|
DEVICE |
OUT |
Column indices of the sparse matrix. Array with |
|
DEVICE |
OUT |
Values of the sparse matrix. Array with |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Index base of |
|
HOST |
OUT |
Datatype of |
See cusparseStatus_t for the description of the return status.
6.5.3.3. cusparseCscSetPointers()
cusparseStatus_t
cusparseCscSetPointers(cusparseSpMatDescr_t spMatDescr,
void* cscColOffsets,
void* cscRowInd,
void* cscValues)
This function sets the pointers of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
DEVICE |
IN |
Col offsets of the sparse matrix. Array with |
|
DEVICE |
IN |
Row indices of the sparse matrix. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
cusparseCscSetPointers() has the following constraints:
cscColOffsets,cscRowInd, andcscValuesmust be aligned to the size of their corresponding datatypes specified inspMatDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.4. Blocked-Ellpack (Blocked-ELL)
6.5.4.1. cusparseCreateBlockedEll()
cusparseStatus_t
cusparseCreateBlockedEll(cusparseSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t ellBlockSize,
int64_t ellCols,
void* ellColInd,
void* ellValue,
cusparseIndexType_t ellIdxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstBlockedEll(cusparseConstSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t ellBlockSize,
int64_t ellCols,
const void* ellColInd,
const void* ellValue,
cusparseIndexType_t ellIdxType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spMatDescr for the Blocked-Ellpack (ELL) format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of rows of the sparse matrix |
|
HOST |
IN |
Number of columns of the sparse matrix |
|
HOST |
IN |
Size of the ELL-Block |
|
HOST |
IN |
Actual number of columns of the Blocked-Ellpack format ( |
|
DEVICE |
IN |
Blocked-ELL Column indices. Array with |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Index base of |
|
HOST |
IN |
Data type of |
Blocked-ELL Column indices (ellColInd) are in the range [0, cols / ellBlockSize -1]. The array can contain -1 values for indicating empty blocks.
See cusparseStatus_t for the description of the return status.
6.5.4.2. cusparseBlockedEllGet()
cusparseStatus_t
cusparseBlockedEllGet(cusparseSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* ellBlockSize,
int64_t* ellCols,
void** ellColInd,
void** ellValue,
cusparseIndexType_t* ellIdxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
cusparseStatus_t
cusparseConstBlockedEllGet(cusparseConstSpMatDescr_t spMatDescr,
int64_t* rows,
int64_t* cols,
int64_t* ellBlockSize,
int64_t* ellCols,
const void** ellColInd,
const void** ellValue,
cusparseIndexType_t* ellIdxType,
cusparseIndexBase_t* idxBase,
cudaDataType* valueType)
This function returns the fields of the sparse matrix descriptor spMatDescr stored in Blocked-Ellpack (ELL) format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of rows of the sparse matrix |
|
HOST |
OUT |
Number of columns of the sparse matrix |
|
HOST |
OUT |
Size of the ELL-Block |
|
HOST |
OUT |
Actual number of columns of the Blocked-Ellpack format |
|
DEVICE |
OUT |
Column indices for the ELL-Block. Array with |
|
DEVICE |
OUT |
Values of the sparse matrix. Array with |
|
HOST |
OUT |
Data type of |
|
HOST |
OUT |
Index base of |
|
HOST |
OUT |
Datatype of |
See cusparseStatus_t for the description of the return status.
6.5.5. Sliced-Ellpack (SELL)
6.5.5.1. cusparseCreateSlicedEll()
cusparseStatus_t
cusparseCreateSlicedEll(cusparseSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
int64_t sellValuesSize,
int64_t sliceSize,
void* sellSliceOffsets,
void* sellColInd,
void* sellValues,
cusparseIndexType_t sellSliceOffsetsType,
cusparseIndexType_t sellColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
cusparseStatus_t
cusparseCreateConstSlicedEll(cusparseConstSpMatDescr_t* spMatDescr,
int64_t rows,
int64_t cols,
int64_t nnz,
int64_t sellValuesSize,
int64_t sliceSize,
const void* sellSliceOffsets,
const void* sellColInd,
const void* sellValues,
cusparseIndexType_t sellSliceOffsetsType,
cusparseIndexType_t sellColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType)
This function initializes the sparse matrix descriptor spMatDescr for the Sliced Ellpack (SELL) format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of rows of the sparse matrix |
|
HOST |
IN |
Number of columns of the sparse matrix |
|
HOST |
IN |
Number of nonzero elements in the sparse matrix |
|
HOST |
IN |
Total number of elements in |
|
HOST |
IN |
The number of rows per slice |
|
DEVICE |
IN |
Slice offsets of the sparse matrix. Array of size \(\left \lceil{\frac{rows}{sliceSize}}\right \rceil + 1\) |
|
DEVICE |
IN |
Column indexes of the sparse matrix. Array of size |
|
DEVICE |
IN |
Values of the sparse matrix. Array of size |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Index base of |
|
HOST |
IN |
Data type of |
Note
Sliced Ellpack Column array sellColInd contains -1 values for indicating padded entries.
cusparseCreateSlicedEll() has the following constraints:
sellSliceOffsets,sellColInd, andsellValuesmust be aligned to the size of the datatypes specified bysellSliceOffsetsType,sellColIndType, andvalueType, respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.6. Block Sparse Row (BSR)
6.5.6.1. cusparseCreateBsr()
cusparseStatus_t
cusparseCreateBsr(cusparseSpMatDescr_t* spMatDescr,
int64_t brows,
int64_t bcols,
int64_t bnnz,
int64_t rowBlockSize,
int64_t colBlockSize,
void* bsrRowOffsets,
void* bsrColInd,
void* bsrValues,
cusparseIndexType_t bsrRowOffsetsType,
cusparseIndexType_t bsrColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType,
cusparseOrder_t order)
cusparseStatus_t
cusparseCreateConstBsr(cusparseConstSpMatDescr_t* spMatDescr,
int64_t brows,
int64_t bcols,
int64_t bnnz,
int64_t rowBlockSize,
int64_t colBlockSize,
const void* bsrRowOffsets,
const void* bsrColInd,
const void* bsrValues,
cusparseIndexType_t bsrRowOffsetsType,
cusparseIndexType_t bsrColIndType,
cusparseIndexBase_t idxBase,
cudaDataType valueType,
cusparseOrder_t order)
This function initializes the sparse matrix descriptor spMatDescr for the Block Compressed Row (BSR) format.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Number of block rows of the sparse matrix |
|
HOST |
IN |
Number of block columns of the sparse matrix |
|
HOST |
IN |
Number of blocks of the sparse matrix |
|
HOST |
IN |
Number of rows of each block |
|
HOST |
IN |
Number of columns of each block |
|
DEVICE |
IN |
Block row offsets of the sparse matrix. Array of size |
|
DEVICE |
IN |
Block column indices of the sparse matrix. Array of size |
|
DEVICE |
IN |
Values of the sparse matrix. Array of size |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Data type of |
|
HOST |
IN |
Base index of |
|
HOST |
IN |
Datatype of |
|
HOST |
IN |
Enumerator specifying the memory layout of values in each block |
cusparseCreateBsr() has the following constraints:
bsrRowOffsets,bsrColInd, andbsrValuesmust be aligned to the size of the datatypes specified bybsrRowOffsetsType,bsrColIndType, andvalueType, respectively. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.6.2. cusparseBsrSetStridedBatch()
cusparseStatus_t
cusparseBsrSetStridedBatch(cusparseSpMatDescr_t spMatDescr,
int batchCount,
int64_t offsetsBatchStride,
int64_t columnsBatchStride,
int64_t valuesBatchStride)
This function sets the batchCount and the batchStride fields of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
IN |
Number of batches of the sparse matrix |
|
HOST |
IN |
Address offset between consecutive batches for the row offset array |
|
HOST |
IN |
Address offset between consecutive batches for the column array |
|
HOST |
IN |
Address offset between consecutive batches for the values array |
See cusparseStatus_t for the description of the return status.
6.5.7. All Sparse Formats
6.5.7.1. cusparseDestroySpMat()
cusparseStatus_t
cusparseDestroySpMat(cusparseConstSpMatDescr_t spMatDescr) // non-const descriptor supported
This function releases the host memory allocated for the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
See cusparseStatus_t for the description of the return status.
6.5.7.2. cusparseSpMatGetSize()
cusparseStatus_t
cusparseSpMatGetSize(cusparseConstSpMatDescr_t spMatDescr, // non-const descriptor supported
int64_t* rows,
int64_t* cols,
int64_t* nnz)
This function returns the sizes of the sparse matrix spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of rows of the sparse matrix |
|
HOST |
OUT |
Number of columns of the sparse matrix |
|
HOST |
OUT |
Number of non-zero entries of the sparse matrix |
See cusparseStatus_t for the description of the return status.
6.5.7.3. cusparseSpMatGetFormat()
cusparseStatus_t
cusparseSpMatGetFormat(cusparseConstSpMatDescr_t spMatDescr, // non-const descriptor supported
cusparseFormat_t* format)
This function returns the format field of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Storage format of the sparse matrix |
See cusparseStatus_t for the description of the return status.
6.5.7.4. cusparseSpMatGetIndexBase()
cusparseStatus_t
cusparseSpMatGetIndexBase(cusparseConstSpMatDescr_t spMatDescr, // non-const descriptor supported
cusparseIndexBase_t* idxBase)
This function returns the idxBase field of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Index base of the sparse matrix |
See cusparseStatus_t for the description of the return status.
6.5.7.5. cusparseSpMatGetValues()
cusparseStatus_t
cusparseSpMatGetValues(cusparseSpMatDescr_t spMatDescr,
void** values)
cusparseStatus_t
cusparseConstSpMatGetValues(cusparseConstSpMatDescr_t spMatDescr,
const void** values)
This function returns the values field of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
DEVICE |
OUT |
Values of the sparse matrix. Array with |
See cusparseStatus_t for the description of the return status.
6.5.7.6. cusparseSpMatSetValues()
cusparseStatus_t
cusparseSpMatSetValues(cusparseSpMatDescr_t spMatDescr,
void* values)
This function sets the values field of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
DEVICE |
IN |
Values of the sparse matrix. Array with |
cusparseSpMatSetValues() has the following constraints:
valuesmust be aligned to the size of its corresponding datatype specified inspMatDescr. See cudaDataType_t for the description of the datatypes.
See cusparseStatus_t for the description of the return status.
6.5.7.7. cusparseSpMatGetStridedBatch()
cusparseStatus_t
cusparseSpMatGetStridedBatch(cusparseConstSpMatDescr_t spMatDescr, // non-const descriptor supported
int* batchCount)
This function returns the batchCount field of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
OUT |
Number of batches of the sparse matrix |
See cusparseStatus_t for the description of the return status.
6.5.7.8. cusparseSpMatGetAttribute()
cusparseStatus_t
cusparseSpMatGetAttribute(cusparseConstSpMatDescr_t spMatDescr, // non-const descriptor supported
cusparseSpMatAttribute_t attribute,
void* data,
size_t dataSize)
The function gets the attributes of the sparse matrix descriptor spMatDescr.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Sparse matrix descriptor |
|
HOST |
IN |
Attribute enumerator |
|
HOST |
OUT |
Attribute value |
|
HOST |
IN |
Size of the attribute in bytes for safety |
Attribute |
Meaning |
Possible Values |
|---|---|---|
|
Indicates if the lower or upper part of a matrix is stored in sparse storage |
|
|
Indicates if the matrix diagonal entries are unity |
|
See cusparseStatus_t for the description of the return status.
6.5.7.9. cusparseSpMatSetAttribute()
cusparseStatus_t
cusparseSpMatSetAttribute(cusparseSpMatDescr_t spMatDescr,
cusparseSpMatAttribute_t attribute,
const void* data,
size_t dataSize)
The function sets the attributes of the sparse matrix descriptor spMatDescr
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
OUT |
Sparse matrix descriptor |
|
HOST |
IN |
Attribute enumerator |
|
HOST |
IN |
Attribute value |
|
HOST |
IN |
Size of the attribute in bytes for safety |
Attribute |
Meaning |
Possible Values |
|---|---|---|
|
Indicates if the lower or upper part of a matrix is stored in sparse storage |
|
|
Indicates if the matrix diagonal entries are unity |
|
See cusparseStatus_t for the description of the return status.
6.6. Generic API Functions
6.6.1. cusparseAxpby()
cusparseStatus_t
cusparseAxpby(cusparseHandle_t handle,
const void* alpha,
cusparseConstSpVecDescr_t vecX, // non-const descriptor supported
const void* beta,
cusparseDnVecDescr_t vecY)
The function computes the sum of a sparse vector vecX and a dense vector vecY.
\(\mathbf{Y} = \alpha\mathbf{X} + \beta\mathbf{Y}\) |
In other words,
for i=0 to n-1
Y[i] = beta * Y[i]
for i=0 to nnz-1
Y[X_indices[i]] += alpha * X_values[i]
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of compute type |
|
HOST |
IN |
Sparse vector |
|
HOST or DEVICE |
IN |
\(\beta\) scalar used for multiplication of compute type |
|
HOST |
IN/OUT |
Dense vector |
cusparseAxpby supports the following index type for representing the sparse vector vecX:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseAxpby supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
|---|---|---|
|
|
|
|
||
|
|
[DEPRECATED] |
|
[DEPRECATED] |
cusparseAxpby() has the following constraints:
The arrays representing the sparse vector
vecXmust be aligned to 16 bytes
cusparseAxpby() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run if the the sparse vector
vecXindices are distinctThe routine allows
indicesofvecXto be unsorted
cusparseAxpby() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseAxpby for a code example.
6.6.2. cusparseGather()
cusparseStatus_t
cusparseGather(cusparseHandle_t handle,
cusparseConstDnVecDescr_t vecY, // non-const descriptor supported
cusparseSpVecDescr_t vecX)
The function gathers the elements of the dense vector vecY into the sparse vector vecX
In other words,
for i=0 to nnz-1
X_values[i] = Y[X_indices[i]]
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
OUT |
Sparse vector |
|
HOST |
IN |
Dense vector |
cusparseGather supports the following index type for representing the sparse vector vecX:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseGather supports the following data types:
|
|---|
|
|
|
|
|
|
|
|
cusparseGather() has the following constraints:
The arrays representing the sparse vector
vecXmust be aligned to 16 bytes
cusparseGather() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run if the the sparse vector
vecXindices are distinctThe routine allows
indicesofvecXto be unsorted
cusparseGather() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseGather for a code example.
6.6.3. cusparseScatter()
cusparseStatus_t
cusparseScatter(cusparseHandle_t handle,
cusparseConstSpVecDescr_t vecX, // non-const descriptor supported
cusparseDnVecDescr_t vecY)
The function scatters the elements of the sparse vector vecX into the dense vector vecY
In other words,
for i=0 to nnz-1
Y[X_indices[i]] = X_values[i]
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Sparse vector |
|
HOST |
OUT |
Dense vector |
cusparseScatter supports the following index type for representing the sparse vector vecX:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseScatter supports the following data types:
|
|---|
|
|
|
|
|
|
|
|
|
cusparseScatter() has the following constraints:
The arrays representing the sparse vector
vecXmust be aligned to 16 bytes
cusparseScatter() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run if the the sparse vector
vecXindices are distinctThe routine allows
indicesofvecXto be unsorted
cusparseScatter() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseScatter for a code example.
6.6.4. cusparseRot() [DEPRECATED]
> The routine will be removed in the next major release
cusparseStatus_t
cusparseRot(cusparseHandle_t handle,
const void* c_coeff,
const void* s_coeff,
cusparseSpVecDescr_t vecX,
cusparseDnVecDescr_t vecY)
The function computes the Givens rotation matrix
\(G = \begin{bmatrix} c & s \\ {- s} & c \\ \end{bmatrix}\) |
to a sparse vecX and a dense vector vecY
In other words,
for i=0 to nnz-1
Y[X_indices[i]] = c * Y[X_indices[i]] - s * X_values[i]
X_values[i] = c * X_values[i] + s * Y[X_indices[i]]
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST or DEVICE |
IN |
cosine element of the rotation matrix |
|
HOST |
IN/OUT |
Sparse vector |
|
HOST or DEVICE |
IN |
sine element of the rotation matrix |
|
HOST |
IN/OUT |
Dense vector |
cusparseRot supports the following index type for representing the sparse vector vecX:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseRot supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
|---|---|---|
|
|
|
|
||
|
|
[DEPRECATED] |
|
[DEPRECATED] |
cusparseRot() has the following constraints:
The arrays representing the sparse vector
vecXmust be aligned to 16 bytes
cusparseRot() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run if the the sparse vector
vecXindices are distinct
cusparseRot() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseRot for a code example.
6.6.5. cusparseSpVV()
cusparseStatus_t
cusparseSpVV_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opX,
cusparseConstSpVecDescr_t vecX, // non-const descriptor supported
cusparseConstDnVecDescr_t vecY, // non-const descriptor supported
void* result,
cudaDataType computeType,
size_t* bufferSize)
cusparseStatus_t
cusparseSpVV(cusparseHandle_t handle,
cusparseOperation_t opX,
cusparseConstSpVecDescr_t vecX, // non-const descriptor supported
cusparseConstDnVecDescr_t vecY, // non-const descriptor supported
void* result,
cudaDataType computeType,
void* externalBuffer)
The function computes the inner dot product of a sparse vector vecX and a dense vector vecY
\(result = \mathbf{X}' \cdot \mathbf{Y}\) |
In other words,
result = 0;
for i=0 to nnz-1
result += X_values[i] * Y[X_indices[i]]
\(\text{op}(X) = \begin{cases} X & \text{if op(X) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ \overline{X} & \text{if op(X) == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The function cusparseSpVV_bufferSize() returns the size of the workspace needed by cusparseSpVV()
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Sparse vector |
|
HOST |
IN |
Dense vector |
|
HOST or DEVICE |
OUT |
The resulting dot product |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to a workspace buffer of at least |
cusparseSpVV supports the following index type for representing the sparse vector vecX:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
The data types combinations currently supported for cusparseSpVV are listed below:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
Notes |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[DEPRECATED] |
|
|
[DEPRECATED] |
cusparseSpVV() has the following constraints:
The arrays representing the sparse vector
vecXmust be aligned to 16 bytes
cusparseSpVV() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run if the the sparse vector
vecXindices are distinctThe routine allows
indicesofvecXto be unsorted
cusparseSpVV() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpVV for a code example.
6.6.6. cusparseSpMV()
cusparseStatus_t
cusparseSpMV_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
const void* beta,
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpMVAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseSpMV_preprocess(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
const void* beta,
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpMVAlg_t alg,
void* externalBuffer)
cusparseStatus_t
cusparseSpMV(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
const void* beta,
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpMVAlg_t alg,
void* externalBuffer)
This function performs the multiplication of a sparse matrix matA and a dense vector vecX
\(\mathbf{Y} = \alpha op\left( \mathbf{A} \right) \cdot \mathbf{X} + \beta\mathbf{Y}\) |
where
op(A)is a sparse matrix of size \(m \times k\)Xis a dense vector of size \(k\)Yis a dense vector of size \(m\)\(\alpha\) and \(\beta\) are scalars
Also, for matrix A
\(\text{op}(A) == \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if op(A) ==CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The function cusparseSpMV_bufferSize() returns the size of the workspace needed by cusparseSpMV_preprocess() and cusparseSpMV()
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of type |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Dense vector |
|
HOST or DEVICE |
IN |
\(\beta\) scalar used for multiplication of type |
|
HOST |
IN/OUT |
Dense vector |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to a workspace buffer of at least |
The sparse matrix formats currently supported are listed below:
CUSPARSE_FORMAT_COOCUSPARSE_FORMAT_CSRCUSPARSE_FORMAT_CSCCUSPARSE_FORMAT_SLICED_ELL
cusparseSpMV supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSpMV supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
Notes |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|||
|
|||
|
|
||
|
|
||
|
|
|
|
|
|
[DEPRECATED] |
|
|
|
[DEPRECATED] |
|
|
|---|---|
|
|
Mixed Regular/Complex computation:
|
|
|---|---|
|
|
|
|
NOTE: CUDA_R_16F, CUDA_R_16BF, CUDA_C_16F, and CUDA_C_16BF data types always imply mixed-precision computation.
cusparseSpMV() supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm for any sparse matrix format. |
|
Default algorithm for COO sparse matrix format. May produce slightly different results during different runs with the same input parameters. |
|
Provides deterministic (bit-wise) results for each run. If |
|
Default algorithm for CSR/CSC sparse matrix format. May produce slightly different results during different runs with the same input parameters. |
|
Provides deterministic (bit-wise) results for each run. If |
|
Default algorithm for Sliced Ellpack sparse matrix format. Provides deterministic (bit-wise) results for each run. |
Performance notes:
CUSPARSE_SPMV_COO_ALG1andCUSPARSE_SPMV_CSR_ALG1provide higher performance thanCUSPARSE_SPMV_COO_ALG2andCUSPARSE_SPMV_CSR_ALG2.In general,
opA == CUSPARSE_OPERATION_NON_TRANSPOSEis 3x faster thanopA != CUSPARSE_OPERATION_NON_TRANSPOSE.Using
cusparseSpMV_preprocess()helps improve performance ofcusparseSpMV()in CSR. It is beneficial when we need to runcusparseSpMV()multiple times with a same matrix (cusparseSpMV_preprocess()is executed only once).
cusparseSpMV() has the following properties:
The routine requires extra storage for CSR/CSC format (all algorithms) and for COO format with
CUSPARSE_SPMV_COO_ALG2algorithm.Provides deterministic (bit-wise) results for each run only for
CUSPARSE_SPMV_COO_ALG2andCUSPARSE_SPMV_CSR_ALG2algorithms, andopA == CUSPARSE_OPERATION_NON_TRANSPOSE.The routine supports asynchronous execution.
compute-sanitizer could report false race conditions for this routine when
beta == 0. This is for optimization purposes and does not affect the correctness of the computation.The routine allows the indices of
matAto be unsorted.
cusparseSpMV() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpMV CSR and cusparseSpMV COO for a code example.
6.6.7. cusparseSpSV()
cusparseStatus_t
cusparseSpSV_createDescr(cusparseSpSVDescr_t* spsvDescr);
cusparseStatus_t
cusparseSpSV_destroyDescr(cusparseSpSVDescr_t spsvDescr);
cusparseStatus_t
cusparseSpSV_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpSVAlg_t alg,
cusparseSpSVDescr_t spsvDescr,
size_t* bufferSize)
cusparseStatus_t
cusparseSpSV_analysis(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpSVAlg_t alg,
cusparseSpSVDescr_t spsvDescr
void* externalBuffer)
cusparseStatus_t
cusparseSpSV_solve(cusparseHandle_t handle,
cusparseOperation_t opA,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnVecDescr_t vecX, // non-const descriptor supported
cusparseDnVecDescr_t vecY,
cudaDataType computeType,
cusparseSpSVAlg_t alg,
cusparseSpSVDescr_t spsvDescr)
cusparseStatus_t
cusparseSpSV_updateMatrix(cusparseHandle_t handle,
cusparseSpSVDescr_t spsvDescr,
void* newValues,
cusparseSpSVUpdate_t updatePart)
The function solves a system of linear equations whose coefficients are represented in a sparse triangular matrix:
\(op\left( \mathbf{A} \right) \cdot \mathbf{Y} = \alpha\mathbf{X}\) |
where
op(A)is a sparse square matrix of size \(m \times m\)Xis a dense vector of size \(m\)Yis a dense vector of size \(m\)\(\alpha\) is a scalar
Also, for matrix A
\(\text{op}(A) = \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if op(A) == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
The function cusparseSpSV_bufferSize() returns the size of the workspace needed by cusparseSpSV_analysis() and cusparseSpSV_solve().
The function cusparseSpSV_analysis() performs the analysis phase, while cusparseSpSV_solve() executes the solve phase for a sparse triangular linear system.
The opaque data structure spsvDescr is used to share information among all functions.
The function cusparseSpSV_updateMatrix() updates spsvDescr with new matrix values.
The routine supports arbitrary sparsity for the input matrix, but only the upper or lower triangular part is taken into account in the computation.
NOTE: all parameters must be consistent across cusparseSpSV API calls and the matrix descriptions and externalBuffer must not be modified between cusparseSpSV_analysis() and cusparseSpSV_solve(). The function cusparseSpSV_updateMatrix() can be used to update the values on the sparse matrix stored inside the opaque data structure spsvDescr
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of type |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Dense vector |
|
HOST |
IN/OUT |
Dense vector |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN/OUT |
Pointer to a workspace buffer of at least |
|
HOST |
IN/OUT |
Opaque descriptor for storing internal data used across the three steps |
The sparse matrix formats currently supported are listed below:
CUSPARSE_FORMAT_CSRCUSPARSE_FORMAT_COOCUSPARSE_FORMAT_SLICED_ELL
The cusparseSpSV() supports the following shapes and properties:
CUSPARSE_FILL_MODE_LOWERandCUSPARSE_FILL_MODE_UPPERfill modesCUSPARSE_DIAG_TYPE_NON_UNITandCUSPARSE_DIAG_TYPE_UNITdiagonal types
The fill mode and diagonal type can be set by cusparseSpMatSetAttribute()
cusparseSpSV() supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSpSV() supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
cusparseSpSV() supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm |
cusparseSpSV() has the following properties:
The routine requires extra storage for the analysis phase which is proportional to number of non-zero entries of the sparse matrix
Provides deterministic (bit-wise) results for each run for the solving phase
cusparseSpSV_solve()The routine supports in-place operation
The
cusparseSpSV_solve()routine supports asynchronous executioncusparseSpSV_bufferSize()andcusparseSpSV_analysis()routines acceptNULLforvecXandvecYThe routine allows the indices of
matAto be unsorted
cusparseSpSV() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
cusparseSpSV_updateMatrix() updates the sparse matrix after calling the analysis phase. This functions supports the following update strategies (updatePart):
Strategy |
Notes |
|---|---|
|
Updates the sparse matrix values with values of |
|
Updates the diagonal part of the matrix with diagonal values stored in |
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpSV CSR and cuSPARSE Library Samples - cusparseSpSV COO for code examples.
6.6.8. cusparseSpMM()
cusparseStatus_t
cusparseSpMM_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpMMAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseSpMM_preprocess(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpMMAlg_t alg,
void* externalBuffer)
cusparseStatus_t
cusparseSpMM(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpMMAlg_t alg,
void* externalBuffer)
The function performs the multiplication of a sparse matrix matA and a dense matrix matB.
\(\mathbf{C} = \alpha op\left( \mathbf{A} \right) \cdot op\left( \mathbf{B} \right) + \beta\mathbf{C}\) |
where
op(A)is a sparse matrix of size \(m \times k\)op(B)is a dense matrix of size \(k \times n\)Cis a dense matrix of size \(m \times n\)\(\alpha\) and \(\beta\) are scalars
The routine can be also used to perform the multiplication of a dense matrix and a sparse matrix by switching the dense matrices layout:
\(\begin{array}{l} \left. \mathbf{C}_{C} = \mathbf{B}_{C} \cdot \mathbf{A} + \beta\mathbf{C}_{C}\rightarrow \right. \\ {\mathbf{C}_{R} = \mathbf{A}^{T} \cdot \mathbf{B}_{R} + \beta\mathbf{C}_{R}} \\ \end{array}\) |
where \(\mathbf{B}_{C}\) , \(\mathbf{C}_{C}\) indicate column-major layout, while \(\mathbf{B}_{R}\) , \(\mathbf{C}_{R}\) refer to row-major layout
Also, for matrix A and B
\(\text{op}(A) = \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if op(A) == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
\(\text{op}(B) = \begin{cases} B & \text{if op(B) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ B^{T} & \text{if op(B) == CUSPARSE_OPERATION_TRANSPOSE} \\ B^{H} & \text{if op(B) == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
When using the (conjugate) transpose of the sparse matrix A, this routine may produce slightly different results during different runs with the same input parameters.
The function cusparseSpMM_bufferSize() returns the size of the workspace needed by cusparseSpMM()
The function cusparseSpMM_preprocess() can be called before cusparseSpMM to speedup the actual computation. It is useful when cusparseSpMM is called multiple times with the same sparsity pattern (matA). The values of the matrices (matA, matB, matC) can change arbitrarily. It provides performance advantages is used with CUSPARSE_SPMM_CSR_ALG1 or CUSPARSE_SPMM_CSR_ALG3. For all other formats and algorithms have no effect.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of type |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Dense matrix |
|
HOST or DEVICE |
IN |
\(\beta\) scalar used for multiplication of type |
|
HOST |
IN/OUT |
Dense matrix |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to workspace buffer of at least |
cusparseSpMM supports the following sparse matrix formats:
CUSPARSE_FORMAT_COOCUSPARSE_FORMAT_CSRCUSPARSE_FORMAT_CSCCUSPARSE_FORMAT_BLOCKED_ELL
(1) |
COO/CSR/CSC FORMATS |
cusparseSpMM supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSpMM supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|||
|
|||
|
|
||
|
|
||
|
|
|
[DEPRECATED] |
|
|
[DEPRECATED] |
NOTE: CUDA_R_16F, CUDA_R_16BF, CUDA_C_16F, and CUDA_C_16BF data types always imply mixed-precision computation.
cusparseSpMM supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm for any sparse matrix format |
|
Algorithm 1 for COO sparse matrix format
|
|
Algorithm 2 for COO sparse matrix format
|
|
Algorithm 3 for COO sparse matrix format
|
|
Algorithm 4 for COO sparse matrix format
|
|
Algorithm 1 for CSR/CSC sparse matrix format
|
|
Algorithm 2 for CSR/CSC sparse matrix format
|
|
Algorithm 3 for CSR/CSC sparse matrix format
|
Performance notes:
Row-major layout provides higher performance than column-major
CUSPARSE_SPMM_COO_ALG4andCUSPARSE_SPMM_CSR_ALG2should be used with row-major layout, whileCUSPARSE_SPMM_COO_ALG1,CUSPARSE_SPMM_COO_ALG2,CUSPARSE_SPMM_COO_ALG3, andCUSPARSE_SPMM_CSR_ALG1with column-major layoutFor
beta != 1, the output matrix is scaled before the actual computationFor
n == 1, the routine usescusparseSpMV()as fallback
cusparseSpMM() with all algorithms support the following batch modes except for CUSPARSE_SPMM_CSR_ALG3:
\(C_{i} = A \cdot B_{i}\)
\(C_{i} = A_{i} \cdot B\)
\(C_{i} = A_{i} \cdot B_{i}\)
The number of batches and their strides can be set by using cusparseCooSetStridedBatch, cusparseCsrSetStridedBatch, and cusparseDnMatSetStridedBatch. The maximum number of batches for cusparseSpMM() is 65,535.
cusparseSpMM() has the following properties:
The routine requires no extra storage for
CUSPARSE_SPMM_COO_ALG1,CUSPARSE_SPMM_COO_ALG3,CUSPARSE_SPMM_COO_ALG4The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run only for
CUSPARSE_SPMM_COO_ALG2andCUSPARSE_SPMM_CSR_ALG3algorithmscompute-sanitizercould report false race conditions for this routine. This is for optimization purposes and does not affect the correctness of the computationThe routine allows the indices of
matAto be unsorted
cusparseSpMM() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
Please visit cuSPARSE Library Samples - cusparseSpMM CSR and cusparseSpMM COO for a code example. For batched computation please visit cusparseSpMM CSR Batched and cusparseSpMM COO Batched.
(2) |
BLOCKED-ELLPACK FORMAT |
cusparseSpMM supports the following data types for CUSPARSE_FORMAT_BLOCKED_ELL format and the following GPU architectures for exploiting NVIDIA Tensor Cores:
|
|
|
|
|
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cusparseSpMM supports the following algorithms with CUSPARSE_FORMAT_BLOCKED_ELL format:
Algorithm |
Notes |
|---|---|
|
Default algorithm for any sparse matrix format |
|
Default algorithm for Blocked-ELL format |
Performance notes:
Blocked-ELL SpMM provides the best performance with Power-of-2 Block-Sizes.
Large Block-Sizes (e.g. ≥ 64) provide the best performance.
The function has the following limitations:
The pointer mode must be equal to
CUSPARSE_POINTER_MODE_HOSTOnly
opA == CUSPARSE_OPERATION_NON_TRANSPOSEis supported.opB == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSEis not supported.Only
CUSPARSE_INDEX_32Iis supported.
Please visit cuSPARSE Library Samples - cusparseSpMM Blocked-ELL for a code example.
See cusparseStatus_t for the description of the return status.
6.6.9. cusparseSpMMOp()
cusparseStatus_t CUSPARSEAPI
cusparseSpMMOp_createPlan(cusparseHandle_t handle,
cusparseSpMMOpPlan_t* plan,
cusparseOperation_t opA,
cusparseOperation_t opB,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpMMOpAlg_t alg,
const void* addOperationNvvmBuffer,
size_t addOperationBufferSize,
const void* mulOperationNvvmBuffer,
size_t mulOperationBufferSize,
const void* epilogueNvvmBuffer,
size_t epilogueBufferSize,
size_t* SpMMWorkspaceSize)
cusparseStatus_t
cusparseSpMMOp_destroyPlan(cusparseSpMMOpPlan_t plan)
cusparseStatus_t
cusparseSpMMOp(cusparseSpMMOpPlan_t plan,
void* externalBuffer)
NOTE 1: NVRTC and nvJitLink are not currently available on Arm64 Android platforms.
NOTE 2: The routine does not support Android and Tegra platforms except Judy (sm87).
Experimental: The function performs the multiplication of a sparse matrix matA and a dense matrix matB with custom operators.
\({C^{\prime}}_{ij} = \text{epilogue}\left( {\sum_{k}^{\oplus}{op\left( A_{ik} \right) \otimes op\left( B_{kj} \right),C_{ij}}} \right)\) |
where
op(A)is a sparse matrix of size \(m \times k\)op(B)is a dense matrix of size \(k \times n\)Cis a dense matrix of size \(m \times n\)\(\oplus\) , \(\otimes\) , and \(\text{epilogue}\) are custom add, mul, and epilogue operators respectively.
Also, for matrix A and B
\(\text{op}(A) = \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ \end{cases}\)
\(\text{op}(B) = \begin{cases} B & {\text{if op(}B\text{) == CUSPARSE_OPERATION_NON_TRANSPOSE}} \\ B^{T} & {\text{if op(}B\text{) == CUSPARSE_OPERATION_TRANSPOSE}} \\ \end{cases}\)
Only opA == CUSPARSE_OPERATION_NON_TRANSPOSE is currently supported
The function cusparseSpMMOp_createPlan() returns the size of the workspace and the compiled kernel needed by cusparseSpMMOp()
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Dense matrix |
|
HOST |
IN/OUT |
Dense matrix |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
IN |
Pointer to the NVVM buffer containing the custom add operator |
|
HOST |
IN |
Size in bytes of |
|
HOST |
IN |
Pointer to the NVVM buffer containing the custom mul operator |
|
HOST |
IN |
Size in bytes of |
|
HOST |
IN |
Pointer to the NVVM buffer containing the custom epilogue operator |
|
HOST |
IN |
Size in bytes of |
|
HOST |
OUT |
Number of bytes of workspace needed by |
The operators must have the following signature and return type
__device__ <computetype> add_op(<computetype> value1, <computetype> value2);
__device__ <computetype> mul_op(<computetype> value1, <computetype> value2);
__device__ <computetype> epilogue(<computetype> value1, <computetype> value2);
<computetype> is one of float, double, cuComplex, cuDoubleComplex, or int,
cusparseSpMMOp supports the following sparse matrix formats:
CUSPARSE_FORMAT_CSR
cusparseSpMMOp supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSpMMOp supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
|---|---|---|
|
|
|
|
|
|
|
||
|
||
|
|
|
|
|
cusparseSpMMOp supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm for any sparse matrix format |
Performance notes:
Row-major layout provides higher performance than column-major.
cusparseSpMMOp() has the following properties:
The routine requires extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run
The routine allows the indices of
matAto be unsorted
cusparseSpMMOp() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
Please visit cuSPARSE Library Samples - cusparseSpMMOp
See cusparseStatus_t for the description of the return status.
6.6.10. cusparseSpSM()
cusparseStatus_t
cusparseSpSM_createDescr(cusparseSpSMDescr_t* spsmDescr);
cusparseStatus_t
cusparseSpSM_destroyDescr(cusparseSpSMDescr_t spsmDescr);
cusparseStatus_t
cusparseSpSM_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpSMAlg_t alg,
cusparseSpSMDescr_t spsmDescr,
size_t* bufferSize)
cusparseStatus_t
cusparseSpSM_analysis(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpSMAlg_t alg,
cusparseSpSMDescr_t spsmDescr,
void* externalBuffer)
cusparseStatus_t
cusparseSpSM_solve(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
cusparseDnMatDescr_t matC,
cudaDataType computeType,
cusparseSpSMAlg_t alg,
cusparseSpSMDescr_t spsmDescr)
cusparseStatus_t
cusparseSpSM_updateMatrix(cusparseHandle_t handle,
cusparseSpSMDescr_t spsmDescr,
void* newValues,
cusparseSpSMUpdate_t updatePart)
The function solves a system of linear equations whose coefficients are represented in a sparse triangular matrix:
\(op\left( \mathbf{A} \right) \cdot \mathbf{C} = \mathbf{\alpha}op\left( \mathbf{B} \right)\) |
where
op(A)is a sparse square matrix of size \(m \times m\)op(B)is a dense matrix of size \(m \times n\)Cis a dense matrix of size \(m \times n\)\(\alpha\) is a scalar
Also, for matrix A
\(\text{op}(A) = \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ A^{H} & \text{if op(A) == CUSPARSE_OPERATION_CONJUGATE_TRANSPOSE} \\ \end{cases}\)
\(\text{op}(B) = \begin{cases} B & \text{if op(B) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ B^{T} & \text{if op(B) == CUSPARSE_OPERATION_TRANSPOSE} \\ & \text{ } \\ \end{cases}\)
The function cusparseSpSM_bufferSize() returns the size of the workspace needed by cusparseSpSM_analysis() and cusparseSpSM_solve().
The function cusparseSpSM_analysis() performs the analysis phase, while cusparseSpSM_solve() executes the solve phase for a sparse triangular linear system.
The opaque data structure spsmDescr is used to share information among all functions.
The function cusparseSpSM_updateMatrix() updates spsmDescr with new matrix values.
The routine supports arbitrary sparsity for the input matrix, but only the upper or lower triangular part is taken into account in the computation.
cusparseSpSM_bufferSize() requires a buffer size for the analysis phase which is proportional to number of non-zero entries of the sparse matrix
The externalBuffer is stored into spsmDescr and used by cusparseSpSM_solve(). For this reason, the device memory buffer must be deallocated only after cusparseSpSM_solve()
NOTE: all parameters must be consistent across cusparseSpSM API calls and the matrix descriptions and externalBuffer must not be modified between cusparseSpSM_analysis() and cusparseSpSM_solve()
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of type |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Dense matrix |
|
HOST |
IN/OUT |
Dense matrix |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN/OUT |
Pointer to a workspace buffer of at least |
|
HOST |
IN/OUT |
Opaque descriptor for storing internal data used across the three steps |
The sparse matrix formats currently supported are listed below:
CUSPARSE_FORMAT_CSRCUSPARSE_FORMAT_COO
The cusparseSpSM() supports the following shapes and properties:
CUSPARSE_FILL_MODE_LOWERandCUSPARSE_FILL_MODE_UPPERfill modesCUSPARSE_DIAG_TYPE_NON_UNITandCUSPARSE_DIAG_TYPE_UNITdiagonal types
The fill mode and diagonal type can be set by cusparseSpMatSetAttribute()
cusparseSpSM() supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSpSM() supports the following data types:
Uniform-precision computation:
|
|---|
|
|
|
|
cusparseSpSM() supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm |
cusparseSpSM() has the following properties:
The routine requires no extra storage
Provides deterministic (bit-wise) results for each run for the solving phase
cusparseSpSM_solve()The
cusparseSpSM_solve()routine supports asynchronous executionThe routine supports in-place operation. The same device pointer must be provided to the
valuesparameter of the dense matricesmatBandmatC. All other dense matrix descriptor parameters (e.g.,order) can be set independentlycusparseSpSM_bufferSize()andcusparseSpSM_analysis()routines accept descriptors ofNULLvalues formatBandmatC. These two routines do not acceptNULLdescriptorsThe routine allows the indices of
matAto be unsorted
cusparseSpSM() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
cusparseSpSM_updateMatrix() updates the sparse matrix after calling the analysis phase. This functions supports the following update strategies (updatePart):
Strategy |
Notes |
|---|---|
|
Updates the sparse matrix values with values of |
|
Updates the diagonal part of the matrix with diagonal values stored in |
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpSM CSR and cuSPARSE Library Samples - cusparseSpSM COO for code examples.
6.6.11. cusparseSDDMM()
cusparseStatus_t
cusparseSDDMM_bufferSize(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSDDMMAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseSDDMM_preprocess(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSDDMMAlg_t alg,
void* externalBuffer)
cusparseStatus_t
cusparseSDDMM(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseConstDnMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSDDMMAlg_t alg,
void* externalBuffer)
This function performs the multiplication of matA and matB, followed by an element-wise multiplication with the sparsity pattern of matC. Formally, it performs the following operation:
\(\mathbf{C} = \alpha({op}(\mathbf{A}) \cdot {op}(\mathbf{B})) \circ {spy}(\mathbf{C}) + \beta\mathbf{C}\) |
where
op(A)is a dense matrix of size \(m \times k\)op(B)is a dense matrix of size \(k \times n\)Cis a sparse matrix of size \(m \times n\)\(\alpha\) and \(\beta\) are scalars
\(\circ\) denotes the Hadamard (entry-wise) matrix product, and \({spy}\left( \mathbf{C} \right)\) is the sparsity pattern matrix of
Cdefined as:\({spy}(\mathbf{C})_{ij} = \left\{ \begin{matrix} 0 & {\text{if}\,\mathbf{C}_{ij} = 0} \\ 1 & \text{otherwise} \\ \end{matrix} \right.\)
Also, for matrix A and B
\(\text{op}(A) = \begin{cases} A & \text{if op(A) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ A^{T} & \text{if op(A) == CUSPARSE_OPERATION_TRANSPOSE} \\ \end{cases}\)
\(\text{op}(B) = \begin{cases} B & \text{if op(B) == CUSPARSE_OPERATION_NON_TRANSPOSE} \\ B^{T} & \text{if op(B) == CUSPARSE_OPERATION_TRANSPOSE} \\ \end{cases}\)
The function cusparseSDDMM_bufferSize() returns the size of the workspace needed by cusparseSDDMM or cusparseSDDMM_preprocess.
The function cusparseSDDMM_preprocess() can be called before cusparseSDDMM to speedup the actual computation. It is useful when cusparseSDDMM is called multiple times with the same sparsity pattern (matC). The values of the dense matrices (matA, matB) can change arbitrarily.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication of type |
|
HOST |
IN |
Dense matrix |
|
HOST |
IN |
Dense matrix |
|
HOST or DEVICE |
IN |
\(\beta\) scalar used for multiplication of type |
|
HOST |
IN/OUT |
Sparse matrix |
|
HOST |
IN |
Datatype in which the computation is executed |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to a workspace buffer of at least |
Currently supported sparse matrix formats:
CUSPARSE_FORMAT_CSRCUSPARSE_FORMAT_BSR
cusparseSDDMM() supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
The data types combinations currently supported for cusparseSDDMM are listed below:
Uniform-precision computation:
|
|---|
|
|
|
|
Mixed-precision computation:
|
|
|
|---|---|---|
|
|
|
|
|
cusparseSDDMM for CUSPARSE_FORMAT_BSR also supports the following mixed-precision computation:
|
|
|
|---|---|---|
|
|
|
|
|
NOTE: CUDA_R_16F, CUDA_R_16BF data types always imply mixed-precision computation.
cusparseSDDMM() for CUSPASRE_FORMAT_BSR supports block sizes of 2, 4, 8, 16, 32, 64 and 128.
cusparseSDDMM() supports the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm. It supports batched computation. |
Performance notes: cuspaseSDDMM() for CUSPARSE_FORMAT_CSR provides the best performance when matA and matB satisfy:
matA:matAis in row-major order andopAisCUSPARSE_OPERATION_NON_TRANSPOSE, ormatAis in col-major order andopAis notCUSPARSE_OPERATION_NON_TRANSPOSE
matB:matBis in col-major order andopBisCUSPARSE_OPERATION_NON_TRANSPOSE, ormatBis in row-major order andopBis notCUSPARSE_OPERATION_NON_TRANSPOSE
cuspaseSDDMM() for CUSPARSE_FORMAT_BSR provides the best performance when matA and matB satisfy:
matA:matAis in row-major order andopAisCUSPARSE_OPERATION_NON_TRANSPOSE, ormatAis in col-major order andopAis notCUSPARSE_OPERATION_NON_TRANSPOSE
matB:matBis in row-major order andopBisCUSPARSE_OPERATION_NON_TRANSPOSE, ormatBis in col-major order andopBis notCUSPARSE_OPERATION_NON_TRANSPOSE
cusparseSDDMM() supports the following batch modes:
\(C_{i} = (A \cdot B) \circ C_{i}\)
\(C_{i} = \left( A_{i} \cdot B \right) \circ C_{i}\)
\(C_{i} = \left( A \cdot B_{i} \right) \circ C_{i}\)
\(C_{i} = \left( A_{i} \cdot B_{i} \right) \circ C_{i}\)
The number of batches and their strides can be set by using cusparseCsrSetStridedBatch and cusparseDnMatSetStridedBatch. The maximum number of batches for cusparseSDDMM() is 65,535.
cusparseSDDMM() has the following properties:
The routine requires no extra storage
Provides deterministic (bit-wise) results for each run
The routine supports asynchronous execution
The routine allows the indices of
matCto be unsorted
cusparseSDDMM() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSDDMM for a code example. For batched computation please visit cusparseSDDMM CSR Batched.
6.6.12. cusparseSpGEMM()
cusparseStatus_t
cusparseSpGEMM_createDescr(cusparseSpGEMMDescr_t* descr)
cusparseStatus_t
cusparseSpGEMM_destroyDescr(cusparseSpGEMMDescr_t descr)
cusparseStatus_t
cusparseSpGEMM_workEstimation(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstSpMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
size_t* bufferSize1,
void* externalBuffer1)
cusparseStatus_t
cusparseSpGEMM_getNumProducts(cusparseSpGEMMDescr_t spgemmDescr,
int64_t* num_prods)
cusparseStatus_t
cusparseSpGEMM_estimateMemory(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstSpMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
float chunk_fraction,
size_t* bufferSize3,
void* externalBuffer3,
size_t* bufferSize2)
cusparseStatus_t
cusparseSpGEMM_compute(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstSpMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
size_t* bufferSize2,
void* externalBuffer2)
cusparseStatus_t
cusparseSpGEMM_copy(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseConstSpMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr)
This function performs the multiplication of two sparse matrices matA and matB.
\(\mathbf{C^{\prime}} = \alpha op\left( \mathbf{A} \right) \cdot op\left( \mathbf{B} \right) + \beta\mathbf{C}\) |
where \(\alpha,\) \(\beta\) are scalars, and \(\mathbf{C},\) \(\mathbf{C^{\prime}}\) have the same sparsity pattern.
The functions cusparseSpGEMM_workEstimation(), cusparseSpGEMM_estimateMemory(), and cusparseSpGEMM_compute() are used for both determining the buffer size and performing the actual computation.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Operation |
|
HOST |
IN |
Operation |
|
HOST or DEVICE |
IN |
\(\alpha\) scalar used for multiplication |
|
HOST |
IN |
Sparse matrix |
|
HOST |
IN |
Sparse matrix |
|
HOST or DEVICE |
IN |
\(\beta\) scalar used for multiplication |
|
HOST |
IN/OUT |
Sparse matrix |
|
HOST |
IN |
Enumerator specifying the datatype in which the computation is executed |
|
HOST |
IN |
Enumerator specifying the algorithm for the computation |
|
HOST |
IN/OUT |
Opaque descriptor for storing internal data used across the three steps |
|
HOST |
OUT |
Pointer to a 64-bit integer that stores the number of intermediate products calculated by |
|
HOST |
IN |
The fraction of total intermediate products being computed in a chunk. Used by |
|
HOST |
IN/OUT |
Number of bytes of workspace requested by |
|
HOST |
IN/OUT |
Number of bytes of workspace requested by |
|
HOST |
IN/OUT |
Number of bytes of workspace requested by |
|
DEVICE |
IN |
Pointer to workspace buffer needed by |
|
DEVICE |
IN |
Pointer to workspace buffer needed by |
|
DEVICE |
IN |
Pointer to workspace buffer needed by |
Currently, the function has the following limitations:
Only 32-bit indices
CUSPARSE_INDEX_32Iis supportedOnly CSR format
CUSPARSE_FORMAT_CSRis supportedOnly
opA,opBequal toCUSPARSE_OPERATION_NON_TRANSPOSEare supported
The data types combinations currently supported for cusparseSpGEMM are listed below :
Uniform-precision computation:
|
|---|
|
|
|
|
|
|
|
|
cusparseSpGEMM routine runs for the following algorithms:
Algorithm |
Notes |
|---|---|
|
Default algorithm. Currently, it is |
|
Algorithm 1
|
|
Algorithm 2
|
|
Algorithm 3
|
cusparseSpGEMM() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine allows the indices of
matAandmatBto be unsortedThe routine guarantees the indices of
matCto be sorted
cusparseSpGEMM() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpGEMM for a code example for CUSPARSE_SPGEMM_DEFAULT and CUSPARSE_SPGEMM_ALG1, and cuSPARSE Library Samples - memory-optimzed cusparseSpGEMM for a code example for CUSPARSE_SPGEMM_ALG2 and CUSPARSE_SPGEMM_ALG3.
6.6.13. cusparseSpGEMMreuse()
cusparseStatus_t
cusparseSpGEMM_createDescr(cusparseSpGEMMDescr_t* descr)
cusparseStatus_t
cusparseSpGEMM_destroyDescr(cusparseSpGEMMDescr_t descr)
cusparseStatus_t
cusparseSpGEMMreuse_workEstimation(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
cusparseSpMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB, // non-const descriptor supported
cusparseSpMatDescr_t matC,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
size_t* bufferSize1,
void* externalBuffer1)
cusparseStatus_t
cusparseSpGEMMreuse_nnz(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
cusparseSpMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB, // non-const descriptor supported
cusparseSpMatDescr_t matC,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
size_t* bufferSize2,
void* externalBuffer2,
size_t* bufferSize3,
void* externalBuffer3,
size_t* bufferSize4,
void* externalBuffer4)
cusparseStatus_t CUSPARSEAPI
cusparseSpGEMMreuse_copy(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
cusparseSpMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB, // non-const descriptor supported
cusparseSpMatDescr_t matC,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr,
size_t* bufferSize5,
void* externalBuffer5)
cusparseStatus_t CUSPARSEAPI
cusparseSpGEMMreuse_compute(cusparseHandle_t handle,
cusparseOperation_t opA,
cusparseOperation_t opB,
const void* alpha,
cusparseSpMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB, // non-const descriptor supported
const void* beta,
cusparseSpMatDescr_t matC,
cudaDataType computeType,
cusparseSpGEMMAlg_t alg,
cusparseSpGEMMDescr_t spgemmDescr)
This function performs the multiplication of two sparse matrices matA and matB where the structure of the output matrix matC can be reused for multiple computations with different values.
\(\mathbf{C^{\prime}} = \alpha op\left( \mathbf{A} \right) \cdot op\left( \mathbf{B} \right) + \beta\mathbf{C}\) |
where \(\alpha\) and \(\beta\) are scalars.
The functions cusparseSpGEMMreuse_workEstimation(), cusparseSpGEMMreuse_nnz(), and cusparseSpGEMMreuse_copy() are used for determining the buffer size and performing the actual computation.
Note: cusparseSpGEMMreuse() output CSR matrix (matC) is sorted by column indices.
MEMORY REQUIREMENT: cusparseSpGEMMreuse requires to keep in memory all intermediate products to reuse the structure of the output matrix. On the other hand, the number of intermediate products is orders of magnitude higher than the number of non-zero entries in general. In order to minimize the memory requirements, the routine uses multiple buffers that can be deallocated after they are no more needed. If the number of intermediate product exceeds 2^31-1, the routine will returns CUSPARSE_STATUS_INSUFFICIENT_RESOURCES status.
Currently, the function has the following limitations:
Only 32-bit indices
CUSPARSE_INDEX_32Iis supportedOnly CSR format
CUSPARSE_FORMAT_CSRis supportedOnly
opA,opBequal toCUSPARSE_OPERATION_NON_TRANSPOSEare supported
The data types combinations currently supported for cusparseSpGEMMreuse are listed below.
Uniform-precision computation:
|
|---|
|
|
|
|
|
|
Mixed-precision computation: [DEPRECATED]
|
|
|
|---|---|---|
|
|
|
|
|
|
cusparseSpGEMMreuse routine runs for the following algorithm:
Algorithm |
Notes |
|---|---|
|
Default algorithm. Provides deterministic (bit-wise) structure for the output matrix for each run, while value computation is not deterministic. |
|
Provides deterministic (bit-wise) structure for the output matrix and value computation for each run. |
cusparseSpGEMMreuse() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
The routine allows the indices of
matAandmatBto be unsortedThe routine guarantees the indices of
matCto be sorted
cusparseSpGEMMreuse() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
Refer to cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSpGEMMreuse for a code example.
6.6.14. cusparseSparseToDense()
cusparseStatus_t
cusparseSparseToDense_bufferSize(cusparseHandle_t handle,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseDnMatDescr_t matB,
cusparseSparseToDenseAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseSparseToDense(cusparseHandle_t handle,
cusparseConstSpMatDescr_t matA, // non-const descriptor supported
cusparseDnMatDescr_t matB,
cusparseSparseToDenseAlg_t alg,
void* buffer)
The function converts the sparse matrix matA in CSR, CSC, or COO format into its dense representation matB. Blocked-ELL is not currently supported.
The function cusparseSparseToDense_bufferSize() returns the size of the workspace needed by cusparseSparseToDense().
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Sparse matrix |
|
HOST |
OUT |
Dense matrix |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to workspace buffer |
cusparseSparseToDense() supports the following index type for representing the sparse matrix matA:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseSparseToDense() supports the following data types:
|
|---|
|
|
|
|
|
|
|
|
|
cusparseSparse2Dense() supports the following algorithm:
Algorithm |
Notes |
|---|---|
|
Default algorithm |
cusparseSparseToDense() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run
The routine allows the indices of
matAto be unsorted
cusparseSparseToDense() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseSparseToDense for a code example.
6.6.15. cusparseDenseToSparse()
cusparseStatus_t
cusparseDenseToSparse_bufferSize(cusparseHandle_t handle,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB,
cusparseDenseToSparseAlg_t alg,
size_t* bufferSize)
cusparseStatus_t
cusparseDenseToSparse_analysis(cusparseHandle_t handle,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB,
cusparseDenseToSparseAlg_t alg,
void* buffer)
cusparseStatus_t
cusparseDenseToSparse_convert(cusparseHandle_t handle,
cusparseConstDnMatDescr_t matA, // non-const descriptor supported
cusparseSpMatDescr_t matB,
cusparseDenseToSparseAlg_t alg,
void* buffer)
The function converts the dense matrix matA into a sparse matrix matB in CSR, CSC, COO, or Blocked-ELL format.
The function cusparseDenseToSparse_bufferSize() returns the size of the workspace needed by cusparseDenseToSparse_analysis().
The function cusparseDenseToSparse_analysis() updates the number of non-zero elements in the sparse matrix descriptor matB. The user is responsible to allocate the memory required by the sparse matrix:
Row/Column indices and value arrays for CSC and CSR respectively
Row, column, value arrays for COO
Column (
ellColInd), value (ellValue) arrays for Blocked-ELL
Finally, we call cusparseDenseToSparse_convert() for filling the arrays allocated in the previous step.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
HOST |
IN |
Handle to the cuSPARSE library context |
|
HOST |
IN |
Dense matrix |
|
HOST |
OUT |
Sparse matrix |
|
HOST |
IN |
Algorithm for the computation |
|
HOST |
OUT |
Number of bytes of workspace needed by |
|
DEVICE |
IN |
Pointer to workspace buffer |
cusparseDenseToSparse() supports the following index type for representing the sparse vector matB:
32-bit indices (
CUSPARSE_INDEX_32I)64-bit indices (
CUSPARSE_INDEX_64I)
cusparseDenseToSparse() supports the following data types:
|
|---|
|
|
|
|
|
|
|
|
|
cusparseDense2Sparse() supports the following algorithm:
Algorithm |
Notes |
|---|---|
|
Default algorithm |
cusparseDenseToSparse() has the following properties:
The routine requires no extra storage
The routine supports asynchronous execution
Provides deterministic (bit-wise) results for each run
The routine does not guarantee the indices of
matBto be sorted
cusparseDenseToSparse() supports the following optimizations:
CUDA graph capture
Hardware Memory Compression
See cusparseStatus_t for the description of the return status.
Please visit cuSPARSE Library Samples - cusparseDenseToSparse (CSR) and cuSPARSE Library Samples - cusparseDenseToSparse (Blocked-ELL) for code examples.
7. cuSPARSE Fortran Bindings
The cuSPARSE library is implemented using the C-based CUDA toolchain, and it thus provides a C-style API that makes interfacing to applications written in C or C++ trivial. There are also many applications implemented in Fortran that would benefit from using cuSPARSE, and therefore a cuSPARSE Fortran interface has been developed.
Unfortunately, Fortran-to-C calling conventions are not standardized and differ by platform and toolchain. In particular, differences may exist in the following areas:
Symbol names (capitalization, name decoration)
Argument passing (by value or reference)
Passing of pointer arguments (size of the pointer)
To provide maximum flexibility in addressing those differences, the cuSPARSE Fortran interface is provided in the form of wrapper functions, which are written in C and are located in the file cusparse_fortran.c. This file also contains a few additional wrapper functions (for cudaMalloc(), cudaMemset, and so on) that can be used to allocate memory on the GPU.
The cuSPARSE Fortran wrapper code is provided as an example only and needs to be compiled into an application for it to call the cuSPARSE API functions. Providing this source code allows users to make any changes necessary for a particular platform and toolchain.
The cuSPARSE Fortran wrapper code has been used to demonstrate interoperability with the compilers g95 0.91 (on 32-bit and 64-bit Linux) and g95 0.92 (on 32-bit and 64-bit Mac OS X). In order to use other compilers, users have to make any changes to the wrapper code that may be required.
The direct wrappers, intended for production code, substitute device pointers for vector and matrix arguments in all cuSPARSE functions. To use these interfaces, existing applications need to be modified slightly to allocate and deallocate data structures in GPU memory space (using CUDA_MALLOC() and CUDA_FREE()) and to copy data between GPU and CPU memory spaces (using the CUDA_MEMCPY() routines). The sample wrappers provided in cusparse_fortran.c map device pointers to the OS-dependent type size_t, which is 32 bits wide on 32-bit platforms and 64 bits wide on a 64-bit platforms.
One approach to dealing with index arithmetic on device pointers in Fortran code is to use C-style macros and to use the C preprocessor to expand them. On Linux and Mac OS X, preprocessing can be done by using the option '-cpp' with g95 or gfortran. The function GET_SHIFTED_ADDRESS(), provided with the cuSPARSE Fortran wrappers, can also be used, as shown in example B.
Example B shows the the C++ of example A implemented in Fortran 77 on the host. This example should be compiled with ARCH_64 defined as 1 on a 64-bit OS system and as undefined on a 32-bit OS system. For example, on g95 or gfortran, it can be done directly on the command line using the option -cpp -DARCH_64=1.
7.1. Fortran Application
c #define ARCH_64 0
c #define ARCH_64 1
program cusparse_fortran_example
implicit none
integer cuda_malloc
external cuda_free
integer cuda_memcpy_c2fort_int
integer cuda_memcpy_c2fort_real
integer cuda_memcpy_fort2c_int
integer cuda_memcpy_fort2c_real
integer cuda_memset
integer cusparse_create
external cusparse_destroy
integer cusparse_get_version
integer cusparse_create_mat_descr
external cusparse_destroy_mat_descr
integer cusparse_set_mat_type
integer cusparse_get_mat_type
integer cusparse_get_mat_fill_mode
integer cusparse_get_mat_diag_type
integer cusparse_set_mat_index_base
integer cusparse_get_mat_index_base
integer cusparse_xcoo2csr
integer cusparse_dsctr
integer cusparse_dcsrmv
integer cusparse_dcsrmm
external get_shifted_address
#if ARCH_64
integer*8 handle
integer*8 descrA
integer*8 cooRowIndex
integer*8 cooColIndex
integer*8 cooVal
integer*8 xInd
integer*8 xVal
integer*8 y
integer*8 z
integer*8 csrRowPtr
integer*8 ynp1
#else
integer*4 handle
integer*4 descrA
integer*4 cooRowIndex
integer*4 cooColIndex
integer*4 cooVal
integer*4 xInd
integer*4 xVal
integer*4 y
integer*4 z
integer*4 csrRowPtr
integer*4 ynp1
#endif
integer status
integer cudaStat1,cudaStat2,cudaStat3
integer cudaStat4,cudaStat5,cudaStat6
integer n, nnz, nnz_vector
parameter (n=4, nnz=9, nnz_vector=3)
integer cooRowIndexHostPtr(nnz)
integer cooColIndexHostPtr(nnz)
real*8 cooValHostPtr(nnz)
integer xIndHostPtr(nnz_vector)
real*8 xValHostPtr(nnz_vector)
real*8 yHostPtr(2*n)
real*8 zHostPtr(2*(n+1))
integer i, j
integer version, mtype, fmode, dtype, ibase
real*8 dzero,dtwo,dthree,dfive
real*8 epsilon
write(*,*) "testing fortran example"
c predefined constants (need to be careful with them)
dzero = 0.0
dtwo = 2.0
dthree= 3.0
dfive = 5.0
c create the following sparse test matrix in COO format
c (notice one-based indexing)
c |1.0 2.0 3.0|
c | 4.0 |
c |5.0 6.0 7.0|
c | 8.0 9.0|
cooRowIndexHostPtr(1)=1
cooColIndexHostPtr(1)=1
cooValHostPtr(1) =1.0
cooRowIndexHostPtr(2)=1
cooColIndexHostPtr(2)=3
cooValHostPtr(2) =2.0
cooRowIndexHostPtr(3)=1
cooColIndexHostPtr(3)=4
cooValHostPtr(3) =3.0
cooRowIndexHostPtr(4)=2
cooColIndexHostPtr(4)=2
cooValHostPtr(4) =4.0
cooRowIndexHostPtr(5)=3
cooColIndexHostPtr(5)=1
cooValHostPtr(5) =5.0
cooRowIndexHostPtr(6)=3
cooColIndexHostPtr(6)=3
cooValHostPtr(6) =6.0
cooRowIndexHostPtr(7)=3
cooColIndexHostPtr(7)=4
cooValHostPtr(7) =7.0
cooRowIndexHostPtr(8)=4
cooColIndexHostPtr(8)=2
cooValHostPtr(8) =8.0
cooRowIndexHostPtr(9)=4
cooColIndexHostPtr(9)=4
cooValHostPtr(9) =9.0
c print the matrix
write(*,*) "Input data:"
do i=1,nnz
write(*,*) "cooRowIndexHostPtr[",i,"]=",cooRowIndexHostPtr(i)
write(*,*) "cooColIndexHostPtr[",i,"]=",cooColIndexHostPtr(i)
write(*,*) "cooValHostPtr[", i,"]=",cooValHostPtr(i)
enddo
c create a sparse and dense vector
c xVal= [100.0 200.0 400.0] (sparse)
c xInd= [0 1 3 ]
c y = [10.0 20.0 30.0 40.0 | 50.0 60.0 70.0 80.0] (dense)
c (notice one-based indexing)
yHostPtr(1) = 10.0
yHostPtr(2) = 20.0
yHostPtr(3) = 30.0
yHostPtr(4) = 40.0
yHostPtr(5) = 50.0
yHostPtr(6) = 60.0
yHostPtr(7) = 70.0
yHostPtr(8) = 80.0
xIndHostPtr(1)=1
xValHostPtr(1)=100.0
xIndHostPtr(2)=2
xValHostPtr(2)=200.0
xIndHostPtr(3)=4
xValHostPtr(3)=400.0
c print the vectors
do j=1,2
do i=1,n
write(*,*) "yHostPtr[",i,",",j,"]=",yHostPtr(i+n*(j-1))
enddo
enddo
do i=1,nnz_vector
write(*,*) "xIndHostPtr[",i,"]=",xIndHostPtr(i)
write(*,*) "xValHostPtr[",i,"]=",xValHostPtr(i)
enddo
c allocate GPU memory and copy the matrix and vectors into it
c cudaSuccess=0
c cudaMemcpyHostToDevice=1
cudaStat1 = cuda_malloc(cooRowIndex,nnz*4)
cudaStat2 = cuda_malloc(cooColIndex,nnz*4)
cudaStat3 = cuda_malloc(cooVal, nnz*8)
cudaStat4 = cuda_malloc(y, 2*n*8)
cudaStat5 = cuda_malloc(xInd,nnz_vector*4)
cudaStat6 = cuda_malloc(xVal,nnz_vector*8)
if ((cudaStat1 /= 0) .OR.
$ (cudaStat2 /= 0) .OR.
$ (cudaStat3 /= 0) .OR.
$ (cudaStat4 /= 0) .OR.
$ (cudaStat5 /= 0) .OR.
$ (cudaStat6 /= 0)) then
write(*,*) "Device malloc failed"
write(*,*) "cudaStat1=",cudaStat1
write(*,*) "cudaStat2=",cudaStat2
write(*,*) "cudaStat3=",cudaStat3
write(*,*) "cudaStat4=",cudaStat4
write(*,*) "cudaStat5=",cudaStat5
write(*,*) "cudaStat6=",cudaStat6
stop 2
endif
cudaStat1 = cuda_memcpy_fort2c_int(cooRowIndex,cooRowIndexHostPtr,
$ nnz*4,1)
cudaStat2 = cuda_memcpy_fort2c_int(cooColIndex,cooColIndexHostPtr,
$ nnz*4,1)
cudaStat3 = cuda_memcpy_fort2c_real(cooVal, cooValHostPtr,
$ nnz*8,1)
cudaStat4 = cuda_memcpy_fort2c_real(y, yHostPtr,
$ 2*n*8,1)
cudaStat5 = cuda_memcpy_fort2c_int(xInd, xIndHostPtr,
$ nnz_vector*4,1)
cudaStat6 = cuda_memcpy_fort2c_real(xVal, xValHostPtr,
$ nnz_vector*8,1)
if ((cudaStat1 /= 0) .OR.
$ (cudaStat2 /= 0) .OR.
$ (cudaStat3 /= 0) .OR.
$ (cudaStat4 /= 0) .OR.
$ (cudaStat5 /= 0) .OR.
$ (cudaStat6 /= 0)) then
write(*,*) "Memcpy from Host to Device failed"
write(*,*) "cudaStat1=",cudaStat1
write(*,*) "cudaStat2=",cudaStat2
write(*,*) "cudaStat3=",cudaStat3
write(*,*) "cudaStat4=",cudaStat4
write(*,*) "cudaStat5=",cudaStat5
write(*,*) "cudaStat6=",cudaStat6
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
stop 1
endif
c initialize cusparse library
c CUSPARSE_STATUS_SUCCESS=0
status = cusparse_create(handle)
if (status /= 0) then
write(*,*) "CUSPARSE Library initialization failed"
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
stop 1
endif
c get version
c CUSPARSE_STATUS_SUCCESS=0
status = cusparse_get_version(handle,version)
if (status /= 0) then
write(*,*) "CUSPARSE Library initialization failed"
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cusparse_destroy(handle)
stop 1
endif
write(*,*) "CUSPARSE Library version",version
c create and setup the matrix descriptor
c CUSPARSE_STATUS_SUCCESS=0
c CUSPARSE_MATRIX_TYPE_GENERAL=0
c CUSPARSE_INDEX_BASE_ONE=1
status= cusparse_create_mat_descr(descrA)
if (status /= 0) then
write(*,*) "Creating matrix descriptor failed"
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cusparse_destroy(handle)
stop 1
endif
status = cusparse_set_mat_type(descrA,0)
status = cusparse_set_mat_index_base(descrA,1)
c print the matrix descriptor
mtype = cusparse_get_mat_type(descrA)
fmode = cusparse_get_mat_fill_mode(descrA)
dtype = cusparse_get_mat_diag_type(descrA)
ibase = cusparse_get_mat_index_base(descrA)
write (*,*) "matrix descriptor:"
write (*,*) "t=",mtype,"m=",fmode,"d=",dtype,"b=",ibase
c exercise conversion routines (convert matrix from COO 2 CSR format)
c cudaSuccess=0
c CUSPARSE_STATUS_SUCCESS=0
c CUSPARSE_INDEX_BASE_ONE=1
cudaStat1 = cuda_malloc(csrRowPtr,(n+1)*4)
if (cudaStat1 /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Device malloc failed (csrRowPtr)"
stop 2
endif
status= cusparse_xcoo2csr(handle,cooRowIndex,nnz,n,
$ csrRowPtr,1)
if (status /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Conversion from COO to CSR format failed"
stop 1
endif
c csrRowPtr = [0 3 4 7 9]
c exercise Level 1 routines (scatter vector elements)
c CUSPARSE_STATUS_SUCCESS=0
c CUSPARSE_INDEX_BASE_ONE=1
call get_shifted_address(y,n*8,ynp1)
status= cusparse_dsctr(handle, nnz_vector, xVal, xInd,
$ ynp1, 1)
if (status /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Scatter from sparse to dense vector failed"
stop 1
endif
c y = [10 20 30 40 | 100 200 70 400]
c exercise Level 2 routines (csrmv)
c CUSPARSE_STATUS_SUCCESS=0
c CUSPARSE_OPERATION_NON_TRANSPOSE=0
status= cusparse_dcsrmv(handle, 0, n, n, nnz, dtwo,
$ descrA, cooVal, csrRowPtr, cooColIndex,
$ y, dthree, ynp1)
if (status /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Matrix-vector multiplication failed"
stop 1
endif
c print intermediate results (y)
c y = [10 20 30 40 | 680 760 1230 2240]
c cudaSuccess=0
c cudaMemcpyDeviceToHost=2
cudaStat1 = cuda_memcpy_c2fort_real(yHostPtr, y, 2*n*8, 2)
if (cudaStat1 /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Memcpy from Device to Host failed"
stop 1
endif
write(*,*) "Intermediate results:"
do j=1,2
do i=1,n
write(*,*) "yHostPtr[",i,",",j,"]=",yHostPtr(i+n*(j-1))
enddo
enddo
c exercise Level 3 routines (csrmm)
c cudaSuccess=0
c CUSPARSE_STATUS_SUCCESS=0
c CUSPARSE_OPERATION_NON_TRANSPOSE=0
cudaStat1 = cuda_malloc(z, 2*(n+1)*8)
if (cudaStat1 /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Device malloc failed (z)"
stop 2
endif
cudaStat1 = cuda_memset(z, 0, 2*(n+1)*8)
if (cudaStat1 /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(z)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Memset on Device failed"
stop 1
endif
status= cusparse_dcsrmm(handle, 0, n, 2, n, nnz, dfive,
$ descrA, cooVal, csrRowPtr, cooColIndex,
$ y, n, dzero, z, n+1)
if (status /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(z)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Matrix-matrix multiplication failed"
stop 1
endif
c print final results (z)
c cudaSuccess=0
c cudaMemcpyDeviceToHost=2
cudaStat1 = cuda_memcpy_c2fort_real(zHostPtr, z, 2*(n+1)*8, 2)
if (cudaStat1 /= 0) then
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(z)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
write(*,*) "Memcpy from Device to Host failed"
stop 1
endif
c z = [950 400 2550 2600 0 | 49300 15200 132300 131200 0]
write(*,*) "Final results:"
do j=1,2
do i=1,n+1
write(*,*) "z[",i,",",j,"]=",zHostPtr(i+(n+1)*(j-1))
enddo
enddo
c check the results
epsilon = 0.00000000000001
if ((DABS(zHostPtr(1) - 950.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(2) - 400.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(3) - 2550.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(4) - 2600.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(5) - 0.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(6) - 49300.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(7) - 15200.0) .GT. epsilon) .OR.
$ (DABS(zHostPtr(8) - 132300.0).GT. epsilon) .OR.
$ (DABS(zHostPtr(9) - 131200.0).GT. epsilon) .OR.
$ (DABS(zHostPtr(10) - 0.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(1) - 10.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(2) - 20.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(3) - 30.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(4) - 40.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(5) - 680.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(6) - 760.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(7) - 1230.0) .GT. epsilon) .OR.
$ (DABS(yHostPtr(8) - 2240.0) .GT. epsilon)) then
write(*,*) "fortran example test FAILED"
else
write(*,*) "fortran example test PASSED"
endif
c deallocate GPU memory and exit
call cuda_free(cooRowIndex)
call cuda_free(cooColIndex)
call cuda_free(cooVal)
call cuda_free(xInd)
call cuda_free(xVal)
call cuda_free(y)
call cuda_free(z)
call cuda_free(csrRowPtr)
call cusparse_destroy_mat_descr(descrA)
call cusparse_destroy(handle)
stop 0
end
8. Acknowledgements
NVIDIA would like to thank the following individuals and institutions for their contributions:
The cusparse<t>gtsv implementation is derived from a version developed by Li-Wen Chang from the University of Illinois.
The cusparse<t>gtsvInterleavedBatch adopts cuThomasBatch developed by Pedro Valero-Lara and Ivan Martínez-Pérez from Barcelona Supercomputing Center and BSC/UPC NVIDIA GPU Center of Excellence.
This product includes {fmt} - A modern formatting library https://fmt.dev Copyright (c) 2012 - present, Victor Zverovich.
9. Bibliography
[1] N. Bell and M. Garland, “Implementing Sparse Matrix-Vector Multiplication on Throughput-Oriented Processors”, Supercomputing, 2009.
[2] R. Grimes, D. Kincaid, and D. Young, “ITPACK 2.0 User’s Guide”, Technical Report CNA-150, Center for Numerical Analysis, University of Texas, 1979.
[3] M. Naumov, “Incomplete-LU and Cholesky Preconditioned Iterative Methods Using cuSPARSE and cuBLAS”, Technical Report and White Paper, 2011.
[4] Pedro Valero-Lara, Ivan Martínez-Pérez, Raül Sirvent, Xavier Martorell, and Antonio J. Peña. NVIDIA GPUs Scalability to Solve Multiple (Batch) Tridiagonal Systems. Implementation of cuThomasBatch. In Parallel Processing and Applied Mathematics - 12th International Conference (PPAM), 2017.
10. Notices
10.1. Notice
This document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.
NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice.
Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.
NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgement, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.
NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk.
NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.
No license, either expressed or implied, is granted under any NVIDIA patent right, copyright, or other NVIDIA intellectual property right under this document. Information published by NVIDIA regarding third-party products or services does not constitute a license from NVIDIA to use such products or services or a warranty or endorsement thereof. Use of such information may require a license from a third party under the patents or other intellectual property rights of the third party, or a license from NVIDIA under the patents or other intellectual property rights of NVIDIA.
Reproduction of information in this document is permissible only if approved in advance by NVIDIA in writing, reproduced without alteration and in full compliance with all applicable export laws and regulations, and accompanied by all associated conditions, limitations, and notices.
THIS DOCUMENT AND ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, “MATERIALS”) ARE BEING PROVIDED “AS IS.” NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE. TO THE EXTENT NOT PROHIBITED BY LAW, IN NO EVENT WILL NVIDIA BE LIABLE FOR ANY DAMAGES, INCLUDING WITHOUT LIMITATION ANY DIRECT, INDIRECT, SPECIAL, INCIDENTAL, PUNITIVE, OR CONSEQUENTIAL DAMAGES, HOWEVER CAUSED AND REGARDLESS OF THE THEORY OF LIABILITY, ARISING OUT OF ANY USE OF THIS DOCUMENT, EVEN IF NVIDIA HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. Notwithstanding any damages that customer might incur for any reason whatsoever, NVIDIA’s aggregate and cumulative liability towards customer for the products described herein shall be limited in accordance with the Terms of Sale for the product.
10.2. OpenCL
OpenCL is a trademark of Apple Inc. used under license to the Khronos Group Inc.
10.3. Trademarks
NVIDIA and the NVIDIA logo are trademarks or registered trademarks of NVIDIA Corporation in the U.S. and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.