Parallel Thread Execution ISA Version 8.4
The programming guide to using PTX (Parallel Thread Execution) and ISA (Instruction Set Architecture).
1. Introduction
This document describes PTX, a low-level parallel thread execution virtual machine and instruction set architecture (ISA). PTX exposes the GPU as a data-parallel computing device.
1.1. Scalable Data-Parallel Computing using GPUs
Driven by the insatiable market demand for real-time, high-definition 3D graphics, the programmable GPU has evolved into a highly parallel, multithreaded, many-core processor with tremendous computational horsepower and very high memory bandwidth. The GPU is especially well-suited to address problems that can be expressed as data-parallel computations - the same program is executed on many data elements in parallel - with high arithmetic intensity - the ratio of arithmetic operations to memory operations. Because the same program is executed for each data element, there is a lower requirement for sophisticated flow control; and because it is executed on many data elements and has high arithmetic intensity, the memory access latency can be hidden with calculations instead of big data caches.
Data-parallel processing maps data elements to parallel processing threads. Many applications that process large data sets can use a data-parallel programming model to speed up the computations. In 3D rendering large sets of pixels and vertices are mapped to parallel threads. Similarly, image and media processing applications such as post-processing of rendered images, video encoding and decoding, image scaling, stereo vision, and pattern recognition can map image blocks and pixels to parallel processing threads. In fact, many algorithms outside the field of image rendering and processing are accelerated by data-parallel processing, from general signal processing or physics simulation to computational finance or computational biology.
PTX defines a virtual machine and ISA for general purpose parallel thread execution. PTX programs are translated at install time to the target hardware instruction set. The PTX-to-GPU translator and driver enable NVIDIA GPUs to be used as programmable parallel computers.
1.2. Goals of PTX
PTX provides a stable programming model and instruction set for general purpose parallel programming. It is designed to be efficient on NVIDIA GPUs supporting the computation features defined by the NVIDIA Tesla architecture. High level language compilers for languages such as CUDA and C/C++ generate PTX instructions, which are optimized for and translated to native target-architecture instructions.
The goals for PTX include the following:
Provide a stable ISA that spans multiple GPU generations.
Achieve performance in compiled applications comparable to native GPU performance.
Provide a machine-independent ISA for C/C++ and other compilers to target.
Provide a code distribution ISA for application and middleware developers.
Provide a common source-level ISA for optimizing code generators and translators, which map PTX to specific target machines.
Facilitate hand-coding of libraries, performance kernels, and architecture tests.
Provide a scalable programming model that spans GPU sizes from a single unit to many parallel units.
1.3. PTX ISA Version 8.4
PTX ISA version 8.4 introduces the following new features:
Extends
ld,standatominstructions with.b128type to support.sysscope.Extends integer
wgmma.mma_asyncinstruction to support.u8.s8and.s8.u8as.atypeand.btyperespectively.Extends
mma,mma.spinstructions to support FP8 types.e4m3and.e5m2.
1.4. Document Structure
The information in this document is organized into the following Chapters:
Programming Model outlines the programming model.
PTX Machine Model gives an overview of the PTX virtual machine model.
Syntax describes the basic syntax of the PTX language.
State Spaces, Types, and Variables describes state spaces, types, and variable declarations.
Instruction Operands describes instruction operands.
Abstracting the ABI describes the function and call syntax, calling convention, and PTX support for abstracting the Application Binary Interface (ABI).
Instruction Set describes the instruction set.
Special Registers lists special registers.
Directives lists the assembly directives supported in PTX.
Release Notes provides release notes for PTX ISA versions 2.x and beyond.
References
754-2008 IEEE Standard for Floating-Point Arithmetic. ISBN 978-0-7381-5752-8, 2008.
The OpenCL Specification, Version: 1.1, Document Revision: 44, June 1, 2011.
CUDA Programming Guide.
https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html
CUDA Dynamic Parallelism Programming Guide.
https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#cuda-dynamic-parallelism
CUDA Atomicity Requirements.
https://nvidia.github.io/cccl/libcudacxx/extended_api/memory_model.html#atomicity
PTX Writers Guide to Interoperability.
https://docs.nvidia.com/cuda/ptx-writers-guide-to-interoperability/index.html
2. Programming Model
2.1. A Highly Multithreaded Coprocessor
The GPU is a compute device capable of executing a very large number of threads in parallel. It operates as a coprocessor to the main CPU, or host: In other words, data-parallel, compute-intensive portions of applications running on the host are off-loaded onto the device.
More precisely, a portion of an application that is executed many times, but independently on different data, can be isolated into a kernel function that is executed on the GPU as many different threads. To that effect, such a function is compiled to the PTX instruction set and the resulting kernel is translated at install time to the target GPU instruction set.
2.2. Thread Hierarchy
The batch of threads that executes a kernel is organized as a grid. A grid consists of either cooperative thread arrays or clusters of cooperative thread arrays as described in this section and illustrated in Figure 1 and Figure 2. Cooperative thread arrays (CTAs) implement CUDA thread blocks and clusters implement CUDA thread block clusters.
2.2.1. Cooperative Thread Arrays
The Parallel Thread Execution (PTX) programming model is explicitly parallel: a PTX program specifies the execution of a given thread of a parallel thread array. A cooperative thread array, or CTA, is an array of threads that execute a kernel concurrently or in parallel.
Threads within a CTA can communicate with each other. To coordinate the communication of the threads within the CTA, one can specify synchronization points where threads wait until all threads in the CTA have arrived.
Each thread has a unique thread identifier within the CTA. Programs use a data parallel
decomposition to partition inputs, work, and results across the threads of the CTA. Each CTA thread
uses its thread identifier to determine its assigned role, assign specific input and output
positions, compute addresses, and select work to perform. The thread identifier is a three-element
vector tid, (with elements tid.x, tid.y, and tid.z) that specifies the thread’s
position within a 1D, 2D, or 3D CTA. Each thread identifier component ranges from zero up to the
number of thread ids in that CTA dimension.
Each CTA has a 1D, 2D, or 3D shape specified by a three-element vector ntid (with elements
ntid.x, ntid.y, and ntid.z). The vector ntid specifies the number of threads in each
CTA dimension.
Threads within a CTA execute in SIMT (single-instruction, multiple-thread) fashion in groups called
warps. A warp is a maximal subset of threads from a single CTA, such that the threads execute
the same instructions at the same time. Threads within a warp are sequentially numbered. The warp
size is a machine-dependent constant. Typically, a warp has 32 threads. Some applications may be
able to maximize performance with knowledge of the warp size, so PTX includes a run-time immediate
constant, WARP_SZ, which may be used in any instruction where an immediate operand is allowed.
2.2.2. Cluster of Cooperative Thread Arrays
Cluster is a group of CTAs that run concurrently or in parallel and can synchronize and communicate with each other via shared memory. The executing CTA has to make sure that the shared memory of the peer CTA exists before communicating with it via shared memory.
Threads within the different CTAs in a cluster can synchronize and communicate with each other via
shared memory. Cluster-wide barriers can be used to synchronize all the threads within the
cluster. Each CTA in a cluster has a unique CTA identifier within its cluster
(cluster_ctaid). Each cluster of CTAs has 1D, 2D or 3D shape specified by the parameter
cluster_nctaid. Each CTA in the cluster also has a unique CTA identifier (cluster_ctarank)
across all dimensions. The total number of CTAs across all the dimensions in the cluster is
specified by cluster_nctarank. Threads may read and use these values through predefined, read-only
special registers %cluster_ctaid, %cluster_nctaid, %cluster_ctarank,
%cluster_nctarank.
Cluster level is applicable only on target architecture sm_90 or higher. Specifying cluster
level during launch time is optional. If the user specifies the cluster dimensions at launch time
then it will be treated as explicit cluster launch, otherwise it will be treated as implicit cluster
launch with default dimension 1x1x1. PTX provides read-only special register
%is_explicit_cluster to differentiate between explicit and implicit cluster launch.
2.2.3. Grid of Clusters
There is a maximum number of threads that a CTA can contain and a maximum number of CTAs that a cluster can contain. However, clusters with CTAs that execute the same kernel can be batched together into a grid of clusters, so that the total number of threads that can be launched in a single kernel invocation is very large. This comes at the expense of reduced thread communication and synchronization, because threads in different clusters cannot communicate and synchronize with each other.
Each cluster has a unique cluster identifier (clusterid) within a grid of clusters. Each grid of
clusters has a 1D, 2D , or 3D shape specified by the parameter nclusterid. Each grid also has a
unique temporal grid identifier (gridid). Threads may read and use these values through
predefined, read-only special registers %tid, %ntid, %clusterid, %nclusterid, and
%gridid.
Each CTA has a unique identifier (ctaid) within a grid. Each grid of CTAs has 1D, 2D, or 3D shape
specified by the parameter nctaid. Thread may use and read these values through predefined,
read-only special registers %ctaid and %nctaid.
Each kernel is executed as a batch of threads organized as a grid of clusters consisting of CTAs
where cluster is optional level and is applicable only for target architectures sm_90 and
higher. Figure 1 shows a grid consisting of CTAs and
Figure 2 shows a grid consisting of clusters.
Grids may be launched with dependencies between one another - a grid may be a dependent grid and/or a prerequisite grid. To understand how grid dependencies may be defined, refer to the section on CUDA Graphs in the Cuda Programming Guide.
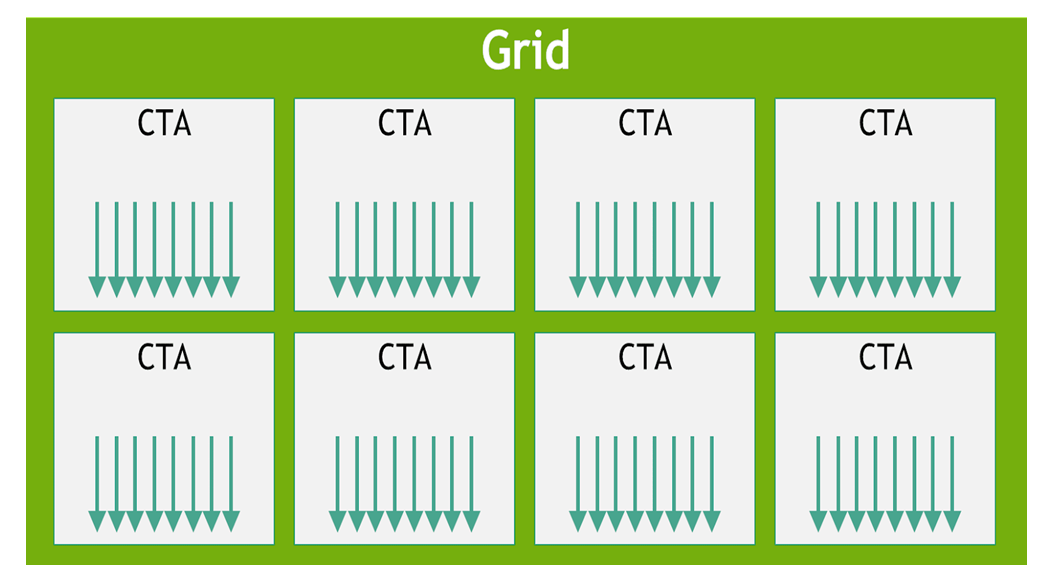
Figure 1 Grid with CTAs
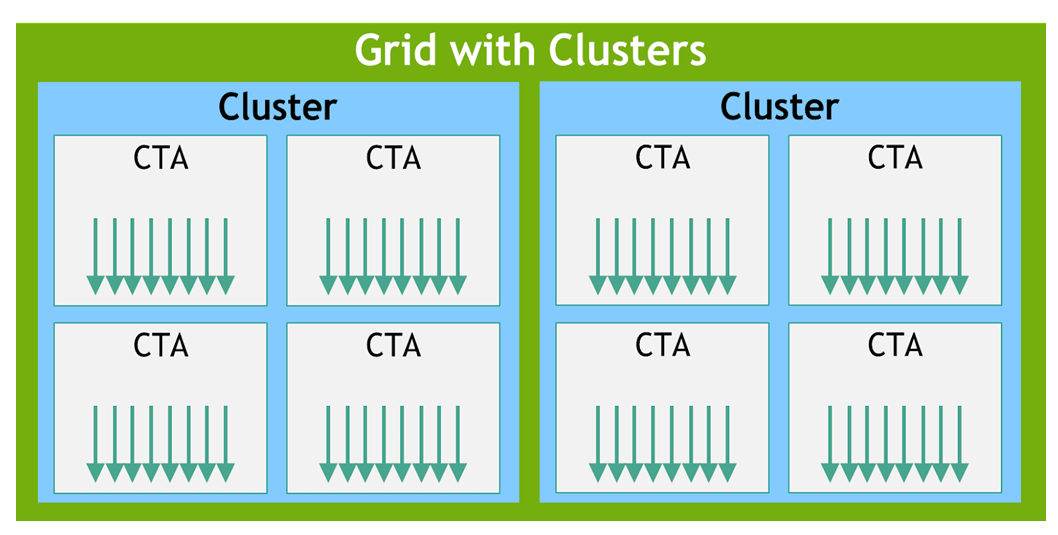
Figure 2 Grid with clusters
A cluster is a set of cooperative thread arrays (CTAs) where a CTA is a set of concurrent threads that execute the same kernel program. A grid is a set of clusters consisting of CTAs that execute independently.
2.3. Memory Hierarchy
PTX threads may access data from multiple state spaces during their execution as illustrated by
Figure 3 where cluster level is introduced from
target architecture sm_90 onwards. Each thread has a private local memory. Each thread block
(CTA) has a shared memory visible to all threads of the block and to all active blocks in the
cluster and with the same lifetime as the block. Finally, all threads have access to the same global
memory.
There are additional state spaces accessible by all threads: the constant, param, texture, and surface state spaces. Constant and texture memory are read-only; surface memory is readable and writable. The global, constant, param, texture, and surface state spaces are optimized for different memory usages. For example, texture memory offers different addressing modes as well as data filtering for specific data formats. Note that texture and surface memory is cached, and within the same kernel call, the cache is not kept coherent with respect to global memory writes and surface memory writes, so any texture fetch or surface read to an address that has been written to via a global or a surface write in the same kernel call returns undefined data. In other words, a thread can safely read some texture or surface memory location only if this memory location has been updated by a previous kernel call or memory copy, but not if it has been previously updated by the same thread or another thread from the same kernel call.
The global, constant, and texture state spaces are persistent across kernel launches by the same application.
Both the host and the device maintain their own local memory, referred to as host memory and device memory, respectively. The device memory may be mapped and read or written by the host, or, for more efficient transfer, copied from the host memory through optimized API calls that utilize the device’s high-performance Direct Memory Access (DMA) engine.
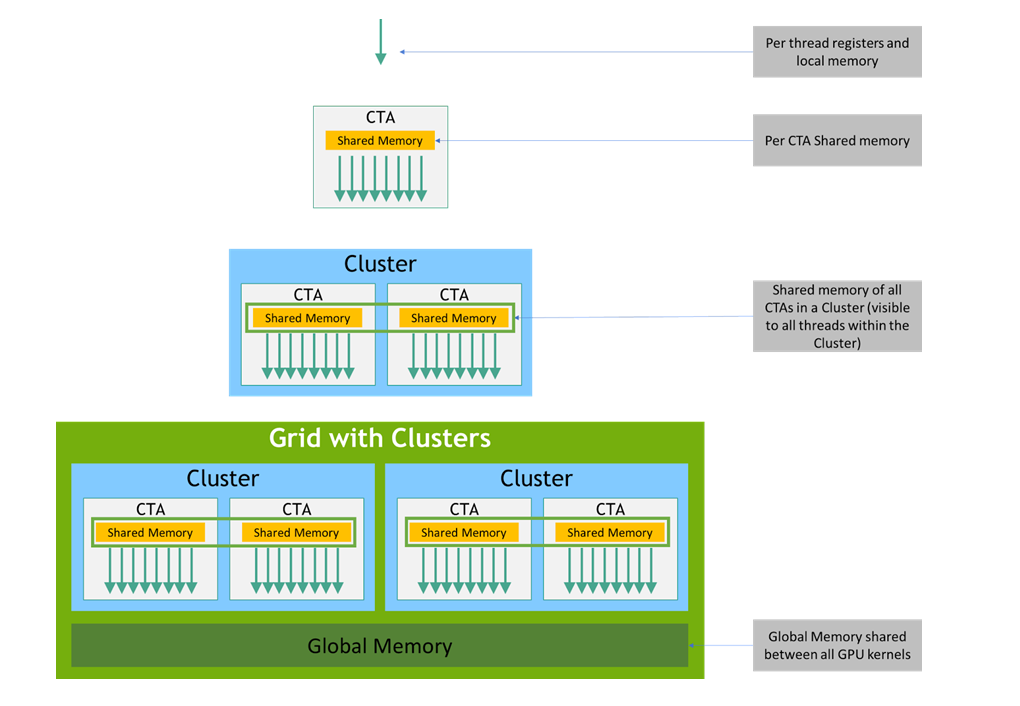
Figure 3 Memory Hierarchy
3. PTX Machine Model
3.1. A Set of SIMT Multiprocessors
The NVIDIA GPU architecture is built around a scalable array of multithreaded Streaming Multiprocessors (SMs). When a host program invokes a kernel grid, the blocks of the grid are enumerated and distributed to multiprocessors with available execution capacity. The threads of a thread block execute concurrently on one multiprocessor. As thread blocks terminate, new blocks are launched on the vacated multiprocessors.
A multiprocessor consists of multiple Scalar Processor (SP) cores, a multithreaded instruction unit, and on-chip shared memory. The multiprocessor creates, manages, and executes concurrent threads in hardware with zero scheduling overhead. It implements a single-instruction barrier synchronization. Fast barrier synchronization together with lightweight thread creation and zero-overhead thread scheduling efficiently support very fine-grained parallelism, allowing, for example, a low granularity decomposition of problems by assigning one thread to each data element (such as a pixel in an image, a voxel in a volume, a cell in a grid-based computation).
To manage hundreds of threads running several different programs, the multiprocessor employs an architecture we call SIMT (single-instruction, multiple-thread). The multiprocessor maps each thread to one scalar processor core, and each scalar thread executes independently with its own instruction address and register state. The multiprocessor SIMT unit creates, manages, schedules, and executes threads in groups of parallel threads called warps. (This term originates from weaving, the first parallel thread technology.) Individual threads composing a SIMT warp start together at the same program address but are otherwise free to branch and execute independently.
When a multiprocessor is given one or more thread blocks to execute, it splits them into warps that get scheduled by the SIMT unit. The way a block is split into warps is always the same; each warp contains threads of consecutive, increasing thread IDs with the first warp containing thread 0.
At every instruction issue time, the SIMT unit selects a warp that is ready to execute and issues the next instruction to the active threads of the warp. A warp executes one common instruction at a time, so full efficiency is realized when all threads of a warp agree on their execution path. If threads of a warp diverge via a data-dependent conditional branch, the warp serially executes each branch path taken, disabling threads that are not on that path, and when all paths complete, the threads converge back to the same execution path. Branch divergence occurs only within a warp; different warps execute independently regardless of whether they are executing common or disjointed code paths.
SIMT architecture is akin to SIMD (Single Instruction, Multiple Data) vector organizations in that a single instruction controls multiple processing elements. A key difference is that SIMD vector organizations expose the SIMD width to the software, whereas SIMT instructions specify the execution and branching behavior of a single thread. In contrast with SIMD vector machines, SIMT enables programmers to write thread-level parallel code for independent, scalar threads, as well as data-parallel code for coordinated threads. For the purposes of correctness, the programmer can essentially ignore the SIMT behavior; however, substantial performance improvements can be realized by taking care that the code seldom requires threads in a warp to diverge. In practice, this is analogous to the role of cache lines in traditional code: Cache line size can be safely ignored when designing for correctness but must be considered in the code structure when designing for peak performance. Vector architectures, on the other hand, require the software to coalesce loads into vectors and manage divergence manually.
How many blocks a multiprocessor can process at once depends on how many registers per thread and how much shared memory per block are required for a given kernel since the multiprocessor’s registers and shared memory are split among all the threads of the batch of blocks. If there are not enough registers or shared memory available per multiprocessor to process at least one block, the kernel will fail to launch.
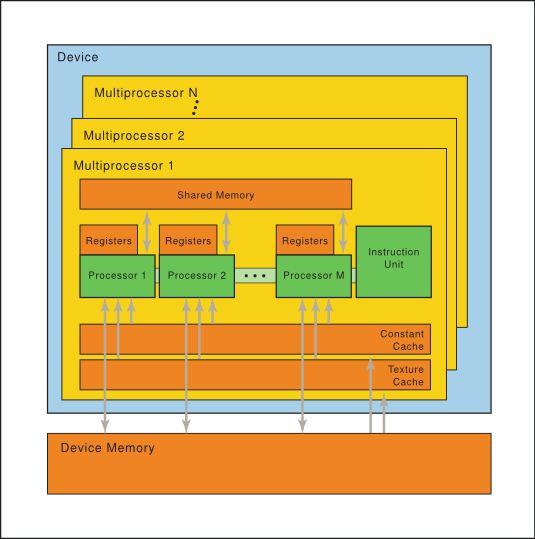
Figure 4 Hardware Model
A set of SIMT multiprocessors with on-chip shared memory.
3.2. Independent Thread Scheduling
On architectures prior to Volta, warps used a single program counter shared amongst all 32 threads in the warp together with an active mask specifying the active threads of the warp. As a result, threads from the same warp in divergent regions or different states of execution cannot signal each other or exchange data, and algorithms requiring fine-grained sharing of data guarded by locks or mutexes can easily lead to deadlock, depending on which warp the contending threads come from.
Starting with the Volta architecture, Independent Thread Scheduling allows full concurrency between threads, regardless of warp. With Independent Thread Scheduling, the GPU maintains execution state per thread, including a program counter and call stack, and can yield execution at a per-thread granularity, either to make better use of execution resources or to allow one thread to wait for data to be produced by another. A schedule optimizer determines how to group active threads from the same warp together into SIMT units. This retains the high throughput of SIMT execution as in prior NVIDIA GPUs, but with much more flexibility: threads can now diverge and reconverge at sub-warp granularity.
Independent Thread Scheduling can lead to a rather different set of threads participating in the executed code than intended if the developer made assumptions about warp-synchronicity of previous hardware architectures. In particular, any warp-synchronous code (such as synchronization-free, intra-warp reductions) should be revisited to ensure compatibility with Volta and beyond. See the section on Compute Capability 7.x in the Cuda Programming Guide for further details.
4. Syntax
PTX programs are a collection of text source modules (files). PTX source modules have an assembly-language style syntax with instruction operation codes and operands. Pseudo-operations specify symbol and addressing management. The ptxas optimizing backend compiler optimizes and assembles PTX source modules to produce corresponding binary object files.
4.1. Source Format
Source modules are ASCII text. Lines are separated by the newline character (\n).
All whitespace characters are equivalent; whitespace is ignored except for its use in separating tokens in the language.
The C preprocessor cpp may be used to process PTX source modules. Lines beginning with # are
preprocessor directives. The following are common preprocessor directives:
#include, #define, #if, #ifdef, #else, #endif, #line, #file
C: A Reference Manual by Harbison and Steele provides a good description of the C preprocessor.
PTX is case sensitive and uses lowercase for keywords.
Each PTX module must begin with a .version directive specifying the PTX language version,
followed by a .target directive specifying the target architecture assumed. See PTX Module
Directives for a more information on these directives.
4.3. Statements
A PTX statement is either a directive or an instruction. Statements begin with an optional label and end with a semicolon.
Examples
.reg .b32 r1, r2;
.global .f32 array[N];
start: mov.b32 r1, %tid.x;
shl.b32 r1, r1, 2; // shift thread id by 2 bits
ld.global.b32 r2, array[r1]; // thread[tid] gets array[tid]
add.f32 r2, r2, 0.5; // add 1/2
4.3.1. Directive Statements
Directive keywords begin with a dot, so no conflict is possible with user-defined identifiers. The directives in PTX are listed in Table 1 and described in State Spaces, Types, and Variables and Directives.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3.2. Instruction Statements
Instructions are formed from an instruction opcode followed by a comma-separated list of zero or
more operands, and terminated with a semicolon. Operands may be register variables, constant
expressions, address expressions, or label names. Instructions have an optional guard predicate
which controls conditional execution. The guard predicate follows the optional label and precedes
the opcode, and is written as @p, where p is a predicate register. The guard predicate may
be optionally negated, written as @!p.
The destination operand is first, followed by source operands.
Instruction keywords are listed in Table 2. All instruction keywords are reserved tokens in PTX.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4. Identifiers
User-defined identifiers follow extended C++ rules: they either start with a letter followed by zero or more letters, digits, underscore, or dollar characters; or they start with an underscore, dollar, or percentage character followed by one or more letters, digits, underscore, or dollar characters:
followsym: [a-zA-Z0-9_$]
identifier: [a-zA-Z]{followsym}* | {[_$%]{followsym}+
PTX does not specify a maximum length for identifiers and suggests that all implementations support a minimum length of at least 1024 characters.
Many high-level languages such as C and C++ follow similar rules for identifier names, except that the percentage sign is not allowed. PTX allows the percentage sign as the first character of an identifier. The percentage sign can be used to avoid name conflicts, e.g., between user-defined variable names and compiler-generated names.
PTX predefines one constant and a small number of special registers that begin with the percentage sign, listed in Table 3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5. Constants
PTX supports integer and floating-point constants and constant expressions. These constants may be
used in data initialization and as operands to instructions. Type checking rules remain the same for
integer, floating-point, and bit-size types. For predicate-type data and instructions, integer
constants are allowed and are interpreted as in C, i.e., zero values are False and non-zero
values are True.
4.5.1. Integer Constants
Integer constants are 64-bits in size and are either signed or unsigned, i.e., every integer
constant has type .s64 or .u64. The signed/unsigned nature of an integer constant is needed
to correctly evaluate constant expressions containing operations such as division and ordered
comparisons, where the behavior of the operation depends on the operand types. When used in an
instruction or data initialization, each integer constant is converted to the appropriate size based
on the data or instruction type at its use.
Integer literals may be written in decimal, hexadecimal, octal, or binary notation. The syntax
follows that of C. Integer literals may be followed immediately by the letter U to indicate that
the literal is unsigned.
hexadecimal literal: 0[xX]{hexdigit}+U?
octal literal: 0{octal digit}+U?
binary literal: 0[bB]{bit}+U?
decimal literal {nonzero-digit}{digit}*U?
Integer literals are non-negative and have a type determined by their magnitude and optional type
suffix as follows: literals are signed (.s64) unless the value cannot be fully represented in
.s64 or the unsigned suffix is specified, in which case the literal is unsigned (.u64).
The predefined integer constant WARP_SZ specifies the number of threads per warp for the target
platform; to date, all target architectures have a WARP_SZ value of 32.
4.5.2. Floating-Point Constants
Floating-point constants are represented as 64-bit double-precision values, and all floating-point constant expressions are evaluated using 64-bit double precision arithmetic. The only exception is the 32-bit hex notation for expressing an exact single-precision floating-point value; such values retain their exact 32-bit single-precision value and may not be used in constant expressions. Each 64-bit floating-point constant is converted to the appropriate floating-point size based on the data or instruction type at its use.
Floating-point literals may be written with an optional decimal point and an optional signed exponent. Unlike C and C++, there is no suffix letter to specify size; literals are always represented in 64-bit double-precision format.
PTX includes a second representation of floating-point constants for specifying the exact machine
representation using a hexadecimal constant. To specify IEEE 754 double-precision floating point
values, the constant begins with 0d or 0D followed by 16 hex digits. To specify IEEE 754
single-precision floating point values, the constant begins with 0f or 0F followed by 8 hex
digits.
0[fF]{hexdigit}{8} // single-precision floating point
0[dD]{hexdigit}{16} // double-precision floating point
Example
mov.f32 $f3, 0F3f800000; // 1.0
4.5.3. Predicate Constants
In PTX, integer constants may be used as predicates. For predicate-type data initializers and
instruction operands, integer constants are interpreted as in C, i.e., zero values are False and
non-zero values are True.
4.5.4. Constant Expressions
In PTX, constant expressions are formed using operators as in C and are evaluated using rules similar to those in C, but simplified by restricting types and sizes, removing most casts, and defining full semantics to eliminate cases where expression evaluation in C is implementation dependent.
Constant expressions are formed from constant literals, unary plus and minus, basic arithmetic
operators (addition, subtraction, multiplication, division), comparison operators, the conditional
ternary operator ( ?: ), and parentheses. Integer constant expressions also allow unary logical
negation (!), bitwise complement (~), remainder (%), shift operators (<< and
>>), bit-type operators (&, |, and ^), and logical operators (&&, ||).
Constant expressions in PTX do not support casts between integer and floating-point.
Constant expressions are evaluated using the same operator precedence as in C. Table 4 gives operator precedence and associativity. Operator precedence is highest for unary operators and decreases with each line in the chart. Operators on the same line have the same precedence and are evaluated right-to-left for unary operators and left-to-right for binary operators.
Kind |
Operator Symbols |
Operator Names |
Associates |
|---|---|---|---|
Primary |
|
parenthesis |
n/a |
Unary |
|
plus, minus, negation, complement |
right |
|
casts |
right |
|
Binary |
|
multiplication, division, remainder |
left |
|
addition, subtraction |
||
|
shifts |
||
|
ordered comparisons |
||
|
equal, not equal |
||
|
bitwise AND |
||
|
bitwise XOR |
||
|
bitwise OR |
||
|
logical AND |
||
|
logical OR |
||
Ternary |
|
conditional |
right |
4.5.5. Integer Constant Expression Evaluation
Integer constant expressions are evaluated at compile time according to a set of rules that
determine the type (signed .s64 versus unsigned .u64) of each sub-expression. These rules
are based on the rules in C, but they’ve been simplified to apply only to 64-bit integers, and
behavior is fully defined in all cases (specifically, for remainder and shift operators).
Literals are signed unless unsigned is needed to prevent overflow, or unless the literal uses a
Usuffix. For example:42,0x1234,0123are signed.0xfabc123400000000,42U,0x1234Uare unsigned.
Unary plus and minus preserve the type of the input operand. For example:
+123,-1,-(-42)are signed.-1U,-0xfabc123400000000are unsigned.
Unary logical negation (
!) produces a signed result with value0or1.Unary bitwise complement (
~) interprets the source operand as unsigned and produces an unsigned result.Some binary operators require normalization of source operands. This normalization is known as the usual arithmetic conversions and simply converts both operands to unsigned type if either operand is unsigned.
Addition, subtraction, multiplication, and division perform the usual arithmetic conversions and produce a result with the same type as the converted operands. That is, the operands and result are unsigned if either source operand is unsigned, and is otherwise signed.
Remainder (
%) interprets the operands as unsigned. Note that this differs from C, which allows a negative divisor but defines the behavior to be implementation dependent.Left and right shift interpret the second operand as unsigned and produce a result with the same type as the first operand. Note that the behavior of right-shift is determined by the type of the first operand: right shift of a signed value is arithmetic and preserves the sign, and right shift of an unsigned value is logical and shifts in a zero bit.
AND (
&), OR (|), and XOR (^) perform the usual arithmetic conversions and produce a result with the same type as the converted operands.AND_OP (
&&), OR_OP (||), Equal (==), and Not_Equal (!=) produce a signed result. The result value is 0 or 1.Ordered comparisons (
<,<=,>,>=) perform the usual arithmetic conversions on source operands and produce a signed result. The result value is0or1.Casting of expressions to signed or unsigned is supported using (
.s64) and (.u64) casts.For the conditional operator (
? :) , the first operand must be an integer, and the second and third operands are either both integers or both floating-point. The usual arithmetic conversions are performed on the second and third operands, and the result type is the same as the converted type.
4.5.6. Summary of Constant Expression Evaluation Rules
Table 5 contains a summary of the constant expression evaluation rules.
Kind |
Operator |
Operand Types |
Operand Interpretation |
Result Type |
|---|---|---|---|---|
Primary |
|
any type |
same as source |
same as source |
constant literal |
n/a |
n/a |
|
|
Unary |
|
any type |
same as source |
same as source |
|
integer |
zero or non-zero |
|
|
|
integer |
|
|
|
Cast |
|
integer |
|
|
|
integer |
|
|
|
Binary |
|
|
|
|
integer |
use usual conversions |
converted type |
||
|
|
|
|
|
integer |
use usual conversions |
|
||
|
|
|
|
|
integer |
use usual conversions |
|
||
|
integer |
|
|
|
|
integer |
1st unchanged, 2nd is |
same as 1st operand |
|
|
integer |
|
|
|
|
integer |
zero or non-zero |
|
|
Ternary |
|
|
same as sources |
|
|
use usual conversions |
converted type |
5. State Spaces, Types, and Variables
While the specific resources available in a given target GPU will vary, the kinds of resources will be common across platforms, and these resources are abstracted in PTX through state spaces and data types.
5.1. State Spaces
A state space is a storage area with particular characteristics. All variables reside in some state space. The characteristics of a state space include its size, addressability, access speed, access rights, and level of sharing between threads.
The state spaces defined in PTX are a byproduct of parallel programming and graphics programming. The list of state spaces is shown in Table 6,and properties of state spaces are shown in Table 7.
Name |
Description |
|---|---|
|
Registers, fast. |
|
Special registers. Read-only; pre-defined; platform-specific. |
|
Shared, read-only memory. |
|
Global memory, shared by all threads. |
|
Local memory, private to each thread. |
|
Kernel parameters, defined per-grid; or Function or local parameters, defined per-thread. |
|
Addressable memory, defined per CTA, accessible to all threads in the cluster throughout the lifetime of the CTA that defines it. |
|
Global texture memory (deprecated). |
Name |
Addressable |
Initializable |
Access |
Sharing |
|---|---|---|---|---|
|
No |
No |
R/W |
per-thread |
|
No |
No |
RO |
per-CTA |
|
Yes |
Yes1 |
RO |
per-grid |
|
Yes |
Yes1 |
R/W |
Context |
|
Yes |
No |
R/W |
per-thread |
|
Yes2 |
No |
RO |
per-grid |
|
Restricted3 |
No |
R/W |
per-thread |
|
Yes |
No |
R/W |
per-cluster5 |
|
No4 |
Yes, via driver |
RO |
Context |
Notes: 1 Variables in 2 Accessible only via the 3 Accessible via 4 Accessible only via the 5 Visible to the owning CTA and other active CTAs in the cluster. |
||||
5.1.1. Register State Space
Registers (.reg state space) are fast storage locations. The number of registers is limited, and
will vary from platform to platform. When the limit is exceeded, register variables will be spilled
to memory, causing changes in performance. For each architecture, there is a recommended maximum
number of registers to use (see the CUDA Programming Guide for details).
Registers may be typed (signed integer, unsigned integer, floating point, predicate) or
untyped. Register size is restricted; aside from predicate registers which are 1-bit, scalar
registers have a width of 8-, 16-, 32-, or 64-bits, and vector registers have a width of 16-, 32-,
64-, or 128-bits. The most common use of 8-bit registers is with ld, st, and cvt
instructions, or as elements of vector tuples.
Registers differ from the other state spaces in that they are not fully addressable, i.e., it is not
possible to refer to the address of a register. When compiling to use the Application Binary
Interface (ABI), register variables are restricted to function scope and may not be declared at
module scope. When compiling legacy PTX code (ISA versions prior to 3.0) containing module-scoped
.reg variables, the compiler silently disables use of the ABI. Registers may have alignment
boundaries required by multi-word loads and stores.
5.1.2. Special Register State Space
The special register (.sreg) state space holds predefined, platform-specific registers, such as
grid, cluster, CTA, and thread parameters, clock counters, and performance monitoring registers. All
special registers are predefined.
5.1.3. Constant State Space
The constant (.const) state space is a read-only memory initialized by the host. Constant memory
is accessed with a ld.const instruction. Constant memory is restricted in size, currently
limited to 64 KB which can be used to hold statically-sized constant variables. There is an
additional 640 KB of constant memory, organized as ten independent 64 KB regions. The driver may
allocate and initialize constant buffers in these regions and pass pointers to the buffers as kernel
function parameters. Since the ten regions are not contiguous, the driver must ensure that constant
buffers are allocated so that each buffer fits entirely within a 64 KB region and does not span a
region boundary.
Statically-sized constant variables have an optional variable initializer; constant variables with no explicit initializer are initialized to zero by default. Constant buffers allocated by the driver are initialized by the host, and pointers to such buffers are passed to the kernel as parameters. See the description of kernel parameter attributes in Kernel Function Parameter Attributes for more details on passing pointers to constant buffers as kernel parameters.
5.1.3.1. Banked Constant State Space (deprecated)
Previous versions of PTX exposed constant memory as a set of eleven 64 KB banks, with explicit bank numbers required for variable declaration and during access.
Prior to PTX ISA version 2.2, the constant memory was organized into fixed size banks. There were
eleven 64 KB banks, and banks were specified using the .const[bank] modifier, where bank
ranged from 0 to 10. If no bank number was given, bank zero was assumed.
By convention, bank zero was used for all statically-sized constant variables. The remaining banks were used to declare incomplete constant arrays (as in C, for example), where the size is not known at compile time. For example, the declaration
.extern .const[2] .b32 const_buffer[];
resulted in const_buffer pointing to the start of constant bank two. This pointer could then be
used to access the entire 64 KB constant bank. Multiple incomplete array variables declared in the
same bank were aliased, with each pointing to the start address of the specified constant bank.
To access data in contant banks 1 through 10, the bank number was required in the state space of the load instruction. For example, an incomplete array in bank 2 was accessed as follows:
.extern .const[2] .b32 const_buffer[];
ld.const[2].b32 %r1, [const_buffer+4]; // load second word
In PTX ISA version 2.2, we eliminated explicit banks and replaced the incomplete array representation of driver-allocated constant buffers with kernel parameter attributes that allow pointers to constant buffers to be passed as kernel parameters.
5.1.4. Global State Space
The global (.global) state space is memory that is accessible by all threads in a context. It is
the mechanism by which threads in different CTAs, clusters, and grids can communicate. Use
ld.global, st.global, and atom.global to access global variables.
Global variables have an optional variable initializer; global variables with no explicit initializer are initialized to zero by default.
5.1.5. Local State Space
The local state space (.local) is private memory for each thread to keep its own data. It is
typically standard memory with cache. The size is limited, as it must be allocated on a per-thread
basis. Use ld.local and st.local to access local variables.
When compiling to use the Application Binary Interface (ABI), .local state-space variables
must be declared within function scope and are allocated on the stack. In implementations that do
not support a stack, all local memory variables are stored at fixed addresses, recursive function
calls are not supported, and .local variables may be declared at module scope. When compiling
legacy PTX code (ISA versions prior to 3.0) containing module-scoped .local variables, the
compiler silently disables use of the ABI.
5.1.6. Parameter State Space
The parameter (.param) state space is used (1) to pass input arguments from the host to the
kernel, (2a) to declare formal input and return parameters for device functions called from within
kernel execution, and (2b) to declare locally-scoped byte array variables that serve as function
call arguments, typically for passing large structures by value to a function. Kernel function
parameters differ from device function parameters in terms of access and sharing (read-only versus
read-write, per-kernel versus per-thread). Note that PTX ISA versions 1.x supports only kernel
function parameters in .param space; device function parameters were previously restricted to the
register state space. The use of parameter state space for device function parameters was introduced
in PTX ISA version 2.0 and requires target architecture sm_20 or higher. Additional sub-qualifiers
::entry or ::func can be specified on instructions with .param state space to indicate
whether the address refers to kernel function parameter or device function parameter. If no
sub-qualifier is specified with the .param state space, then the default sub-qualifier is specific
to and dependent on the exact instruction. For example, st.param is equivalent to st.param::func
whereas isspacep.param is equivalent to isspacep.param::entry. Refer to the instruction
description for more details on default sub-qualifier assumption.
Note
The location of parameter space is implementation specific. For example, in some implementations
kernel parameters reside in global memory. No access protection is provided between parameter and
global space in this case. Though the exact location of the kernel parameter space is
implementation specific, the kernel parameter space window is always contained within the global
space window. Similarly, function parameters are mapped to parameter passing registers and/or
stack locations based on the function calling conventions of the Application Binary Interface
(ABI). Therefore, PTX code should make no assumptions about the relative locations or ordering
of .param space variables.
5.1.6.1. Kernel Function Parameters
Each kernel function definition includes an optional list of parameters. These parameters are
addressable, read-only variables declared in the .param state space. Values passed from the host
to the kernel are accessed through these parameter variables using ld.param instructions. The
kernel parameter variables are shared across all CTAs from all clusters within a grid.
The address of a kernel parameter may be moved into a register using the mov instruction. The
resulting address is in the .param state space and is accessed using ld.param instructions.
Example
.entry foo ( .param .b32 N, .param .align 8 .b8 buffer[64] )
{
.reg .u32 %n;
.reg .f64 %d;
ld.param.u32 %n, [N];
ld.param.f64 %d, [buffer];
...
Example
.entry bar ( .param .b32 len )
{
.reg .u32 %ptr, %n;
mov.u32 %ptr, len;
ld.param.u32 %n, [%ptr];
...
Kernel function parameters may represent normal data values, or they may hold addresses to objects in constant, global, local, or shared state spaces. In the case of pointers, the compiler and runtime system need information about which parameters are pointers, and to which state space they point. Kernel parameter attribute directives are used to provide this information at the PTX level. See Kernel Function Parameter Attributes for a description of kernel parameter attribute directives.
Note
The current implementation does not allow creation of generic pointers to constant variables
(cvta.const) in programs that have pointers to constant buffers passed as kernel parameters.
5.1.6.2. Kernel Function Parameter Attributes
Kernel function parameters may be declared with an optional .ptr attribute to indicate that a
parameter is a pointer to memory, and also indicate the state space and alignment of the memory
being pointed to. Kernel Parameter Attribute: .ptr
describes the .ptr kernel parameter attribute.
5.1.6.3. Kernel Parameter Attribute: .ptr
.ptr
Kernel parameter alignment attribute.
Syntax
.param .type .ptr .space .align N varname
.param .type .ptr .align N varname
.space = { .const, .global, .local, .shared };
Description
Used to specify the state space and, optionally, the alignment of memory pointed to by a pointer type kernel parameter. The alignment value N, if present, must be a power of two. If no state space is specified, the pointer is assumed to be a generic address pointing to one of const, global, local, or shared memory. If no alignment is specified, the memory pointed to is assumed to be aligned to a 4 byte boundary.
Spaces between .ptr, .space, and .align may be eliminated to improve readability.
PTX ISA Notes
Introduced in PTX ISA version 2.2.
Support for generic addressing of .const space added in PTX ISA version 3.1.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo ( .param .u32 param1,
.param .u32 .ptr.global.align 16 param2,
.param .u32 .ptr.const.align 8 param3,
.param .u32 .ptr.align 16 param4 // generic address
// pointer
) { .. }
5.1.6.4. Device Function Parameters
PTX ISA version 2.0 extended the use of parameter space to device function parameters. The most
common use is for passing objects by value that do not fit within a PTX register, such as C
structures larger than 8 bytes. In this case, a byte array in parameter space is used. Typically,
the caller will declare a locally-scoped .param byte array variable that represents a flattened
C structure or union. This will be passed by value to a callee, which declares a .param formal
parameter having the same size and alignment as the passed argument.
Example
// pass object of type struct { double d; int y; };
.func foo ( .reg .b32 N, .param .align 8 .b8 buffer[12] )
{
.reg .f64 %d;
.reg .s32 %y;
ld.param.f64 %d, [buffer];
ld.param.s32 %y, [buffer+8];
...
}
// code snippet from the caller
// struct { double d; int y; } mystruct; is flattened, passed to foo
...
.reg .f64 dbl;
.reg .s32 x;
.param .align 8 .b8 mystruct;
...
st.param.f64 [mystruct+0], dbl;
st.param.s32 [mystruct+8], x;
call foo, (4, mystruct);
...
See the section on function call syntax for more details.
Function input parameters may be read via ld.param and function return parameters may be written
using st.param; it is illegal to write to an input parameter or read from a return parameter.
Aside from passing structures by value, .param space is also required whenever a formal
parameter has its address taken within the called function. In PTX, the address of a function input
parameter may be moved into a register using the mov instruction. Note that the parameter will
be copied to the stack if necessary, and so the address will be in the .local state space and is
accessed via ld.local and st.local instructions. It is not possible to use mov to get
the address of or a locally-scoped .param space variable. Starting PTX ISA version 6.0, it is
possible to use mov instruction to get address of return parameter of device function.
Example
// pass array of up to eight floating-point values in buffer
.func foo ( .param .b32 N, .param .b32 buffer[32] )
{
.reg .u32 %n, %r;
.reg .f32 %f;
.reg .pred %p;
ld.param.u32 %n, [N];
mov.u32 %r, buffer; // forces buffer to .local state space
Loop:
setp.eq.u32 %p, %n, 0;
@%p: bra Done;
ld.local.f32 %f, [%r];
...
add.u32 %r, %r, 4;
sub.u32 %n, %n, 1;
bra Loop;
Done:
...
}
5.1.8. Texture State Space (deprecated)
The texture (.tex) state space is global memory accessed via the texture instruction. It is
shared by all threads in a context. Texture memory is read-only and cached, so accesses to texture
memory are not coherent with global memory stores to the texture image.
The GPU hardware has a fixed number of texture bindings that can be accessed within a single kernel
(typically 128). The .tex directive will bind the named texture memory variable to a hardware
texture identifier, where texture identifiers are allocated sequentially beginning with
zero. Multiple names may be bound to the same physical texture identifier. An error is generated if
the maximum number of physical resources is exceeded. The texture name must be of type .u32 or
.u64.
Physical texture resources are allocated on a per-kernel granularity, and .tex variables are
required to be defined in the global scope.
Texture memory is read-only. A texture’s base address is assumed to be aligned to a 16 byte boundary.
Example
.tex .u32 tex_a; // bound to physical texture 0
.tex .u32 tex_c, tex_d; // both bound to physical texture 1
.tex .u32 tex_d; // bound to physical texture 2
.tex .u32 tex_f; // bound to physical texture 3
Note
Explicit declarations of variables in the texture state space is deprecated, and programs should
instead reference texture memory through variables of type .texref. The .tex directive is
retained for backward compatibility, and variables declared in the .tex state space are
equivalent to module-scoped .texref variables in the .global state space.
For example, a legacy PTX definitions such as
.tex .u32 tex_a;
is equivalent to:
.global .texref tex_a;
See Texture Sampler and Surface Types for the
description of the .texref type and Texture Instructions
for its use in texture instructions.
5.2. Types
5.2.1. Fundamental Types
In PTX, the fundamental types reflect the native data types supported by the target architectures. A fundamental type specifies both a basic type and a size. Register variables are always of a fundamental type, and instructions operate on these types. The same type-size specifiers are used for both variable definitions and for typing instructions, so their names are intentionally short.
Table 8 lists the fundamental type specifiers for each basic type:
Basic Type |
Fundamental Type Specifiers |
|---|---|
Signed integer |
|
Unsigned integer |
|
Floating-point |
|
Bits (untyped) |
|
Predicate |
|
Most instructions have one or more type specifiers, needed to fully specify instruction behavior. Operand types and sizes are checked against instruction types for compatibility.
Two fundamental types are compatible if they have the same basic type and are the same size. Signed and unsigned integer types are compatible if they have the same size. The bit-size type is compatible with any fundamental type having the same size.
In principle, all variables (aside from predicates) could be declared using only bit-size types, but typed variables enhance program readability and allow for better operand type checking.
5.2.2. Restricted Use of Sub-Word Sizes
The .u8, .s8, and .b8 instruction types are restricted to ld, st, and cvt
instructions. The .f16 floating-point type is allowed only in conversions to and from .f32,
.f64 types, in half precision floating point instructions and texture fetch instructions. The
.f16x2 floating point type is allowed only in half precision floating point arithmetic
instructions and texture fetch instructions.
For convenience, ld, st, and cvt instructions permit source and destination data
operands to be wider than the instruction-type size, so that narrow values may be loaded, stored,
and converted using regular-width registers. For example, 8-bit or 16-bit values may be held
directly in 32-bit or 64-bit registers when being loaded, stored, or converted to other types and
sizes.
5.2.3. Alternate Floating-Point Data Formats
The fundamental floating-point types supported in PTX have implicit bit representations that
indicate the number of bits used to store exponent and mantissa. For example, the .f16 type
indicates 5 bits reserved for exponent and 10 bits reserved for mantissa. In addition to the
floating-point representations assumed by the fundamental types, PTX allows the following alternate
floating-point data formats:
bf16data format:This data format is a 16-bit floating point format with 8 bits for exponent and 7 bits for mantissa. A register variable containing
bf16data must be declared with.b16type.e4m3data format:This data format is an 8-bit floating point format with 4 bits for exponent and 3 bits for mantissa. The
e4m3encoding does not support infinity andNaNvalues are limited to0x7fand0xff. A register variable containinge4m3value must be declared using bit-size type.e5m2data format:This data format is an 8-bit floating point format with 5 bits for exponent and 2 bits for mantissa. A register variable containing
e5m2value must be declared using bit-size type.tf32data format:This data format is a special 32-bit floating point format supported by the matrix multiply-and-accumulate instructions, with the same range as
.f32and reduced precision (>=10 bits). The internal layout oftf32format is implementation defined. PTX facilitates conversion from single precision.f32type totf32format. A register variable containingtf32data must be declared with.b32type.
Alternate data formats cannot be used as fundamental types. They are supported as source or destination formats by certain instructions.
5.2.4. Packed Data Types
Certain PTX instructions operate on two sets of inputs in parallel, and produce two outputs. Such instructions can use the data stored in a packed format. PTX supports packing two values of the same scalar data type into a single, larger value. The packed value is considered as a value of a packed data type. In this section we describe the packed data types supported in PTX.
5.2.4.1. Packed Floating Point Data Types
PTX supports the following four variants of packed floating point data types:
.f16x2packed type containing two.f16floating point values..bf16x2packed type containing two.bf16alternate floating point values..e4m3x2packed type containing two.e4m3alternate floating point values..e5m2x2packed type containing two.e5m2alternate floating point values.
.f16x2 is supported as a fundamental type. .bf16x2, .e4m3x2 and .e5m2x2 cannot be
used as fundamental types - they are supported as instruction types on certain instructions. A
register variable containing .bf16x2 data must be declared with .b32 type. A register
variable containing .e4m3x2 or .e5m2x2 data must be declared with .b16 type.
5.2.4.2. Packed Integer Data Types
PTX supports two variants of packed integer data types: .u16x2 and .s16x2. The packed data
type consists of two .u16 or .s16 values. A register variable containing .u16x2 or
.s16x2 data must be declared with .b32 type. Packed integer data types cannot be used as
fundamental types. They are supported as instruction types on certain instructions.
5.3. Texture Sampler and Surface Types
PTX includes built-in opaque types for defining texture, sampler, and surface descriptor variables. These types have named fields similar to structures, but all information about layout, field ordering, base address, and overall size is hidden to a PTX program, hence the term opaque. The use of these opaque types is limited to:
Variable definition within global (module) scope and in kernel entry parameter lists.
Static initialization of module-scope variables using comma-delimited static assignment expressions for the named members of the type.
Referencing textures, samplers, or surfaces via texture and surface load/store instructions (
tex,suld,sust,sured).Retrieving the value of a named member via query instructions (
txq,suq).Creating pointers to opaque variables using
mov, e.g.,mov.u64 reg, opaque_var;. The resulting pointer may be stored to and loaded from memory, passed as a parameter to functions, and de-referenced by texture and surface load, store, and query instructions, but the pointer cannot otherwise be treated as an address, i.e., accessing the pointer withldandstinstructions, or performing pointer arithmetic will result in undefined results.Opaque variables may not appear in initializers, e.g., to initialize a pointer to an opaque variable.
Note
Indirect access to textures and surfaces using pointers to opaque variables is supported
beginning with PTX ISA version 3.1 and requires target sm_20 or later.
Indirect access to textures is supported only in unified texture mode (see below).
The three built-in types are .texref, .samplerref, and .surfref. For working with
textures and samplers, PTX has two modes of operation. In the unified mode, texture and sampler
information is accessed through a single .texref handle. In the independent mode, texture and
sampler information each have their own handle, allowing them to be defined separately and combined
at the site of usage in the program. In independent mode, the fields of the .texref type that
describe sampler properties are ignored, since these properties are defined by .samplerref
variables.
Table 9 and
Table 10 list the named members
of each type for unified and independent texture modes. These members and their values have
precise mappings to methods and values defined in the texture HW class as well as
exposed values via the API.
Member |
.texref values |
.surfref values |
|---|---|---|
|
in elements |
|
|
in elements |
|
|
in elements |
|
|
|
|
|
|
|
|
|
N/A |
|
|
N/A |
|
|
N/A |
|
as number of textures in a texture array |
as number of surfaces in a surface array |
|
as number of levels in a mipmapped texture |
N/A |
|
as number of samples in a multi-sample texture |
N/A |
|
N/A |
|
5.3.1. Texture and Surface Properties
Fields width, height, and depth specify the size of the texture or surface in number of
elements in each dimension.
The channel_data_type and channel_order fields specify these properties of the texture or
surface using enumeration types corresponding to the source language API. For example, see Channel
Data Type and Channel Order Fields for
the OpenCL enumeration types currently supported in PTX.
5.3.2. Sampler Properties
The normalized_coords field indicates whether the texture or surface uses normalized coordinates
in the range [0.0, 1.0) instead of unnormalized coordinates in the range [0, N). If no value is
specified, the default is set by the runtime system based on the source language.
The filter_mode field specifies how the values returned by texture reads are computed based on
the input texture coordinates.
The addr_mode_{0,1,2} fields define the addressing mode in each dimension, which determine how
out-of-range coordinates are handled.
See the CUDA C++ Programming Guide for more details of these properties.
Member |
.samplerref values |
.texref values |
.surfref values |
|---|---|---|---|
|
N/A |
in elements |
|
|
N/A |
in elements |
|
|
N/A |
in elements |
|
|
N/A |
|
|
|
N/A |
|
|
|
N/A |
|
N/A |
|
|
N/A |
N/A |
|
|
ignored |
N/A |
|
|
N/A |
N/A |
|
N/A |
as number of textures in a texture array |
as number of surfaces in a surface array |
|
N/A |
as number of levels in a mipmapped texture |
N/A |
|
N/A |
as number of samples in a multi-sample texture |
N/A |
|
N/A |
N/A |
|
In independent texture mode, the sampler properties are carried in an independent .samplerref
variable, and these fields are disabled in the .texref variables. One additional sampler
property, force_unnormalized_coords, is available in independent texture mode.
The force_unnormalized_coords field is a property of .samplerref variables that allows the
sampler to override the texture header normalized_coords property. This field is defined only in
independent texture mode. When True, the texture header setting is overridden and unnormalized
coordinates are used; when False, the texture header setting is used.
The force_unnormalized_coords property is used in compiling OpenCL; in OpenCL, the property of
normalized coordinates is carried in sampler headers. To compile OpenCL to PTX, texture headers are
always initialized with normalized_coords set to True, and the OpenCL sampler-based
normalized_coords flag maps (negated) to the PTX-level force_unnormalized_coords flag.
Variables using these types may be declared at module scope or within kernel entry parameter
lists. At module scope, these variables must be in the .global state space. As kernel
parameters, these variables are declared in the .param state space.
Example
.global .texref my_texture_name;
.global .samplerref my_sampler_name;
.global .surfref my_surface_name;
When declared at module scope, the types may be initialized using a list of static expressions assigning values to the named members.
Example
.global .texref tex1;
.global .samplerref tsamp1 = { addr_mode_0 = clamp_to_border,
filter_mode = nearest
};
5.3.3. Channel Data Type and Channel Order Fields
The channel_data_type and channel_order fields have enumeration types corresponding to the
source language API. Currently, OpenCL is the only source language that defines these
fields. Table 12 and
Table 11 show the
enumeration values defined in OpenCL version 1.0 for channel data type and channel order.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.4. Variables
In PTX, a variable declaration describes both the variable’s type and its state space. In addition to fundamental types, PTX supports types for simple aggregate objects such as vectors and arrays.
5.4.1. Variable Declarations
All storage for data is specified with variable declarations. Every variable must reside in one of the state spaces enumerated in the previous section.
A variable declaration names the space in which the variable resides, its type and size, its name, an optional array size, an optional initializer, and an optional fixed address for the variable.
Predicate variables may only be declared in the register state space.
Examples
.global .u32 loc;
.reg .s32 i;
.const .f32 bias[] = {-1.0, 1.0};
.global .u8 bg[4] = {0, 0, 0, 0};
.reg .v4 .f32 accel;
.reg .pred p, q, r;
5.4.2. Vectors
Limited-length vector types are supported. Vectors of length 2 and 4 of any non-predicate
fundamental type can be declared by prefixing the type with .v2 or .v4. Vectors must be
based on a fundamental type, and they may reside in the register space. Vectors cannot exceed
128-bits in length; for example, .v4 .f64 is not allowed. Three-element vectors may be
handled by using a .v4 vector, where the fourth element provides padding. This is a common case
for three-dimensional grids, textures, etc.
Examples
.global .v4 .f32 V; // a length-4 vector of floats
.shared .v2 .u16 uv; // a length-2 vector of unsigned ints
.global .v4 .b8 v; // a length-4 vector of bytes
By default, vector variables are aligned to a multiple of their overall size (vector length times base-type size), to enable vector load and store instructions which require addresses aligned to a multiple of the access size.
5.4.3. Array Declarations
Array declarations are provided to allow the programmer to reserve space. To declare an array, the variable name is followed with dimensional declarations similar to fixed-size array declarations in C. The size of each dimension is a constant expression.
Examples
.local .u16 kernel[19][19];
.shared .u8 mailbox[128];
The size of the array specifies how many elements should be reserved. For the declaration of array kernel above, 19*19 = 361 halfwords are reserved, for a total of 722 bytes.
When declared with an initializer, the first dimension of the array may be omitted. The size of the first array dimension is determined by the number of elements in the array initializer.
Examples
.global .u32 index[] = { 0, 1, 2, 3, 4, 5, 6, 7 };
.global .s32 offset[][2] = { {-1, 0}, {0, -1}, {1, 0}, {0, 1} };
Array index has eight elements, and array offset is a 4x2 array.
5.4.4. Initializers
Declared variables may specify an initial value using a syntax similar to C/C++, where the variable name is followed by an equals sign and the initial value or values for the variable. A scalar takes a single value, while vectors and arrays take nested lists of values inside of curly braces (the nesting matches the dimensionality of the declaration).
As in C, array initializers may be incomplete, i.e., the number of initializer elements may be less than the extent of the corresponding array dimension, with remaining array locations initialized to the default value for the specified array type.
Examples
.const .f32 vals[8] = { 0.33, 0.25, 0.125 };
.global .s32 x[3][2] = { {1,2}, {3} };
is equivalent to
.const .f32 vals[8] = { 0.33, 0.25, 0.125, 0.0, 0.0, 0.0, 0.0, 0.0 };
.global .s32 x[3][2] = { {1,2}, {3,0}, {0,0} };
Currently, variable initialization is supported only for constant and global state spaces. Variables in constant and global state spaces with no explicit initializer are initialized to zero by default. Initializers are not allowed in external variable declarations.
Variable names appearing in initializers represent the address of the variable; this can be used to
statically initialize a pointer to a variable. Initializers may also contain var+offset
expressions, where offset is a byte offset added to the address of var. Only variables in
.global or .const state spaces may be used in initializers. By default, the resulting
address is the offset in the variable’s state space (as is the case when taking the address of a
variable with a mov instruction). An operator, generic(), is provided to create a generic
address for variables used in initializers.
Starting PTX ISA version 7.1, an operator mask() is provided, where mask is an integer
immediate. The only allowed expressions in the mask() operator are integer constant expression
and symbol expression representing address of variable. The mask() operator extracts n
consecutive bits from the expression used in initializers and inserts these bits at the lowest
position of the initialized variable. The number n and the starting position of the bits to be
extracted is specified by the integer immediate mask. PTX ISA version 7.1 only supports
extracting a single byte starting at byte boundary from the address of the variable. PTX ISA version
7.3 supports Integer constant expression as an operand in the mask() operator.
Supported values for mask are: 0xFF, 0xFF00, 0XFF0000, 0xFF000000, 0xFF00000000, 0xFF0000000000,
0xFF000000000000, 0xFF00000000000000.
Examples
.const .u32 foo = 42;
.global .u32 bar[] = { 2, 3, 5 };
.global .u32 p1 = foo; // offset of foo in .const space
.global .u32 p2 = generic(foo); // generic address of foo
// array of generic-address pointers to elements of bar
.global .u32 parr[] = { generic(bar), generic(bar)+4,
generic(bar)+8 };
// examples using mask() operator are pruned for brevity
.global .u8 addr[] = {0xff(foo), 0xff00(foo), 0xff0000(foo), ...};
.global .u8 addr2[] = {0xff(foo+4), 0xff00(foo+4), 0xff0000(foo+4),...}
.global .u8 addr3[] = {0xff(generic(foo)), 0xff00(generic(foo)),...}
.global .u8 addr4[] = {0xff(generic(foo)+4), 0xff00(generic(foo)+4),...}
// mask() operator with integer const expression
.global .u8 addr5[] = { 0xFF(1000 + 546), 0xFF00(131187), ...};
Note
PTX 3.1 redefines the default addressing for global variables in initializers, from generic
addresses to offsets in the global state space. Legacy PTX code is treated as having an implicit
generic() operator for each global variable used in an initializer. PTX 3.1 code should
either include explicit generic() operators in initializers, use cvta.global to form
generic addresses at runtime, or load from the non-generic address using ld.global.
Device function names appearing in initializers represent the address of the first instruction in the function; this can be used to initialize a table of function pointers to be used with indirect calls. Beginning in PTX ISA version 3.1, kernel function names can be used as initializers e.g. to initialize a table of kernel function pointers, to be used with CUDA Dynamic Parallelism to launch kernels from GPU. See the CUDA Dynamic Parallelism Programming Guide for details.
Labels cannot be used in initializers.
Variables that hold addresses of variables or functions should be of type .u8 or .u32 or
.u64.
Type .u8 is allowed only if the mask() operator is used.
Initializers are allowed for all types except .f16, .f16x2 and .pred.
Examples
.global .s32 n = 10;
.global .f32 blur_kernel[][3]
= {{.05,.1,.05},{.1,.4,.1},{.05,.1,.05}};
.global .u32 foo[] = { 2, 3, 5, 7, 9, 11 };
.global .u64 ptr = generic(foo); // generic address of foo[0]
.global .u64 ptr = generic(foo)+8; // generic address of foo[2]
5.4.5. Alignment
Byte alignment of storage for all addressable variables can be specified in the variable
declaration. Alignment is specified using an optional .alignbyte-count specifier immediately
following the state-space specifier. The variable will be aligned to an address which is an integer
multiple of byte-count. The alignment value byte-count must be a power of two. For arrays, alignment
specifies the address alignment for the starting address of the entire array, not for individual
elements.
The default alignment for scalar and array variables is to a multiple of the base-type size. The default alignment for vector variables is to a multiple of the overall vector size.
Examples
// allocate array at 4-byte aligned address. Elements are bytes.
.const .align 4 .b8 bar[8] = {0,0,0,0,2,0,0,0};
Note that all PTX instructions that access memory require that the address be aligned to a multiple
of the access size. The access size of a memory instruction is the total number of bytes accessed in
memory. For example, the access size of ld.v4.b32 is 16 bytes, while the access size of
atom.f16x2 is 4 bytes.
5.4.6. Parameterized Variable Names
Since PTX supports virtual registers, it is quite common for a compiler frontend to generate a large number of register names. Rather than require explicit declaration of every name, PTX supports a syntax for creating a set of variables having a common prefix string appended with integer suffixes.
For example, suppose a program uses a large number, say one hundred, of .b32 variables, named
%r0, %r1, …, %r99. These 100 register variables can be declared as follows:
.reg .b32 %r<100>; // declare %r0, %r1, ..., %r99
This shorthand syntax may be used with any of the fundamental types and with any state space, and may be preceded by an alignment specifier. Array variables cannot be declared this way, nor are initializers permitted.
5.4.7. Variable Attributes
Variables may be declared with an optional .attribute directive which allows specifying special
attributes of variables. Keyword .attribute is followed by attribute specification inside
parenthesis. Multiple attributes are separated by comma.
Variable and Function Attribute Directive: .attribute describes the .attribute
directive.
5.4.8. Variable and Function Attribute Directive: .attribute
.attribute
Variable and function attributes
Description
Used to specify special attributes of a variable or a function.
The following attributes are supported.
.managed.managedattribute specifies that variable will be allocated at a location in unified virtual memory environment where host and other devices in the system can reference the variable directly. This attribute can only be used with variables in .global state space. See the CUDA UVM-Lite Programming Guide for details..unified.unifiedattribute specifies that function has the same memory address on the host and on other devices in the system. Integer constantsuuid1anduuid2respectively specify upper and lower 64 bits of the unique identifier associated with the function or the variable. This attribute can only be used on device functions or on variables in the.globalstate space. Variables with.unifiedattribute are read-only and must be loaded by specifying.unifiedqualifier on the address operand ofldinstruction, otherwise the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 4.0.
Support for function attributes introduced in PTX ISA version 8.0.
Target ISA Notes
.managedattribute requiressm_30or higher..unifiedattribute requiressm_90or higher.
Examples
.global .attribute(.managed) .s32 g;
.global .attribute(.managed) .u64 x;
.global .attribute(.unified(19,95)) .f32 f;
.func .attribute(.unified(0xAB, 0xCD)) bar() { ... }
5.5. Tensors
A tensor is a multi-dimensional matrix structure in the memory. Tensor is defined by the following properties:
Dimensionality
Dimension sizes across each dimension
Individual element types
Tensor stride across each dimension
PTX supports instructions which can operate on the tensor data. PTX Tensor instructions include:
Copying data between global and shared memories
Reducing the destination tensor data with the source.
The Tensor data can be operated on by various wmma.mma, mma and wgmma.mma_async
instructions.
PTX Tensor instructions treat the tensor data in the global memory as a multi-dimensional structure and treat the data in the shared memory as a linear data.
5.5.1. Tensor Dimension, size and format
Tensors can have dimensions: 1D, 2D, 3D, 4D or 5D.
Each dimension has a size which represents the number of elements along the dimension. The elements can have one the following types:
Bit-sized type:
.b32,.b64Integer:
.u8,.u16,.u32,.s32,.u64,.s64Floating point and alternate floating point:
.f16,.bf16,.tf32,.f32,.f64(rounded to nearest even).
Tensor can have padding at the end in each of the dimensions to provide alignment for the data in the subsequent dimensions. Tensor stride can be used to specify the amount of padding in each dimension.
5.5.2. Tensor Access Modes
Tensor data can be accessed in two modes:
Tiled mode:
In tiled mode, the source multi-dimensional tensor layout is preserved at the destination.
Im2col mode:
In im2col mode, the elements in the Bounding Box of the source tensor are rearranged into columns at the destination. Refer here for more details.
5.5.3. Tiled Mode
This section talks about how Tensor and Tensor access work in tiled mode.
5.5.3.1. Bounding Box
A tensor can be accessed in chunks known as Bounding Box. The Bounding Box has the same dimensionality as the tensor they are accessing into. Size of each bounding Box must be a multiple of 16 bytes. The address of the bounding Box must also be aligned to 16 bytes.
Bounding Box has the following access properties:
Bounding Box dimension sizes
Out of boundary access mode
Traversal strides
The tensor-coordinates, specified in the PTX tensor instructions, specify the starting offset of the bounding box. Starting offset of the bounding box along with the rest of the bounding box information together are used to determine the elements which are to be accessed.
5.5.3.2. Traversal-Stride
While the Bounding Box is iterating the tensor across a dimension, the traversal stride specifies the exact number of elements to be skipped. If no jump over is required, default value of 1 must be specified.
The traversal stride in dimension 0 can be used for the Interleave layout. For non-interleaved layout, the traversal stride in dimension 0 must always be 1.
Figure 5 illustrates tensor, tensor size, tensor stride, Bounding Box size and traversal stride.
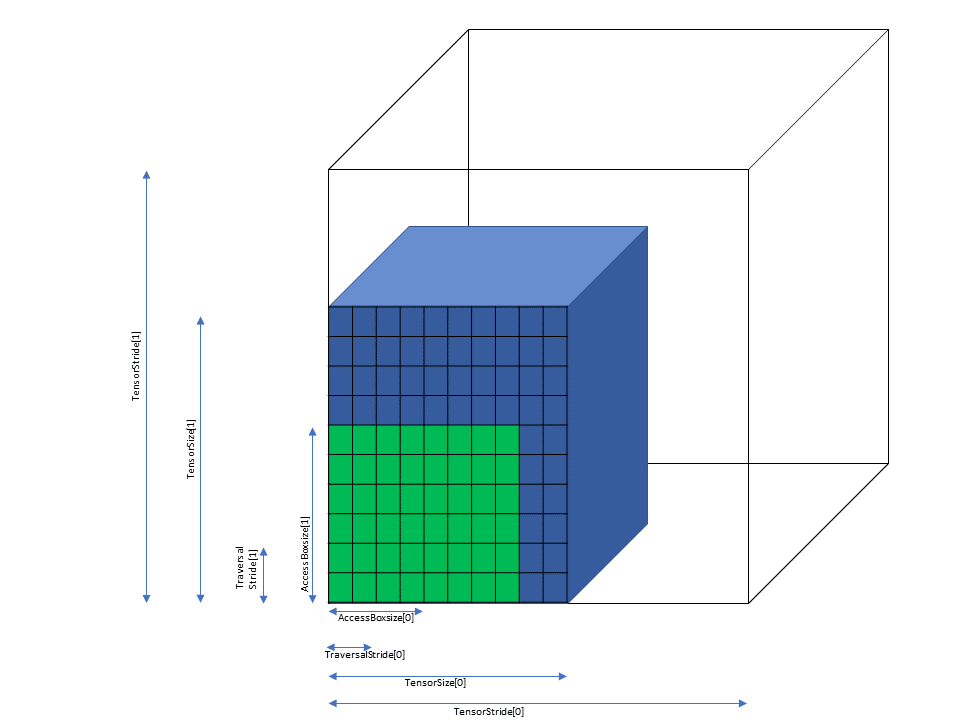
Figure 5 Tiled mode bounding box, tensor size and traversal stride
5.5.3.3. Out of Boundary Access
PTX Tensor operation can detect and handle the case when the Bounding Box crosses the tensor boundary in any dimension. There are 2 modes:
Zero fill mode:
Elements in the Bounding Box which fall outside of the tensor boundary are set to 0.
OOB-NaNfill mode:Elements in the Bounding Box which fall outside of the tensor boundary are set to a special NaN called
OOB-NaN.
Figure 6 shows an example of the out of boundary access.
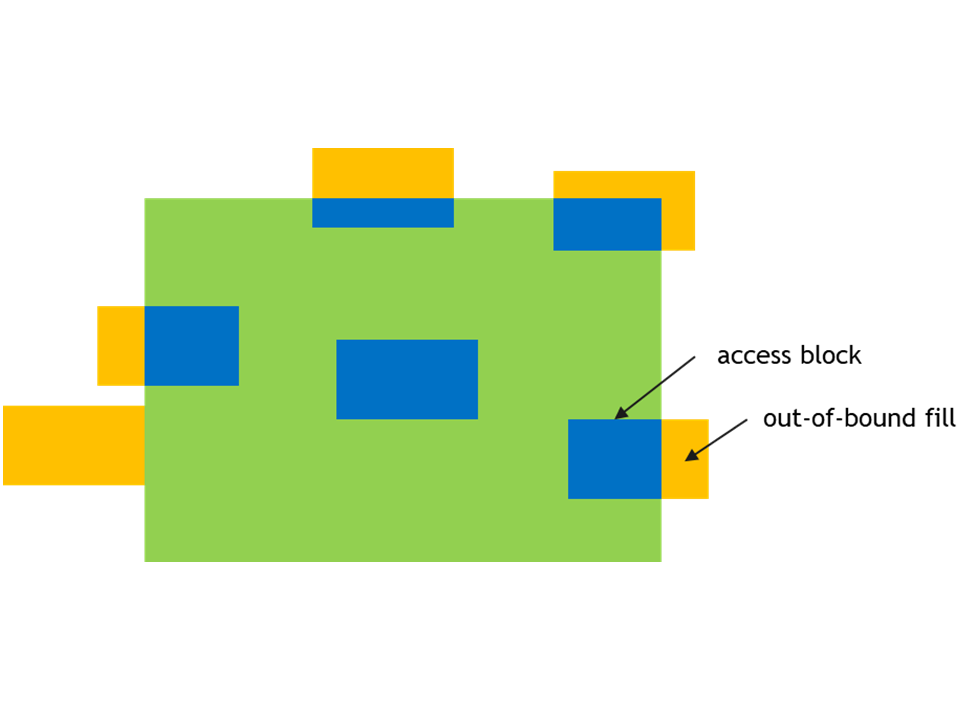
Figure 6 Out of boundary access
5.5.4. Im2col mode
Im2col mode supports the following tensor dimensions : 3D, 4D and 5D. In this mode, the tensor data is treated as a batch of images with the following properties:
N : number of images in the batch
D, H, W : size of a 3D image (depth, height and width)
C: channels per image element
The above properties are associated with 3D, 4D and 5D tensors as follows:
Dimension |
N/D/H/W/C applicability |
|---|---|
3D |
NWC |
4D |
NHWC |
5D |
NDHWC |
5.5.4.1. Bounding Box
In im2col mode, the Bounding Box is defined in DHW space. Boundaries along other dimensions are specified by Pixels-per-Column and Channels-per-Pixel parameters as described below.
The dimensionality of the Bounding Box is two less than the tensor dimensionality.
The following properties describe how to access of the elements in im2col mode:
Bounding-Box Lower-Corner
Bounding-Box Upper-Corner
Pixels-per-Column
Channels-per-Pixel
Bounding-box Lower-Corner and Bounding-box Upper-Corner specify the two opposite corners of the Bounding Box in the DHW space. Bounding-box Lower-Corner specifies the corner with the smallest coordinate and Bounding-box Upper-Corner specifies the corner with the largest coordinate.
Bounding-box Upper- and Lower-Corners are 16-bit signed values whose limits varies across the dimensions and are as shown below:
3D |
4D |
5D |
|
|---|---|---|---|
Upper- / Lower- Corner sizes |
[-215, 215-1] |
[-27, 27-1] |
[-24, 24-1] |
Figure 7 and Figure 8 show the Upper-Corners and Lower-Corners.
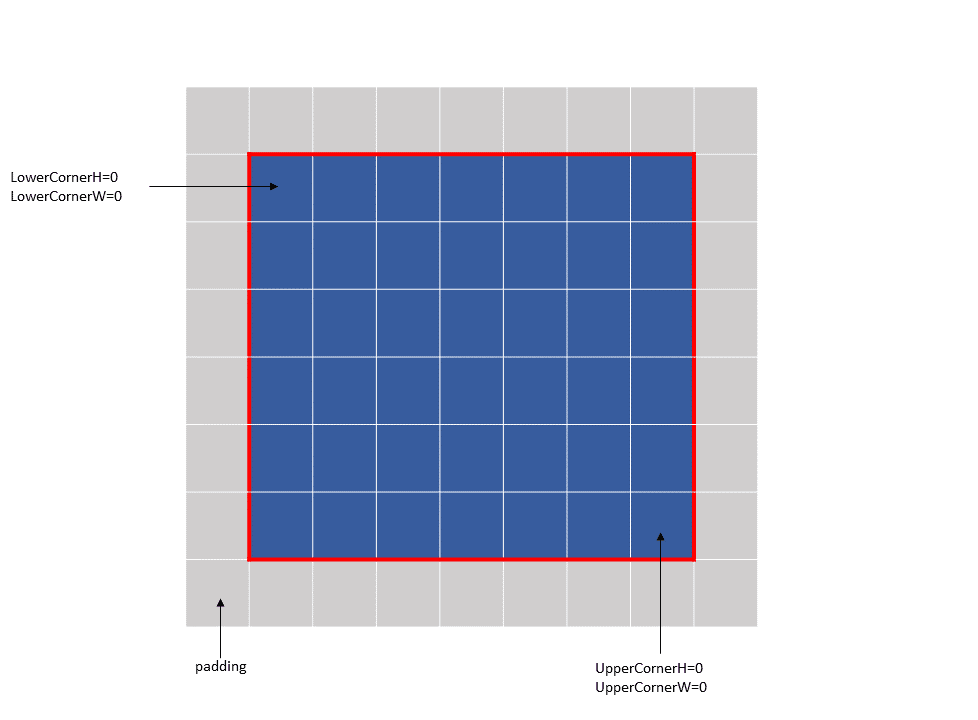
Figure 7 im2col mode bounding box example 1
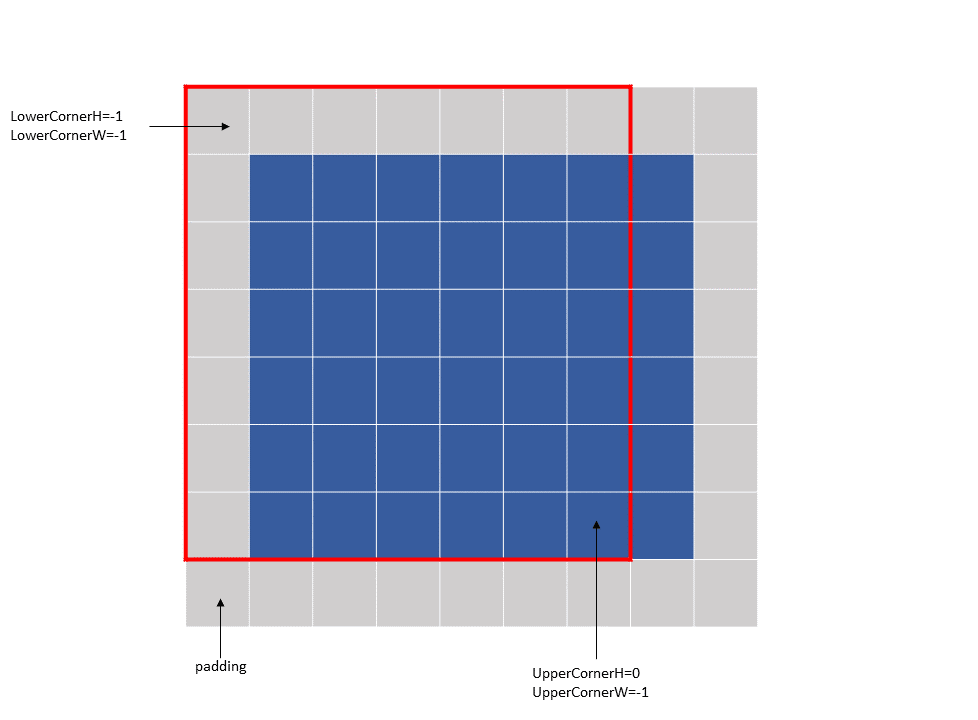
Figure 8 im2col mode bounding box example 2
The Bounding-box Upper- and Lower- Corners specify only the boundaries and not the number of elements to be accessed. Pixels-per-Column specifies the number of elements to be accessed in the NDHW space.
Channels-per-Pixel specifies the number of elements to access across the C dimension.
The tensor coordinates, specified in the PTX tensor instructions, behaves differently in different dimensions:
Across N and C dimensions: specify the starting offsets along the dimension, similar to the tiled mode.
Across DHW dimensions: specify the location of the convolution filter base in the tensor space. The filter corner location must be within the bounding box.
The im2col offsets, specified in the PTX tensor instructions in im2col mode, are added to the filter base coordinates to determine the starting location in the tensor space from where the elements are accessed.
The size of the im2col offsets varies across the dimensions and their valid ranges are as shown below:
3D |
4D |
5D |
|
|---|---|---|---|
im2col offsets range |
[0, 216-1] |
[0, 28-1] |
[0, 25-1] |
Following are some examples of the im2col mode accesses:
Example 1 (Figure 9):
Tensor Size[0] = 64 Tensor Size[1] = 9 Tensor Size[2] = 14 Tensor Size[3] = 64 Pixels-per-Column = 64 channels-per-pixel = 8 Bounding-Box Lower-Corner W = -1 Bounding-Box Lower-Corner H = -1 Bounding-Box Upper-Corner W = -1 Bounding-Box Upper-Corner H = -1. tensor coordinates = (7, 7, 4, 0) im2col offsets : (0, 0)
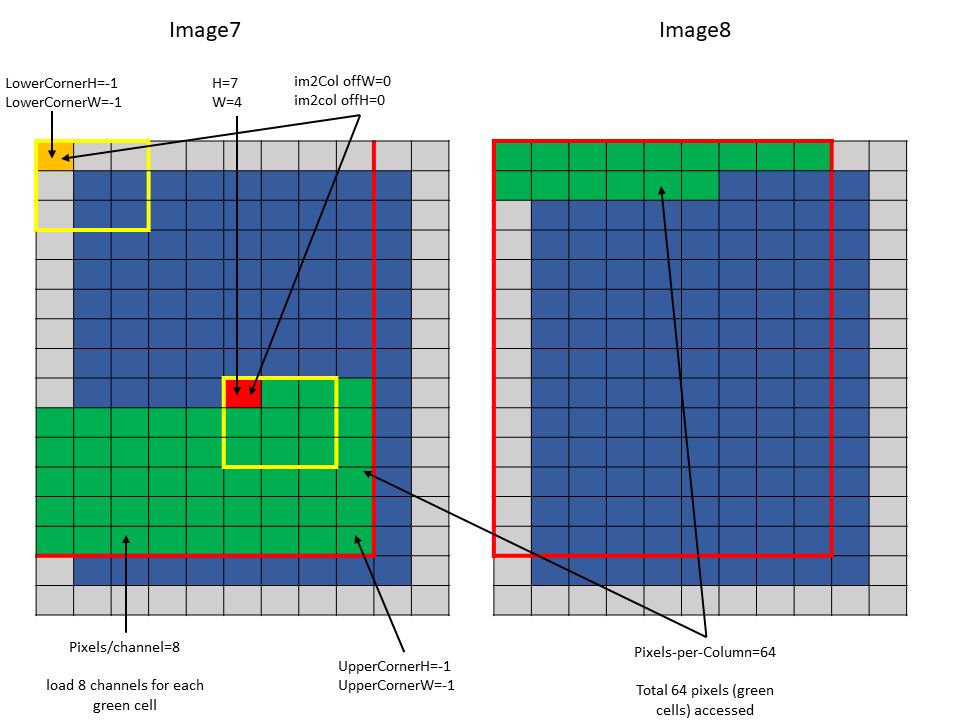
Figure 9 im2col mode example 1
Example 2 (Figure 10):
Tensor Size[0] = 64 Tensor Size[1] = 9 Tensor Size[2] = 14 Tensor Size[3] = 64 Pixels-per-Column = 64 channels-per-pixel = 8 Bounding-Box Lower-Corner W = 0 Bounding-Box Lower-Corner H = 0 Bounding-Box Upper-Corner W = -2 Bounding-Box Upper-Corner H = -2 tensor coordinates = (7, 7, 4, 0) im2col offsets: (2, 2)
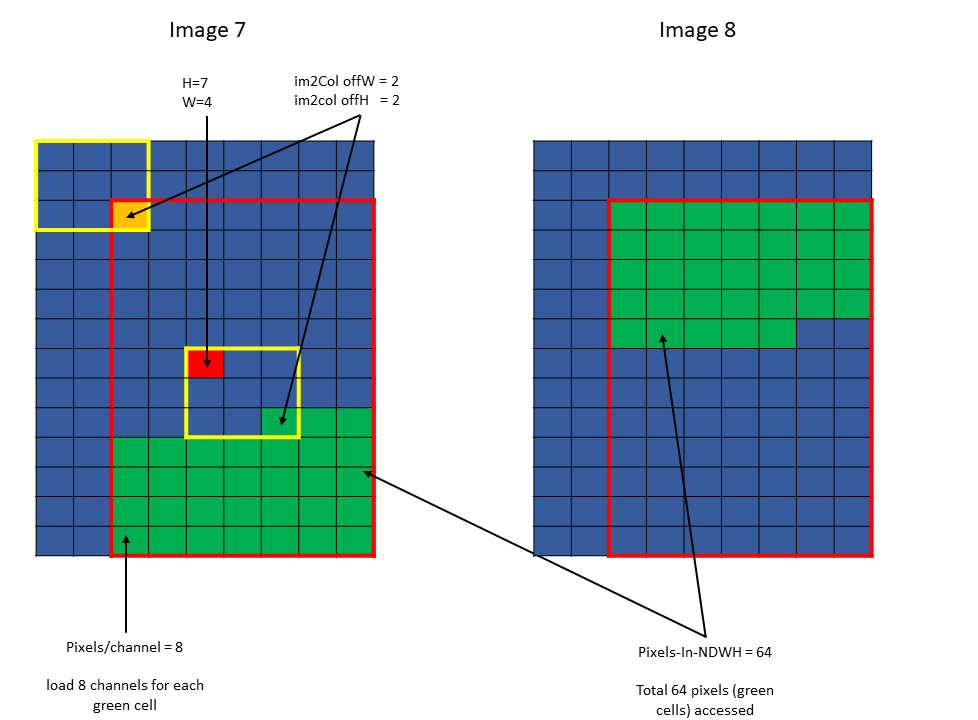
Figure 10 im2col mode example 2
5.5.4.2. Traversal Stride
The traversal stride, in im2col mode, does not impact the total number of elements (or pixels) being accessed unlike the tiled mode. Pixels-per-Column determines the total number of elements being accessed, in im2col mode.
The number of elements traversed along the D, H and W dimensions is strided by the traversal stride for that dimension.
The following example with Figure 11 illustrates accesse with traversal-strides:
Tensor Size[0] = 64
Tensor Size[1] = 8
Tensor Size[2] = 14
Tensor Size[3] = 64
Traversal Stride = 2
Pixels-per-Column = 32
channels-per-pixel = 16
Bounding-Box Lower-Corner W = -1
Bounding-Box Lower-Corner H = -1
Bounding-Box Upper-Corner W = -1
Bounding-Box Upper-Corner H = -1.
Tensor coordinates in the instruction = (7, 7, 5, 0)
Im2col offsets in the instruction : (1, 1)
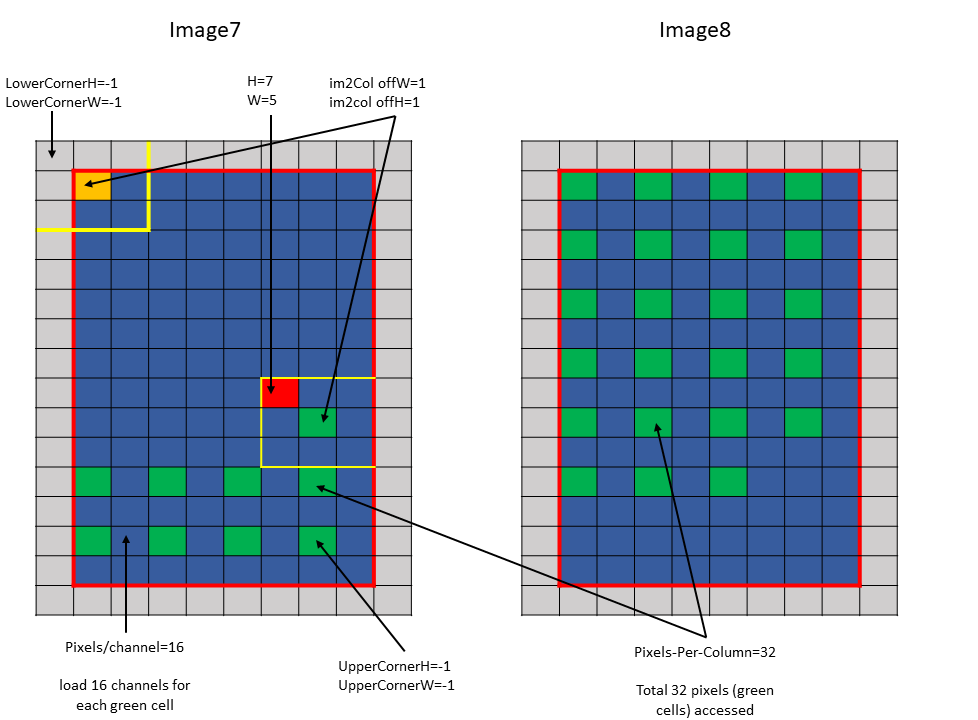
Figure 11 im2col mode traversal stride example
5.5.4.3. Out of Boundary Access
In im2col mode, when the number of requested pixels in NDHW space specified by Pixels-per-Column exceeds the number of available pixels in the image batch then out-of-bounds access is performed.
Similar to tiled mode, zero fill or OOB-NaN fill can be performed based on the Fill-Mode
specified.
5.5.5. Interleave layout
Tensor can be interleaved and the following interleave layouts are supported:
No interleave (NDHWC)
8 byte interleave (NC/8DHWC8) : C8 utilizes 16 bytes in memory assuming 2B per channel.
16 byte interleave (NC/16HWC16) : C16 utilizes 32 bytes in memory assuming 4B per channel.
The C information is organized in slices where sequential C elements are grouped in 16 byte or 32 byte quantities.
If the total number of channels is not a multiple of the number of channels per slice, then the last slice must be padded with zeros to make it complete 16B or 32B slice.
Interleaved layouts are supported only for the dimensionalities : 3D, 4D and 5D.
5.5.6. Swizzling Modes
The layout of the data in the shared memory can be different to that of global memory, for access performance reasons. The following describes various swizzling modes:
No swizzle mode:
There is no swizzling in this mode and the destination data layout is exactly similar to the source data layout.
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
… Pattern repeats …
32 byte swizzle mode:
The following table, where each elements (numbered cell) is 16 byte and the starting address is 256 bytes aligned, shows the pattern of the destination data layout:
0
1
2
3
4
5
6
7
1
0
3
2
5
4
7
6
… Pattern repeats …
An example of the 32 byte swizzle mode for NC/(32B)HWC(32B) tensor of 1x2x10x10xC16 dimension, with the innermost dimension holding slice of 16 channels with 2 byte/channel, is shown in Figure 12.
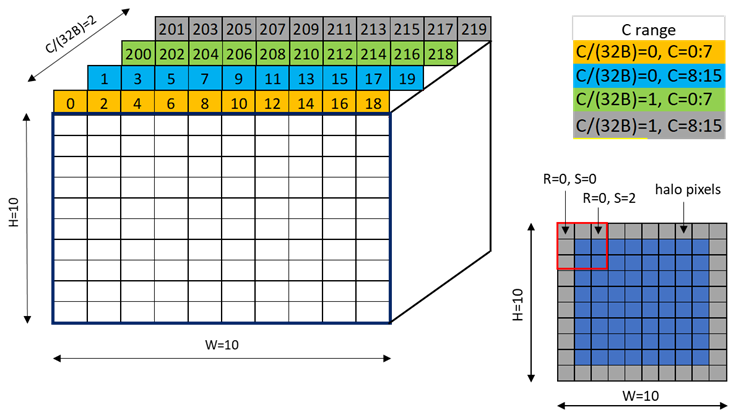
Figure 12 32-byte swizzle mode example
Figure 13 shows the two fragments of the tensor : one for C/(32B) = 0 and another for C/(32B) = 1.
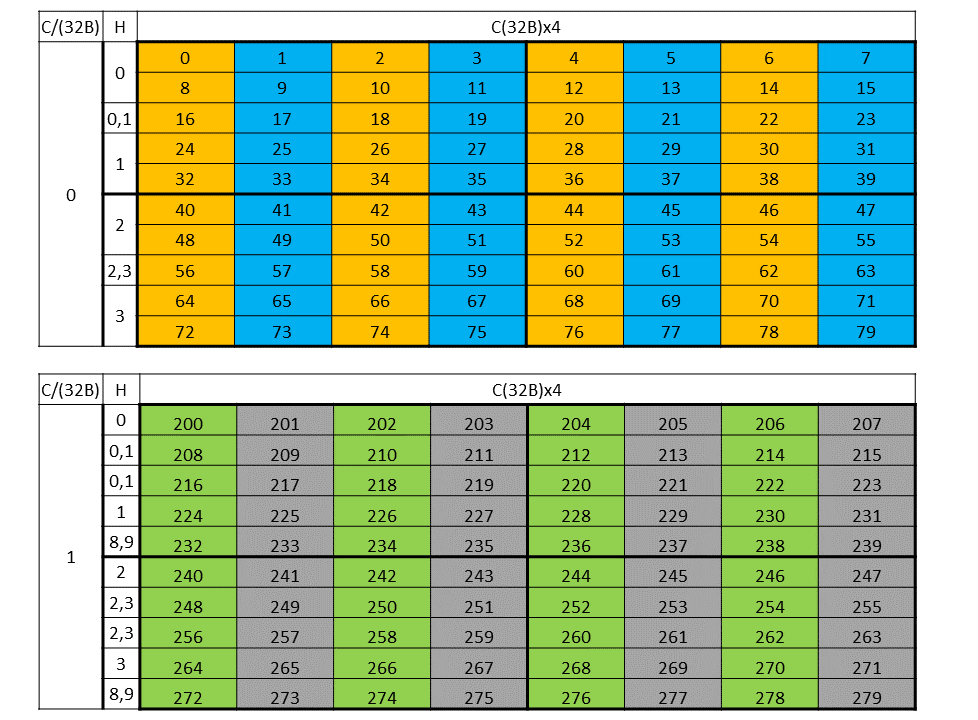
Figure 13 32-byte swizzle mode fragments
Figure 14 shows the destination data layout with 32 byte swizzling.
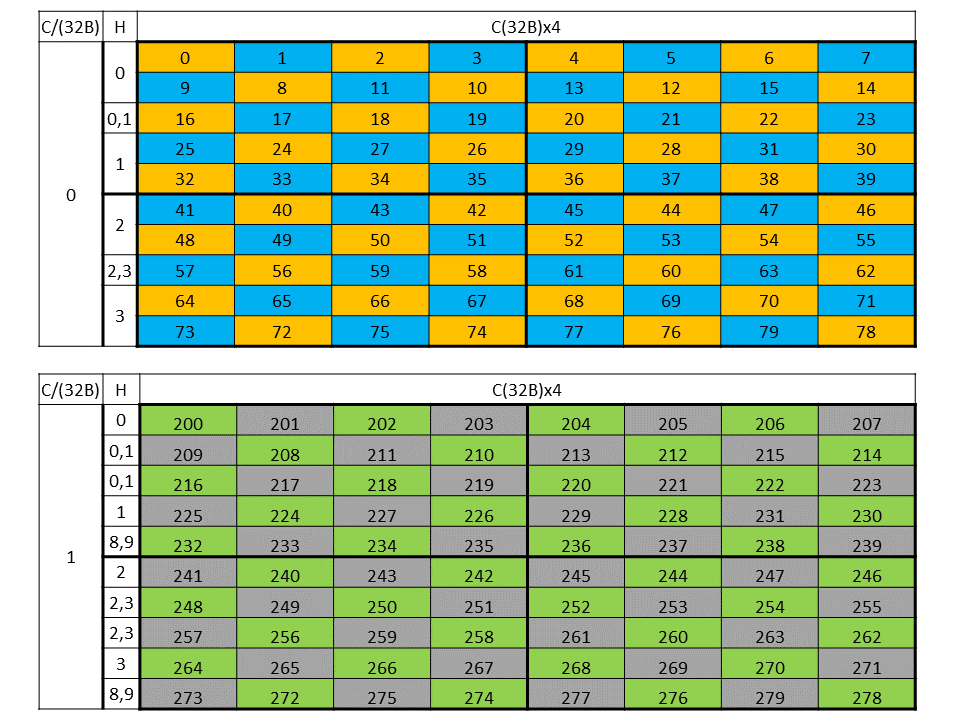
Figure 14 32-byte swizzle mode destination data layout
64 byte swizzle mode:
The following table, where each elements (numbered cell) is 16 byte and the starting address is 512 bytes aligned, shows the pattern of the destination data layout:
0
1
2
3
4
5
6
7
1
0
3
2
5
4
7
6
2
3
0
1
6
7
4
5
3
2
1
0
7
6
5
4
… Pattern repeats …
An example of the 64 byte swizzle mode for NHWC tensor of 1x10x10x64 dimension, with 2 bytes / channel and 32 channels, is shown in Figure 15.
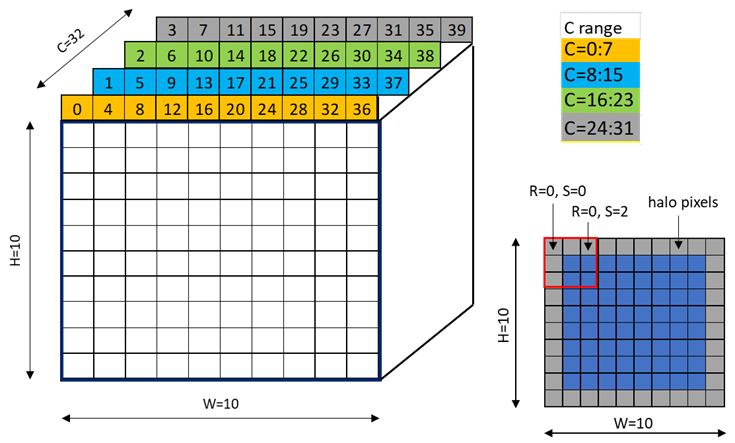
Figure 15 64-byte swizzle mode example
Each colored cell represents 8 channels. Figure 16 shows the source data layout.
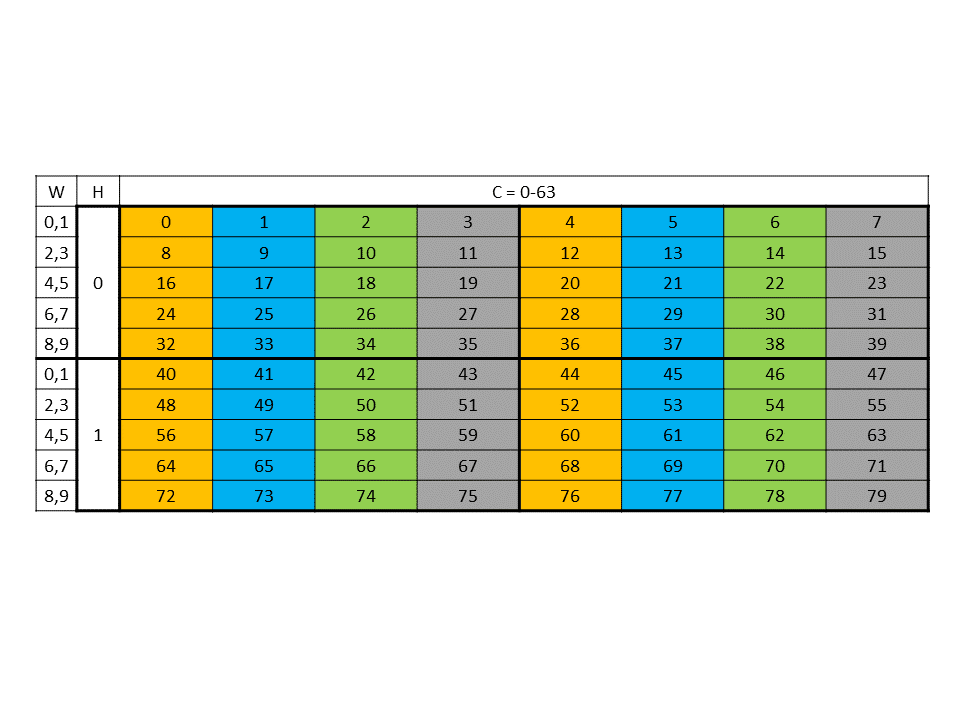
Figure 16 64-byte swizzle mode source data layout
Figure 17 shows the destination data layout with 64 byte swizzling.
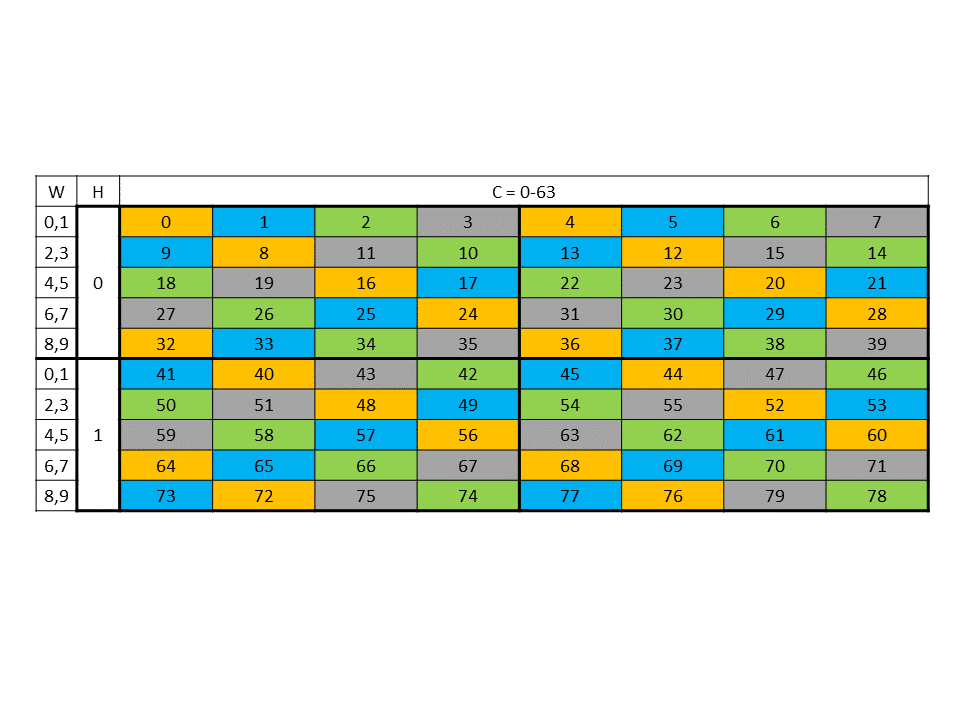
Figure 17 64-byte swizzle mode destination data layout
128 byte swizzle mode:
The following table, where each elements (numbered cell) is 16 byte and the starting address is 1024 bytes aligned, shows the pattern of the destination data layout:
0
1
2
3
4
5
6
7
1
0
3
2
5
4
7
6
2
3
0
1
6
7
4
5
3
2
1
0
7
6
5
4
4
5
6
7
0
1
2
3
5
4
7
6
1
0
3
2
6
7
4
5
2
3
0
1
… Pattern repeats …
An example of the 128 byte swizzle mode for NHWC tensor of 1x10x10x64 dimension, with 2 bytes / channel and 64 channels, is shown in Figure 18.
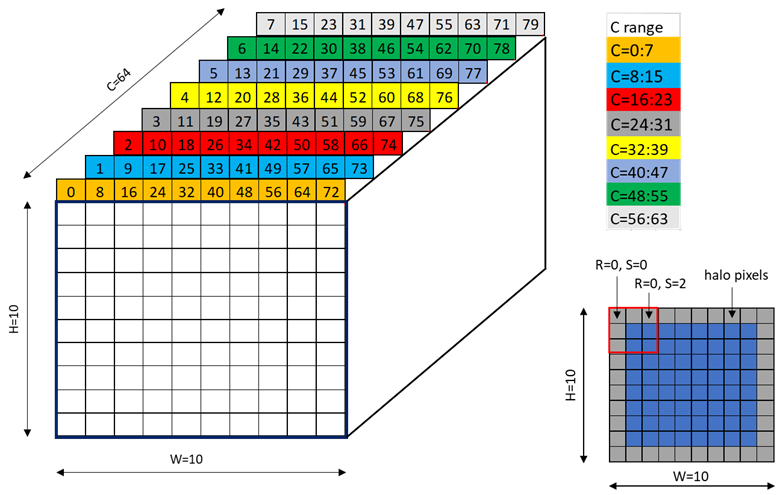
Figure 18 128-byte swizzle mode example
Each colored cell represents 8 channels. Figure 19 shows the source data layout.
Figure 19 128-byte swizzle mode source data layout
Figure 20 shows the destination data layout with 128 byte swizzling.
Figure 20 128-byte swizzle mode destination data layout
5.5.7. Tensor-map
The tensor-map is a 128-byte opaque object either in .const space or .param (kernel function
parameter) space or .global space which describes the tensor properties and the access properties
of the tensor data described in previous sections.
Tensor-Map can be created using CUDA APIs. Refer to CUDA programming guide for more details.
6. Instruction Operands
6.1. Operand Type Information
All operands in instructions have a known type from their declarations. Each operand type must be compatible with the type determined by the instruction template and instruction type. There is no automatic conversion between types.
The bit-size type is compatible with every type having the same size. Integer types of a common size are compatible with each other. Operands having type different from but compatible with the instruction type are silently cast to the instruction type.
6.2. Source Operands
The source operands are denoted in the instruction descriptions by the names a, b, and
c. PTX describes a load-store machine, so operands for ALU instructions must all be in variables
declared in the .reg register state space. For most operations, the sizes of the operands must
be consistent.
The cvt (convert) instruction takes a variety of operand types and sizes, as its job is to
convert from nearly any data type to any other data type (and size).
The ld, st, mov, and cvt instructions copy data from one location to
another. Instructions ld and st move data from/to addressable state spaces to/from
registers. The mov instruction copies data between registers.
Most instructions have an optional predicate guard that controls conditional execution, and a few
instructions have additional predicate source operands. Predicate operands are denoted by the names
p, q, r, s.
6.3. Destination Operands
PTX instructions that produce a single result store the result in the field denoted by d (for
destination) in the instruction descriptions. The result operand is a scalar or vector variable in
the register state space.
6.4. Using Addresses, Arrays, and Vectors
Using scalar variables as operands is straightforward. The interesting capabilities begin with addresses, arrays, and vectors.
6.4.1. Addresses as Operands
All the memory instructions take an address operand that specifies the memory location being accessed. This addressable operand is one of:
[var]the name of an addressable variable
var.[reg]an integer or bit-size type register
regcontaining a byte address.[reg+immOff]a sum of register
regcontaining a byte address plus a constant integer byte offset (signed, 32-bit).[var+immOff]a sum of address of addressable variable
varcontaining a byte address plus a constant integer byte offset (signed, 32-bit).[immAddr]an immediate absolute byte address (unsigned, 32-bit).
var[immOff]an array element as described in Arrays as Operands.
The register containing an address may be declared as a bit-size type or integer type.
The access size of a memory instruction is the total number of bytes accessed in memory. For
example, the access size of ld.v4.b32 is 16 bytes, while the access size of atom.f16x2 is 4
bytes.
The address must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined. For example, among other things, the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
The address size may be either 32-bit or 64-bit. 128-bit adresses are not supported. Addresses are zero-extended to the specified width as needed, and truncated if the register width exceeds the state space address width for the target architecture.
Address arithmetic is performed using integer arithmetic and logical instructions. Examples include pointer arithmetic and pointer comparisons. All addresses and address computations are byte-based; there is no support for C-style pointer arithmetic.
The mov instruction can be used to move the address of a variable into a pointer. The address is
an offset in the state space in which the variable is declared. Load and store operations move data
between registers and locations in addressable state spaces. The syntax is similar to that used in
many assembly languages, where scalar variables are simply named and addresses are de-referenced by
enclosing the address expression in square brackets. Address expressions include variable names,
address registers, address register plus byte offset, and immediate address expressions which
evaluate at compile-time to a constant address.
Here are a few examples:
.shared .u16 x;
.reg .u16 r0;
.global .v4 .f32 V;
.reg .v4 .f32 W;
.const .s32 tbl[256];
.reg .b32 p;
.reg .s32 q;
ld.shared.u16 r0,[x];
ld.global.v4.f32 W, [V];
ld.const.s32 q, [tbl+12];
mov.u32 p, tbl;
6.4.1.1. Generic Addressing
If a memory instruction does not specify a state space, the operation is performed using generic
addressing. The state spaces .const, Kernel Function Parameters (.param), .local and .shared are modeled as
windows within the generic address space. Each window is defined by a window base and a window size
that is equal to the size of the corresponding state space. A generic address maps to global
memory unless it falls within the window for const, local, or shared memory. The Kernel
Function Parameters (.param) window is contained
within the .global window. Within each window, a generic address maps to an address in the
underlying state space by subtracting the window base from the generic address.
6.4.2. Arrays as Operands
Arrays of all types can be declared, and the identifier becomes an address constant in the space where the array is declared. The size of the array is a constant in the program.
Array elements can be accessed using an explicitly calculated byte address, or by indexing into the array using square-bracket notation. The expression within square brackets is either a constant integer, a register variable, or a simple register with constant offset expression, where the offset is a constant expression that is either added or subtracted from a register variable. If more complicated indexing is desired, it must be written as an address calculation prior to use. Examples are:
ld.global.u32 s, a[0];
ld.global.u32 s, a[N-1];
mov.u32 s, a[1]; // move address of a[1] into s
6.4.3. Vectors as Operands
Vector operands are supported by a limited subset of instructions, which include mov, ld,
st, atom, red and tex. Vectors may also be passed as arguments to called functions.
Vector elements can be extracted from the vector with the suffixes .x, .y, .z and
.w, as well as the typical color fields .r, .g, .b and .a.
A brace-enclosed list is used for pattern matching to pull apart vectors.
.reg .v4 .f32 V;
.reg .f32 a, b, c, d;
mov.v4.f32 {a,b,c,d}, V;
Vector loads and stores can be used to implement wide loads and stores, which may improve memory performance. The registers in the load/store operations can be a vector, or a brace-enclosed list of similarly typed scalars. Here are examples:
ld.global.v4.f32 {a,b,c,d}, [addr+16];
ld.global.v2.u32 V2, [addr+8];
Elements in a brace-enclosed vector, say {Ra, Rb, Rc, Rd}, correspond to extracted elements as follows:
Ra = V.x = V.r
Rb = V.y = V.g
Rc = V.z = V.b
Rd = V.w = V.a
6.4.4. Labels and Function Names as Operands
Labels and function names can be used only in bra/brx.idx and call instructions
respectively. Function names can be used in mov instruction to get the address of the function
into a register, for use in an indirect call.
Beginning in PTX ISA version 3.1, the mov instruction may be used to take the address of kernel
functions, to be passed to a system call that initiates a kernel launch from the GPU. This feature
is part of the support for CUDA Dynamic Parallelism. See the CUDA Dynamic Parallelism Programming
Guide for details.
6.5. Type Conversion
All operands to all arithmetic, logic, and data movement instruction must be of the same type and size, except for operations where changing the size and/or type is part of the definition of the instruction. Operands of different sizes or types must be converted prior to the operation.
6.5.1. Scalar Conversions
Table 13 shows what
precision and format the cvt instruction uses given operands of differing types. For example, if a
cvt.s32.u16 instruction is given a u16 source operand and s32 as a destination operand,
the u16 is zero-extended to s32.
Conversions to floating-point that are beyond the range of floating-point numbers are represented
with the maximum floating-point value (IEEE 754 Inf for f32 and f64, and ~131,000 for
f16).
Destination Format |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
s8 |
s16 |
s32 |
s64 |
u8 |
u16 |
u32 |
u64 |
f16 |
f32 |
f64 |
||
Source Format |
s8 |
– |
sext |
sext |
sext |
– |
sext |
sext |
sext |
s2f |
s2f |
s2f |
s16 |
chop1 |
– |
sext |
sext |
chop1 |
– |
sext |
sext |
s2f |
s2f |
s2f |
|
s32 |
chop1 |
chop1 |
– |
sext |
chop1 |
chop1 |
– |
sext |
s2f |
s2f |
s2f |
|
s64 |
chop1 |
chop1 |
chop |
– |
chop1 |
chop1 |
chop |
– |
s2f |
s2f |
s2f |
|
u8 |
– |
zext |
zext |
zext |
– |
zext |
zext |
zext |
u2f |
u2f |
u2f |
|
u16 |
chop1 |
– |
zext |
zext |
chop1 |
– |
zext |
zext |
u2f |
u2f |
u2f |
|
u32 |
chop1 |
chop1 |
– |
zext |
chop1 |
chop1 |
– |
zext |
u2f |
u2f |
u2f |
|
u64 |
chop1 |
chop1 |
chop |
– |
chop1 |
chop1 |
chop |
– |
u2f |
u2f |
u2f |
|
f16 |
f2s |
f2s |
f2s |
f2s |
f2u |
f2u |
f2u |
f2u |
– |
f2f |
f2f |
|
f32 |
f2s |
f2s |
f2s |
f2s |
f2u |
f2u |
f2u |
f2u |
f2f |
– |
f2f |
|
f64 |
f2s |
f2s |
f2s |
f2s |
f2u |
f2u |
f2u |
f2u |
f2f |
f2f |
– |
|
Notes |
sext = sign-extend; zext = zero-extend; chop = keep only low bits that fit; s2f = signed-to-float; f2s = float-to-signed; u2f = unsigned-to-float; f2u = float-to-unsigned; f2f = float-to-float. 1 If the destination register is wider than the destination format, the result is extended to the destination register width after chopping. The type of extension (sign or zero) is based on the destination format. For example, cvt.s16.u32 targeting a 32-bit register first chops to 16-bit, then sign-extends to 32-bit. |
|||||||||||
6.5.2. Rounding Modifiers
Conversion instructions may specify a rounding modifier. In PTX, there are four integer rounding modifiers and four floating-point rounding modifiers. Table 14 and Table 15 summarize the rounding modifiers.
Modifier |
Description |
|---|---|
|
mantissa LSB rounds to nearest even |
|
mantissa LSB rounds to nearest, ties away from zero |
|
mantissa LSB rounds towards zero |
|
mantissa LSB rounds towards negative infinity |
|
mantissa LSB rounds towards positive infinity |
Modifier |
Description |
|---|---|
|
round to nearest integer, choosing even integer if source is equidistant between two integers. |
|
round to nearest integer in the direction of zero |
|
round to nearest integer in direction of negative infinity |
|
round to nearest integer in direction of positive infinity |
6.6. Operand Costs
Operands from different state spaces affect the speed of an operation. Registers are fastest, while global memory is slowest. Much of the delay to memory can be hidden in a number of ways. The first is to have multiple threads of execution so that the hardware can issue a memory operation and then switch to other execution. Another way to hide latency is to issue the load instructions as early as possible, as execution is not blocked until the desired result is used in a subsequent (in time) instruction. The register in a store operation is available much more quickly. Table 16 gives estimates of the costs of using different kinds of memory.
Space |
Time |
Notes |
|---|---|---|
Register |
0 |
|
Shared |
0 |
|
Constant |
0 |
Amortized cost is low, first access is high |
Local |
> 100 clocks |
|
Parameter |
0 |
|
Immediate |
0 |
|
Global |
> 100 clocks |
|
Texture |
> 100 clocks |
|
Surface |
> 100 clocks |
7. Abstracting the ABI
Rather than expose details of a particular calling convention, stack layout, and Application Binary
Interface (ABI), PTX provides a slightly higher-level abstraction and supports multiple ABI
implementations. In this section, we describe the features of PTX needed to achieve this hiding of
the ABI. These include syntax for function definitions, function calls, parameter passing, support
for variadic functions (varargs), and memory allocated on the stack (alloca).
Refer to PTX Writers Guide to Interoperability for details on generating PTX compliant with Application Binary Interface (ABI) for the CUDA® architecture.
7.1. Function Declarations and Definitions
In PTX, functions are declared and defined using the .func directive. A function declaration
specifies an optional list of return parameters, the function name, and an optional list of input
parameters; together these specify the function’s interface, or prototype. A function definition
specifies both the interface and the body of the function. A function must be declared or defined
prior to being called.
The simplest function has no parameters or return values, and is represented in PTX as follows:
.func foo
{
...
ret;
}
...
call foo;
...
Here, execution of the call instruction transfers control to foo, implicitly saving the
return address. Execution of the ret instruction within foo transfers control to the
instruction following the call.
Scalar and vector base-type input and return parameters may be represented simply as register variables. At the call, arguments may be register variables or constants, and return values may be placed directly into register variables. The arguments and return variables at the call must have type and size that match the callee’s corresponding formal parameters.
Example
.func (.reg .u32 %res) inc_ptr ( .reg .u32 %ptr, .reg .u32 %inc )
{
add.u32 %res, %ptr, %inc;
ret;
}
...
call (%r1), inc_ptr, (%r1,4);
...
When using the ABI, .reg state space parameters must be at least 32-bits in size. Subword scalar
objects in the source language should be promoted to 32-bit registers in PTX, or use .param
state space byte arrays described next.
Objects such as C structures and unions are flattened into registers or byte arrays in PTX and are
represented using .param space memory. For example, consider the following C structure, passed
by value to a function:
struct {
double dbl;
char c[4];
};
In PTX, this structure will be flattened into a byte array. Since memory accesses are required to be
aligned to a multiple of the access size, the structure in this example will be a 12 byte array with
8 byte alignment so that accesses to the .f64 field are aligned. The .param state space is
used to pass the structure by value:
Example
.func (.reg .s32 out) bar (.reg .s32 x, .param .align 8 .b8 y[12])
{
.reg .f64 f1;
.reg .b32 c1, c2, c3, c4;
...
ld.param.f64 f1, [y+0];
ld.param.b8 c1, [y+8];
ld.param.b8 c2, [y+9];
ld.param.b8 c3, [y+10];
ld.param.b8 c4, [y+11];
...
... // computation using x,f1,c1,c2,c3,c4;
}
{
.param .b8 .align 8 py[12];
...
st.param.b64 [py+ 0], %rd;
st.param.b8 [py+ 8], %rc1;
st.param.b8 [py+ 9], %rc2;
st.param.b8 [py+10], %rc1;
st.param.b8 [py+11], %rc2;
// scalar args in .reg space, byte array in .param space
call (%out), bar, (%x, py);
...
In this example, note that .param space variables are used in two ways. First, a .param
variable y is used in function definition bar to represent a formal parameter. Second, a
.param variable py is declared in the body of the calling function and used to set up the
structure being passed to bar.
The following is a conceptual way to think about the .param state space use in device functions.
For a caller,
The
.paramstate space is used to set values that will be passed to a called function and/or to receive return values from a called function. Typically, a.parambyte array is used to collect together fields of a structure being passed by value.
For a callee,
The
.paramstate space is used to receive parameter values and/or pass return values back to the caller.
The following restrictions apply to parameter passing.
For a caller,
Arguments may be
.paramvariables,.regvariables, or constants.In the case of
.paramspace formal parameters that are byte arrays, the argument must also be a.paramspace byte array with matching type, size, and alignment. A.paramargument must be declared within the local scope of the caller.In the case of
.paramspace formal parameters that are base-type scalar or vector variables, the corresponding argument may be either a.paramor.regspace variable with matching type and size, or a constant that can be represented in the type of the formal parameter.In the case of
.regspace formal parameters, the corresponding argument may be either a.paramor.regspace variable of matching type and size, or a constant that can be represented in the type of the formal parameter.In the case of
.regspace formal parameters, the register must be at least 32-bits in size.All
st.paraminstructions used for passing arguments to function call must immediately precede the correspondingcallinstruction andld.paraminstruction used for collecting return value must immediately follow thecallinstruction without any control flow alteration.st.paramandld.paraminstructions used for argument passing cannot be predicated. This enables compiler optimization and ensures that the.paramvariable does not consume extra space in the caller’s frame beyond that needed by the ABI. The.paramvariable simply allows a mapping to be made at the call site between data that may be in multiple locations (e.g., structure being manipulated by caller is located in registers and memory) to something that can be passed as a parameter or return value to the callee.
For a callee,
Input and return parameters may be
.paramvariables or.regvariables.Parameters in
.parammemory must be aligned to a multiple of 1, 2, 4, 8, or 16 bytes.Parameters in the
.regstate space must be at least 32-bits in size.The
.regstate space can be used to receive and return base-type scalar and vector values, including sub-word size objects when compiling in non-ABI mode. Supporting the.regstate space provides legacy support.
Note that the choice of .reg or .param state space for parameter passing has no impact on
whether the parameter is ultimately passed in physical registers or on the stack. The mapping of
parameters to physical registers and stack locations depends on the ABI definition and the order,
size, and alignment of parameters.
7.1.1. Changes from PTX ISA Version 1.x
In PTX ISA version 1.x, formal parameters were restricted to .reg state space, and there was no support for array parameters. Objects such as C structures were flattened and passed or returned using multiple registers. PTX ISA version 1.x supports multiple return values for this purpose.
Beginning with PTX ISA version 2.0, formal parameters may be in either .reg or .param state
space, and .param space parameters support arrays. For targets sm_20 or higher, PTX
restricts functions to a single return value, and a .param byte array should be used to return
objects that do not fit into a register. PTX continues to support multiple return registers for
sm_1x targets.
Note
PTX implements a stack-based ABI only for targets sm_20 or higher.
PTX ISA versions prior to 3.0 permitted variables in .reg and .local state spaces to be
defined at module scope. When compiling to use the ABI, PTX ISA version 3.0 and later disallows
module-scoped .reg and .local variables and restricts their use to within function
scope. When compiling without use of the ABI, module-scoped .reg and .local variables are
supported as before. When compiling legacy PTX code (ISA versions prior to 3.0) containing
module-scoped .reg or .local variables, the compiler silently disables use of the ABI.
7.2. Variadic Functions
Note
Support for variadic functions which was unimplemented has been removed from the spec.
PTX version 6.0 supports passing unsized array parameter to a function which can be used to implement variadic functions.
Refer to Kernel and Function Directives: .func for details
7.3. Alloca
PTX provides alloca instruction for allocating storage at runtime on the per-thread local memory
stack. The allocated stack memory can be accessed with ld.local and st.local instructions
using the pointer returned by alloca.
In order to facilitate deallocation of memory allocated with alloca, PTX provides two additional
instructions: stacksave which allows reading the value of stack pointer in a local variable, and
stackrestore which can restore the stack pointer with the saved value.
alloca, stacksave, and stackrestore instructions are described in Stack Manipulation
Instructions.
- Preview Feature:
Stack manipulation instructions
alloca,stacksaveandstackrestoreare preview features in PTX ISA version 7.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
8. Memory Consistency Model
In multi-threaded executions, the side-effects of memory operations performed by each thread become visible to other threads in a partial and non-identical order. This means that any two operations may appear to happen in no order, or in different orders, to different threads. The axioms introduced by the memory consistency model specify exactly which contradictions are forbidden between the orders observed by different threads.
In the absence of any constraint, each read operation returns the value committed by some write operation to the same memory location, including the initial write to that memory location. The memory consistency model effectively constrains the set of such candidate writes from which a read operation can return a value.
8.1. Scope and applicability of the model
The constraints specified under this model apply to PTX programs with any PTX ISA version number,
running on sm_70 or later architectures.
The memory consistency model does not apply to texture (including ld.global.nc) and surface
accesses.
8.1.1. Limitations on atomicity at system scope
When communicating with the host CPU, certain strong operations with system scope may not be performed atomically on some systems. For more details on atomicity guarantees to host memory, see the CUDA Atomicity Requirements.
8.2. Memory operations
The fundamental storage unit in the PTX memory model is a byte, consisting of 8 bits. Each state space available to a PTX program is a sequence of contiguous bytes in memory. Every byte in a PTX state space has a unique address relative to all threads that have access to the same state space.
Each PTX memory instruction specifies an address operand and a data type. The address operand contains a virtual address that gets converted to a physical address during memory access. The physical address and the size of the data type together define a physical memory location, which is the range of bytes starting from the physical address and extending up to the size of the data type in bytes.
The memory consistency model specification uses the terms “address” or “memory address” to indicate a virtual address, and the term “memory location” to indicate a physical memory location.
Each PTX memory instruction also specifies the operation — either a read, a write or an atomic read-modify-write — to be performed on all the bytes in the corresponding memory location.
8.2.1. Overlap
Two memory locations are said to overlap when the starting address of one location is within the range of bytes constituting the other location. Two memory operations are said to overlap when they specify the same virtual address and the corresponding memory locations overlap. The overlap is said to be complete when both memory locations are identical, and it is said to be partial otherwise.
8.2.2. Aliases
Two distinct virtual addresses are said to be aliases if they map to the same memory location.
8.2.3. Multimem Addresses
A multimem address is a virtual address which points to multiple distinct memory locations across devices.
Only multimem.* operations are valid on multimem addresses. That is, the behavior of accessing a multimem address in any other memory operation is undefined.
8.2.4. Memory Operations on Vector Data Types
The memory consistency model relates operations executed on memory locations with scalar data types, which have a maximum size and alignment of 64 bits. Memory operations with a vector data type are modelled as a set of equivalent memory operations with a scalar data type, executed in an unspecified order on the elements in the vector.
8.2.5. Memory Operations on Packed Data Types
A packed data type consists of two values of the same scalar data type, as described in Packed Data Types. These values are accessed in adjacent memory locations. A memory operation on a packed data type is modelled as a pair of equivalent memory operations on the scalar data type, executed in an unspecified order on each element of the packed data.
8.2.6. Initialization
Each byte in memory is initialized by a hypothetical write W0 executed before starting any thread in the program. If the byte is included in a program variable, and that variable has an initial value, then W0 writes the corresponding initial value for that byte; else W0 is assumed to have written an unknown but constant value to the byte.
8.3. State spaces
The relations defined in the memory consistency model are independent of state spaces. In
particular, causality order closes over all memory operations across all the state spaces. But the
side-effect of a memory operation in one state space can be observed directly only by operations
that also have access to the same state space. This further constrains the synchronizing effect of a
memory operation in addition to scope. For example, the synchronizing effect of the PTX instruction
ld.relaxed.shared.sys is identical to that of ld.relaxed.shared.cluster, since no thread
outside the same cluster can execute an operation that accesses the same memory location.
8.4. Operation types
For simplicity, the rest of the document refers to the following operation types, instead of mentioning specific instructions that give rise to them.
Operation Type |
Instruction/Operation |
|---|---|
atomic operation |
|
read operation |
All variants of |
write operation |
All variants of |
memory operation |
A read or write operation. |
volatile operation |
An instruction with |
acquire operation |
A memory operation with |
release operation |
A memory operation with |
mmio operation |
An |
memory fence operation |
A |
proxy fence operation |
A |
strong operation |
A memory fence operation, or a memory operation with a |
weak operation |
An |
synchronizing operation |
A |
8.4.1. mmio Operation
An mmio operation is a memory operation with .mmio qualifier specified. It is usually performed
on a memory location which is mapped to the control registers of peer I/O devices. It can also be
used for communication between threads but has poor performance relative to non-mmio operations.
The semantic meaning of mmio operations cannot be defined precisely as it is defined by the underlying I/O device. For formal specification of semantics of mmio operation from Memory Consistency Model perspective, it is equivalent to the semantics of a strong operation. But it follows a few implementation-specific properties, if it meets the CUDA atomicity requirements at the specified scope:
Writes are always performed and are never combined within the scope specified.
Reads are always performed, and are not forwarded, prefetched, combined, or allowed to hit any cache within the scope specified.
As an exception, in some implementations, the surrounding locations may also be loaded. In such cases the amount of data loaded is implementation specific and varies between 32 and 128 bytes in size.
8.5. Scope
Each strong operation must specify a scope, which is the set of threads that may interact directly with that operation and establish any of the relations described in the memory consistency model. There are four scopes:
Scope |
Description |
|---|---|
|
The set of all threads executing in the same CTA as the current thread. |
|
The set of all threads executing in the same cluster as the current thread. |
|
The set of all threads in the current program executing on the same compute device as the current thread. This also includes other kernel grids invoked by the host program on the same compute device. |
|
The set of all threads in the current program, including all kernel grids invoked by the host program on all compute devices, and all threads constituting the host program itself. |
Note that the warp is not a scope; the CTA is the smallest collection of threads that qualifies as a scope in the memory consistency model.
8.6. Proxies
A memory proxy, or a proxy is an abstract label applied to a method of memory access. When two memory operations use distinct methods of memory access, they are said to be different proxies.
Memory operations as defined in Operation types use generic method of memory access, i.e. a generic proxy. Other operations such as textures and surfaces all use distinct methods of memory access, also distinct from the generic method.
A proxy fence is required to synchronize memory operations across different proxies. Although virtual aliases use the generic method of memory access, since using distinct virtual addresses behaves as if using different proxies, they require a proxy fence to establish memory ordering.
8.7. Morally strong operations
Two operations are said to be morally strong relative to each other if they satisfy all of the following conditions:
The operations are related in program order (i.e, they are both executed by the same thread), or each operation is strong and specifies a scope that includes the thread executing the other operation.
Both operations are performed via the same proxy.
If both are memory operations, then they overlap completely.
Most (but not all) of the axioms in the memory consistency model depend on relations between morally strong operations.
8.7.1. Conflict and Data-races
Two overlapping memory operations are said to conflict when at least one of them is a write.
Two conflicting memory operations are said to be in a data-race if they are not related in causality order and they are not morally strong.
8.7.2. Limitations on Mixed-size Data-races
A data-race between operations that overlap completely is called a uniform-size data-race, while a data-race between operations that overlap partially is called a mixed-size data-race.
The axioms in the memory consistency model do not apply if a PTX program contains one or more mixed-size data-races. But these axioms are sufficient to describe the behavior of a PTX program with only uniform-size data-races.
Atomicity of mixed-size RMW operations
In any program with or without mixed-size data-races, the following property holds for every pair of overlapping atomic operations A1 and A2 such that each specifies a scope that includes the other: Either the read-modify-write operation specified by A1 is performed completely before A2 is initiated, or vice versa. This property holds irrespective of whether the two operations A1 and A2 overlap partially or completely.
8.8. Release and Acquire Patterns
Some sequences of instructions give rise to patterns that participate in memory synchronization as described later. The release pattern makes prior operations from the current thread1 visible to some operations from other threads. The acquire pattern makes some operations from other threads visible to later operations from the current thread.
A release pattern on a location M consists of one of the following:
A release operation on M
E.g.:
st.release [M];oratom.acq_rel [M];ormbarrier.arrive.release [M];Or a release operation on M followed by a strong write on M in program order
E.g.:
st.release [M];st.relaxed [M];Or a memory fence followed by a strong write on M in program order
E.g.:
fence; st.relaxed [M];
Any memory synchronization established by a release pattern only affects operations occurring in program order before the first instruction in that pattern.
An acquire pattern on a location M consists of one of the following:
An acquire operation on M
E.g.:
ld.acquire [M];oratom.acq_rel [M];ormbarrier.test_wait.acquire [M];Or a strong read on M followed by an acquire operation on M in program order
E.g.:
ld.relaxed [M]; ld.acquire [M];Or a strong read on M followed by a memory fence in program order
E.g.:
ld.relaxed [M]; fence;
Any memory synchronization established by an acquire pattern only affects operations occurring in program order after the last instruction in that pattern.
1 For both release and acquire patterns, this effect is further extended to operations in other threads through the transitive nature of causality order.
8.9. Ordering of memory operations
The sequence of operations performed by each thread is captured as program order while memory synchronization across threads is captured as causality order. The visibility of the side-effects of memory operations to other memory operations is captured as communication order. The memory consistency model defines contradictions that are disallowed between communication order on the one hand, and causality order and program order on the other.
8.9.1. Program Order
The program order relates all operations performed by a thread to the order in which a sequential processor will execute instructions in the corresponding PTX source. It is a transitive relation that forms a total order over the operations performed by the thread, but does not relate operations from different threads.
8.9.1.1. Asynchronous Operations
Some PTX instructions (all variants of cp.async, cp.async.bulk, cp.reduce.async.bulk,
wgmma.mma_async) perform operations that are asynchronous to the thread that executed the
instruction. These asynchronous operations are ordered after prior instructions in the same thread
(except in the case of wgmma.mma_async), but they are not part of the program order for that
thread. Instead, they provide weaker ordering guarantees as documented in the instruction
description.
For example, the loads and stores performed as part of a cp.async are ordered with respect to
each other, but not to those of any other cp.async instructions initiated by the same thread,
nor any other instruction subsequently issued by the thread with the exception of
cp.async.commit_group or cp.async.mbarrier.arrive. The asynchronous mbarrier arrive-on operation
performed by a cp.async.mbarrier.arrive instruction is ordered with respect to the memory
operations performed by all prior cp.async operations initiated by the same thread, but not to
those of any other instruction issued by the thread. The implicit mbarrier complete-tx
operation that is part of all variants of cp.async.bulk and cp.reduce.async.bulk
instructions is ordered only with respect to the memory operations performed by the same
asynchronous instruction, and in particular it does not transitively establish ordering with respect
to prior instructions from the issuing thread.
8.9.2. Observation Order
Observation order relates a write W to a read R through an optional sequence of atomic read-modify-write operations.
A write W precedes a read R in observation order if:
R and W are morally strong and R reads the value written by W, or
For some atomic operation Z, W precedes Z and Z precedes R in observation order.
8.9.3. Fence-SC Order
The Fence-SC order is an acyclic partial order, determined at runtime, that relates every pair of morally strong fence.sc operations.
8.9.4. Memory synchronization
Synchronizing operations performed by different threads synchronize with each other at runtime as described here. The effect of such synchronization is to establish causality order across threads.
A fence.sc operation X synchronizes with a fence.sc operation Y if X precedes Y in the Fence-SC order.
A bar{.cta}.sync or bar{.cta}.red or bar{.cta}.arrive operation synchronizes with a bar{.cta}.sync or bar{.cta}.red operation executed on the same barrier.
A
barrier.cluster.arriveoperation synchronizes with abarrier.cluster.waitoperation.A release pattern X synchronizes with an acquire pattern Y, if a write operation in X precedes a read operation in Y in observation order, and the first operation in X and the last operation in Y are morally strong.
API synchronization
A synchronizes relation can also be established by certain CUDA APIs.
Completion of a task enqueued in a CUDA stream synchronizes with the start of the following task in the same stream, if any.
For purposes of the above, recording or waiting on a CUDA event in a stream, or causing a cross-stream barrier to be inserted due to
cudaStreamLegacy, enqueues tasks in the associated streams even if there are no direct side effects. An event record task synchronizes with matching event wait tasks, and a barrier arrival task synchronizes with matching barrier wait tasks.Start of a CUDA kernel synchronizes with start of all threads in the kernel. End of all threads in a kernel synchronize with end of the kernel.
Start of a CUDA graph synchronizes with start of all source nodes in the graph. Completion of all sink nodes in a CUDA graph synchronizes with completion of the graph. Completion of a graph node synchronizes with start of all nodes with a direct dependency.
Start of a CUDA API call to enqueue a task synchronizes with start of the task.
Completion of the last task queued to a stream, if any, synchronizes with return from
cudaStreamSynchronize. Completion of the most recently queued matching event record task, if any, synchronizes with return fromcudaEventSynchronize. Synchronizing a CUDA device or context behaves as if synchronizing all streams in the context, including ones that have been destroyed.Returning
cudaSuccessfrom an API to query a CUDA handle, such as a stream or event, behaves the same as return from the matching synchronization API.
In addition to establishing a synchronizes relation, the CUDA API synchronization mechanisms above also participate in proxy-preserved base causality order.
8.9.5. Causality Order
Causality order captures how memory operations become visible across threads through synchronizing operations. The axiom “Causality” uses this order to constrain the set of write operations from which a read operation may read a value.
Relations in the causality order primarily consist of relations in Base causality order1 , which is a transitive order, determined at runtime.
Base causality order
An operation X precedes an operation Y in base causality order if:
X precedes Y in program order, or
X synchronizes with Y, or
For some operation Z,
X precedes Z in program order and Z precedes Y in base causality order, or
X precedes Z in base causality order and Z precedes Y in program order, or
X precedes Z in base causality order and Z precedes Y in base causality order.
Proxy-preserved base causality order
A memory operation X precedes a memory operation Y in proxy-preserved base causality order if X precedes Y in base causality order, and:
X and Y are performed to the same address, using the generic proxy, or
X and Y are performed to the same address, using the same proxy, and by the same thread block, or
X and Y are aliases and there is an alias proxy fence along the base causality path from X to Y.
Causality order
Causality order combines base causality order with some non-transitive relations as follows:
An operation X precedes an operation Y in causality order if:
X precedes Y in proxy-preserved base causality order, or
For some operation Z, X precedes Z in observation order, and Z precedes Y in proxy-preserved base causality order.
1 The transitivity of base causality order accounts for the “cumulativity” of synchronizing operations.
8.9.6. Coherence Order
There exists a partial transitive order that relates overlapping write operations, determined at runtime, called the coherence order1. Two overlapping write operations are related in coherence order if they are morally strong or if they are related in causality order. Two overlapping writes are unrelated in coherence order if they are in a data-race, which gives rise to the partial nature of coherence order.
1 Coherence order cannot be observed directly since it consists entirely of write operations. It may be observed indirectly by its use in constraining the set of candidate writes that a read operation may read from.
8.9.7. Communication Order
The communication order is a non-transitive order, determined at runtime, that relates write operations to other overlapping memory operations.
A write W precedes an overlapping read R in communication order if R returns the value of any byte that was written by W.
A write W precedes a write W’ in communication order if W precedes W’ in coherence order.
A read R precedes an overlapping write W in communication order if, for any byte accessed by both R and W, R returns the value written by a write W’ that precedes W in coherence order.
Communication order captures the visibility of memory operations — when a memory operation X1 precedes a memory operation X2 in communication order, X1 is said to be visible to X2.
8.10. Axioms
8.10.1. Coherence
If a write W precedes an overlapping write W’ in causality order, then W must precede W’ in coherence order.
8.10.2. Fence-SC
Fence-SC order cannot contradict causality order. For a pair of morally strong fence.sc operations F1 and F2, if F1 precedes F2 in causality order, then F1 must precede F2 in Fence-SC order.
8.10.3. Atomicity
Single-Copy Atomicity
Conflicting morally strong operations are performed with single-copy atomicity. When a read R and a write W are morally strong, then the following two communications cannot both exist in the same execution, for the set of bytes accessed by both R and W:
R reads any byte from W.
R reads any byte from any write W’ which precedes W in coherence order.
Atomicity of read-modify-write (RMW) operations
When an atomic operation A and a write W overlap and are morally strong, then the following two communications cannot both exist in the same execution, for the set of bytes accessed by both A and W:
A reads any byte from a write W’ that precedes W in coherence order.
A follows W in coherence order.
Litmus Test 1:
.global .u32 x = 0;
|
|
T1 |
T2 |
A1: atom.sys.inc.u32 %r0, [x];
|
A2: atom.sys.inc.u32 %r0, [x];
|
FINAL STATE: x == 2
|
|
Atomicity is guaranteed when the operations are morally strong.
Litmus Test 2:
.global .u32 x = 0;
|
|
T1 |
T2 (In a different CTA) |
A1: atom.cta.inc.u32 %r0, [x];
|
A2: atom.gpu.inc.u32 %r0, [x];
|
FINAL STATE: x == 1 OR x == 2
|
|
Atomicity is not guaranteed if the operations are not morally strong.
8.10.4. No Thin Air
Values may not appear “out of thin air”: an execution cannot speculatively produce a value in such a way that the speculation becomes self-satisfying through chains of instruction dependencies and inter-thread communication. This matches both programmer intuition and hardware reality, but is necessary to state explicitly when performing formal analysis.
Litmus Test: Load Buffering
.global .u32 x = 0;
.global .u32 y = 0;
|
|
T1 |
T2 |
A1: ld.global.u32 %r0, [x];
B1: st.global.u32 [y], %r0;
|
A2: ld.global.u32 %r1, [y];
B2: st.global.u32 [x], %r1;
|
FINAL STATE: x == 0 AND y == 0
|
|
The litmus test known as “LB” (Load Buffering) checks such forbidden values that may arise out of thin air. Two threads T1 and T2 each read from a first variable and copy the observed result into a second variable, with the first and second variable exchanged between the threads. If each variable is initially zero, the final result shall also be zero. If A1 reads from B2 and A2 reads from B1, then values passing through the memory operations in this example form a cycle: A1->B1->A2->B2->A1. Only the values x == 0 and y == 0 are allowed to satisfy this cycle. If any of the memory operations in this example were to speculatively associate a different value with the corresponding memory location, then such a speculation would become self-fulfilling, and hence forbidden.
8.10.5. Sequential Consistency Per Location
Within any set of overlapping memory operations that are pairwise morally strong, communication order cannot contradict program order, i.e., a concatenation of program order between overlapping operations and morally strong relations in communication order cannot result in a cycle. This ensures that each program slice of overlapping pairwise morally strong operations is strictly sequentially-consistent.
Litmus Test: CoRR
.global .u32 x = 0;
|
|
T1 |
T2 |
W1: st.global.relaxed.sys.u32 [x], 1;
|
R1: ld.global.relaxed.sys.u32 %r0, [x];
R2: ld.global.relaxed.sys.u32 %r1, [x];
|
IF %r0 == 1 THEN %r1 == 1
|
|
The litmus test “CoRR” (Coherent Read-Read), demonstrates one consequence of this guarantee. A thread T1 executes a write W1 on a location x, and a thread T2 executes two (or an infinite sequence of) reads R1 and R2 on the same location x. No other writes are executed on x, except the one modelling the initial value. The operations W1, R1 and R2 are pairwise morally strong. If R1 reads from W1, then the subsequent read R2 must also observe the same value. If R2 observed the initial value of x instead, then this would form a sequence of morally-strong relations R2->W1->R1 in communication order that contradicts the program order R1->R2 in thread T2. Hence R2 cannot read the initial value of x in such an execution.
8.10.6. Causality
Relations in communication order cannot contradict causality order. This constrains the set of candidate write operations that a read operation may read from:
If a read R precedes an overlapping write W in causality order, then R cannot read from W.
If a write W precedes an overlapping read R in causality order, then for any byte accessed by both R and W, R cannot read from any write W’ that precedes W in coherence order.
Litmus Test: Message Passing
.global .u32 data = 0;
.global .u32 flag = 0;
|
|
T1 |
T2 |
W1: st.global.u32 [data], 1;
F1: fence.sys;
W2: st.global.relaxed.sys.u32 [flag], 1;
|
R1: ld.global.relaxed.sys.u32 %r0, [flag];
F2: fence.sys;
R2: ld.global.u32 %r1, [data];
|
IF %r0 == 1 THEN %r1 == 1
|
|
The litmus test known as “MP” (Message Passing) represents the essence of typical synchronization algorithms. A vast majority of useful programs can be reduced to sequenced applications of this pattern.
Thread T1 first writes to a data variable and then to a flag variable while a second thread T2 first reads from the flag variable and then from the data variable. The operations on the flag are morally strong and the memory operations in each thread are separated by a fence, and these fences are morally strong.
If R1 observes W2, then the release pattern “F1; W2” synchronizes with the acquire pattern “R1; F2”. This establishes the causality order W1 -> F1 -> W2 -> R1 -> F2 -> R2. Then axiom causality guarantees that R2 cannot read from any write that precedes W1 in coherence order. In the absence of any other writes in this example, R2 must read from W1.
Litmus Test: CoWR
// These addresses are aliases
.global .u32 data_alias_1;
.global .u32 data_alias_2;
|
T1 |
W1: st.global.u32 [data_alias_1], 1;
F1: fence.proxy.alias;
R1: ld.global.u32 %r1, [data_alias_2];
|
%r1 == 1
|
Virtual aliases require an alias proxy fence along the synchronization path.
Litmus Test: Store Buffering
The litmus test known as “SB” (Store Buffering) demonstrates the sequential consistency enforced
by the fence.sc. A thread T1 writes to a first variable, and then reads the value of a second
variable, while a second thread T2 writes to the second variable and then reads the value of the
first variable. The memory operations in each thread are separated by fence.sc instructions,
and these fences are morally strong.
.global .u32 x = 0;
.global .u32 y = 0;
|
|
T1 |
T2 |
W1: st.global.u32 [x], 1;
F1: fence.sc.sys;
R1: ld.global.u32 %r0, [y];
|
W2: st.global.u32 [y], 1;
F2: fence.sc.sys;
R2: ld.global.u32 %r1, [x];
|
%r0 == 1 OR %r1 == 1
|
|
In any execution, either F1 precedes F2 in Fence-SC order, or vice versa. If F1 precedes F2 in
Fence-SC order, then F1 synchronizes with F2. This establishes the causality order in W1 -> F1
-> F2 -> R2. Axiom causality ensures that R2 cannot read from any write that precedes W1 in
coherence order. In the absence of any other write to that variable, R2 must read from
W1. Similarly, in the case where F2 precedes F1 in Fence-SC order, R1 must read from W2. If each
fence.sc in this example were replaced by a fence.acq_rel instruction, then this outcome is
not guaranteed. There may be an execution where the write from each thread remains unobserved from
the other thread, i.e., an execution is possible, where both R1 and R2 return the initial value “0”
for variables y and x respectively.
9. Instruction Set
9.1. Format and Semantics of Instruction Descriptions
This section describes each PTX instruction. In addition to the name and the format of the instruction, the semantics are described, followed by some examples that attempt to show several possible instantiations of the instruction.
9.2. PTX Instructions
PTX instructions generally have from zero to four operands, plus an optional guard predicate
appearing after an @ symbol to the left of the opcode:
@p opcode;@p opcode a;@p opcode d, a;@p opcode d, a, b;@p opcode d, a, b, c;
For instructions that create a result value, the d operand is the destination operand, while
a, b, and c are source operands.
The setp instruction writes two destination registers. We use a | symbol to separate
multiple destination registers.
setp.lt.s32 p|q, a, b; // p = (a < b); q = !(a < b);
For some instructions the destination operand is optional. A bit bucket operand denoted with an
underscore (_) may be used in place of a destination register.
9.3. Predicated Execution
In PTX, predicate registers are virtual and have .pred as the type specifier. So, predicate
registers can be declared as
.reg .pred p, q, r;
All instructions have an optional guard predicate which controls conditional execution of the
instruction. The syntax to specify conditional execution is to prefix an instruction with @{!}p,
where p is a predicate variable, optionally negated. Instructions without a guard predicate are
executed unconditionally.
Predicates are most commonly set as the result of a comparison performed by the setp
instruction.
As an example, consider the high-level code
if (i < n)
j = j + 1;
This can be written in PTX as
setp.lt.s32 p, i, n; // p = (i < n)
@p add.s32 j, j, 1; // if i < n, add 1 to j
To get a conditional branch or conditional function call, use a predicate to control the execution of the branch or call instructions. To implement the above example as a true conditional branch, the following PTX instruction sequence might be used:
setp.lt.s32 p, i, n; // compare i to n
@!p bra L1; // if False, branch over
add.s32 j, j, 1;
L1: ...
9.3.1. Comparisons
9.3.1.1. Integer and Bit-Size Comparisons
The signed integer comparisons are the traditional eq (equal), ne (not-equal), lt
(less-than), le (less-than-or-equal), gt (greater-than), and ge
(greater-than-or-equal). The unsigned comparisons are eq, ne, lo (lower), ls
(lower-or-same), hi (higher), and hs (higher-or-same). The bit-size comparisons are eq
and ne; ordering comparisons are not defined for bit-size types.
Table 19 shows the operators for signed integer, unsigned integer, and bit-size types.
Meaning |
Signed Operator |
Unsigned Operator |
Bit-Size Operator |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
n/a |
|
|
|
n/a |
|
|
|
n/a |
|
|
|
n/a |
9.3.1.2. Floating Point Comparisons
The ordered floating-point comparisons are eq, ne, lt, le, gt, and ge. If
either operand is NaN, the result is
False. Table 20 lists the floating-point
comparison operators.
Meaning |
Floating-Point Operator |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
To aid comparison operations in the presence of NaN values, unordered floating-point comparisons
are provided: equ, neu, ltu, leu, gtu, and geu. If both operands are numeric
values (not NaN), then the comparison has the same result as its ordered counterpart. If either
operand is NaN, then the result of the comparison is True.
Table 21 lists the floating-point
comparison operators accepting NaN values.
Meaning |
Floating-Point Operator |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
To test for NaN values, two operators num (numeric) and nan (isNaN) are
provided. num returns True if both operands are numeric values (not NaN), and nan
returns True if either operand is
NaN. Table 22 lists the
floating-point comparison operators testing for NaN values.
Meaning |
Floating-Point Operator |
|---|---|
|
|
|
|
9.3.2. Manipulating Predicates
Predicate values may be computed and manipulated using the following instructions: and, or,
xor, not, and mov.
There is no direct conversion between predicates and integer values, and no direct way to load or
store predicate register values. However, setp can be used to generate a predicate from an
integer, and the predicate-based select (selp) instruction can be used to generate an integer
value based on the value of a predicate; for example:
selp.u32 %r1,1,0,%p; // convert predicate to 32-bit value
9.4. Type Information for Instructions and Operands
Typed instructions must have a type-size modifier. For example, the add instruction requires
type and size information to properly perform the addition operation (signed, unsigned, float,
different sizes), and this information must be specified as a suffix to the opcode.
Example
.reg .u16 d, a, b;
add.u16 d, a, b; // perform a 16-bit unsigned add
Some instructions require multiple type-size modifiers, most notably the data conversion instruction
cvt. It requires separate type-size modifiers for the result and source, and these are placed in
the same order as the operands. For example:
.reg .u16 a;
.reg .f32 d;
cvt.f32.u16 d, a; // convert 16-bit unsigned to 32-bit float
In general, an operand’s type must agree with the corresponding instruction-type modifier. The rules for operand and instruction type conformance are as follows:
Bit-size types agree with any type of the same size.
Signed and unsigned integer types agree provided they have the same size, and integer operands are silently cast to the instruction type if needed. For example, an unsigned integer operand used in a signed integer instruction will be treated as a signed integer by the instruction.
Floating-point types agree only if they have the same size; i.e., they must match exactly.
Table 23 summarizes these type checking rules.
Operand Type |
|||||
|---|---|---|---|---|---|
.bX |
.sX |
.uX |
.fX |
||
Instruction Type |
.bX |
okay |
okay |
okay |
okay |
.sX |
okay |
okay |
okay |
invalid |
|
.uX |
okay |
okay |
okay |
invalid |
|
.fX |
okay |
invalid |
invalid |
okay |
|
Note
Some operands have their type and size defined independently from the instruction type-size. For
example, the shift amount operand for left and right shift instructions always has type .u32,
while the remaining operands have their type and size determined by the instruction type.
Example
// 64-bit arithmetic right shift; shift amount 'b' is .u32
shr.s64 d,a,b;
9.4.1. Operand Size Exceeding Instruction-Type Size
For convenience, ld, st, and cvt instructions permit source and destination data
operands to be wider than the instruction-type size, so that narrow values may be loaded, stored,
and converted using regular-width registers. For example, 8-bit or 16-bit values may be held
directly in 32-bit or 64-bit registers when being loaded, stored, or converted to other types and
sizes. The operand type checking rules are relaxed for bit-size and integer (signed and unsigned)
instruction types; floating-point instruction types still require that the operand type-size matches
exactly, unless the operand is of bit-size type.
When a source operand has a size that exceeds the instruction-type size, the source data is truncated (chopped) to the appropriate number of bits specified by the instruction type-size.
Table 24
summarizes the relaxed type-checking rules for source operands. Note that some combinations may
still be invalid for a particular instruction; for example, the cvt instruction does not support
.bX instruction types, so those rows are invalid for cvt.
Source Operand Type |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
b8 |
b16 |
b32 |
b64 |
b128 |
s8 |
s16 |
s32 |
s64 |
u8 |
u16 |
u32 |
u64 |
f16 |
f32 |
f64 |
||
Instruction Type |
b8 |
– |
chop |
chop |
chop |
chop |
– |
chop |
chop |
chop |
– |
chop |
chop |
chop |
chop |
chop |
chop |
b16 |
inv |
– |
chop |
chop |
chop |
inv |
– |
chop |
chop |
inv |
– |
chop |
chop |
– |
chop |
chop |
|
b32 |
inv |
inv |
– |
chop |
chop |
inv |
inv |
– |
chop |
inv |
inv |
– |
chop |
inv |
– |
chop |
|
b64 |
inv |
inv |
inv |
– |
chop |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
– |
|
b128 |
inv |
inv |
inv |
inv |
– |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
|
s8 |
– |
chop |
chop |
chop |
chop |
– |
chop |
chop |
chop |
– |
chop |
chop |
chop |
inv |
inv |
inv |
|
s16 |
inv |
– |
chop |
chop |
chop |
inv |
– |
chop |
chop |
inv |
– |
chop |
chop |
inv |
inv |
inv |
|
s32 |
inv |
inv |
– |
chop |
chop |
inv |
inv |
– |
chop |
inv |
inv |
– |
chop |
inv |
inv |
inv |
|
s64 |
inv |
inv |
inv |
– |
chop |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
inv |
|
u8 |
– |
chop |
chop |
chop |
chop |
– |
chop |
chop |
chop |
– |
chop |
chop |
chop |
inv |
inv |
inv |
|
u16 |
inv |
– |
chop |
chop |
chop |
inv |
– |
chop |
chop |
inv |
– |
chop |
chop |
inv |
inv |
inv |
|
u32 |
inv |
inv |
– |
chop |
chop |
inv |
inv |
– |
chop |
inv |
inv |
– |
chop |
inv |
inv |
inv |
|
u64 |
inv |
inv |
inv |
– |
chop |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
inv |
|
f16 |
inv |
– |
chop |
chop |
chop |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
inv |
inv |
|
f32 |
inv |
inv |
– |
chop |
chop |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
inv |
|
f64 |
inv |
inv |
inv |
– |
chop |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
|
Notes |
chop = keep only low bits that fit; “–” = allowed, but no conversion needed; inv = invalid, parse error.
|
||||||||||||||||
When a destination operand has a size that exceeds the instruction-type size, the destination data is zero- or sign-extended to the size of the destination register. If the corresponding instruction type is signed integer, the data is sign-extended; otherwise, the data is zero-extended.
Table 25 summarizes the relaxed type-checking rules for destination operands.
Destination Operand Type |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
b8 |
b16 |
b32 |
b64 |
b128 |
s8 |
s16 |
s32 |
s64 |
u8 |
u16 |
u32 |
u64 |
f16 |
f32 |
f64 |
||
Instruction Type |
b8 |
– |
zext |
zext |
zext |
zext |
– |
zext |
zext |
zext |
– |
zext |
zext |
zext |
zext |
zext |
zext |
b16 |
inv |
– |
zext |
zext |
zext |
inv |
– |
zext |
zext |
inv |
– |
zext |
zext |
– |
zext |
zext |
|
b32 |
inv |
inv |
– |
zext |
zext |
inv |
inv |
– |
zext |
inv |
inv |
– |
zext |
inv |
– |
zext |
|
b64 |
inv |
inv |
inv |
– |
zext |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
– |
|
b128 |
inv |
inv |
inv |
inv |
– |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
|
s8 |
– |
sext |
sext |
sext |
sext |
– |
sext |
sext |
sext |
– |
sext |
sext |
sext |
inv |
inv |
inv |
|
s16 |
inv |
– |
sext |
sext |
sext |
inv |
– |
sext |
sext |
inv |
– |
sext |
sext |
inv |
inv |
inv |
|
s32 |
inv |
inv |
– |
sext |
sext |
inv |
inv |
– |
sext |
inv |
inv |
– |
sext |
inv |
inv |
inv |
|
s64 |
inv |
inv |
inv |
– |
sext |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
inv |
|
u8 |
– |
zext |
zext |
zext |
zext |
– |
zext |
zext |
zext |
– |
zext |
zext |
zext |
inv |
inv |
inv |
|
u16 |
inv |
– |
zext |
zext |
zext |
inv |
– |
zext |
zext |
inv |
– |
zext |
zext |
inv |
inv |
inv |
|
u32 |
inv |
inv |
– |
zext |
zext |
inv |
inv |
– |
zext |
inv |
inv |
– |
zext |
inv |
inv |
inv |
|
u64 |
inv |
inv |
inv |
– |
zext |
inv |
inv |
inv |
– |
inv |
inv |
inv |
– |
inv |
inv |
inv |
|
f16 |
inv |
– |
zext |
zext |
zext |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
inv |
inv |
|
f32 |
inv |
inv |
– |
zext |
zext |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
inv |
|
f64 |
inv |
inv |
inv |
– |
zext |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
inv |
– |
|
Notes |
sext = sign-extend; zext = zero-extend; “–” = allowed, but no conversion needed; inv = invalid, parse error.
|
||||||||||||||||
9.5. Divergence of Threads in Control Constructs
Threads in a CTA execute together, at least in appearance, until they come to a conditional control construct such as a conditional branch, conditional function call, or conditional return. If threads execute down different control flow paths, the threads are called divergent. If all of the threads act in unison and follow a single control flow path, the threads are called uniform. Both situations occur often in programs.
A CTA with divergent threads may have lower performance than a CTA with uniformly executing threads,
so it is important to have divergent threads re-converge as soon as possible. All control constructs
are assumed to be divergent points unless the control-flow instruction is marked as uniform, using
the .uni suffix. For divergent control flow, the optimizing code generator automatically
determines points of re-convergence. Therefore, a compiler or code author targeting PTX can ignore
the issue of divergent threads, but has the opportunity to improve performance by marking branch
points as uniform when the compiler or author can guarantee that the branch point is non-divergent.
9.6. Semantics
The goal of the semantic description of an instruction is to describe the results in all cases in as simple language as possible. The semantics are described using C, until C is not expressive enough.
9.6.1. Machine-Specific Semantics of 16-bit Code
A PTX program may execute on a GPU with either a 16-bit or a 32-bit data path. When executing on a 32-bit data path, 16-bit registers in PTX are mapped to 32-bit physical registers, and 16-bit computations are promoted to 32-bit computations. This can lead to computational differences between code run on a 16-bit machine versus the same code run on a 32-bit machine, since the promoted computation may have bits in the high-order half-word of registers that are not present in 16-bit physical registers. These extra precision bits can become visible at the application level, for example, by a right-shift instruction.
At the PTX language level, one solution would be to define semantics for 16-bit code that is consistent with execution on a 16-bit data path. This approach introduces a performance penalty for 16-bit code executing on a 32-bit data path, since the translated code would require many additional masking instructions to suppress extra precision bits in the high-order half-word of 32-bit registers.
Rather than introduce a performance penalty for 16-bit code running on 32-bit GPUs, the semantics of 16-bit instructions in PTX is machine-specific. A compiler or programmer may chose to enforce portable, machine-independent 16-bit semantics by adding explicit conversions to 16-bit values at appropriate points in the program to guarantee portability of the code. However, for many performance-critical applications, this is not desirable, and for many applications the difference in execution is preferable to limiting performance.
9.7. Instructions
All PTX instructions may be predicated. In the following descriptions, the optional guard predicate is omitted from the syntax.
9.7.1. Integer Arithmetic Instructions
Integer arithmetic instructions operate on the integer types in register and constant immediate forms. The integer arithmetic instructions are:
addsubmulmadmul24mad24saddivremabsnegminmaxpopcclzbfindfnsbrevbfebfibmskszextdp4adp2a
9.7.1.1. Integer Arithmetic Instructions: add
add
Add two values.
Syntax
add.type d, a, b;
add{.sat}.s32 d, a, b; // .sat applies only to .s32
.type = { .u16, .u32, .u64,
.s16, .s32, .s64,
.u16x2, .s16x2 };
Description
Performs addition and writes the resulting value into a destination register.
For .u16x2, .s16x2 instruction types, forms input vectors by half word values from source
operands. Half-word operands are then added in parallel to produce .u16x2, .s16x2 result in
destination.
Operands d, a and b have type .type. For instruction types .u16x2, .s16x2,
operands d, a and b have type .b32.
Semantics
if (type == u16x2 || type == s16x2) {
iA[0] = a[0:15];
iA[1] = a[16:31];
iB[0] = b[0:15];
iB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = iA[i] + iB[i];
}
} else {
d = a + b;
}
Notes
Saturation modifier:
- .sat
limits result to
MININT..MAXINT(no overflow) for the size of the operation. Applies only to.s32type.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
add.u16x2 and add.s16x2 introduced in PTX ISA version 8.0.
Target ISA Notes
Supported on all target architectures.
add.u16x2 and add.s16x2 require sm_90 or higher.
Examples
@p add.u32 x,y,z;
add.sat.s32 c,c,1;
add.u16x2 u,v,w;
9.7.1.2. Integer Arithmetic Instructions: sub
sub
Subtract one value from another.
Syntax
sub.type d, a, b;
sub{.sat}.s32 d, a, b; // .sat applies only to .s32
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Performs subtraction and writes the resulting value into a destination register.
Semantics
d = a - b;
Notes
Saturation modifier:
.satlimits result to
MININT..MAXINT(no overflow) for the size of the operation. Applies only to.s32type.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
sub.s32 c,a,b;
9.7.1.3. Integer Arithmetic Instructions: mul
mul
Multiply two values.
Syntax
mul.mode.type d, a, b;
.mode = { .hi, .lo, .wide };
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Compute the product of two values.
Semantics
t = a * b;
n = bitwidth of type;
d = t; // for .wide
d = t<2n-1..n>; // for .hi variant
d = t<n-1..0>; // for .lo variant
Notes
The type of the operation represents the types of the a and b operands. If .hi or
.lo is specified, then d is the same size as a and b, and either the upper or lower
half of the result is written to the destination register. If .wide is specified, then d is
twice as wide as a and b to receive the full result of the multiplication.
The .wide suffix is supported only for 16- and 32-bit integer types.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
mul.wide.s16 fa,fxs,fys; // 16*16 bits yields 32 bits
mul.lo.s16 fa,fxs,fys; // 16*16 bits, save only the low 16 bits
mul.wide.s32 z,x,y; // 32*32 bits, creates 64 bit result
9.7.1.4. Integer Arithmetic Instructions: mad
mad
Multiply two values, optionally extract the high or low half of the intermediate result, and add a third value.
Syntax
mad.mode.type d, a, b, c;
mad.hi.sat.s32 d, a, b, c;
.mode = { .hi, .lo, .wide };
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Multiplies two values, optionally extracts the high or low half of the intermediate result, and adds a third value. Writes the result into a destination register.
Semantics
t = a * b;
n = bitwidth of type;
d = t + c; // for .wide
d = t<2n-1..n> + c; // for .hi variant
d = t<n-1..0> + c; // for .lo variant
Notes
The type of the operation represents the types of the a and b operands. If .hi or .lo is
specified, then d and c are the same size as a and b, and either the upper or lower
half of the result is written to the destination register. If .wide is specified, then d and
c are twice as wide as a and b to receive the result of the multiplication.
The .wide suffix is supported only for 16-bit and 32-bit integer types.
Saturation modifier:
.satlimits result to
MININT..MAXINT(no overflow) for the size of the operation.Applies only to
.s32type in.himode.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
@p mad.lo.s32 d,a,b,c;
mad.lo.s32 r,p,q,r;
9.7.1.5. Integer Arithmetic Instructions: mul24
mul24
Multiply two 24-bit integer values.
Syntax
mul24.mode.type d, a, b;
.mode = { .hi, .lo };
.type = { .u32, .s32 };
Description
Compute the product of two 24-bit integer values held in 32-bit source registers, and return either the high or low 32-bits of the 48-bit result.
Semantics
t = a * b;
d = t<47..16>; // for .hi variant
d = t<31..0>; // for .lo variant
Notes
Integer multiplication yields a result that is twice the size of the input operands, i.e., 48-bits.
mul24.hi performs a 24x24-bit multiply and returns the high 32 bits of the 48-bit result.
mul24.lo performs a 24x24-bit multiply and returns the low 32 bits of the 48-bit result.
All operands are of the same type and size.
mul24.hi may be less efficient on machines without hardware support for 24-bit multiply.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
mul24.lo.s32 d,a,b; // low 32-bits of 24x24-bit signed multiply.
9.7.1.6. Integer Arithmetic Instructions: mad24
mad24
Multiply two 24-bit integer values and add a third value.
Syntax
mad24.mode.type d, a, b, c;
mad24.hi.sat.s32 d, a, b, c;
.mode = { .hi, .lo };
.type = { .u32, .s32 };
Description
Compute the product of two 24-bit integer values held in 32-bit source registers, and add a third, 32-bit value to either the high or low 32-bits of the 48-bit result. Return either the high or low 32-bits of the 48-bit result.
Semantics
t = a * b;
d = t<47..16> + c; // for .hi variant
d = t<31..0> + c; // for .lo variant
Notes
Integer multiplication yields a result that is twice the size of the input operands, i.e., 48-bits.
mad24.hi performs a 24x24-bit multiply and adds the high 32 bits of the 48-bit result to a third
value.
mad24.lo performs a 24x24-bit multiply and adds the low 32 bits of the 48-bit result to a third
value.
All operands are of the same type and size.
Saturation modifier:
.satlimits result of 32-bit signed addition to
MININT..MAXINT(no overflow). Applies only to.s32type in .hi mode.
mad24.hi may be less efficient on machines without hardware support for 24-bit multiply.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
mad24.lo.s32 d,a,b,c; // low 32-bits of 24x24-bit signed multiply.
9.7.1.7. Integer Arithmetic Instructions: sad
sad
Sum of absolute differences.
Syntax
sad.type d, a, b, c;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Adds the absolute value of a-b to c and writes the resulting value into d.
Semantics
d = c + ((a<b) ? b-a : a-b);
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
sad.s32 d,a,b,c;
sad.u32 d,a,b,d; // running sum
9.7.1.8. Integer Arithmetic Instructions: div
div
Divide one value by another.
Syntax
div.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Divides a by b, stores result in d.
Semantics
d = a / b;
Notes
Division by zero yields an unspecified, machine-specific value.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
div.s32 b,n,i;
9.7.1.9. Integer Arithmetic Instructions: rem
rem
The remainder of integer division.
Syntax
rem.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Divides a by b, store the remainder in d.
Semantics
d = a % b;
Notes
The behavior for negative numbers is machine-dependent and depends on whether divide rounds towards zero or negative infinity.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
rem.s32 x,x,8; // x = x%8;
9.7.1.10. Integer Arithmetic Instructions: abs
abs
Absolute value.
Syntax
abs.type d, a;
.type = { .s16, .s32, .s64 };
Description
Take the absolute value of a and store it in d.
Semantics
d = |a|;
Notes
Only for signed integers.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
abs.s32 r0,a;
9.7.1.11. Integer Arithmetic Instructions: neg
neg
Arithmetic negate.
Syntax
neg.type d, a;
.type = { .s16, .s32, .s64 };
Description
Negate the sign of a and store the result in d.
Semantics
d = -a;
Notes
Only for signed integers.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
neg.s32 r0,a;
9.7.1.12. Integer Arithmetic Instructions: min
min
Find the minimum of two values.
Syntax
min.atype d, a, b;
min{.relu}.btype d, a, b;
.atype = { .u16, .u32, .u64,
.u16x2, .s16, .s64 };
.btype = { .s16x2, .s32 };
Description
Store the minimum of a and b in d.
For .u16x2, .s16x2 instruction types, forms input vectors by half word values from source
operands. Half-word operands are then processed in parallel to produce .u16x2, .s16x2 result
in destination.
Operands d, a and b have the same type as the instruction type. For instruction types
.u16x2, .s16x2, operands d, a and b have type .b32.
Semantics
if (type == u16x2 || type == s16x2) {
iA[0] = a[0:15];
iA[1] = a[16:31];
iB[0] = b[0:15];
iB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = (iA[i] < iB[i]) ? iA[i] : iB[i];
}
} else {
d = (a < b) ? a : b; // Integer (signed and unsigned)
}
Notes
Signed and unsigned differ.
- Saturation modifier:
min.relu.{s16x2, s32}clamps the result to 0 if negative.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
min.u16x2, min{.relu}.s16x2 and min.relu.s32 introduced in PTX ISA version 8.0.
Target ISA Notes
Supported on all target architectures.
min.u16x2, min{.relu}.s16x2 and min.relu.s32 require sm_90 or higher.
Examples
min.s32 r0,a,b;
@p min.u16 h,i,j;
min.s16x2.relu u,v,w;
9.7.1.13. Integer Arithmetic Instructions: max
max
Find the maximum of two values.
Syntax
max.atype d, a, b;
max{.relu}.btype d, a, b;
.atype = { .u16, .u32, .u64,
.u16x2, .s16, .s64 };
.btype = { .s16x2, .s32 };
Description
Store the maximum of a and b in d.
For .u16x2, .s16x2 instruction types, forms input vectors by half word values from source
operands. Half-word operands are then processed in parallel to produce .u16x2, .s16x2 result
in destination.
Operands d, a and b have the same type as the instruction type. For instruction types
.u16x2, .s16x2, operands d, a and b have type .b32.
Semantics
if (type == u16x2 || type == s16x2) {
iA[0] = a[0:15];
iA[1] = a[16:31];
iB[0] = b[0:15];
iB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = (iA[i] > iB[i]) ? iA[i] : iB[i];
}
} else {
d = (a > b) ? a : b; // Integer (signed and unsigned)
}
Notes
Signed and unsigned differ.
- Saturation modifier:
max.relu.{s16x2, s32}clamps the result to 0 if negative.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
max.u16x2, max{.relu}.s16x2 and max.relu.s32 introduced in PTX ISA version 8.0.
Target ISA Notes
Supported on all target architectures.
max.u16x2, max{.relu}.s16x2 and max.relu.s32 require sm_90 or higher.
Examples
max.u32 d,a,b;
max.s32 q,q,0;
max.relu.s16x2 t,t,u;
9.7.1.14. Integer Arithmetic Instructions: popc
popc
Population count.
Syntax
popc.type d, a;
.type = { .b32, .b64 };
Description
Count the number of one bits in a and place the resulting population count in 32-bit
destination register d. Operand a has the instruction type and destination d has type
.u32.
Semantics
.u32 d = 0;
while (a != 0) {
if (a & 0x1) d++;
a = a >> 1;
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
popc requires sm_20 or higher.
Examples
popc.b32 d, a;
popc.b64 cnt, X; // cnt is .u32
9.7.1.15. Integer Arithmetic Instructions: clz
clz
Count leading zeros.
Syntax
clz.type d, a;
.type = { .b32, .b64 };
Description
Count the number of leading zeros in a starting with the most-significant bit and place the
result in 32-bit destination register d. Operand a has the instruction type, and destination
d has type .u32. For .b32 type, the number of leading zeros is between 0 and 32,
inclusively. For.b64 type, the number of leading zeros is between 0 and 64, inclusively.
Semantics
.u32 d = 0;
if (.type == .b32) { max = 32; mask = 0x80000000; }
else { max = 64; mask = 0x8000000000000000; }
while (d < max && (a&mask == 0) ) {
d++;
a = a << 1;
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
clz requires sm_20 or higher.
Examples
clz.b32 d, a;
clz.b64 cnt, X; // cnt is .u32
9.7.1.16. Integer Arithmetic Instructions: bfind
bfind
Find most significant non-sign bit.
Syntax
bfind.type d, a;
bfind.shiftamt.type d, a;
.type = { .u32, .u64,
.s32, .s64 };
Description
Find the bit position of the most significant non-sign bit in a and place the result in
d. Operand a has the instruction type, and destination d has type .u32. For unsigned
integers, bfind returns the bit position of the most significant 1. For signed integers,
bfind returns the bit position of the most significant 0 for negative inputs and the most
significant 1 for non-negative inputs.
If .shiftamt is specified, bfind returns the shift amount needed to left-shift the found bit
into the most-significant bit position.
bfind returns 0xffffffff if no non-sign bit is found.
Semantics
msb = (.type==.u32 || .type==.s32) ? 31 : 63;
// negate negative signed inputs
if ( (.type==.s32 || .type==.s64) && (a & (1<<msb)) ) {
a = ~a;
}
.u32 d = 0xffffffff;
for (.s32 i=msb; i>=0; i--) {
if (a & (1<<i)) { d = i; break; }
}
if (.shiftamt && d != 0xffffffff) { d = msb - d; }
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
bfind requires sm_20 or higher.
Examples
bfind.u32 d, a;
bfind.shiftamt.s64 cnt, X; // cnt is .u32
9.7.1.17. Integer Arithmetic Instructions: fns
fns
Find the n-th set bit
Syntax
fns.b32 d, mask, base, offset;
Description
Given a 32-bit value mask and an integer value base (between 0 and 31), find the n-th (given
by offset) set bit in mask from the base bit, and store the bit position in d. If not
found, store 0xffffffff in d.
Operand mask has a 32-bit type. Operand base has .b32, .u32 or .s32
type. Operand offset has .s32 type. Destination d has type .b32.
Operand base must be <= 31, otherwise behavior is undefined.
Semantics
d = 0xffffffff;
if (offset == 0) {
if (mask[base] == 1) {
d = base;
}
} else {
pos = base;
count = |offset| - 1;
inc = (offset > 0) ? 1 : -1;
while ((pos >= 0) && (pos < 32)) {
if (mask[pos] == 1) {
if (count == 0) {
d = pos;
break;
} else {
count = count – 1;
}
}
pos = pos + inc;
}
}
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
fns requires sm_30 or higher.
Examples
fns.b32 d, 0xaaaaaaaa, 3, 1; // d = 3
fns.b32 d, 0xaaaaaaaa, 3, -1; // d = 3
fns.b32 d, 0xaaaaaaaa, 2, 1; // d = 3
fns.b32 d, 0xaaaaaaaa, 2, -1; // d = 1
9.7.1.18. Integer Arithmetic Instructions: brev
brev
Bit reverse.
Syntax
brev.type d, a;
.type = { .b32, .b64 };
Description
Perform bitwise reversal of input.
Semantics
msb = (.type==.b32) ? 31 : 63;
for (i=0; i<=msb; i++) {
d[i] = a[msb-i];
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
brev requires sm_20 or higher.
Examples
brev.b32 d, a;
9.7.1.19. Integer Arithmetic Instructions: bfe
bfe
Bit Field Extract.
Syntax
bfe.type d, a, b, c;
.type = { .u32, .u64,
.s32, .s64 };
Description
Extract bit field from a and place the zero or sign-extended result in d. Source b gives
the bit field starting bit position, and source c gives the bit field length in bits.
Operands a and d have the same type as the instruction type. Operands b and c are
type .u32, but are restricted to the 8-bit value range 0..255.
The sign bit of the extracted field is defined as:
.u32,.u64:zero
.s32,.s64:msbof input a if the extracted field extends beyond themsbof amsbof extracted field, otherwise
If the bit field length is zero, the result is zero.
The destination d is padded with the sign bit of the extracted field. If the start position is
beyond the msb of the input, the destination d is filled with the replicated sign bit of the
extracted field.
Semantics
msb = (.type==.u32 || .type==.s32) ? 31 : 63;
pos = b & 0xff; // pos restricted to 0..255 range
len = c & 0xff; // len restricted to 0..255 range
if (.type==.u32 || .type==.u64 || len==0)
sbit = 0;
else
sbit = a[min(pos+len-1,msb)];
d = 0;
for (i=0; i<=msb; i++) {
d[i] = (i<len && pos+i<=msb) ? a[pos+i] : sbit;
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
bfe requires sm_20 or higher.
Examples
bfe.b32 d,a,start,len;
9.7.1.20. Integer Arithmetic Instructions: bfi
bfi
Bit Field Insert.
Syntax
bfi.type f, a, b, c, d;
.type = { .b32, .b64 };
Description
Align and insert a bit field from a into b, and place the result in f. Source c
gives the starting bit position for the insertion, and source d gives the bit field length in
bits.
Operands a, b, and f have the same type as the instruction type. Operands c and
d are type .u32, but are restricted to the 8-bit value range 0..255.
If the bit field length is zero, the result is b.
If the start position is beyond the msb of the input, the result is b.
Semantics
msb = (.type==.b32) ? 31 : 63;
pos = c & 0xff; // pos restricted to 0..255 range
len = d & 0xff; // len restricted to 0..255 range
f = b;
for (i=0; i<len && pos+i<=msb; i++) {
f[pos+i] = a[i];
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
bfi requires sm_20 or higher.
Examples
bfi.b32 d,a,b,start,len;
9.7.1.21. Integer Arithmetic Instructions: szext
szext
Sign-extend or Zero-extend.
Syntax
szext.mode.type d, a, b;
.mode = { .clamp, .wrap };
.type = { .u32, .s32 };
Description
Sign-extends or zero-extends an N-bit value from operand a where N is specified in operand
b. The resulting value is stored in the destination operand d.
For the .s32 instruction type, the value in a is treated as an N-bit signed value and the
most significant bit of this N-bit value is replicated up to bit 31. For the .u32 instruction
type, the value in a is treated as an N-bit unsigned number and is zero-extended to 32
bits. Operand b is an unsigned 32-bit value.
If the value of N is 0, then the result of szext is 0. If the value of N is 32 or higher, then
the result of szext depends upon the value of the .mode qualifier as follows:
If
.modeis.clamp, then the result is the same as the source operanda.If
.modeis.wrap, then the result is computed using the wrapped value of N.
Semantics
b1 = b & 0x1f;
too_large = (b >= 32 && .mode == .clamp) ? true : false;
mask = too_large ? 0 : (~0) << b1;
sign_pos = (b1 - 1) & 0x1f;
if (b1 == 0 || too_large || .type != .s32) {
sign_bit = false;
} else {
sign_bit = (a >> sign_pos) & 1;
}
d = (a & ~mask) | (sign_bit ? mask | 0);
PTX ISA Notes
Introduced in PTX ISA version 7.6.
Target ISA Notes
szext requires sm_70 or higher.
Examples
szext.clamp.s32 rd, ra, rb;
szext.wrap.u32 rd, 0xffffffff, 0; // Result is 0.
9.7.1.22. Integer Arithmetic Instructions: bmsk
bmsk
Bit Field Mask.
Syntax
bmsk.mode.b32 d, a, b;
.mode = { .clamp, .wrap };
Description
Generates a 32-bit mask starting from the bit position specified in operand a, and of the width
specified in operand b. The generated bitmask is stored in the destination operand d.
The resulting bitmask is 0 in the following cases:
When the value of
ais 32 or higher and.modeis.clamp.When either the specified value of
bor the wrapped value ofb(when.modeis specified as.wrap) is 0.
Semantics
a1 = a & 0x1f;
mask0 = (~0) << a1;
b1 = b & 0x1f;
sum = a1 + b1;
mask1 = (~0) << sum;
sum-overflow = sum >= 32 ? true : false;
bit-position-overflow = false;
bit-width-overflow = false;
if (.mode == .clamp) {
if (a >= 32) {
bit-position-overflow = true;
mask0 = 0;
}
if (b >= 32) {
bit-width-overflow = true;
}
}
if (sum-overflow || bit-position-overflow || bit-width-overflow) {
mask1 = 0;
} else if (b1 == 0) {
mask1 = ~0;
}
d = mask0 & ~mask1;
Notes
The bitmask width specified by operand b is limited to range 0..32 in .clamp mode and to
range 0..31 in .wrap mode.
PTX ISA Notes
Introduced in PTX ISA version 7.6.
Target ISA Notes
bmsk requires sm_70 or higher.
Examples
bmsk.clamp.b32 rd, ra, rb;
bmsk.wrap.b32 rd, 1, 2; // Creates a bitmask of 0x00000006.
9.7.1.23. Integer Arithmetic Instructions: dp4a
dp4a
Four-way byte dot product-accumulate.
Syntax
dp4a.atype.btype d, a, b, c;
.atype = .btype = { .u32, .s32 };
Description
Four-way byte dot product which is accumulated in 32-bit result.
Operand a and b are 32-bit inputs which hold 4 byte inputs in packed form for dot product.
Operand c has type .u32 if both .atype and .btype are .u32 else operand c
has type .s32.
Semantics
d = c;
// Extract 4 bytes from a 32bit input and sign or zero extend
// based on input type.
Va = extractAndSignOrZeroExt_4(a, .atype);
Vb = extractAndSignOrZeroExt_4(b, .btype);
for (i = 0; i < 4; ++i) {
d += Va[i] * Vb[i];
}
PTX ISA Notes
Introduced in PTX ISA version 5.0.
Target ISA Notes
Requires sm_61 or higher.
Examples
dp4a.u32.u32 d0, a0, b0, c0;
dp4a.u32.s32 d1, a1, b1, c1;
9.7.1.24. Integer Arithmetic Instructions: dp2a
dp2a
Two-way dot product-accumulate.
Syntax
dp2a.mode.atype.btype d, a, b, c;
.atype = .btype = { .u32, .s32 };
.mode = { .lo, .hi };
Description
Two-way 16-bit to 8-bit dot product which is accumulated in 32-bit result.
Operand a and b are 32-bit inputs. Operand a holds two 16-bits inputs in packed form and
operand b holds 4 byte inputs in packed form for dot product.
Depending on the .mode specified, either lower half or upper half of operand b will be used
for dot product.
Operand c has type .u32 if both .atype and .btype are .u32 else operand c
has type .s32.
Semantics
d = c;
// Extract two 16-bit values from a 32-bit input and sign or zero extend
// based on input type.
Va = extractAndSignOrZeroExt_2(a, .atype);
// Extract four 8-bit values from a 32-bit input and sign or zer extend
// based on input type.
Vb = extractAndSignOrZeroExt_4(b, .btype);
b_select = (.mode == .lo) ? 0 : 2;
for (i = 0; i < 2; ++i) {
d += Va[i] * Vb[b_select + i];
}
PTX ISA Notes
Introduced in PTX ISA version 5.0.
Target ISA Notes
Requires sm_61 or higher.
Examples
dp2a.lo.u32.u32 d0, a0, b0, c0;
dp2a.hi.u32.s32 d1, a1, b1, c1;
9.7.2. Extended-Precision Integer Arithmetic Instructions
Instructions add.cc, addc, sub.cc, subc, mad.cc and madc reference an
implicitly specified condition code register (CC) having a single carry flag bit (CC.CF)
holding carry-in/carry-out or borrow-in/borrow-out. These instructions support extended-precision
integer addition, subtraction, and multiplication. No other instructions access the condition code,
and there is no support for setting, clearing, or testing the condition code. The condition code
register is not preserved across calls and is mainly intended for use in straight-line code
sequences for computing extended-precision integer addition, subtraction, and multiplication.
The extended-precision arithmetic instructions are:
add.cc,addcsub.cc,subcmad.cc,madc
9.7.2.1. Extended-Precision Arithmetic Instructions: add.cc
add.cc
Add two values with carry-out.
Syntax
add.cc.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };
Description
Performs integer addition and writes the carry-out value into the condition code register.
Semantics
d = a + b;
carry-out written to CC.CF
Notes
No integer rounding modifiers.
No saturation.
Behavior is the same for unsigned and signed integers.
PTX ISA Notes
32-bit add.cc introduced in PTX ISA version 1.2.
64-bit add.cc introduced in PTX ISA version 4.3.
Target ISA Notes
32-bit add.cc is supported on all target architectures.
64-bit add.cc requires sm_20 or higher.
Examples
@p add.cc.u32 x1,y1,z1; // extended-precision addition of
@p addc.cc.u32 x2,y2,z2; // two 128-bit values
@p addc.cc.u32 x3,y3,z3;
@p addc.u32 x4,y4,z4;
9.7.2.2. Extended-Precision Arithmetic Instructions: addc
addc
Add two values with carry-in and optional carry-out.
Syntax
addc{.cc}.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };
Description
Performs integer addition with carry-in and optionally writes the carry-out value into the condition code register.
Semantics
d = a + b + CC.CF;
if .cc specified, carry-out written to CC.CF
Notes
No integer rounding modifiers.
No saturation.
Behavior is the same for unsigned and signed integers.
PTX ISA Notes
32-bit addc introduced in PTX ISA version 1.2.
64-bit addc introduced in PTX ISA version 4.3.
Target ISA Notes
32-bit addc is supported on all target architectures.
64-bit addc requires sm_20 or higher.
Examples
@p add.cc.u32 x1,y1,z1; // extended-precision addition of
@p addc.cc.u32 x2,y2,z2; // two 128-bit values
@p addc.cc.u32 x3,y3,z3;
@p addc.u32 x4,y4,z4;
9.7.2.3. Extended-Precision Arithmetic Instructions: sub.cc
sub.cc
Subtract one value from another, with borrow-out.
Syntax
sub.cc.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };
Description
Performs integer subtraction and writes the borrow-out value into the condition code register.
Semantics
d = a - b;
borrow-out written to CC.CF
Notes
No integer rounding modifiers.
No saturation.
Behavior is the same for unsigned and signed integers.
PTX ISA Notes
32-bit sub.cc introduced in PTX ISA version 1.2.
64-bit sub.cc introduced in PTX ISA version 4.3.
Target ISA Notes
32-bit sub.cc is supported on all target architectures.
64-bit sub.cc requires sm_20 or higher.
Examples
@p sub.cc.u32 x1,y1,z1; // extended-precision subtraction
@p subc.cc.u32 x2,y2,z2; // of two 128-bit values
@p subc.cc.u32 x3,y3,z3;
@p subc.u32 x4,y4,z4;
9.7.2.4. Extended-Precision Arithmetic Instructions: subc
subc
Subtract one value from another, with borrow-in and optional borrow-out.
Syntax
subc{.cc}.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };
Description
Performs integer subtraction with borrow-in and optionally writes the borrow-out value into the condition code register.
Semantics
d = a - (b + CC.CF);
if .cc specified, borrow-out written to CC.CF
Notes
No integer rounding modifiers.
No saturation.
Behavior is the same for unsigned and signed integers.
PTX ISA Notes
32-bit subc introduced in PTX ISA version 1.2.
64-bit subc introduced in PTX ISA version 4.3.
Target ISA Notes
32-bit subc is supported on all target architectures.
64-bit subc requires sm_20 or higher.
Examples
@p sub.cc.u32 x1,y1,z1; // extended-precision subtraction
@p subc.cc.u32 x2,y2,z2; // of two 128-bit values
@p subc.cc.u32 x3,y3,z3;
@p subc.u32 x4,y4,z4;
9.7.2.5. Extended-Precision Arithmetic Instructions: mad.cc
mad.cc
Multiply two values, extract high or low half of result, and add a third value with carry-out.
Syntax
mad{.hi,.lo}.cc.type d, a, b, c;
.type = { .u32, .s32, .u64, .s64 };
Description
Multiplies two values, extracts either the high or low part of the result, and adds a third value. Writes the result to the destination register and the carry-out from the addition into the condition code register.
Semantics
t = a * b;
d = t<63..32> + c; // for .hi variant
d = t<31..0> + c; // for .lo variant
carry-out from addition is written to CC.CF
Notes
Generally used in combination with madc and addc to implement extended-precision multi-word
multiplication. See madc for an example.
PTX ISA Notes
32-bit mad.cc introduced in PTX ISA version 3.0.
64-bit mad.cc introduced in PTX ISA version 4.3.
Target ISA Notes
Requires target sm_20 or higher.
Examples
@p mad.lo.cc.u32 d,a,b,c;
mad.lo.cc.u32 r,p,q,r;
9.7.2.6. Extended-Precision Arithmetic Instructions: madc
madc
Multiply two values, extract high or low half of result, and add a third value with carry-in and optional carry-out.
Syntax
madc{.hi,.lo}{.cc}.type d, a, b, c;
.type = { .u32, .s32, .u64, .s64 };
Description
Multiplies two values, extracts either the high or low part of the result, and adds a third value along with carry-in. Writes the result to the destination register and optionally writes the carry-out from the addition into the condition code register.
Semantics
t = a * b;
d = t<63..32> + c + CC.CF; // for .hi variant
d = t<31..0> + c + CC.CF; // for .lo variant
if .cc specified, carry-out from addition is written to CC.CF
Notes
Generally used in combination with mad.cc and addc to implement extended-precision
multi-word multiplication. See example below.
PTX ISA Notes
32-bit madc introduced in PTX ISA version 3.0.
64-bit madc introduced in PTX ISA version 4.3.
Target ISA Notes
Requires target sm_20 or higher.
Examples
// extended-precision multiply: [r3,r2,r1,r0] = [r5,r4] * [r7,r6]
mul.lo.u32 r0,r4,r6; // r0=(r4*r6).[31:0], no carry-out
mul.hi.u32 r1,r4,r6; // r1=(r4*r6).[63:32], no carry-out
mad.lo.cc.u32 r1,r5,r6,r1; // r1+=(r5*r6).[31:0], may carry-out
madc.hi.u32 r2,r5,r6,0; // r2 =(r5*r6).[63:32]+carry-in,
// no carry-out
mad.lo.cc.u32 r1,r4,r7,r1; // r1+=(r4*r7).[31:0], may carry-out
madc.hi.cc.u32 r2,r4,r7,r2; // r2+=(r4*r7).[63:32]+carry-in,
// may carry-out
addc.u32 r3,0,0; // r3 = carry-in, no carry-out
mad.lo.cc.u32 r2,r5,r7,r2; // r2+=(r5*r7).[31:0], may carry-out
madc.hi.u32 r3,r5,r7,r3; // r3+=(r5*r7).[63:32]+carry-in
9.7.3. Floating-Point Instructions
Floating-point instructions operate on .f32 and .f64 register operands and constant
immediate values. The floating-point instructions are:
testpcopysignaddsubmulfmamaddivabsnegminmaxrcpsqrtrsqrtsincoslg2ex2tanh
Instructions that support rounding modifiers are IEEE-754 compliant. Double-precision instructions
support subnormal inputs and results. Single-precision instructions support subnormal inputs and
results by default for sm_20 and subsequent targets, and flush subnormal inputs and results to
sign-preserving zero for sm_1x targets. The optional .ftz modifier on single-precision
instructions provides backward compatibility with sm_1x targets by flushing subnormal inputs and
results to sign-preserving zero regardless of the target architecture.
Single-precision add, sub, mul, and mad support saturation of results to the range
[0.0, 1.0], with NaNs being flushed to positive zero. NaN payloads are supported for
double-precision instructions (except for rcp.approx.ftz.f64 and rsqrt.approx.ftz.f64, which
maps input NaNs to a canonical NaN). Single-precision instructions return an unspecified
NaN. Note that future implementations may support NaN payloads for single-precision
instructions, so PTX programs should not rely on the specific single-precision NaNs being
generated.
Table 26 summarizes floating-point instructions in PTX.
Instruction |
.rn |
.rz |
.rm |
.rp |
.ftz |
.sat |
Notes |
|---|---|---|---|---|---|---|---|
|
x |
x |
x |
x |
x |
x |
If no rounding modifier is specified,
default is |
|
x |
x |
x |
x |
n/a |
n/a |
If no rounding modifier is specified,
default is |
|
n/a |
n/a |
n/a |
n/a |
x |
x |
No rounding modifier. |
|
x |
x |
x |
x |
x |
x |
|
|
x |
x |
x |
x |
n/a |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
No rounding modifier. |
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
n/a |
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
|
|
x |
x |
x |
x |
x |
n/a |
|
|
x |
x |
x |
x |
n/a |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
n/a |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
n/a |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
x |
n/a |
|
|
n/a |
n/a |
n/a |
n/a |
n/a |
n/a |
|
9.7.3.1. Floating Point Instructions: testp
testp
Test floating-point property.
Syntax
testp.op.type p, a; // result is .pred
.op = { .finite, .infinite,
.number, .notanumber,
.normal, .subnormal };
.type = { .f32, .f64 };
Description
testp tests common properties of floating-point numbers and returns a predicate value of 1
if True and 0 if False.
testp.finiteTrueif the input is not infinite orNaNtestp.infiniteTrueif the input is positive or negative infinitytestp.numberTrueif the input is notNaNtestp.notanumberTrueif the input isNaNtestp.normalTrueif the input is a normal number (notNaN, not infinity)testp.subnormalTrueif the input is a subnormal number (notNaN, not infinity)
As a special case, positive and negative zero are considered normal numbers.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
Requires sm_20 or higher.
Examples
testp.notanumber.f32 isnan, f0;
testp.infinite.f64 p, X;
9.7.3.2. Floating Point Instructions: copysign
copysign
Copy sign of one input to another.
Syntax
copysign.type d, a, b;
.type = { .f32, .f64 };
Description
Copy sign bit of a into value of b, and return the result as d.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
Requires sm_20 or higher.
Examples
copysign.f32 x, y, z;
copysign.f64 A, B, C;
9.7.3.3. Floating Point Instructions: add
add
Add two values.
Syntax
add{.rnd}{.ftz}{.sat}.f32 d, a, b;
add{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };
Description
Performs addition and writes the resulting value into a destination register.
Semantics
d = a + b;
Notes
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
The default value of rounding modifier is .rn. Note that an add instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. An add instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/add sequences with no rounding modifiers may be optimized to
use fused-multiply-add instructions on the target device.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
add.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xadd.f64supports subnormal numbers.add.f32flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
add.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
add.f32 supported on all target architectures.
add.f64 requires sm_13 or higher.
Rounding modifiers have the following target requirements:
.rn,.rzavailable for all targets
.rm,.rpfor
add.f64, requiressm_13or higher.for
add.f32, requiressm_20or higher.
Examples
@p add.rz.ftz.f32 f1,f2,f3;
9.7.3.4. Floating Point Instructions: sub
sub
Subtract one value from another.
Syntax
sub{.rnd}{.ftz}{.sat}.f32 d, a, b;
sub{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };
Description
Performs subtraction and writes the resulting value into a destination register.
Semantics
d = a - b;
Notes
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
The default value of rounding modifier is .rn. Note that a sub instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. A sub instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/sub sequences with no rounding modifiers may be optimized to
use fused-multiply-add instructions on the target device.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
sub.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xsub.f64supports subnormal numbers.sub.f32flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
sub.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
sub.f32 supported on all target architectures.
sub.f64 requires sm_13 or higher.
Rounding modifiers have the following target requirements:
.rn,.rzavailable for all targets
.rm,.rpfor
sub.f64, requiressm_13or higher.for
sub.f32, requiressm_20or higher.
Examples
sub.f32 c,a,b;
sub.rn.ftz.f32 f1,f2,f3;
9.7.3.5. Floating Point Instructions: mul
mul
Multiply two values.
Syntax
mul{.rnd}{.ftz}{.sat}.f32 d, a, b;
mul{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };
Description
Compute the product of two values.
Semantics
d = a * b;
Notes
For floating-point multiplication, all operands must be the same size.
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
The default value of rounding modifier is .rn. Note that a mul instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. A mul instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/add and mul/sub sequences with no rounding modifiers may be
optimized to use fused-multiply-add instructions on the target device.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
mul.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xmul.f64supports subnormal numbers.mul.f32flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
mul.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
mul.f32 supported on all target architectures.
mul.f64 requires sm_13 or higher.
Rounding modifiers have the following target requirements:
.rn,.rzavailable for all targets
.rm,.rpfor
mul.f64, requiressm_13or higher.for
mul.f32, requiressm_20or higher.
Examples
mul.ftz.f32 circumf,radius,pi // a single-precision multiply
9.7.3.6. Floating Point Instructions: fma
fma
Fused multiply-add.
Syntax
fma.rnd{.ftz}{.sat}.f32 d, a, b, c;
fma.rnd.f64 d, a, b, c;
.rnd = { .rn, .rz, .rm, .rp };
Description
Performs a fused multiply-add with no loss of precision in the intermediate product and addition.
Semantics
d = a*b + c;
Notes
fma.f32 computes the product of a and b to infinite precision and then adds c to
this product, again in infinite precision. The resulting value is then rounded to single precision
using the rounding mode specified by .rnd.
fma.f64 computes the product of a and b to infinite precision and then adds c to
this product, again in infinite precision. The resulting value is then rounded to double precision
using the rounding mode specified by .rnd.
fma.f64 is the same as mad.f64.
Rounding modifiers (no default):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
fma.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xfma.f64supports subnormal numbers.fma.f32is unimplemented forsm_1xtargets.
Saturation:
fma.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes
fma.f64 introduced in PTX ISA version 1.4.
fma.f32 introduced in PTX ISA version 2.0.
Target ISA Notes
fma.f32 requires sm_20 or higher.
fma.f64 requires sm_13 or higher.
Examples
fma.rn.ftz.f32 w,x,y,z;
@p fma.rn.f64 d,a,b,c;
9.7.3.7. Floating Point Instructions: mad
mad
Multiply two values and add a third value.
Syntax
mad{.ftz}{.sat}.f32 d, a, b, c; // .target sm_1x
mad.rnd{.ftz}{.sat}.f32 d, a, b, c; // .target sm_20
mad.rnd.f64 d, a, b, c; // .target sm_13 and higher
.rnd = { .rn, .rz, .rm, .rp };
Description
Multiplies two values and adds a third, and then writes the resulting value into a destination register.
Semantics
d = a*b + c;
Notes
For .target sm_20 and higher:
mad.f32computes the product ofaandbto infinite precision and then addscto this product, again in infinite precision. The resulting value is then rounded to single precision using the rounding mode specified by.rnd.mad.f64computes the product ofaandbto infinite precision and then addscto this product, again in infinite precision. The resulting value is then rounded to double precision using the rounding mode specified by.rnd.mad.{f32,f64}is the same asfma.{f32,f64}.
For .target sm_1x:
mad.f32computes the product ofaandbat double precision, and then the mantissa is truncated to 23 bits, but the exponent is preserved. Note that this is different from computing the product withmul, where the mantissa can be rounded and the exponent will be clamped. The exception formad.f32is whenc = +/-0.0,mad.f32is identical to the result computed using separate mul and add instructions. When JIT-compiled for SM 2.0 devices,mad.f32is implemented as a fused multiply-add (i.e.,fma.rn.ftz.f32). In this case,mad.f32can produce slightly different numeric results and backward compatibility is not guaranteed in this case.mad.f64computes the product ofaandbto infinite precision and then addscto this product, again in infinite precision. The resulting value is then rounded to double precision using the rounding mode specified by.rnd. Unlikemad.f32, the treatment of subnormal inputs and output follows IEEE 754 standard.mad.f64is the same asfma.f64.
Rounding modifiers (no default):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
mad.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xmad.f64supports subnormal numbers.mad.f32flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
mad.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
In PTX ISA versions 1.4 and later, a rounding modifier is required for mad.f64.
Legacy mad.f64 instructions having no rounding modifier will map to mad.rn.f64.
In PTX ISA versions 2.0 and later, a rounding modifier is required for mad.f32 for sm_20 and higher targets.
Errata
mad.f32 requires a rounding modifier for sm_20 and higher targets. However for PTX ISA
version 3.0 and earlier, ptxas does not enforce this requirement and mad.f32 silently defaults
to mad.rn.f32. For PTX ISA version 3.1, ptxas generates a warning and defaults to
mad.rn.f32, and in subsequent releases ptxas will enforce the requirement for PTX ISA version
3.2 and later.
Target ISA Notes
mad.f32 supported on all target architectures.
mad.f64 requires sm_13 or higher.
Rounding modifiers have the following target requirements:
.rn,.rz,.rm,.rpformad.f64, requiressm_13or higher..rn,.rz,.rm,.rpformad.f32, requiressm_20or higher.
Examples
@p mad.f32 d,a,b,c;
9.7.3.8. Floating Point Instructions: div
div
Divide one value by another.
Syntax
div.approx{.ftz}.f32 d, a, b; // fast, approximate divide
div.full{.ftz}.f32 d, a, b; // full-range approximate divide
div.rnd{.ftz}.f32 d, a, b; // IEEE 754 compliant rounding
div.rnd.f64 d, a, b; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };
Description
Divides a by b, stores result in d.
Semantics
d = a / b;
Notes
Fast, approximate single-precision divides:
div.approx.f32implements a fast approximation to divide, computed asd = a * (1/b). For|b|in [2-126, 2126], the maximumulperror is 2. For 2126 <|b|< 2128, ifais infinity,div.approx.f32returnsNaN, otherwise it returns 0.div.full.f32implements a relatively fast, full-range approximation that scales operands to achieve better accuracy, but is not fully IEEE 754 compliant and does not support rounding modifiers. The maximumulperror is 2 across the full range of inputs.Subnormal inputs and results are flushed to sign-preserving zero. Fast, approximate division by zero creates a value of infinity (with same sign as
a).
Divide with IEEE 754 compliant rounding:
Rounding modifiers (no default):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
div.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xdiv.f64supports subnormal numbers.div.f32flushes subnormal inputs and results to sign-preserving zero.
PTX ISA Notes
div.f32 and div.f64 introduced in PTX ISA version 1.0.
Explicit modifiers .approx, .full, .ftz, and rounding introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, one of .approx, .full, or .rnd is required.
For PTX ISA versions 1.0 through 1.3, div.f32 defaults to div.approx.ftz.f32, and
div.f64 defaults to div.rn.f64.
Target ISA Notes
div.approx.f32 and div.full.f32 supported on all target architectures.
div.rnd.f32 requires sm_20 or higher.
div.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.
div.{rz,rm,rp}.f64 requires sm_20 or higher.
Examples
div.approx.ftz.f32 diam,circum,3.14159;
div.full.ftz.f32 x, y, z;
div.rn.f64 xd, yd, zd;
9.7.3.9. Floating Point Instructions: abs
abs
Absolute value.
Syntax
abs{.ftz}.f32 d, a;
abs.f64 d, a;
Description
Take the absolute value of a and store the result in d.
Semantics
d = |a|;
Notes
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
abs.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xabs.f64supports subnormal numbers.abs.f32flushes subnormal inputs and results to sign-preserving zero.
For abs.f32, NaN input yields unspecified NaN. For abs.f64, NaN input is passed
through unchanged. Future implementations may comply with the IEEE 754 standard by preserving
payload and modifying only the sign bit.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
abs.f32 supported on all target architectures.
abs.f64 requires sm_13 or higher.
Examples
abs.ftz.f32 x,f0;
9.7.3.10. Floating Point Instructions: neg
neg
Arithmetic negate.
Syntax
neg{.ftz}.f32 d, a;
neg.f64 d, a;
Description
Negate the sign of a and store the result in d.
Semantics
d = -a;
Notes
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
neg.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xneg.f64supports subnormal numbers.neg.f32flushes subnormal inputs and results to sign-preserving zero.
NaN inputs yield an unspecified NaN. Future implementations may comply with the IEEE 754
standard by preserving payload and modifying only the sign bit.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
neg.f32 supported on all target architectures.
neg.f64 requires sm_13 or higher.
Examples
neg.ftz.f32 x,f0;
9.7.3.11. Floating Point Instructions: min
min
Find the minimum of two values.
Syntax
min{.ftz}{.NaN}{.xorsign.abs}.f32 d, a, b;
min.f64 d, a, b;
Description
Store the minimum of a and b in d.
If .NaN modifier is specified, then the result is canonical NaN if either of the inputs is
NaN.
If .abs modifier is specified, the magnitude of destination operand d is the minimum of
absolute values of both the input arguments.
If .xorsign modifier is specified, the sign bit of destination d is equal to the XOR of the
sign bits of both the inputs.
Modifiers .abs and .xorsign must be specified together and .xorsign considers the sign
bit of both inputs before applying .abs operation.
If the result of min is NaN then the .xorsign and .abs modifiers will be ignored.
Semantics
if (.xorsign) {
xorsign = getSignBit(a) ^ getSignBit(b);
if (.abs) {
a = |a|;
b = |b|;
}
}
if (isNaN(a) && isNaN(b)) d = NaN;
else if (.NaN && (isNaN(a) || isNaN(b))) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a < b) ? a : b;
if (.xorsign && !isNaN(d)) {
setSignBit(d, xorsign);
}
Notes
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
min.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xmin.f64supports subnormal numbers.min.f32flushes subnormal inputs and results to sign-preserving zero.
If values of both inputs are 0.0, then +0.0 > -0.0.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
min.NaNintroduced in PTX ISA version 7.0.
min.xorsign.abs introduced in PTX ISA version 7.2.
Target ISA Notes
min.f32 supported on all target architectures.
min.f64 requires sm_13 or higher.
min.NaNrequires sm_80 or higher.
min.xorsign.abs requires sm_86 or higher.
Examples
@p min.ftz.f32 z,z,x;
min.f64 a,b,c;
// fp32 min with .NaN
min.NaN.f32 f0,f1,f2;
// fp32 min with .xorsign.abs
min.xorsign.abs.f32 Rd, Ra, Rb;
9.7.3.12. Floating Point Instructions: max
max
Find the maximum of two values.
Syntax
max{.ftz}{.NaN}{.xorsign.abs}.f32 d, a, b;
max.f64 d, a, b;
Description
Store the maximum of a and b in d.
If .NaN modifier is specified, the result is canonical NaN if either of the inputs is
NaN.
If .abs modifier is specified, the magnitude of destination operand d is the maximum of
absolute values of both the input arguments.
If .xorsign modifier is specified, the sign bit of destination d is equal to the XOR of the
sign bits of both the inputs.
Modifiers .abs and .xorsign must be specified together and .xorsign considers the sign
bit of both inputs before applying .abs operation.
If the result of max is NaN then the .xorsign and .abs modifiers will be ignored.
Semantics
if (.xorsign) {
xorsign = getSignBit(a) ^ getSignBit(b);
if (.abs) {
a = |a|;
b = |b|;
}
}
if (isNaN(a) && isNaN(b)) d = NaN;
else if (.NaN && (isNaN(a) || isNaN(b))) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a > b) ? a : b;
if (.xorsign && !isNaN(d)) {
setSignBit(d, xorsign);
}
Notes
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
max.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xmax.f64supports subnormal numbers.max.f32flushes subnormal inputs and results to sign-preserving zero.
If values of both inputs are 0.0, then +0.0 > -0.0.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
max.NaNintroduced in PTX ISA version 7.0.
max.xorsign.abs introduced in PTX ISA version 7.2.
Target ISA Notes
max.f32 supported on all target architectures.
max.f64 requires sm_13 or higher.
max.NaNrequires sm_80 or higher.
max.xorsign.abs requires sm_86 or higher.
Examples
max.ftz.f32 f0,f1,f2;
max.f64 a,b,c;
// fp32 max with .NaN
max.NaN.f32 f0,f1,f2;
// fp32 max with .xorsign.abs
max.xorsign.abs.f32 Rd, Ra, Rb;
9.7.3.13. Floating Point Instructions: rcp
rcp
Take the reciprocal of a value.
Syntax
rcp.approx{.ftz}.f32 d, a; // fast, approximate reciprocal
rcp.rnd{.ftz}.f32 d, a; // IEEE 754 compliant rounding
rcp.rnd.f64 d, a; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };
Description
Compute 1/a, store result in d.
Semantics
d = 1 / a;
Notes
Fast, approximate single-precision reciprocal:
rcp.approx.f32 implements a fast approximation to reciprocal. The maximum absolute error is 2-23.0 over the range 1.0-2.0.
Input |
Result |
|---|---|
-Inf |
-0.0 |
-subnormal |
-Inf |
-0.0 |
-Inf |
+0.0 |
+Inf |
+subnormal |
+Inf |
+Inf |
+0.0 |
NaN |
NaN |
Reciprocal with IEEE 754 compliant rounding:
Rounding modifiers (no default):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
rcp.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xrcp.f64supports subnormal numbers.rcp.f32flushes subnormal inputs and results to sign-preserving zero.
PTX ISA Notes
rcp.f32 and rcp.f64 introduced in PTX ISA version 1.0. rcp.rn.f64 and explicit modifiers
.approx and .ftz were introduced in PTX ISA version 1.4. General rounding modifiers were
added in PTX ISA version 2.0.
For PTX ISA version 1.4 and later, one of .approx or .rnd is required.
For PTX ISA versions 1.0 through 1.3, rcp.f32 defaults to rcp.approx.ftz.f32, and
rcp.f64 defaults to rcp.rn.f64.
Target ISA Notes
rcp.approx.f32 supported on all target architectures.
rcp.rnd.f32 requires sm_20 or higher.
rcp.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.
rcp.{rz,rm,rp}.f64 requires sm_20 or higher.
Examples
rcp.approx.ftz.f32 ri,r;
rcp.rn.ftz.f32 xi,x;
rcp.rn.f64 xi,x;
9.7.3.14. Floating Point Instructions: rcp.approx.ftz.f64
rcp.approx.ftz.f64
Compute a fast, gross approximation to the reciprocal of a value.
Syntax
rcp.approx.ftz.f64 d, a;
Description
Compute a fast, gross approximation to the reciprocal as follows:
extract the most-significant 32 bits of
.f64operandain 1.11.20 IEEE floating-point format (i.e., ignore the least-significant 32 bits ofa),compute an approximate
.f64reciprocal of this value using the most-significant 20 bits of the mantissa of operanda,place the resulting 32-bits in 1.11.20 IEEE floating-point format in the most-significant 32-bits of destination
d,andzero the least significant 32 mantissa bits of
.f64destinationd.
Semantics
tmp = a[63:32]; // upper word of a, 1.11.20 format
d[63:32] = 1.0 / tmp;
d[31:0] = 0x00000000;
Notes
rcp.approx.ftz.f64 implements a fast, gross approximation to reciprocal.
Input a[63:32] |
Result d[63:32] |
|---|---|
-Inf |
-0.0 |
-subnormal |
-Inf |
-0.0 |
-Inf |
+0.0 |
+Inf |
+subnormal |
+Inf |
+Inf |
+0.0 |
NaN |
NaN |
Input NaNs map to a canonical NaN with encoding 0x7fffffff00000000.
Subnormal inputs and results are flushed to sign-preserving zero.
PTX ISA Notes
rcp.approx.ftz.f64 introduced in PTX ISA version 2.1.
Target ISA Notes
rcp.approx.ftz.f64 requires sm_20 or higher.
Examples
rcp.ftz.f64 xi,x;
9.7.3.15. Floating Point Instructions: sqrt
sqrt
Take the square root of a value.
Syntax
sqrt.approx{.ftz}.f32 d, a; // fast, approximate square root
sqrt.rnd{.ftz}.f32 d, a; // IEEE 754 compliant rounding
sqrt.rnd.f64 d, a; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };
Description
Compute sqrt(a) and store the result in d.
Semantics
d = sqrt(a);
Notes
sqrt.approx.f32 implements a fast approximation to square root.
Input |
Result |
|---|---|
-Inf |
NaN |
-normal |
NaN |
-subnormal |
-0.0 |
-0.0 |
-0.0 |
+0.0 |
+0.0 |
+subnormal |
+0.0 |
+Inf |
+Inf |
NaN |
NaN |
Square root with IEEE 754 compliant rounding:
Rounding modifiers (no default):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
sqrt.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xsqrt.f64supports subnormal numbers.sqrt.f32flushes subnormal inputs and results to sign-preserving zero.
PTX ISA Notes
sqrt.f32 and sqrt.f64 introduced in PTX ISA version 1.0. sqrt.rn.f64 and explicit
modifiers .approx and .ftz were introduced in PTX ISA version 1.4. General rounding
modifiers were added in PTX ISA version 2.0.
For PTX ISA version 1.4 and later, one of .approx or .rnd is required.
For PTX ISA versions 1.0 through 1.3, sqrt.f32 defaults to sqrt.approx.ftz.f32, and
sqrt.f64 defaults to sqrt.rn.f64.
Target ISA Notes
sqrt.approx.f32 supported on all target architectures.
sqrt.rnd.f32 requires sm_20 or higher.
sqrt.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.
sqrt.{rz,rm,rp}.f64 requires sm_20 or higher.
Examples
sqrt.approx.ftz.f32 r,x;
sqrt.rn.ftz.f32 r,x;
sqrt.rn.f64 r,x;
9.7.3.16. Floating Point Instructions: rsqrt
rsqrt
Take the reciprocal of the square root of a value.
Syntax
rsqrt.approx{.ftz}.f32 d, a;
rsqrt.approx.f64 d, a;
Description
Compute 1/sqrt(a) and store the result in d.
Semantics
d = 1/sqrt(a);
Notes
rsqrt.approx implements an approximation to the reciprocal square root.
Input |
Result |
|---|---|
-Inf |
NaN |
-normal |
NaN |
-subnormal |
-Inf |
-0.0 |
-Inf |
+0.0 |
+Inf |
+subnormal |
+Inf |
+Inf |
+0.0 |
NaN |
NaN |
The maximum absolute error for rsqrt.f32 is 2-22.4 over the range 1.0-4.0.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
rsqrt.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xrsqrt.f64supports subnormal numbers.rsqrt.f32flushes subnormal inputs and results to sign-preserving zero.
Note that rsqrt.approx.f64 is emulated in software and are relatively slow.
PTX ISA Notes
rsqrt.f32 and rsqrt.f64 were introduced in PTX ISA version 1.0. Explicit modifiers
.approx and .ftz were introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, the .approx modifier is required.
For PTX ISA versions 1.0 through 1.3, rsqrt.f32 defaults to rsqrt.approx.ftz.f32, and
rsqrt.f64 defaults to rsqrt.approx.f64.
Target ISA Notes
rsqrt.f32 supported on all target architectures.
rsqrt.f64 requires sm_13 or higher.
Examples
rsqrt.approx.ftz.f32 isr, x;
rsqrt.approx.f64 ISR, X;
9.7.3.17. Floating Point Instructions: rsqrt.approx.ftz.f64
rsqrt.approx.ftz.f64
Compute an approximation of the square root reciprocal of a value.
Syntax
rsqrt.approx.ftz.f64 d, a;
Description
Compute a double-precision (.f64) approximation of the square root reciprocal of a value. The
least significant 32 bits of the double-precision (.f64) destination d are all zeros.
Semantics
tmp = a[63:32]; // upper word of a, 1.11.20 format
d[63:32] = 1.0 / sqrt(tmp);
d[31:0] = 0x00000000;
Notes
rsqrt.approx.ftz.f64 implements a fast approximation of the square root reciprocal of a value.
Input |
Result |
|---|---|
-Inf |
NaN |
-subnormal |
-Inf |
-0.0 |
-Inf |
+0.0 |
+Inf |
+subnormal |
+Inf |
+Inf |
+0.0 |
NaN |
NaN |
Input NaNs map to a canonical NaN with encoding 0x7fffffff00000000.
Subnormal inputs and results are flushed to sign-preserving zero.
PTX ISA Notes
rsqrt.approx.ftz.f64 introduced in PTX ISA version 4.0.
Target ISA Notes
rsqrt.approx.ftz.f64 requires sm_20 or higher.
Examples
rsqrt.approx.ftz.f64 xi,x;
9.7.3.18. Floating Point Instructions: sin
sin
Find the sine of a value.
Syntax
sin.approx{.ftz}.f32 d, a;
Description
Find the sine of the angle a (in radians).
Semantics
d = sin(a);
Notes
sin.approx.f32 implements a fast approximation to sine.
Input |
Result |
|---|---|
-Inf |
NaN |
-subnormal |
-0.0 |
-0.0 |
-0.0 |
+0.0 |
+0.0 |
+subnormal |
+0.0 |
+Inf |
NaN |
NaN |
NaN |
The maximum absolute error is 2-20.9 in quadrant 00.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
sin.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xSubnormal inputs and results to sign-preserving zero.
PTX ISA Notes
sin.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz
introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, the .approx modifier is required.
For PTX ISA versions 1.0 through 1.3, sin.f32 defaults to sin.approx.ftz.f32.
Target ISA Notes
Supported on all target architectures.
Examples
sin.approx.ftz.f32 sa, a;
9.7.3.19. Floating Point Instructions: cos
cos
Find the cosine of a value.
Syntax
cos.approx{.ftz}.f32 d, a;
Description
Find the cosine of the angle a (in radians).
Semantics
d = cos(a);
Notes
cos.approx.f32 implements a fast approximation to cosine.
Input |
Result |
|---|---|
-Inf |
NaN |
-subnormal |
+1.0 |
-0.0 |
+1.0 |
+0.0 |
+1.0 |
+subnormal |
+1.0 |
+Inf |
NaN |
NaN |
NaN |
The maximum absolute error is 2-20.9 in quadrant 00.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
cos.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xSubnormal inputs and results to sign-preserving zero.
PTX ISA Notes
cos.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz
introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, the .approx modifier is required.
For PTX ISA versions 1.0 through 1.3, cos.f32 defaults to cos.approx.ftz.f32.
Target ISA Notes
Supported on all target architectures.
Examples
cos.approx.ftz.f32 ca, a;
9.7.3.20. Floating Point Instructions: lg2
lg2
Find the base-2 logarithm of a value.
Syntax
lg2.approx{.ftz}.f32 d, a;
Description
Determine the log2 of a.
Semantics
d = log(a) / log(2);
Notes
lg2.approx.f32 implements a fast approximation to log2(a).
Input |
Result |
|---|---|
-Inf |
NaN |
-subnormal |
-Inf |
-0.0 |
-Inf |
+0.0 |
-Inf |
+subnormal |
-Inf |
+Inf |
+Inf |
NaN |
NaN |
The maximum absolute error is 2-22.6 for mantissa.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
lg2.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xSubnormal inputs and results to sign-preserving zero.
PTX ISA Notes
lg2.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz
introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, the .approx modifier is required.
For PTX ISA versions 1.0 through 1.3, lg2.f32 defaults to lg2.approx.ftz.f32.
Target ISA Notes
Supported on all target architectures.
Examples
lg2.approx.ftz.f32 la, a;
9.7.3.21. Floating Point Instructions: ex2
ex2
Find the base-2 exponential of a value.
Syntax
ex2.approx{.ftz}.f32 d, a;
Description
Raise 2 to the power a.
Semantics
d = 2 ^ a;
Notes
ex2.approx.f32 implements a fast approximation to 2a.
Input |
Result |
|---|---|
-Inf |
+0.0 |
-subnormal |
+1.0 |
-0.0 |
+1.0 |
+0.0 |
+1.0 |
+subnormal |
+1.0 |
+Inf |
+Inf |
NaN |
NaN |
The maximum absolute error is 2-22.5 for fraction in the primary range.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
ex2.ftz.f32flushes subnormal inputs and results to sign-preserving zero.sm_1xSubnormal inputs and results to sign-preserving zero.
PTX ISA Notes
ex2.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz
introduced in PTX ISA version 1.4.
For PTX ISA version 1.4 and later, the .approx modifier is required.
For PTX ISA versions 1.0 through 1.3, ex2.f32 defaults to ex2.approx.ftz.f32.
Target ISA Notes
Supported on all target architectures.
Examples
ex2.approx.ftz.f32 xa, a;
9.7.3.22. Floating Point Instructions: tanh
tanh
Find the hyperbolic tangent of a value (in radians)
Syntax
tanh.approx.f32 d, a;
Description
Take hyperbolic tangent value of a.
The operands d and a are of type .f32.
Semantics
d = tanh(a);
Notes
tanh.approx.f32 implements a fast approximation to FP32 hyperbolic-tangent.
Results of tanh for various corner-case inputs are as follows:
Input |
Result |
|---|---|
-Inf |
-1.0 |
-subnormal |
Same as input |
-0.0 |
-0.0 |
+0.0 |
+0.0 |
+subnormal |
Same as input |
+Inf |
1.0 |
NaN |
NaN |
The subnormal numbers are supported.
Note
The subnormal inputs gets passed through to the output since the value of tanh(x) for small
values of x is approximately the same as x.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Target ISA Notes
Requires sm_75 or higher.
Examples
tanh.approx.f32 sa, a;
9.7.4. Half Precision Floating-Point Instructions
Half precision floating-point instructions operate on .f16 and .f16x2 register operands. The
half precision floating-point instructions are:
addsubmulfmanegabsminmaxtanhex2
Half-precision add, sub, mul, and fma support saturation of results to the range
[0.0, 1.0], with NaNs being flushed to positive zero. Half-precision instructions return an
unspecified NaN.
9.7.4.1. Half Precision Floating Point Instructions: add
add
Add two values.
Syntax
add{.rnd}{.ftz}{.sat}.f16 d, a, b;
add{.rnd}{.ftz}{.sat}.f16x2 d, a, b;
add{.rnd}.bf16 d, a, b;
add{.rnd}.bf16x2 d, a, b;
.rnd = { .rn };
Description
Performs addition and writes the resulting value into a destination register.
For .f16x2 and .bf16x2 instruction type, forms input vectors by half word values from source
operands. Half-word operands are then added in parallel to produce .f16x2 or .bf16x2 result
in destination.
For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For
.f16x2 instruction type, operands d, a and b have .b32 type. For .bf16
instruction type, operands d, a, b have .b16 type. For .bf16x2 instruction type,
operands d, a, b have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = a + b;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = fA[i] + fB[i];
}
}
Notes
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
The default value of rounding modifier is .rn. Note that an add instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. An add instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/add sequences with no rounding modifiers may be optimized to
use fused-multiply-add instructions on the target device.
- Subnormal numbers:
By default, subnormal numbers are supported.
add.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.- Saturation modifier:
add.sat.{f16, f16x2}clamps the result to [0.0, 1.0].NaNresults are flushed to+0.0f.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
add{.rnd}.bf16 and add{.rnd}.bf16x2 introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_53 or higher.
add{.rnd}.bf16 and add{.rnd}.bf16x2 requires sm_90 or higher.
Examples
// scalar f16 additions
add.f16 d0, a0, b0;
add.rn.f16 d1, a1, b1;
add.bf16 bd0, ba0, bb0;
add.rn.bf16 bd1, ba1, bb1;
// SIMD f16 addition
cvt.rn.f16.f32 h0, f0;
cvt.rn.f16.f32 h1, f1;
cvt.rn.f16.f32 h2, f2;
cvt.rn.f16.f32 h3, f3;
mov.b32 p1, {h0, h1}; // pack two f16 to 32bit f16x2
mov.b32 p2, {h2, h3}; // pack two f16 to 32bit f16x2
add.f16x2 p3, p1, p2; // SIMD f16x2 addition
// SIMD bf16 addition
cvt.rn.bf16x2.f32 p4, f4, f5; // Convert two f32 into packed bf16x2
cvt.rn.bf16x2.f32 p5, f6, f7; // Convert two f32 into packed bf16x2
add.bf16x2 p6, p4, p5; // SIMD bf16x2 addition
// SIMD fp16 addition
ld.global.b32 f0, [addr]; // load 32 bit which hold packed f16x2
ld.global.b32 f1, [addr + 4]; // load 32 bit which hold packed f16x2
add.f16x2 f2, f0, f1; // SIMD f16x2 addition
ld.global.b32 f3, [addr + 8]; // load 32 bit which hold packed bf16x2
ld.global.b32 f4, [addr + 12]; // load 32 bit which hold packed bf16x2
add.bf16x2 f5, f3, f4; // SIMD bf16x2 addition
9.7.4.2. Half Precision Floating Point Instructions: sub
sub
Subtract two values.
Syntax
sub{.rnd}{.ftz}{.sat}.f16 d, a, b;
sub{.rnd}{.ftz}{.sat}.f16x2 d, a, b;
sub{.rnd}.bf16 d, a, b;
sub{.rnd}.bf16x2 d, a, b;
.rnd = { .rn };
Description
Performs subtraction and writes the resulting value into a destination register.
For .f16x2 and .bf16x2 instruction type, forms input vectors by half word values from source
operands. Half-word operands are then subtracted in parallel to produce .f16x2 or .bf16x2
result in destination.
For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For
.f16x2 instruction type, operands d, a and b have .b32 type. For .bf16
instruction type, operands d, a, b have .b16 type. For .bf16x2 instruction type,
operands d, a, b have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = a - b;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = fA[i] - fB[i];
}
}
Notes
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
The default value of rounding modifier is .rn. Note that a sub instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. A sub instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/sub sequences with no rounding modifiers may be optimized to
use fused-multiply-add instructions on the target device.
- Subnormal numbers:
By default, subnormal numbers are supported.
sub.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.- Saturation modifier:
sub.sat.{f16, f16x2}clamps the result to [0.0, 1.0].NaNresults are flushed to+0.0f.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
sub{.rnd}.bf16 and sub{.rnd}.bf16x2 introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_53 or higher.
sub{.rnd}.bf16 and sub{.rnd}.bf16x2 requires sm_90 or higher.
Examples
// scalar f16 subtractions
sub.f16 d0, a0, b0;
sub.rn.f16 d1, a1, b1;
sub.bf16 bd0, ba0, bb0;
sub.rn.bf16 bd1, ba1, bb1;
// SIMD f16 subtraction
cvt.rn.f16.f32 h0, f0;
cvt.rn.f16.f32 h1, f1;
cvt.rn.f16.f32 h2, f2;
cvt.rn.f16.f32 h3, f3;
mov.b32 p1, {h0, h1}; // pack two f16 to 32bit f16x2
mov.b32 p2, {h2, h3}; // pack two f16 to 32bit f16x2
sub.f16x2 p3, p1, p2; // SIMD f16x2 subtraction
// SIMD bf16 subtraction
cvt.rn.bf16x2.f32 p4, f4, f5; // Convert two f32 into packed bf16x2
cvt.rn.bf16x2.f32 p5, f6, f7; // Convert two f32 into packed bf16x2
sub.bf16x2 p6, p4, p5; // SIMD bf16x2 subtraction
// SIMD fp16 subtraction
ld.global.b32 f0, [addr]; // load 32 bit which hold packed f16x2
ld.global.b32 f1, [addr + 4]; // load 32 bit which hold packed f16x2
sub.f16x2 f2, f0, f1; // SIMD f16x2 subtraction
// SIMD bf16 subtraction
ld.global.b32 f3, [addr + 8]; // load 32 bit which hold packed bf16x2
ld.global.b32 f4, [addr + 12]; // load 32 bit which hold packed bf16x2
sub.bf16x2 f5, f3, f4; // SIMD bf16x2 subtraction
9.7.4.3. Half Precision Floating Point Instructions: mul
mul
Multiply two values.
Syntax
mul{.rnd}{.ftz}{.sat}.f16 d, a, b;
mul{.rnd}{.ftz}{.sat}.f16x2 d, a, b;
mul{.rnd}.bf16 d, a, b;
mul{.rnd}.bf16x2 d, a, b;
.rnd = { .rn };
Description
Performs multiplication and writes the resulting value into a destination register.
For .f16x2 and .bf16x2 instruction type, forms input vectors by half word values from source
operands. Half-word operands are then multiplied in parallel to produce .f16x2 or .bf16x2
result in destination.
For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For
.f16x2 instruction type, operands d, a and b have .b32 type. For .bf16
instruction type, operands d, a, b have .b16 type. For .bf16x2 instruction type,
operands d, a, b have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = a * b;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = fA[i] * fB[i];
}
}
Notes
Rounding modifiers:
.rnmantissa LSB rounds to nearest even
The default value of rounding modifier is .rn. Note that a mul instruction with an explicit
rounding modifier is treated conservatively by the code optimizer. A mul instruction with no
rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code
optimizer. In particular, mul/add and mul/sub sequences with no rounding modifiers may
be optimized to use fused-multiply-add instructions on the target device.
- Subnormal numbers:
By default, subnormal numbers are supported.
mul.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.- Saturation modifier:
mul.sat.{f16, f16x2}clamps the result to [0.0, 1.0].NaNresults are flushed to+0.0f.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
mul{.rnd}.bf16 and mul{.rnd}.bf16x2 introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_53 or higher.
mul{.rnd}.bf16 and mul{.rnd}.bf16x2 requires sm_90 or higher.
Examples
// scalar f16 multiplications
mul.f16 d0, a0, b0;
mul.rn.f16 d1, a1, b1;
mul.bf16 bd0, ba0, bb0;
mul.rn.bf16 bd1, ba1, bb1;
// SIMD f16 multiplication
cvt.rn.f16.f32 h0, f0;
cvt.rn.f16.f32 h1, f1;
cvt.rn.f16.f32 h2, f2;
cvt.rn.f16.f32 h3, f3;
mov.b32 p1, {h0, h1}; // pack two f16 to 32bit f16x2
mov.b32 p2, {h2, h3}; // pack two f16 to 32bit f16x2
mul.f16x2 p3, p1, p2; // SIMD f16x2 multiplication
// SIMD bf16 multiplication
cvt.rn.bf16x2.f32 p4, f4, f5; // Convert two f32 into packed bf16x2
cvt.rn.bf16x2.f32 p5, f6, f7; // Convert two f32 into packed bf16x2
mul.bf16x2 p6, p4, p5; // SIMD bf16x2 multiplication
// SIMD fp16 multiplication
ld.global.b32 f0, [addr]; // load 32 bit which hold packed f16x2
ld.global.b32 f1, [addr + 4]; // load 32 bit which hold packed f16x2
mul.f16x2 f2, f0, f1; // SIMD f16x2 multiplication
// SIMD bf16 multiplication
ld.global.b32 f3, [addr + 8]; // load 32 bit which hold packed bf16x2
ld.global.b32 f4, [addr + 12]; // load 32 bit which hold packed bf16x2
mul.bf16x2 f5, f3, f4; // SIMD bf16x2 multiplication
9.7.4.4. Half Precision Floating Point Instructions: fma
fma
Fused multiply-add
Syntax
fma.rnd{.ftz}{.sat}.f16 d, a, b, c;
fma.rnd{.ftz}{.sat}.f16x2 d, a, b, c;
fma.rnd{.ftz}.relu.f16 d, a, b, c;
fma.rnd{.ftz}.relu.f16x2 d, a, b, c;
fma.rnd{.relu}.bf16 d, a, b, c;
fma.rnd{.relu}.bf16x2 d, a, b, c;
fma.rnd.oob.{relu}.type d, a, b, c;
.rnd = { .rn };
Description
Performs a fused multiply-add with no loss of precision in the intermediate product and addition.
For .f16x2 and .bf16x2 instruction type, forms input vectors by half word values from source
operands. Half-word operands are then operated in parallel to produce .f16x2 or .bf16x2
result in destination.
For .f16 instruction type, operands d, a, b and c have .f16 or .b16
type. For .f16x2 instruction type, operands d, a, b and c have .b32
type. For .bf16 instruction type, operands d, a, b and c have .b16 type. For
.bf16x2 instruction type, operands d, a, b and c have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = a * b + c;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
fC[0] = c[0:15];
fC[1] = c[16:31];
for (i = 0; i < 2; i++) {
d[i] = fA[i] * fB[i] + fC[i];
}
}
Notes
Rounding modifiers (default is .rn):
.rnmantissa LSB rounds to nearest even
- Subnormal numbers:
By default, subnormal numbers are supported.
fma.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.- Saturation modifier:
fma.sat.{f16, f16x2}clamps the result to [0.0, 1.0].NaNresults are flushed to+0.0f.fma.relu.{f16, f16x2, bf16, bf16x2}clamps the result to 0 if negative.NaNresult is converted to canonicalNaN.- Out Of Bounds modifier:
fma.oob.{f16, f16x2, bf16, bf16x2}clamps the result to 0 if either of the operands isOOB NaN(defined under Tensors) value. The test for the specialNaNvalue and resultant forcing of the result to +0.0 is performed independently for each of the two SIMD operations.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
fma.relu.{f16, f16x2} and fma{.relu}.{bf16, bf16x2} introduced in PTX ISA version 7.0.
Support for modifier .oob introduced in PTX ISA version 8.1.
Target ISA Notes
Requires sm_53 or higher.
fma.relu.{f16, f16x2} and fma{.relu}.{bf16, bf16x2} require sm_80 or higher.
fma{.oob}.{f16, f16x2, bf16, bf16x2} requires sm_90 or higher.
Examples
// scalar f16 fused multiply-add
fma.rn.f16 d0, a0, b0, c0;
fma.rn.f16 d1, a1, b1, c1;
fma.rn.relu.f16 d1, a1, b1, c1;
fma.rn.oob.f16 d1, a1, b1, c1;
fma.rn.oob.relu.f16 d1, a1, b1, c1;
// scalar bf16 fused multiply-add
fma.rn.bf16 d1, a1, b1, c1;
fma.rn.relu.bf16 d1, a1, b1, c1;
fma.rn.oob.bf16 d1, a1, b1, c1;
fma.rn.oob.relu.bf16 d1, a1, b1, c1;
// SIMD f16 fused multiply-add
cvt.rn.f16.f32 h0, f0;
cvt.rn.f16.f32 h1, f1;
cvt.rn.f16.f32 h2, f2;
cvt.rn.f16.f32 h3, f3;
mov.b32 p1, {h0, h1}; // pack two f16 to 32bit f16x2
mov.b32 p2, {h2, h3}; // pack two f16 to 32bit f16x2
fma.rn.f16x2 p3, p1, p2, p2; // SIMD f16x2 fused multiply-add
fma.rn.relu.f16x2 p3, p1, p2, p2; // SIMD f16x2 fused multiply-add with relu saturation mode
fma.rn.oob.f16x2 p3, p1, p2, p2; // SIMD f16x2 fused multiply-add with oob modifier
fma.rn.oob.relu.f16x2 p3, p1, p2, p2; // SIMD f16x2 fused multiply-add with oob modifier and relu saturation mode
// SIMD fp16 fused multiply-add
ld.global.b32 f0, [addr]; // load 32 bit which hold packed f16x2
ld.global.b32 f1, [addr + 4]; // load 32 bit which hold packed f16x2
fma.rn.f16x2 f2, f0, f1, f1; // SIMD f16x2 fused multiply-add
// SIMD bf16 fused multiply-add
fma.rn.bf16x2 f2, f0, f1, f1; // SIMD bf16x2 fused multiply-add
fma.rn.relu.bf16x2 f2, f0, f1, f1; // SIMD bf16x2 fused multiply-add with relu saturation mode
fma.rn.oob.bf16x2 f2, f0, f1, f1; // SIMD bf16x2 fused multiply-add with oob modifier
fma.rn.oob.relu.bf16x2 f2, f0, f1, f1; // SIMD bf16x2 fused multiply-add with oob modifier and relu saturation mode
9.7.4.5. Half Precision Floating Point Instructions: neg
neg
Arithmetic negate.
Syntax
neg{.ftz}.f16 d, a;
neg{.ftz}.f16x2 d, a;
neg.bf16 d, a;
neg.bf16x2 d, a;
Description
Negate the sign of a and store the result in d.
For .f16x2 and .bf16x2 instruction type, forms input vector by extracting half word values
from the source operand. Half-word operands are then negated in parallel to produce .f16x2 or
.bf16x2 result in destination.
For .f16 instruction type, operands d and a have .f16 or .b16 type. For
.f16x2 instruction type, operands d and a have .b32 type. For .bf16 instruction
type, operands d and a have .b16 type. For .bf16x2 instruction type, operands d
and a have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = -a;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
for (i = 0; i < 2; i++) {
d[i] = -fA[i];
}
}
Notes
- Subnormal numbers:
By default, subnormal numbers are supported.
neg.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.
NaN inputs yield an unspecified NaN. Future implementations may comply with the IEEE 754
standard by preserving payload and modifying only the sign bit.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
neg.bf16 and neg.bf16x2 introduced in PTX ISA 7.0.
Target ISA Notes
Requires sm_53 or higher.
neg.bf16 and neg.bf16x2 requires architecture sm_80 or higher.
Examples
neg.ftz.f16 x,f0;
neg.bf16 x,b0;
neg.bf16x2 x1,b1;
9.7.4.6. Half Precision Floating Point Instructions: abs
abs
Absolute value
Syntax
abs{.ftz}.f16 d, a;
abs{.ftz}.f16x2 d, a;
abs.bf16 d, a;
abs.bf16x2 d, a;
Description
Take absolute value of a and store the result in d.
For .f16x2 and .bf16x2 instruction type, forms input vector by extracting half word values
from the source operand. Absolute values of half-word operands are then computed in parallel to
produce .f16x2 or .bf16x2 result in destination.
For .f16 instruction type, operands d and a have .f16 or .b16 type. For
.f16x2 instruction type, operands d and a have .f16x2 or .b32 type. For
.bf16 instruction type, operands d and a have .b16 type. For .bf16x2 instruction
type, operands d and a have .b32 type.
Semantics
if (type == f16 || type == bf16) {
d = |a|;
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
for (i = 0; i < 2; i++) {
d[i] = |fA[i]|;
}
}
Notes
- Subnormal numbers:
By default, subnormal numbers are supported.
abs.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.
NaN inputs yield an unspecified NaN. Future implementations may comply with the IEEE 754
standard by preserving payload and modifying only the sign bit.
PTX ISA Notes
Introduced in PTX ISA version 6.5.
abs.bf16 and abs.bf16x2 introduced in PTX ISA 7.0.
Target ISA Notes
Requires sm_53 or higher.
abs.bf16 and abs.bf16x2 requires architecture sm_80 or higher.
Examples
abs.ftz.f16 x,f0;
abs.bf16 x,b0;
abs.bf16x2 x1,b1;
9.7.4.7. Half Precision Floating Point Instructions: min
min
Find the minimum of two values.
Syntax
min{.ftz}{.NaN}{.xorsign.abs}.f16 d, a, b;
min{.ftz}{.NaN}{.xorsign.abs}.f16x2 d, a, b;
min{.NaN}{.xorsign.abs}.bf16 d, a, b;
min{.NaN}{.xorsign.abs}.bf16x2 d, a, b;
Description
Store the minimum of a and b in d.
For .f16x2 and .bf16x2 instruction types, input vectors are formed with half-word values
from source operands. Half-word operands are then processed in parallel to store .f16x2 or
.bf16x2 result in destination.
For .f16 instruction type, operands d and a have .f16 or .b16 type. For
.f16x2 instruction type, operands d and a have .f16x2 or .b32 type. For
.bf16 instruction type, operands d and a have .b16 type. For .bf16x2 instruction
type, operands d and a have .b32 type.
If .NaN modifier is specified, then the result is canonical NaN if either of the inputs is
NaN.
If .abs modifier is specified, the magnitude of destination operand d is the minimum of
absolute values of both the input arguments.
If .xorsign modifier is specified, the sign bit of destination d is equal to the XOR of the
sign bits of both the inputs.
Modifiers .abs and .xorsign must be specified together and .xorsign considers the sign
bit of both inputs before applying .abs operation.
If the result of min is NaN then the .xorsign and .abs modifiers will be ignored.
Semantics
if (type == f16 || type == bf16) {
if (.xorsign) {
xorsign = getSignBit(a) ^ getSignBit(b);
if (.abs) {
a = |a|;
b = |b|;
}
}
if (isNaN(a) && isNaN(b)) d = NaN;
if (.NaN && (isNaN(a) || isNaN(b))) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a < b) ? a : b;
if (.xorsign && !isNaN(d)) {
setSignBit(d, xorsign);
}
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
if (.xorsign) {
xorsign = getSignBit(fA[i]) ^ getSignBit(fB[i]);
if (.abs) {
fA[i] = |fA[i]|;
fB[i] = |fB[i]|;
}
}
if (isNaN(fA[i]) && isNaN(fB[i])) d[i] = NaN;
if (.NaN && (isNaN(fA[i]) || isNaN(fB[i]))) d[i] = NaN;
else if (isNaN(fA[i])) d[i] = fB[i];
else if (isNaN(fB[i])) d[i] = fA[i];
else d[i] = (fA[i] < fB[i]) ? fA[i] : fB[i];
if (.xorsign && !isNaN(d[i])) {
setSignBit(d[i], xorsign);
}
}
}
Notes
- Subnormal numbers:
By default, subnormal numbers are supported.
min.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.
If values of both inputs are 0.0, then +0.0 > -0.0.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
min.xorsign introduced in PTX ISA version 7.2.
Target ISA Notes
Requires sm_80 or higher.
min.xorsign.abs support requires sm_86 or higher.
Examples
min.ftz.f16 h0,h1,h2;
min.f16x2 b0,b1,b2;
// SIMD fp16 min with .NaN
min.NaN.f16x2 b0,b1,b2;
min.bf16 h0, h1, h2;
// SIMD bf16 min with NaN
min.NaN.bf16x2 b0, b1, b2;
// scalar bf16 min with xorsign.abs
min.xorsign.abs.bf16 Rd, Ra, Rb
9.7.4.8. Half Precision Floating Point Instructions: max
max
Find the maximum of two values.
Syntax
max{.ftz}{.NaN}{.xorsign.abs}.f16 d, a, b;
max{.ftz}{.NaN}{.xorsign.abs}.f16x2 d, a, b;
max{.NaN}{.xorsign.abs}.bf16 d, a, b;
max{.NaN}{.xorsign.abs}.bf16x2 d, a, b;
Description
Store the maximum of a and b in d.
For .f16x2 and .bf16x2 instruction types, input vectors are formed with half-word values
from source operands. Half-word operands are then processed in parallel to store .f16x2 or
.bf16x2 result in destination.
For .f16 instruction type, operands d and a have .f16 or .b16 type. For
.f16x2 instruction type, operands d and a have .f16x2 or .b32 type. For
.bf16 instruction type, operands d and a have .b16 type. For .bf16x2 instruction
type, operands d and a have .b32 type.
If .NaN modifier is specified, the result is canonical NaN if either of the inputs is
NaN.
If .abs modifier is specified, the magnitude of destination operand d is the maximum of
absolute values of both the input arguments.
If .xorsign modifier is specified, the sign bit of destination d is equal to the XOR of the
sign bits of both the inputs.
Modifiers .abs and .xorsign must be specified together and .xorsign considers the sign
bit of both inputs before applying .abs operation.
If the result of max is NaN then the .xorsign and .abs modifiers will be ignored.
Semantics
if (type == f16 || type == bf16) {
if (.xorsign) {
xorsign = getSignBit(a) ^ getSignBit(b);
if (.abs) {
a = |a|;
b = |b|;
}
}
if (isNaN(a) && isNaN(b)) d = NaN;
if (.NaN && (isNaN(a) || isNaN(b))) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a > b) ? a : b;
if (.xorsign && !isNaN(d)) {
setSignBit(d, xorsign);
}
} else if (type == f16x2 || type == bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
if (.xorsign) {
xorsign = getSignBit(fA[i]) ^ getSignBit(fB[i]);
if (.abs) {
fA[i] = |fA[i]|;
fB[i] = |fB[i]|;
}
}
if (isNaN(fA[i]) && isNaN(fB[i])) d[i] = NaN;
if (.NaN && (isNaN(fA[i]) || isNaN(fB[i]))) d[i] = NaN;
else if (isNaN(fA[i])) d[i] = fB[i];
else if (isNaN(fB[i])) d[i] = fA[i];
else d[i] = (fA[i] > fB[i]) ? fA[i] : fB[i];
if (.xorsign && !isNaN(fA[i])) {
setSignBit(d[i], xorsign);
}
}
}
Notes
- Subnormal numbers:
By default, subnormal numbers are supported.
max.ftz.{f16, f16x2}flushes subnormal inputs and results to sign-preserving zero.
If values of both inputs are 0.0, then +0.0 > -0.0.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
max.xorsign.abs introduced in PTX ISA version 7.2.
Target ISA Notes
Requires sm_80 or higher.
max.xorsign.abs support requires sm_86 or higher.
Examples
max.ftz.f16 h0,h1,h2;
max.f16x2 b0,b1,b2;
// SIMD fp16 max with NaN
max.NaN.f16x2 b0,b1,b2;
// scalar f16 max with xorsign.abs
max.xorsign.abs.f16 Rd, Ra, Rb;
max.bf16 h0, h1, h2;
// scalar bf16 max and NaN
max.NaN.bf16x2 b0, b1, b2;
// SIMD bf16 max with xorsign.abs
max.xorsign.abs.bf16x2 Rd, Ra, Rb;
9.7.4.9. Half Precision Floating Point Instructions: tanh
tanh
Find the hyperbolic tangent of a value (in radians)
Syntax
tanh.approx.type d, a;
.type = {.f16, .f16x2, .bf16, .bf16x2}
Description
Take hyperbolic tangent value of a.
The type of operands d and a are as specified by .type.
For .f16x2 or .bf16x2 instruction type, each of the half-word operands are operated in
parallel and the results are packed appropriately into a .f16x2 or .bf16x2.
Semantics
if (.type == .f16 || .type == .bf16) {
d = tanh(a)
} else if (.type == .f16x2 || .type == .bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
d[0] = tanh(fA[0])
d[1] = tanh(fA[1])
}
Notes
tanh.approx.{f16, f16x2, bf16, bf16x2} implements an approximate hyperbolic tangent in the
target format.
Results of tanh for various corner-case inputs are as follows:
Input |
Result |
|---|---|
-Inf |
-1.0 |
-0.0 |
-0.0 |
+0.0 |
+0.0 |
+Inf |
1.0 |
NaN |
NaN |
The maximum absolute error for .f16 type is 2-10.987. The maximum absolute error for .bf16
type is 2-8.
The subnormal numbers are supported.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
tanh.approx.{bf16/bf16x2} introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_75 or higher.
tanh.approx.{bf16/bf16x2} requires sm_90 or higher.
Examples
tanh.approx.f16 h1, h0;
tanh.approx.f16x2 hd1, hd0;
tanh.approx.bf16 b1, b0;
tanh.approx.bf16x2 hb1, hb0;
9.7.4.10. Half Precision Floating Point Instructions: ex2
ex2
Find the base-2 exponent of input.
Syntax
ex2.approx.atype d, a;
ex2.approx.ftz.btype d, a;
.atype = { .f16, .f16x2}
.btype = { .bf16, .bf16x2}
Description
Raise 2 to the power a.
The type of operands d and a are as specified by .type.
For .f16x2 or .bf16x2 instruction type, each of the half-word operands are operated in
parallel and the results are packed appropriately into a .f16x2 or .bf16x2.
Semantics
if (.type == .f16 || .type == .bf16) {
d = 2 ^ a
} else if (.type == .f16x2 || .type == .bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
d[0] = 2 ^ fA[0]
d[1] = 2 ^ fA[1]
}
Notes
ex2.approx.{f16, f16x2, bf16, bf16x2} implement a fast approximation to 2a.
For the .f16 type, subnormal inputs are supported. ex2.approx.ftz.bf16 flushes subnormal
inputs and results to sign-preserving zero.
Results of ex2.approx.ftz.bf16 for various corner-case inputs are as follows:
Input |
Result |
|---|---|
-Inf |
+0.0 |
-subnormal |
+1.0 |
-0.0 |
+1.0 |
+0.0 |
+1.0 |
+subnormal |
+1.0 |
+Inf |
+Inf |
NaN |
NaN |
Results of ex2.approx.f16 for various corner-case inputs are as follows:
Input |
Result |
|---|---|
-Inf |
+0.0 |
-0.0 |
+1.0 |
+0.0 |
+1.0 |
+Inf |
+Inf |
NaN |
NaN |
The maximum relative error for .f16 type is 2-9.9. The maximum relative error for .bf16 type
is 2-7.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
ex2.approx.ftz.{bf16/bf16x2} introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_75 or higher.
ex2.approx.ftz.{bf16/bf16x2} requires sm_90 or higher.
Examples
ex2.approx.f16 h1, h0;
ex2.approx.f16x2 hd1, hd0;
ex2.approx.ftz.bf16 b1, b2;
ex2.approx.ftz.bf16x2 hb1, hb2;
9.7.5. Comparison and Selection Instructions
The comparison select instructions are:
setsetpselpslct
As with single-precision floating-point instructions, the set, setp, and slct
instructions support subnormal numbers for sm_20 and higher targets and flush single-precision
subnormal inputs to sign-preserving zero for sm_1x targets. The optional .ftz modifier
provides backward compatibility with sm_1x targets by flushing subnormal inputs and results to
sign-preserving zero regardless of the target architecture.
9.7.5.1. Comparison and Selection Instructions: set
set
Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.
Syntax
set.CmpOp{.ftz}.dtype.stype d, a, b;
set.CmpOp.BoolOp{.ftz}.dtype.stype d, a, b, {!}c;
.CmpOp = { eq, ne, lt, le, gt, ge, lo, ls, hi, hs,
equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.dtype = { .u32, .s32, .f32 };
.stype = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f32, .f64 };
Description
Compares two numeric values and optionally combines the result with another predicate value by
applying a Boolean operator. If this result is True, 1.0f is written for floating-point
destination types, and 0xffffffff is written for integer destination types. Otherwise,
0x00000000 is written.
Operand dhas type .dtype; operands a and b have type .stype; operand c has
type .pred.
Semantics
t = (a CmpOp b) ? 1 : 0;
if (isFloat(dtype))
d = BoolOp(t, c) ? 1.0f : 0x00000000;
else
d = BoolOp(t, c) ? 0xffffffff : 0x00000000;
Integer Notes
The signed and unsigned comparison operators are eq, ne, lt, le, gt, ge.
For unsigned values, the comparison operators lo, ls, hi, and hs for lower,
lower-or-same, higher, and higher-or-same may be used instead of lt, le, gt, ge,
respectively.
The untyped, bit-size comparisons are eq and ne.
Floating Point Notes
The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.
To aid comparison operations in the presence of NaN values, unordered versions are included:
equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not
NaN), then these comparisons have the same result as their ordered counterparts. If either
operand is NaN, then the result of these comparisons is True.
num returns True if both operands are numeric values (not NaN), and nan returns
True if either operand is NaN.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
set.ftz.dtype.f32flushes subnormal inputs to sign-preserving zero.sm_1xset.dtype.f64supports subnormal numbers.set.dtype.f32flushes subnormal inputs to sign-preserving zero.
Modifier .ftz applies only to .f32 comparisons.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
set with .f64 source type requires sm_13 or higher.
Examples
@p set.lt.and.f32.s32 d,a,b,r;
set.eq.u32.u32 d,i,n;
9.7.5.2. Comparison and Selection Instructions: setp
setp
Compare two numeric values with a relational operator, and (optionally) combine this result with a predicate value by applying a Boolean operator.
Syntax
setp.CmpOp{.ftz}.type p[|q], a, b;
setp.CmpOp.BoolOp{.ftz}.type p[|q], a, b, {!}c;
.CmpOp = { eq, ne, lt, le, gt, ge, lo, ls, hi, hs,
equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.type = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f32, .f64 };
Description
Compares two values and combines the result with another predicate value by applying a Boolean operator. This result is written to the first destination operand. A related value computed using the complement of the compare result is written to the second destination operand.
Applies to all numeric types. Operands a and b have type .type; operands p, q,
and c have type .pred. The sink symbol ‘_’ may be used in place of any one of the
destination operands.
Semantics
t = (a CmpOp b) ? 1 : 0;
p = BoolOp(t, c);
q = BoolOp(!t, c);
Integer Notes
The signed and unsigned comparison operators are eq, ne, lt, le, gt, ge.
For unsigned values, the comparison operators lo, ls, hi, and hs for lower,
lower-or-same, higher, and higher-or-same may be used instead of lt, le, gt, ge,
respectively.
The untyped, bit-size comparisons are eq and ne.
Floating Point Notes
The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.
To aid comparison operations in the presence of NaN values, unordered versions are included:
equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not
NaN), then these comparisons have the same result as their ordered counterparts. If either
operand is NaN, then the result of these comparisons is True.
num returns True if both operands are numeric values (not NaN), and nan returns
True if either operand is NaN.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
setp.ftz.dtype.f32flushes subnormal inputs to sign-preserving zero.sm_1xsetp.dtype.f64supports subnormal numbers.setp.dtype.f32flushes subnormal inputs to sign-preserving zero.
Modifier .ftz applies only to .f32 comparisons.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
setp with .f64 source type requires sm_13 or higher.
Examples
setp.lt.and.s32 p|q,a,b,r;
@q setp.eq.u32 p,i,n;
9.7.5.3. Comparison and Selection Instructions: selp
selp
Select between source operands, based on the value of the predicate source operand.
Syntax
selp.type d, a, b, c;
.type = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f32, .f64 };
Description
Conditional selection. If c is True, a is stored in d, b otherwise. Operands
d, a, and b must be of the same type. Operand c is a predicate.
Semantics
d = (c == 1) ? a : b;
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
selp.f64 requires sm_13 or higher.
Examples
selp.s32 r0,r,g,p;
@q selp.f32 f0,t,x,xp;
9.7.5.4. Comparison and Selection Instructions: slct
slct
Select one source operand, based on the sign of the third operand.
Syntax
slct.dtype.s32 d, a, b, c;
slct{.ftz}.dtype.f32 d, a, b, c;
.dtype = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f32, .f64 };
Description
Conditional selection. If c ≥ 0, a is stored in d, otherwise b is stored in
d. Operands d, a, and b are treated as a bitsize type of the same width as the first
instruction type; operand c must match the second instruction type (.s32 or .f32). The
selected input is copied to the output without modification.
Semantics
d = (c >= 0) ? a : b;
Floating Point Notes
For .f32 comparisons, negative zero equals zero.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
slct.ftz.dtype.f32flushes subnormal values of operandcto sign-preserving zero, and operandais selected.sm_1xslct.dtype.f32flushes subnormal values of operandcto sign-preserving zero, and operandais selected.
Modifier .ftz applies only to .f32 comparisons.
If operand c is NaN, the comparison is unordered and operand b is selected.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
slct.f64 requires sm_13 or higher.
Examples
slct.u32.s32 x, y, z, val;
slct.ftz.u64.f32 A, B, C, fval;
9.7.6. Half Precision Comparison Instructions
The comparison instructions are:
setsetp
9.7.6.1. Half Precision Comparison Instructions: set
set
Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.
Syntax
set.CmpOp{.ftz}.f16.stype d, a, b;
set.CmpOp.BoolOp{.ftz}.f16.stype d, a, b, {!}c;
set.CmpOp.bf16.stype d, a, b;
set.CmpOp.BoolOp.bf16.stype d, a, b, {!}c;
set.CmpOp{.ftz}.dtype.f16 d, a, b;
set.CmpOp.BoolOp{.ftz}.dtype.f16 d, a, b, {!}c;
.dtype = { .u16, .s16, .u32, .s32}
set.CmpOp.dtype.bf16 d, a, b;
set.CmpOp.BoolOp.dtype.bf16 d, a, b, {!}c;
.dtype = { .u16, .s16, .u32, .s32}
set.CmpOp{.ftz}.dtype.f16x2 d, a, b;
set.CmpOp.BoolOp{.ftz}.dtype.f16x2 d, a, b, {!}c;
.dtype = { .f16x2, .u32, .s32}
set.CmpOp.dtype.bf16x2 d, a, b;
set.CmpOp.BoolOp.dtype.bf16x2 d, a, b, {!}c;
.dtype = { .bf16x2, .u32, .s32}
.CmpOp = { eq, ne, lt, le, gt, ge,
equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.stype = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f16, .f32, .f64};
Description
Compares two numeric values and optionally combines the result with another predicate value by applying a Boolean operator.
Result of this computation is written in destination register in the following way:
If result is
True,0xffffffffis written for destination types.u32/.s32.0xffffis written for destination types.u16/.s16.1.0in target precision floating point format is written for destination type.f16,.bf16.
If result is
False,0x0is written for all integer destination types.0.0in target precision floating point format is written for destination type.f16,.bf16.
If the source type is .f16x2 or .bf16x2 then result of individual operations are packed in
the 32-bit destination operand.
Operand c has type .pred.
Semantics
if (stype == .f16x2 || stype == .bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
if (dtype == .f16x2 || stype == .bf16x2) {
for (i = 0; i < 2; i++) {
d[i] = BoolOp(t[i], c) ? 1.0 : 0.0;
}
} else {
for (i = 0; i < 2; i++) {
d[i] = BoolOp(t[i], c) ? 0xffff : 0;
}
}
} else if (dtype == .f16 || stype == .bf16) {
t = (a CmpOp b) ? 1 : 0;
d = BoolOp(t, c) ? 1.0 : 0.0;
} else { // Integer destination type
trueVal = (isU16(dtype) || isS16(dtype)) ? 0xffff : 0xffffffff;
t = (a CmpOp b) ? 1 : 0;
d = BoolOp(t, c) ? trueVal : 0;
}
Floating Point Notes
The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is
NaN, the result is False.
To aid comparison operations in the presence of NaN values, unordered versions are included:
equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not
NaN), then these comparisons have the same result as their ordered counterparts. If either
operand is NaN, then the result of these comparisons is True.
num returns True if both operands are numeric values (not NaN), and nan returns
True if either operand is NaN.
- Subnormal numbers:
By default, subnormal numbers are supported.
When
.ftzmodifier is specified then subnormal inputs and results are flushed to sign preserving zero.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
set.{u16, u32, s16, s32}.f16 and set.{u32, s32}.f16x2 are introduced in PTX ISA version 6.5.
set.{u16, u32, s16, s32}.bf16, set.{u32, s32, bf16x2}.bf16x2,
set.bf16.{s16,u16,f16,b16,s32,u32,f32,b32,s64,u64,f64,b64} are introduced in PTX ISA version
7.8.
Target ISA Notes
Requires sm_53 or higher.
set.{u16, u32, s16, s32}.bf16, set.{u32, s32, bf16x2}.bf16x2,
set.bf16.{s16,u16,f16,b16,s32,u32,f32,b32,s64,u64,f64,b64} require sm_90 or higher.
Examples
set.lt.and.f16.f16 d,a,b,r;
set.eq.f16x2.f16x2 d,i,n;
set.eq.u32.f16x2 d,i,n;
set.lt.and.u16.f16 d,a,b,r;
set.ltu.or.bf16.f16 d,u,v,s;
set.equ.bf16x2.bf16x2 d,j,m;
set.geu.s32.bf16x2 d,j,m;
set.num.xor.s32.bf16 d,u,v,s;
9.7.6.2. Half Precision Comparison Instructions: setp
setp
Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.
Syntax
setp.CmpOp{.ftz}.f16 p, a, b;
setp.CmpOp.BoolOp{.ftz}.f16 p, a, b, {!}c;
setp.CmpOp{.ftz}.f16x2 p|q, a, b;
setp.CmpOp.BoolOp{.ftz}.f16x2 p|q, a, b, {!}c;
setp.CmpOp.bf16 p, a, b;
setp.CmpOp.BoolOp.bf16 p, a, b, {!}c;
setp.CmpOp.bf16x2 p|q, a, b;
setp.CmpOp.BoolOp.bf16x2 p|q, a, b, {!}c;
.CmpOp = { eq, ne, lt, le, gt, ge,
equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
Description
Compares two values and combines the result with another predicate value by applying a Boolean operator. This result is written to the destination operand.
Operand c, p and q has type .pred.
For instruction type .f16, operands a and b have type .b16 or .f16.
For instruction type .f16x2, operands a and b have type .b32.
For instruction type .bf16, operands a and b have type .b16.
For instruction type .bf16x2, operands a and b have type .b32.
Semantics
if (type == .f16 || type == .bf16) {
t = (a CmpOp b) ? 1 : 0;
p = BoolOp(t, c);
} else if (type == .f16x2 || type == .bf16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
p = BoolOp(t[0], c);
q = BoolOp(t[1], c);
}
Floating Point Notes
The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is
NaN, the result is False.
To aid comparison operations in the presence of NaN values, unordered versions are included:
equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not
NaN), then these comparisons have the same result as their ordered counterparts. If either
operand is NaN, then the result of these comparisons is True.
num returns True if both operands are numeric values (not NaN), and nan returns
True if either operand is NaN.
- Subnormal numbers:
By default, subnormal numbers are supported.
setp.ftz.{f16,f16x2}flushes subnormal inputs to sign-preserving zero.
PTX ISA Notes
Introduced in PTX ISA version 4.2.
setp.{bf16/bf16x2} introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_53 or higher.
setp.{bf16/bf16x2} requires sm_90 or higher.
Examples
setp.lt.and.f16x2 p|q,a,b,r;
@q setp.eq.f16 p,i,n;
setp.gt.or.bf16x2 u|v,c,d,s;
@q setp.eq.bf16 u,j,m;
9.7.7. Logic and Shift Instructions
The logic and shift instructions are fundamentally untyped, performing bit-wise operations on
operands of any type, provided the operands are of the same size. This permits bit-wise operations
on floating point values without having to define a union to access the bits. Instructions and,
or, xor, and not also operate on predicates.
The logical shift instructions are:
andorxornotcnotlop3shfshlshr
9.7.7.1. Logic and Shift Instructions: and
and
Bitwise AND.
Syntax
and.type d, a, b;
.type = { .pred, .b16, .b32, .b64 };
Description
Compute the bit-wise and operation for the bits in a and b.
Semantics
d = a & b;
Notes
The size of the operands must match, but not necessarily the type.
Allowed types include predicate registers.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
and.b32 x,q,r;
and.b32 sign,fpvalue,0x80000000;
9.7.7.2. Logic and Shift Instructions: or
or
Biwise OR.
Syntax
or.type d, a, b;
.type = { .pred, .b16, .b32, .b64 };
Description
Compute the bit-wise or operation for the bits in a and b.
Semantics
d = a | b;
Notes
The size of the operands must match, but not necessarily the type.
Allowed types include predicate registers.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
or.b32 mask mask,0x00010001
or.pred p,q,r;
9.7.7.3. Logic and Shift Instructions: xor
xor
Bitwise exclusive-OR (inequality).
Syntax
xor.type d, a, b;
.type = { .pred, .b16, .b32, .b64 };
Description
Compute the bit-wise exclusive-or operation for the bits in a and b.
Semantics
d = a ^ b;
Notes
The size of the operands must match, but not necessarily the type.
Allowed types include predicate registers.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
xor.b32 d,q,r;
xor.b16 d,x,0x0001;
9.7.7.4. Logic and Shift Instructions: not
not
Bitwise negation; one’s complement.
Syntax
not.type d, a;
.type = { .pred, .b16, .b32, .b64 };
Description
Invert the bits in a.
Semantics
d = ~a;
Notes
The size of the operands must match, but not necessarily the type.
Allowed types include predicates.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
not.b32 mask,mask;
not.pred p,q;
9.7.7.5. Logic and Shift Instructions: cnot
cnot
C/C++ style logical negation.
Syntax
cnot.type d, a;
.type = { .b16, .b32, .b64 };
Description
Compute the logical negation using C/C++ semantics.
Semantics
d = (a==0) ? 1 : 0;
Notes
The size of the operands must match, but not necessarily the type.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
cnot.b32 d,a;
9.7.7.6. Logic and Shift Instructions: lop3
lop3
Arbitrary logical operation on 3 inputs.
Syntax
lop3.b32 d, a, b, c, immLut;
lop3.BoolOp.b32 d|p, a, b, c, immLut, q;
.BoolOp = { .or , .and };
Description
Compute bitwise logical operation on inputs a, b, c and store the result in destination
d.
Optionally, .BoolOp can be specified to compute the predicate result p by performing a
Boolean operation on the destination operand d with the predicate q in the following manner:
p = (d != 0) BoolOp q;
The sink symbol ‘_’ may be used in place of the destination operand d when .BoolOp qualifier
is specified.
The logical operation is defined by a look-up table which, for 3 inputs, can be represented as an
8-bit value specified by operand immLut as described below. immLut is an integer constant
that can take values from 0 to 255, thereby allowing up to 256 distinct logical operations on inputs
a, b, c.
For a logical operation F(a, b, c) the value of immLut can be computed by applying the same
operation to three predefined constant values as follows:
ta = 0xF0;
tb = 0xCC;
tc = 0xAA;
immLut = F(ta, tb, tc);
Examples:
If F = (a & b & c);
immLut = 0xF0 & 0xCC & 0xAA = 0x80
If F = (a | b | c);
immLut = 0xF0 | 0xCC | 0xAA = 0xFE
If F = (a & b & ~c);
immLut = 0xF0 & 0xCC & (~0xAA) = 0x40
If F = ((a & b | c) ^ a);
immLut = (0xF0 & 0xCC | 0xAA) ^ 0xF0 = 0x1A
The following table illustrates computation of immLut for various logical operations:
ta |
tb |
tc |
Oper 0 (False) |
Oper 1 (ta & tb & tc) |
Oper 2 (ta & tb & ~tc) |
… |
Oper 254 (ta | tb | tc) |
Oper 255 (True) |
|---|---|---|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
immLut |
0x0 |
0x80 |
0x40 |
… |
0xFE |
0xFF |
||
Semantics
F = GetFunctionFromTable(immLut); // returns the function corresponding to immLut value
d = F(a, b, c);
if (BoolOp specified) {
p = (d != 0) BoolOp q;
}
PTX ISA Notes
Introduced in PTX ISA version 4.3.
Support for .BoolOp qualifier introduced in PTX ISA version 8.2.
Target ISA Notes
Requires sm_50 or higher.
Qualifier .BoolOp requires sm_70 or higher.
Examples
lop3.b32 d, a, b, c, 0x40;
lop3.or.b32 d|p, a, b, c, 0x3f, q;
lop3.and.b32 _|p, a, b, c, 0x3f, q;
9.7.7.7. Logic and Shift Instructions: shf
shf
Funnel shift.
Syntax
shf.l.mode.b32 d, a, b, c; // left shift
shf.r.mode.b32 d, a, b, c; // right shift
.mode = { .clamp, .wrap };
Description
Shift the 64-bit value formed by concatenating operands a and b left or right by the amount
specified by the unsigned 32-bit value in c. Operand b holds bits 63:32 and operand a
holds bits 31:0 of the 64-bit source value. The source is shifted left or right by the clamped
or wrapped value in c. For shf.l, the most-significant 32-bits of the result are written
into d; for shf.r, the least-significant 32-bits of the result are written into d.
Semantics
u32 n = (.mode == .clamp) ? min(c, 32) : c & 0x1f;
switch (shf.dir) { // shift concatenation of [b, a]
case shf.l: // extract 32 msbs
u32 d = (b << n) | (a >> (32-n));
case shf.r: // extract 32 lsbs
u32 d = (b << (32-n)) | (a >> n);
}
Notes
Use funnel shift for multi-word shift operations and for rotate operations. The shift amount is
limited to the range 0..32 in clamp mode and 0..31 in wrap mode, so shifting multi-word
values by distances greater than 32 requires first moving 32-bit words, then using shf to shift
the remaining 0..31 distance.
To shift data sizes greater than 64 bits to the right, use repeated shf.r instructions applied
to adjacent words, operating from least-significant word towards most-significant word. At each
step, a single word of the shifted result is computed. The most-significant word of the result is
computed using a shr.{u32,s32} instruction, which zero or sign fills based on the instruction
type.
To shift data sizes greater than 64 bits to the left, use repeated shf.l instructions applied to
adjacent words, operating from most-significant word towards least-significant word. At each step, a
single word of the shifted result is computed. The least-significant word of the result is computed
using a shl instruction.
Use funnel shift to perform 32-bit left or right rotate by supplying the same value for source
arguments a and b.
PTX ISA Notes
Introduced in PTX ISA version 3.1.
Target ISA Notes
Requires sm_32 or higher.
Example
shf.l.clamp.b32 r3,r1,r0,16;
// 128-bit left shift; n < 32
// [r7,r6,r5,r4] = [r3,r2,r1,r0] << n
shf.l.clamp.b32 r7,r2,r3,n;
shf.l.clamp.b32 r6,r1,r2,n;
shf.l.clamp.b32 r5,r0,r1,n;
shl.b32 r4,r0,n;
// 128-bit right shift, arithmetic; n < 32
// [r7,r6,r5,r4] = [r3,r2,r1,r0] >> n
shf.r.clamp.b32 r4,r0,r1,n;
shf.r.clamp.b32 r5,r1,r2,n;
shf.r.clamp.b32 r6,r2,r3,n;
shr.s32 r7,r3,n; // result is sign-extended
shf.r.clamp.b32 r1,r0,r0,n; // rotate right by n; n < 32
shf.l.clamp.b32 r1,r0,r0,n; // rotate left by n; n < 32
// extract 32-bits from [r1,r0] starting at position n < 32
shf.r.clamp.b32 r0,r0,r1,n;
9.7.7.8. Logic and Shift Instructions: shl
shl
Shift bits left, zero-fill on right.
Syntax
shl.type d, a, b;
.type = { .b16, .b32, .b64 };
Description
Shift a left by the amount specified by unsigned 32-bit value in b.
Semantics
d = a << b;
Notes
Shift amounts greater than the register width N are clamped to N.
The sizes of the destination and first source operand must match, but not necessarily the type. The
b operand must be a 32-bit value, regardless of the instruction type.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Example
shl.b32 q,a,2;
9.7.7.9. Logic and Shift Instructions: shr
shr
Shift bits right, sign or zero-fill on left.
Syntax
shr.type d, a, b;
.type = { .b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64 };
Description
Shift a right by the amount specified by unsigned 32-bit value in b. Signed shifts fill with
the sign bit, unsigned and untyped shifts fill with 0.
Semantics
d = a >> b;
Notes
Shift amounts greater than the register width N are clamped to N.
The sizes of the destination and first source operand must match, but not necessarily the type. The
b operand must be a 32-bit value, regardless of the instruction type.
Bit-size types are included for symmetry with shl.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Example
shr.u16 c,a,2;
shr.s32 i,i,1;
shr.b16 k,i,j;
9.7.8. Data Movement and Conversion Instructions
These instructions copy data from place to place, and from state space to state space, possibly
converting it from one format to another. mov, ld, ldu, and st operate on both
scalar and vector types. The isspacep instruction is provided to query whether a generic address
falls within a particular state space window. The cvta instruction converts addresses between
generic and const, global, local, or shared state spaces.
Instructions ld, st, suld, and sust support optional cache operations.
The Data Movement and Conversion Instructions are:
movshfl.syncprmtldldustst.asyncmultimem.ld_reduce,multimem.st,multimem.redprefetch,prefetchuisspacepcvtacvtcvt.packcp.asynccp.async.commit_groupcp.async.wait_group,cp.async.wait_allcp.async.bulkcp.reduce.async.bulkcp.async.bulk.prefetchcp.async.bulk.tensorcp.reduce.async.bulk.tensorcp.async.bulk.prefetch.tensorcp.async.bulk.commit_groupcp.async.bulk.wait_grouptensormap.replace
9.7.8.1. Cache Operators
PTX ISA version 2.0 introduced optional cache operators on load and store instructions. The cache
operators require a target architecture of sm_20 or higher.
Cache operators on load or store instructions are treated as performance hints only. The use of a
cache operator on an ld or st instruction does not change the memory consistency behavior of
the program.
For sm_20 and higher, the cache operators have the following definitions and behavior.
Operator |
Meaning |
|---|---|
|
Cache at all levels, likely to be accessed again. The default load instruction cache operation is ld.ca, which allocates cache lines in all
levels (L1 and L2) with normal eviction policy. Global data is coherent at the L2 level, but
multiple L1 caches are not coherent for global data. If one thread stores to global memory
via one L1 cache, and a second thread loads that address via a second L1 cache with |
|
Cache at global level (cache in L2 and below, not L1). Use |
|
Cache streaming, likely to be accessed once. The |
|
Last use. The compiler/programmer may use |
|
Don’t cache and fetch again (consider cached system memory lines stale, fetch again). The ld.cv load operation applied to a global System Memory address invalidates (discards) a matching L2 line and re-fetches the line on each new load. |
Operator |
Meaning |
|---|---|
|
Cache write-back all coherent levels. The default store instruction cache operation is If one thread stores to global memory, bypassing its L1 cache, and a second thread in a
different SM later loads from that address via a different L1 cache with The driver must invalidate global L1 cache lines between dependent grids of thread arrays.
Stores by the first grid program are then correctly missed in L1 and fetched by the second grid
program issuing default |
|
Cache at global level (cache in L2 and below, not L1). Use |
|
Cache streaming, likely to be accessed once. The |
|
Cache write-through (to system memory). The |
9.7.8.2. Cache Eviction Priority Hints
PTX ISA version 7.4 adds optional cache eviction priority hints on load and store
instructions. Cache eviction priority requires target architecture sm_70 or higher.
Cache eviction priority on load or store instructions is treated as a performance hint. It is
supported for .global state space and generic addresses where the address points to .global
state space.
Cache Eviction Priority |
Meaning |
|---|---|
|
Cache data with normal eviction priority. This is the default eviction priority. |
|
Data cached with this priority will be first in the eviction priority order and will likely be evicted when cache eviction is required. This priority is suitable for streaming data. |
|
Data cached with this priority will be last in the eviction priority order and will
likely be evicted only after other data with |
|
Do not change eviction priority order as part of this operation. |
|
Do not allocate data to cache. This priority is suitable for streaming data. |
9.7.8.3. Data Movement and Conversion Instructions: mov
mov
Set a register variable with the value of a register variable or an immediate value. Take the non-generic address of a variable in global, local, or shared state space.
Syntax
mov.type d, a;
mov.type d, sreg;
mov.type d, avar; // get address of variable
mov.type d, avar+imm; // get address of variable with offset
mov.u32 d, fname; // get address of device function
mov.u64 d, fname; // get address of device function
mov.u32 d, kernel; // get address of entry function
mov.u64 d, kernel; // get address of entry function
.type = { .pred,
.b16, .b32, .b64,
.u16, .u32, .u64,
.s16, .s32, .s64,
.f32, .f64 };
Description
Write register d with the value of a.
Operand a may be a register, special register, variable with optional offset in an addressable
memory space, or function name.
For variables declared in .const, .global, .local, and .shared state spaces, mov
places the non-generic address of the variable (i.e., the address of the variable in its state
space) into the destination register. The generic address of a variable in const, global,
local, or shared state space may be generated by first taking the address within the state
space with mov and then converting it to a generic address using the cvta instruction;
alternately, the generic address of a variable declared in const, global, local, or
shared state space may be taken directly using the cvta instruction.
Note that if the address of a device function parameter is moved to a register, the parameter will be copied onto the stack and the address will be in the local state space.
Semantics
d = a;
d = sreg;
d = &avar; // address is non-generic; i.e., within the variable's declared state space
d = &avar+imm;
Notes
Although only predicate and bit-size types are required, we include the arithmetic types for the programmer’s convenience: their use enhances program readability and allows additional type checking.
When moving address of a kernel or a device function, only
.u32or.u64instruction types are allowed. However, if a signed type is used, it is not treated as a compilation error. The compiler issues a warning in this case.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Taking the address of kernel entry functions requires PTX ISA version 3.1 or later. Kernel function addresses should only be used in the context of CUDA Dynamic Parallelism system calls. See the CUDA Dynamic Parallelism Programming Guide for details.
Target ISA Notes
mov.f64 requires sm_13 or higher.
Taking the address of kernel entry functions requires sm_35 or higher.
Examples
mov.f32 d,a;
mov.u16 u,v;
mov.f32 k,0.1;
mov.u32 ptr, A; // move address of A into ptr
mov.u32 ptr, A[5]; // move address of A[5] into ptr
mov.u32 ptr, A+20; // move address with offset into ptr
mov.u32 addr, myFunc; // get address of device function 'myFunc'
mov.u64 kptr, main; // get address of entry function 'main'
9.7.8.4. Data Movement and Conversion Instructions: mov
mov
Move vector-to-scalar (pack) or scalar-to-vector (unpack).
Syntax
mov.type d, a;
.type = { .b16, .b32, .b64, .b128 };
Description
Write scalar register d with the packed value of vector register a, or write vector register
d with the unpacked values from scalar register a.
When destination operand d is a vector register, the sink symbol '_' may be used for one or
more elements provided that at least one element is a scalar register.
For bit-size types, mov may be used to pack vector elements into a scalar register or unpack
sub-fields of a scalar register into a vector. Both the overall size of the vector and the size of
the scalar must match the size of the instruction type.
Semantics
// pack two 8-bit elements into .b16
d = a.x | (a.y << 8)
// pack four 8-bit elements into .b32
d = a.x | (a.y << 8) | (a.z << 16) | (a.w << 24)
// pack two 16-bit elements into .b32
d = a.x | (a.y << 16)
// pack four 16-bit elements into .b64
d = a.x | (a.y << 16) | (a.z << 32) | (a.w << 48)
// pack two 32-bit elements into .b64
d = a.x | (a.y << 32)
// pack four 32-bit elements into .b128
d = a.x | (a.y << 32) | (a.z << 64) | (a.w << 96)
// pack two 64-bit elements into .b128
d = a.x | (a.y << 64)
// unpack 8-bit elements from .b16
{ d.x, d.y } = { a[0..7], a[8..15] }
// unpack 8-bit elements from .b32
{ d.x, d.y, d.z, d.w }
{ a[0..7], a[8..15], a[16..23], a[24..31] }
// unpack 16-bit elements from .b32
{ d.x, d.y } = { a[0..15], a[16..31] }
// unpack 16-bit elements from .b64
{ d.x, d.y, d.z, d.w } =
{ a[0..15], a[16..31], a[32..47], a[48..63] }
// unpack 32-bit elements from .b64
{ d.x, d.y } = { a[0..31], a[32..63] }
// unpack 32-bit elements from .b128
{ d.x, d.y, d.z, d.w } =
{ a[0..31], a[32..63], a[64..95], a[96..127] }
// unpack 64-bit elements from .b128
{ d.x, d.y } = { a[0..63], a[64..127] }
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Support for .b128 type introduced in PTX ISA version 8.3.
Target ISA Notes
Supported on all target architectures.
Support for .b128 type requires sm_70 or higher.
Examples
mov.b32 %r1,{a,b}; // a,b have type .u16
mov.b64 {lo,hi}, %x; // %x is a double; lo,hi are .u32
mov.b32 %r1,{x,y,z,w}; // x,y,z,w have type .b8
mov.b32 {r,g,b,a},%r1; // r,g,b,a have type .u8
mov.b64 {%r1, _}, %x; // %x is.b64, %r1 is .b32
mov.b128 {%b1, %b2}, %y; // %y is.b128, %b1 and % b2 are .b64
mov.b128 %y, {%b1, %b2}; // %y is.b128, %b1 and % b2 are .b64
9.7.8.5. Data Movement and Conversion Instructions: shfl (deprecated)
shfl (deprecated)
Register data shuffle within threads of a warp.
Syntax
shfl.mode.b32 d[|p], a, b, c;
.mode = { .up, .down, .bfly, .idx };
Deprecation Note
The shfl instruction without a .sync qualifier is deprecated in PTX ISA version 6.0.
Support for this instruction with
.targetlower thansm_70may be removed in a future PTX ISA version.
Removal Note
Support for shfl instruction without a .sync qualifier is removed in PTX ISA version 6.4 for .targetsm_70 or higher.
Description
Exchange register data between threads of a warp.
Each thread in the currently executing warp will compute a source lane index j based on input
operands b and c and the mode. If the computed source lane index j is in range, the
thread will copy the input operand a from lane j into its own destination register d;
otherwise, the thread will simply copy its own input a to destination d. The optional
destination predicate p is set to True if the computed source lane is in range, and
otherwise set to False.
Note that an out of range value of b may still result in a valid computed source lane index
j. In this case, a data transfer occurs and the destination predicate p is True.
Note that results are undefined in divergent control flow within a warp, if an active thread sources a register from an inactive thread.
Operand b specifies a source lane or source lane offset, depending on the mode.
Operand c contains two packed values specifying a mask for logically splitting warps into
sub-segments and an upper bound for clamping the source lane index.
Semantics
lane[4:0] = [Thread].laneid; // position of thread in warp
bval[4:0] = b[4:0]; // source lane or lane offset (0..31)
cval[4:0] = c[4:0]; // clamp value
mask[4:0] = c[12:8];
// get value of source register a if thread is active and
// guard predicate true, else unpredictable
if (isActive(Thread) && isGuardPredicateTrue(Thread)) {
SourceA[lane] = a;
} else {
// Value of SourceA[lane] is unpredictable for
// inactive/predicated-off threads in warp
}
maxLane = (lane[4:0] & mask[4:0]) | (cval[4:0] & ~mask[4:0]);
minLane = (lane[4:0] & mask[4:0]);
switch (.mode) {
case .up: j = lane - bval; pval = (j >= maxLane); break;
case .down: j = lane + bval; pval = (j <= maxLane); break;
case .bfly: j = lane ^ bval; pval = (j <= maxLane); break;
case .idx: j = minLane | (bval[4:0] & ~mask[4:0]);
pval = (j <= maxLane); break;
}
if (!pval) j = lane; // copy from own lane
d = SourceA[j]; // copy input a from lane j
if (dest predicate selected)
p = pval;
PTX ISA Notes
Introduced in PTX ISA version 3.0.
Deprecated in PTX ISA version 6.0 in favor of shfl.sync.
Not supported in PTX ISA version 6.4 for .target sm_70 or higher.
Target ISA Notes
shfl requires sm_30 or higher.
shfl is not supported on sm_70 or higher starting PTX ISA version 6.4.
Examples
// Warp-level INCLUSIVE PLUS SCAN:
//
// Assumes input in following registers:
// - Rx = sequence value for this thread
//
shfl.up.b32 Ry|p, Rx, 0x1, 0x0;
@p add.f32 Rx, Ry, Rx;
shfl.up.b32 Ry|p, Rx, 0x2, 0x0;
@p add.f32 Rx, Ry, Rx;
shfl.up.b32 Ry|p, Rx, 0x4, 0x0;
@p add.f32 Rx, Ry, Rx;
shfl.up.b32 Ry|p, Rx, 0x8, 0x0;
@p add.f32 Rx, Ry, Rx;
shfl.up.b32 Ry|p, Rx, 0x10, 0x0;
@p add.f32 Rx, Ry, Rx;
// Warp-level INCLUSIVE PLUS REVERSE-SCAN:
//
// Assumes input in following registers:
// - Rx = sequence value for this thread
//
shfl.down.b32 Ry|p, Rx, 0x1, 0x1f;
@p add.f32 Rx, Ry, Rx;
shfl.down.b32 Ry|p, Rx, 0x2, 0x1f;
@p add.f32 Rx, Ry, Rx;
shfl.down.b32 Ry|p, Rx, 0x4, 0x1f;
@p add.f32 Rx, Ry, Rx;
shfl.down.b32 Ry|p, Rx, 0x8, 0x1f;
@p add.f32 Rx, Ry, Rx;
shfl.down.b32 Ry|p, Rx, 0x10, 0x1f;
@p add.f32 Rx, Ry, Rx;
// BUTTERFLY REDUCTION:
//
// Assumes input in following registers:
// - Rx = sequence value for this thread
//
shfl.bfly.b32 Ry, Rx, 0x10, 0x1f; // no predicate dest
add.f32 Rx, Ry, Rx;
shfl.bfly.b32 Ry, Rx, 0x8, 0x1f;
add.f32 Rx, Ry, Rx;
shfl.bfly.b32 Ry, Rx, 0x4, 0x1f;
add.f32 Rx, Ry, Rx;
shfl.bfly.b32 Ry, Rx, 0x2, 0x1f;
add.f32 Rx, Ry, Rx;
shfl.bfly.b32 Ry, Rx, 0x1, 0x1f;
add.f32 Rx, Ry, Rx;
//
// All threads now hold sum in Rx
9.7.8.6. Data Movement and Conversion Instructions: shfl.sync
shfl.sync
Register data shuffle within threads of a warp.
Syntax
shfl.sync.mode.b32 d[|p], a, b, c, membermask;
.mode = { .up, .down, .bfly, .idx };
Description
Exchange register data between threads of a warp.
shfl.sync will cause executing thread to wait until all non-exited threads corresponding to
membermask have executed shfl.sync with the same qualifiers and same membermask value
before resuming execution.
Operand membermask specifies a 32-bit integer which is a mask indicating threads participating
in barrier where the bit position corresponds to thread’s laneid.
shfl.sync exchanges register data between threads in membermask.
Each thread in the currently executing warp will compute a source lane index j based on input
operands b and c and the mode. If the computed source lane index j is in range, the
thread will copy the input operand a from lane j into its own destination register d;
otherwise, the thread will simply copy its own input a to destination d. The optional
destination predicate p is set to True if the computed source lane is in range, and
otherwise set to False.
Note that an out of range value of b may still result in a valid computed source lane index
j. In this case, a data transfer occurs and the destination predicate p is True.
Note that results are undefined if a thread sources a register from an inactive thread or a thread
that is not in membermask.
Operand b specifies a source lane or source lane offset, depending on the mode.
Operand c contains two packed values specifying a mask for logically splitting warps into
sub-segments and an upper bound for clamping the source lane index.
The behavior of shfl.sync is undefined if the executing thread is not in the membermask.
Note
For .target sm_6x or below, all threads in membermask must execute the same shfl.sync
instruction in convergence, and only threads belonging to some membermask can be active when
the shfl.sync instruction is executed. Otherwise, the behavior is undefined.
Semantics
// wait for all threads in membermask to arrive
wait_for_specified_threads(membermask);
lane[4:0] = [Thread].laneid; // position of thread in warp
bval[4:0] = b[4:0]; // source lane or lane offset (0..31)
cval[4:0] = c[4:0]; // clamp value
segmask[4:0] = c[12:8];
// get value of source register a if thread is active and
// guard predicate true, else unpredictable
if (isActive(Thread) && isGuardPredicateTrue(Thread)) {
SourceA[lane] = a;
} else {
// Value of SourceA[lane] is unpredictable for
// inactive/predicated-off threads in warp
}
maxLane = (lane[4:0] & segmask[4:0]) | (cval[4:0] & ~segmask[4:0]);
minLane = (lane[4:0] & segmask[4:0]);
switch (.mode) {
case .up: j = lane - bval; pval = (j >= maxLane); break;
case .down: j = lane + bval; pval = (j <= maxLane); break;
case .bfly: j = lane ^ bval; pval = (j <= maxLane); break;
case .idx: j = minLane | (bval[4:0] & ~segmask[4:0]);
pval = (j <= maxLane); break;
}
if (!pval) j = lane; // copy from own lane
d = SourceA[j]; // copy input a from lane j
if (dest predicate selected)
p = pval;
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
Requires sm_30 or higher.
Examples
shfl.sync.up.b32 Ry|p, Rx, 0x1, 0x0, 0xffffffff;
9.7.8.7. Data Movement and Conversion Instructions: prmt
prmt
Permute bytes from register pair.
Syntax
prmt.b32{.mode} d, a, b, c;
.mode = { .f4e, .b4e, .rc8, .ecl, .ecr, .rc16 };
Description
Pick four arbitrary bytes from two 32-bit registers, and reassemble them into a 32-bit destination register.
In the generic form (no mode specified), the permute control consists of four 4-bit selection
values. The bytes in the two source registers are numbered from 0 to 7: {b, a} = {{b7, b6, b5,
b4}, {b3, b2, b1, b0}}. For each byte in the target register, a 4-bit selection value is defined.
The 3 lsbs of the selection value specify which of the 8 source bytes should be moved into the
target position. The msb defines if the byte value should be copied, or if the sign (msb of the
byte) should be replicated over all 8 bits of the target position (sign extend of the byte value);
msb=0 means copy the literal value; msb=1 means replicate the sign. Note that the sign
extension is only performed as part of generic form.
Thus, the four 4-bit values fully specify an arbitrary byte permute, as a 16b permute code.
default mode |
source select |
source select |
source select |
source select |
|---|---|---|---|---|
index |
|
|
|
|
The more specialized form of the permute control uses the two lsb’s of operand c (which is
typically an address pointer) to control the byte extraction.
mode |
selector
|
source |
source |
source |
source |
|---|---|---|---|---|---|
|
0 |
3 |
2 |
1 |
0 |
1 |
4 |
3 |
2 |
1 |
|
2 |
5 |
4 |
3 |
2 |
|
3 |
6 |
5 |
4 |
3 |
|
|
0 |
5 |
6 |
7 |
0 |
1 |
6 |
7 |
0 |
1 |
|
2 |
7 |
0 |
1 |
2 |
|
3 |
0 |
1 |
2 |
3 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
|
|
0 |
3 |
2 |
1 |
0 |
1 |
3 |
2 |
1 |
1 |
|
2 |
3 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
2 |
2 |
2 |
1 |
0 |
|
3 |
3 |
2 |
1 |
0 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
3 |
2 |
3 |
2 |
|
2 |
1 |
0 |
1 |
0 |
|
3 |
3 |
2 |
3 |
2 |
Semantics
tmp64 = (b<<32) | a; // create 8 byte source
if ( ! mode ) {
ctl[0] = (c >> 0) & 0xf;
ctl[1] = (c >> 4) & 0xf;
ctl[2] = (c >> 8) & 0xf;
ctl[3] = (c >> 12) & 0xf;
} else {
ctl[0] = ctl[1] = ctl[2] = ctl[3] = (c >> 0) & 0x3;
}
tmp[07:00] = ReadByte( mode, ctl[0], tmp64 );
tmp[15:08] = ReadByte( mode, ctl[1], tmp64 );
tmp[23:16] = ReadByte( mode, ctl[2], tmp64 );
tmp[31:24] = ReadByte( mode, ctl[3], tmp64 );
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
prmt requires sm_20 or higher.
Examples
prmt.b32 r1, r2, r3, r4;
prmt.b32.f4e r1, r2, r3, r4;
9.7.8.8. Data Movement and Conversion Instructions: ld
ld
Load a register variable from an addressable state space variable.
Syntax
ld{.weak}{.ss}{.cop}{.level::cache_hint}{.level::prefetch_size}{.vec}.type d, [a]{.unified}{, cache-policy};
ld{.weak}{.ss}{.level::eviction_priority}{.level::cache_hint}{.level::prefetch_size}{.vec}.type d, [a]{.unified}{, cache-policy};
ld.volatile{.ss}{.level::prefetch_size}{.vec}.type d, [a];
ld.relaxed.scope{.ss}{.level::eviction_priority}{.level::cache_hint}{.level::prefetch_size}{.vec}.type d, [a]{, cache-policy};
ld.acquire.scope{.ss}{.level::eviction_priority}{.level::cache_hint}{.level::prefetch_size}{.vec}.type d, [a]{, cache-policy};
ld.mmio.relaxed.sys{.global}.type d, [a];
.ss = { .const, .global, .local, .param{::entry, ::func}, .shared{::cta, ::cluster} };
.cop = { .ca, .cg, .cs, .lu, .cv };
.level::eviction_priority = { .L1::evict_normal, .L1::evict_unchanged,
.L1::evict_first, .L1::evict_last, .L1::no_allocate };
.level::cache_hint = { .L2::cache_hint };
.level::prefetch_size = { .L2::64B, .L2::128B, .L2::256B }
.scope = { .cta, .cluster, .gpu, .sys };
.vec = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64, .b128,
.u8, .u16, .u32, .u64,
.s8, .s16, .s32, .s64,
.f32, .f64 };
Description
Load register variable d from the location specified by the source address operand a in
specified state space. If no state space is given, perform the load using Generic Addressing.
If no sub-qualifier is specified with .shared state space, then ::cta is assumed by default.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
If no sub-qualifier is specified with .param state space, then :
::funcis assumed when access is inside a device function.::entryis assumed when accessing kernel function parameters from entry function. Otherwise, when accessing device function parameters or any other.paramvariables from entry function::funcis assumed by default.
For ld.param::entry instruction, operand a must be a kernel parameter address, otherwise behavior
is undefined. For ld.param::func instruction, operand a must be a device function parameter address,
otherwise behavior is undefined.
Instruction ld.param{::func} used for reading value returned from device function call cannot be
predicated. See Parameter State Space and
Function Declarations and Definitions for descriptions
of the proper use of ld.param.
The .relaxed and .acquire qualifiers indicate memory synchronization as described in the
Memory Consistency Model. The .scope qualifier
indicates the set of threads with which an ld.relaxed or ld.acquire instruction can directly
synchronize1. The .weak qualifier indicates a memory instruction with no synchronization.
The effects of this instruction become visible to other threads only when synchronization is established
by other means.
The semantic details of .mmio qualifier are described in the Memory Consistency Model. Only .sys thread scope is valid for ld.mmio operation. The
qualifiers .mmio and .relaxed must be specified together.
The .weak, .volatile, .relaxed and .acquire qualifiers are mutually exclusive. When
none of these is specified, the .weak qualifier is assumed by default.
An ld.volatile operation is always performed and it will not be reordered with respect to other
volatile operations to the same memory location. volatile and non-volatile load operations
to the same memory location may be reordered. ld.volatile has the same memory synchronization
semantics as ld.relaxed.sys.
The qualifiers .volatile, .relaxed and .acquire may be used only with .global and
.shared spaces and with generic addressing, where the address points to .global or
.shared space. Cache operations are not permitted with these qualifiers. The qualifier .mmio
may be used only with .global space and with generic addressing, where the address points to
.global space.
The optional qualifier .unified must be specified on operand a if a is the address of a
variable declared with .unified attribute as described in Variable and Function Attribute
Directive: .attribute.
The qualifier .level::eviction_priority specifies the eviction policy that will be used during
memory access.
The .level::prefetch_size qualifier is a hint to fetch additional data of the specified size
into the respective cache level.The sub-qualifier prefetch_size can be set to either of 64B,
128B, 256B thereby allowing the prefetch size to be 64 Bytes, 128 Bytes or 256 Bytes
respectively.
The qualifier .level::prefetch_size may only be used with .global state space and with
generic addressing where the address points to .global state space. If the generic address does
not fall within the address window of the global memory, then the prefetching behavior is undefined.
The .level::prefetch_size qualifier is treated as a performance hint only.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
The qualifiers .unified and .level::cache_hint are only supported for .global state
space and for generic addressing where the address points to the .global state space.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
1 This synchronization is further extended to other threads through the transitive nature of causality order, as described in the memory consistency model.
Semantics
d = a; // named variable a
d = *(&a+immOff) // variable-plus-offset
d = *a; // register
d = *(a+immOff); // register-plus-offset
d = *(immAddr); // immediate address
Notes
Destination d must be in the .reg state space.
A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types. See Table 25 for a description of these relaxed type-checking rules.
.f16 data may be loaded using ld.b16, and then converted to .f32 or .f64 using
cvt or can be used in half precision floating point instructions.
.f16x2 data may be loaded using ld.b32 and then used in half precision floating point
instructions.
PTX ISA Notes
ld introduced in PTX ISA version 1.0. ld.volatile introduced in PTX ISA version 1.1.
Generic addressing and cache operations introduced in PTX ISA version 2.0.
Support for scope qualifier, .relaxed, .acquire, .weak qualifiers introduced in PTX ISA
version 6.0.
Support for generic addressing of .const space added in PTX ISA version 3.1.
Support for .level::eviction_priority, .level::prefetch_size and .level::cache_hint
qualifiers introduced in PTX ISA version 7.4.
Support for .cluster scope qualifier introduced in PTX ISA version 7.8.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for .unified qualifier introduced in PTX ISA version 8.0.
Support for .mmio qualifier introduced in PTX ISA version 8.2.
Support for ::entry and ::func sub-qualifiers on .param space introduced in PTX ISA
version 8.3.
Support for .b128 type introduced in PTX ISA version 8.3.
Support for .sys scope with .b128 type introduced in PTX ISA version 8.4.
Target ISA Notes
ld.f64 requires sm_13 or higher.
Support for scope qualifier, .relaxed, .acquire, .weak qualifiers require sm_70 or
higher.
Generic addressing requires sm_20 or higher.
Cache operations require sm_20 or higher.
Support for .level::eviction_priority qualifier requires sm_70 or higher.
Support for .level::prefetch_size qualifier requires sm_75 or higher.
Support for .L2::256B and .L2::cache_hint qualifiers requires sm_80 or higher.
Support for .cluster scope qualifier requires sm_90 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for .unified qualifier requires sm_90 or higher.
Support for .mmio qualifier requires sm_70 or higher.
Support for .b128 type requires sm_70 or higher.
Examples
ld.global.f32 d,[a];
ld.shared.v4.b32 Q,[p];
ld.const.s32 d,[p+4];
ld.local.b32 x,[p+-8]; // negative offset
ld.local.b64 x,[240]; // immediate address
ld.global.b16 %r,[fs]; // load .f16 data into 32-bit reg
cvt.f32.f16 %r,%r; // up-convert f16 data to f32
ld.global.b32 %r0, [fs]; // load .f16x2 data in 32-bit reg
ld.global.b32 %r1, [fs + 4]; // load .f16x2 data in 32-bit reg
add.rn.f16x2 %d0, %r0, %r1; // addition of f16x2 data
ld.global.relaxed.gpu.u32 %r0, [gbl];
ld.shared.acquire.gpu.u32 %r1, [sh];
ld.global.relaxed.cluster.u32 %r2, [gbl];
ld.shared::cta.acquire.gpu.u32 %r2, [sh + 4];
ld.shared::cluster.u32 %r3, [sh + 8];
ld.global.mmio.relaxed.sys.u32 %r3, [gbl];
ld.global.f32 d,[ugbl].unified;
ld.b32 %r0, [%r1].unified;
ld.global.L1::evict_last.u32 d, [p];
ld.global.L2::64B.b32 %r0, [gbl]; // Prefetch 64B to L2
ld.L2::128B.f64 %r1, [gbl]; // Prefetch 128B to L2
ld.global.L2::256B.f64 %r2, [gbl]; // Prefetch 256B to L2
createpolicy.fractional.L2::evict_last.L2::evict_unchanged.b64 cache-policy, 1;
ld.global.L2::cache_hint.b64 x, [p], cache-policy;
ld.param::entry.b32 %rp1, [kparam1];
ld.global.b128 %r0, [gbl]; // 128-bit load
9.7.8.9. Data Movement and Conversion Instructions: ld.global.nc
ld.global.nc
Load a register variable from global state space via non-coherent cache.
Syntax
ld.global{.cop}.nc{.level::cache_hint}{.level::prefetch_size}.type d, [a]{, cache-policy};
ld.global{.cop}.nc{.level::cache_hint}{.level::prefetch_size}.vec.type d, [a]{, cache-policy};
ld.global.nc{.level::eviction_priority}{.level::cache_hint}{.level::prefetch_size}.type d, [a]{, cache-policy};
ld.global.nc{.level::eviction_priority}{.level::cache_hint}{.level::prefetch_size}.vec.type d, [a]{, cache-policy};
.cop = { .ca, .cg, .cs }; // cache operation
.level::eviction_priority = { .L1::evict_normal, .L1::evict_unchanged,
.L1::evict_first, .L1::evict_last, .L1::no_allocate};
.level::cache_hint = { .L2::cache_hint };
.level::prefetch_size = { .L2::64B, .L2::128B, .L2::256B }
.vec = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64, .b128,
.u8, .u16, .u32, .u64,
.s8, .s16, .s32, .s64,
.f32, .f64 };
Description
Load register variable d from the location specified by the source address operand a in the
global state space, and optionally cache in non-coherent read-only cache.
Note
On some architectures, the texture cache is larger, has higher bandwidth, and longer latency than
the global memory cache. For applications with sufficient parallelism to cover the longer
latency, ld.global.nc should offer better performance than ld.global on such
architectures.
The address operand a may contain a generic address pointing to the
.global state space. Supported addressing modes for operand a and alignment requirements are
described in Addresses as Operands
The qualifier .level::eviction_priority specifies the eviction policy that will be used during
memory access.
The .level::prefetch_size qualifier is a hint to fetch additional data of the specified size
into the respective cache level.The sub-qualifier prefetch_size can be set to either of 64B,
128B, 256B thereby allowing the prefetch size to be 64 Bytes, 128 Bytes or 256 Bytes
respectively.
The .level::prefetch_size qualifier is treated as a performance hint only.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
Semantics
d = a; // named variable a
d = *(&a+immOff) // variable-plus-offset
d = *a; // register
d = *(a+immOff); // register-plus-offset
d = *(immAddr); // immediate address
Notes
Destination d must be in the .reg state space.
A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types.
.f16 data may be loaded using ld.b16, and then converted to .f32 or .f64 using cvt.
PTX ISA Notes
Introduced in PTX ISA version 3.1.
Support for .level::eviction_priority, .level::prefetch_size and .level::cache_hint
qualifiers introduced in PTX ISA version 7.4.
Support for .b128 type introduced in PTX ISA version 8.3.
Target ISA Notes
Requires sm_32 or higher.
Support for .level::eviction_priority qualifier requires sm_70 or higher.
Support for .level::prefetch_size qualifier requires sm_75 or higher.
Support for .level::cache_hint qualifier requires sm_80 or higher.
Support for .b128 type requires sm_70 or higher.
Examples
ld.global.nc.f32 d, [a];
ld.gloal.nc.L1::evict_last.u32 d, [a];
createpolicy.fractional.L2::evict_last.b64 cache-policy, 0.5;
ld.global.nc.L2::cache_hint.f32 d, [a], cache-policy;
ld.global.nc.L2::64B.b32 d, [a]; // Prefetch 64B to L2
ld.global.nc.L2::256B.f64 d, [a]; // Prefetch 256B to L2
ld.global.nc.b128 d, [a];
9.7.8.10. Data Movement and Conversion Instructions: ldu
ldu
Load read-only data from an address that is common across threads in the warp.
Syntax
ldu{.ss}.type d, [a]; // load from address
ldu{.ss}.vec.type d, [a]; // vec load from address
.ss = { .global }; // state space
.vec = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64, .b128,
.u8, .u16, .u32, .u64,
.s8, .s16, .s32, .s64,
.f32, .f64 };
Description
Load read-only data into register variable d from the location specified by the source address
operand a in the global state space, where the address is guaranteed to be the same across all
threads in the warp. If no state space is given, perform the load using Generic Addressing.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
Semantics
d = a; // named variable a
d = *(&a+immOff) // variable-plus-offset
d = *a; // register
d = *(a+immOff); // register-plus-offset
d = *(immAddr); // immediate address
Notes
Destination d must be in the .reg state space.
A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types. See Table 25 for a description of these relaxed type-checking rules.
.f16 data may be loaded using ldu.b16, and then converted to .f32 or .f64 using
cvtor can be used in half precision floating point instructions.
.f16x2 data may be loaded using ldu.b32 and then used in half precision floating point
instructions.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Support for .b128 type introduced in PTX ISA version 8.3.
Target ISA Notes
ldu.f64 requires sm_13 or higher.
Support for .b128 type requires sm_70 or higher.
Examples
ldu.global.f32 d,[a];
ldu.global.b32 d,[p+4];
ldu.global.v4.f32 Q,[p];
ldu.global.b128 d,[a];
9.7.8.11. Data Movement and Conversion Instructions: st
st
Store data to an addressable state space variable.
Syntax
st{.weak}{.ss}{.cop}{.level::cache_hint}{.vec}.type [a], b{, cache-policy};
st{.weak}{.ss}{.level::eviction_priority}{.level::cache_hint}{.vec}.type
[a], b{, cache-policy};
st.volatile{.ss}{.vec}.type [a], b;
st.relaxed.scope{.ss}{.level::eviction_priority}{.level::cache_hint}{.vec}.type
[a], b{, cache-policy};
st.release.scope{.ss}{.level::eviction_priority}{.level::cache_hint}{.vec}.type
[a], b{, cache-policy};
st.mmio.relaxed.sys{.global}.type [a], b;
.ss = { .global, .local, .param{::func}, .shared{::cta, ::cluster} };
.level::eviction_priority = { .L1::evict_normal, .L1::evict_unchanged,
.L1::evict_first, .L1::evict_last, .L1::no_allocate };
.level::cache_hint = { .L2::cache_hint };
.cop = { .wb, .cg, .cs, .wt };
.sem = { .relaxed, .release };
.scope = { .cta, .cluster, .gpu, .sys };
.vec = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64, .b128,
.u8, .u16, .u32, .u64,
.s8, .s16, .s32, .s64,
.f32, .f64 };
Description
Store the value of operand b in the location specified by the destination address
operand a in specified state space. If no state space is given, perform the store using Generic
Addressing. Stores to const memory are illegal.
If no sub-qualifier is specified with .shared state space, then ::cta is assumed by default.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
If .param is specified without any sub-qualifiers then it defaults to .param::func.
Instruction st.param{::func} used for passing arguments to device function cannot be predicated.
See Parameter State Space and Function Declarations and
Definitions for descriptions of the proper use
of st.param.
The qualifiers .relaxed and .release indicate memory synchronization as described in the
Memory Consistency Model. The .scope qualifier
indicates the set of threads with which an st.relaxed or st.release instruction can directly
synchronize1. The .weak qualifier indicates a memory instruction with no synchronization.
The effects of this instruction become visible to other threads only when synchronization is established
by other means.
The semantic details of .mmio qualifier are described in the Memory Consistency Model. Only .sys thread scope is valid for st.mmio operation. The
qualifiers .mmio and .relaxed must be specified together.
The .weak, .volatile, .relaxed and .release qualifiers are mutually exclusive. When
none of these is specified, the .weak qualifier is assumed by default.
An st.volatile operation is always performed and it will not be reordered with respect to other
volatile operations to the same memory location. st.volatile has the same memory
synchronization semantics as st.relaxed.sys.
The qualifiers .volatile, .relaxed and .release may be used only with .global and
.shared spaces and with generic addressing, where the address points to .global or
.shared space. Cache operations are not permitted with these qualifiers. The qualifier .mmio
may be used only with .global space and with generic addressing, where the address points to
.global space.
The qualifier .level::eviction_priority specifies the eviction policy that will be used during
memory access.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
The qualifier .level::cache_hint is only supported for .global state space and for generic
addressing where the address points to the .global state space.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
1 This synchronization is further extended to other threads through the transitive nature of causality order, as described in the memory consistency model.
Semantics
d = a; // named variable d
*(&a+immOffset) = b; // variable-plus-offset
*a = b; // register
*(a+immOffset) = b; // register-plus-offset
*(immAddr) = b; // immediate address
Notes
Operand b must be in the .reg state space.
A source register wider than the specified type may be used. The lower n bits corresponding to
the instruction-type width are stored to memory. See
Table 24
for a description of these relaxed type-checking rules.
.f16 data resulting from a cvt instruction may be stored using st.b16.
.f16x2 data may be stored using st.b32.
PTX ISA Notes
st introduced in PTX ISA version 1.0. st.volatile introduced in PTX ISA version 1.1.
Generic addressing and cache operations introduced in PTX ISA version 2.0.
Support for scope qualifier, .relaxed, .release, .weak qualifiers introduced in PTX ISA
version 6.0.
Support for .level::eviction_priority and .level::cache_hint qualifiers introduced in PTX
ISA version 7.4.
Support for .cluster scope qualifier introduced in PTX ISA version 7.8.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for .mmio qualifier introduced in PTX ISA version 8.2.
Support for ::func sub-qualifier on .param space introduced in PTX ISA version 8.3.
Support for .b128 type introduced in PTX ISA version 8.3.
Support for .sys scope with .b128 type introduced in PTX ISA version 8.4.
Target ISA Notes
st.f64 requires sm_13 or higher.
Support for scope qualifier, .relaxed, .release, .weak qualifiers require sm_70 or
higher.
Generic addressing requires sm_20 or higher.
Cache operations require sm_20 or higher.
Support for .level::eviction_priority qualifier requires sm_70 or higher.
Support for .level::cache_hint qualifier requires sm_80 or higher.
Support for .cluster scope qualifier requires sm_90 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for .mmio qualifier requires sm_70 or higher.
Support for .b128 type requires sm_70 or higher.
Examples
st.global.f32 [a],b;
st.local.b32 [q+4],a;
st.global.v4.s32 [p],Q;
st.local.b32 [q+-8],a; // negative offset
st.local.s32 [100],r7; // immediate address
cvt.f16.f32 %r,%r; // %r is 32-bit register
st.b16 [fs],%r; // store lower
st.global.relaxed.sys.u32 [gbl], %r0;
st.shared.release.cta.u32 [sh], %r1;
st.global.relaxed.cluster.u32 [gbl], %r2;
st.shared::cta.release.cta.u32 [sh + 4], %r1;
st.shared::cluster.u32 [sh + 8], %r1;
st.global.mmio.relaxed.sys.u32 [gbl], %r1;
st.global.L1::no_allocate.f32 [p], a;
createpolicy.fractional.L2::evict_last.b64 cache-policy, 0.25;
st.global.L2::cache_hint.b32 [a], b, cache-policy;
st.param::func.b64 [param1], %rp1;
st.global.b128 [a], b; // 128-bit store
9.7.8.12. Data Movement and Conversion Instructions: st.async
st.async
Asynchronous store operation on shared memory.
Syntax
st.async{.weak}{.ss}{.completion_mechanism}{.vec}.type [a], b, [mbar];
.ss = { .shared::cluster };
.type = { .b32, .b64,
.u32, .u64,
.s32, .s64,
.f32, .f64 };
.vec = { .v2, .v4 };
.completion_mechanism = { .mbarrier::complete_tx::bytes };
Description
st.async is a non-blocking instruction which initiates an asynchronous store operation that
stores the value specified by source operand b to the destination memory location
specified by operand a.
The modifier .completion_mechanism specifies that upon completion of the asynchronous operation,
complete-tx
operation, with completeCount argument equal to amount of data stored in bytes, will be
performed on the mbarrier object specified by the operand mbar.
Operand a represents destination address and must be a register or of the form register +
immOff as described in Addresses as Operands.
The shared memory addresses of destination operand a and the mbarrier object mbar, must
meet all of the following conditions:
They belong to the same CTA.
They are different to the CTA of the executing thread but must be within the same cluster.
Otherwise, the behavior is undefined.
The state space of the address {.ss}, if specified, is applicable to both operands a and
mbar. If not specified, then Generic Addressing is used for
both a and mbar. If the generic addresses specified do not fall within the address window of
.shared::cluster state space, then the behaviour is undefined.
The store operation in st.async is treated as a weak memory operation and the complete_tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 8.1.
Target ISA Notes
Requires sm_90 or higher.
Examples
st.async.shared::cluster.mbarrier::complete_tx::bytes.u32 [addr], b, [mbar_addr]
9.7.8.13. Data Movement and Conversion Instructions: multimem.ld_reduce, multimem.st, multimem.red
The multimem.* operations operate on multimem addresses and accesses all of the multiple memory locations which the multimem address points to.
Multimem addresses can only be accessed only by multimem.* operations. Accessing a multimem address
with ld, st or any other memory operations results in undefined behavior.
Refer to CUDA programming guide for creation and management of the multimem addresses.
multimem.ld_reduce, multimem.st, multimem.red
Perform memory operations on the multimem address.
Syntax
// Integer type:
multimem.ld_reduce{.ldsem}{.scope}{.ss}.op.type d, [a];
multimem.st{.stsem}{.scope}{.ss}.type [a], b;
multimem.red{.redsem}{.scope}{.ss}.op.type [a], b;
.ss = { .global }
.ldsem = { .weak, .relaxed, .acquire }
.stsem = { .weak, .relaxed, .release }
.redsem = { .relaxed, .release }
.scope = { .cta, .cluster, .gpu, .sys }
.op = { .min, .max, .add, .and, .or, .xor }
.type = { .b32, .b64, .u32, .u64, .s32, .s64 }
// Floating point type:
multimem.ld_reduce{.ldsem}{.scope}{.ss}.op{.acc_prec}{.vec}.type d, [a];
multimem.st{.stsem}{.scope}{.ss}{.vec}.type [a], b;
multimem.red{.redsem}{.scope}{.ss}.redop{.vec}.type [a], b;
.ss = { .global }
.ldsem = { .weak, .relaxed, .acquire }
.stsem = { .weak, .relaxed, .release }
.redsem = { .relaxed, .release }
.scope = { .cta, .cluster, .gpu, .sys }
.op = { .min, .max, .add }
.redop = { .add }
.acc_prec = { .acc::f32 }
.vec = { .v2, .v4, .v8 }
.type= { .f16, .f16x2, .bf16, .bf16x2, .f32, .f64 }
Description
Instruction multimem.ld_reduce performs the following operations:
load operation on the multimem address
a, which involves loading of data from all of the multiple memory locations pointed to by the multimem addressa,reduction operation specified by
.opon the multiple data loaded from the multimem addressa.
The result of the reduction operation in returned in register d.
Instruction multimem.st performs a store operation of the input operand b to all the memory
locations pointed to by the multimem address a.
Instruction multimem.red performs a reduction operation on all the memory locations pointed to
by the multimem address a, with operand b.
Instruction multimem.ld_reduce performs reduction on the values loaded from all the memory
locations that the multimem address points to. In contrast, the multimem.red perform reduction
on all the memory locations that the multimem address points to.
Address operand a must be a multimem address. Otherwise, the behavior is undefined. Supported
addressing modes for operand a and alignment requirements are described in Addresses as Operands.
If no state space is specified then Generic Addressing is
used. If the address specified by a does not fall within the address window of .global state
space then the behavior is undefined.
For floating-point type multi- operations, the size of the specified type along with .vec must
equal either 32-bits or 64-bits or 128-bits. No other combinations of .vec and type are
allowed. Type .f64 cannot be used with .vec qualifier.
The following table describes the valid combinations of .op and base type:
op |
Base type |
|---|---|
|
.u32, .u64, .s32.f16, .f16x2, .bf16, .bf16x2.f32, .f64 |
|
|
|
.u32, .s32, .u64, .s644.f16, .f16x2, .bf16, .bf16x2 |
For multimem.ld_reduce, the default precision of the intermediate accumulation is same as the
specified type. Optionally for .f16, .f16x2, .bf16 and .bf16x2 types, .acc::f32
can be specified to change the precision of the intermediate accumulation to .f32.
Optional qualifiers .ldsem, .stsem and .redsem specify the memory synchronizing effect
of the multimem.ld_reduce, multimem.st and multimem.red respectively, as described in
Memory Consistency Model. If explicit semantics qualifiers
are not specified, then multimem.ld_reduce and multimem.st default to .weak and
multimem.red defaults to .relaxed.
The optional .scope qualifier specifies the set of threads that can directly observe the memory
synchronizing effect of this operation, as described in Memory Consistency Model. If the .scope qualifier is not specified for
multimem.red then .sys scope is assumed by default.
PTX ISA Notes
Introduced in PTX ISA version 8.1.
Support for .acc::f32 qualifier introduced in PTX ISA version 8.2.
Target ISA Notes
Requires sm_90 or higher.
Examples
multimem.ld_reduce.and.b32 val1_b32, [addr1];
multimem.ld_reduce.acquire.gpu.global.add.u32 val2_u32, [addr2];
multimem.st.relaxed.gpu.b32 [addr3], val3_b32;
multimem.st.release.cta.global.u32 [addr4], val4_u32;
multimem.red.relaxed.gpu.max.f64 [addr5], val5_f64;
multimem.red.release.cta.global.add.v4.f32 [addr6], {val6, val7, val8, val9};
multimem.ld_reduce.add.acc::f32.v2.f16x2 {val_10, val_11}, [addr7];
9.7.8.14. Data Movement and Conversion Instructions: prefetch, prefetchu
prefetch, prefetchu
Prefetch line containing a generic address at a specified level of memory hierarchy, in specified state space.
Syntax
prefetch{.space}.level [a]; // prefetch to data cache
prefetch.global.level::eviction_priority [a]; // prefetch to data cache
prefetchu.L1 [a]; // prefetch to uniform cache
prefetch{.tensormap_space}.tensormap [a]; // prefetch the tensormap
.space = { .global, .local };
.level = { .L1, .L2 };
.level::eviction_priority = { .L2::evict_last, .L2::evict_normal };
.tensormap_space = { .const, .param };
Description
The prefetch instruction brings the cache line containing the specified address in global or
local memory state space into the specified cache level.
If the .tensormap qualifier is specified then the prefetch instruction brings the cache line
containing the specified address in the .const or .param memory state space for subsequent
use by the cp.async.bulk.tensor instruction.
If no state space is given, the prefetch uses Generic Addressing.
Optionally, the eviction priority to be applied on the prefetched cache line can be specified by the
modifier .level::eviction_priority.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
The prefetchu instruction brings the cache line containing the specified generic address into
the specified uniform cache level.
A prefetch to a shared memory location performs no operation.
A prefetch into the uniform cache requires a generic address, and no operation occurs if the
address maps to a const, local, or shared memory location.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Support for .level::eviction_priority qualifier introduced in PTX ISA version 7.4.
Support for the .tensormap qualifier is introduced in PTX ISA version 8.0.
Target ISA Notes
prefetch and prefetchu require sm_20 or higher.
Support for .level::eviction_priority qualifier requires sm_80 or higher.
Support for the .tensormap qualifier requires sm_90 or higher.
Examples
prefetch.global.L1 [ptr];
prefetch.global.L2::evict_last [ptr];
prefetchu.L1 [addr];
prefetch.global.tensormap [ptr];
9.7.8.15. Data Movement and Conversion Instructions: applypriority
applypriority
Apply the cache eviction priority to the specified address in the specified cache level.
Syntax
applypriority{.global}.level::eviction_priority [a], size;
.level::eviction_priority = { .L2::evict_normal };
Description
The applypriority instruction applies the cache eviction priority specified by the
.level::eviction_priority qualifier to the address range [a..a+size) in the specified cache
level.
If no state space is specified then Generic Addressing is
used. If the specified address does not fall within the address window of .global state space
then the behavior is undefined.
The operand size is an integer constant that specifies the amount of data, in bytes, in the
specified cache level on which the priority is to be applied. The only supported value for the
size operand is 128.
Supported addressing modes for operand a are described in Addresses as Operands. a must be aligned to 128 bytes.
If the data pointed to by address a is not already present in the specified cache level, then
the data will be prefetched before applying the specified priority.
PTX ISA Notes
Introduced in PTX ISA version 7.4.
Target ISA Notes
Requires sm_80 or higher.
Examples
applypriority.global.L2::evict_normal [ptr], 128;
9.7.8.16. Data Movement and Conversion Instructions: discard
discard
Invalidate the data in cache at the specified address and cache level.
Syntax
discard{.global}.level [a], size;
.level = { .L2 };
Description
The discard instruction invalidates the data at the address range [a .. a + (size - 1)] in
the cache level specified by the .level qualifier without writing back the data in the cache to
the memory. Therefore after the discard operation, the data at the address range [a .. a+ (size -
1)] has undetermined value.
The operand size is an integer constant that specifies the amount of data, in bytes, in the
cache level specified by the .level qualifier to be discarded. The only supported value for the
size operand is 128.
If no state space is specified then Generic Addressing is
used. If the specified address does not fall within the address window of .global state space
then the behavior is undefined.
Supported addressing modes for address operand a are described in Addresses as Operands. a must be aligned to 128 bytes.
PTX ISA Notes
Introduced in PTX ISA version 7.4.
Target ISA Notes
Requires sm_80 or higher.
Examples
discard.global.L2 [ptr], 128;
9.7.8.17. Data Movement and Conversion Instructions: createpolicy
createpolicy
Create a cache eviction policy for the specified cache level.
Syntax
// Range-based policy
createpolicy.range{.global}.level::primary_priority{.level::secondary_priority}.b64
cache-policy, [a], primary-size, total-size;
// Fraction-based policy
createpolicy.fractional.level::primary_priority{.level::secondary_priority}.b64
cache-policy{, fraction};
// Converting the access property from CUDA APIs
createpolicy.cvt.L2.b64 cache-policy, access-property;
.level::primary_priority = { .L2::evict_last, .L2::evict_normal,
.L2::evict_first, .L2::evict_unchanged };
.level::secondary_priority = { .L2::evict_first, .L2::evict_unchanged };
Description
The createpolicy instruction creates a cache eviction policy for the specified cache level in an
opaque 64-bit register specified by the destination operand cache-policy. The cache eviction
policy specifies how cache eviction priorities are applied to global memory addresses used in memory
operations with .level::cache_hint qualifier.
There are two types of cache eviction policies:
Range-based policy
The cache eviction policy created using
createpolicy.rangespecifies the cache eviction behaviors for the following three address ranges:[a .. a + (primary-size - 1)]referred to as primary range.[a + primary-size .. a + (total-size - 1)]referred to as trailing secondary range.[a - (total-size - primary-size) .. (a - 1)]referred to as preceding secondary range.
When a range-based cache eviction policy is used in a memory operation with
.level::cache_hintqualifier, the eviction priorities are applied as follows:If the memory address falls in the primary range, the eviction priority specified by
.L2::primary_priorityis applied.If the memory address falls in any of the secondary ranges, the eviction priority specified by
.L2::secondary_priorityis applied.If the memory address does not fall in either of the above ranges, then the applied eviction priority is unspecified.
The 32-bit operand
primary-sizespecifies the size, in bytes, of the primary range. The 32-bit operandtotal-sizespecifies the combined size, in bytes, of the address range including primary and secondary ranges. The value ofprimary-sizemust be less than or equal to the value oftotal-size. Maximum allowed value oftotal-sizeis 4GB.If
.L2::secondary_priorityis not specified, then it defaults to.L2::evict_unchanged.If no state space is specified then Generic Addressing is used. If the specified address does not fall within the address window of
.globalstate space then the behavior is undefined.Fraction-based policy
A memory operation with
.level::cache_hintqualifier can use the fraction-based cache eviction policy to request the cache eviction priority specified by.L2:primary_priorityto be applied to a fraction of cache accesses specified by the 32-bit floating point operandfraction. The remainder of the cache accesses get the eviction priority specified by.L2::secondary_priority. This implies that in a memory operation that uses a fraction-based cache policy, the memory access has a probability specified by the operandfractionof getting the cache eviction priority specified by.L2::primary_priority.The valid range of values for the operand
fractionis(0.0,.., 1.0]. If the operandfractionis not specified, it defaults to 1.0.If
.L2::secondary_priorityis not specified, then it defaults to.L2::evict_unchanged.
The access property created using the CUDA APIs can be converted into cache eviction policy by the
instruction createpolicy.cvt. The source operand access-property is a 64-bit opaque
register. Refer to CUDA programming guide for more details.
PTX ISA Notes
Introduced in PTX ISA version 7.4.
Target ISA Notes
Requires sm_80 or higher.
Examples
createpolicy.fractional.L2::evict_last.b64 policy, 1.0;
createpolicy.fractional.L2::evict_last.L2::evict_unchanged.b64 policy, 0.5;
createpolicy.range.L2::evict_last.L2::evict_first.b64
policy, [ptr], 0x100000, 0x200000;
// access-prop is created by CUDA APIs.
createpolicy.cvt.L2.b64 policy, access-prop;
9.7.8.18. Data Movement and Conversion Instructions: isspacep
isspacep
Query whether a generic address falls within a specified state space window.
Syntax
isspacep.space p, a; // result is .pred
.space = { const, .global, .local, .shared{::cta, ::cluster}, .param{::entry} };
Description
Write predicate register p with 1 if generic address a falls within the specified state
space window and with 0 otherwise. Destination p has type .pred; the source address
operand must be of type .u32 or .u64.
isspacep.param{::entry} returns 1 if the generic address falls within the window of
Kernel Function Parameters, otherwise returns 0. If .param
is specified without any sub-qualifiers then it defaults to .param::entry.
isspacep.global returns 1 for Kernel Function Parameters as .param window is contained within the .global
window.
If no sub-qualifier is specified with .shared state space, then ::cta is assumed by default.
Note
ispacep.shared::cluster will return 1 for every shared memory address that is accessible to
the threads in the cluster, whereas ispacep.shared::cta will return 1 only if the address is
of a variable declared in the executing CTA.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
isspacep.const introduced in PTX ISA version 3.1.
isspacep.param introduced in PTX ISA version 7.7.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for sub-qualifier ::entry on .param space introduced in PTX ISA version 8.3.
Target ISA Notes
isspacep requires sm_20 or higher.
isspacep.param{::entry} requires sm_70 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Examples
isspacep.const iscnst, cptr;
isspacep.global isglbl, gptr;
isspacep.local islcl, lptr;
isspacep.shared isshrd, sptr;
isspacep.param::entry isparam, pptr;
isspacep.shared::cta isshrdcta, sptr;
isspacep.shared::cluster ishrdany sptr;
9.7.8.19. Data Movement and Conversion Instructions: cvta
cvta
Convert address from .const, Kernel Function Parameters (.param), .global, .local, or .shared
state space to generic, or vice-versa. Take the generic address of a variable declared in
.const, Kernel Function Parameters (.param),
.global, .local, or .shared state space.
Syntax
// convert const, global, local, or shared address to generic address
cvta.space.size p, a; // source address in register a
cvta.space.size p, var; // get generic address of var
cvta.space.size p, var+imm; // generic address of var+offset
// convert generic address to const, global, local, or shared address
cvta.to.space.size p, a;
.space = { .const, .global, .local, .shared{::cta, ::cluster}, .param{::entry} };
.size = { .u32, .u64 };
Description
Convert a const, Kernel Function Parameters
(.param), global, local, or shared address to a generic address, or vice-versa. The
source and destination addresses must be the same size. Use cvt.u32.u64 or cvt.u64.u32 to
truncate or zero-extend addresses.
For variables declared in .const, Kernel Function Parameters (.param), .global, .local, or .shared
state space, the generic address of the variable may be taken using cvta. The source is either a
register or a variable defined in const, Kernel Function Parameters (.param), global, local, or shared memory
with an optional offset.
When converting a generic address into a const, Kernel Function Parameters (.param), global, local, or shared
address, the resulting address is undefined in cases where the generic address does not fall within
the address window of the specified state space. A program may use isspacep to guard against
such incorrect behavior.
For cvta with .shared state space, the address must belong to the space specified by
::cta or ::cluster sub-qualifier, otherwise the behavior is undefined. If no sub-qualifier
is specified with .shared state space, then ::cta is assumed by default.
If .param is specified without any sub-qualifiers then it defaults to .param::entry.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
cvta.const and cvta.to.const introduced in PTX ISA version 3.1.
cvta.param and cvta.to.param introduced in PTX ISA version 7.7.
Note: The current implementation does not allow generic pointers to const space variables in
programs that contain pointers to constant buffers passed as kernel parameters.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for sub-qualifier ::entry on .param space introduced in PTX ISA version 8.3.
Target ISA Notes
cvta requires sm_20 or higher.
cvta.param{::entry} and cvta.to.param{::entry} requires sm_70 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Examples
cvta.const.u32 ptr,cvar;
cvta.local.u32 ptr,lptr;
cvta.shared::cta.u32 p,As+4;
cvta.shared::cluster.u32 ptr, As;
cvta.to.global.u32 p,gptr;
cvta.param.u64 ptr,pvar;
cvta.to.param::entry.u64 epptr, ptr;
9.7.8.20. Data Movement and Conversion Instructions: cvt
cvt
Convert a value from one type to another.
Syntax
cvt{.irnd}{.ftz}{.sat}.dtype.atype d, a; // integer rounding
cvt{.frnd}{.ftz}{.sat}.dtype.atype d, a; // fp rounding
cvt.frnd2{.relu}{.satfinite}.f16.f32 d, a;
cvt.frnd2{.relu}{.satfinite}.f16x2.f32 d, a, b;
cvt.frnd2{.relu}{.satfinite}.bf16.f32 d, a;
cvt.frnd2{.relu}{.satfinite}.bf16x2.f32 d, a, b;
cvt.rna{.satfinite}.tf32.f32 d, a;
cvt.frnd2{.relu}.tf32.f32 d, a;
cvt.rn.satfinite{.relu}.f8x2type.f32 d, a, b;
cvt.rn.satfinite{.relu}.f8x2type.f16x2 d, a;
cvt.rn.{.relu}.f16x2.f8x2type d, a;
.irnd = { .rni, .rzi, .rmi, .rpi };
.frnd = { .rn, .rz, .rm, .rp };
.frnd2 = { .rn, .rz };
.dtype = .atype = { .u8, .u16, .u32, .u64,
.s8, .s16, .s32, .s64,
.bf16, .f16, .f32, .f64 };
.f8x2type = { .e4m3x2, .e5m2x2 };
Description
Convert between different types and sizes.
For .f16x2 and .bf16x2 instruction type, two inputs a and b of .f32 type are
converted into .f16 or .bf16 type and the converted values are packed in the destination
register d, such that the value converted from input a is stored in the upper half of d
and the value converted from input b is stored in the lower half of d
For .f16x2 instruction type, destination operand d has .f16x2 or .b32 type. For
.bf16 instruction type, operand d has .b16 type. For .bf16x2 instruction type,
operand d has .b32 type. For .tf32 instruction type, operand d has .b32 type.
When converting to .e4m3x2/.e5m2x2 data formats, the destination operand d has .b16
type. When converting two .f32 inputs to .e4m3x2/.e5m2x2, each input is converted to the
specified format, and the converted values are packed in the destination operand d such that the
value converted from input a is stored in the upper 8 bits of d and the value converted from
input b is stored in the lower 8 bits of d. When converting an .f16x2 input to
.e4m3x2/ .e5m2x2, each .f16 input from operand a is converted to the specified
format. The converted values are packed in the destination operand d such that the value
converted from the upper 16 bits of input a is stored in the upper 8 bits of d and the value
converted from the lower 16 bits of input a is stored in the lower 8 bits of d.
When converting from .e4m3x2/.e5m2x2 to .f16x2, source operand a has .b16
type. Each 8-bit input value in operand a is converted to .f16 type. The converted values
are packed in the destination operand d such that the value converted from the upper 8 bits of
a is stored in the upper 16 bits of d and the value converted from the lower 8 bits of a
is stored in the lower 16 bits of d.
Rounding modifier is mandatory in all of the following cases:
float-to-float conversions, when destination type is smaller than source type
All float-to-int conversions
All int-to-float conversions
All conversions involving
.f16x2,.e4m3x2, .e5m2x2,.bf16x2and.tf32instruction types.
.satfinite modifier is only supported for conversions involving the following types:
.e4m3x2and.e5m2x2destination types..satfinitemodifier is mandatory for such conversions..f16,.bf16,.f16x2,.bf16x2as destination types..tf32as destination type with rounding mode specified as round to nearest, ties away from zero.
Semantics
if (/* inst type is .f16x2 or .bf16x2 */) {
d[31:16] = convert(a);
d[15:0] = convert(b);
} else {
d = convert(a);
}
Integer Notes
Integer rounding is required for float-to-integer conversions, and for same-size float-to-float conversions where the value is rounded to an integer. Integer rounding is illegal in all other instances.
Integer rounding modifiers:
.rniround to nearest integer, choosing even integer if source is equidistant between two integers
.rziround to nearest integer in the direction of zero
.rmiround to nearest integer in direction of negative infinity
.rpiround to nearest integer in direction of positive infinity
In float-to-integer conversion, NaN inputs are converted to 0.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported.
For
cvt.ftz.dtype.f32float-to-integer conversions andcvt.ftz.f32.f32float-to-float conversions with integer rounding, subnormal inputs are flushed to sign-preserving zero. Modifier.ftzcan only be specified when either.dtypeor.atypeis.f32and applies only to single precision (.f32) inputs and results.sm_1xFor
cvt.ftz.dtype.f32float-to-integer conversions andcvt.ftz.f32.f32float-to-float conversions with integer rounding, subnormal inputs are flushed to sign-preserving zero. The optional.ftzmodifier may be specified in these cases for clarity.Note: In PTX ISA versions 1.4 and earlier, the
cvtinstruction did not flush single-precision subnormal inputs or results to zero if the destination type size was 64-bits. The compiler will preserve this behavior for legacy PTX code.
Saturation modifier:
.satFor integer destination types,
.satlimits the result toMININT..MAXINTfor the size of the operation. Note that saturation applies to both signed and unsigned integer types.The saturation modifier is allowed only in cases where the destination type’s value range is not a superset of the source type’s value range; i.e., the
.satmodifier is illegal in cases where saturation is not possible based on the source and destination types.For float-to-integer conversions, the result is clamped to the destination range by default; i.e,
.satis redundant.
Floating Point Notes
Floating-point rounding is required for float-to-float conversions that result in loss of precision, and for integer-to-float conversions. Floating-point rounding is illegal in all other instances.
Floating-point rounding modifiers:
.rnmantissa LSB rounds to nearest even
.rnamantissa LSB rounds to nearest, ties away from zero
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
A floating-point value may be rounded to an integral value using the integer rounding modifiers (see Integer Notes). The operands must be of the same size. The result is an integral value, stored in floating-point format.
Subnormal numbers:
sm_20+By default, subnormal numbers are supported. Modifier
.ftzmay be specified to flush single-precision subnormal inputs and results to sign-preserving zero. Modifier.ftzcan only be specified when either.dtypeor.atypeis.f32and applies only to single precision (.f32) inputs and results.sm_1xSingle-precision subnormal inputs and results are flushed to sign-preserving zero. The optional
.ftzmodifier may be specified in these cases for clarity.
Note: In PTX ISA versions 1.4 and earlier, the cvt instruction did not flush
single-precision subnormal inputs or results to zero if either source or destination type was
.f64. The compiler will preserve this behavior for legacy PTX code. Specifically, if the PTX
ISA version is 1.4 or earlier, single-precision subnormal inputs and results are flushed to
sign-preserving zero only for cvt.f32.f16, cvt.f16.f32, and cvt.f32.f32 instructions.
Saturation modifier:
.sat:For floating-point destination types,
.satlimits the result to the range [0.0, 1.0].NaNresults are flushed to positive zero. Applies to.f16,.f32, and.f64types..relu:For
.f16,.f16x2,.bf16,.bf16x2,.e4m3x2,.e5m2x2and.tf32destination types,.reluclamps the result to 0 if negative.NaNresults are converted to canonicalNaN..satfinite:For
.f16,.f16x2,.bf16,.bf16x2,.e4m3x2,.e5m2x2and.tf32destination formats, if the input value isNaN, then the result isNaNin the specified destination format. If the absolute value of input (ignoring sign) is greater than MAX_NORM of the specified destination format, then the result is sign-preserved MAX_NORM of the destination format.
Notes
A source register wider than the specified type may be used, except when the source operand has
.bf16 or .bf16x2 format. The lower n bits corresponding to the instruction-type width
are used in the conversion. See Operand Size Exceeding Instruction-Type Size for a description of these relaxed
type-checking rules.
A destination register wider than the specified type may be used, except when the destination
operand has .bf16, .bf16x2 or .tf32 format. The result of conversion is sign-extended to
the destination register width for signed integers, and is zero-extended to the destination register
width for unsigned, bit-size, and floating-point types. See Operand Size Exceeding Instruction-Type
Size for a description of these relaxed
type-checking rules.
For cvt.f32.bf16, NaN input yields unspecified NaN.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
.relu modifier and {.f16x2, .bf16, .bf16x2, .tf32} destination formats
introduced in PTX ISA version 7.0.
cvt.bf16.{u8/s8/u16/s16/u32/s32/u64/s64/f16/f64/bf16},
cvt.{u8/s8/u16/s16/u32/s32/u64/s64/f16/f64}.bf16, and cvt.tf32.f32.{relu}.{rn/rz} introduced
in PTX ISA 7.8.
cvt with .e4m3x2/.e5m2x2 for sm_90 or higher introduced in PTX ISA version 7.8.
cvt.satfinite.{e4m3x2, e5m2x2}.{f32, f16x2} for sm_90 or higher introduced in PTX ISA version 7.8.
cvt with .e4m3x2/.e5m2x2 for sm_89 introduced in PTX ISA version 8.1.
cvt.satfinite.{e4m3x2, e5m2x2}.{f32, f16x2} for sm_89 introduced in PTX ISA version 8.1.
cvt.satfinite.{f16, bf16, f16x2, bf16x2, tf32}.f32 introduced in PTX ISA version 8.1.
Target ISA Notes
cvt to or from .f64 requires sm_13 or higher.
.relu modifier and {.f16x2, .bf16, .bf16x2, .tf32} destination formats require
sm_80 or higher.
cvt.bf16.{u8/s8/u16/s16/u32/s32/u64/s64/f16/f64/bf16},
cvt.{u8/s8/u16/s16/u32/s32/u64/s64/f16/f64}.bf16, and cvt.tf32.f32.{relu}.{rn/rz} require
sm_90 or higher.
cvt with .e4m3x2/.e5m2x2 requires sm89 or higher.
cvt.satfinite.{e4m3x2, e5m2x2}.{f32, f16x2} requires sm_89 or higher.
Examples
cvt.f32.s32 f,i;
cvt.s32.f64 j,r; // float-to-int saturates by default
cvt.rni.f32.f32 x,y; // round to nearest int, result is fp
cvt.f32.f32 x,y; // note .ftz behavior for sm_1x targets
cvt.rn.relu.f16.f32 b, f; // result is saturated with .relu saturation mode
cvt.rz.f16x2.f32 b1, f, f1; // convert two fp32 values to packed fp16 outputs
cvt.rn.relu.satfinite.f16x2.f32 b1, f, f1; // convert two fp32 values to packed fp16 outputs with .relu saturation on each output
cvt.rn.bf16.f32 b, f; // convert fp32 to bf16
cvt.rz.relu.satfinite.bf16.f3 2 b, f; // convert fp32 to bf16 with .relu and .satfinite saturation
cvt.rz.satfinite.bf16x2.f32 b1, f, f1; // convert two fp32 values to packed bf16 outputs
cvt.rn.relu.bf16x2.f32 b1, f, f1; // convert two fp32 values to packed bf16 outputs with .relu saturation on each output
cvt.rna.satfinite.tf32.f32 b1, f; // convert fp32 to tf32 format
cvt.rn.relu.tf32.f32 d, a; // convert fp32 to tf32 format
cvt.f64.bf16.rp f, b; // convert bf16 to f64 format
cvt.bf16.f16.rz b, f // convert f16 to bf16 format
cvt.bf16.u64.rz b, u // convert u64 to bf16 format
cvt.s8.bf16.rpi s, b // convert bf16 to s8 format
cvt.bf16.bf16.rpi b1, b2 // convert bf16 to corresponding int represented in bf16 format
cvt.rn.satfinite.e4m3x2.f32 d, a, b; // convert a, b to .e4m3 and pack as .e4m3x2 output
cvt.rn.relu.satfinite.e5m2x2.f16x2 d, a; // unpack a and convert the values to .e5m2 outputs with .relu
// saturation on each output and pack as .e5m2x2
cvt.rn.f16x2.e4m3x2 d, a; // unpack a, convert two .e4m3 values to packed f16x2 output
9.7.8.21. Data Movement and Conversion Instructions: cvt.pack
cvt.pack
Convert two integer values from one integer type to another and pack the results.
Syntax
cvt.pack.sat.convertType.abType d, a, b;
.convertType = { .u16, .s16 }
.abType = { .s32 }
cvt.pack.sat.convertType.abType.cType d, a, b, c;
.convertType = { .u2, .s2, .u4, .s4, .u8, .s8 }
.abType = { .s32 }
.cType = { .b32 }
Description
Convert two 32-bit integers a and b into specified type and pack the results into d.
Destination d is an unsigned 32-bit integer. Source operands a and b are integers of
type .abType and the source operand c is an integer of type .cType.
The inputs a and b are converted to values of type specified by .convertType with
saturation and the results after conversion are packed into lower bits of d.
If operand c is specified then remaining bits of d are copied from lower bits of c.
Semantics
ta = a < MIN(convertType) ? MIN(convertType) : a;
ta = a > MAX(convertType) ? MAX(convertType) : a;
tb = b < MIN(convertType) ? MIN(convertType) : b;
tb = b > MAX(convertType) ? MAX(convertType) : b;
size = sizeInBits(convertType);
td = tb ;
for (i = size; i <= 2 * size - 1; i++) {
td[i] = ta[i - size];
}
if (isU16(convertType) || isS16(convertType)) {
d = td;
} else {
for (i = 0; i < 2 * size; i++) {
d[i] = td[i];
}
for (i = 2 * size; i <= 31; i++) {
d[i] = c[i - 2 * size];
}
}
.sat modifier limits the converted values to MIN(convertType)..MAX(convertedType) (no
overflow) if the corresponding inputs are not in the range of datatype specified as
.convertType.
PTX ISA Notes
Introduced in PTX ISA version 6.5.
Target ISA Notes
Requires sm_72 or higher.
Sub byte types (.u4/.s4 and .u2/.s2) requires sm_75 or higher.
Examples
cvt.pack.sat.s16.s32 %r1, %r2, %r3; // 32-bit to 16-bit conversion
cvt.pack.sat.u8.s32.b32 %r4, %r5, %r6, 0; // 32-bit to 8-bit conversion
cvt.pack.sat.u8.s32.b32 %r7, %r8, %r9, %r4; // %r7 = { %r5, %r6, %r8, %r9 }
cvt.pack.sat.u4.s32.b32 %r10, %r12, %r13, %r14; // 32-bit to 4-bit conversion
cvt.pack.sat.s2.s32.b32 %r15, %r16, %r17, %r18; // 32-bits to 2-bit conversion
9.7.8.22. Data Movement and Conversion Instructions: mapa
mapa
Map the address of the shared variable in the target CTA.
Syntax
mapa{.space}.type d, a, b;
// Maps shared memory address in register a into CTA b.
mapa.shared::cluster.type d, a, b;
// Maps shared memory variable into CTA b.
mapa.shared::cluster.type d, sh, b;
// Maps shared memory variable into CTA b.
mapa.shared::cluster.type d, sh + imm, b;
// Maps generic address in register a into CTA b.
mapa.type d, a, b;
.space = { .shared::cluster }
.type = { .u32, .u64 }
Description
Get address in the CTA specified by operand b which corresponds to the address specified by
operand a.
Instruction type .type indicates the type of the destination operand d and the source
operand a.
When space is .shared::cluster, source a is either a shared memory variable or a register
containing a valid shared memory address and register d contains a shared memory address. When
the optional qualifier .space is not specified, both a and d are registers containing
generic addresses pointing to shared memory.
b is a 32-bit integer operand representing the rank of the target CTA.
Destination register d will hold an address in CTA b corresponding to operand a.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
mapa.shared::cluster.u64 d1, %reg1, cta;
mapa.shared::cluster.u32 d2, sh, 3;
mapa.u64 d3, %reg2, cta;
9.7.8.23. Data Movement and Conversion Instructions: getctarank
getctarank
Generate the CTA rank of the address.
Syntax
getctarank{.space}.type d, a;
// Get cta rank from source shared memory address in register a.
getctarank.shared::cluster.type d, a;
// Get cta rank from shared memory variable.
getctarank.shared::cluster.type d, var;
// Get cta rank from shared memory variable+offset.
getctarank.shared::cluster.type d, var + imm;
// Get cta rank from generic address of shared memory variable in register a.
getctarank.type d, a;
.space = { .shared::cluster }
.type = { .u32, .u64 }
Description
Write the destination register d with the rank of the CTA which contains the address specified
in operand a.
Instruction type .type indicates the type of source operand a.
When space is .shared::cluster, source a is either a shared memory variable or a register
containing a valid shared memory address. When the optional qualifier .space is not specified,
a is a register containing a generic addresses pointing to shared memory. Destination d is
always a 32-bit register which holds the rank of the CTA.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
getctarank.shared::cluster.u32 d1, addr;
getctarank.shared::cluster.u64 d2, sh + 4;
getctarank.u64 d3, src;
9.7.8.24. Data Movement and Conversion Instructions: Asynchronous copy
An asynchronous copy operation performs the underlying operation asynchronously in the background, thus allowing the issuing threads to perform subsequent tasks.
An asynchronous copy operation can be a bulk operation that operates on a large amount of data, or a non-bulk operation that operates on smaller sized data. The amount of data handled by a bulk asynchronous operation must be a multiple of 16 bytes.
9.7.8.24.1. Completion Mechanisms for Asynchronous Copy Operations
A thread must explicitly wait for the completion of an asynchronous copy operation in order to access the result of the operation. Once an asynchronous copy operation is initiated, modifying the source memory location or reading from the destination memory location before the asynchronous operation completes, will cause unpredictable results.
This section describes two asynchronous copy operation completion mechanisms supported in PTX: Async-group mechanism and mbarrier-based mechanism.
Async-group mechanism
When using the async-group completion mechanism, the issuing thread specifies a group of asynchronous operations, called async-group, using a commit operation and tracks the completion of this group using a wait operation. The thread issuing the asynchronous operation must create separate async-groups for bulk and non-bulk asynchronous operations.
A commit operation creates a per-thread async-group containing all prior asynchronous operations initiated by the executing thread but none of the asynchronous operations following the commit operation. A committed asynchronous operation belongs to a single async-group.
When an async-group completes, all the asynchronous operations belonging to that group are complete and the executing thread that initiated the asynchronous operations can read the result of the asynchronous operations. All async-groups committed by an executing thread always complete in the order in which they were committed. There is no ordering between asynchronous operations within an async-group.
A typical pattern of using async-group as the completion mechanism is as follows:
Initiate the asynchronous operations.
Group the asynchronous operations into an async-group using a commit operation.
Wait for the completion of the async-group using the wait operation.
Once the async-group completes, access the results of all asynchronous operations in that async-group.
Mbarrier-based mechanism
A thread can track the completion of one or more asynchronous operations using the current phase of an mbarrier object. When the current phase of the mbarrier object is complete, it implies that all asynchronous operations tracked by this phase are complete, and all threads participating in that mbarrier object can access the result of the asynchronous operations.
The mbarrier object to be used for tracking the completion of an asynchronous operation can be either specified along with the asynchronous operation as part of its syntax, or as a separate operation. For a bulk asynchronous operation, the mbarrier object must be specified in the asynchronous operation, whereas for non-bulk operations, it can be specified after the asynchronous operation.
A typical pattern of using mbarrier-based completion mechanism is as follows:
Initiate the asynchronous operations.
Set up an mbarrier object to track the asynchronous operations in its current phase, either as part of the asynchronous operation or as a separate operation.
Wait for the mbarrier object to complete its current phase using
mbarrier.test_waitormbarrier.try_wait.Once the
mbarrier.test_waitormbarrier.try_waitoperation returnsTrue, access the results of the asynchronous operations tracked by the mbarrier object.
9.7.8.24.2. Async Proxy
The cp{.reduce}.async.bulk operations are performed in the asynchronous proxy (or async
proxy).
Accessing the same memory location across multiple proxies needs a cross-proxy fence. For the
async proxy, fence.proxy.async should be used to synchronize memory between generic
proxy and the async proxy.
The completion of a cp{.reduce}.async.bulk operation is followed by an implicit generic-async
proxy fence. So the result of the asynchronous operation is made visible to the generic proxy as
soon as its completion is observed. Async-group OR mbarrier-based completion mechanism must
be used to wait for the completion of the cp{.reduce}.async.bulk instructions.
9.7.8.24.3. Data Movement and Conversion Instructions: cp.async
cp.async
Initiates an asynchronous copy operation from one state space to another.
Syntax
cp.async.ca.shared{::cta}.global{.level::cache_hint}{.level::prefetch_size}
[dst], [src], cp-size{, src-size}{, cache-policy} ;
cp.async.cg.shared{::cta}.global{.level::cache_hint}{.level::prefetch_size}
[dst], [src], 16{, src-size}{, cache-policy} ;
cp.async.ca.shared{::cta}.global{.level::cache_hint}{.level::prefetch_size}
[dst], [src], cp-size{, ignore-src}{, cache-policy} ;
cp.async.cg.shared{::cta}.global{.level::cache_hint}{.level::prefetch_size}
[dst], [src], 16{, ignore-src}{, cache-policy} ;
.level::cache_hint = { .L2::cache_hint }
.level::prefetch_size = { .L2::64B, .L2::128B, .L2::256B }
cp-size = { 4, 8, 16 }
Description
cp.async is a non-blocking instruction which initiates an asynchronous copy operation of data
from the location specified by source address operand src to the location specified by
destination address operand dst. Operand src specifies a location in the global state space
and dst specifies a location in the shared state space.
Operand cp-size is an integer constant which specifies the size of data in bytes to be copied to
the destination dst. cp-size can only be 4, 8 and 16.
Instruction cp.async allows optionally specifying a 32-bit integer operand src-size. Operand
src-size represents the size of the data in bytes to be copied from src to dst and must
be less than cp-size. In such case, remaining bytes in destination dst are filled with
zeros. Specifying src-size larger than cp-size results in undefined behavior.
The optional and non-immediate predicate argument ignore-src specifies whether the data from the
source location src should be ignored completely. If the source data is ignored then zeros will
be copied to destination dst. If the argument ignore-src is not specified then it defaults
to False.
Supported alignment requirements and addressing modes for operand src and dst are described
in Addresses as Operands.
The mandatory .async qualifier indicates that the cp instruction will initiate the memory
copy operation asynchronously and control will return to the executing thread before the copy
operation is complete. The executing thread can then use cp.async.wait_all or
cp.async.wait_group or mbarrier instructions to wait for
completion of the asynchronous copy operation. No other synchronization mechanisms described in
Memory Consistency Model can be used to guarantee the
completion of the asynchronous copy operations.
There is no ordering guarantee between two cp.async operations if they are not explicitly
synchronized using cp.async.wait_all or cp.async.wait_group or mbarrier instructions.
As described in Cache Operators, the .cg qualifier indicates
caching of data only at global level cache L2 and not at L1 whereas .ca qualifier indicates
caching of data at all levels including L1 cache. Cache operator are treated as performance hints
only.
cp.async is treated as a weak memory operation in the Memory Consistency Model.
The .level::prefetch_size qualifier is a hint to fetch additional data of the specified size
into the respective cache level.The sub-qualifier prefetch_size can be set to either of 64B,
128B, 256B thereby allowing the prefetch size to be 64 Bytes, 128 Bytes or 256 Bytes
respectively.
The qualifier .level::prefetch_size may only be used with .global state space and with
generic addressing where the address points to .global state space. If the generic address does
not fall within the address window of the global memory, then the prefetching behavior is undefined.
The .level::prefetch_size qualifier is treated as a performance hint only.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
The qualifier .level::cache_hint is only supported for .global state space and for generic
addressing where the address points to the .global state space.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for .level::cache_hint and .level::prefetch_size qualifiers introduced in PTX ISA
version 7.4.
Support for ignore-src operand introduced in PTX ISA version 7.5.
Support for sub-qualifier ::cta introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_80 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Examples
cp.async.ca.shared.global [shrd], [gbl + 4], 4;
cp.async.ca.shared::cta.global [%r0 + 8], [%r1], 8;
cp.async.cg.shared.global [%r2], [%r3], 16;
cp.async.cg.shared.global.L2::64B [%r2], [%r3], 16;
cp.async.cg.shared.global.L2::128B [%r0 + 16], [%r1], 16;
cp.async.cg.shared.global.L2::256B [%r2 + 32], [%r3], 16;
createpolicy.fractional.L2::evict_last.L2::evict_unchanged.b64 cache-policy, 0.25;
cp.async.ca.shared.global.L2::cache_hint [%r2], [%r1], 4, cache-policy;
cp.async.ca.shared.global [shrd], [gbl], 4, p;
cp.async.cg.shared.global.L2::chache_hint [%r0], [%r2], 16, q, cache-policy;
9.7.8.24.4. Data Movement and Conversion Instructions: cp.async.commit_group
cp.async.commit_group
Commits all prior initiated but uncommitted cp.async instructions into a cp.async-group.
Syntax
cp.async.commit_group ;
Description
cp.async.commit_group instruction creates a new cp.async-group per thread and batches all
prior cp.async instructions initiated by the executing thread but not committed to any
cp.async-group into the new cp.async-group. If there are no uncommitted cp.async
instructions then cp.async.commit_group results in an empty cp.async-group.
An executing thread can wait for the completion of all cp.async operations in a cp.async-group
using cp.async.wait_group.
There is no memory ordering guarantee provided between any two cp.async operations within the
same cp.async-group. So two or more cp.async operations within a cp.async-group copying data
to the same location results in undefined behavior.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Target ISA Notes
Requires sm_80 or higher.
Examples
// Example 1:
cp.async.ca.shared.global [shrd], [gbl], 4;
cp.async.commit_group ; // Marks the end of a cp.async group
// Example 2:
cp.async.ca.shared.global [shrd1], [gbl1], 8;
cp.async.ca.shared.global [shrd1+8], [gbl1+8], 8;
cp.async.commit_group ; // Marks the end of cp.async group 1
cp.async.ca.shared.global [shrd2], [gbl2], 16;
cp.async.cg.shared.global [shrd2+16], [gbl2+16], 16;
cp.async.commit_group ; // Marks the end of cp.async group 2
9.7.8.24.5. Data Movement and Conversion Instructions: cp.async.wait_group / cp.async.wait_all
cp.async.wait_group/cp.async.wait_all
Wait for completion of prior asynchronous copy operations.
Syntax
cp.async.wait_group N;
cp.async.wait_all ;
Description
cp.async.wait_group instruction will cause executing thread to wait till only N or fewer of
the most recent cp.async-groups are pending and all the prior cp.async-groups committed by
the executing threads are complete. For example, when N is 0, the executing thread waits on all
the prior cp.async-groups to complete. Operand N is an integer constant.
cp.async.wait_all is equivalent to :
cp.async.commit_group;
cp.async.wait_group 0;
An empty cp.async-group is considered to be trivially complete.
Writes performed by cp.async operations are made visible to the executing thread only after:
The completion of
cp.async.wait_allorThe completion of
cp.async.wait_groupon the cp.async-group in which thecp.asyncbelongs to ormbarrier.test_wait returns
Trueon an mbarrier object which is tracking the completion of thecp.asyncoperation.
There is no ordering between two cp.async operations that are not synchronized with
cp.async.wait_all or cp.async.wait_group or mbarrier objects.
cp.async.wait_group and cp.async.wait_all does not provide any ordering and visibility
guarantees for any other memory operation apart from cp.async.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Target ISA Notes
Requires sm_80 or higher.
Examples
// Example of .wait_all:
cp.async.ca.shared.global [shrd1], [gbl1], 4;
cp.async.cg.shared.global [shrd2], [gbl2], 16;
cp.async.wait_all; // waits for all prior cp.async to complete
// Example of .wait_group :
cp.async.ca.shared.global [shrd3], [gbl3], 8;
cp.async.commit_group; // End of group 1
cp.async.cg.shared.global [shrd4], [gbl4], 16;
cp.async.commit_group; // End of group 2
cp.async.cg.shared.global [shrd5], [gbl5], 16;
cp.async.commit_group; // End of group 3
cp.async.wait_group 1; // waits for group 1 and group 2 to complete
9.7.8.24.6. Data Movement and Conversion Instructions: cp.async.bulk
cp.async.bulk
Initiates an asynchronous copy operation from one state space to another.
Syntax
cp.async.bulk.dst.src.completion_mechanism{.multicast}{.level::cache_hint}
[dstMem], [srcMem], size, [mbar] {, ctaMask} {, cache-policy}
.dst = { .shared::cluster }
.src = { .global }
.completion_mechanism = { .mbarrier::complete_tx::bytes }
.level::cache_hint = { .L2::cache_hint }
.multicast = { .multicast::cluster }
cp.async.bulk.dst.src.completion_mechanism [dstMem], [srcMem], size, [mbar]
.dst = { .shared::cluster }
.src = { .shared::cta }
.completion_mechanism = { .mbarrier::complete_tx::bytes }
cp.async.bulk.dst.src.completion_mechanism{.level::cache_hint} [dstMem], [srcMem], size{, cache-policy}
.dst = { .global }
.src = { .shared::cta }
.completion_mechanism = { .bulk_group }
.level::cache_hint = { .L2::cache_hint }
Description
cp.async.bulk is a non-blocking instruction which initiates an asynchronous bulk-copy operation
from the location specified by source address operand srcMem to the location specified by
destination address operand dstMem.
The direction of bulk-copy is from the state space specified by the .src modifier to the state
space specified by the .dst modifiers.
The 32-bit operand size specifies the amount of memory to be copied, in terms of number of
bytes. size must be a multiple of 16. If the value is not a multiple of 16, then the behavior is
undefined. The memory range [dstMem, dstMem + size - 1] must not overflow the destination memory
space and the memory range [srcMem, srcMem + size - 1] must not overflow the source memory
space. Otherwise, the behavior is undefined. The addresses dstMem and srcMem must be aligned
to 16 bytes.
When the source of the copy is .shared::cta and the destination is .shared::cluster, the
destination has to be in the shared memory of a different CTA within the cluster.
The modifier .completion_mechanism specifies the completion mechanism that is supported on the
instruction variant. The completion mechanisms that are supported for different variants are
summarized in the following table:
Completion mechanism |
|
|
Description |
|---|---|---|---|
|
|
|
mbarrier based completion mechanism |
|
|
||
|
|
|
Bulk async-group based completion mechanism |
The modifier .mbarrier::complete_tx::bytes specifies that the cp.async.bulk variant uses
mbarrier based completion mechanism. The complete-tx
operation, with completeCount argument equal to amount of data copied in bytes, will be
performed on the mbarrier object specified by the operand mbar.
The modifier .bulk_group specifies that the cp.async.bulk variant uses bulk async-group
based completion mechanism.
The optional modifier .multicast::cluster allows copying of data from global memory to shared
memory of multiple CTAs in the cluster. Operand ctaMask specifies the destination CTAs in the
cluster such that each bit position in the 16-bit ctaMask operand corresponds to the %ctaid
of the destination CTA. The source data is multicast to the same CTA-relative offset as dstMem
in the shared memory of each destination CTA. The mbarrier signal is also multicast to the same
CTA-relative offset as mbar in the shared memory of the destination CTA.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program. The
qualifier .level::cache_hint is only supported when at least one of the .src or .dst
statespaces is .global state space.
The copy operation in cp.async.bulk is treated as a weak memory operation and the complete-tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
Notes
.multicast::cluster qualifier is optimized for target architecture sm_90a and may have
substantially reduced performance on other targets and hence .multicast::cluster is advised to
be used with .target sm_90a.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
.multicast::cluster qualifier advised to be used with .target sm_90a.
Examples
// .global -> .shared::cluster:
cp.async.bulk.shared::cluster.global.mbarrier::complete_tx::bytes [dstMem], [srcMem], size, [mbar];
cp.async.bulk.shared::cluster.global.mbarrier::complete_tx::bytes.multicast::cluster
[dstMem], [srcMem], size, [mbar], ctaMask;
cp.async.bulk.shared::cluster.global.mbarrier::complete_tx::bytes.L2::cache_hint
[dstMem], [srcMem], size, [mbar], cache-policy;
// .shared::cta -> .shared::cluster (strictly remote):
cp.async.bulk.shared::cluster.shared::cta.mbarrier::complete_tx::bytes [dstMem], [srcMem], size, [mbar];
// .shared::cta -> .global:
cp.async.bulk.global.shared::cta.bulk_group [dstMem], [srcMem], size;
cp.async.bulk.global.shared::cta.bulk_group.L2::cache_hint} [dstMem], [srcMem], size, cache-policy;
9.7.8.24.7. Data Movement and Conversion Instructions: cp.reduce.async.bulk
cp.reduce.async.bulk
Initiates an asynchronous reduction operation.
Syntax
cp.reduce.async.bulk.dst.src.completion_mechanism.redOp.type
[dstMem], [srcMem], size, [mbar]
.dst = { .shared::cluster }
.src = { .shared::cta }
.completion_mechanism = { .mbarrier::complete_tx::bytes }
.redOp= { .and, .or, .xor,
.add, .inc, .dec,
.min, .max }
.type = { .b32, .u32, .s32, .b64, .u64 }
cp.reduce.async.bulk.dst.src.completion_mechanism{.level::cache_hint}.redOp.type
[dstMem], [srcMem], size{, cache-policy}
.dst = { .global }
.src = { .shared::cta }
.completion_mechanism = { .bulk_group }
.level::cache_hint = { .L2::cache_hint }
.redOp= { .and, .or, .xor,
.add, .inc, .dec,
.min, .max }
.type = { .f16, .bf16, .b32, .u32, .s32, .b64, .u64, .s64, .f32, .f64 }
cp.reduce.async.bulk.dst.src.completion_mechanism{.level::cache_hint}.add.noftz.type
[dstMem], [srcMem], size{, cache-policy}
.dst = { .global }
.src = { .shared::cta }
.completion_mechanism = { .bulk_group }
.type = { .f16, .bf16 }
Description
cp.reduce.async.bulk is a non-blocking instruction which initiates an asynchronous reduction
operation on an array of memory locations specified by the destination address operand dstMem
with the source array whose location is specified by the source address operand srcMem. The size
of the source and the destination array must be the same and is specified by the operand size.
Each data element in the destination array is reduced inline with the corresponding data element in
the source array with the reduction operation specified by the modifier .redOp. The type of each
data element in the source and the destination array is specified by the modifier .type.
The source address operand srcMem is located in the state space specified by .src and the
destination address operand dstMem is located in the state specified by the .dst.
The 32-bit operand size specifies the amount of memory to be copied from the source location and
used in the reduction operation, in terms of number of bytes. size must be a multiple of 16. If
the value is not a multiple of 16, then the behavior is undefined. The memory range [dstMem,
dstMem + size - 1] must not overflow the destination memory space and the memory range [srcMem,
srcMem + size - 1] must not overflow the source memory space. Otherwise, the behavior is
undefined. The addresses dstMem and srcMem must be aligned to 16 bytes.
The operations supported by .redOp are classified as follows:
The bit-size operations are
.and,.or, and.xor.The integer operations are
.add,.inc,.dec,.min, and.max. The.incand.decoperations return a result in the range[0..x]wherexis the value at the source state space.The floating point operation
.addrounds to the nearest even. The current implementation ofcp.reduce.async.bulk.add.f32flushes subnormal inputs and results to sign-preserving zero. Thecp.reduce.async.bulk.add.f16andcp.reduce.async.bulk.add.bf16operations require.noftzqualifier. It preserves input and result subnormals, and does not flush them to zero.
The following table describes the valid combinations of .redOp and element type:
|
|
Element type |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The modifier .completion_mechanism specifies the completion mechanism that is supported on the
instruction variant. The completion mechanisms that are supported for different variants are
summarized in the following table:
Completion mechanism |
|
|
Description |
|---|---|---|---|
|
|
|
mbarrier based completion mechanism |
|
|
||
|
|
|
Bulk async-group based completion mechanism |
The modifier .mbarrier::complete_tx::bytes specifies that the cp.reduce.async.bulk variant
uses mbarrier based completion mechanism. The complete-tx
operation, with completeCount argument equal to amount of data copied in bytes, will be
performed on the mbarrier object specified by the operand mbar.
The modifier .bulk_group specifies that the cp.reduce.async.bulk variant uses bulk
async-group based completion mechanism.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program. The
qualifier .level::cache_hint is only supported when at least one of the .src or .dst
statespaces is .global state space.
Each reduction operation performed by the cp.reduce.async.bulk has individually .relaxed.gpu
memory ordering semantics. The load operations in cp.reduce.async.bulk are treated as weak
memory operation and the complete-tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
cp.reduce.async.bulk.shared::cluster.shared::cta.mbarrier::complete_tx::bytes.add.u64
[dstMem], [srcMem], size, [mbar];
cp.reduce.async.bulk.shared::cluster.shared::cta.mbarrier::complete_tx::bytes.min.s32
[dstMem], [srcMem], size, [mbar];
cp.reduce.async.bulk.global.shared::cta.bulk_group.min.f16 [dstMem], [srcMem], size;
cp.reduce.async.bulk.global.shared::cta.bulk_group.L2::cache_hint.xor.s32 [dstMem], [srcMem], size, policy;
cp.reduce.async.bulk.global.shared::cta.bulk_group.add.noftz.f16 [dstMem], [srcMem], size;
9.7.8.24.8. Data Movement and Conversion Instructions: cp.async.bulk.prefetch
cp.async.bulk.prefetch
Provides a hint to the system to initiate the asynchronous prefetch of data to the cache.
Syntax
cp.async.bulk.prefetch.L2.src{.level::cache_hint} [srcMem], size {, cache-policy}
.src = { .global }
.level::cache_hint = { .L2::cache_hint }
Description
cp.async.bulk.prefetch is a non-blocking instruction which may initiate an asynchronous prefetch
of data from the location specified by source address operand srcMem, in .src statespace, to
the L2 cache.
The 32-bit operand size specifies the amount of memory to be prefetched in terms of number of
bytes. size must be a multiple of 16. If the value is not a multiple of 16, then the behavior is
undefined. The memory range [dstMem, dstMem + size - 1] must not overflow the destination memory
space and the memory range [srcMem, srcMem + size - 1] must not overflow the source memory
space. Otherwise, the behavior is undefined. The address srcMem must be aligned to 16 bytes.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
cp.async.bulk.prefetch.L2.global [srcMem], size;
cp.async.bulk.prefetch.L2.global.L2::cache_hint [srcMem], size, policy;
9.7.8.24.9. Data Movement and Conversion Instructions: cp.async.bulk.tensor
cp.async.bulk.tensor
Initiates an asynchronous copy operation on the tensor data from one state space to another.
Syntax
// global -> shared::cluster:
cp.async.bulk.tensor.dim.dst.src{.load_mode}.completion_mechanism{.multicast}{.level::cache_hint}
[dstMem], [tensorMap, tensorCoords], [mbar]{, im2colOffsets}
{, ctaMask} {, cache-policy}
.dst = { .shared::cluster }
.src = { .global }
.dim = { .1d, .2d, .3d, .4d, .5d }
.completion_mechanism = { .mbarrier::complete_tx::bytes }
.load_mode = { .tile, .im2col }
.level::cache_hint = { .L2::cache_hint }
.multicast = { .multicast::cluster }
// shared::cta -> global:
cp.async.bulk.tensor.dim.dst.src{.load_mode}.completion_mechanism{.level::cache_hint}
[tensorMap, tensorCoords], [srcMem] {, cache-policy}
.dst = { .global }
.src = { .shared::cta }
.dim = { .1d, .2d, .3d, .4d, .5d }
.completion_mechanism = { .bulk_group }
.load_mode = { .tile, .im2col_no_offs }
.level::cache_hint = { .L2::cache_hint }
Description
cp.async.bulk.tensor is a non-blocking instruction which initiates an asynchronous copy
operation of tensor data from the location in .src state space to the location in the .dst
state space.
The operand dstMem specifies the location in the .dst state space into which the tensor data
has to be copied and srcMem specifies the location in the .src state space from which the
tensor data has to be copied.
The operand tensorMap is the generic address of the opaque tensor-map object which resides
either in .param space or .const space or .global space. The operand tensorMap specifies
the properties of the tensor copy operation, as described in Tensor-map.
The tensorMap is accessed in tensormap proxy. Refer to the CUDA programming guide for creating
the tensor-map objects on the host side.
The dimension of the tensor data is specified by the .dim modifier.
The vector operand tensorCoords specifies the starting coordinates in the tensor data in the
global memory from or to which the copy operation has to be performed. The number of tensor
coordinates in the vector argument tensorCoords should be equal to the dimension specified by
the modifier .dim. The individual tensor coordinates in tensorCoords are of type .s32.
The modifier .completion_mechanism specifies the completion mechanism that is supported on the
instruction variant. The completion mechanisms that are supported for different variants are
summarized in the following table:
Completion mechanism |
|
|
Description |
|---|---|---|---|
|
|
|
mbarrier based completion mechanism |
|
|
|
Bulk async-group based completion mechanism |
The modifier .mbarrier::complete_tx::bytes specifies that the cp.async.bulk.tensor variant
uses mbarrier based completion mechanism. The complete-tx
operation, with completeCount argument equal to amount of data copied in bytes, will be
performed on the mbarrier object specified by the operand mbar.
The modifier .bulk_group specifies that the cp.async.bulk.tensor variant uses bulk
async-group based completion mechanism.
The qualifier .load_mode specifies how the data in the source location is copied into the
destination location. If .load_mode is not specified, it defaults to .tile. In .tile
mode, the multi-dimensional layout of the source tensor is preserved at the destination. In
.im2col mode, some dimensions of the source tensors are unrolled in a single dimensional column
at the destination. Details of the im2col mode are described in Im2col mode. In .im2col mode, the tensor has to be at least
3-dimensional. The vector operand im2colOffsets can be specified only when .load_mode is
.im2col. The length of the vector operand im2colOffsets is two less than the number of dimension
.dim of the tensor operation. The modifier .im2col_no_offs is the same as .im2col mode
except there is no im2colOffsets vector involved.
The optional modifier .multicast::cluster allows copying of data from global memory to shared
memory of multiple CTAs in the cluster. Operand ctaMask specifies the destination CTAs in the
cluster such that each bit position in the 16-bit ctaMask operand corresponds to the %ctaid
of the destination CTA. The source data is multicast to the same offset as dstMem in the shared
memory of each destination CTA. The mbarrier signal is also multicast to the same offset as mbar
in the shared memory of the destination CTA.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program. The
qualifier .level::cache_hint is only supported when at least one of the .src or .dst
statespaces is .global state space.
The copy operation in cp.async.bulk.tensor is treated as a weak memory operation and the
complete-tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
Notes
.multicast::cluster qualifier is optimized for target architecture sm_90a and may have
substantially reduced performance on other targets and hence .multicast::cluster is advised to
be used with .target sm_90a.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
.multicast::cluster qualifier advised to be used with .target sm_90a.
Examples
.reg .b16 ctaMask;
.reg .u16 i2cOffW, i2cOffH, i2cOffD;
.reg .b64 l2CachePolicy;
cp.async.bulk.tensor.1d.shared::cluster.global.tile [sMem0], [tensorMap0, {tc0}], [mbar0];
@p cp.async.bulk.tensor.2d.shared::cluster.global.mbarrier::complete_tx::bytes.multicast::cluster
[sMem1], [tensorMap1, {tc0, tc1}], [mbar2], ctaMask;
@p cp.async.bulk.tensor.5d.shared::cluster.global.im2col.mbarrier::complete_tx::bytes
[sMem2], [tensorMap2, {tc0, tc1, tc2, tc3, tc4}], [mbar2], {i2cOffW, i2cOffH, i2cOffD};
@p cp.async.bulk.tensor.3d.im2col.shared::cluster.global.mbarrier::complete_tx::bytes.L2::cache_hint
[sMem3], [tensorMap3, {tc0, tc1, tc2}], [mbar3], {i2cOffW}, policy;
@p cp.async.bulk.tensor.1d.global.shared::cta.bulk_group [tensorMap3, {tc0}], [sMem3];
9.7.8.24.10. Data Movement and Conversion Instructions: cp.reduce.async.bulk.tensor
cp.reduce.async.bulk.tensor
Initiates an asynchronous reduction operation on the tensor data.
Syntax
// shared::cta -> global:
cp.reduce.async.bulk.tensor.dim.dst.src.redOp{.load_mode}.completion_mechanism{.level::cache_hint}
[tensorMap, tensorCoords], [srcMem] {,cache-policy}
.dst = { .global }
.src = { .shared::cta }
.dim = { .1d, .2d, .3d, .4d, .5d }
.completion_mechanism = { .bulk_group }
.load_mode = { .tile, .im2col_no_offs }
.redOp = { .add, .min, .max, .inc, .dec, .and, .or, .xor}
Description
cp.reduce.async.bulk.tensor is a non-blocking instruction which initiates an asynchronous
reduction operation of tensor data in the .dst state space with tensor data in the .src
state space.
The operand srcMem specifies the location of the tensor data in the .src state space using
which the reduction operation has to be performed.
The operand tensorMap is the generic address of the opaque tensor-map object which resides
either in .param space or .const space or .global space. The operand tensorMap specifies
the properties of the tensor copy operation, as described in Tensor-map.
The tensorMap is accessed in tensormap proxy. Refer to the CUDA programming guide for creating
the tensor-map objects on the host side.
Each element of the tensor data in the .dst state space is reduced inline with the corresponding
element from the tensor data in the .src state space. The modifier .redOp specifies the
reduction operation used for the inline reduction. The type of each tensor data element in the
source and the destination tensor is specified in Tensor-map.
The dimension of the tensor is specified by the .dim modifier.
The vector operand tensorCoords specifies the starting coordinates of the tensor data in the
global memory on which the reduce operation is to be performed. The number of tensor coordinates in
the vector argument tensorCoords should be equal to the dimension specified by the modifier
.dim. The individual tensor coordinates are of the type .s32.
The following table describes the valid combinations of .redOp and element type:
|
Element type |
|---|---|
|
|
|
|
|
|
|
|
The modifier .completion_mechanism specifies the completion mechanism that is supported on the
instruction variant. Value .bulk_group of the modifier .completion_mechanism specifies that
cp.reduce.async.bulk.tensor instruction uses bulk async-group based completion mechanism.
The qualifier .load_mode specifies how the data in the source location is copied into the
destination location. If .load_mode is not specified, it defaults to .tile. In .tile
mode, the multi-dimensional layout of the source tensor is preserved at the destination. In
.im2col_no_offs mode, some dimensions of the source tensors are unrolled in a single dimensional
column at the destination. Details of the im2col mode are described in Im2col mode. In .im2col mode, the tensor has to be at least
3-dimensional.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program. The
qualifier .level::cache_hint is only supported when at least one of the .src or .dst
statespaces is .global state space.
Each reduction operation performed by cp.reduce.async.bulk.tensor has individually
.relaxed.gpu memory ordering semantics. The load operations in cp.reduce.async.bulk.tensor
are treated as weak memory operations and the complete-tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
cp.reduce.async.bulk.tensor.1d.global.shared::cta.add.tile.bulk_group
[tensorMap0, {tc0}], [sMem0];
cp.reduce.async.bulk.tensor.2d.global.shared::cta.and.bulk_group.L2::cache_hint
[tensorMap1, {tc0, tc1}], [sMem1] , policy;
cp.reduce.async.bulk.tensor.3d.global.shared::cta.xor.im2col.bulk_group
[tensorMap2, {tc0, tc1, tc2}], [sMem2]
9.7.8.24.11. Data Movement and Conversion Instructions: cp.async.bulk.prefetch.tensor
cp.async.bulk.prefetch.tensor
Provides a hint to the system to initiate the asynchronous prefetch of tensor data to the cache.
Syntax
// global -> shared::cluster:
cp.async.bulk.prefetch.tensor.dim.L2.src{.load_mode}{.level::cache_hint} [tensorMap, tensorCoords]
{, im2colOffsets } {, cache-policy}
.src = { .global }
.dim = { .1d, .2d, .3d, .4d, .5d }
.load_mode = { .tile, .im2col }
.level::cache_hint = { .L2::cache_hint }
Description
cp.async.bulk.prefetch.tensor is a non-blocking instruction which may initiate an asynchronous
prefetch of tensor data from the location in .src statespace to the L2 cache.
The operand tensorMap is the generic address of the opaque tensor-map object which resides
either in .param space or .const space or .global space. The operand tensorMap specifies
the properties of the tensor copy operation, as described in Tensor-map.
The tensorMap is accessed in tensormap proxy. Refer to the CUDA programming guide for creating
the tensor-map objects on the host side.
The dimension of the tensor data is specified by the .dim modifier.
The vector operand tensorCoords specifies the starting coordinates in the tensor data in the
global memory from or to which the copy operation has to be performed. The number of tensor
coordinates in the vector argument tensorCoords should be equal to the dimension specified by
the modifier .dim. The individual tensor coordinates in tensorCoords are of type .s32.
The qualifier .load_mode specifies how the data in the source location is copied into the
destination location. If .load_mode is not specified, it defaults to .tile. In .tile
mode, the multi-dimensional layout of the source tensor is preserved at the destination. In
.im2col mode, some dimensions of the source tensors are unrolled in a single dimensional column
at the destination. Details of the im2col mode are described in Im2col mode. In .im2col mode, the tensor has to be at least
3-dimensional. The vector operand im2colOffsets can be specified only when .load_mode is
.im2col. The length of the vector operand im2colOffsets is two less than the number of dimension
.dim of the tensor operation.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
cp.async.bulk.prefetch.tensor is treated as a weak memory operation in the Memory Consistency
Model.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b16 ctaMask;
.reg .u16 i2cOffW, i2cOffH, i2cOffD;
.reg .b64 l2CachePolicy;
cp.async.bulk.prefetch.tensor.1d.L2.global.tile [tensorMap0, {tc0}];
@p cp.async.bulk.prefetch.tensor.2d.L2.global [tensorMap1, {tc0, tc1}];
@p cp.async.bulk.prefetch.tensor.5d.L2.global.im2col
[tensorMap2, {tc0, tc1, tc2, tc3, tc4}], {i2cOffW, i2cOffH, i2cOffD};
@p cp.async.bulk.prefetch.tensor.3d.L2.global.im2col.L2::cache_hint
[tensorMap3, {tc0, tc1, tc2}], {i2cOffW}, policy;
9.7.8.24.12. Data Movement and Conversion Instructions: cp.async.bulk.commit_group
cp.async.bulk.commit_group
Commits all prior initiated but uncommitted cp.async.bulk instructions into a
cp.async.bulk-group.
Syntax
cp.async.bulk.commit_group;
Description
cp.async.bulk.commit_group instruction creates a new per-thread bulk async-group and batches
all prior cp{.reduce}.async.bulk.{.prefetch}{.tensor} instructions satisfying the following
conditions into the new bulk async-group:
The prior
cp{.reduce}.async.bulk.{.prefetch}{.tensor}instructions use bulk_group based completion mechanism, andThey are initiated by the executing thread but not committed to any bulk async-group.
If there are no uncommitted cp{.reduce}.async.bulk.{.prefetch}{.tensor} instructions then
cp.async.bulk.commit_group results in an empty bulk async-group.
An executing thread can wait for the completion of all
cp{.reduce}.async.bulk.{.prefetch}{.tensor} operations in a bulk async-group using
cp.async.wait_group.
There is no memory ordering guarantee provided between any two
cp{.reduce}.async.bulk.{.prefetch}{.tensor} operations within the same bulk async-group.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
cp.async.bulk.commit_group;
9.7.8.24.13. Data Movement and Conversion Instructions: cp.async.bulk.wait_group
cp.async.bulk.wait_group
Wait for completion of bulk async-groups.
Syntax
cp.async.bulk.wait_group{.read} N;
Description
cp.async.bulk.wait_group instruction will cause the executing thread to wait until only N or
fewer of the most recent bulk async-groups are pending and all the prior bulk async-groups
committed by the executing threads are complete. For example, when N is 0, the executing thread
waits on all the prior bulk async-groups to complete. Operand N is an integer constant.
By default, cp.async.bulk.wait_group instruction will cause the executing thread to wait till
all the bulk async operations in the specified bulk async-group have completed all of the
following:
Reading from the source locations.
Writing to their respective destination locations.
Writes being made visible to the executing thread.
The optional .read modifier indicates that the waiting has to be done until all the bulk async
operations in the specified bulk async-group have completed reading from their source locations.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
cp.async.bulk.wait_group.read 0;
cp.async.bulk.wait_group 2;
9.7.8.25. Data Movement and Conversion Instructions: tensormap.replace
tensormap.replace
Modifies the field of a tensor-map object.
Syntax
tensormap.replace.mode.field1{.ss}.b1024.type [addr], new_val;
tensormap.replace.mode.field2{.ss}.b1024.type [addr], ord, new_val;
tensormap.replace.mode.field3{.ss}.b1024.type [addr], new_val;
.mode = { .tile }
.field1 = { .global_address, .rank }
.field2 = { .box_dim, .global_dim, .global_stride, .element_stride }
.field3 = { .elemtype, .interleave_layout, .swizzle_mode, .fill_mode }
.ss = { .global, .shared::cta }
.type = { .b32, .b64 }
Description
The tensormap.replace instruction replaces the field, specified by .field qualifier,
of the tensor-map object at the location specified by the address operand addr with a
new value. The new value is specified by the argument new_val.
Qualifier .mode specifies the mode of the tensor-map object
located at the address operand addr.
Instruction type .b1024 indicates the size of the tensor-map
object, which is 1024 bits.
Operand new_val has the type .type. When .field is specified as .global_address
or .global_stride, .type must be .b64. Otherwise, .type must be .b32.
The immediate integer operand ord specifies the ordinal of the field across the rank of the
tensor which needs to be replaced in the tensor-map object.
For field .rank, the operand new_val must be ones less than the desired tensor rank as
this field uses zero-based numbering.
When .field3 is specified, the operand new_val must be an immediate and the
Table 30 shows the mapping of the operand new_val across various fields.
new_val |
.field3 |
|||
|---|---|---|---|---|
.elemtype |
.interleave_layout |
.swizzle_mode |
.fill_mode |
|
0 |
|
No interleave |
No swizzling |
Zero fill |
1 |
|
16B interleave |
32B swizzling |
OOB-NaN fill |
2 |
|
32B interleave |
64B swizzling |
x |
3 |
|
x |
128B swizzling |
x |
4 |
|
x |
x |
x |
5 |
|
x |
x |
x |
6 |
|
x |
x |
x |
7 |
|
x |
x |
x |
8 |
|
x |
x |
x |
9 |
|
x |
x |
x |
10 |
|
x |
x |
x |
11 |
|
x |
x |
x |
12 |
|
x |
x |
x |
If no state space is specified then Generic Addressing is used.
If the address specified by addr does not fall within the address window of .global
or .shared::cta state space then the behavior is undefined.
tensormap.replace is treated as a weak memory operation, on the entire 1024-bit opaque
tensor-map object, in the Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 8.3.
Target ISA Notes
Requires sm_90a.
Examples
tensormap.replace.tile.global_address.shared::cta.b1024.b64 [sMem], new_val;
9.7.9. Texture Instructions
This section describes PTX instructions for accessing textures and samplers. PTX supports the following operations on texture and sampler descriptors:
Static initialization of texture and sampler descriptors.
Module-scope and per-entry scope definitions of texture and sampler descriptors.
Ability to query fields within texture and sampler descriptors.
9.7.9.1. Texturing Modes
For working with textures and samplers, PTX has two modes of operation. In the unified mode,
texture and sampler information is accessed through a single .texref handle. In the independent
mode, texture and sampler information each have their own handle, allowing them to be defined
separately and combined at the site of usage in the program.
The advantage of unified mode is that it allows 256 samplers per kernel (128 for architectures prior
to sm_3x), with the restriction that they correspond 1-to-1 with the 256 possible textures per
kernel (128 for architectures prior to sm_3x). The advantage of independent mode is that
textures and samplers can be mixed and matched, but the number of samplers is greatly restricted to
32 per kernel (16 for architectures prior to sm_3x).
Table 31 summarizes the number of textures, samplers and surfaces available in different texturing modes.
Texturing mode |
Resource |
|
|
|---|---|---|---|
Unified mode |
Textures |
128 |
256 |
Samplers |
128 |
256 |
|
Surfaces |
8 |
16 |
|
Independent mode |
Textures |
128 |
256 |
Samplers |
16 |
32 |
|
Surfaces |
8 |
16 |
The texturing mode is selected using .target options texmode_unified and
texmode_independent. A PTX module may declare only one texturing mode. If no texturing mode is
declared, the module is assumed to use unified mode.
Example: calculate an element’s power contribution as element’s power/total number of elements.
.target texmode_independent
.global .samplerref tsamp1 = { addr_mode_0 = clamp_to_border,
filter_mode = nearest
};
...
.entry compute_power
( .param .texref tex1 )
{
txq.width.b32 r6, [tex1]; // get tex1's width
txq.height.b32 r5, [tex1]; // get tex1's height
tex.2d.v4.f32.f32 {r1,r2,r3,r4}, [tex1, tsamp1, {f1,f2}];
mul.u32 r5, r5, r6;
add.f32 r1, r1, r2;
add.f32 r3, r3, r4;
add.f32 r1, r1, r3;
cvt.f32.u32 r5, r5;
div.f32 r1, r1, r5;
}
9.7.9.2. Mipmaps
A mipmap is a sequence of textures, each of which is a progressively lower resolution representation of the same image. The height and width of each image, or level of detail (LOD), in the mipmap is a power of two smaller than the previous level. Mipmaps are used in graphics applications to improve rendering speed and reduce aliasing artifacts. For example, a high-resolution mipmap image is used for objects that are close to the user; lower-resolution images are used as the object appears farther away. Mipmap filtering modes are provided when switching between two levels of detail (LODs) in order to avoid abrupt changes in visual fidelity.
Example: If the texture has a basic size of 256 by 256 pixels, then the associated mipmap set may contain a series of eight images, each one-fourth the total area of the previous one: 128×128 pixels, 64×64, 32×32, 16×16, 8×8, 4×4, 2×2, 1×1 (a single pixel). If, for example, a scene is rendering this texture in a space of 40×40 pixels, then either a scaled up version of the 32×32 (without trilinear interpolation) or an interpolation of the 64×64 and the 32×32 mipmaps (with trilinear interpolation) would be used.
The total number of LODs in a complete mipmap pyramid is calculated through the following equation:
numLODs = 1 + floor(log2(max(w, h, d)))
The finest LOD is called the base level and is the 0th level. The next (coarser) level is the 1st level, and so on. The coarsest level is the level of size (1 x 1 x 1). Each successively smaller mipmap level has half the {width, height, depth} of the previous level, but if this half value is a fractional value, it’s rounded down to the next largest integer. Essentially, the size of a mipmap level can be specified as:
max(1, floor(w_b / 2^i)) x
max(1, floor(h_b / 2^i)) x
max(1, floor(d_b / 2^i))
where i is the ith level beyond the 0th level (the base level). And w_b, h_b and d_b are the width, height and depth of the base level respectively.
PTX support for mipmaps
The PTX tex instruction supports three modes for specifying the LOD: base, level, and
gradient. In base mode, the instruction always picks level 0. In level mode, an additional
argument is provided to specify the LOD to fetch from. In gradmode, two floating-point vector
arguments provide partials (e.g., {ds/dx, dt/dx} and {ds/dy, dt/dy} for a 2d texture),
which the tex instruction uses to compute the LOD.
These instructions provide access to texture memory.
textld4txq
9.7.9.3. Texture Instructions: tex
tex
Perform a texture memory lookup.
Syntax
tex.geom.v4.dtype.ctype d, [a, c] {, e} {, f};
tex.geom.v4.dtype.ctype d[|p], [a, b, c] {, e} {, f}; // explicit sampler
tex.geom.v2.f16x2.ctype d[|p], [a, c] {, e} {, f};
tex.geom.v2.f16x2.ctype d[|p], [a, b, c] {, e} {, f}; // explicit sampler
// mipmaps
tex.base.geom.v4.dtype.ctype d[|p], [a, {b,} c] {, e} {, f};
tex.level.geom.v4.dtype.ctype d[|p], [a, {b,} c], lod {, e} {, f};
tex.grad.geom.v4.dtype.ctype d[|p], [a, {b,} c], dPdx, dPdy {, e} {, f};
tex.base.geom.v2.f16x2.ctype d[|p], [a, {b,} c] {, e} {, f};
tex.level.geom.v2.f16x2.ctype d[|p], [a, {b,} c], lod {, e} {, f};
tex.grad.geom.v2.f16x2.ctype d[|p], [a, {b,} c], dPdx, dPdy {, e} {, f};
.geom = { .1d, .2d, .3d, .a1d, .a2d, .cube, .acube, .2dms, .a2dms };
.dtype = { .u32, .s32, .f16, .f32 };
.ctype = { .s32, .f32 }; // .cube, .acube require .f32
// .2dms, .a2dms require .s32
Description
tex.{1d,2d,3d}
Texture lookup using a texture coordinate vector. The instruction loads data from the texture named
by operand a at coordinates given by operand c into destination d. Operand c is a
scalar or singleton tuple for 1d textures; is a two-element vector for 2d textures; and is a
four-element vector for 3d textures, where the fourth element is ignored. An optional texture
sampler b may be specified. If no sampler is specified, the sampler behavior is a property of
the named texture. The optional destination predicate p is set to True if data from texture
at specified coordinates is resident in memory, False otherwise. When optional destination
predicate p is set to False, data loaded will be all zeros. Memory residency of Texture Data
at specified coordinates is dependent on execution environment setup using Driver API calls, prior
to kernel launch. Refer to Driver API documentation for more details including any
system/implementation specific behavior.
An optional operand e may be specified. Operand e is a vector of .s32 values that
specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset
value is in the range of -8 to +7. Operand e is a singleton tuple for 1d textures; is a two
element vector 2d textures; and is four-element vector for 3d textures, where the fourth element is
ignored.
An optional operand f may be specified for depth textures. Depth textures are special type
of textures which hold data from the depth buffer. Depth buffer contains depth information of each
pixel. Operand f is .f32 scalar value that specifies depth compare value for depth
textures. Each element fetched from texture is compared against value given in f operand. If
comparison passes, result is 1.0; otherwise result is 0.0. These per-element comparison results are
used for the filtering. When using depth compare operand, the elements in texture coordinate vector
c have .f32 type.
Depth compare operand is not supported for 3d textures.
The instruction returns a two-element vector for destination type .f16x2. For all other
destination types, the instruction returns a four-element vector. Coordinates may be given in either
signed 32-bit integer or 32-bit floating point form.
A texture base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
tex.{a1d,a2d}
Texture array selection, followed by texture lookup. The instruction first selects a texture from
the texture array named by operand a using the index given by the first element of the array
coordinate vector c. The instruction then loads data from the selected texture at coordinates
given by the remaining elements of operand c into destination d. Operand c is a bit-size
type vector or tuple containing an index into the array of textures followed by coordinates within
the selected texture, as follows:
For 1d texture arrays, operand
chas type.v2.b32. The first element is interpreted as an unsigned integer index (.u32) into the texture array, and the second element is interpreted as a 1d texture coordinate of type.ctype.For 2d texture arrays, operand
chas type.v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the texture array, and the next two elements are interpreted as 2d texture coordinates of type.ctype. The fourth element is ignored.
An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior
is a property of the named texture.
An optional operand e may be specified. Operand e is a vector of .s32 values that
specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset
value is in the range of -8 to +7. Operand e is a singleton tuple for 1d texture arrays; and is
a two element vector 2d texture arrays.
An optional operand f may be specified for depth textures arrays. Operand f is .f32
scalar value that specifies depth compare value for depth textures. When using depth compare
operand, the coordinates in texture coordinate vector c have .f32 type.
The instruction returns a two-element vector for destination type .f16x2. For all other
destination types, the instruction returns a four-element vector. The texture array index is a
32-bit unsigned integer, and texture coordinate elements are 32-bit signed integer or floating point
values.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
tex.cube
Cubemap texture lookup. The instruction loads data from the cubemap texture named by operand a
at coordinates given by operand c into destination d. Cubemap textures are special
two-dimensional layered textures consisting of six layers that represent the faces of a cube. All
layers in a cubemap are of the same size and are square (i.e., width equals height).
When accessing a cubemap, the texture coordinate vector c has type .v4.f32, and comprises
three floating-point coordinates (s, t, r) and a fourth padding argument which is
ignored. Coordinates (s, t, r) are projected onto one of the six cube faces. The (s,
t, r) coordinates can be thought of as a direction vector emanating from the center of the
cube. Of the three coordinates (s, t, r), the coordinate of the largest magnitude (the
major axis) selects the cube face. Then, the other two coordinates (the minor axes) are divided by
the absolute value of the major axis to produce a new (s, t) coordinate pair to lookup into
the selected cube face.
An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior
is a property of the named texture.
Offset vector operand e is not supported for cubemap textures.
an optional operand f may be specified for cubemap depth textures. operand f is .f32
scalar value that specifies depth compare value for cubemap depth textures.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
tex.acube
Cubemap array selection, followed by cubemap lookup. The instruction first selects a cubemap texture
from the cubemap array named by operand a using the index given by the first element of the
array coordinate vector c. The instruction then loads data from the selected cubemap texture at
coordinates given by the remaining elements of operand c into destination d.
Cubemap array textures consist of an array of cubemaps, i.e., the total number of layers is a
multiple of six. When accessing a cubemap array texture, the coordinate vector c has type
.v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the
cubemap array, and the remaining three elements are interpreted as floating-point cubemap
coordinates (s, t, r), used to lookup in the selected cubemap as described above.
An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior
is a property of the named texture.
Offset vector operand e is not supported for cubemap texture arrays.
An optional operand f may be specified for cubemap depth texture arrays. Operand f is
.f32 scalar value that specifies depth compare value for cubemap depth textures.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
tex.2dms
Multi-sample texture lookup using a texture coordinate vector. Multi-sample textures consist of
multiple samples per data element. The instruction loads data from the texture named by operand
a from sample number given by first element of the operand c, at coordinates given by
remaining elements of operand c into destination d. When accessing a multi-sample texture,
texture coordinate vector c has type .v4.b32. The first element in operand c is
interpreted as unsigned integer sample number (.u32), and the next two elements are interpreted
as signed integer (.s32) 2d texture coordinates. The fourth element is ignored. An optional
texture sampler b may be specified. If no sampler is specified, the sampler behavior is a
property of the named texture.
An optional operand e may be specified. Operand e is a vector of type .v2.s32 that
specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset
value is in the range of -8 to +7.
Depth compare operand f is not supported for multi-sample textures.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
tex.a2dms
Multi-sample texture array selection, followed by multi-sample texture lookup. The instruction first
selects a multi-sample texture from the multi-sample texture array named by operand a using the
index given by the first element of the array coordinate vector c. The instruction then loads
data from the selected multi-sample texture from sample number given by second element of the
operand c, at coordinates given by remaining elements of operand c into destination
d. When accessing a multi-sample texture array, texture coordinate vector c has type
.v4.b32. The first element in operand c is interpreted as unsigned integer sampler number, the
second element is interpreted as unsigned integer index (.u32) into the multi-sample texture
array and the next two elements are interpreted as signed integer (.s32) 2d texture
coordinates. An optional texture sampler b may be specified. If no sampler is specified, the
sampler behavior is a property of the named texture.
An optional operand e may be specified. Operand e is a vector of type .v2.s32 values
that specifies coordinate offset. Offset is applied to coordinates before doing texture
lookup. Offset value is in the range of -8 to +7.
Depth compare operand f is not supported for multi-sample texture arrays.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
Mipmaps
.base(lod zero)Pick level 0 (base level). This is the default if no mipmap mode is specified. No additional arguments.
.level(lod explicit)Requires an additional 32-bit scalar argument,
lod, which contains the LOD to fetch from. The type oflodfollows.ctype(either.s32or.f32). Geometries.2dmsand.a2dmsare not supported in this mode..grad(lod gradient)Requires two
.f32vectors,dPdxanddPdy, that specify the partials. The vectors are singletons for 1d and a1d textures; are two-element vectors for 2d and a2d textures; and are four-element vectors for 3d, cube and acube textures, where the fourth element is ignored for 3d and cube geometries. Geometries.2dmsand.a2dmsare not supported in this mode.
For mipmap texture lookup, an optional operand e may be specified. Operand e is a vector of
.s32 that specifies coordinate offset. Offset is applied to coordinates before doing texture
lookup. Offset value is in the range of -8 to +7. Offset vector operand is not supported for cube
and cubemap geometries.
An optional operand f may be specified for mipmap textures. Operand f is .f32 scalar
value that specifies depth compare value for depth textures. When using depth compare operand, the
coordinates in texture coordinate vector c have .f32 type.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
Depth compare operand is not supported for 3d textures.
Indirect texture access
Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target
architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding
the address of a .texref variable.
Notes
For compatibility with prior versions of PTX, the square brackets are not required and .v4
coordinate vectors are allowed for any geometry, with the extra elements being ignored.
PTX ISA Notes
Unified mode texturing introduced in PTX ISA version 1.0. Extension using opaque .texref and
.samplerref types and independent mode texturing introduced in PTX ISA version 1.5.
Texture arrays tex.{a1d,a2d} introduced in PTX ISA version 2.3.
Cubemaps and cubemap arrays introduced in PTX ISA version 3.0.
Support for mipmaps introduced in PTX ISA version 3.1.
Indirect texture access introduced in PTX ISA version 3.1.
Multi-sample textures and multi-sample texture arrays introduced in PTX ISA version 3.2.
Support for textures returning .f16 and .f16x2 data introduced in PTX ISA version 4.2.
Support for tex.grad.{cube, acube} introduced in PTX ISA version 4.3.
Offset vector operand introduced in PTX ISA version 4.3.
Depth compare operand introduced in PTX ISA version 4.3.
Support for optional destination predicate introduced in PTX ISA version 7.1.
Target ISA Notes
Supported on all target architectures.
The cubemap array geometry (.acube) requires sm_20 or higher.
Mipmaps require sm_20 or higher.
Indirect texture access requires sm_20 or higher.
Multi-sample textures and multi-sample texture arrays require sm_30 or higher.
Texture fetch returning .f16 and .f16x2 data require sm_53 or higher.
tex.grad.{cube, acube} requires sm_20 or higher.
Offset vector operand requires sm_30 or higher.
Depth compare operand requires sm_30 or higher.
Support for optional destination predicate requires sm_60 or higher.
Examples
// Example of unified mode texturing
// - f4 is required to pad four-element tuple and is ignored
tex.3d.v4.s32.s32 {r1,r2,r3,r4}, [tex_a,{f1,f2,f3,f4}];
// Example of independent mode texturing
tex.1d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,smpl_x,{f1}];
// Example of 1D texture array, independent texturing mode
tex.a1d.v4.s32.s32 {r1,r2,r3,r4}, [tex_a,smpl_x,{idx,s1}];
// Example of 2D texture array, unified texturing mode
// - f3 is required to pad four-element tuple and is ignored
tex.a2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{idx,f1,f2,f3}];
// Example of cubemap array, unified textureing mode
tex.acube.v4.f32.f32 {r0,r1,r2,r3}, [tex_cuarray,{idx,f1,f2,f3}];
// Example of multi-sample texture, unified texturing mode
tex.2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ms,{sample,r6,r7,r8}];
// Example of multi-sample texture, independent texturing mode
tex.2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ms, smpl_x,{sample,r6,r7,r8}];
// Example of multi-sample texture array, unified texturing mode
tex.a2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ams,{idx,sample,r6,r7}];
// Example of texture returning .f16 data
tex.1d.v4.f16.f32 {h1,h2,h3,h4}, [tex_a,smpl_x,{f1}];
// Example of texture returning .f16x2 data
tex.1d.v2.f16x2.f32 {h1,h2}, [tex_a,smpl_x,{f1}];
// Example of 3d texture array access with tex.grad,unified texturing mode
tex.grad.3d.v4.f32.f32 {%f4,%f5,%f6,%f7},[tex_3d,{%f0,%f0,%f0,%f0}],
{fl0,fl1,fl2,fl3},{fl0,fl1,fl2,fl3};
// Example of cube texture array access with tex.grad,unified texturing mode
tex.grad.cube.v4.f32.f32{%f4,%f5,%f6,%f7},[tex_cube,{%f0,%f0,%f0,%f0}],
{fl0,fl1,fl2,fl3},{fl0,fl1,fl2,fl3};
// Example of 1d texture lookup with offset, unified texturing mode
tex.1d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a, {f1}], {r5};
// Example of 2d texture array lookup with offset, unified texturing mode
tex.a2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{idx,f1,f2}], {f5,f6};
// Example of 2d mipmap texture lookup with offset, unified texturing mode
tex.level.2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{f1,f2}],
flvl, {r7, r8};
// Example of 2d depth texture lookup with compare, unified texturing mode
tex.1d.v4.f32.f32 {f1,f2,f3,f4}, [tex_a, {f1}], f0;
// Example of depth 2d texture array lookup with offset, compare
tex.a2d.v4.s32.f32 {f0,f1,f2,f3}, [tex_a,{idx,f4,f5}], {r5,r6}, f6;
// Example of destination predicate use
tex.3d.v4.s32.s32 {r1,r2,r3,r4}|p, [tex_a,{f1,f2,f3,f4}];
9.7.9.4. Texture Instructions: tld4
tld4
Perform a texture fetch of the 4-texel bilerp footprint.
Syntax
tld4.comp.2d.v4.dtype.f32 d[|p], [a, c] {, e} {, f};
tld4.comp.geom.v4.dtype.f32 d[|p], [a, b, c] {, e} {, f}; // explicit sampler
.comp = { .r, .g, .b, .a };
.geom = { .2d, .a2d, .cube, .acube };
.dtype = { .u32, .s32, .f32 };
Description
Texture fetch of the 4-texel bilerp footprint using a texture coordinate vector. The instruction
loads the bilerp footprint from the texture named by operand a at coordinates given by operand
c into vector destination d. The texture component fetched for each texel sample is
specified by .comp. The four texel samples are placed into destination vector d in
counter-clockwise order starting at lower left.
An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior
is a property of the named texture.
The optional destination predicate p is set to True if data from texture at specified
coordinates is resident in memory, False otherwise. When optional destination predicate p is
set to False, data loaded will be all zeros. Memory residency of Texture Data at specified
coordinates is dependent on execution environment setup using Driver API calls, prior to kernel
launch. Refer to Driver API documentation for more details including any system/implementation
specific behavior.
An optional operand f may be specified for depth textures. Depth textures are special type of
textures which hold data from the depth buffer. Depth buffer contains depth information of each
pixel. Operand f is .f32 scalar value that specifies depth compare value for depth
textures. Each element fetched from texture is compared against value given in f operand. If
comparison passes, result is 1.0; otherwise result is 0.0. These per-element comparison results are
used for the filtering.
A texture base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
tld4.2d
For 2D textures, operand c specifies coordinates as a two-element, 32-bit floating-point vector.
An optional operand e may be specified. Operand e is a vector of type .v2.s32 that
specifies coordinate offset. Offset is applied to coordinates before doing texture fetch. Offset
value is in the range of -8 to +7.
tld4.a2d
Texture array selection, followed by tld4 texture fetch of 2d texture. For 2d texture arrays
operand c is a four element, 32-bit vector. The first element in operand c is interpreted as an
unsigned integer index (.u32) into the texture array, and the next two elements are interpreted
as 32-bit floating point coordinates of 2d texture. The fourth element is ignored.
An optional operand e may be specified. Operand e is a vector of type .v2.s32 that
specifies coordinate offset. Offset is applied to coordinates before doing texture fetch. Offset
value is in the range of -8 to +7.
tld4.cube
For cubemap textures, operand c specifies four-element vector which comprises three
floating-point coordinates (s, t, r) and a fourth padding argument which is ignored.
Cubemap textures are special two-dimensional layered textures consisting of six layers that represent the faces of a cube. All layers in a cubemap are of the same size and are square (i.e., width equals height).
Coordinates (s, t, r) are projected onto one of the six cube faces. The (s, t, r) coordinates can be thought of as a direction vector emanating from the center of the cube. Of the three coordinates (s, t, r), the coordinate of the largest magnitude (the major axis) selects the cube face. Then, the other two coordinates (the minor axes) are divided by the absolute value of the major axis to produce a new (s, t) coordinate pair to lookup into the selected cube face.
Offset vector operand e is not supported for cubemap textures.
tld4.acube
Cubemap array selection, followed by tld4 texture fetch of cubemap texture. The first element in
operand c is interpreted as an unsigned integer index (.u32) into the cubemap texture array,
and the remaining three elements are interpreted as floating-point cubemap coordinates (s, t, r),
used to lookup in the selected cubemap.
Offset vector operand e is not supported for cubemap texture arrays.
Indirect texture access
Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target
architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding
the address of a .texref variable.
PTX ISA Notes
Introduced in PTX ISA version 2.2.
Indirect texture access introduced in PTX ISA version 3.1.
tld4.{a2d,cube,acube} introduced in PTX ISA version 4.3.
Offset vector operand introduced in PTX ISA version 4.3.
Depth compare operand introduced in PTX ISA version 4.3.
Support for optional destination predicate introduced in PTX ISA version 7.1.
Target ISA Notes
tld4 requires sm_20 or higher.
Indirect texture access requires sm_20 or higher.
tld4.{a2d,cube,acube} requires sm_30 or higher.
Offset vector operand requires sm_30 or higher.
Depth compare operand requires sm_30 or higher.
Support for optional destination predicate requires sm_60 or higher.
Examples
//Example of unified mode texturing
tld4.r.2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{f1,f2}];
// Example of independent mode texturing
tld4.r.2d.v4.u32.f32 {u1,u2,u3,u4}, [tex_a,smpl_x,{f1,f2}];
// Example of unified mode texturing using offset
tld4.r.2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{f1,f2}], {r5, r6};
// Example of unified mode texturing using compare
tld4.r.2d.v4.f32.f32 {f1,f2,f3,f4}, [tex_a,{f5,f6}], f7;
// Example of optional destination predicate
tld4.r.2d.v4.f32.f32 {f1,f2,f3,f4}|p, [tex_a,{f5,f6}], f7;
9.7.9.5. Texture Instructions: txq
txq
Query texture and sampler attributes.
Syntax
txq.tquery.b32 d, [a]; // texture attributes
txq.level.tlquery.b32 d, [a], lod; // texture attributes
txq.squery.b32 d, [a]; // sampler attributes
.tquery = { .width, .height, .depth,
.channel_data_type, .channel_order,
.normalized_coords, .array_size,
.num_mipmap_levels, .num_samples};
.tlquery = { .width, .height, .depth };
.squery = { .force_unnormalized_coords, .filter_mode,
.addr_mode_0, addr_mode_1, addr_mode_2 };
Description
Query an attribute of a texture or sampler. Operand a is either a .texref or .samplerref variable, or a .u64 register.
Query |
Returns |
|---|---|
|
value in elements |
|
Unsigned integer corresponding to source language’s channel data type
enumeration. If the source language combines channel data type and channel
order into a single enumeration type, that value is returned for both
|
|
Unsigned integer corresponding to source language’s channel order
enumeration. If the source language combines channel data type and channel
order into a single enumeration type, that value is returned for both
|
|
|
|
|
|
Integer from |
|
Integer from
|
|
For a texture array, number of textures in array, 0 otherwise. |
|
For a mipmapped texture, number of levels of details (LOD), 0 otherwise. |
|
For a multi-sample texture, number of samples, 0 otherwise. |
Texture attributes are queried by supplying a .texref argument to txq. In unified mode,
sampler attributes are also accessed via a .texref argument, and in independent mode sampler
attributes are accessed via a separate .samplerref argument.
txq.level
txq.level requires an additional 32bit integer argument, lod, which specifies LOD and
queries requested attribute for the specified LOD.
Indirect texture access
Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target
architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding
the address of a .texref variable.
PTX ISA Notes
Introduced in PTX ISA version 1.5.
Channel data type and channel order queries were added in PTX ISA version 2.1.
The .force_unnormalized_coords query was added in PTX ISA version 2.2.
Indirect texture access introduced in PTX ISA version 3.1.
.array_size, .num_mipmap_levels, .num_samples samples queries were added in PTX ISA
version 4.1.
txq.level introduced in PTX ISA version 4.3.
Target ISA Notes
Supported on all target architectures.
Indirect texture access requires sm_20 or higher.
Querying the number of mipmap levels requires sm_20 or higher.
Querying the number of samples requires sm_30 or higher.
txq.level requires sm_30 or higher.
Examples
txq.width.b32 %r1, [tex_A];
txq.filter_mode.b32 %r1, [tex_A]; // unified mode
txq.addr_mode_0.b32 %r1, [smpl_B]; // independent mode
txq.level.width.b32 %r1, [tex_A], %r_lod;
9.7.9.6. Texture Instructions: istypep
istypep
Query whether a register points to an opaque variable of a specified type.
Syntax
istypep.type p, a; // result is .pred
.type = { .texref, .samplerref, .surfref };
Description
Write predicate register p with 1 if register a points to an opaque variable of the
specified type, and with 0 otherwise. Destination p has type .pred; the source address
operand must be of type .u64.
PTX ISA Notes
Introduced in PTX ISA version 4.0.
Target ISA Notes
istypep requires sm_30 or higher.
Examples
istypep.texref istex, tptr;
istypep.samplerref issampler, sptr;
istypep.surfref issurface, surfptr;
9.7.10. Surface Instructions
This section describes PTX instructions for accessing surfaces. PTX supports the following operations on surface descriptors:
Static initialization of surface descriptors.
Module-scope and per-entry scope definitions of surface descriptors.
Ability to query fields within surface descriptors.
These instructions provide access to surface memory.
suldsustsuredsuq
9.7.10.1. Surface Instructions: suld
suld
Load from surface memory.
Syntax
suld.b.geom{.cop}.vec.dtype.clamp d, [a, b]; // unformatted
.geom = { .1d, .2d, .3d, .a1d, .a2d };
.cop = { .ca, .cg, .cs, .cv }; // cache operation
.vec = { none, .v2, .v4 };
.dtype = { .b8 , .b16, .b32, .b64 };
.clamp = { .trap, .clamp, .zero };
Description
suld.b.{1d,2d,3d}
Load from surface memory using a surface coordinate vector. The instruction loads data from the
surface named by operand a at coordinates given by operand b into destination d. Operand
a is a .surfref variable or .u64 register. Operand b is a scalar or singleton tuple
for 1d surfaces; is a two-element vector for 2d surfaces; and is a four-element vector for 3d
surfaces, where the fourth element is ignored. Coordinate elements are of type .s32.
suld.b performs an unformatted load of binary data. The lowest dimension coordinate represents a
byte offset into the surface and is not scaled, and the size of the data transfer matches the size
of destination operand d.
suld.b.{a1d,a2d}
Surface layer selection, followed by a load from the selected surface. The instruction first selects
a surface layer from the surface array named by operand a using the index given by the first
element of the array coordinate vector b. The instruction then loads data from the selected
surface at coordinates given by the remaining elements of operand b into destination
d. Operand a is a .surfref variable or .u64 register. Operand b is a bit-size
type vector or tuple containing an index into the array of surfaces followed by coordinates within
the selected surface, as follows:
For 1d surface arrays, operand b has type .v2.b32. The first element is interpreted as an
unsigned integer index (.u32) into the surface array, and the second element is interpreted as a
1d surface coordinate of type .s32.
For 2d surface arrays, operand b has type .v4.b32. The first element is interpreted as an
unsigned integer index (.u32) into the surface array, and the next two elements are interpreted
as 2d surface coordinates of type .s32. The fourth element is ignored.
A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
The .clamp field specifies how to handle out-of-bounds addresses:
.trapcauses an execution trap on out-of-bounds addresses
.clamploads data at the nearest surface location (sized appropriately)
.zeroloads zero for out-of-bounds addresses
Indirect surface access
Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture
sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of
a .surfref variable.
PTX ISA Notes
suld.b.trap introduced in PTX ISA version 1.5.
Additional clamp modifiers and cache operations introduced in PTX ISA version 2.0.
suld.b.3d andsuld.b.{a1d,a2d} introduced in PTX ISA version 3.0.
Indirect surface access introduced in PTX ISA version 3.1.
Target ISA Notes
suld.b supported on all target architectures.
sm_1x targets support only the .trap clamping modifier.
suld.3d andsuld.{a1d,a2d} require sm_20 or higher.
Indirect surface access requires sm_20 or higher.
Cache operations require sm_20 or higher.
Examples
suld.b.1d.v4.b32.trap {s1,s2,s3,s4}, [surf_B, {x}];
suld.b.3d.v2.b64.trap {r1,r2}, [surf_A, {x,y,z,w}];
suld.b.a1d.v2.b32 {r0,r1}, [surf_C, {idx,x}];
suld.b.a2d.b32 r0, [surf_D, {idx,x,y,z}]; // z ignored
9.7.10.2. Surface Instructions: sust
sust
Store to surface memory.
Syntax
sust.b.{1d,2d,3d}{.cop}.vec.ctype.clamp [a, b], c; // unformatted
sust.p.{1d,2d,3d}.vec.b32.clamp [a, b], c; // formatted
sust.b.{a1d,a2d}{.cop}.vec.ctype.clamp [a, b], c; // unformatted
.cop = { .wb, .cg, .cs, .wt }; // cache operation
.vec = { none, .v2, .v4 };
.ctype = { .b8 , .b16, .b32, .b64 };
.clamp = { .trap, .clamp, .zero };
Description
sust.{1d,2d,3d}
Store to surface memory using a surface coordinate vector. The instruction stores data from operand
c to the surface named by operand a at coordinates given by operand b. Operand a is
a .surfref variable or .u64 register. Operand b is a scalar or singleton tuple for 1d
surfaces; is a two-element vector for 2d surfaces; and is a four-element vector for 3d surfaces,
where the fourth element is ignored. Coordinate elements are of type .s32.
sust.b performs an unformatted store of binary data. The lowest dimension coordinate represents
a byte offset into the surface and is not scaled. The size of the data transfer matches the size of
source operand c.
sust.p performs a formatted store of a vector of 32-bit data values to a surface sample. The
source vector elements are interpreted left-to-right as R, G, B, and A surface
components. These elements are written to the corresponding surface sample components. Source
elements that do not occur in the surface sample are ignored. Surface sample components that do not
occur in the source vector will be written with an unpredictable value. The lowest dimension
coordinate represents a sample offset rather than a byte offset.
The source data interpretation is based on the surface sample format as follows: If the surface
format contains UNORM, SNORM, or FLOAT data, then .f32 is assumed; if the surface
format contains UINT data, then .u32 is assumed; if the surface format contains SINT
data, then .s32 is assumed. The source data is then converted from this type to the surface
sample format.
sust.b.{a1d,a2d}
Surface layer selection, followed by an unformatted store to the selected surface. The instruction
first selects a surface layer from the surface array named by operand a using the index given by
the first element of the array coordinate vector b. The instruction then stores the data in
operand c to the selected surface at coordinates given by the remaining elements of operand
b. Operand a is a .surfref variable or .u64 register. Operand b is a bit-size type
vector or tuple containing an index into the array of surfaces followed by coordinates within the
selected surface, as follows:
For 1d surface arrays, operand
bhas type.v2.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the second element is interpreted as a 1d surface coordinate of type.s32.For 2d surface arrays, operand
bhas type.v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the next two elements are interpreted as 2d surface coordinates of type.s32. The fourth element is ignored.
A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
The .clamp field specifies how to handle out-of-bounds addresses:
.trapcauses an execution trap on out-of-bounds addresses
.clampstores data at the nearest surface location (sized appropriately)
.zerodrops stores to out-of-bounds addresses
Indirect surface access
Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture
sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of
a .surfref variable.
PTX ISA Notes
sust.b.trap introduced in PTX ISA version 1.5. sust.p, additional clamp modifiers, and
cache operations introduced in PTX ISA version 2.0.
sust.b.3d and sust.b.{a1d,a2d} introduced in PTX ISA version 3.0.
Indirect surface access introduced in PTX ISA version 3.1.
Target ISA Notes
sust.b supported on all target architectures.
sm_1x targets support only the .trap clamping modifier.
sust.3d and sust.{a1d,a2d} require sm_20 or higher.
sust.p requires sm_20 or higher.
Indirect surface access requires sm_20 or higher.
Cache operations require sm_20 or higher.
Examples
sust.p.1d.v4.b32.trap [surf_B, {x}], {f1,f2,f3,f4};
sust.b.3d.v2.b64.trap [surf_A, {x,y,z,w}], {r1,r2};
sust.b.a1d.v2.b64 [surf_C, {idx,x}], {r1,r2};
sust.b.a2d.b32 [surf_D, {idx,x,y,z}], r0; // z ignored
9.7.10.3. Surface Instructions: sured
sured
Reduce surface memory.
Syntax
sured.b.op.geom.ctype.clamp [a,b],c; // byte addressing
sured.p.op.geom.ctype.clamp [a,b],c; // sample addressing
.op = { .add, .min, .max, .and, .or };
.geom = { .1d, .2d, .3d };
.ctype = { .u32, .u64, .s32, .b32, .s64 }; // for sured.b
.ctype = { .b32, .b64 }; // for sured.p
.clamp = { .trap, .clamp, .zero };
Description
Reduction to surface memory using a surface coordinate vector. The instruction performs a reduction
operation with data from operand c to the surface named by operand a at coordinates given by
operand b. Operand a is a .surfref variable or .u64 register. Operand b is a
scalar or singleton tuple for 1d surfaces; is a two-element vector for 2d surfaces; and is a
four-element vector for 3d surfaces, where the fourth element is ignored. Coordinate elements are of
type .s32.
sured.b performs an unformatted reduction on .u32, .s32, .b32, .u64, or .s64
data. The lowest dimension coordinate represents a byte offset into the surface and is not
scaled. Operation add applies to .u32, .u64, and .s32 types; min and max
apply to .u32, .s32, .u64 and .s64 types; operations and and or apply to
.b32 type.
sured.p performs a reduction on sample-addressed data. The lowest dimension coordinate
represents a sample offset rather than a byte offset. The instruction type .b64 is restricted to
min and max operations. For type .b32, the data is interpreted as .u32 or .s32
based on the surface sample format as follows: if the surface format contains UINT data, then
.u32 is assumed; if the surface format contains SINT data, then .s32 is assumed. For
type .b64, if the surface format contains UINT data, then .u64 is assumed; if the
surface format contains SINT data, then .s64 is assumed.
A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.
The .clamp field specifies how to handle out-of-bounds addresses:
.trapcauses an execution trap on out-of-bounds addresses
.clampstores data at the nearest surface location (sized appropriately)
.zerodrops stores to out-of-bounds addresses
Indirect surface access
Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture
sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of
a .surfref variable.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Indirect surface access introduced in PTX ISA version 3.1.
.u64/.s64/.b64 types with .min/.max operations introduced in PTX ISA version
8.1.
Target ISA Notes
sured requires sm_20 or higher.
Indirect surface access requires sm_20 or higher.
.u64/.s64/.b64 types with .min/.max operations requires sm_50 or higher.
Examples
sured.b.add.2d.u32.trap [surf_A, {x,y}], r1;
sured.p.min.1d.u32.trap [surf_B, {x}], r1;
sured.b.max.1d.u64.trap [surf_C, {x}], r1;
sured.p.min.1d.b64.trap [surf_D, {x}], r1;
9.7.10.4. Surface Instructions: suq
suq
Query a surface attribute.
Syntax
suq.query.b32 d, [a];
.query = { .width, .height, .depth,
.channel_data_type, .channel_order,
.array_size, .memory_layout };
Description
Query an attribute of a surface. Operand a is a .surfref variable or a .u64 register.
Query |
Returns |
|---|---|
|
value in elements |
|
Unsigned integer corresponding to source language’s channel data
type enumeration. If the source language combines channel data
type and channel order into a single enumeration type, that value
is returned for both |
|
Unsigned integer corresponding to source language’s channel order
enumeration. If the source language combines channel data type and
channel order into a single enumeration type, that value is
returned for both |
|
For a surface array, number of surfaces in array, 0 otherwise. |
|
|
Indirect surface access
Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture
sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of
a .surfref variable.
PTX ISA Notes
Introduced in PTX ISA version 1.5.
Channel data type and channel order queries added in PTX ISA version 2.1.
Indirect surface access introduced in PTX ISA version 3.1.
The .array_size query was added in PTX ISA version 4.1.
The .memory_layout query was added in PTX ISA version 4.2.
Target ISA Notes
Supported on all target architectures.
Indirect surface access requires sm_20 or higher.
Examples
suq.width.b32 %r1, [surf_A];
9.7.11. Control Flow Instructions
The following PTX instructions and syntax are for controlling execution in a PTX program:
{}@bracallretexit
9.7.11.1. Control Flow Instructions: {}
{}
Instruction grouping.
Syntax
{ instructionList }
Description
The curly braces create a group of instructions, used primarily for defining a function body. The curly braces also provide a mechanism for determining the scope of a variable: any variable declared within a scope is not available outside the scope.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
{ add.s32 a,b,c; mov.s32 d,a; }
9.7.11.2. Control Flow Instructions: @
@
Predicated execution.
Syntax
@{!}p instruction;
Description
Execute an instruction or instruction block for threads that have the guard predicate
True. Threads with a False guard predicate do nothing.
Semantics
If {!}p then instruction
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
setp.eq.f32 p,y,0; // is y zero?
@!p div.f32 ratio,x,y // avoid division by zero
@q bra L23; // conditional branch
9.7.11.3. Control Flow Instructions: bra
bra
Branch to a target and continue execution there.
Syntax
@p bra{.uni} tgt; // tgt is a label
bra{.uni} tgt; // unconditional branch
Description
Continue execution at the target. Conditional branches are specified by using a guard predicate. The branch target must be a label.
bra.uni is guaranteed to be non-divergent, i.e. all active threads in a warp that are currently
executing this instruction have identical values for the guard predicate and branch target.
Semantics
if (p) {
pc = tgt;
}
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Unimplemented indirect branch introduced in PTX ISA version 2.1 has been removed from the spec.
Target ISA Notes
Supported on all target architectures.
Examples
bra.uni L_exit; // uniform unconditional jump
@q bra L23; // conditional branch
9.7.11.4. Control Flow Instructions: brx.idx
brx.idx
Branch to a label indexed from a list of potential branch targets.
Syntax
@p brx.idx{.uni} index, tlist;
brx.idx{.uni} index, tlist;
Description
Index into a list of possible destination labels, and continue execution from the chosen label. Conditional branches are specified by using a guard predicate.
brx.idx.uni guarantees that the branch is non-divergent, i.e. all active threads in a warp that
are currently executing this instruction have identical values for the guard predicate and the
index argument.
The index operand is a .u32 register. The tlist operand must be the label of a
.branchtargets directive. It is accessed as a zero-based sequence using index. Behaviour is
undefined if the value of index is greater than or equal to the length of tlist.
The .branchtargets directive must be defined in the local function scope before it is used. It
must refer to labels within the current function.
Semantics
if (p) {
if (index < length(tlist)) {
pc = tlist[index];
} else {
pc = undefined;
}
}
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
Requires sm_30 or higher.
Examples
.function foo () {
.reg .u32 %r0;
...
L1:
...
L2:
...
L3:
...
ts: .branchtargets L1, L2, L3;
@p brx.idx %r0, ts;
...
}
9.7.11.5. Control Flow Instructions: call
call
Call a function, recording the return location.
Syntax
// direct call to named function, func is a symbol
call{.uni} (ret-param), func, (param-list);
call{.uni} func, (param-list);
call{.uni} func;
// indirect call via pointer, with full list of call targets
call{.uni} (ret-param), fptr, (param-list), flist;
call{.uni} fptr, (param-list), flist;
call{.uni} fptr, flist;
// indirect call via pointer, with no knowledge of call targets
call{.uni} (ret-param), fptr, (param-list), fproto;
call{.uni} fptr, (param-list), fproto;
call{.uni} fptr, fproto;
Description
The call instruction stores the address of the next instruction, so execution can resume at that
point after executing a ret instruction. A call is assumed to be divergent unless the
.uni suffix is present. The .uni suffix indicates that the call is guaranteed to be
non-divergent, i.e. all active threads in a warp that are currently executing this instruction have
identical values for the guard predicate and call target.
For direct calls, the called location func must be a symbolic function name; for indirect calls,
the called location fptr must be an address of a function held in a register. Input arguments
and return values are optional. Arguments may be registers, immediate constants, or variables in
.param space. Arguments are pass-by-value.
Indirect calls require an additional operand, flist or fproto, to communicate the list of
potential call targets or the common function prototype of all call targets,
respectively. In the first case, flist gives a complete list of potential call targets and
the optimizing backend is free to optimize the calling convention. In the second case, where the
complete list of potential call targets may not be known, the common function prototype is given
and the call must obey the ABI’s calling convention.
The flist operand is either the name of an array (call table) initialized to a list of function
names; or a label associated with a .calltargets directive, which declares a list of potential
call targets. In both cases the fptr register holds the address of a function listed in the call
table or .calltargets list, and the call operands are type-checked against the type
signature of the functions indicated by flist.
The fproto operand is the name of a label associated with a .callprototype directive. This
operand is used when a complete list of potential targets is not known. The call operands are
type-checked against the prototype, and code generation will follow the ABI calling convention. If a
function that doesn’t match the prototype is called, the behavior is undefined.
Call tables may be declared at module scope or local scope, in either the constant or global state
space. The .calltargets and .callprototype directives must be declared within a function
body. All functions must be declared prior to being referenced in a call table initializer or
.calltargets directive.
PTX ISA Notes
Direct call introduced in PTX ISA version 1.0. Indirect call introduced in PTX ISA version 2.1.
Target ISA Notes
Direct call supported on all target architectures. Indirect call requires sm_20 or higher.
Examples
// examples of direct call
call init; // call function 'init'
call.uni g, (a); // call function 'g' with parameter 'a'
@p call (d), h, (a, b); // return value into register d
// call-via-pointer using jump table
.func (.reg .u32 rv) foo (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) bar (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) baz (.reg .u32 a, .reg .u32 b) ...
.global .u32 jmptbl[5] = { foo, bar, baz };
...
@p ld.global.u32 %r0, [jmptbl+4];
@p ld.global.u32 %r0, [jmptbl+8];
call (retval), %r0, (x, y), jmptbl;
// call-via-pointer using .calltargets directive
.func (.reg .u32 rv) foo (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) bar (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) baz (.reg .u32 a, .reg .u32 b) ...
...
@p mov.u32 %r0, foo;
@q mov.u32 %r0, baz;
Ftgt: .calltargets foo, bar, baz;
call (retval), %r0, (x, y), Ftgt;
// call-via-pointer using .callprototype directive
.func dispatch (.reg .u32 fptr, .reg .u32 idx)
{
...
Fproto: .callprototype _ (.param .u32 _, .param .u32 _);
call %fptr, (x, y), Fproto;
...
9.7.11.6. Control Flow Instructions: ret
ret
Return from function to instruction after call.
Syntax
ret{.uni};
Description
Return execution to caller’s environment. A divergent return suspends threads until all threads are
ready to return to the caller. This allows multiple divergent ret instructions.
A ret is assumed to be divergent unless the .uni suffix is present, indicating that the
return is guaranteed to be non-divergent.
Any values returned from a function should be moved into the return parameter variables prior to
executing the ret instruction.
A return instruction executed in a top-level entry routine will terminate thread execution.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
ret;
@p ret;
9.7.11.7. Control Flow Instructions: exit
exit
Terminate a thread.
Syntax
exit;
Description
Ends execution of a thread.
As threads exit, barriers waiting on all threads are checked to see if the exiting threads are the
only threads that have not yet made it to a barrier{.cta} for all threads in the CTA or to a
barrier.cluster for all threads in the cluster. If the exiting threads are holding up the
barrier, the barrier is released.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
exit;
@p exit;
9.7.12. Parallel Synchronization and Communication Instructions
These instructions are:
bar{.cta},barrier{.cta}barrier.clusterbar.warp.syncmembaratomredred.asyncvotematch.syncactivemaskredux.syncgriddepcontrolelect.syncmbarrier.initmbarrier.invalmbarrier.arrivembarrier.arrive_dropmbarrier.test_waitmbarrier.try_waitmbarrier.pending_countcp.async.mbarrier.arrivetensormap.cp_fenceproxy
9.7.12.1. Parallel Synchronization and Communication Instructions: bar, barrier
bar{.cta}, barrier{.cta}
Barrier synchronization.
Syntax
barrier{.cta}.sync{.aligned} a{, b};
barrier{.cta}.arrive{.aligned} a, b;
barrier{.cta}.red.popc{.aligned}.u32 d, a{, b}, {!}c;
barrier{.cta}.red.op{.aligned}.pred p, a{, b}, {!}c;
bar{.cta}.sync a{, b};
bar{.cta}.arrive a, b;
bar{.cta}.red.popc.u32 d, a{, b}, {!}c;
bar{.cta}.red.op.pred p, a{, b}, {!}c;
.op = { .and, .or };
Description
Performs barrier synchronization and communication within a CTA. Each CTA instance has sixteen
barriers numbered 0..15.
barrier{.cta} instructions can be used by the threads within the CTA for synchronization and
communication.
Operands a, b, and d have type .u32; operands p and c are predicates. Source
operand a specifies a logical barrier resource as an immediate constant or register with value
0 through 15. Operand b specifies the number of threads participating in the barrier. If
no thread count is specified, all threads in the CTA participate in the barrier. When specifying a
thread count, the value must be a multiple of the warp size. Note that a non-zero thread count is
required for barrier{.cta}.arrive.
Depending on operand b, either specified number of threads (in multiple of warp size) or all
threads in the CTA participate in barrier{.cta} instruction. The barrier{.cta} instructions
signal the arrival of the executing threads at the named barrier.
barrier{.cta} instruction causes executing thread to wait for all non-exited threads from its
warp and marks warps’ arrival at barrier. In addition to signaling its arrival at the barrier, the
barrier{.cta}.red and barrier{.cta}.sync instructions causes executing thread to wait for
non-exited threads of all other warps participating in the barrier to
arrive. barrier{.cta}.arrive does not cause executing thread to wait for threads of other
participating warps.
When a barrier completes, the waiting threads are restarted without delay, and the barrier is reinitialized so that it can be immediately reused.
The barrier{.cta}.sync or barrier{.cta}.red or barrier{.cta}.arrive instruction
guarantees that when the barrier completes, prior memory accesses requested by this thread are
performed relative to all threads participating in the barrier. The barrier{.cta}.sync and
barrier{.cta}.red instruction further guarantees that no new memory access is requested by this
thread before the barrier completes.
A memory read (e.g., by ld or atom) has been performed when the value read has been
transmitted from memory and cannot be modified by another thread participating in the barrier. A
memory write (e.g., by st, red or atom) has been performed when the value written has
become visible to other threads participating in the barrier, that is, when the previous value can
no longer be read.
barrier{.cta}.red performs a reduction operation across threads. The c predicate (or its
complement) from all threads in the CTA are combined using the specified reduction operator. Once
the barrier count is reached, the final value is written to the destination register in all threads
waiting at the barrier.
The reduction operations for barrier{.cta}.red are population-count (.popc),
all-threads-True (.and), and any-thread-True (.or). The result of .popc is the number of
threads with a True predicate, while .and and .or indicate if all the threads had a
True predicate or if any of the threads had a True predicate.
Instruction barrier{.cta} has optional .aligned modifier. When specified, it indicates that
all threads in CTA will execute the same barrier{.cta} instruction. In conditionally executed
code, an aligned barrier{.cta} instruction should only be used if it is known that all threads
in CTA evaluate the condition identically, otherwise behavior is undefined.
Different warps may execute different forms of the barrier{.cta} instruction using the same
barrier name and thread count. One example mixes barrier{.cta}.sync and barrier{.cta}.arrive
to implement producer/consumer models. The producer threads execute barrier{.cta}.arrive to
announce their arrival at the barrier and continue execution without delay to produce the next
value, while the consumer threads execute the barrier{.cta}.sync to wait for a resource to be
produced. The roles are then reversed, using a different barrier, where the producer threads execute
a barrier{.cta}.sync to wait for a resource to consumed, while the consumer threads announce
that the resource has been consumed with barrier{.cta}.arrive. Care must be taken to keep a warp
from executing more barrier{.cta} instructions than intended (barrier{.cta}.arrive followed
by any other barrier{.cta} instruction to the same barrier) prior to the reset of the
barrier. barrier{.cta}.red should not be intermixed with barrier{.cta}.sync or
barrier{.cta}.arrive using the same active barrier. Execution in this case is unpredictable.
The optional .cta qualifier simply indicates CTA-level applicability of the barrier and it
doesn’t change the semantics of the instruction.
bar{.cta}.sync is equivalent to barrier{.cta}.sync.aligned. bar{.cta}.arrive is
equivalent to barrier{.cta}.arrive.aligned. bar{.cta}.red is equivalent to
barrier{.cta}.red.aligned.
Note
For .target sm_6x or below,
barrier{.cta}instruction without.alignedmodifier is equivalent to.alignedvariant and has the same restrictions as of.alignedvariant.All threads in warp (except for those have exited) must execute
barrier{.cta}instruction in convergence.
PTX ISA Notes
bar.sync without a thread count introduced in PTX ISA version 1.0.
Register operands, thread count, and bar.{arrive,red} introduced in PTX ISA version 2.0.
barrier instruction introduced in PTX ISA version 6.0.
.cta qualifier introduced in PTX ISA version 7.8.
Target ISA Notes
Register operands, thread count, and bar{.cta}.{arrive,red} require sm_20 or higher.
Only bar{.cta}.sync with an immediate barrier number is supported for sm_1x targets.
barrier{.cta} instruction requires sm_30 or higher.
Examples
// Use bar.sync to arrive at a pre-computed barrier number and
// wait for all threads in CTA to also arrive:
st.shared [r0],r1; // write my result to shared memory
bar.cta.sync 1; // arrive, wait for others to arrive
ld.shared r2,[r3]; // use shared results from other threads
// Use bar.sync to arrive at a pre-computed barrier number and
// wait for fixed number of cooperating threads to arrive:
#define CNT1 (8*12) // Number of cooperating threads
st.shared [r0],r1; // write my result to shared memory
bar.cta.sync 1, CNT1; // arrive, wait for others to arrive
ld.shared r2,[r3]; // use shared results from other threads
// Use bar.red.and to compare results across the entire CTA:
setp.eq.u32 p,r1,r2; // p is True if r1==r2
bar.cta.red.and.pred r3,1,p; // r3=AND(p) forall threads in CTA
// Use bar.red.popc to compute the size of a group of threads
// that have a specific condition True:
setp.eq.u32 p,r1,r2; // p is True if r1==r2
bar.cta.red.popc.u32 r3,1,p; // r3=SUM(p) forall threads in CTA
/* Producer/consumer model. The producer deposits a value in
* shared memory, signals that it is complete but does not wait
* using bar.arrive, and begins fetching more data from memory.
* Once the data returns from memory, the producer must wait
* until the consumer signals that it has read the value from
* the shared memory location. In the meantime, a consumer
* thread waits until the data is stored by the producer, reads
* it, and then signals that it is done (without waiting).
*/
// Producer code places produced value in shared memory.
st.shared [r0],r1;
bar.arrive 0,64;
ld.global r1,[r2];
bar.sync 1,64;
...
// Consumer code, reads value from shared memory
bar.sync 0,64;
ld.shared r1,[r0];
bar.arrive 1,64;
...
// Examples of barrier.cta.sync
st.shared [r0],r1;
barrier.cta.sync 0;
ld.shared r1, [r0];
9.7.12.2. Parallel Synchronization and Communication Instructions: bar.warp.sync
bar.warp.sync
Barrier synchronization for threads in a warp.
Syntax
bar.warp.sync membermask;
Description
bar.warp.sync will cause executing thread to wait until all threads corresponding to
membermask have executed a bar.warp.sync with the same membermask value before resuming
execution.
Operand membermask specifies a 32-bit integer which is a mask indicating threads participating
in barrier where the bit position corresponds to thread’s laneid.
The behavior of bar.warp.sync is undefined if the executing thread is not in the membermask.
bar.warp.sync also guarantee memory ordering among threads participating in barrier. Thus,
threads within warp that wish to communicate via memory can store to memory, execute
bar.warp.sync, and then safely read values stored by other threads in warp.
Note
For .target sm_6x or below, all threads in membermask must execute the same
bar.warp.sync instruction in convergence, and only threads belonging to some membermask
can be active when the bar.warp.sync instruction is executed. Otherwise, the behavior is
undefined.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
Requires sm_30 or higher.
Examples
st.shared.u32 [r0],r1; // write my result to shared memory
bar.warp.sync 0xffffffff; // arrive, wait for others to arrive
ld.shared.u32 r2,[r3]; // read results written by other threads
9.7.12.3. Parallel Synchronization and Communication Instructions: barrier.cluster
barrier.cluster
Barrier synchronization within a cluster.
Syntax
barrier.cluster.arrive{.sem}{.aligned};
barrier.cluster.wait{.acquire}{.aligned};
.sem = {.release, .relaxed}
Description
Performs barrier synchronization and communication within a cluster.
barrier.cluster instructions can be used by the threads within the cluster for synchronization
and communication.
barrier.cluster.arrive instruction marks warps’ arrival at barrier without causing executing
thread to wait for threads of other participating warps.
barrier.cluster.wait instruction causes the executing thread to wait for all non-exited threads
of the cluster to perform barrier.cluster.arrive.
In addition, barrier.cluster instructions cause the executing thread to wait for all non-exited
threads from its warp.
When all non-exited threads that executed barrier.cluster.arrive have executed
barrier.cluster.wait, the barrier completes and is reinitialized so it can be reused
immediately. Each thread must arrive at the barrier only once before the barrier completes.
The barrier.cluster.wait instruction guarantees that when it completes the execution, memory
accesses (except asynchronous operations) requested, in program order, prior to the preceding
barrier.cluster.arrive by all threads in the cluster are complete and visible to the executing
thread.
There is no memory ordering and visibility guarantee for memory accesses requested by the executing
thread, in program order, after barrier.cluster.arrive and prior to barrier.cluster.wait.
The optional .relaxed qualifier on barrier.cluster.arrive specifies that there are no memory
ordering and visibility guarantees provided for the memory accesses performed prior to
barrier.cluster.arrive.
The optional .sem and .acquire qualifiers on instructions barrier.cluster.arrive and
barrier.cluster.wait specify the memory synchronization as described in the Memory Consistency
Model. If the optional .sem qualifier is absent for
barrier.cluster.arrive, .release is assumed by default. If the optional .acquire
qualifier is absent for barrier.cluster.wait, .acquire is assumed by default.
The optional .aligned qualifier indicates that all threads in the warp must execute the same
barrier.cluster instruction. In conditionally executed code, an aligned barrier.cluster
instruction should only be used if it is known that all threads in the warp evaluate the condition
identically, otherwise behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Support for .acquire, .relaxed, .release qualifiers introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
// use of arrive followed by wait
ld.shared::cluster.u32 r0, [addr];
barrier.cluster.arrive.aligned;
...
barrier.cluster.wait.aligned;
st.shared::cluster.u32 [addr], r1;
// use memory fence prior to arrive for relaxed barrier
@cta0 ld.shared::cluster.u32 r0, [addr];
fence.cluster.acq_rel;
barrier.cluster.arrive.relaxed.aligned;
...
barrier.cluster.wait.aligned;
@cta1 st.shared::cluster.u32 [addr], r1;
9.7.12.4. Parallel Synchronization and Communication Instructions: membar/fence
membar/fence
Enforce an ordering of memory operations.
Syntax
// Thread fence :
fence{.sem}.scope;
// Operation fence :
fence.op_restrict.release.cluster;
// Proxy fence (bi-directional) :
fence.proxy.proxykind;
// Proxy fence (uni-directional) :
fence.proxy.to_proxykind::from_proxykind.release.scope;
fence.proxy.to_proxykind::from_proxykind.acquire.scope [addr], size;
// Old style membar :
membar.level;
membar.proxy.proxykind;
.sem = { .sc, .acq_rel };
.scope = { .cta, .cluster, .gpu, .sys };
.level = { .cta, .gl, .sys };
.proxykind = { .alias, .async, async.global, .async.shared::{cta, cluster} };
.op_restrict = { .mbarrier_init };
.to_proxykind::from_proxykind = {.tensormap::generic};
Description
The membar instruction guarantees that prior memory accesses requested by this thread (ld,
st, atom and red instructions) are performed at the specified level, before later
memory operations requested by this thread following the membar instruction. The level
qualifier specifies the set of threads that may observe the ordering effect of this operation.
A memory read (e.g., by ld or atom) has been performed when the value read has been
transmitted from memory and cannot be modified by another thread at the indicated level. A memory
write (e.g., by st, red or atom) has been performed when the value written has become
visible to other threads at the specified level, that is, when the previous value can no longer be
read.
The fence instruction establishes an ordering between memory accesses requested by this thread
(ld, st, atom and red instructions) as described in the Memory Consistency Model. The scope qualifier specifies the set of threads that may
observe the ordering effect of this operation.
fence.acq_rel is a light-weight fence that is sufficient for memory synchronization in most
programs. Instances of fence.acq_rel synchronize when combined with additional memory operations
as described in acquire and release patterns in the Memory Consistency Model. If the optional .sem qualifier is absent, .acq_rel
is assumed by default.
fence.sc is a slower fence that can restore sequential consistency when used in sufficient
places, at the cost of performance. Instances of fence.sc with sufficient scope always
synchronize by forming a total order per scope, determined at runtime. This total order can be
constrained further by other synchronization in the program.
Qualifier .op_restrict restricts the class of prior memory operations for which the fence
instruction provides the memory ordering guarantees. When .op_restrict is .mbarrier_init,
the fence only applies to the prior mbarrier.init operations executed by the same thread on
mbarrier objects in .shared::cta state space.
The address operand addr and the operand size together specifies the memory range
[addr, addr+size-1] on which the ordering guarantees on the memory accesses across the proxies is to be
provided. The only supported value for the size operand is 128. Generic Addressing
is used unconditionally, and the address specified by the operand addr must fall within the .global
state space. Otherwise, the behavior is undefined.
On sm_70 and higher membar is a synonym for fence.sc1, and the membar
levels cta, gl and sys are synonymous with the fence scopes cta, gpu and
sys respectively.
membar.proxy and fence.proxy instructions establish an ordering between memory accesses that
may happen through different proxies.
A uni-directional proxy ordering from the from-proxykind to the to-proxykind establishes ordering between a prior memory access performed via the from-proxykind and a subsequent memory access performed via the to-proxykind.
A bi-directional proxy ordering between two proxykinds establishes two uni-directional proxy orderings : one from the first proxykind to the second proxykind and the other from the second proxykind to the first proxykind.
The .proxykind qualifier indicates the bi-directional proxy ordering that is established between the memory
accesses done between the generic proxy and the proxy specified by .proxykind.
Value .alias of the .proxykind qualifier refers to memory accesses performed using virtually
aliased addresses to the same memory location. Value .async of the .proxykind qualifier specifies
that the memory ordering is established between the async proxy and the generic proxy. The memory
ordering is limited only to the state space specified. If no state space is specified, then the memory
ordering applies on all state spaces.
A .release proxy fence can form a release sequence that synchronizes with an acquire
sequence that contains a .acquire proxy fence. The .to_proxykind and
.from_proxykind qualifiers indicate the uni-directional proxy ordering that is established.
On sm_70 and higher, membar.proxy is a synonym for fence.proxy.
1 The semantics of fence.sc introduced with sm_70 is a superset of the semantics of
membar and the two are compatible; when executing on sm_70 or later architectures,
membar acquires the full semantics of fence.sc.
PTX ISA Notes
membar.{cta,gl} introduced in PTX ISA version 1.4.
membar.sys introduced in PTX ISA version 2.0.
fence introduced in PTX ISA version 6.0.
membar.proxy and fence.proxy introduced in PTX ISA version 7.5.
.cluster scope qualifier introduced in PTX ISA version 7.8.
.op_restrict qualifier introduced in PTX ISA version 8.0.
fence.proxy.async is introduced in PTX ISA version 8.0.
.to_proxykind::from_proxykind qualifier introduced in PTX ISA version 8.3.
Target ISA Notes
membar.{cta,gl} supported on all target architectures.
membar.sys requires sm_20 or higher.
fence requires sm_70 or higher.
membar.proxy requires sm_60 or higher.
fence.proxy requires sm_70 or higher.
.cluster scope qualifier requires sm_90 or higher.
.op_restrict qualifier requires sm_90 or higher.
fence.proxy.async requires sm_90 or higher.
.to_proxykind::from_proxykind qualifier requires sm_90 or higher.
Examples
membar.gl;
membar.cta;
membar.sys;
fence.sc;
fence.sc.cluster;
fence.proxy.alias;
membar.proxy.alias;
fence.mbarrier_init.release.cluster;
fence.proxy.async;
fence.proxy.async.shared::cta;
fence.proxy.async.shared::cluster;
fence.proxy.async.global;
tensormap.replace.tile.global_address.global.b1024.b64 [gbl], new_addr;
fence.proxy.tensormap::generic.release.gpu;
fence.proxy.tensormap::generic.acquire.gpu [tmap], 128;
cvta.global.u64 tmap, gbl;
cp.async.bulk.tensor.1d.shared::cluster.global.tile [addr0], [tmap, {tc0}], [mbar0];
9.7.12.5. Parallel Synchronization and Communication Instructions: atom
atom
Atomic reduction operations for thread-to-thread communication.
Syntax
Atomic operation with scalar type:
atom{.sem}{.scope}{.space}.op{.level::cache_hint}.type d, [a], b{, cache-policy};
atom{.sem}{.scope}{.space}.op.type d, [a], b, c;
atom{.sem}{.scope}{.space}.cas.b16 d, [a], b, c;
atom{.sem}{.scope}{.space}.cas.b128 d, [a], b, c {, cache-policy};
atom{.sem}{.scope}{.space}.exch{.level::cache_hint}.b128 d, [a], b {, cache-policy};
atom{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.f16 d, [a], b{, cache-policy};
atom{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.f16x2 d, [a], b{, cache-policy};
atom{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.bf16 d, [a], b{, cache-policy};
atom{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.bf16x2 d, [a], b{, cache-policy};
.space = { .global, .shared{::cta, ::cluster} };
.sem = { .relaxed, .acquire, .release, .acq_rel };
.scope = { .cta, .cluster, .gpu, .sys };
.op = { .and, .or, .xor,
.cas, .exch,
.add, .inc, .dec,
.min, .max };
.level::cache_hint = { .L2::cache_hint };
.type = { .b32, .b64, .u32, .u64, .s32, .s64, .f32, .f64 };
Atomic operation with vector type:
atom{.sem}{.scope}{.global}.add{.level::cache_hint}.vec_32_bit.f32 d, [a], b{, cache-policy};
atom{.sem}{.scope}{.global}.op.noftz{.level::cache_hint}.vec_16_bit.half_word_type d, [a], b{, cache-policy};
atom{.sem}{.scope}{.global}.op.noftz{.level::cache_hint}.vec_32_bit.packed_type d, [a], b{, cache-policy};
.sem = { .relaxed, .acquire, .release, .acq_rel };
.scope = { .cta, .gpu, .sys };
.op = { .add, .min, .max };
.half_word_type = { .f16, .bf16 };
.packed_type = { .f16x2, .bf16x2 };
.vec_16_bit = { .v2, .v4, .v8 }
.vec_32_bit = { .v2, .v4 };
.level::cache_hint = { .L2::cache_hint }
Description
Atomically loads the original value at location a into destination register d, performs a
reduction operation with operand b and the value in location a, and stores the result of the
specified operation at location a, overwriting the original value. Operand a specifies a
location in the specified state space. If no state space is given, perform the memory accesses using
Generic Addressing. atom with scalar type may be used only
with .global and .shared spaces and with generic addressing, where the address points to
.global or .shared space. atom with vector type may be used only with .global space
and with generic addressing where the address points to .global space.
For atom with vector type, operands d and b are brace-enclosed vector expressions, size
of which is equal to the size of vector qualifier.
If no sub-qualifier is specified with .shared state space, then ::cta is assumed by default.
The optional .sem qualifier specifies a memory synchronizing effect as described in the Memory
Consistency Model. If the .sem qualifier is absent,
.relaxed is assumed by default.
The optional .scope qualifier specifies the set of threads that can directly observe the memory
synchronizing effect of this operation, as described in the Memory Consistency Model. If the .scope qualifier is absent, .gpu scope is
assumed by default.
For atom with vector type, the supported combinations of vector qualifier and types, and atomic
operations supported on these combinations are depicted in the following table:
Vector qualifier |
Types |
||
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Not supported |
Not Supported |
Two atomic operations {atom or red} are performed atomically with respect to each other only
if each operation specifies a scope that includes the other. When this condition is not met, each
operation observes the other operation being performed as if it were split into a read followed by a
dependent write.
atom instruction on packed type or vector type, accesses adjacent scalar elements in memory. In
such cases, the atomicity is guaranteed separately for each of the individual scalar elements; the
entire atom is not guaranteed to be atomic as a single access.
For sm_6x and earlier architectures, atom operations on .shared state space do not
guarantee atomicity with respect to normal store instructions to the same address. It is the
programmer’s responsibility to guarantee correctness of programs that use shared memory atomic
instructions, e.g., by inserting barriers between normal stores and atomic operations to a common
address, or by using atom.exch to store to locations accessed by other atomic operations.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
The bit-size operations are .and, .or, .xor, .cas (compare-and-swap), and .exch
(exchange).
The integer operations are .add, .inc, .dec, .min, .max. The .inc and
.dec operations return a result in the range [0..b].
The floating-point operation .add operation rounds to nearest even. Current implementation of
atom.add.f32 on global memory flushes subnormal inputs and results to sign-preserving zero;
whereas atom.add.f32 on shared memory supports subnormal inputs and results and doesn’t flush
them to zero.
atom.add.f16, atom.add.f16x2, atom.add.bf16 and atom.add.bf16x2 operation requires
the .noftz qualifier; it preserves subnormal inputs and results, and does not flush them to
zero.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
The qualifier .level::cache_hint is only supported for .global state space and for generic
addressing where the address points to the .global state space.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
Semantics
atomic {
d = *a;
*a = (operation == cas) ? operation(*a, b, c)
: operation(*a, b);
}
where
inc(r, s) = (r >= s) ? 0 : r+1;
dec(r, s) = (r==0 || r > s) ? s : r-1;
exch(r, s) = s;
cas(r,s,t) = (r == s) ? t : r;
Notes
Simple reductions may be specified by using the bit bucket destination operand _.
PTX ISA Notes
32-bit atom.global introduced in PTX ISA version 1.1.
atom.shared and 64-bitatom.global.{add,cas,exch} introduced in PTX ISA 1.2.
atom.add.f32 and 64-bitatom.shared.{add,cas,exch} introduced in PTX ISA 2.0.
64-bit atom.{and,or,xor,min,max} introduced in PTX ISA 3.1.
atom.add.f64 introduced in PTX ISA 5.0.
.scope qualifier introduced in PTX ISA 5.0.
.sem qualifier introduced in PTX ISA version 6.0.
atom.add.noftz.f16x2 introduced in PTX ISA 6.2.
atom.add.noftz.f16 and atom.cas.b16 introduced in PTX ISA 6.3.
Per-element atomicity of atom.f16x2 clarified in PTX ISA version 6.3, with retrospective effect
from PTX ISA version 6.2.
Support for .level::cache_hint qualifier introduced in PTX ISA version 7.4.
atom.add.noftz.bf16 and atom.add.noftz.bf16x2 introduced in PTX ISA 7.8.
Support for .cluster scope qualifier introduced in PTX ISA version 7.8.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for vector types introduced in PTX ISA version 8.1.
Support for .b128 type introduced in PTX ISA version 8.3.
Support for .sys scope with .b128 type introduced in PTX ISA version 8.4.
Target ISA Notes
atom.global requires sm_11 or higher.
atom.shared requires sm_12 or higher.
64-bit atom.global.{add,cas,exch} require sm_12 or higher.
64-bit atom.shared.{add,cas,exch} require sm_20 or higher.
64-bit atom.{and,or,xor,min,max} require sm_32 or higher.
atom.add.f32 requires sm_20 or higher.
atom.add.f64 requires sm_60 or higher.
.scope qualifier requires sm_60 or higher.
.sem qualifier requires sm_70 or higher.
Use of generic addressing requires sm_20 or higher.
atom.add.noftz.f16x2 requires sm_60 or higher.
atom.add.noftz.f16 and atom.cas.b16 requires sm_70 or higher.
Support for .level::cache_hint qualifier requires sm_80 or higher.
atom.add.noftz.bf16 and atom.add.noftz.bf16x2 require sm_90 or higher.
Support for .cluster scope qualifier requires sm_90 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for vector types requires sm_90 or higher.
Support for .b128 type requires sm_90 or higher.
Examples
atom.global.add.s32 d,[a],1;
atom.shared::cta.max.u32 d,[x+4],0;
@p atom.global.cas.b32 d,[p],my_val,my_new_val;
atom.global.sys.add.u32 d, [a], 1;
atom.global.acquire.sys.inc.u32 ans, [gbl], %r0;
atom.add.noftz.f16x2 d, [a], b;
atom.add.noftz.f16 hd, [ha], hb;
atom.global.cas.b16 hd, [ha], hb, hc;
atom.add.noftz.bf16 hd, [a], hb;
atom.add.noftz.bf16x2 bd, [b], bb;
atom.add.shared::cluster.noftz.f16 hd, [ha], hb;
atom.shared.b128.cas d, a, b, c; // 128-bit atom
atom.global.b128.exch d, a, b; // 128-bit atom
atom.global.cluster.relaxed.add.u32 d, [a], 1;
createpolicy.fractional.L2::evict_last.b64 cache-policy, 0.25;
atom.global.add.L2::cache_hint.s32 d, [a], 1, cache-policy;
atom.global.v8.f16.max.noftz {%hd0, %hd1, %hd2, %hd3, %hd4, %hd5, %hd6, %hd7}, [gbl],
{%h0, %h1, %h2, %h3, %h4, %h5, %h6, %h7};
atom.global.v8.bf16.add.noftz {%hd0, %hd1, %hd2, %hd3, %hd4, %hd5, %hd6, %hd7}, [gbl],
{%h0, %h1, %h2, %h3, %h4, %h5, %h6, %h7};
atom.global.v2.f16.add.noftz {%hd0, %hd1}, [gbl], {%h0, %h1};
atom.global.v2.bf16.add.noftz {%hd0, %hd1}, [gbl], {%h0, %h1};
atom.global.v4.b16x2.min.noftz {%hd0, %hd1, %hd2, %hd3}, [gbl], {%h0, %h1, %h2, %h3};
atom.global.v4.f32.add {%f0, %f1, %f2, %f3}, [gbl], {%f0, %f1, %f2, %f3};
atom.global.v2.f16x2.min.noftz {%bd0, %bd1}, [g], {%b0, %b1};
atom.global.v2.bf16x2.max.noftz {%bd0, %bd1}, [g], {%b0, %b1};
atom.global.v2.f32.add {%f0, %f1}, [g], {%f0, %f1};
9.7.12.6. Parallel Synchronization and Communication Instructions: red
red
Reduction operations on global and shared memory.
Syntax
Reduction operation with scalar type:
red{.sem}{.scope}{.space}.op{.level::cache_hint}.type [a], b{, cache-policy};
red{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.f16 [a], b{, cache-policy};
red{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.f16x2 [a], b{, cache-policy};
red{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.bf16
[a], b {, cache-policy};
red{.sem}{.scope}{.space}.add.noftz{.level::cache_hint}.bf16x2
[a], b {, cache-policy};
.space = { .global, .shared{::cta, ::cluster} };
.sem = {.relaxed, .release};
.scope = {.cta, .cluster, .gpu, .sys};
.op = { .and, .or, .xor,
.add, .inc, .dec,
.min, .max };
.level::cache_hint = { .L2::cache_hint };
.type = { .b32, .b64, .u32, .u64, .s32, .s64, .f32, .f64 };
Reduction operation with vector type:
red{.sem}{.scope}{.global}.add{.level::cache_hint}.vec_32_bit.f32 [a], b{, cache-policy};
red{.sem}{.scope}{.global}.op.noftz{.level::cache_hint}. vec_16_bit.half_word_type [a], b{, cache-policy};
red{.sem}{.scope}{.global}.op.noftz{.level::cache_hint}.vec_32_bit.packed_type [a], b {, cache-policy};
.sem = { .relaxed, .release };
.scope = { .cta, .gpu, .sys };
.op = { .add, .min, .max };
.half_word_type = { .f16, .bf16 };
.packed_type = { .f16x2,.bf16x2 };
.vec_16_bit = { .v2, .v4, .v8 }
.vec_32_bit = { .v2, .v4 };
.level::cache_hint = { .L2::cache_hint }
Description
Performs a reduction operation with operand b and the value in location a, and stores the
result of the specified operation at location a, overwriting the original value. Operand a
specifies a location in the specified state space. If no state space is given, perform the memory
accesses using Generic Addressing. red with scalar type may
be used only with .global and .shared spaces and with generic addressing, where the address
points to .global or .shared space. red with vector type may be used only with
.global space and with generic addressing where the address points to .global space.
For red with vector type, operand b is brace-enclosed vector expressions, size of which is
equal to the size of vector qualifier.
If no sub-qualifier is specified with .shared state space, then ::cta is assumed by default.
The optional .sem qualifier specifies a memory synchronizing effect as described in the Memory
Consistency Model. If the .sem qualifier is absent,
.relaxed is assumed by default.
The optional .scope qualifier specifies the set of threads that can directly observe the memory
synchronizing effect of this operation, as described in the Memory Consistency Model. If the .scope qualifier is absent, .gpu scope is
assumed by default.
For red with vector type, the supported combinations of vector qualifier, types and reduction
operations supported on these combinations are depicted in following table:
Vector qualifier |
Types |
||
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Not supported |
Not Supported |
Two atomic operations {atom or red} are performed atomically with respect to each other only
if each operation specifies a scope that includes the other. When this condition is not met, each
operation observes the other operation being performed as if it were split into a read followed by a
dependent write.
red instruction on packed type or vector type, accesses adjacent scalar elements in memory. In
such case, the atomicity is guaranteed separately for each of the individual scalar elements; the
entire red is not guaranteed to be atomic as a single access.
For sm_6x and earlier architectures, red operations on .shared state space do not
guarantee atomicity with respect to normal store instructions to the same address. It is the
programmer’s responsibility to guarantee correctness of programs that use shared memory reduction
instructions, e.g., by inserting barriers between normal stores and reduction operations to a common
address, or by using atom.exch to store to locations accessed by other reduction operations.
Supported addressing modes for operand a and alignment requirements are described in Addresses
as Operands
The bit-size operations are .and, .or, and .xor.
The integer operations are .add, .inc, .dec, .min, .max. The .inc and
.dec operations return a result in the range [0..b].
The floating-point operation .add operation rounds to nearest even. Current implementation of
red.add.f32 on global memory flushes subnormal inputs and results to sign-preserving zero;
whereas red.add.f32 on shared memory supports subnormal inputs and results and doesn’t flush
them to zero.
red.add.f16, red.add.f16x2, red.add.bf16 and red.add.bf16x2 operation requires the
.noftz qualifier; it preserves subnormal inputs and results, and does not flush them to zero.
When the optional argument cache-policy is specified, the qualifier .level::cache_hint is
required. The 64-bit operand cache-policy specifies the cache eviction policy that may be used
during the memory access.
The qualifier .level::cache_hint is only supported for .global state space and for generic
addressing where the address points to the .global state space.
cache-policy is a hint to the cache subsystem and may not always be respected. It is treated as
a performance hint only, and does not change the memory consistency behavior of the program.
Semantics
*a = operation(*a, b);
where
inc(r, s) = (r >= s) ? 0 : r+1;
dec(r, s) = (r==0 || r > s) ? s : r-1;
PTX ISA Notes
Introduced in PTX ISA version 1.2.
red.add.f32 and red.shared.add.u64 introduced in PTX ISA 2.0.
64-bit red.{and,or,xor,min,max} introduced in PTX ISA 3.1.
red.add.f64 introduced in PTX ISA 5.0.
.scope qualifier introduced in PTX ISA 5.0.
.sem qualifier introduced in PTX ISA version 6.0.
red.add.noftz.f16x2 introduced in PTX ISA 6.2.
red.add.noftz.f16 introduced in PTX ISA 6.3.
Per-element atomicity of red.f16x2 clarified in PTX ISA version 6.3, with retrospective effect
from PTX ISA version 6.2
Support for .level::cache_hint qualifier introduced in PTX ISA version 7.4.
red.add.noftz.bf16 and red.add.noftz.bf16x2 introduced in PTX ISA 7.8.
Support for .cluster scope qualifier introduced in PTX ISA version 7.8.
Support for ::cta and ::cluster sub-qualifiers introduced in PTX ISA version 7.8.
Support for vector types introduced in PTX ISA version 8.1.
Target ISA Notes
red.global requires sm_11 or higher
red.shared requires sm_12 or higher.
red.global.add.u64 requires sm_12 or higher.
red.shared.add.u64 requires sm_20 or higher.
64-bit red.{and,or,xor,min,max} require sm_32 or higher.
red.add.f32 requires sm_20 or higher.
red.add.f64 requires sm_60 or higher.
.scope qualifier requires sm_60 or higher.
.sem qualifier requires sm_70 or higher.
Use of generic addressing requires sm_20 or higher.
red.add.noftz.f16x2 requires sm_60 or higher.
red.add.ftz.f16 requires sm_70 or higher.
Support for .level::cache_hint qualifier requires sm_80 or higher.
red.add.noftz.bf16 and red.add.noftz.bf16x2 require sm_90 or higher.
Support for .cluster scope qualifier requires sm_90 or higher.
Sub-qualifier ::cta requires sm_30 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for vector types requires sm_90 or higher.
Examples
red.global.add.s32 [a],1;
red.shared::cluster.max.u32 [x+4],0;
@p red.global.and.b32 [p],my_val;
red.global.sys.add.u32 [a], 1;
red.global.acquire.sys.add.u32 [gbl], 1;
red.add.noftz.f16x2 [a], b;
red.add.noftz.bf16 [a], hb;
red.add.noftz.bf16x2 [b], bb;
red.global.cluster.relaxed.add.u32 [a], 1;
red.shared::cta.min.u32 [x+4],0;
createpolicy.fractional.L2::evict_last.b64 cache-policy, 0.25;
red.global.and.L2::cache_hint.b32 [a], 1, cache-policy;
red.global.v8.f16.add.noftz [gbl], {%h0, %h1, %h2, %h3, %h4, %h5, %h6, %h7};
red.global.v8.bf16.min.noftz [gbl], {%h0, %h1, %h2, %h3, %h4, %h5, %h6, %h7};
red.global.v2.f16.add.noftz [gbl], {%h0, %h1};
red.global.v2.bf16.add.noftz [gbl], {%h0, %h1};
red.global.v4.f16x2.max.noftz [gbl], {%h0, %h1, %h2, %h3};
red.global.v4.f32.add [gbl], {%f0, %f1, %f2, %f3};
red.global.v2.f16x2.max.noftz {%bd0, %bd1}, [g], {%b0, %b1};
red.global.v2.bf16x2.add.noftz {%bd0, %bd1}, [g], {%b0, %b1};
red.global.v2.f32.add {%f0, %f1}, [g], {%f0, %f1};
9.7.12.7. Parallel Synchronization and Communication Instructions: red.async
red.async
Asynchronous reduction operation on shared memory.
Syntax
// Increment and Decrement reductions
red.async.relaxed.cluster{.ss}.completion_mechanism.op.type [a], b, [mbar];
.ss = { .shared::cluster };
.op = { .inc, .dec };
.type = { .u32 };
.completion_mechanism = { .mbarrier::complete_tx::bytes };
// MIN and MAX reductions
red.async.relaxed.cluster{.ss}.completion_mechanism.op.type [a], b, [mbar];
.ss = { .shared::cluster };
.op = { .min, .max };
.type = { .u32, .s32 };
.completion_mechanism = { .mbarrier::complete_tx::bytes };
// Bitwise AND, OR and XOR reductions
red.async.relaxed.cluster{.ss}.completion_mechanism.op.type [a], b, [mbar];
.ss = { .shared::cluster };
.op = { .and, .or, .xor };
.type = { .b32 };
.completion_mechanism = { .mbarrier::complete_tx::bytes };
// ADD reductions
red.async.relaxed.cluster{.ss}.completion_mechanism.add.type [a], b, [mbar];
.ss = { .shared::cluster };
.type = { .u32, .s32, .u64 };
.completion_mechanism = { .mbarrier::complete_tx::bytes };
Description
red.async is a non-blocking instruction which initiates an asynchronous reduction operation
specified by .op, with the operand b and the value at destination shared memory location
specified by operand a.
The .inc and .dec operations return a result in the range [0..b].
The modifier .completion_mechanism specifies that upon completion of the asynchronous operation,
complete-tx
operation, with completeCount argument equal to amount of data stored in bytes, will be
performed on the mbarrier object specified by the operand mbar.
Operand a represents destination address and must be a register or of the form register +
immOff as described in Addresses as Operands.
The shared memory addresses of destination operand a and the mbarrier object mbar, must
meet all of the following conditions:
They Belong to the same CTA.
They are different to the CTA of the executing thread but must be within the same cluster.
Otherwise, the behavior is undefined.
The state space of the address {.ss}, if specified, is applicable to both operands a and
mbar. If not specified, then Generic Addressing is used for
both a and mbar.
With .shared::cluster, if the addresses specified do not fall within the address window of
.shared::cluster state space, then the behaviour is undefined.
The reduce operation in red.async is treated as a relaxed memory operation and the complete_tx
operation on the mbarrier has .release semantics at the .cluster scope as described in the
Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 8.1.
Target ISA Notes
Requires sm_90 or higher.
Examples
red.async.relaxed.cluster.shared::cluster.mbarrier::complete_tx::bytes.min.u32 [addr], b, [mbar_addr];
9.7.12.8. Parallel Synchronization and Communication Instructions: vote (deprecated)
vote (deprecated)
Vote across thread group.
Syntax
vote.mode.pred d, {!}a;
vote.ballot.b32 d, {!}a; // 'ballot' form, returns bitmask
.mode = { .all, .any, .uni };
Deprecation Note
The vote instruction without a .sync qualifier is deprecated in PTX ISA version 6.0.
Support for this instruction with
.targetlower thansm_70may be removed in a future PTX ISA version.
Removal Note
Support for vote instruction without a .sync qualifier is removed in PTX ISA version 6.4 for
.targetsm_70 or higher.
Description
Performs a reduction of the source predicate across all active threads in a warp. The destination predicate value is the same across all threads in the warp.
The reduction modes are:
.allTrueif source predicate isTruefor all active threads in warp. Negate the source predicate to compute.none..anyTrueif source predicate isTruefor some active thread in warp. Negate the source predicate to compute.not_all..uniTrueif source predicate has the same value in all active threads in warp. Negating the source predicate also computes.uni.
In the ballot form, vote.ballot.b32 simply copies the predicate from each thread in a warp
into the corresponding bit position of destination register d, where the bit position
corresponds to the thread’s lane id.
An inactive thread in warp will contribute a 0 for its entry when participating in
vote.ballot.b32.
PTX ISA Notes
Introduced in PTX ISA version 1.2.
Deprecated in PTX ISA version 6.0 in favor of vote.sync.
Not supported in PTX ISA version 6.4 for .target sm_70 or higher.
Target ISA Notes
vote requires sm_12 or higher.
vote.ballot.b32 requires sm_20 or higher.
vote is not supported on sm_70 or higher starting PTX ISA version 6.4.
Release Notes
Note that vote applies to threads in a single warp, not across an entire CTA.
Examples
vote.all.pred p,q;
vote.uni.pred p,q;
vote.ballot.b32 r1,p; // get 'ballot' across warp
9.7.12.9. Parallel Synchronization and Communication Instructions: vote.sync
vote.sync
Vote across thread group.
Syntax
vote.sync.mode.pred d, {!}a, membermask;
vote.sync.ballot.b32 d, {!}a, membermask; // 'ballot' form, returns bitmask
.mode = { .all, .any, .uni };
Description
vote.sync will cause executing thread to wait until all non-exited threads corresponding to
membermask have executed vote.sync with the same qualifiers and same membermask value
before resuming execution.
Operand membermask specifies a 32-bit integer which is a mask indicating threads participating
in this instruction where the bit position corresponds to thread’s laneid. Operand a is a
predicate register.
In the mode form, vote.sync performs a reduction of the source predicate across all non-exited
threads in membermask. The destination operand d is a predicate register and its value is
the same across all threads in membermask.
The reduction modes are:
.allTrueif source predicate isTruefor all non-exited threads inmembermask. Negate the source predicate to compute.none..anyTrueif source predicate isTruefor some thread inmembermask. Negate the source predicate to compute.not_all..uniTrueif source predicate has the same value in all non-exited threads inmembermask. Negating the source predicate also computes.uni.
In the ballot form, the destination operand d is a .b32 register. In this form,
vote.sync.ballot.b32 simply copies the predicate from each thread in membermask into the
corresponding bit position of destination register d, where the bit position corresponds to the
thread’s lane id.
A thread not specified in membermask will contribute a 0 for its entry in
vote.sync.ballot.b32.
The behavior of vote.sync is undefined if the executing thread is not in the membermask.
Note
For .target sm_6x or below, all threads in membermask must execute the same vote.sync
instruction in convergence, and only threads belonging to some membermask can be active when
the vote.sync instruction is executed. Otherwise, the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
Requires sm_30 or higher.
Examples
vote.sync.all.pred p,q,0xffffffff;
vote.sync.ballot.b32 r1,p,0xffffffff; // get 'ballot' across warp
9.7.12.10. Parallel Synchronization and Communication Instructions: match.sync
match.sync
Broadcast and compare a value across threads in warp.
Syntax
match.any.sync.type d, a, membermask;
match.all.sync.type d[|p], a, membermask;
.type = { .b32, .b64 };
Description
match.sync will cause executing thread to wait until all non-exited threads from membermask
have executed match.sync with the same qualifiers and same membermask value before resuming
execution.
Operand membermask specifies a 32-bit integer which is a mask indicating threads participating
in this instruction where the bit position corresponds to thread’s laneid.
match.sync performs broadcast and compare of operand a across all non-exited threads in
membermask and sets destination d and optional predicate p based on mode.
Operand a has instruction type and d has .b32 type.
Destination d is a 32-bit mask where bit position in mask corresponds to thread’s laneid.
The matching operation modes are:
.alldis set to mask corresponding to non-exited threads inmembermaskif all non-exited threads inmembermaskhave same value of operanda; otherwisedis set to 0. Optionally predicatepis set to true if all non-exited threads inmembermaskhave same value of operanda; otherwisepis set to false. The sink symbol ‘_’ may be used in place of any one of the destination operands..anydis set to mask of non-exited threads inmembermaskthat have same value of operanda.
The behavior of match.sync is undefined if the executing thread is not in the membermask.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
Target ISA Notes
Requires sm_70 or higher.
Release Notes
Note that match.sync applies to threads in a single warp, not across an entire CTA.
Examples
match.any.sync.b32 d, a, 0xffffffff;
match.all.sync.b64 d|p, a, mask;
9.7.12.11. Parallel Synchronization and Communication Instructions: activemask
activemask
Queries the active threads within a warp.
Syntax
activemask.b32 d;
Description
activemask queries predicated-on active threads from the executing warp and sets the destination
d with 32-bit integer mask where bit position in the mask corresponds to the thread’s
laneid.
Destination d is a 32-bit destination register.
An active thread will contribute 1 for its entry in the result and exited or inactive or predicated-off thread will contribute 0 for its entry in the result.
PTX ISA Notes
Introduced in PTX ISA version 6.2.
Target ISA Notes
Requires sm_30 or higher.
Examples
activemask.b32 %r1;
9.7.12.12. Parallel Synchronization and Communication Instructions: redux.sync
redux.sync
Perform reduction operation on the data from each predicated active thread in the thread group.
Syntax
redux.sync.op.type dst, src, membermask;
.op = {.add, .min, .max}
.type = {.u32, .s32}
redux.sync.op.b32 dst, src, membermask;
.op = {.and, .or, .xor}
Description
redux.sync will cause the executing thread to wait until all non-exited threads corresponding to
membermask have executed redux.sync with the same qualifiers and same membermask value
before resuming execution.
Operand membermask specifies a 32-bit integer which is a mask indicating threads participating
in this instruction where the bit position corresponds to thread’s laneid.
redux.sync performs a reduction operation .op of the 32 bit source register src across
all non-exited threads in the membermask. The result of the reduction operation is written to
the 32 bit destination register dst.
Reduction operation can be one of the bitwise operation in .and, .or, .xor or arithmetic
operation in .add, .min , .max.
For the .add operation result is truncated to 32 bits.
The behavior of redux.sync is undefined if the executing thread is not in the membermask.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Target ISA Notes
Requires sm_80 or higher.
Release Notes
Note that redux.sync applies to threads in a single warp, not across an entire CTA.
Examples
.reg .b32 dst, src, init, mask;
redux.sync.add.s32 dst, src, 0xff;
redux.sync.xor.b32 dst, src, mask;
9.7.12.13. Parallel Synchronization and Communication Instructions: griddepcontrol
griddepcontrol
Control execution of dependent grids.
Syntax
griddepcontrol.action;
.action = { .launch_dependents, .wait }
Description
The griddepcontrol instruction allows the dependent grids and prerequisite grids as defined by
the runtime, to control execution in the following way:
.launch_dependents modifier signals that specific dependents the runtime system designated to
react to this instruction can be scheduled as soon as all other CTAs in the grid issue the same
instruction or have completed. The dependent may launch before the completion of the current
grid. There is no guarantee that the dependent will launch before the completion of the current
grid. Repeated invocations of this instruction by threads in the current CTA will have no additional
side effects past that of the first invocation.
.wait modifier causes the executing thread to wait until all prerequisite grids in flight have
completed and all the memory operations from the prerequisite grids are performed and made visible
to the current grid.
Note
If the prerequisite grid is using griddepcontrol.launch_dependents, then the dependent grid
must use griddepcontrol.wait to ensure correct functional execution.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
griddepcontrol.launch_dependents;
griddepcontrol.wait;
9.7.12.14. Parallel Synchronization and Communication Instructions: elect.sync
elect.sync
Elect a leader thread from a set of threads.
Syntax
elect.sync d|p, membermask;
Description
elect.sync elects one predicated active leader thread from among a set of threads specified by
membermask. laneid of the elected thread is returned in the 32-bit destination operand
d. The sink symbol ‘_’ can be used for destination operand d. The predicate destination
p is set to True for the leader thread, and False for all other threads.
Operand membermask specifies a 32-bit integer indicating the set of threads from which a leader
is to be elected. The behavior is undefined if the executing thread is not in membermask.
Election of a leader thread happens deterministically, i.e. the same leader thread is elected for
the same membermask every time.
The mandatory .sync qualifier indicates that elect causes the executing thread to wait until
all threads in the membermask execute the elect instruction before resuming execution.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
elect.sync %r0|%p0, 0xffffffff;
9.7.12.15. Parallel Synchronization and Communication Instructions: mbarrier
mbarrier is a barrier created in shared memory that supports :
Synchronizing any subset of threads within a CTA
One-way synchronization of threads across CTAs of a cluster. As noted in mbarrier support with shared memory, threads can perform only arrive operations but not *_wait on an mbarrier located in
shared::clusterspace.Waiting for completion of asynchronous memory operations initiated by a thread and making them visible to other threads.
An mbarrier object is an opaque object in memory which can be initialized and invalidated using :
mbarrier.initmbarrier.inval
Operations supported on mbarrier objects are :
mbarrier.expect_txmbarrier.complete_txmbarrier.arrivembarrier.arrive_dropmbarrier.test_waitmbarrier.try_waitmbarrier.pending_countcp.async.mbarrier.arrive
Performing any mbarrier operation except mbarrier.init on an uninitialized mbarrier object
results in undefined behavior.
Unlike bar{.cta}/barrier{.cta} instructions which can access a limited number of barriers
per CTA, mbarrier objects are used defined and are only limited by the total shared memory size
available.
mbarrier operations enable threads to perform useful work after the arrival at the mbarrier and before waiting for the mbarrier to complete.
9.7.12.15.1. Size and alignment of mbarrier object
An mbarrier object is an opaque object with the following type and alignment requirements :
Type |
Alignment (bytes) |
Memory space |
|---|---|---|
|
8 |
|
9.7.12.15.2. Contents of the mbarrier object
An opaque mbarrier object keeps track of the following information :
Current phase of the mbarrier object
Count of pending arrivals for the current phase of the mbarrier object
Count of expected arrivals for the next phase of the mbarrier object
Count of pending asynchronous memory operations (or transactions) tracked by the current phase of the mbarrier object. This is also referred to as tx-count.
An mbarrier object progresses through a sequence of phases where each phase is defined by threads performing an expected number of arrive-on operations.
The valid range of each of the counts is as shown below:
Count name |
Minimum value |
Maximum value |
|---|---|---|
Expected arrival count |
1 |
220 - 1 |
Pending arrival count |
0 |
220 - 1 |
tx-count |
-(220 - 1) |
220 - 1 |
9.7.12.15.3. Lifecycle of the mbarrier object
The mbarrier object must be initialized prior to use.
An mbarrier object is used to synchronize threads and asynchronous memory operations.
An mbarrier object may be used to perform a sequence of such synchronizations.
An mbarrier object must be invalidated to repurpose its memory.
9.7.12.15.4. Phase of the mbarrier object
The phase of an mbarrier object is the number of times the mbarrier object has been used to synchronize threads and cp.async operations. In each phase {0, 1, 2, …}, threads perform in program order :
arrive-on operations to complete the current phase and
test_wait / try_wait operations to check for the completion of the current phase.
An mbarrier object is automatically reinitialized upon completion of the current phase for immediate use in the next phase. The current phase is incomplete and all prior phases are complete.
For each phase of the mbarrier object, at least one test_wait or try_wait operation must be
performed which returns True for waitComplete before an arrive-on operation
in the subsequent phase.
9.7.12.15.5. Tracking asynchronous operations by the mbarrier object
Starting with the Hopper architecture (sm_9x), mbarrier object supports a new count, called
tx-count, which is used for tracking the completion of asynchronous memory operations or
transactions. tx-count tracks the number of asynchronous transactions, in units specified by the
asynchronous memory operation, that are outstanding and yet to be complete.
The tx-count of an mbarrier object must be set to the total amount of asynchronous memory operations, in units as specified by the asynchronous operations, to be tracked by the current phase. Upon completion of each of the asynchronous operations, the complete-tx operation will be performed on the mbarrier object and thus progress the mbarrier towards the completion of the current phase.
9.7.12.15.5.1. expect-tx operation
The expect-tx operation, with an expectCount argument, increases the tx-count of an
mbarrier object by the value specified by expectCount. This makes the current phase of the
mbarrier object to expect and track the completion of additional asynchronous transactions.
9.7.12.15.5.2. complete-tx operation
The complete-tx operation, with an completeCount argument, on an mbarrier object consists of the following:
- mbarrier signaling
Signals the completion of asynchronous transactions that were tracked by the current phase. As a result of this, tx-count is decremented by
completeCount.- mbarrier potentially completing the current phase
If the current phase has been completed then the mbarrier transitions to the next phase. Refer to Phase Completion of the mbarrier object for details on phase completion requirements and phase transition process.
9.7.12.15.6. Phase Completion of the mbarrier object
The requirements for completion of the current phase are described below. Upon completion of the current phase, the phase transitions to the subsequent phase as described below.
- Current phase completion requirements
An mbarrier object completes the current phase when all of the following conditions are met:
The count of the pending arrivals has reached zero.
The tx-count has reached zero.
- Phase transition
When an mbarrier object completes the current phase, the following actions are performed atomically:
The mbarrier object transitions to the next phase.
The pending arrival count is reinitialized to the expected arrival count.
9.7.12.15.7. Arrive-on operation on mbarrier object
An arrive-on operation, with an optional count argument, on an mbarrier object consists of the following 2 steps :
mbarrier signalling:
Signals the arrival of the executing thread OR completion of the
cp.asyncinstruction which signals the arrive-on operation initiated by the executing thread on the mbarrier object. As a result of this, the pending arrival count is decremented by count. If the count argument is not specified, then it defaults to 1.mbarrier potentially completing the current phase:
If the current phase has been completed then the mbarrier transitions to the next phase. Refer to Phase Completion of the mbarrier object for details on phase completion requirements and phase transition process.
9.7.12.15.9. Parallel Synchronization and Communication Instructions: mbarrier.init
mbarrier.init
Initialize the mbarrier object.
Syntax
mbarrier.init{.shared{::cta}}.b64 [addr], count;
Description
mbarrier.init initializes the mbarrier object at the location specified by the address operand
addr with the unsigned 32-bit integer count. The value of operand count must be in the range
as specified in Contents of the mbarrier object.
Initialization of the mbarrier object involves :
Initializing the current phase to 0.
Initializing the expected arrival count to
count.Initializing the pending arrival count to
count.Initializing the tx-count to 0.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_80 or higher.
Examples
.shared .b64 shMem, shMem2;
.reg .b64 addr;
.reg .b32 %r1;
cvta.shared.u64 addr, shMem2;
mbarrier.init.b64 [addr], %r1;
bar.cta.sync 0;
// ... other mbarrier operations on addr
mbarrier.init.shared::cta.b64 [shMem], 12;
bar.sync 0;
// ... other mbarrier operations on shMem
9.7.12.15.10. Parallel Synchronization and Communication Instructions: mbarrier.inval
mbarrier.inval
Invalidates the mbarrier object.
Syntax
mbarrier.inval{.shared{::cta}}.b64 [addr];
Description
mbarrier.inval invalidates the mbarrier object at the location specified by the address
operand addr.
An mbarrier object must be invalidated before using its memory location for any other purpose.
Performing any mbarrier operation except mbarrier.init on an invalidated mbarrier object
results in undefined behaviour.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_80 or higher.
Examples
.shared .b64 shmem;
.reg .b64 addr;
.reg .b32 %r1;
.reg .pred t0;
// Example 1 :
bar.sync 0;
@t0 mbarrier.init.b64 [addr], %r1;
// ... other mbarrier operations on addr
bar.sync 0;
@t0 mbarrier.inval.b64 [addr];
// Example 2 :
bar.cta.sync 0;
mbarrier.init.shared.b64 [shmem], 12;
// ... other mbarrier operations on shmem
bar.cta.sync 0;
@t0 mbarrier.inval.shared.b64 [shmem];
// shmem can be reused here for unrelated use :
bar.cta.sync 0;
st.shared.b64 [shmem], ...;
// shmem can be re-initialized as mbarrier object :
bar.cta.sync 0;
@t0 mbarrier.init.shared.b64 [shmem], 24;
// ... other mbarrier operations on shmem
bar.cta.sync 0;
@t0 mbarrier.inval.shared::cta.b64 [shmem];
9.7.12.15.11. Parallel Synchronization and Communication Instructions: mbarrier.expect_tx
mbarrier.expect_tx
Perfoms expect-tx operation on the mbarrier object.
Syntax
mbarrier.expect_tx{.sem}{.scope}{.space}.b64 [addr], txCount;
.sem = { .relaxed }
.scope = { .cta, .cluster }
.space = { .shared{::cta}, .shared::cluster }
Description
A thread executing mbarrier.expect_tx performs an expect-tx
operation on the mbarrier object at the location specified by the address operand addr. The
32-bit unsigned integer operand txCount specifies the expectCount argument to the
expect-tx operation.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta or .shared::cluster state space then the behavior is undefined.
Supported addressing modes for operand addr are as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
This operation does not provide any memory ordering semantics and thus is a relaxed operation.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
mbarrier.expect_tx.b64 [addr], 32;
mbarrier.expect_tx.relaxed.cta.shared.b64 [mbarObj1], 512;
mbarrier.expect_tx.relaxed.cta.shared.b64 [mbarObj2], 512;
9.7.12.15.12. Parallel Synchronization and Communication Instructions: mbarrier.complete_tx
mbarrier.complete_tx
Perfoms complete-tx operation on the mbarrier object.
Syntax
mbarrier.complete_tx{.sem}{.scope}{.space}.b64 [addr], txCount;
.sem = { .relaxed }
.scope = { .cta, .cluster }
.space = { .shared{::cta}, .shared::cluster }
Description
A thread executing mbarrier.complete_tx performs a complete-tx
operation on the mbarrier object at the location specified by the address operand addr. The
32-bit unsigned integer operand txCount specifies the completeCount argument to the
complete-tx operation.
mbarrier.complete_tx does not involve any asynchronous memory operations and only simulates the
completion of an asynchronous memory operation and its side effect of signaling to the mbarrier
object.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta or .shared::cluster state space then the behavior is undefined.
Supported addressing modes for operand addr are as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
This operation does not provide any memory ordering semantics and thus is a relaxed operation.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90 or higher.
Examples
mbarrier.complete_tx.b64 [addr], 32;
mbarrier.complete_tx.shared.b64 [mbarObj1], 512;
mbarrier.complete_tx.relaxed.cta.b64 [addr2], 32;
9.7.12.15.13. Parallel Synchronization and Communication Instructions: mbarrier.arrive
mbarrier.arrive
Performs arrive-on operation on the mbarrier object.
Syntax
mbarrier.arrive{.sem}{.scope}{.shared{::cta}}.b64 state, [addr]{, count};
mbarrier.arrive{.sem}{.scope}{.shared::cluster}.b64 _, [addr] {,count}
mbarrier.arrive.expect_tx{.sem}{.scope}{.shared{::cta}}.b64 state, [addr], txCount;
mbarrier.arrive.expect_tx{.sem}{.scope}{.shared::cluster}.b64 _, [addr], txCount;
mbarrier.arrive.noComplete{.sem}{.cta}{.shared{::cta}}.b64 state, [addr], count;
.sem = { .release }
.scope = { .cta, .cluster }
Description
A thread executing mbarrier.arrive performs an arrive-on operation
on the mbarrier object at the location specified by the address operand addr. The 32-bit
unsigned integer operand count specifies the count argument to the arrive-on
operation.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
The optional qualifier .expect_tx specifies that an expect-tx
operation is performed prior to the arrive-on
operation. The 32-bit unsigned integer operand txCount specifies the expectCount argument to
the expect-tx operation. When both qualifiers .arrive and .expect_tx are specified, then
the count argument of the arrive-on operation is assumed to be 1.
A mbarrier.arrive operation with .noComplete qualifier must not cause the mbarrier to
complete its current phase, otherwise the behavior is undefined.
The value of the operand count must be in the range as specified in Contents of the mbarrier
object.
Note: for sm_8x, when the argument count is specified, the modifier .noComplete is
required.
mbarrier.arrive operation on an mbarrier object located in .shared::cta returns an opaque
64-bit register capturing the phase of the mbarrier object prior to the arrive-on operation in the
destination operand state. Contents of the state operand are implementation
specific. Optionally, sink symbol '_' can be used for the state argument.
mbarrier.arrive operation on an mbarrier object located in .shared::cluster but not in
.shared::cta cannot return a value. Sink symbol ‘_’ is mandatory for the destination operand for
such cases.
The optional .sem qualifier specifies a memory synchronizing effect as described in the Memory
Consistency Model. If the .sem qualifier is absent,
.release is assumed by default.
The optional .scope qualifier indicates the set of threads that directly observe the memory
synchronizing effect of this operation, as described in the Memory Consistency Model. If the .scope qualifier is not specified then it
defaults to .cta. In contrast, the .shared::<scope> indicates the state space where the
mbarrier resides.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for sink symbol ‘_’ as the destination operand is introduced in PTX ISA version 7.1.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Support for count argument without the modifier .noComplete introduced in PTX ISA version
7.8.
Support for sub-qualifier ::cluster introduced in PTX ISA version 8.0.
Support for qualifier .expect_tx is introduced in PTX ISA version 8.0.
Support for .scope and .sem qualifiers introduced in PTX ISA version 8.0
Target ISA Notes
Requires sm_80 or higher.
Support for count argument without the modifier .noComplete requires sm_90 or higher.
Qualifier .expect_tx requires sm_90 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for .cluster scope requires sm_90 or higher.
Examples
.reg .b32 cnt, remoteAddr32, remoteCTAId, addr32;
.reg .b64 %r<3>, addr, remoteAddr64;
.shared .b64 shMem, shMem2;
cvta.shared.u64 addr, shMem2;
mov.b32 addr32, shMem2;
mapa.shared::cluster.u32 remoteAddr32, addr32, remoteCTAId;
mapa.u64 remoteAddr64, addr, remoteCTAId;
cvta.shared.u64 addr, shMem2;
mbarrier.arrive.shared.b64 %r0, [shMem];
mbarrier.arrive.shared::cta.b64 %r0, [shMem2];
mbarrier.arrive.release.cta.shared::cluster.b64 _, [remoteAddr32];
mbarrier.arrive.release.cluster.b64 _, [remoteAddr64], cnt;
mbarrier.arrive.expect_tx.release.cluster.b64 _, [remoteAddr64], tx_count;
mbarrier.arrive.noComplete.b64 %r1, [addr], 2;
mbarrier.arrive.b64 %r2, [addr], cnt;
9.7.12.15.14. Parallel Synchronization and Communication Instructions: mbarrier.arrive_drop
mbarrier.arrive_drop
Decrements the expected count of the mbarrier object and performs arrive-on operation.
Syntax
mbarrier.arrive_drop{.sem}{.scope}{.shared{::cta}}.b64 state, [addr]{, count};
mbarrier.arrive_drop{.sem}{.scope}{.shared::cluster}.b64 _, [addr] {,count};
mbarrier.arrive_drop.expect_tx{.shared{::cta}}{.sem}{.scope}.b64 state, [addr], tx_count;
mbarrier.arrive_drop.expect_tx{.shared::cluster}{.sem}{.scope}.b64 _, [addr], tx_count;
mbarrier.arrive_drop.noComplete{.sem}{.cta}{.shared{::cta}}.b64 state, [addr], count;
.sem = { .release }
.scope = { .cta, .cluster }
Description
A thread executing mbarrier.arrive_drop on the mbarrier object at the location specified by
the address operand addr performs the following steps:
Decrements the expected arrival count of the mbarrier object by the value specified by the 32-bit integer operand
count. Ifcountoperand is not specified, it defaults to 1.Performs an arrive-on operation on the mbarrier object. The operand
countspecifies the count argument to the arrive-on operation.
The decrement done in the expected arrivals count of the mbarrier object will be for all the subsequent phases of the mbarrier object.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta or .shared::cluster state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
The optional qualifier .expect_tx specifies that an expect-tx
operation is performed prior to the arrive-on
operation. The 32-bit unsigned integer operand txCount specifies the expectCount argument to
the expect-tx operation. When both qualifiers .arrive and .expect_tx are specified, then
the count argument of the arrive-on operation is assumed to be 1.
mbarrier.arrive_drop operation forms the release pattern as described in the Memory
Consistency Model and synchronizes with the acquire patterns.
The optional .scope qualifier indicates the set of threads that an mbarrier.arrive_drop
instruction can directly synchronize. If the .scope qualifier is not specified then it defaults
to .cta. In contrast, the .shared::<scope> indicates the state space where the mbarrier
resides.
A mbarrier.arrive_drop with .noComplete qualifier must not complete the mbarrier,
otherwise the behavior is undefined.
The value of the operand count must be in the range as specified in Contents of the mbarrier
object.
Note: for sm_8x, when the argument count is specified, the modifier .noComplete is
required.
A thread that wants to either exit or opt out of participating in the arrive-on operation can use
mbarrier.arrive_drop to drop itself from the mbarrier.
mbarrier.arrive_drop operation on an mbarrier object located in .shared::cta returns an
opaque 64-bit register capturing the phase of the mbarrier object prior to the arrive-on
operation
in the destination operand state. Contents of the returned state are implementation
specific. Optionally, sink symbol '_' can be used for the state argument.
mbarrier.arrive_drop operation on an mbarrier object located in .shared::cluster but not
in .shared::cta cannot return a value. Sink symbol ‘_’ is mandatory for the destination operand
for such cases.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Support for count argument without the modifier .noComplete introduced in PTX ISA version
7.8.
Support for qualifier .expect_tx is introduced in PTX ISA version 8.0.
Support for sub-qualifier ::cluster introduced in PTX ISA version 8.0.
Support for .scope and .sem qualifiers introduced in PTX ISA version 8.0
Target ISA Notes
Requires sm_80 or higher.
Support for count argument without the modifier .noComplete requires sm_90 or higher.
Qualifier .expect_tx requires sm_90 or higher.
Sub-qualifier ::cluster requires sm_90 or higher.
Support for .cluster scope requires sm_90 or higher.
Examples
.reg .b32 cnt;
.reg .b64 %r1;
.shared .b64 shMem;
// Example 1
@p mbarrier.arrive_drop.shared.b64 _, [shMem];
@p exit;
@p2 mbarrier.arrive_drop.noComplete.shared.b64 _, [shMem], %a;
@p2 exit;
..
@!p mbarrier.arrive.shared.b64 %r1, [shMem];
@!p mbarrier.test_wait.shared.b64 q, [shMem], %r1;
// Example 2
mbarrier.arrive_drop.shared::cluster.b64 _, [addr];
mbarrier.arrive_drop.shared::cta.release.cluster.b64 _, [addr], cnt;
// Example 3
mbarrier.arrive_drop.expect_tx.shared::cta.release.cta.b64 state, [addr], tx_count;
9.7.12.15.15. Parallel Synchronization and Communication Instructions: cp.async.mbarrier.arrive
cp.async.mbarrier.arrive
Makes the mbarrier object track all prior cp.async operations initiated by the executing thread.
Syntax
cp.async.mbarrier.arrive{.noinc}{.shared{::cta}}.b64 [addr];
Description
Causes an arrive-on operation to be
triggered by the system on the mbarrier object upon the completion of all prior cp.async operations initiated by the
executing thread. The mbarrier object is at the location specified by the operand addr. The
arrive-on operation is
asynchronous to execution of cp.async.mbarrier.arrive.
When .noinc modifier is not specified, the pending count of the mbarrier object is incremented
by 1 prior to the asynchronous arrive-on operation. This
results in a zero-net change for the pending count from the asynchronous arrive-on operation
during the current phase. The pending count of the mbarrier object after the increment should not
exceed the limit as mentioned in Contents of the mbarrier object. Otherwise,
the behavior is undefined.
When the .noinc modifier is specified, the increment to the pending count of the mbarrier
object is not performed. Hence the decrement of the pending count done by the asynchronous
arrive-on operation must be
accounted for in the initialization of the mbarrier object.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_80 or higher.
Examples
// Example 1: no .noinc
mbarrier.init.shared.b64 [shMem], threadCount;
....
cp.async.ca.shared.global [shard1], [gbl1], 4;
cp.async.cg.shared.global [shard2], [gbl2], 16;
....
// Absence of .noinc accounts for arrive-on from completion of prior cp.async operations.
// So mbarrier.init must only account for arrive-on from mbarrier.arrive.
cp.async.mbarrier.arrive.shared.b64 [shMem];
....
mbarrier.arrive.shared.b64 state, [shMem];
waitLoop:
mbarrier.test_wait.shared.b64 p, [shMem], state;
@!p bra waitLoop;
// Example 2: with .noinc
// Tracks arrive-on from mbarrier.arrive and cp.async.mbarrier.arrive.
// All threads participating in the mbarrier perform cp.async
mov.b32 copyOperationCnt, threadCount;
// 3 arrive-on operations will be triggered per-thread
mul.lo.u32 copyArrivalCnt, copyOperationCnt, 3;
add.u32 totalCount, threadCount, copyArrivalCnt;
mbarrier.init.shared.b64 [shMem], totalCount;
....
cp.async.ca.shared.global [shard1], [gbl1], 4;
cp.async.cg.shared.global [shard2], [gbl2], 16;
...
// Presence of .noinc requires mbarrier initalization to have accounted for arrive-on from cp.async
cp.async.mbarrier.arrive.noinc.shared.b64 [shMem]; // 1st instance
....
cp.async.ca.shared.global [shard3], [gbl3], 4;
cp.async.ca.shared.global [shard4], [gbl4], 16;
cp.async.mbarrier.arrive.noinc.shared::cta.b64 [shMem]; // 2nd instance
....
cp.async.ca.shared.global [shard5], [gbl5], 4;
cp.async.cg.shared.global [shard6], [gbl6], 16;
cp.async.mbarrier.arrive.noinc.shared.b64 [shMem]; // 3rd and last instance
....
mbarrier.arrive.shared.b64 state, [shMem];
waitLoop:
mbarrier.test_wait.shared.b64 p, [shMem], state;
@!p bra waitLoop;
9.7.12.15.16. Parallel Synchronization and Communication Instructions: mbarrier.test_wait/mbarrier.try_wait
mbarrier.test_wait/mbarrier.try_wait
Checks whether the mbarrier object has completed the phase.
Syntax
mbarrier.test_wait{.sem}{.scope}{.shared{::cta}}.b64 waitComplete, [addr], state;
mbarrier.test_wait.parity{.sem}{.scope}{.shared{::cta}}.b64 waitComplete, [addr], phaseParity;
mbarrier.try_wait{.sem}{.scope}{.shared{::cta}}.b64 waitComplete, [addr], state
{, suspendTimeHint};
mbarrier.try_wait.parity{.sem}{.scope}{.shared{::cta}}.b64 waitComplete, [addr], phaseParity
{, suspendTimeHint};
.sem = { .acquire }
.scope = { .cta, .cluster }
Description
The test_wait and try_wait operations test for the completion of the current or the immediately
preceding phase of an mbarrier object at the location specified by the operand addr.
mbarrier.test_wait is a non-blocking instruction which tests for the completion of the phase.
mbarrier.try_wait is a potentially blocking instruction which tests for the completion of the
phase. If the phase is not complete, the executing thread may be suspended. Suspended thread resumes
execution when the specified phase completes OR before the phase completes following a
system-dependent time limit. The optional 32-bit unsigned integer operand suspendTimeHint
specifies the time limit, in nanoseconds, that may be used for the time limit instead of the
system-dependent limit.
mbarrier.test_wait and mbarrier.try_wait test for completion of the phase :
Specified by the operand
state, which was returned by anmbarrier.arriveinstruction on the same mbarrier object during the current or the immediately preceding phase. OrIndicated by the operand
phaseParity, which is the integer parity of either the current phase or the immediately preceding phase of the mbarrier object.
The .parity variant of the instructions test for the completion of the phase indicated by the
operand phaseParity, which is the integer parity of either the current phase or the immediately
preceding phase of the mbarrier object. An even phase has integer parity 0 and an odd phase has
integer parity of 1. So the valid values of phaseParity operand are 0 and 1.
Note: the use of the .parity variants of the instructions requires tracking the phase of an
mbarrier object throughout its lifetime.
The test_wait and try_wait operations are valid only for :
the current incomplete phase, for which
waitCompletereturnsFalse.the immediately preceding phase, for which
waitCompletereturnsTrue.
If no state space is specified then Generic Addressing is
used. If the address specified by addr does not fall within the address window of
.shared::cta state space then the behavior is undefined.
Supported addressing modes for operand addr is as described in Addresses as Operands. Alignment for operand addr is as described in the Size
and alignment of mbarrier object.
When mbarrier.test_wait and mbarrier.try_wait operations return True, they form the
acquire pattern as described in the Memory Consistency Model.
The optional .scope qualifier indicates the set of threads that the mbarrier.test_wait and
mbarrier.try_wait instructions can directly synchronize. If the .scope qualifier is not
specified then it defaults to .cta. In contrast, the .shared::<scope> indicates the state
space where the mbarrier resides.
The following ordering of memory operations hold for the executing thread when
mbarrier.test_wait or mbarrier.try_wait returns True :
All memory accesses (except async operations ) requested prior, in program order, to
mbarrier.arriveduring the completed phase by the participating threads of the CTA are performed and are visible to the executing thread.All cp.async operations requested prior, in program order, to
cp.async.mbarrier.arriveduring the completed phase by the participating threads of the CTA are performed and made visible to the executing thread.All
cp.async.bulkasynchronous operations using the same mbarrier object requested prior, in program order, tombarrier.arriveduring the completed phase by the participating threads of the CTA are performed and made visible to the executing thread.All memory accesses requested after the
mbarrier.test_waitormbarrier.try_wait, in program order, are not performed and not visible to memory accesses performed prior tombarrier.arrive, in program order, by other threads participating in thembarrier.There is no ordering and visibility guarantee for memory accesses requested by the thread after
mbarrier.arriveand prior tombarrier.test_wait, in program order.
PTX ISA Notes
mbarrier.test_wait introduced in PTX ISA version 7.0.
Modifier .parity is introduced in PTX ISA version 7.1.
mbarrier.try_wait introduced in PTX ISA version 7.8.
Support for sub-qualifier ::cta on .shared introduced in PTX ISA version 7.8.
Support for .scope and .sem qualifiers introduced in PTX ISA version 8.0
Target ISA Notes
mbarrier.test_wait requires sm_80 or higher.
mbarrier.try_wait requires sm_90 or higher.
Support for .cluster scope requires sm_90 or higher.
Examples
// Example 1a, thread synchronization with test_wait:
.reg .b64 %r1;
.shared .b64 shMem;
mbarrier.init.shared.b64 [shMem], N; // N threads participating in the mbarrier.
...
mbarrier.arrive.shared.b64 %r1, [shMem]; // N threads executing mbarrier.arrive
// computation not requiring mbarrier synchronization...
waitLoop:
mbarrier.test_wait.shared.b64 complete, [shMem], %r1;
@!complete nanosleep.u32 20;
@!complete bra waitLoop;
// Example 1b, thread synchronization with try_wait :
.reg .b64 %r1;
.shared .b64 shMem;
mbarrier.init.shared.b64 [shMem], N; // N threads participating in the mbarrier.
...
mbarrier.arrive.shared.b64 %r1, [shMem]; // N threads executing mbarrier.arrive
// computation not requiring mbarrier synchronization...
waitLoop:
mbarrier.try_wait.shared.b64 complete, [shMem], %r1;
@!complete bra waitLoop;
// Example 2, thread synchronization using phase parity :
.reg .b32 i, parArg;
.reg .b64 %r1;
.shared .b64 shMem;
mov.b32 i, 0;
mbarrier.init.shared.b64 [shMem], N; // N threads participating in the mbarrier.
...
loopStart : // One phase per loop iteration
...
mbarrier.arrive.shared.b64 %r1, [shMem]; // N threads
...
and.b32 parArg, i, 1;
waitLoop:
mbarrier.test_wait.parity.shared.b64 complete, [shMem], parArg;
@!complete nanosleep.u32 20;
@!complete bra waitLoop;
...
add.u32 i, i, 1;
setp.lt.u32 p, i, IterMax;
@p bra loopStart;
// Example 3, Asynchronous copy completion waiting :
.reg .b64 state;
.shared .b64 shMem2;
.shared .b64 shard1, shard2;
.global .b64 gbl1, gbl2;
mbarrier.init.shared.b64 [shMem2], threadCount;
...
cp.async.ca.shared.global [shard1], [gbl1], 4;
cp.async.cg.shared.global [shard2], [gbl2], 16;
// Absence of .noinc accounts for arrive-on from prior cp.async operation
cp.async.mbarrier.arrive.shared.b64 [shMem2];
...
mbarrier.arrive.shared.b64 state, [shMem2];
waitLoop:
mbarrier.test_wait.shared::cta.b64 p, [shMem2], state;
@!p bra waitLoop;
// Example 4, Synchronizing the CTA0 threads with cluster threads
.reg .b64 %r1, addr, remAddr;
.shared .b64 shMem;
cvta.shared.u64 addr, shMem;
mapa.u64 remAddr, addr, 0; // CTA0’s shMem instance
// One thread from CTA0 executing the below initialization operation
@p0 mbarrier.init.shared::cta.b64 [shMem], N; // N = no of cluster threads
barrier.cluster.arrive;
barrier.cluster.wait;
// Entire cluster executing the below arrive operation
mbarrier.arrive.release.cluster.b64 _, [remAddr];
// computation not requiring mbarrier synchronization ...
// Only CTA0 threads executing the below wait operation
waitLoop:
mbarrier.try_wait.parity.acquire.cluser.shared::cta.b64 complete, [shMem], 0;
@!complete bra waitLoop;
9.7.12.15.17. Parallel Synchronization and Communication Instructions: mbarrier.pending_count
mbarrier.pending_count
Query the pending arrival count from the opaque mbarrier state.
Syntax
mbarrier.pending_count.b64 count, state;
Description
The pending count can be queried from the opaque mbarrier state using mbarrier.pending_count.
The state operand is a 64-bit register that must be the result of a prior
mbarrier.arrive.noComplete or mbarrier.arrive_drop.noComplete instruction. Otherwise, the
behavior is undefined.
The destination register count is a 32-bit unsigned integer representing the pending count of
the mbarrier object prior to the arrive-on operation from
which the state register was obtained.
PTX ISA Notes
Introduced in PTX ISA version 7.0.
Target ISA Notes
Requires sm_80 or higher.
Examples
.reg .b32 %r1;
.reg .b64 state;
.shared .b64 shMem;
mbarrier.arrive.noComplete.b64 state, [shMem], 1;
mbarrier.pending_count.b64 %r1, state;
9.7.12.15.18. Parallel Synchronization and Communication Instructions: tensormap.cp_fenceproxy
tensormap.cp_fenceproxy
A fused copy and fence operation.
Syntax
tensormap.cp_fenceproxy.cp_qualifiers.fence_qualifiers.sync.aligned [dst], [src], size;
.cp_qualifiers = { .global.shared::cta }
.fence_qualifiers = { .to_proxy::from_proxy.release.scope }
.to_proxy::from_proxy = { .tensormap::generic }
.scope = { .cta, .cluster, .gpu , .sys }
Description
The tensormap.cp_fence instructions perform the following operations in order :
Copies data of size specified by the
sizeargument, in bytes, from the location specified by the address operandsrcin shared memory to the location specified by the address operanddstin the global memory, in the generic proxy.Establishes a uni-directional proxy release pattern on the ordering from the copy operation to the subsequent access performed in the tensormap proxy on the address
dst.
The valid value of size operand is 128.
The operands src and dst specify non-generic addresses in shared::cta and global
state space respectively.
The optional .scope qualifier specifies the set of threads that can directly observe the proxy
synchronizing effect of this operation, as described in Memory Consistency Model.
The mandatory .sync qualifier indicates that tensormap.cp_fenceproxy causes the executing
thread to wait until all threads in the warp execute the same tensormap.cp_fenceproxy
instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
tensormap.cp_fenceproxy instruction. In conditionally executed code, an aligned tensormap.cp_fenceproxy
instruction should only be used if it is known that all threads in the warp evaluate the condition
identically, otherwise behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.3.
Target ISA Notes
Requires sm_90 or higher.
Examples
// Example: manipulate a tensor-map object and then consume it in cp.async.bulk.tensor
.reg .b64 new_addr;
.global .align 128 .b8 gbl[128];
.shared .align 128 .b8 sMem[128];
cp.async.bulk.shared::cluster.global.mbarrier::complete_tx::bytes [sMem], [gMem], 128, [mbar];
...
try_wait_loop:
mbarrier.try_wait.shared.b64 p, [mbar], state;
@!p bra try_wait loop;
tensormap.replace.tile.global_address.shared.b1024.b64 [sMem], new_addr;
tensormap.cp_fenceproxy.global.shared::cta.proxy.tensormap::generic.release.gpu
.sync.aligned [gbl], [sMem], 128;
fence.proxy.tensormap::generic.acquire.gpu [gbl], 128;
cp.async.bulk.tensor.1d.shared::cluster.global.tile [addr0], [gbl, {tc0}], [mbar0];
9.7.13. Warp Level Matrix Multiply-Accumulate Instructions
The matrix multiply and accumulate operation has the following form:
D = A * B + C
where D and C are called accumulators and may refer to the same matrix.
PTX provides two ways to perform matrix multiply-and-accumulate computation:
Using
wmmainstructions:This warp-level computation is performed collectively by all threads in the warp as follows:
Load matrices A, B and C from memory into registers using the
wmma.loadoperation. When the operation completes, the destination registers in each thread hold a fragment of the loaded matrix.Perform the matrix multiply and accumulate operation using the
wmma.mmaoperation on the loaded matrices. When the operation completes, the destination registers in each thread hold a fragment of the result matrix returned by thewmma.mmaoperation.Store result Matrix D back to memory using the
wmma.storeoperation. Alternately, result matrix D can also be used as argument C for a subsequentwmma.mmaoperation.
The
wmma.loadandwmma.storeinstructions implicitly handle the organization of matrix elements when loading the input matrices from memory for thewmma.mmaoperation and when storing the result back to memory.
Using
mmainstruction:Similar to
wmma,mmaalso requires computation to be performed collectively by all threads in the warp however distribution of matrix elements across different threads in warp needs to be done explicitly before invoking themmaoperation. Themmainstruction supports both dense as well as sparse matrix A. The sparse variant can be used when A is a structured sparse matrix as described in Sparse matrix storage.
9.7.13.1. Matrix Shape
The matrix multiply and accumulate operations support a limited set of shapes for the operand
matrices A, B and C. The shapes of all three matrix operands are collectively described by the tuple
MxNxK, where A is an MxK matrix, B is a KxN matrix, while C and D are MxN matrices.
The following matrix shapes are supported for the specified types:
Instruction |
Sparsity |
Multiplicand Data-type |
Shape |
PTX ISA version |
|---|---|---|---|---|
|
Dense |
Floating-point - |
|
PTX ISA version 6.0 |
|
Dense |
Alternate floating-point format - |
|
PTX ISA version 7.0 |
|
Dense |
Alternate floating-point format - |
|
PTX ISA version 7.0 |
|
Dense |
Integer - |
|
PTX ISA version 6.3 |
|
Dense |
Sub-byte integer - |
|
PTX ISA version 6.3 (preview feature) |
|
Dense |
Single-bit - |
|
PTX ISA version 6.3 (preview feature) |
|
Dense |
Floating-point - |
|
PTX ISA version 7.0 |
|
PTX ISA version 7.8 |
|||
|
Dense |
Floating-point - |
|
PTX ISA version 6.4 |
|
PTX ISA version 6.5 |
|||
|
PTX ISA version 7.0 |
|||
|
Dense |
Alternate floating-point format - |
|
PTX ISA version 7.0 |
|
Dense |
Alternate floating-point format - |
|
PTX ISA version 7.0 |
|
Dense |
Integer - |
|
PTX ISA version 6.5 |
|
PTX ISA version 7.0 |
|||
|
Dense |
Sub-byte integer - |
|
PTX ISA version 6.5 |
|
PTX ISA version 7.0 |
|||
|
Dense |
Single-bit - |
|
PTX ISA version 7.0 |
|
Dense |
Alternate floating-point format - |
|
PTX ISA version 8.4 |
|
Sparse |
Floating-point - |
|
PTX ISA version 7.1 |
|
Sparse |
Alternate floating-point format - |
|
PTX ISA version 7.1 |
|
Sparse |
Alternate floating-point format - |
|
PTX ISA version 7.1 |
|
Sparse |
Integer - |
|
PTX ISA version 7.1 |
|
Sparse |
Sub-byte integer - |
|
PTX ISA version 7.1 |
|
Sparse |
Alternate floating-point format - |
|
PTX ISA version 8.4 |
9.7.13.2. Matrix Data-types
The matrix multiply and accumulate operation is supported separately on integer, floating-point, sub-byte integer and single bit data-types. All operands must contain the same basic type kind, i.e., integer or floating-point.
For floating-point matrix multiply and accumulate operation, different matrix operands may have different precision, as described later.
Data-type |
Multiplicands (A or B) |
Accumulators (C or D) |
|---|---|---|
Integer |
|
|
Floating Point |
|
|
Alternate floating Point |
|
|
Alternate floating Point |
|
|
Alternate floating Point |
|
|
Floating Point |
|
|
Sub-byte integer |
both |
|
Single-bit integer |
|
|
9.7.13.3. Matrix multiply-accumulate operation using wmma instructions
This section describes warp level wmma.load, wmma.mma and wmma.store instructions and the
organization of various matrices invovled in these instruction.
9.7.13.3.1. Matrix Fragments for WMMA
Each thread in the warp holds a fragment of the matrix. The distribution of fragments loaded by the
threads in a warp is unspecified and is target architecture dependent, and hence the identity of the
fragment within the matrix is also unspecified and is target architecture dependent. The fragment
returned by a wmma operation can be used as an operand for another wmma operation if the
shape, layout and element type of the underlying matrix matches. Since fragment layout is
architecture dependent, using the fragment returned by a wmma operation in one function as an
operand for a wmma operation in a different function may not work as expected if the two
functions are linked together but were compiled for different link-compatible SM architectures. Note
passing wmma fragment to a function having .weak linkage is unsafe since at link time
references to such function may get resolved to a function in different compilation module.
Each fragment is a vector expression whose contents are determined as follows. The identity of individual matrix elements in the fragment is unspecified.
- Integer fragments
Multiplicands (A or B):
Data-type
Shape
Matrix
Fragment
.u8or.s8.m16n16k16A
A vector expression of two
.b32registers, with each register containing four elements from the matrix.B
A vector expression of two
.b32registers, with each register containing four elements from the matrix..m8n32k16A
A vector expression containing a single
.b32register containing four elements from the matrix.B
A vector expression of four
.b32registers, with each register containing four elements from the matrix..m32n8k16A
A vector expression of four
.b32registers, with each register containing four elements from the matrix.B
A vector expression containing single
.b32register, with each containing four elements from the matrix.Accumulators (C or D):
Data-type
Shape
Fragment
.s32.m16n16k16A vector expression of eight
.s32registers..m8n32k16.m32n8k16
Floating point fragments
Data-type
Matrix
Fragment
.f16A or B
A vector expression of eight
.f16x2registers.
.f16C or D
A vector expression of four
.f16x2registers.
.f32A vector expression of eight
.f32registers.
Floating point fragments for .bf16 data format
Multiplicands (A or B):
Data-type
Shape
Matrix
Fragment
.bf16
.m16n16k16A
A vector expression of four
.b32registers, with each register containing two elements from the matrix.B
.m8n32k16A
A vector expression containing a two
.b32registers, with containing two elements from the matrix.B
A vector expression of eight
.b32registers, with each register containing two elements from the matrix.
.m32n8k16A
A vector expression of eight
.b32registers, with each register containing two elements from the matrix.B
A vector expression containing two
.b32registers, with each containing two elements from the matrix.Accumulators (C or D):
Data-type
Matrix
Fragment
.f32C or D
A vector expression containing eight
.f32registers.
Floating point fragments for .tf32 data format
Multiplicands (A or B):
Data-type
Shape
Matrix
Fragment
.tf32
.m16n16k8A
A vector expression of four
.b32registers.B
A vector expression of four
.b32registers.Accumulators (C or D):
Data-type
Shape
Matrix
Fragment
.f32
.m16n16k8C or D
A vector expression containing eight
.f32registers.
Double precision floating point fragments
Multiplicands (A or B):
Data-type
Shape
Matrix
Fragment
.f64
.m8n8k4A or B
A vector expression of single
.f64register.Accumulators (C or D):
Data-type
Shape
Matrix
Fragment
.f64
.m8n8k4C or D
A vector expression containing single
.f64register.
Sub-byte integer and single-bit fragments
Multiplicands (A or B):
Data-type
Shape
Fragment
.u4or.s4
.m8n8k32A vector expression containing a single
.b32register, containing eight elements from the matrix.
.b1
.m8n8k128A vector expression containing a single
.b32register, containing 32 elements from the matrix.Accumulators (C or D):
Data-type
Shape
Fragment
.s32
.m8n8k32A vector expression of two
.s32registers.
.m8n8k128A vector expression of two
.s32registers.
Manipulating fragment contents
The contents of a matrix fragment can be manipulated by reading and writing to individual registers in the fragment, provided the following conditions are satisfied:
All matrix element in the fragment are operated on uniformly across threads, using the same parameters.
The order of the matrix elements is not changed.
For example, if each register corresponding to a given matrix is multiplied by a uniform constant value, then the resulting matrix is simply the scaled version of the original matrix.
Note that type conversion between
.f16and.f32accumulator fragments is not supported in either direction. The result is undefined even if the order of elements in the fragment remains unchanged.
9.7.13.3.2. Matrix Storage for WMMA
Each matrix can be stored in memory with a row-major or column-major layout. In a row-major format, consecutive elements of each row are stored in contiguous memory locations, and the row is called the leading dimension of the matrix. In a column-major format, consecutive elements of each column are stored in contiguous memory locations and the column is called the leading dimension of the matrix.
Consecutive instances of the leading dimension (rows or columns) need not be stored contiguously
in memory. The wmma.load and wmma.store operations accept an optional argument stride
that specifies the offset from the beginning of each row (or column) to the next, in terms of matrix
elements (and not bytes). For example, the matrix being accessed by a wmma operation may be a
submatrix from a larger matrix stored in memory. This allows the programmer to compose a
multiply-and-accumulate operation on matrices that are larger than the shapes supported by the
wmma operation.
Address Alignment:
The starting address of each instance of the leading dimension (row or column) must be aligned with the size of the corresponding fragment in bytes. Note that the starting address is determined by the base pointer and the optional
stride.
Consider the following instruction as an example:
wmma.load.a.sync.aligned.row.m16n16k16.f16 {x0,...,x7}, [p], s;
Fragment size in bytes = 32 (eight elements of type
.f16x2)Actual
stridein bytes = 2 *s(sincestrideis specified in terms of.f16elements, not bytes)For each row of this matrix to be aligned at fragment size the following must be true:
pis a multiple of 32.2*sis a multiple of 32.
Default value for stride:
The default value of the
strideis the size of the leading dimension of the matrix. For example, for anMxKmatrix, thestrideisKfor a row-major layout andMfor a column-major layout. In particular, the default strides for the supported matrix shapes are as follows:
Shape
A (row)
A (column)
B (row)
B (column)
Accumulator (row)
Accumulator (column)
16x16x16
16
16
16
16
16
16
8x32x16
16
8
32
16
32
8
32x8x16
16
32
8
16
8
32
8x8x32
32
8
8
32
8
8
8x8x128
128
8
8
128
8
8
16x16x8
8
16
16
8
16
16
8x8x4
4
8
8
4
8
8
9.7.13.3.3. Warp-level Matrix Load Instruction: wmma.load
wmma.load
Collectively load a matrix from memory for WMMA
Syntax
Floating point format .f16 loads:
wmma.load.a.sync.aligned.layout.shape{.ss}.atype r, [p] {, stride};
wmma.load.b.sync.aligned.layout.shape{.ss}.btype r, [p] {, stride};
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride};
.layout = {.row, .col};
.shape = {.m16n16k16, .m8n32k16, .m32n8k16};
.ss = {.global, .shared{::cta}};
.atype = {.f16, .s8, .u8};
.btype = {.f16, .s8, .u8};
.ctype = {.f16, .f32, .s32};
Alternate floating point format .bf16 loads:
wmma.load.a.sync.aligned.layout.shape{.ss}.atype r, [p] {, stride}
wmma.load.b.sync.aligned.layout.shape{.ss}.btype r, [p] {, stride}
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride}
.layout = {.row, .col};
.shape = {.m16n16k16, .m8n32k16, .m32n8k16};
.ss = {.global, .shared{::cta}};
.atype = {.bf16 };
.btype = {.bf16 };
.ctype = {.f32 };
Alternate floating point format .tf32 loads:
wmma.load.a.sync.aligned.layout.shape{.ss}.atype r, [p] {, stride}
wmma.load.b.sync.aligned.layout.shape{.ss}.btype r, [p] {, stride}
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride}
.layout = {.row, .col};
.shape = {.m16n16k8 };
.ss = {.global, .shared{::cta}};
.atype = {.tf32 };
.btype = {.tf32 };
.ctype = {.f32 };
Double precision Floating point .f64 loads:
wmma.load.a.sync.aligned.layout.shape{.ss}.atype r, [p] {, stride}
wmma.load.b.sync.aligned.layout.shape{.ss}.btype r, [p] {, stride}
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride}
.layout = {.row, .col};
.shape = {.m8n8k4 };
.ss = {.global, .shared{::cta}};
.atype = {.f64 };
.btype = {.f64 };
.ctype = {.f64 };
Sub-byte loads:
wmma.load.a.sync.aligned.row.shape{.ss}.atype r, [p] {, stride}
wmma.load.b.sync.aligned.col.shape{.ss}.btype r, [p] {, stride}
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride}
.layout = {.row, .col};
.shape = {.m8n8k32};
.ss = {.global, .shared{::cta}};
.atype = {.s4, .u4};
.btype = {.s4, .u4};
.ctype = {.s32};
Single-bit loads:
wmma.load.a.sync.aligned.row.shape{.ss}.atype r, [p] {, stride}
wmma.load.b.sync.aligned.col.shape{.ss}.btype r, [p] {, stride}
wmma.load.c.sync.aligned.layout.shape{.ss}.ctype r, [p] {, stride}
.layout = {.row, .col};
.shape = {.m8n8k128};
.ss = {.global, .shared{::cta}};
.atype = {.b1};
.btype = {.b1};
.ctype = {.s32};
Description
Collectively load a matrix across all threads in a warp from the location indicated by address
operand p in the specified state space into destination register r.
If no state space is given, perform the memory accesses using Generic Addressing. wmma.load operation may be used only with .global and
.shared spaces and with generic addressing, where the address points to .global or
.shared space.
The mutually exclusive qualifiers .a, .b and .c indicate whether matrix A, B or C is
being loaded respectively for the wmma computation.
The destination operand r is a brace-enclosed vector expression that can hold the fragment
returned by the load operation, as described in Matrix Fragments for WMMA.
The .shape qualifier indicates the dimensions of all the matrix arguments involved in the
intended wmma computation.
The .layout qualifier indicates whether the matrix to be loaded is stored in row-major or
column-major format.
stride is an optional 32-bit integer operand that provides an offset in terms of matrix elements
between the start of consecutive instances of the leading dimension (rows or columns). The default
value of stride is described in Matrix Storage for WMMA and must be specified if the actual value is larger than
the default. For example, if the matrix is a sub-matrix of a larger matrix, then the value of stride
is the leading dimension of the larger matrix. Specifying a value lower than the default value
results in undefined behavior.
The required alignment for address p and stride is described in the Matrix Storage for WMMA.
The mandatory .sync qualifier indicates that wmma.load causes the executing thread to wait
until all threads in the warp execute the same wmma.load instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
wmma.load instruction. In conditionally executed code, a wmma.load instruction should only
be used if it is known that all threads in the warp evaluate the condition identically, otherwise
behavior is undefined.
The behavior of wmma.load is undefined if all threads do not use the same qualifiers and the
same values of p and stride, or if any thread in the warp has exited.
wmma.load is treated as a weak memory operation in the Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
.m8n32k16 and .m32n8k16 introduced in PTX ISA version 6.1.
Integer, sub-byte integer and single-bit wmma introduced in PTX ISA version 6.3.
.m8n8k4 and .m16n16k8 on wmma introduced in PTX ISA version 7.0.
Double precision and alternate floating point precision wmma introduced in PTX ISA version 7.0.
Modifier .aligned is required from PTX ISA version 6.3 onwards, and considered implicit in PTX
ISA versions less than 6.3.
Support for ::cta sub-qualifier introduced in PTX ISA version 7.8.
- Preview Feature:
Sub-byte
wmmaand single-bitwmmaare preview features in PTX ISA version 6.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
Floating point wmma requires sm_70 or higher.
Integer wmma requires sm_72 or higher.
Sub-byte and single-bit wmma requires sm_75 or higher.
Double precision and alternate floating point precision wmma requires sm_80 or higher.
Examples
// Load elements from f16 row-major matrix B
.reg .b32 x<8>;
wmma.load.b.sync.aligned.m16n16k16.row.f16 {x0,x1,x2,x3,x4,x5,x,x7}, [ptr];
// Now use {x0, ..., x7} for the actual wmma.mma
// Load elements from f32 column-major matrix C and scale the values:
.reg .b32 x<8>;
wmma.load.c.sync.aligned.m16n16k16.col.f32
{x0,x1,x2,x3,x4,x5,x6,x7}, [ptr];
mul.f32 x0, x0, 0.1;
// repeat for all registers x<8>;
...
mul.f32 x7, x7, 0.1;
// Now use {x0, ..., x7} for the actual wmma.mma
// Load elements from integer matrix A:
.reg .b32 x<4>
// destination registers x<4> contain four packed .u8 values each
wmma.load.a.sync.aligned.m32n8k16.row.u8 {x0,x1,x2,x3}, [ptr];
// Load elements from sub-byte integer matrix A:
.reg .b32 x0;
// destination register x0 contains eight packed .s4 values
wmma.load.a.sync.aligned.m8n8k32.row.s4 {x0}, [ptr];
// Load elements from .bf16 matrix A:
.reg .b32 x<4>;
wmma.load.a.sync.aligned.m16n16k16.row.bf16
{x0,x1,x2,x3}, [ptr];
// Load elements from .tf32 matrix A:
.reg .b32 x<4>;
wmma.load.a.sync.aligned.m16n16k8.row.tf32
{x0,x1,x2,x3}, [ptr];
// Load elements from .f64 matrix A:
.reg .b32 x<4>;
wmma.load.a.sync.aligned.m8n8k4.row.f64
{x0}, [ptr];
9.7.13.3.4. Warp-level Matrix Store Instruction: wmma.store
wmma.store
Collectively store a matrix into memory for WMMA
Syntax
wmma.store.d.sync.aligned.layout.shape{.ss}.type [p], r {, stride};
.layout = {.row, .col};
.shape = {.m16n16k16, .m8n32k16, .m32n8k16};
.ss = {.global, .shared{::cta}};
.type = {.f16, .f32, .s32};
wmma.store.d.sync.aligned.layout.shape{.ss}.type [p], r {, stride}
.layout = {.row, .col};
.shape = {.m8n8k32, .m8n8k128};
.ss = {.global, .shared{::cta}};
.type = {.s32};
wmma.store.d.sync.aligned.layout.shape{.ss}.type [p], r {, stride}
.layout = {.row, .col};
.shape = {.m16n16k8};
.ss = {.global, .shared{::cta}};
.type = {.f32};
wmma.store.d.sync.aligned.layout.shape{.ss}.type [p], r {, stride}
.layout = {.row, .col};
.shape = {.m8n8k4 };
.ss = {.global, .shared{::cta}};
.type = {.f64};
Description
Collectively store a matrix across all threads in a warp at the location indicated by address
operand p in the specified state space from source register r.
If no state space is given, perform the memory accesses using Generic Addressing. wmma.load operation may be used only with .global and
.shared spaces and with generic addressing, where the address points to .global or
.shared space.
The source operand r is a brace-enclosed vector expression that matches the shape of the
fragment expected by the store operation, as described in Matrix Fragments for WMMA.
The .shape qualifier indicates the dimensions of all the matrix arguments involved in the
intended wmma computation. It must match the .shape qualifier specified on the wmma.mma
instruction that produced the D matrix being stored.
The .layout qualifier indicates whether the matrix to be loaded is stored in row-major or
column-major format.
stride is an optional 32-bit integer operand that provides an offset in terms of matrix elements
between the start of consecutive instances of the leading dimension (rows or columns). The default
value of stride is described in Matrix Storage for WMMA and must be specified if the actual value is larger than
the default. For example, if the matrix is a sub-matrix of a larger matrix, then the value of stride
is the leading dimension of the larger matrix. Specifying a value lower than the default value
results in undefined behavior.
The required alignment for address p and stride is described in the Matrix Storage for WMMA.
The mandatory .sync qualifier indicates that wmma.store causes the executing thread to wait
until all threads in the warp execute the same wmma.store instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
wmma.store instruction. In conditionally executed code, a wmma.store instruction should only
be used if it is known that all threads in the warp evaluate the condition identically, otherwise
behavior is undefined.
The behavior of wmma.store is undefined if all threads do not use the same qualifiers and the
same values of p and stride, or if any thread in the warp has exited.
wmma.store is treated as a weak memory operation in the Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
.m8n32k16 and .m32n8k16 introduced in PTX ISA version 6.1.
Integer, sub-byte integer and single-bit wmma introduced in PTX ISA version 6.3.
.m16n16k8 introduced in PTX ISA version 7.0.
Double precision wmma introduced in PTX ISA version 7.0.
Modifier .aligned is required from PTX ISA version 6.3 onwards, and considered implicit in PTX
ISA versions less than 6.3.
Support for ::cta sub-qualifier introduced in PTX ISA version 7.8.
- Preview Feature:
Sub-byte
wmmaand single-bitwmmaare preview features in PTX ISA version 6.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
Floating point wmma requires sm_70 or higher.
Integer wmma requires sm_72 or higher.
Sub-byte and single-bit wmma requires sm_75 or higher.
Double precision wmma and shape .m16n16k8 requires sm_80 or higher.
Examples
// Storing f32 elements computed by a wmma.mma
.reg .b32 x<8>;
wmma.mma.sync.m16n16k16.row.col.f32.f32
{d0, d1, d2, d3, d4, d5, d6, d7}, ...;
wmma.store.d.sync.m16n16k16.row.f32
[ptr], {d0, d1, d2, d3, d4, d5, d6, d7};
// Store s32 accumulator for m16n16k16 shape:
.reg .b32 d<8>;
wmma.store.d.sync.aligned.m16n16k16.row.s32
[ptr], {d0, d1, d2, d3, d4, d5, d6, d7};
// Store s32 accumulator for m8n8k128 shape:
.reg .b32 d<2>
wmma.store.d.sync.aligned.m8n8k128.row.s32
[ptr], {d0, d1};
// Store f64 accumulator for m8n8k4 shape:
.reg .f64 d<2>;
wmma.store.d.sync.aligned.m8n8k4.row.f64
[ptr], {d0, d1};
9.7.13.3.5. Warp-level Matrix Multiply-and-Accumulate Instruction: wmma.mma
wmma.mma
Perform a single matrix multiply-and-accumulate operation across a warp
Syntax
// Floating point (.f16 multiplicands) wmma.mma
wmma.mma.sync.aligned.alayout.blayout.shape.dtype.ctype d, a, b, c;
// Integer (.u8/.s8 multiplicands) wmma.mma
wmma.mma.sync.aligned.alayout.blayout.shape.s32.atype.btype.s32{.satfinite} d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.shape = {.m16n16k16, .m8n32k16, .m32n8k16};
.dtype = {.f16, .f32};
.atype = {.s8, .u8};
.btype = {.s8, .u8};
.ctype = {.f16, .f32};
Floating point format .bf16wmma.mma:
wmma.mma.sync.aligned.alayout.blayout.shape.f32.atype.btype.f32 d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.shape = {.m16n16k16, .m8n32k16, .m32n8k16};
.atype = {.bf16 };
.btype = {.bf16};
Floating point format .tf32wmma.mma:
wmma.mma.sync.aligned.alayout.blayout.shape.f32.atype.btype.f32 d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.shape = {.m16n16k8 };
.atype = {.tf32 };
.btype = {.tf32};
Floating point Double precision wmma.mma:
wmma.mma.sync.aligned.alayout.blayout.shape{.rnd}.f64.f64.f64.f64 d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.shape = {.m8n8k4 };
.rnd = { .rn, .rz, .rm, .rp };
Sub-byte (.u4/.s4 multiplicands) wmma.mma:
wmma.mma.sync.aligned.row.col.shape.s32.atype.btype.s32{.satfinite} d, a, b, c;
.shape = {.m8n8k32};
.atype = {.s4, .u4};
.btype = {.s4, .u4};
Single-bit (.b1 multiplicands) wmma.mma:
wmma.mma.op.popc.sync.aligned.row.col.shape.s32.atype.btype.s32 d, a, b, c;
.shape = {.m8n8k128};
.atype = {.b1};
.btype = {.b1};
.op = {.xor, .and}
Description
Perform a warp-level matrix multiply-and-accumulate computation D = A * B + C using matrices A,
B and C loaded in registers a, b and c respectively, and store the result matrix in
register d. The register arguments a, b, c and d hold unspecified fragments of
the corresponding matrices as described in Matrix Fragments for WMMA
The qualifiers .dtype, .atype, .btype and .ctype indicate the data-type of the
elements in the matrices D, A, B and C respectively.
For wmma.mma without explicit .atype and .btype: .atype and .btype are
implicitly set to .f16.
For integer wmma, .ctype and .dtype must be specified as .s32. Also, the values for
.atype and .btype must be the same, i.e., either both are .s8 or both are .u8.
For sub-byte single-bit wmma, .ctype and .dtype must be specified as .s32. Also, the
values for .atype and .btype must be the same; i.e., either both are .s4, both are
.u4, or both are .b1.
For single-bit wmma, multiplication is replaced by a sequence of logical operations;
specifically, wmma.xor.popc and wmma.and.popc computes the XOR, AND respectively of a
128-bit row of A with a 128-bit column of B, then counts the number of set bits in the result
(popc). This result is added to the corresponding element of C and written into D.
The qualifiers .alayout and .blayout must match the layout specified on the wmma.load
instructions that produce the contents of operands a and b respectively. Similarly, the
qualifiers .atype, .btype and .ctype must match the corresponding qualifiers on the
wmma.load instructions that produce the contents of operands a, b and c
respectively.
The .shape qualifier must match the .shape qualifier used on the wmma.load instructions
that produce the contents of all three input operands a, b and c respectively.
The destination operand d is a brace-enclosed vector expression that matches the .shape of
the fragment computed by the wmma.mma instruction.
- Saturation at the output:
The optional qualifier
.satfiniteindicates that the final values in the destination register are saturated as follows:The output is clamped to the minimum or maximum 32-bit signed integer value. Otherwise, if the accumulation would overflow, the value wraps.
- Precision and rounding for
.f16floating point operations: Element-wise multiplication of matrix A and B is performed with at least single precision. When
.ctypeor.dtypeis.f32, accumulation of the intermediate values is performed with at least single precision. When both.ctypeand.dtypeare specified as.f16, the accumulation is performed with at least half precision.The accumulation order, rounding and handling of subnormal inputs is unspecified.
- Precision and rounding for
.bf16,.tf32floating point operations: Element-wise multiplication of matrix A and B is performed with specified precision. Accumulation of the intermediate values is performed with at least single precision.
The accumulation order, rounding and handling of subnormal inputs is unspecified.
Rounding modifiers on double precision wmma.mma (default is .rn):
.rnmantissa LSB rounds to nearest even
.rzmantissa LSB rounds towards zero
.rmmantissa LSB rounds towards negative infinity
.rpmantissa LSB rounds towards positive infinity
The mandatory .sync qualifier indicates that wmma.mma causes the executing thread to wait
until all threads in the warp execute the same wmma.mma instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
wmma.mma instruction. In conditionally executed code, a wmma.mma instruction should only be
used if it is known that all threads in the warp evaluate the condition identically, otherwise
behavior is undefined.
The behavior of wmma.mma is undefined if all threads in the same warp do not use the same
qualifiers, or if any thread in the warp has exited.
PTX ISA Notes
Introduced in PTX ISA version 6.0.
.m8n32k16 and .m32n8k16 introduced in PTX ISA version 6.1.
Integer, sub-byte integer and single-bit wmma introduced in PTX ISA version 6.3.
Double precision and alternate floating point precision wmma introduced in PTX ISA version 7.0.
Support for .and operation in single-bit wmma introduced in PTX ISA version 7.1.
Modifier .aligned is required from PTX ISA version 6.3 onwards, and considered implicit in PTX
ISA versions less than 6.3.
Support for .satfinite on floating point wmma.mma is deprecated in PTX ISA version 6.4 and
is removed from PTX ISA version 6.5.
- Preview Feature:
Sub-byte
wmmaand single-bitwmmaare preview features in PTX ISA. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
Floating point wmma requires sm_70 or higher.
Integer wmma requires sm_72 or higher.
Sub-byte and single-bit wmma requires sm_75 or higher.
Double precision, alternate floating point precision wmma require sm_80 or higher.
.and operation in single-bit wmma requires sm_80 or higher.
Examples
.global .align 32 .f16 A[256], B[256];
.global .align 32 .f32 C[256], D[256];
.reg .b32 a<8> b<8> c<8> d<8>;
wmma.load.a.sync.aligned.m16n16k16.global.row.f16
{a0, a1, a2, a3, a4, a5, a6, a7}, [A];
wmma.load.b.sync.aligned.m16n16k16.global.col.f16
{b0, b1, b2, b3, b4, b5, b6, b7}, [B];
wmma.load.c.sync.aligned.m16n16k16.global.row.f32
{c0, c1, c2, c3, c4, c5, c6, c7}, [C];
wmma.mma.sync.aligned.m16n16k16.row.col.f32.f32
{d0, d1, d2, d3, d4, d5, d6, d7},
{a0, a1, a2, a3, a4, a5, a6, a7},
{b0, b1, b2, b3, b4, b5, b6, b7},
{c0, c1, c2, c3, c4, c5, c6, c7};
wmma.store.d.sync.aligned.m16n16k16.global.col.f32
[D], {d0, d1, d2, d3, d4, d5, d6, d7};
// Compute an integer WMMA:
.reg .b32 a, b<4>;
.reg .b32 c<8>, d<8>;
wmma.mma.sync.aligned.m8n32k16.row.col.s32.s8.s8.s32
{d0, d1, d2, d3, d4, d5, d6, d7},
{a}, {b0, b1, b2, b3},
{c0, c1, c2, c3, c4, c5, c6, c7};
// Compute sub-byte WMMA:
.reg .b32 a, b, c<2> d<2>
wmma.mma.sync.aligned.m8n8k32.row.col.s32.s4.s4.s32
{d0, d1}, {a}, {b}, {c0, c1};
// Compute single-bit type WMMA:
.reg .b32 a, b, c<2> d<2>
wmma.mma.xor.popc.sync.aligned.m8n8k128.row.col.s32.b1.b1.s32
{d0, d1}, {a}, {b}, {c0, c1};
// Compute double precision wmma
.reg .f64 a, b, c<2>, d<2>;
wmma.mma.sync.aligned.m8n8k4.row.col.f64.f64.f64.f64
{d0, d1}, {a}, {b}, {c0, c1};
// Compute alternate floating point precision wmma
.reg .b32 a<2>, b<2>, c<8>, d<8>;
wmma.mma.sync.aligned.m16n16k8.row.col.f32.tf32.tf32.f32
{d0, d1, d2, d3, d4, d5, d6, d7},
{a0, a1, a2, a3}, {b0, b1, b2, b3},
{c0, c1, c2, c3, c4, c5, c6, c7};
9.7.13.4. Matrix multiply-accumulate operation using mma instruction
This section describes warp-level mma, ldmatrix, stmatrix, and movmatrix
instructions and the organization of various matrices involved in these instructions.
9.7.13.4.1. Matrix Fragments for mma.m8n8k4 with .f16 floating point type
A warp executing mma.m8n8k4 with .f16 floating point type will compute 4 MMA operations of shape
.m8n8k4.
Elements of 4 matrices need to be distributed across the threads in a warp. The following table shows distribution of matrices for MMA operations.
MMA Computation |
Threads participating in MMA computation |
|---|---|
MMA computation 1 |
Threads with |
MMA computation 2 |
Threads with |
MMA computation 3 |
Threads with |
MMA computation 4 |
Threads with |
For each of the individual MMA computation shown above, each of the required thread holds a fragment of the matrix for performing mma operation as follows:
Multiplicand A:
.atype
Fragment
Elements (low to high)
.f16A vector expression containing two
.f16x2registers, with each register containing two.f16elements from the matrix A.a0, a1, a2, a3
The layout of the fragments held by different threads is shown below:
Fragment layout for Row Major matrix A is shown in Figure 21.
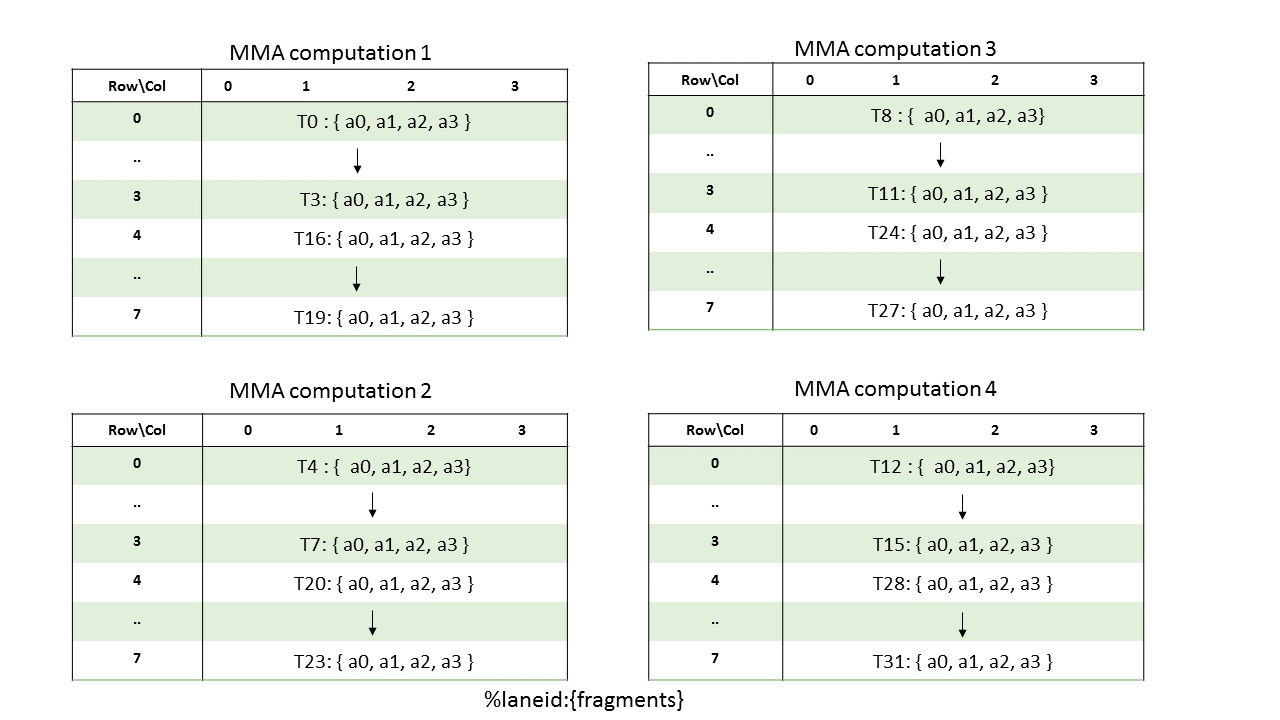
Figure 21 MMA .m8n8k4 fragment layout for row-major matrix A with
.f16typeThe row and column of a matrix fragment can be computed as:
row = %laneid % 4 if %laneid < 16 (%laneid % 4) + 4 otherwise col = i for ai where i = {0,..,3}
Fragment layout for Column Major matrix A is shown in Figure 22.
The layout of the fragments held by different threads is shown below:

Figure 22 MMA .m8n8k4 fragment layout for column-major matrix A with
.f16typeThe row and column of a matrix fragment can be computed as:
row = i % 4 for ai where i = {0,..,3} if %laneid < 16 (i % 4) + 4 for ai where i = {0,..,3} otherwise col = %laneid % 4
Multiplicand B:
.btype
Fragment
Elements (low to high)
.f16A vector expression containing two
.f16x2registers, with each register containing two.f16elements from the matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown below:
Fragment layout for Row Major matrix B is shown in Figure 23.
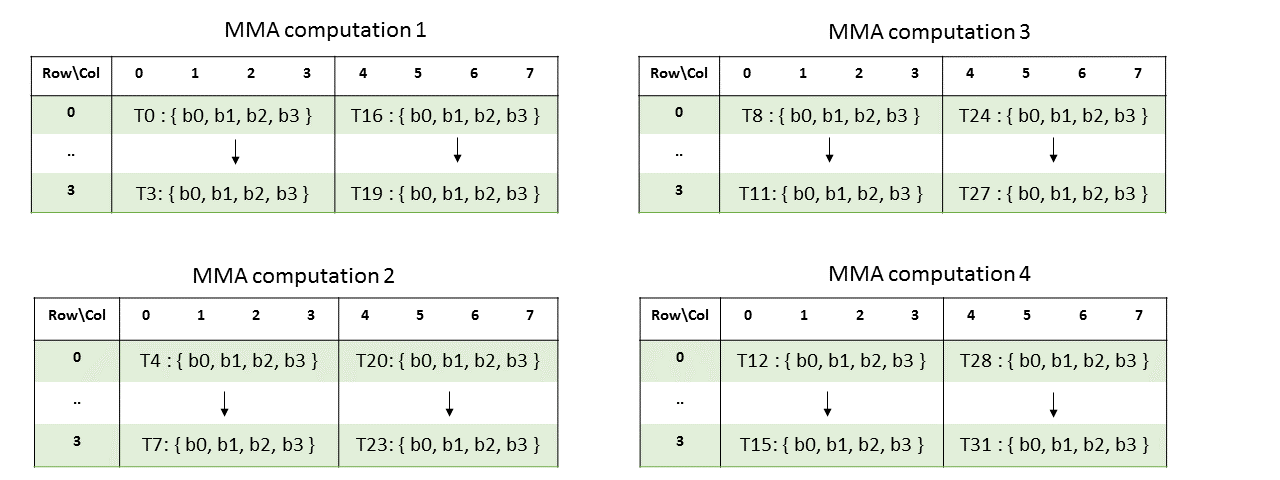
Figure 23 MMA .m8n8k4 fragment layout for row-major matrix B with
.f16typeThe row and column of a matrix fragment can be computed as:
row = %laneid % 4 col = i for bi where i = {0,..,3} if %laneid < 16 i+4 for bi where i = {0,..,3} otherwise
Fragment layout for Column Major matrix B is shown in Figure 24.
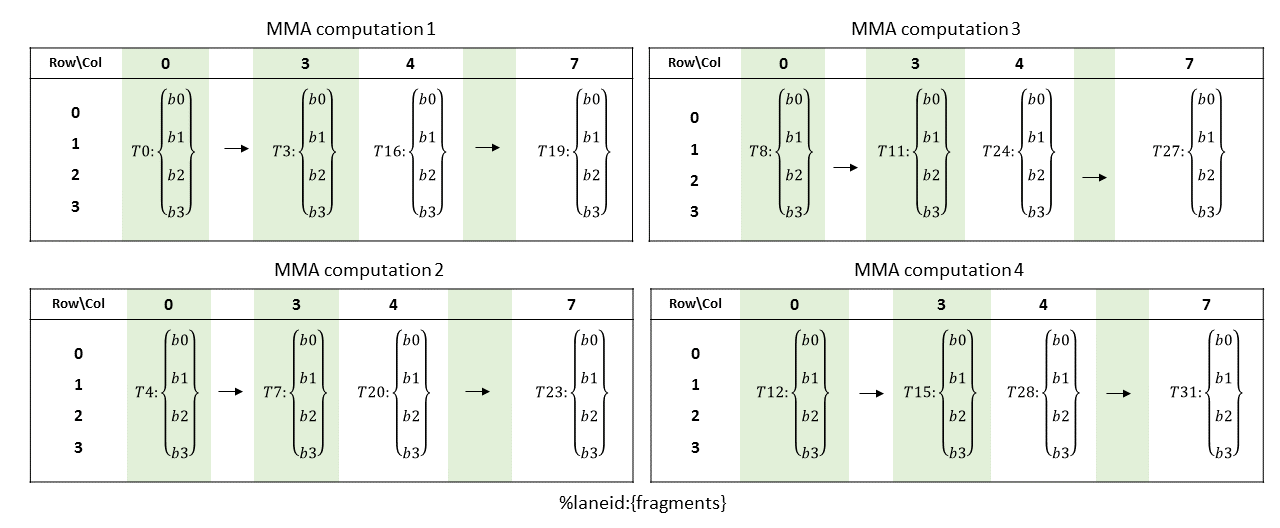
Figure 24 MMA .m8n8k4 fragment layout for column-major matrix B with
.f16typeThe row and column of a matrix fragment can be computed as:
row = i for bi where i = {0,..,3} col = %laneid % 4 if %laneid < 16 (%laneid % 4) + 4 otherwise
Accumulators C (or D):
.ctype / .dtype
Fragment
Elements (low to high)
.f16A vector expression containing four
.f16x2registers, with each register containing two.f16elements from the matrix C (or D).c0, c1, c2, c3, c4, c5, c6, c7
.f32A vector expression of eight
.f32registers.The layout of the fragments held by different threads is shown below:
Fragment layout for accumulator matrix when
.ctypeis.f16is shown in Figure 25.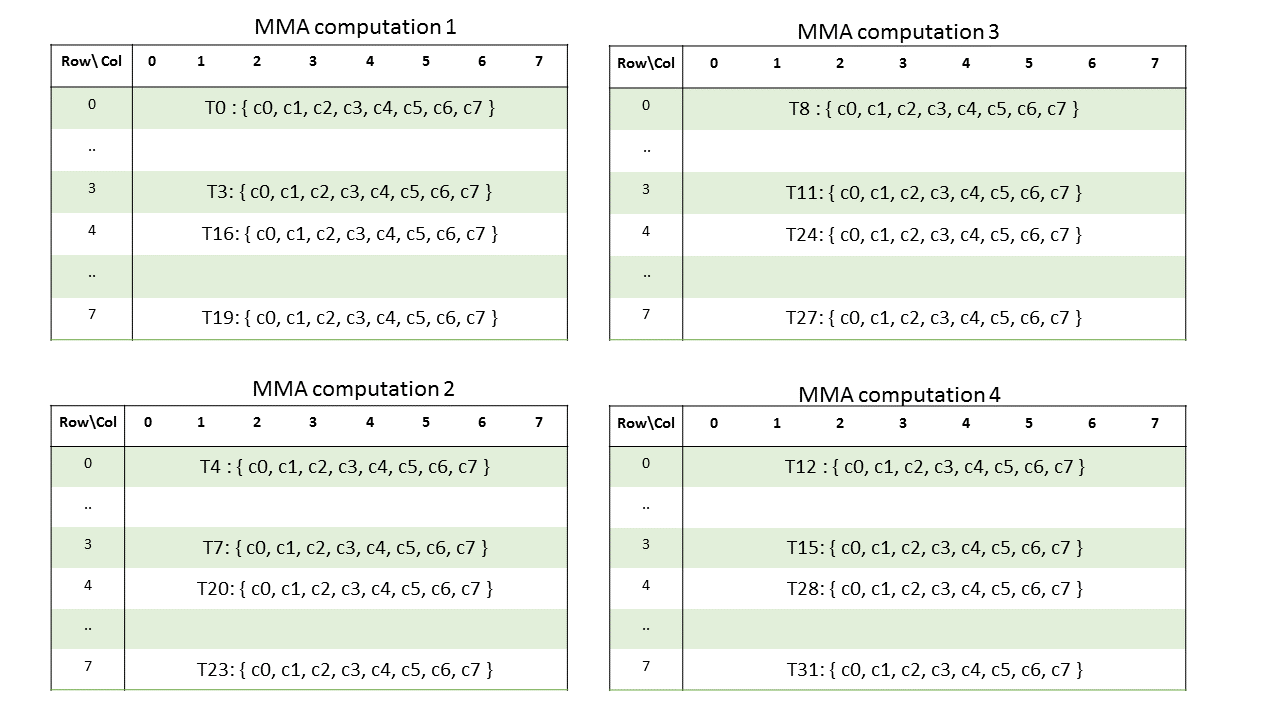
Figure 25 MMA .m8n8k4 fragment layout for matrix C/D with
.ctype=.f16The row and column of a matrix fragment can be computed as:
row = %laneid % 4 if %laneid < 16 (%laneid % 4) + 4 otherwise col = i for ci where i = {0,..,7}
Fragment layout for accumulator matrix when
.ctypeis.f32is shown in Figure 26 and Figure 27.
Figure 26 MMA .m8n8k4 computation 1 and 2 fragment layout for matrix C/D with
.ctype=.f32
Figure 27 MMA .m8n8k4 computation 3 and 4 fragment layout for matrix C/D with
.ctype=.f32The row and column of a matrix fragment can be computed as:
row = X if %laneid < 16 X + 4 otherwise where X = (%laneid & 0b1) + (i & 0b10) for ci where i = {0,..,7} col = (i & 0b100) + (%laneid & 0b10) + (i & 0b1) for ci where i = {0,..,7}
9.7.13.4.2. Matrix Fragments for mma.m8n8k4 with .f64 floating point type
A warp executing mma.m8n8k4 with .f64 floating point type will compute an MMA operation of
shape .m8n8k4.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.f64A vector expression containing a single
.f64register, containing single.f64element from the matrix A.a0
The layout of the fragments held by different threads is shown in Figure 28.
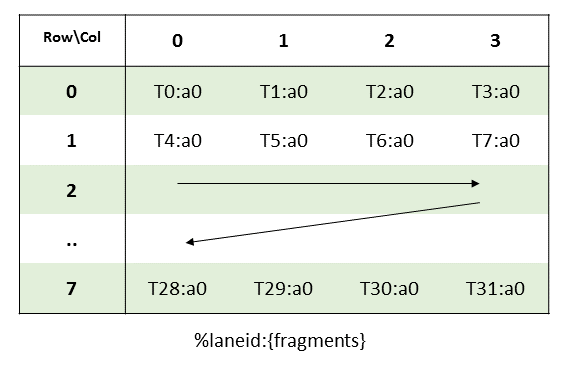
Figure 28 MMA .m8n8k4 fragment layout for matrix A with
.f64typeThe row and column of a matrix fragment can be computed as:
row = %laneid >> 2 col = %laneid % 4
Multiplicand B:
.btype
Fragment
Elements (low to high)
.f64A vector expression containing a single
.f64register, containing a single.f64element from the matrix B.b0
The layout of the fragments held by different threads is shown in Figure 29.
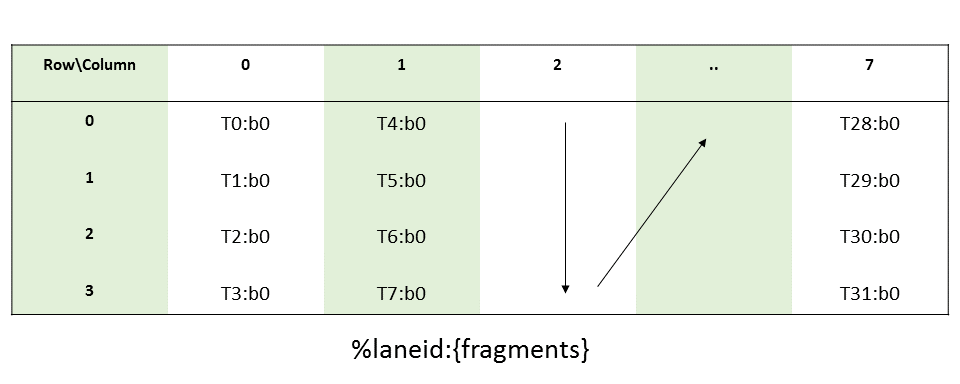
Figure 29 MMA .m8n8k4 fragment layout for matrix B with
.f64typeThe row and column of a matrix fragment can be computed as:
row = %laneid % 4 col = %laneid >> 2
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.f64A vector expression containing of two
.f64registers containing two.f64elements from the matrix C.c0, c1
The layout of the fragments held by different threads is shown in Figure 30.
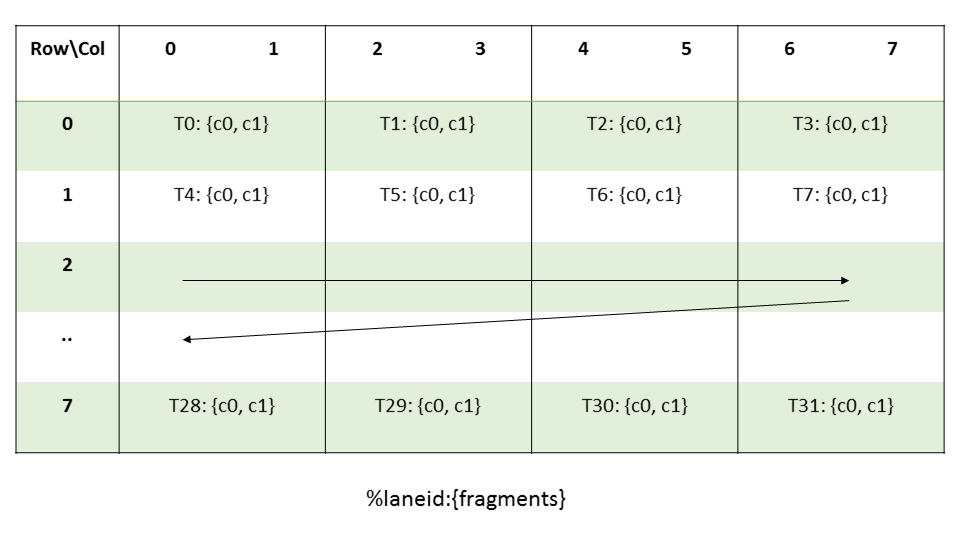
Figure 30 MMA .m8n8k4 fragment layout for accumulator matrix C/D with
.f64typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0, 1}
9.7.13.4.3. Matrix Fragments for mma.m8n8k16
A warp executing mma.m8n8k16 will compute an MMA operation of shape .m8n8k16.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.s8/.u8A vector expression containing a single
.b32register, containing four.s8or.u8elements from the matrix A.a0, a1, a2, a3
The layout of the fragments held by different threads is shown in Figure 31.
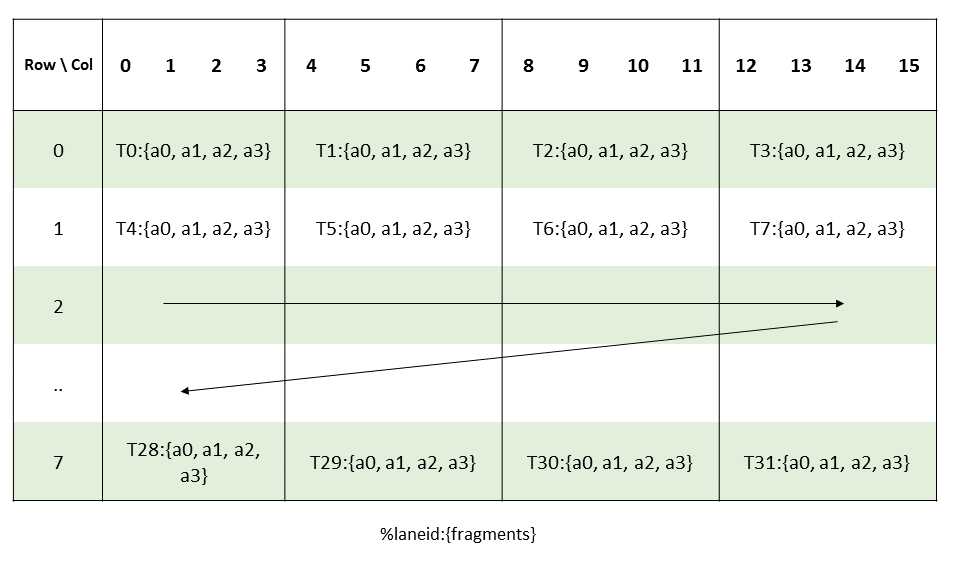
Figure 31 MMA .m8n8k16 fragment layout for matrix A with
.u8/.s8typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 4) + i for ai where i = {0,..,3}
Multiplicand B:
.btype
Fragment
Elements (low to high)
.s8/.u8A vector expression containing a single
.b32register, containing four.s8or.u8elements from the matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 32.
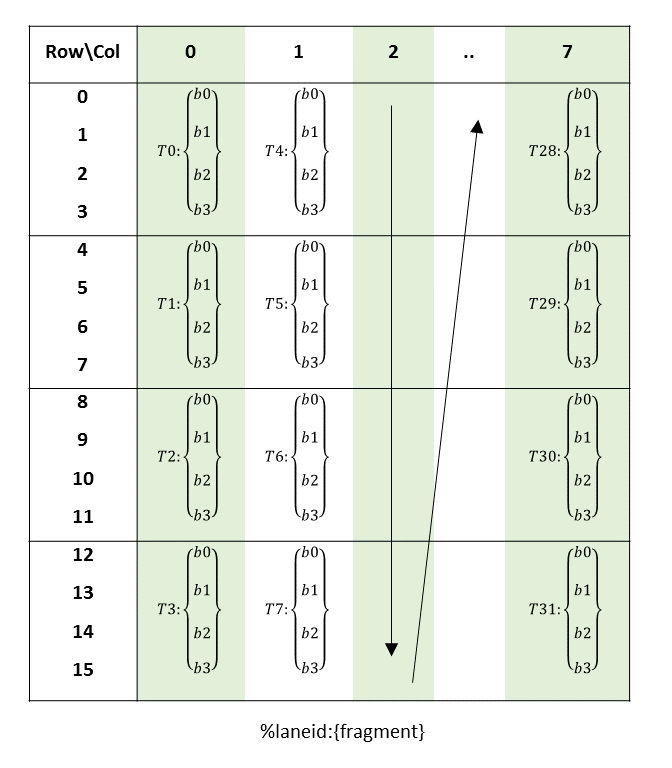
Figure 32 MMA .m8n8k16 fragment layout for matrix B with
.u8/.s8typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 4) + i for bi where i = {0,..,3} col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing of two
.s32registers.c0, c1
The layout of the fragments held by different threads is shown in Figure 33.
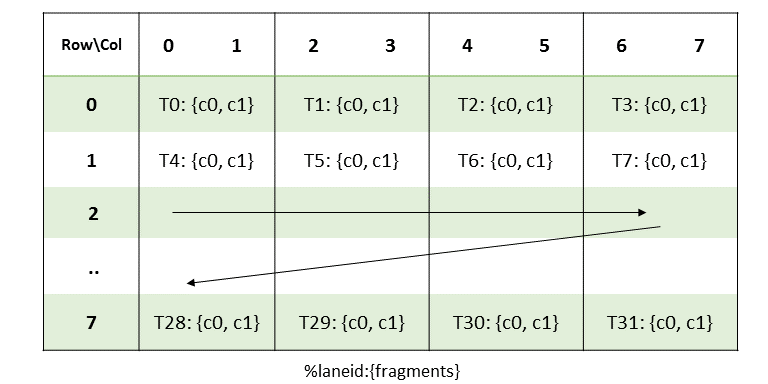
Figure 33 MMA .m8n8k16 fragment layout for accumulator matrix C/D with
.s32typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 2) + i for ci where i = {0, 1}
9.7.13.4.4. Matrix Fragments for mma.m8n8k32
A warp executing mma.m8n8k32 will compute an MMA operation of shape .m8n8k32.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing a single
.b32register, containing eight.s4or.u4elements from the matrix A.a0, a1, a2, a3, a4, a5, a6, a7
The layout of the fragments held by different threads is shown in Figure 34.

Figure 34 MMA .m8n8k32 fragment layout for matrix A with
.u4/.s4typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 8) + i for ai where i = {0,..,7}
Multiplicand B:
.btype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing a single
.b32register, containing eight.s4or.u4elements from the matrix B.b0, b1, b2, b3, b4, b5, b6, b7
The layout of the fragments held by different threads is shown in Figure 35.
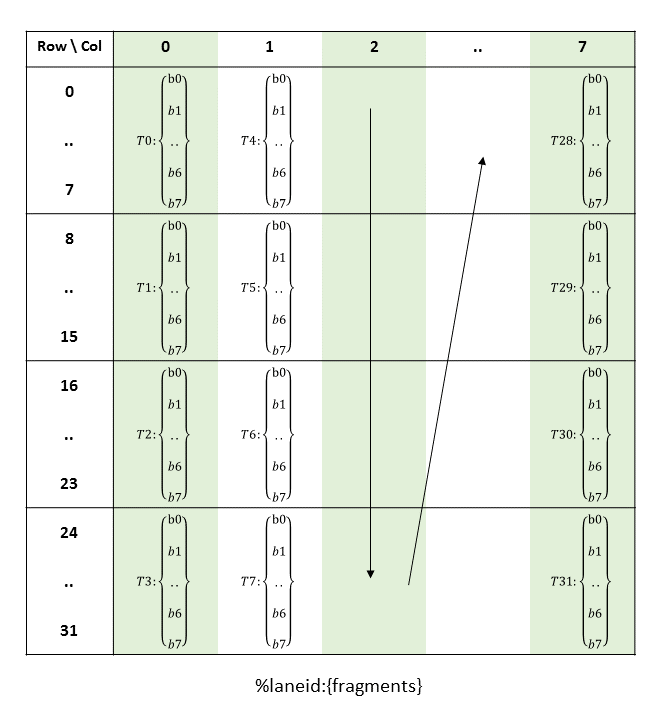
Figure 35 MMA .m8n8k32 fragment layout for matrix B with
.u4/.s4typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 8) + i for bi where i = {0,..,7} col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression of two
.s32registers.c0, c1
The layout of the fragments held by different threads is shown in Figure 36:
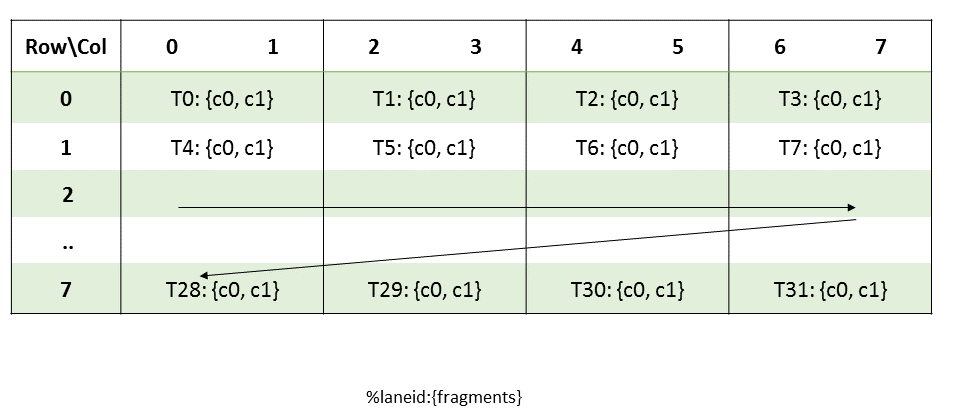
Figure 36 MMA .m8n8k32 fragment layout for accumulator matrix C/D with
.s32typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 2) + i for ci where i = {0, 1}
9.7.13.4.5. Matrix Fragments for mma.m8n8k128
A warp executing mma.m8n8k128 will compute an MMA operation of shape .m8n8k128.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.b1A vector expression containing a single
.b32register, containing thirty two.b1elements from the matrix A.a0, a1, … a30, a31
The layout of the fragments held by different threads is shown in Figure 37.

Figure 37 MMA .m8n8k128 fragment layout for matrix A with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 32) + i for ai where i = {0,..,31}
Multiplicand B:
.btype
Fragment
Elements (low to high)
.b1A vector expression containing a single
.b32register, containing thirty two.b1elements from the matrix B.b0, b1, …, b30, b31
The layout of the fragments held by different threads is shown in Figure 38.
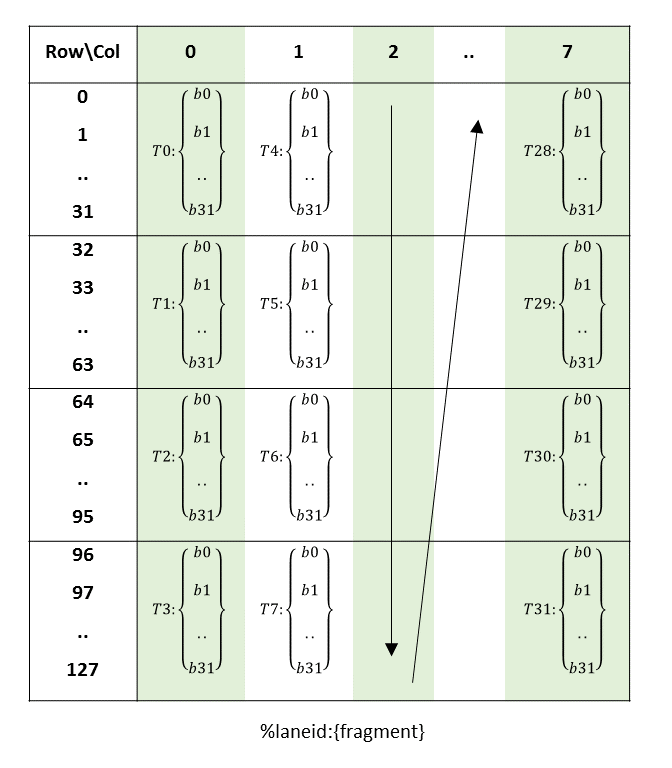
Figure 38 MMA .m8n8k128 fragment layout for matrix B with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 32) + i for bi where i = {0,..,31} col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing two
.s32registers, containing two.s32elements from the matrix C (or D).c0, c1
The layout of the fragments held by different threads is shown in Figure 39.
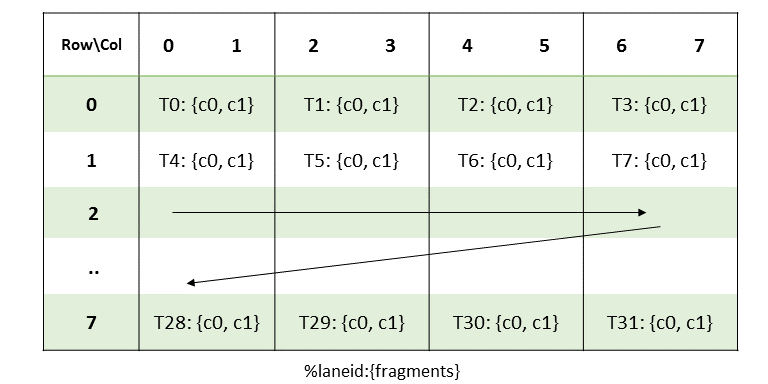
Figure 39 MMA .m8n8k128 fragment layout for accumulator matrix C/D with
.s32typeThe row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID col = (threadID_in_group * 2) + i for ci where i = {0, 1}
9.7.13.4.6. Matrix Fragments for mma.m16n8k4
A warp executing mma.m16n8k4 will compute an MMA operation of shape .m16n8k4.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.tf32:.atype
Fragment
Elements (low to high)
.tf32A vector expression containing two
.b32registers, containing two.tf32elements from the matrix A.a0, a1
The layout of the fragments held by different threads is shown in Figure 40.
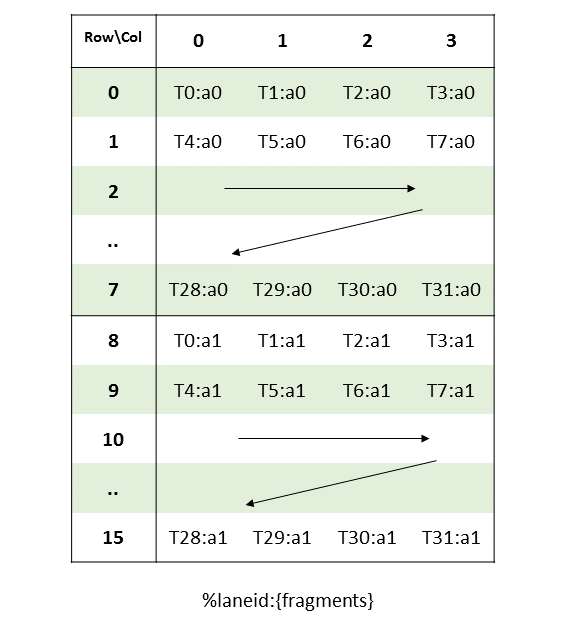
Figure 40 MMA .m16n8k4 fragment layout for matrix A with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 groupID + 8 for a1 col = threadID_in_group
.f64:.atype
Fragment
Elements (low to high)
.f64A vector expression containing two
.f64registers, containing two.f64elements from the matrix A.a0, a1
The layout of the fragments held by different threads is shown in Figure 41.

Figure 41 MMA .m16n8k4 fragment layout for matrix A with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 groupID + 8 for a1 col = threadID_in_group
Multiplicand B:
.tf32:.btype
Fragment
Elements (low to high)
.tf32A vector expression of a single
.b32register, containing a single.tf32element from the matrix B.b0
The layout of the fragments held by different threads is shown in Figure 42.
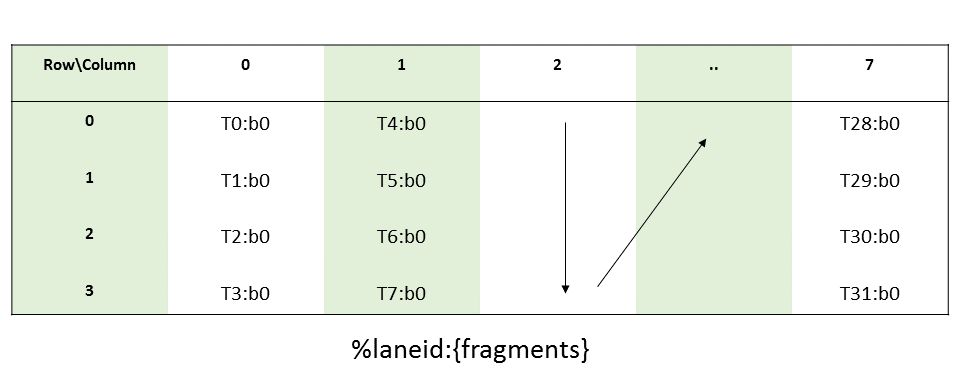
Figure 42 MMA .m16n8k4 fragment layout for matrix B with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = threadID_in_group col = groupID
.f64:.btype
Fragment
Elements (low to high)
.f64A vector expression of a single
.f64register, containing a single.f64element from the matrix B.b0
The layout of the fragments held by different threads is shown in Figure 43.

Figure 43 MMA .m16n8k4 fragment layout for matrix B with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = threadID_in_group col = groupID
Accumulators (C or D):
.tf32:.ctype / .dtype
Fragment
Elements (low to high)
.f32A vector expression containing four
.f32registers, containing four.f32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 44.
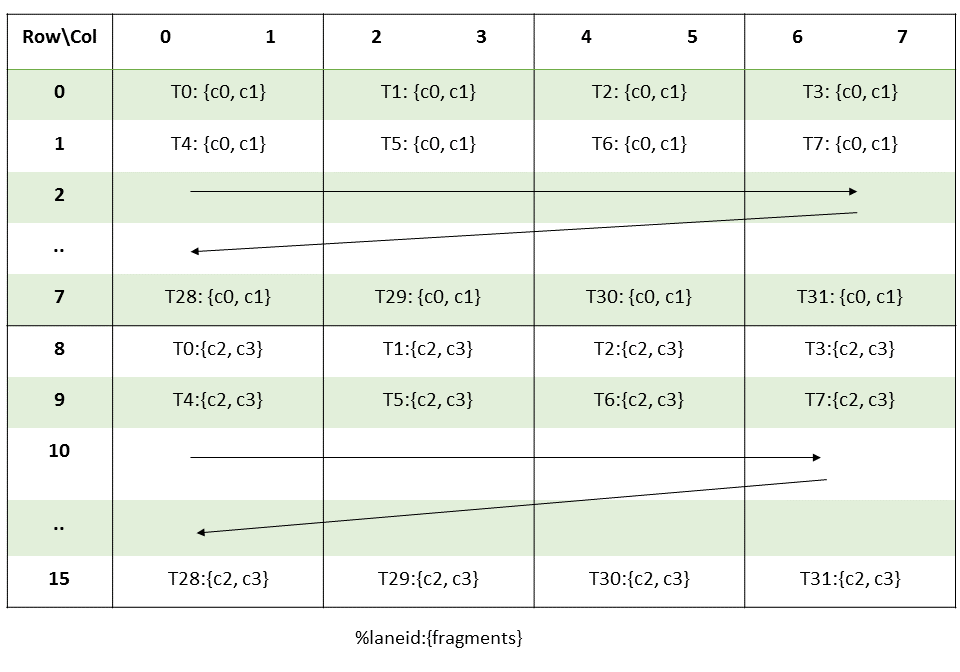
Figure 44 MMA .m16n8k4 fragment layout for accumulator matrix C/D with
.f32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for c0 and c1 groupID + 8 for c2 and c3 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
.f64:.ctype / .dtype
Fragment
Elements (low to high)
.f64A vector expression containing four
.f64registers, containing four.f64elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 45.

Figure 45 MMA .m16n8k4 fragment layout for accumulator matrix C/D with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for c0 and c1 groupID + 8 for c2 and c3 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.7. Matrix Fragments for mma.m16n8k8
A warp executing mma.m16n8k8 will compute an MMA operation of shape .m16n8k8.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.f16and.bf16:.atype
Fragment
Elements (low to high)
.f16/.bf16A vector expression containing two
.f16x2registers, with each register containing two.f16/.bf16elements from the matrix A.a0, a1, a2, a3
The layout of the fragments held by different threads is shown in Figure 46.

Figure 46 MMA .m16n8k8 fragment layout for matrix A with
.f16/.bf16type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 and a1 groupID + 8 for a2 and a3 col = threadID_in_group * 2 + (i & 0x1) for ai where i = {0,..,3}
.tf32:.atype
Fragment
Elements (low to high)
.tf32A vector expression containing four
.b32registers, containing four.tf32elements from the matrix A.a0, a1, a2, a3
The layout of the fragments held by different threads is shown in Figure 47.
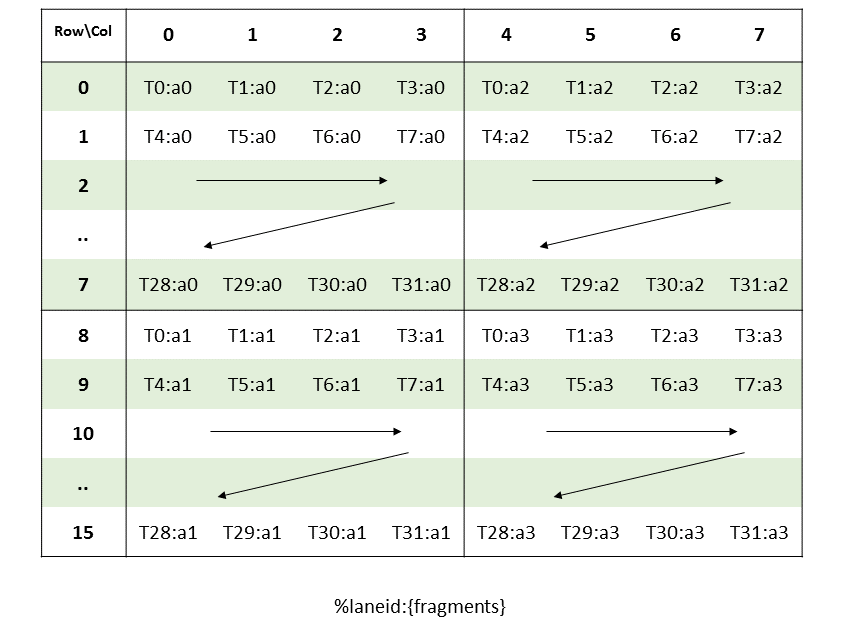
Figure 47 MMA .m16n8k8 fragment layout for matrix A with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 and a2 groupID + 8 for a1 and a3 col = threadID_in_group for a0 and a1 threadID_in_group + 4 for a2 and a3
.f64:.atype
Fragment
Elements (low to high)
.f64A vector expression containing four
.f64registers, containing four.f64elements from the matrix A.a0, a1, a2, a3
The layout of the fragments held by different threads is shown in Figure 48.

Figure 48 MMA .m16n8k8 fragment layout for matrix A with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 and a2 groupID + 8 for a1 and a3 col = threadID_in_group for a0 and a1 threadID_in_group + 4 for a2 and a3
Multiplicand B:
.f16and.bf16:.btype
Fragment
Elements (low to high)
.f16/.bf16A vector expression containing a single
.f16x2register, containing two.f16/.bf16elements from the matrix B.b0, b1
The layout of the fragments held by different threads is shown in Figure 49.
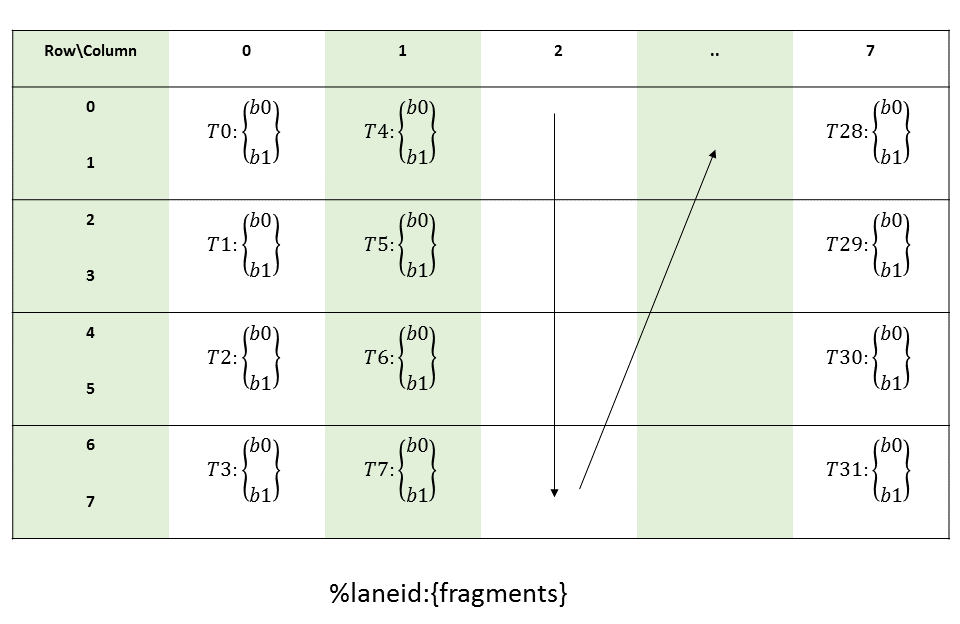
Figure 49 MMA .m16n8k8 fragment layout for matrix B with
.f16/.bf16type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 2) + i for bi where i = {0, 1} col = groupID
.tf32:.btype
Fragment
Elements (low to high)
.tf32A vector expression containing two
.b32registers, containing two.tf32elements from the matrix B.b0, b1
The layout of the fragments held by different threads is shown in Figure 50.
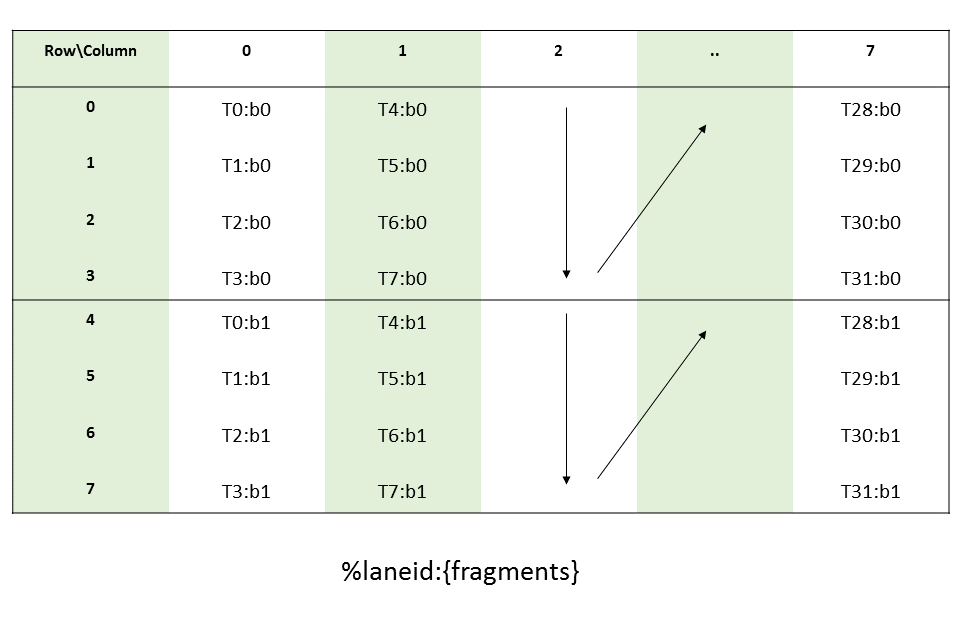
Figure 50 MMA .m16n8k8 fragment layout for matrix B with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = threadID_in_group for b0 threadID_in_group + 4 for b1 col = groupID
.f64:.btype
Fragment
Elements (low to high)
.f64A vector expression containing two
.f64registers, containing two.f64elements from the matrix B.b0, b1
The layout of the fragments held by different threads is shown in Figure 51.

Figure 51 MMA .m16n8k8 fragment layout for matrix B with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = threadID_in_group for b0 threadID_in_group + 4 for b1 col = groupID
Accumulators (C or D):
.f16,.bf16and.tf32:.ctype / .dtype
Fragment
Elements (low to high)
.f16A vector expression containing two
.f16x2registers, with each register containing two.f16elements from the matrix C (or D).c0, c1, c2, c3
.f32A vector expression of four
.f32registers.The layout of the fragments held by different threads is shown in Figure 52.
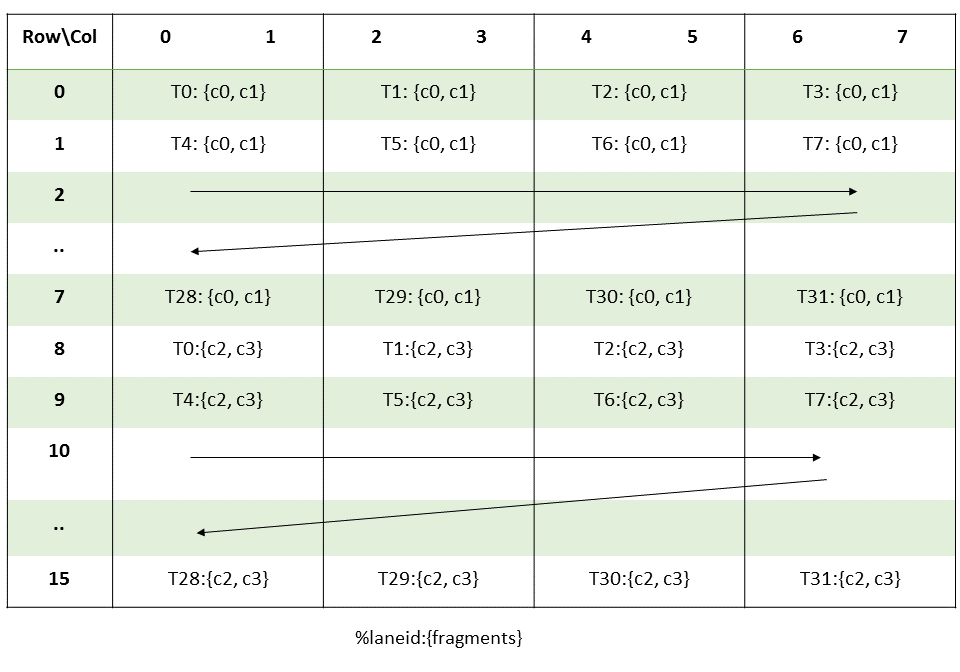
Figure 52 MMA .m16n8k8 fragment layout for accumulator matrix C/D with
.f16x2/.f32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for c0 and c1 groupID + 8 for c2 and c3 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
.f64:.ctype / .dtype
Fragment
Elements (low to high)
.f64A vector expression of four
.f64registers containing four.f64elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 53.

Figure 53 MMA .m16n8k8 fragment layout for accumulator matrix C/D with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for c0 and c1 groupID + 8 for c2 and c3 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.8. Matrix Fragments for mma.m16n8k16 with floating point type
A warp executing mma.m16n8k16 floating point types will compute an MMA operation of shape
.m16n8k16.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.f16and.bf16:.atype
Fragment
Elements (low to high)
.f16/.bf16A vector expression containing four
.f16x2registers, with each register containing two.f16/.bf16elements from the matrix A.a0, a1, a2, a3, a4, a5, a6, a7
The layout of the fragments held by different threads is shown in Figure 54.

Figure 54 MMA .m16n8k16 fragment layout for matrix A with
.f16/.bf16type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 2 || 4 <= i < 6 groupID + 8 Otherwise col = (threadID_in_group * 2) + (i & 0x1) for ai where i < 4 (threadID_in_group * 2) + (i & 0x1) + 8 for ai where i >= 4
.f64:.atype
Fragment
Elements (low to high)
.f64A vector expression containing eight
.f64registers, with each register containing one.f64element from the matrix A.a0, a1, a2, a3, a4, a5, a6, a7
The layout of the fragments held by different threads is shown in Figure 55.
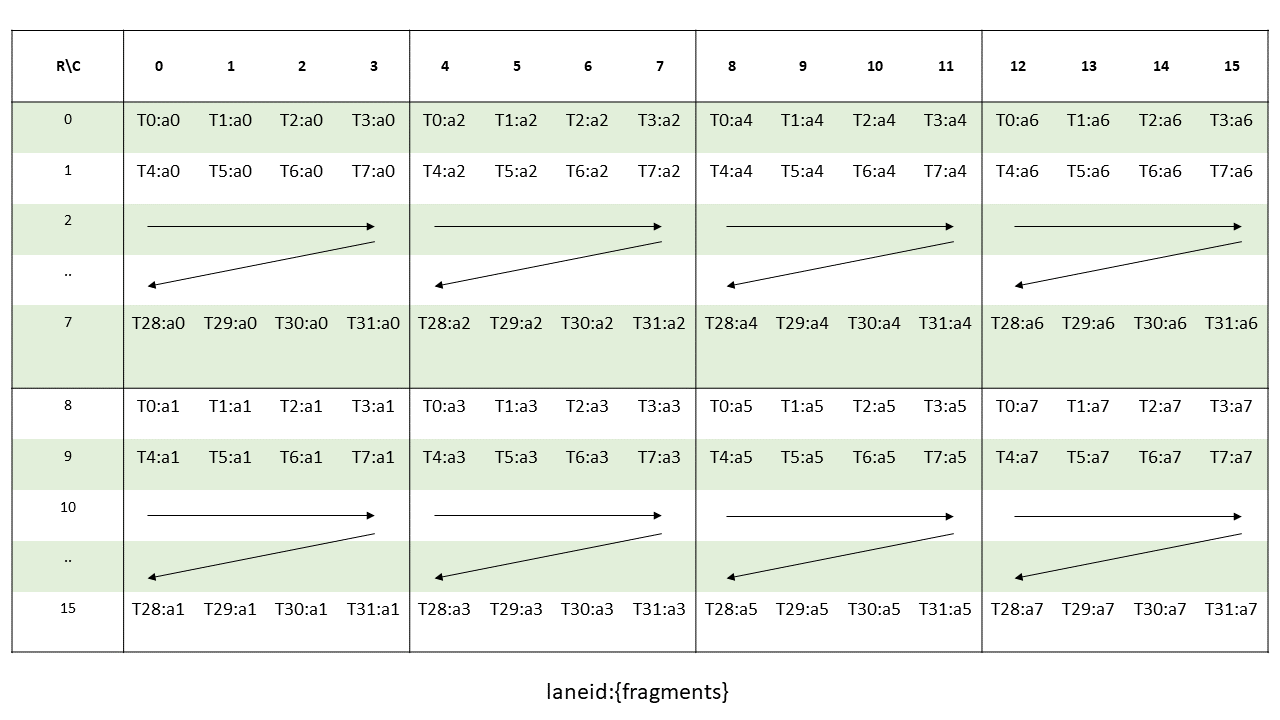
Figure 55 MMA .m16n8k16 fragment layout for matrix A with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where i % 2 = 0 groupID + 8 Otherwise col = (i * 2) + threadID_in_group for ai where i % 2 = 0 (i * 2) - 2 + (threadID_in_group Otherwise
Multiplicand B:
.f16and.bf16:.btype
Fragment
Elements (low to high)
.f16/.bf16A vector expression containing two
.f16x2registers, with each register containing two.f16/.bf16elements from the matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 56.
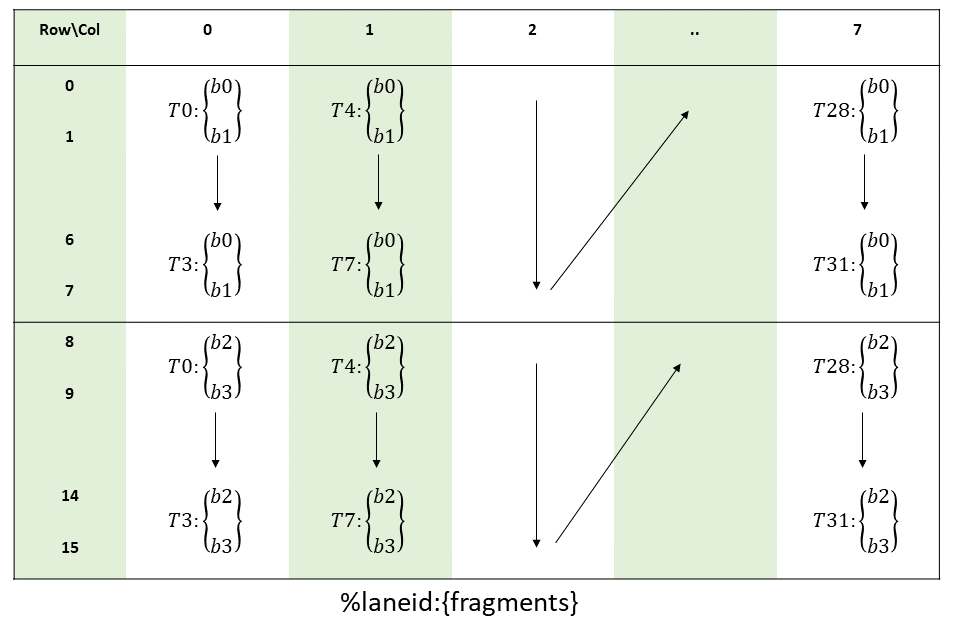
Figure 56 MMA .m16n8k16 fragment layout for matrix B with
.f16/.bf16type.where the row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 2) + (i & 0x1) for bi where i < 2 (threadID_in_group * 2) + (i & 0x1) + 8 for bi where i >= 2 col = groupID
.f64:.atype
Fragment
Elements (low to high)
.f64A vector expression containing four
.f64registers, with each register containing one.f64element from the matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 57.
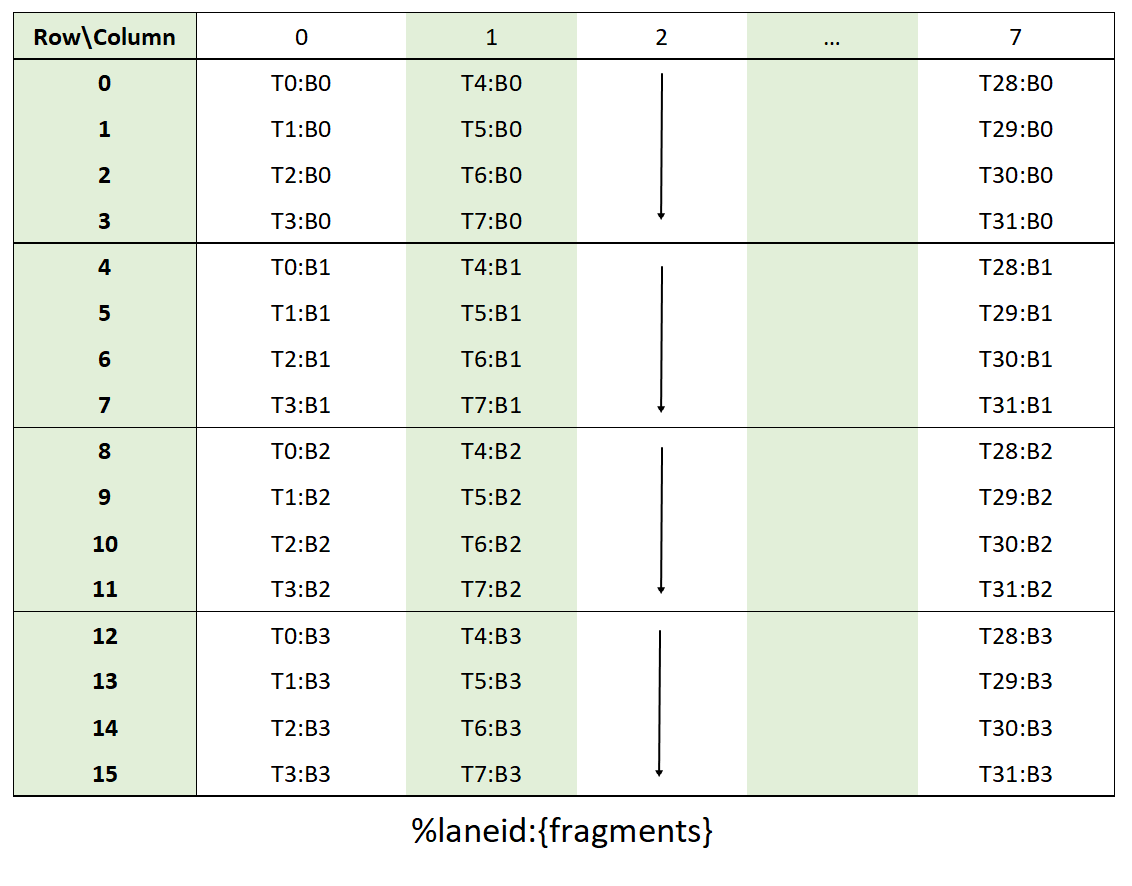
Figure 57 MMA .m16n8k16 fragment layout for matrix B with
.f64type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = threadID_in_group + (i * 4) for bi where i < 4 col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.f64A vector expression containing four
.f64registers containing.f64elements from the matrix C (or D).c0, c1, c2, c3
.f32A vector expression containing four
.f32registers containing four.f32elements from the matrix C (or D)..f16A vector expression containing two
.f16x2registers, with each register containing two.f16elements from the matrix C (or D).The layout of the fragments held by different threads is shown in Figure 58.
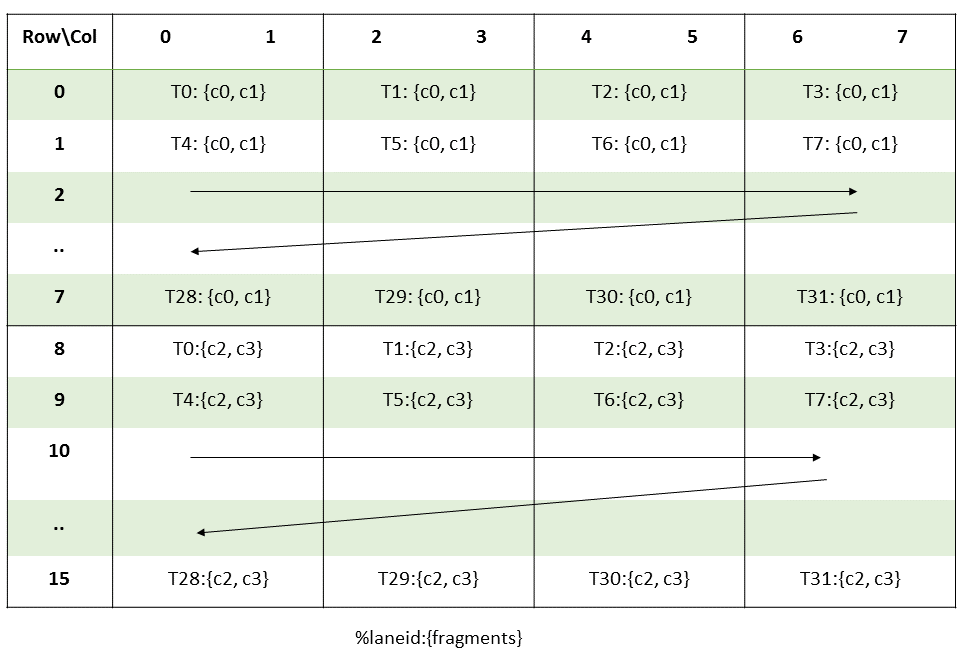
Figure 58 MMA .m16n8k16 fragment layout for accumulator matrix matrix C/D.
The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.9. Matrix Fragments for mma.m16n8k16 with integer type
A warp executing mma.m16n8k16 with .u8 or .s8 integer type will compute an MMA operation
of shape .m16n8k16.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.u8/.s8A vector expression containing two
.b32registers, with each register containing four.u8/.s8elements from the matrix A.a0, a1, a2, a3, a4, a5, a6, a7
The layout of the fragments held by different threads is shown in Figure 59.
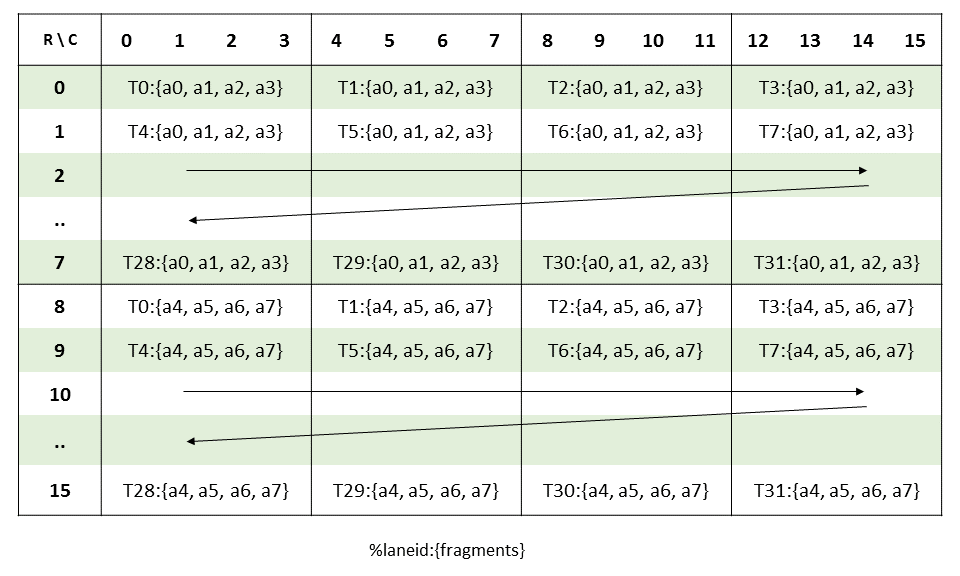
Figure 59 MMA .m16n8k16 fragment layout for matrix A with
.u8/.s8type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where i < 4 groupID + 8 for ai where i >= 4 col = (threadID_in_group * 4) + (i & 0x3) for ai where i = {0,..,7}
Multiplicand B:
.btype
Fragment
Elements (low to high)
.u8/.s8A vector expression containing a single
.b32register, containing four.u8/.s8elements from the matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 60.
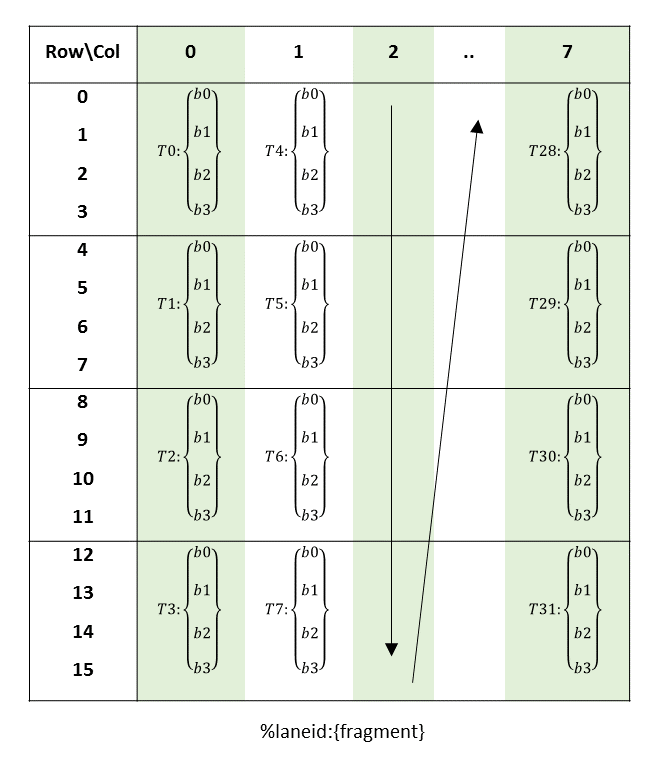
Figure 60 MMA .m16n8k16 fragment layout for matrix B with
.u8/.s8type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 4) + i for bi where i = {0,..,3} col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing four
.s32registers, containing four.s32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 61.
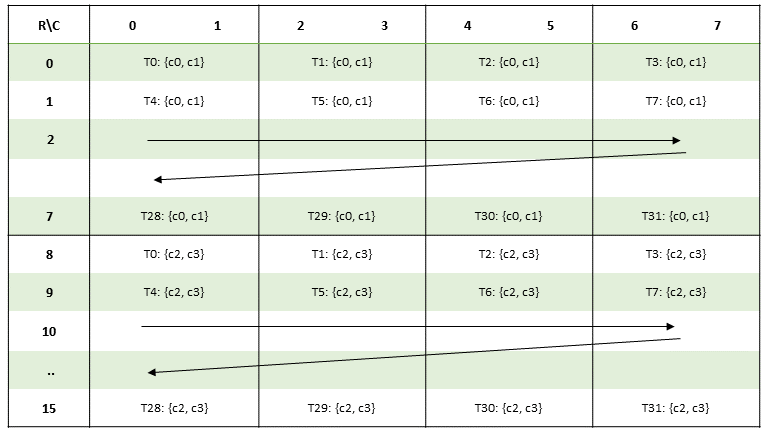
Figure 61 MMA .m16n8k16 fragment layout for accumulator matrix C/D with
.s32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.10. Matrix Fragments for mma.m16n8k32
A warp executing mma.m16n8k32 will compute an MMA operation of shape .m16n8k32.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.s4or.u4:.atype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing two
.b32registers, with each register containing eight.u4/.s4elements from the matrix A.a0, a1, …, a14, a15
The layout of the fragments held by different threads is shown in Figure 62.
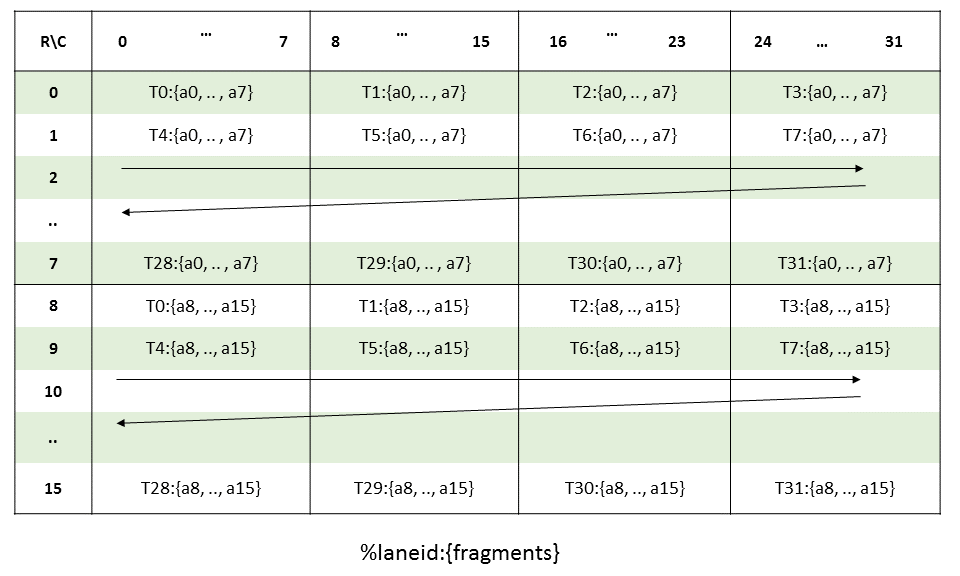
Figure 62 MMA .m16n8k32 fragment layout for matrix A with
.u4/.s4type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where i < 8 groupID + 8 for ai where i >= 8 col = (threadID_in_group * 8) + (i & 0x7) for ai where i = {0,..,15}
.s8or.u8or.e4m3or.e5m2:.atype
Fragment
Elements (low to high)
.s8/.u8A vector expression containing four
.b32registers, with each register containing four.s8/.u8elements from the matrix A.a0, a1, .., a14, a15
.e4m3/.e5m2A vector expression containing four
.b32registers, with each register containing four.e4m3/.e5m2elements from the matrix A.a0, a1, …, a14, a15
The layout of the fragments held by different threads is shown in Figure 63.
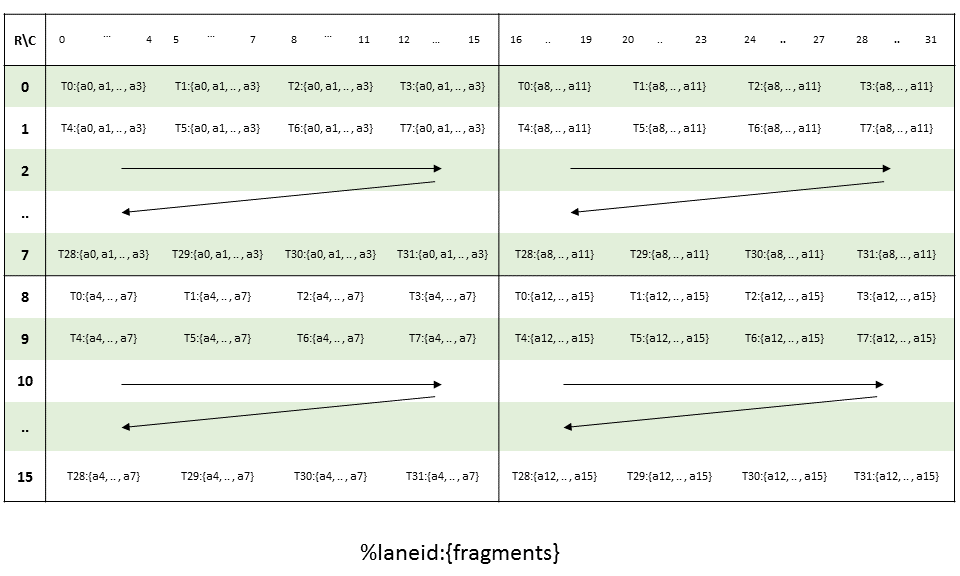
Figure 63 MMA .m16n8k32 fragment layout for matrix A with
.u8/.s8type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 4 || 8 <= i < 12 groupID + 8 otherwise col = (threadID_in_group * 4) + (i & 0x3) for ai where i < 8 (threadID_in_group * 4) + (i & 0x3) + 16 for ai where i >= 8
Multiplicand B:
.s4or.u4:.btype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing a single
.b32register, containing eight.s4/.u4elements from the matrix B.b0, b1, b2, b3, b4, b5, b6, b7
The layout of the fragments held by different threads is shown in Figure 64.
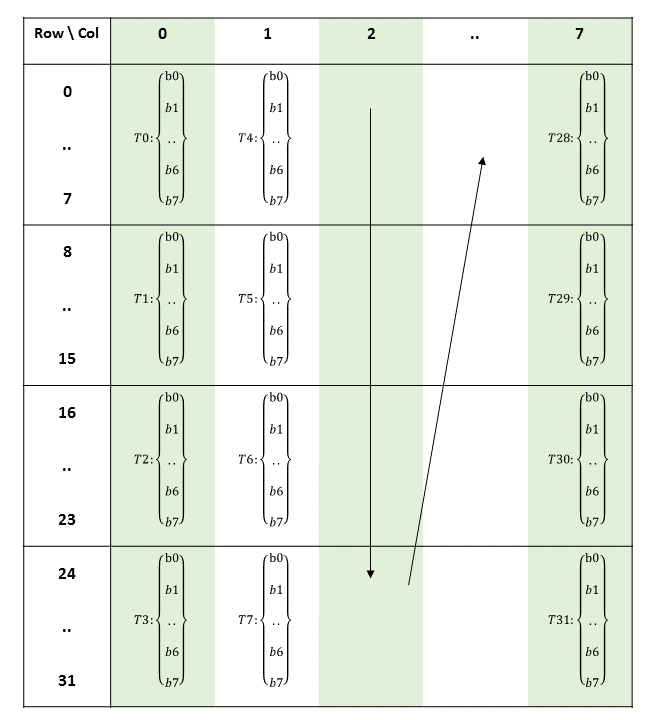
Figure 64 MMA .m16n8k32 fragment layout for matrix B with
.u4/.s4type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 8) + (i & 0x7) for bi where i = {0,..,7} col = groupID
.s8or.u8or.e4m3or.e5m2:.btype
Fragment
Elements (low to high)
.s8/.u8A vector expression containing two
.b32registers, with each register containing four.s8/.u8elements from the matrix B.b0, b1, b2, b3, b4, b5, b6, b7
.e4m3/.e5m2A vector expression containing two
.b32registers, with each register containing four.e4m3/.e5m2elements from the matrix B.b0, b1, b2, b3, b4, b5, b6, b7
The layout of the fragments held by different threads is shown in Figure 65 and Figure 66.
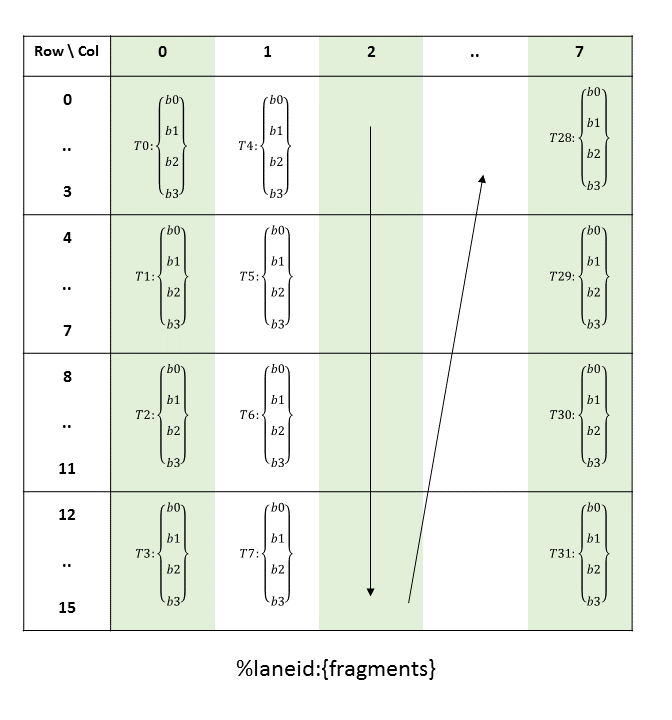
Figure 65 MMA .m16n8k32 fragment layout for rows 0–15 of matrix B with
.u8/.s8type.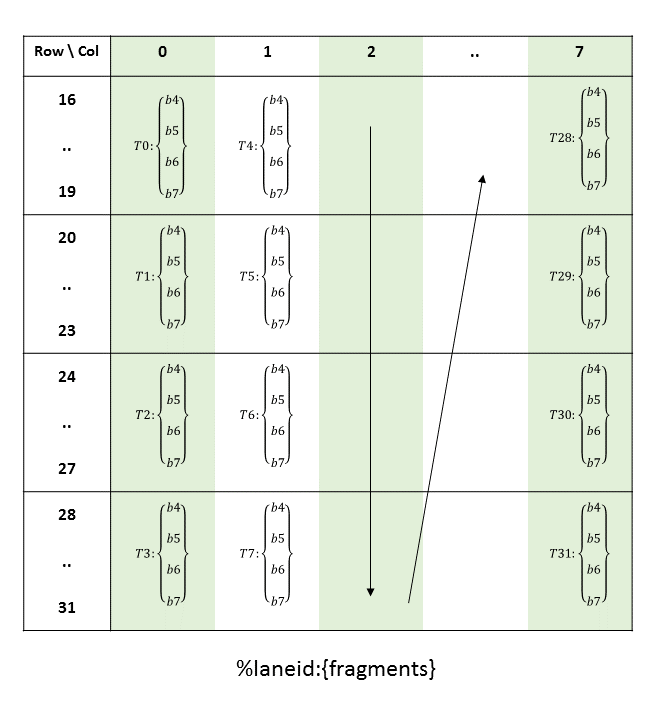
Figure 66 MMA .m16n8k32 fragment layout for rows 16–31 of matrix B with
.u8/.s8type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 4) + (i & 0x3) for bi where i < 4 (threadID_in_group * 4) + (i & 0x3) + 16 for bi where i >= 4 col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing four
.s32registers, containing four.s32elements from the matrix C (or D).c0, c1, c2, c3
.f32A vector expression containing four
.f32registers, containing four.f32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 67.
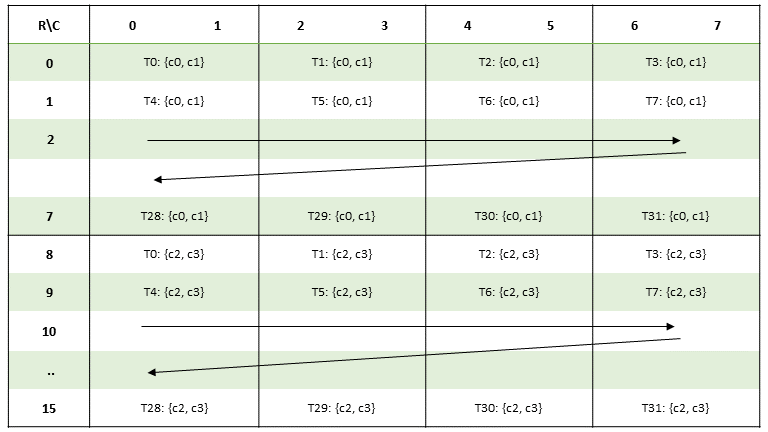
Figure 67 MMA .m16n8k32 fragment layout for accumulator matrix C/D with
.s32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.11. Matrix Fragments for mma.m16n8k64
A warp executing mma.m16n8k64 will compute an MMA operation of shape .m16n8k64.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing four
.b32registers, with each register containing eight.s4/.u4elements from the matrix A.a0, a1, …, a30, a31
The layout of the fragments held by different threads is shown in Figure 68.

Figure 68 MMA .m16n8k64 fragment layout for matrix A with
.u4/.s4type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 8 || 16 <= i < 24 groupID + 8 otherwise col = (threadID_in_group * 8) + (i & 0x7) for ai where i < 16 (threadID_in_group * 8) + (i & 0x7) + 32 for ai where i >= 16
Multiplicand B:
.btype
Fragment
Elements (low to high)
.s4/.u4A vector expression containing two
.b32registers, with each register containing eight.s4/.u4elements from the matrix B.b0, b1, …, b14, b15
The layout of the fragments held by different threads is shown in Figure 69 and Figure 70.
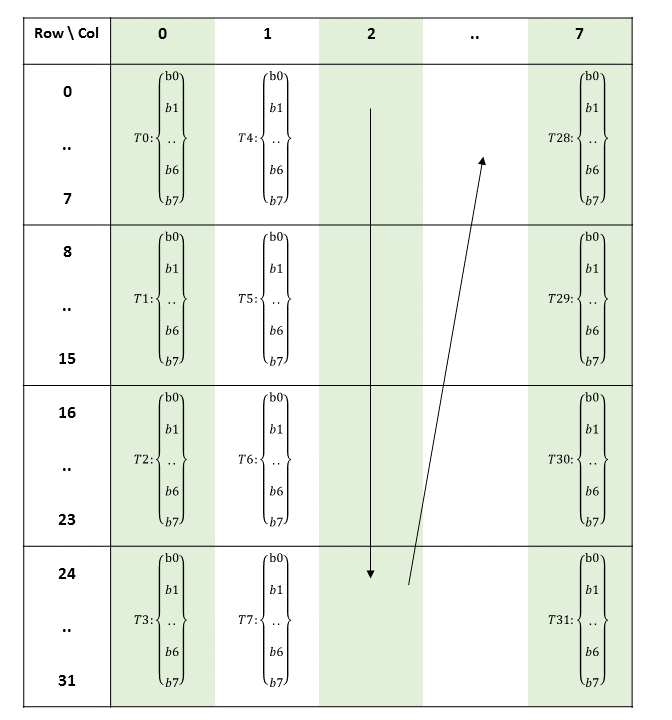
Figure 69 MMA .m16n8k64 fragment layout for rows 0–31 of matrix B with
.u4/.s4type.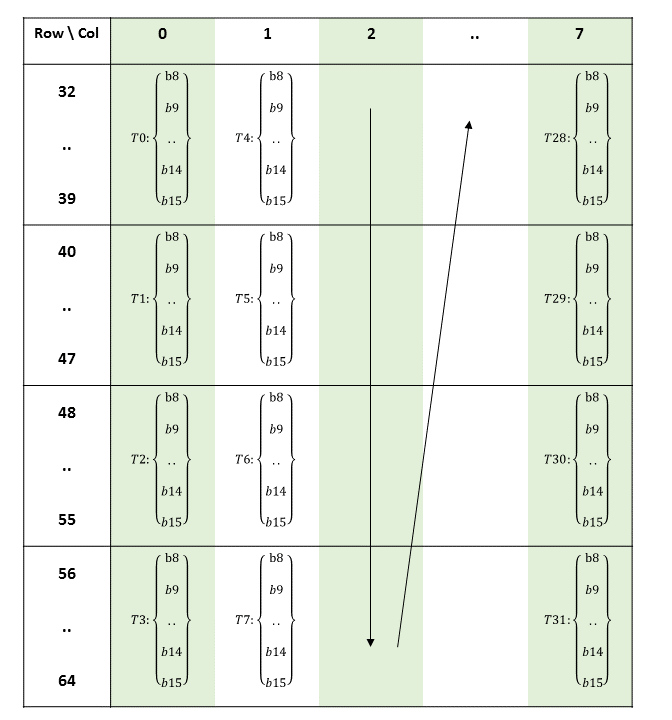
Figure 70 MMA .m16n8k64 fragment layout for rows 32–63 of matrix B with
.u4/.s4type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 8) + (i & 0x7) for bi where i < 8 (threadID_in_group * 8) + (i & 0x7) + 32 for bi where i >= 8 col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing four
.s32registers, containing four.s32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 71.
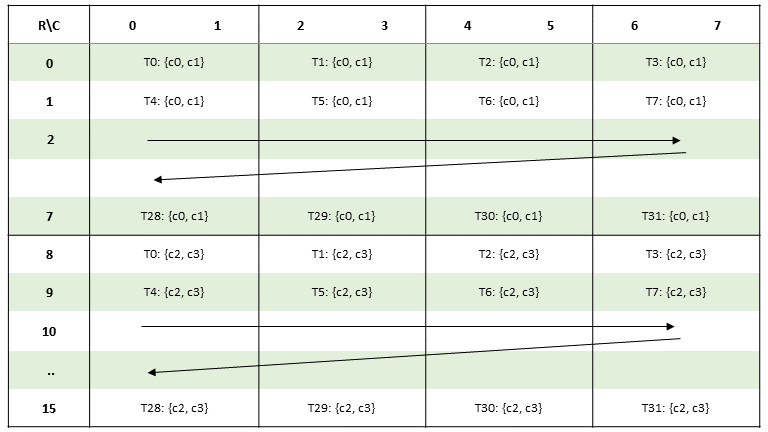
Figure 71 MMA .m16n8k64 fragment layout for accumulator matrix C/D with
.s32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0,..,3}
9.7.13.4.12. Matrix Fragments for mma.m16n8k128
A warp executing mma.m16n8k128 will compute an MMA operation of shape .m16n8k128.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.b1A vector expression containing two
.b32registers, with each register containing thirty two.b1elements from the matrix A.a0, a1, …, a62, a63
The layout of the fragments held by different threads is shown in Figure 72.
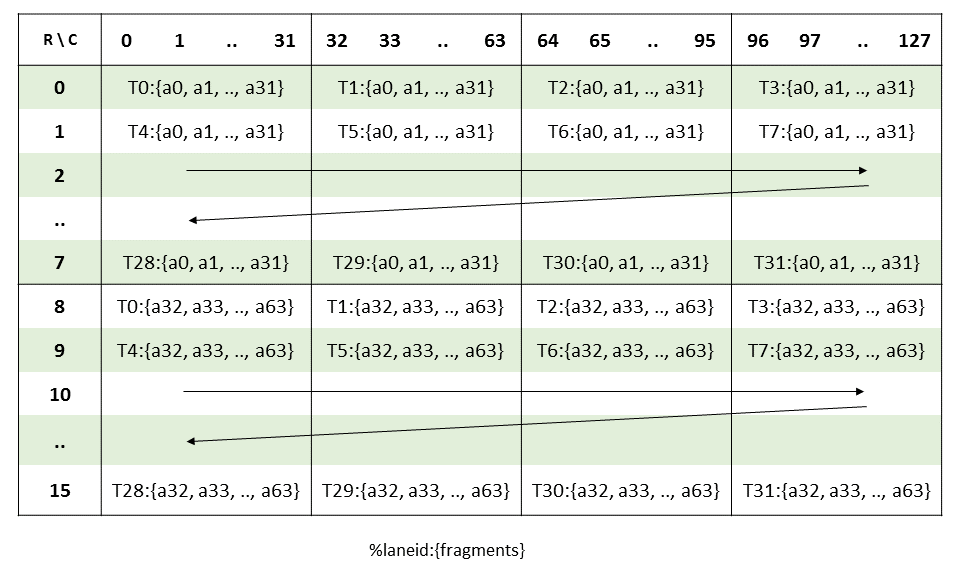
Figure 72 MMA .m16n8k128 fragment layout for matrix A with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where i < 32 groupID + 8 for ai where i >= 32 col = (threadID_in_group * 32) + (i & 0x1F) for ai where i = {0, ...,63}
Multiplicand B:
.btype
Fragment
Elements (low to high)
.b1A vector expression containing a single
.b32register containing thirty two.b1elements from the matrix B.b0, b1, … , b30, b31
The layout of the fragments held by different threads is shown in Figure 73.
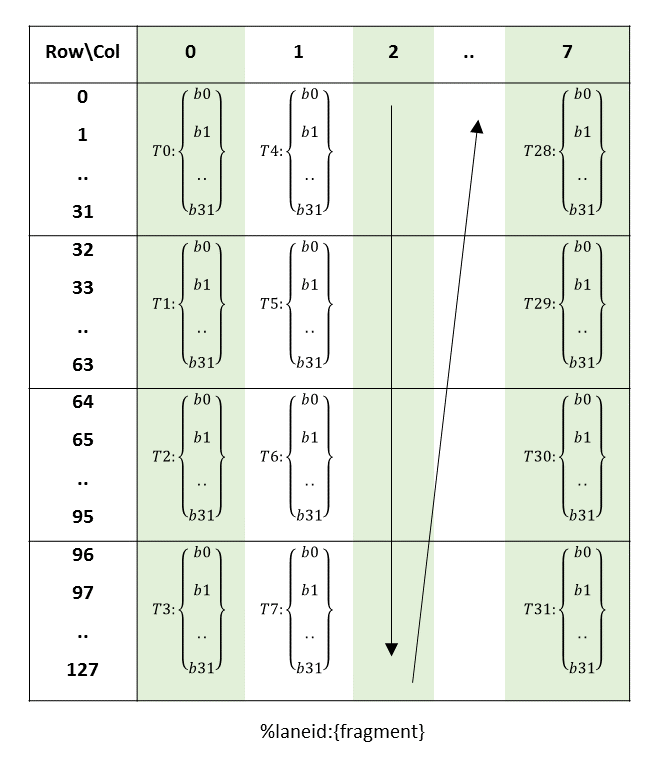
Figure 73 MMA .m16n8k128 fragment layout for matrix B with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 32) + i for bi where i = {0,...,31} col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing four
.s32registers, containing four.s32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 74.
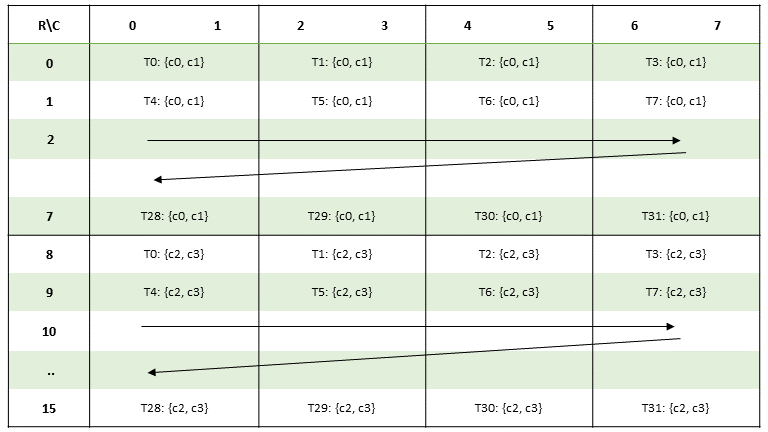
Figure 74 MMA .m16n8k128 fragment layout for accumulator matrix C/D with
.s32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0, 1, 2, 3}
9.7.13.4.13. Matrix Fragments for mma.m16n8k256
A warp executing mma.m16n8k256 will compute an MMA operation of shape .m16n8k256.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements (low to high)
.b1A vector expression containing four
.b32registers, with each register containing thirty two.b1elements from the matrix A.a0, a1, …, a126, a127
The layout of the fragments held by different threads is shown in Figure 75.
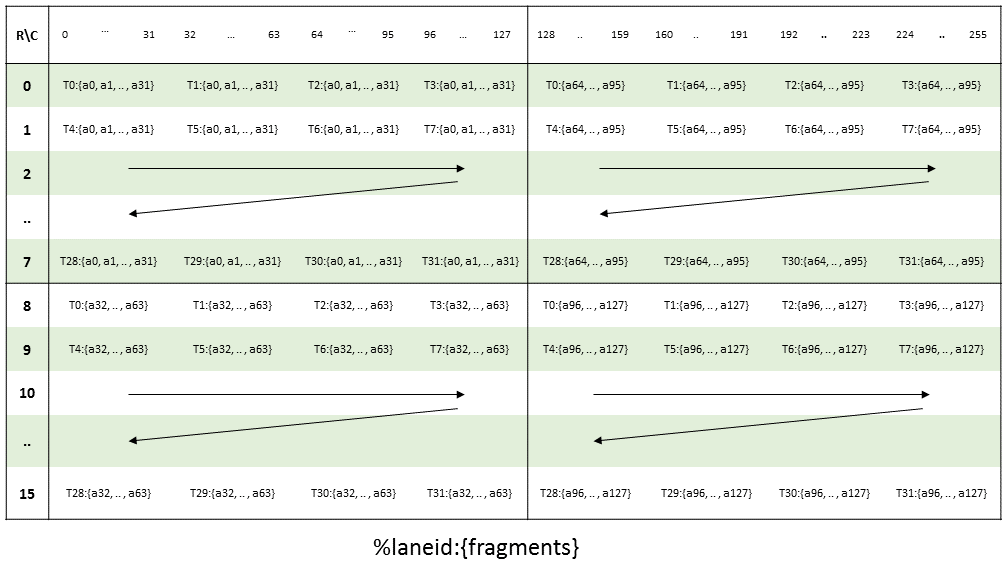
Figure 75 MMA .m16n8k256 fragment layout for matrix A with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 32 || 64 <= i < 96 groupID + 8 otherwise col = (threadID_in_group * 32) + i for ai where i < 64 (threadID_in_group * 32) + (i & 0x1F) + 128 for ai where i >= 64
Multiplicand B:
.btype
Fragment
Elements (low to high)
.b1A vector expression containing two
.b32registers, with each register containing thirty two.b1elements from the matrix B.b0, b1, …, b62, b63
The layout of the fragments held by different threads is shown in Figure 76 and Figure 77.
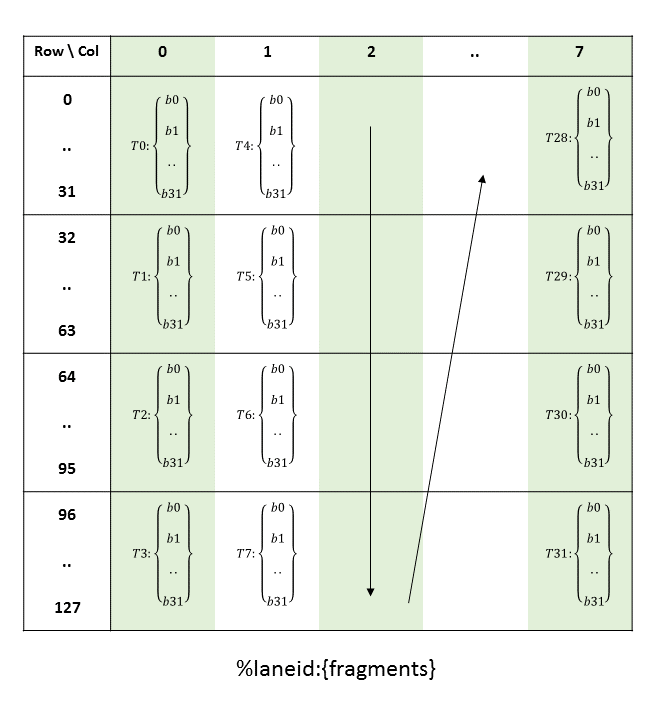
Figure 76 MMA .m16n8k256 fragment layout for rows 0–127 of matrix B with
.b1type.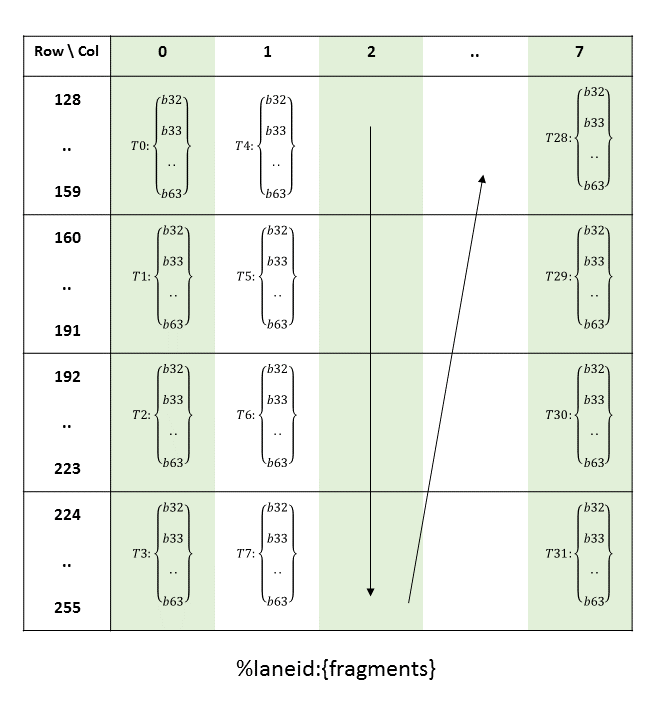
Figure 77 MMA .m16n8k256 fragment layout for rows 128–255 of matrix B with
.b1type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = (threadID_in_group * 32) + (i & 0x1F) for bi where i < 32 (threadID_in_group * 32) + (i & 0x1F) + 128 for bi where i >= 32 col = groupID
Accumulators (C or D):
.ctype / .dtype
Fragment
Elements (low to high)
.s32A vector expression containing four
.s32registers, containing four.s32elements from the matrix C (or D).c0, c1, c2, c3
The layout of the fragments held by different threads is shown in Figure 78.
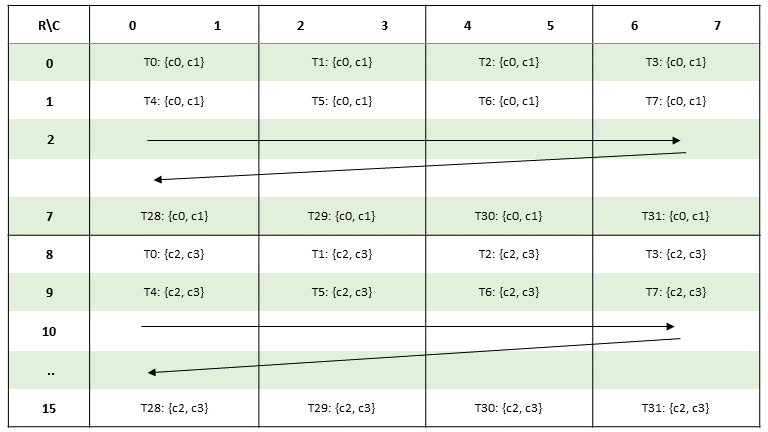
Figure 78 MMA .m16n8k256 fragment layout for accumulator matrix C/D with
.s32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ci where i < 2 groupID + 8 for ci where i >= 2 col = (threadID_in_group * 2) + (i & 0x1) for ci where i = {0, 1, 2, 3}
9.7.13.4.14. Multiply-and-Accumulate Instruction: mma
mma
Perform matrix multiply-and-accumulate operation
Syntax
Half precision floating point type:
mma.sync.aligned.m8n8k4.alayout.blayout.dtype.f16.f16.ctype d, a, b, c;
mma.sync.aligned.m16n8k8.row.col.dtype.f16.f16.ctype d, a, b, c;
mma.sync.aligned.m16n8k16.row.col.dtype.f16.f16.ctype d, a, b, c;
.alayout = {.row, .col};
.blayout = {.row, .col};
.ctype = {.f16, .f32};
.dtype = {.f16, .f32};
Alternate floating point type :
mma.sync.aligned.m16n8k4.row.col.f32.tf32.tf32.f32 d, a, b, c;
mma.sync.aligned.m16n8k8.row.col.f32.atype.btype.f32 d, a, b, c;
mma.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32 d, a, b, c;
mma.sync.aligned.m16n8k32.row.col.f32.f8type.f8type.f32 d, a, b, c;
.atype = {.bf16, .tf32};
.btype = {.bf16, .tf32};
.f8type = {.e4m3, .e5m2};
Double precision floating point type:
mma.sync.aligned.shape.row.col.f64.f64.f64.f64 d, a, b, c;
.shape = {.m8n84, .m16n8k4, .m16n8k8, .m16n8k16};
Integer type:
mma.sync.aligned.shape.row.col{.satfinite}.s32.atype.btype.s32 d, a, b, c;
.shape = {.m8n8k16, .m16n8k16, .m16n8k32}
.atype = {.u8, .s8};
.btype = {.u8, .s8};
mma.sync.aligned.shape.row.col{.satfinite}.s32.atype.btype.s32 d, a, b, c;
.shape = {.m8n8k32, .m16n8k32, .m16n8k64}
.atype = {.u4, .s4};
.btype = {.u4, .s4};
Single bit:
mma.sync.aligned.shape.row.col.s32.b1.b1.s32.bitOp.popc d, a, b, c;
.bitOp = {.xor, .and}
.shape = {.m8n8k128, .m16n8k128, .m16n8k256}
Description
Perform a MxNxK matrix multiply and accumulate operation, D = A*B+C, where the A matrix is
MxK, the B matrix is KxN, and the C and D matrices are MxN.
A warp executing mma.sync.m8n8k4 instruction computes 4 matrix multiply and accumulate
operations. Rest of the mma.sync operations compute a single matrix mutliply and accumulate
operation per warp.
For single-bit mma.sync, multiplication is replaced by a sequence of logical operations;
specifically, mma.xor.popcand mma.and.popc computes the XOR, AND respectively of a k-bit
row of A with a k-bit column of B, then counts the number of set bits in the result (popc). This
result is added to the corresponding element of C and written into D.
Operands a and b represent two multiplicand matrices A and B, while c and d
represent the accumulator and destination matrices, distributed across the threads in warp.
The registers in each thread hold a fragment of matrix as described in Matrix multiply-accumulate operation using mma instruction.
The qualifiers .dtype, .atype, .btype and .ctype indicate the data-type of the
elements in the matrices D, A, B and C respectively. Specific shapes have type restrictions :
.m8n8k4: When.ctypeis.f32,.dtypemust also be.f32..m16n8k8:.dtypemust be the same as.ctype..atypemust be the same as.btype.
The qualifiers .alayout and .blayout indicate the row-major or column-major layouts of
matrices A and B respectively.
- Precision and rounding :
.f16floating point operations:Element-wise multiplication of matrix A and B is performed with at least single precision. When
.ctypeor.dtypeis.f32, accumulation of the intermediate values is performed with at least single precision. When both.ctypeand.dtypeare specified as.f16, the accumulation is performed with at least half precision.The accumulation order, rounding and handling of subnormal inputs are unspecified.
.e4m3and.e5m2floating point operations :Element-wise multiplication of matrix A and B is performed with specified precision. Accumulation of the intermediate values is performed with at least single precision.
The accumulation order, rounding, and handling of subnormal inputs are unspecified.
.bf16and.tf32floating point operations :Element-wise multiplication of matrix A and B is performed with specified precision. Accumulation of the intermediate values is performed with at least single precision.
The accumulation order, rounding, and handling of subnormal inputs are unspecified.
.f64floating point operations :
Precision of the element-wise multiplication and addition operation is identical to that of .f64
precision fused multiply-add. Supported rounding modifiers are :
.rn: mantissa LSB rounds to nearest even. This is the default..rz: mantissa LSB rounds towards zero..rm: mantissa LSB rounds towards negative infinity..rp: mantissa LSB rounds towards positive infinity.Integer operations :
The integer
mmaoperation is performed with.s32accumulators. The.satfinitequalifier indicates that on overflow, the accumulated value is limited to the range MIN_INT32..MAX_INT32 (where the bounds are defined as the minimum negative signed 32-bit integer and the maximum positive signed 32-bit integer respectively).If
.satfiniteis not specified, the accumulated value is wrapped instead.
The mandatory .sync qualifier indicates that mma instruction causes the executing thread to
wait until all threads in the warp execute the same mma instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
mma instruction. In conditionally executed code, a mma instruction should only be used if it
is known that all threads in the warp evaluate the condition identically, otherwise behavior is
undefined.
The behavior of mma instruction is undefined if all threads in the same warp do not use the same
qualifiers, or if any thread in the warp has exited.
Notes
Programs using double precision floating point mma instruction with shapes .m16n8k4,
.m16n8k8, and .m16n8k16 require at least 64 registers for compilation.
PTX ISA Notes
Introduced in PTX ISA version 6.4.
.f16 floating point type mma operation with .m8n8k4 shape introduced in PTX ISA version
6.4.
.f16 floating point type mma operation with .m16n8k8 shape introduced in PTX ISA version
6.5.
.u8/.s8 integer type mma operation with .m8n8k16 shape introduced in PTX ISA version
6.5.
.u4/.s4 integer type mma operation with .m8n8k32 shape introduced in PTX ISA version
6.5.
.f64 floating point type mma operation with .m8n8k4 shape introduced in PTX ISA version
7.0.
.f16 floating point type mma operation with .m16n8k16 shape introduced in PTX ISA
version 7.0.
.bf16 alternate floating point type mma operation with .m16n8k8 and .m16n8k16 shapes
introduced in PTX ISA version 7.0.
.tf32 alternate floating point type mma operation with .m16n8k4 and .m16n8k8 shapes
introduced in PTX ISA version 7.0.
.u8/.s8 integer type mma operation with .m16n8k16 and .m16n8k32 shapes introduced in
PTX ISA version 7.0.
.u4/.s4 integer type mma operation with .m16n8k32 and .m16n8k64 shapes introduced in
PTX ISA version 7.0.
.b1 single-bit integer type mma operation with .m8n8k128, .m16n8k128 and
.m16n8k256 shapes introduced in PTX ISA version 7.0.
Support for .and operation in single-bit mma introduced in PTX ISA version 7.1.
.f64 floating point typemma operation with .m16n8k4, .m16n8k8, and .m16n8k16
shapes introduced in PTX ISA version 7.8.
Support for .e4m3 and .e5m2 alternate floating point type mma operation introduced in
PTX ISA version 8.4.
Target ISA Notes
Requires sm_70 or higher.
.f16 floating point type mma operation with .m8n8k4 shape requires sm_70 or higher.
Note
mma.sync.m8n8k4 is optimized for target architecture sm_70 and may have substantially
reduced performance on other target architectures.
.f16 floating point type mma operation with .m16n8k8 shape requires sm_75 or higher.
.u8/.s8 integer type mma operation with .m8n8k16 shape requires sm_75 or higher.
.u4/.s4 integer type mma operation with .m8n8k32 shape sm_75 or higher.
.b1 single-bit integer type mma operation with .m8n8k128 shape sm_75 or higher.
.f64 floating point type mma operation with .m8n8k4 shape requires sm_80 or higher.
.f16 floating point type mma operation with .m16n8k16 shape requires sm_80 or
higher.
.bf16 alternate floating point type mma operation with .m16n8k8 and .m16n8k16 shapes
requires sm_80 or higher.
.tf32 alternate floating point type mma operation with .m16n8k4 and .m16n8k8 shapes
requires sm_80 or higher.
.u8/.s8 integer type mma operation with .m16n8k16 and .m16n8k32 shapes requires
sm_80 or higher.
.u4/.s4 integer type mma operation with .m16n8k32 and .m16n8k64 shapes requires
sm_80 or higher.
.b1 single-bit integer type mma operation with .m16n8k128 and .m16n8k256 shapes
requires sm_80 or higher.
.and operation in single-bit mma requires sm_80 or higher.
.f64 floating point type mma operation with .m16n8k4, .m16n8k8, and .m16n8k16
shapes require sm_90 or higher.
.e4m3 and .e5m2 alternate floating point type mma operation requires sm_89 or higher.
Examples of half precision floating point type
// f16 elements in C and D matrix
.reg .f16x2 %Ra<2> %Rb<2> %Rc<4> %Rd<4>
mma.sync.aligned.m8n8k4.row.col.f16.f16.f16.f16
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
// f16 elements in C and f32 elements in D
.reg .f16x2 %Ra<2> %Rb<2> %Rc<4>
.reg .f32 %Rd<8>
mma.sync.aligned.m8n8k4.row.col.f32.f16.f16.f16
{%Rd0, %Rd1, %Rd2, %Rd3, %Rd4, %Rd5, %Rd6, %Rd7},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
// f32 elements in C and D
.reg .f16x2 %Ra<2>, %Rb<1>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k8.row.col.f32.f16.f16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .f16x2 %Ra<4>, %Rb<2>, %Rc<2>, %Rd<2>;
mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16
{%Rd0, %Rd1},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1};
.reg .f16 %Ra<4>, %Rb<2>;
.reg .f32 %Rc<2>, %Rd<2>;
mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
Examples of alternate floating point type
.reg .b32 %Ra<2>, %Rb<1>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k4.row.col.f32.tf32.tf32.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .f16x2 %Ra<2>, %Rb<1>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k8.row.col.f32.bf16.bf16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .b32 %Ra<2>, %Rb<1>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k8.row.col.f32.tf32.tf32.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Rb2, %Rb3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .f16x2 %Ra<2>, %Rb<1>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .b32 %Ra<4>, %Rb<4>;
.reg .f32 %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k32.row.col.f32.e4m3.e5m2.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
Examples of integer type
.reg .b32 %Ra, %Rb, %Rc<2>, %Rd<2>;
// s8 elements in A and u8 elements in B
mma.sync.aligned.m8n8k16.row.col.satfinite.s32.s8.u8.s32
{%Rd0, %Rd1},
{%Ra},
{%Rb},
{%Rc0, %Rc1};
// u4 elements in A and B matrix
mma.sync.aligned.m8n8k32.row.col.satfinite.s32.u4.u4.s32
{%Rd0, %Rd1},
{%Ra},
{%Rb},
{%Rc0, %Rc1};
// s8 elements in A and u8 elements in B
.reg .b32 %Ra<2>, %Rb, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k16.row.col.satfinite.s32.s8.u8.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb},
{%Rc0, %Rc1, %Rc2, %Rc3};
// u4 elements in A and s4 elements in B
.reg .b32 %Ra<2>, %Rb, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k32.row.col.satfinite.s32.u4.s4.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb},
{%Rc0, %Rc1, %Rc2, %Rc3};
// s8 elements in A and s8 elements in B
.reg .b32 %Ra<4>, %Rb<2>, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k32.row.col.satfinite.s32.s8.s8.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
// u8 elements in A and u8 elements in B
.reg .b32 %Ra<4>, %Rb<2>, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k64.row.col.satfinite.s32.u4.u4.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1 },
{%Rc0, %Rc1, %Rc2, %Rc3};
Examples of single bit type
// b1 elements in A and B
.reg .b32 %Ra, %Rb, %Rc<2>, %Rd<2>;
mma.sync.aligned.m8n8k128.row.col.s32.b1.b1.s32.and.popc
{%Rd0, %Rd1},
{%Ra},
{%Rb},
{%Rc0, %Rc1};
// b1 elements in A and B
.reg .b32 %Ra, %Rb, %Rc<2>, %Rd<2>;
mma.sync.aligned.m8n8k128.row.col.s32.b1.b1.s32.xor.popc
{%Rd0, %Rd1},
{%Ra},
{%Rb},
{%Rc0, %Rc1};
.reg .b32 %Ra<2>, %Rb, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k128.row.col.s32.b1.b1.s32.xor.popc
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .b32 %Ra<2>, %Rb, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k128.row.col.s32.b1.b1.s32.and.popc
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .b32 %Ra<4>, %Rb<2>, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k256.row.col.s32.b1.b1.s32.xor.popc
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
.reg .b32 %Ra<4>, %Rb<2>, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k256.row.col.s32.b1.b1.s32.and.popc
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
Examples of .f64 floating point type
.reg .f64 %Ra, %Rb, %Rc<2>, %Rd<2>;
mma.sync.aligned.m8n8k4.row.col.f64.f64.f64.f64
{%Rd0, %Rd1},
{%Ra},
{%Rb},
{%Rc0, %Rc1};
.reg .f64 %Ra<8>, %Rb<4>, %Rc<4>, %Rd<4>;
mma.sync.aligned.m16n8k4.row.col.f64.f64.f64.f64.rn
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0},
{%Rc0, %Rc1, %Rc2, %Rc3};
mma.sync.aligned.m16n8k8.row.col.f64.f64.f64.f64.rn
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3};
mma.sync.aligned.m16n8k16.row.col.f64.f64.f64.f64.rn
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3, %Ra4, %Ra5, %Ra6, %Ra7},
{%Rb0, %Rb1, %Rb2, %Rb3},
{%Rc0, %Rc1, %Rc2, %Rc3};
9.7.13.4.15. Warp-level matrix load instruction: ldmatrix
ldmatrix
Collectively load one or more matrices from shared memory for mma instruction
Syntax
ldmatrix.sync.aligned.shape.num{.trans}{.ss}.type r, [p];
.shape = {.m8n8};
.num = {.x1, .x2, .x4};
.ss = {.shared{::cta}};
.type = {.b16};
Description
Collectively load one or more matrices across all threads in a warp from the location indicated by
the address operand p, from .shared state space into destination register r. If no state
space is provided, generic addressing is used, such that the address in p points into
.shared space. If the generic address doesn’t fall in .shared state space, then the behavior
is undefined.
The .shape qualifier indicates the dimensions of the matrices being loaded. Each matrix element
holds 16-bit data as indicated by the .type qualifier.
The values .x1, .x2 and .x4 for .num indicate one, two or four matrices
respectively.
The mandatory .sync qualifier indicates that ldmatrix causes the executing thread to wait
until all threads in the warp execute the same ldmatrix instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
ldmatrix instruction. In conditionally executed code, an ldmatrix instruction should only be
used if it is known that all threads in the warp evaluate the condition identically, otherwise the
behavior is undefined.
The behavior of ldmatrix is undefined if all threads do not use the same qualifiers, or if any
thread in the warp has exited.
The destination operand r is a brace-enclosed vector expression consisting of 1, 2, or 4 32-bit
registers as per the value of .num. Each component of the vector expression holds a fragment
from the corresponding matrix.
Supported addressing modes for p are described in Addresses as Operands.
Consecutive instances of row need not be stored contiguously in memory. The eight addresses required
for each matrix are provided by eight threads, depending upon the value of .num as shown in the
following table. Each address corresponds to the start of a matrix row. Addresses addr0–addr7
correspond to the rows of the first matrix, addresses addr8–addr15 correspond to the rows of the
second matrix, and so on.
|
Threads 0–7 |
Threads 8–15 |
Threads 16–23 |
Threads 24–31 |
|---|---|---|---|---|
|
addr0–addr7 |
– |
– |
– |
|
addr0–addr7 |
addr8–addr15 |
– |
– |
|
addr0–addr7 |
addr8–addr15 |
addr16–addr23 |
addr24–addr31 |
Note
For .target sm_75 or below, all threads must contain valid addresses. Otherwise, the behavior
is undefined. For .num = .x1 and .num = .x2, addresses contained in lower threads can be
copied to higher threads to achieve the expected behavior.
When reading 8x8 matrices, a group of four consecutive threads loads 16 bytes. The matrix addresses must be naturally aligned accordingly.
Each thread in a warp loads fragments of a row, with thread 0 receiving the first fragment in its
register r, and so on. A group of four threads loads an entire row of the matrix as shown in
Figure 79.
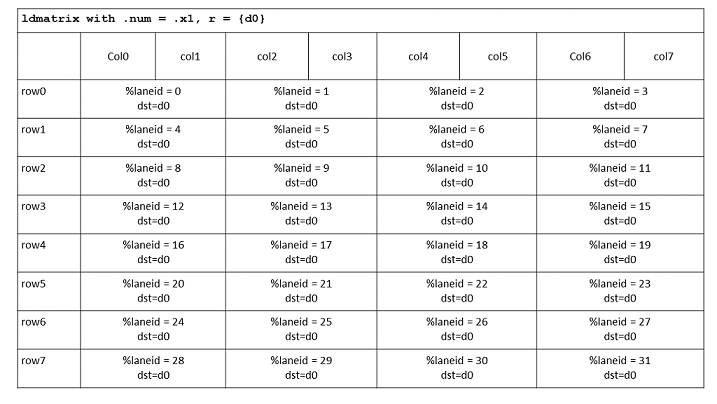
Figure 79 ldmatrix fragment layout
When .num = .x2, the elements of the second matrix are loaded in the next destination
register in each thread as per the layout in above table. Similarly, when .num = .x4,
elements of the third and fourth matrices are loaded in the subsequent destination registers in each
thread.
Optional qualifier .trans indicates that the matrix is loaded in column-major format.
The ldmatrix instruction is treated as a weak memory operation in the Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 6.5.
Support for ::cta sub-qualifier introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_75 or higher.
Examples
// Load a single 8x8 matrix using 64-bit addressing
.reg .b64 addr;
.reg .b32 d;
ldmatrix.sync.aligned.m8n8.x1.shared::cta.b16 {d}, [addr];
// Load two 8x8 matrices in column-major format
.reg .b64 addr;
.reg .b32 d<2>;
ldmatrix.sync.aligned.m8n8.x2.trans.shared.b16 {d0, d1}, [addr];
// Load four 8x8 matrices
.reg .b64 addr;
.reg .b32 d<4>;
ldmatrix.sync.aligned.m8n8.x4.b16 {d0, d1, d2, d3}, [addr];
9.7.13.4.16. Warp-level matrix store instruction: stmatrix
stmatrix
Collectively store one or more matrices to shared memory.
Syntax
stmatrix.sync.aligned.shape.num{.trans}{.ss}.type [p], r;
.shape = {.m8n8};
.num = {.x1, .x2, .x4};
.ss = {.shared{::cta}};
.type = {.b16};
Description
Collectively store one or more matrices across all threads in a warp to the location indicated by
the address operand p, in .shared state space. If no state space is provided, generic
addressing is used, such that the address in p points into .shared space. If the generic
address doesn’t fall in .shared state space, then the behavior is undefined.
The .shape qualifier indicates the dimensions of the matrices being loaded. Each matrix element
holds 16-bit data as indicated by the .type qualifier.
The values .x1, .x2 and .x4 for .num indicate one, two or four matrices
respectively.
The mandatory .sync qualifier indicates that stmatrix causes the executing thread to wait
until all threads in the warp execute the same stmatrix instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
stmatrix instruction. In conditionally executed code, an stmatrix instruction should only be
used if it is known that all threads in the warp evaluate the condition identically, otherwise the
behavior is undefined.
The behavior of stmatrix is undefined if all threads do not use the same qualifiers, or if any
thread in the warp has exited.
The source operand r is a brace-enclosed vector expression consisting of 1, 2, or 4 32-bit
registers as per the value of .num. Each component of the vector expression holds a fragment
from the corresponding matrix.
Supported addressing modes for p are described in Addresses as Operands.
Consecutive instances of row need not be stored contiguously in memory. The eight addresses required
for each matrix are provided by eight threads, depending upon the value of .num as shown in the
following table. Each address corresponds to the start of a matrix row. Addresses addr0–addr7
correspond to the rows of the first matrix, addresses addr8–addr15 correspond to the rows of the
second matrix, and so on.
|
Threads 0–7 |
Threads 8–15 |
Threads 16–23 |
Threads 24–31 |
|---|---|---|---|---|
|
addr0–addr7 |
– |
– |
– |
|
addr0–addr7 |
addr8–addr15 |
– |
– |
|
addr0–addr7 |
addr8–addr15 |
addr16–addr23 |
addr24–addr31 |
When storing 8x8 matrices, a group of four consecutive threads stores 16 bytes. The matrix addresses must be naturally aligned accordingly.
Each thread in a warp stores fragments of a row, with thread 0 storing the first fragment from its
register r, and so on. A group of four threads stores an entire row of the matrix as shown in
Figure 80.
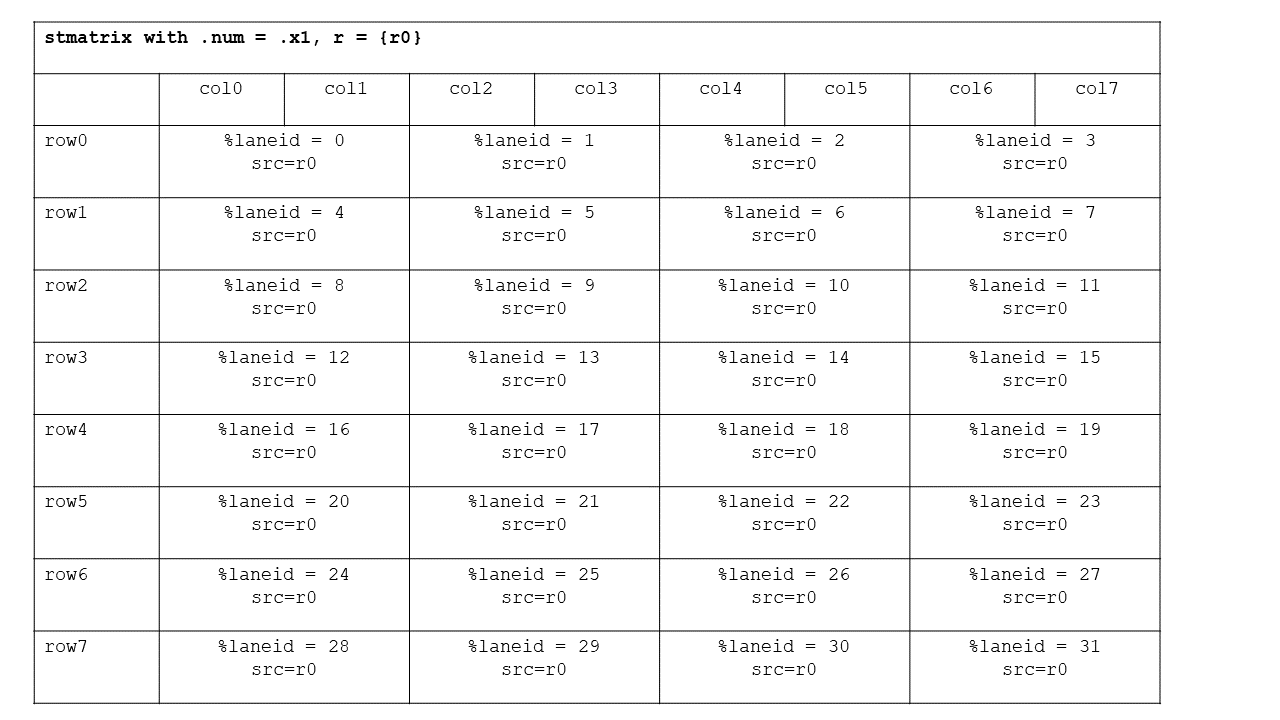
Figure 80 stmatrix fragment layout
When .num = .x2, the elements of the second matrix are storedd from the next source register
in each thread as per the layout in above table. Similarly, when .num = .x4, elements of the
third and fourth matrices are stored from the subsequent source registers in each thread.
Optional qualifier .trans indicates that the matrix is stored in column-major format.
The stmatrix instruction is treated as a weak memory operation in the Memory Consistency Model.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
// Store a single 8x8 matrix using 64-bit addressing
.reg .b64 addr;
.reg .b32 r;
stmatrix.sync.aligned.m8n8.x1.shared.b16 [addr], {r};
// Store two 8x8 matrices in column-major format
.reg .b64 addr;
.reg .b32 r<2>;
stmatrix.sync.aligned.m8n8.x2.trans.shared::cta.b16 [addr], {r0, r1};
// Store four 8x8 matrices
.reg .b64 addr;
.reg .b32 r<4>;
stmatrix.sync.aligned.m8n8.x4.b16 [addr], {r0, r1, r2, r3};
9.7.13.4.17. Warp-level matrix transpose instruction: movmatrix
movmatrix
Transpose a matrix in registers across the warp.
Syntax
movmatrix.sync.aligned.shape.trans.type d, a;
.shape = {.m8n8};
.type = {.b16};
Description
Move a row-major matrix across all threads in a warp, reading elements from source a, and
writing the transposed elements to destination d.
The .shape qualifier indicates the dimensions of the matrix being transposed. Each matrix
element holds 16-bit data as indicated by the .type qualifier.
The mandatory .sync qualifier indicates that movmatrix causes the executing thread to wait
until all threads in the warp execute the same movmatrix instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
movmatrix instruction. In conditionally executed code, a movmatrix instruction should only
be used if it is known that all threads in the warp evaluate the condition identically, otherwise
the behavior is undefined.
Operands a and d are 32-bit registers containing fragments of the input matrix and the
resulting matrix respectively. The mandatory qualifier .trans indicates that the resulting
matrix in d is a transpose of the input matrix specified by a.
Each thread in a warp holds a fragment of a row of the input matrix, with thread 0 holding the first
fragment in register a, and so on. A group of four threads holds an entire row of the input
matrix as shown in Figure 81.
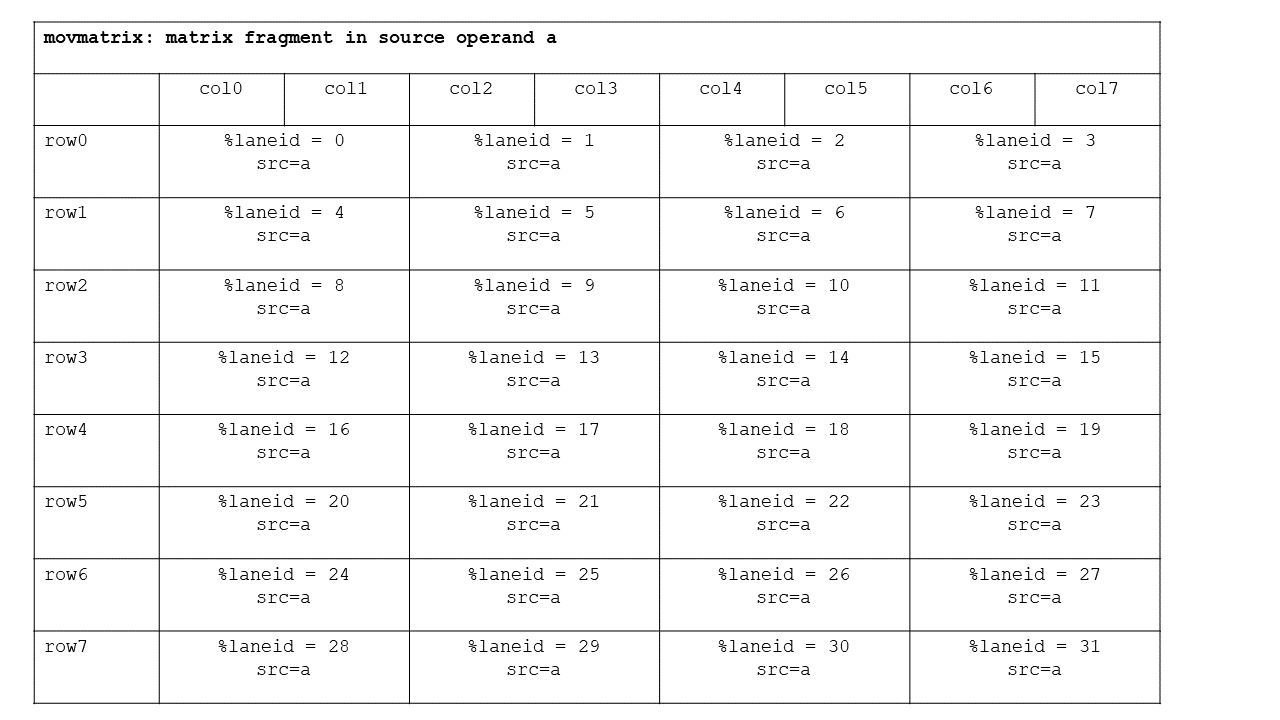
Figure 81 movmatrix source matrix fragment layout
Each thread in a warp holds a fragment of a column of the result matrix, with thread 0 holding the
first fragment in register d, and so on. A group of four threads holds an entire column of the
result matrix as shown in Figure 82.
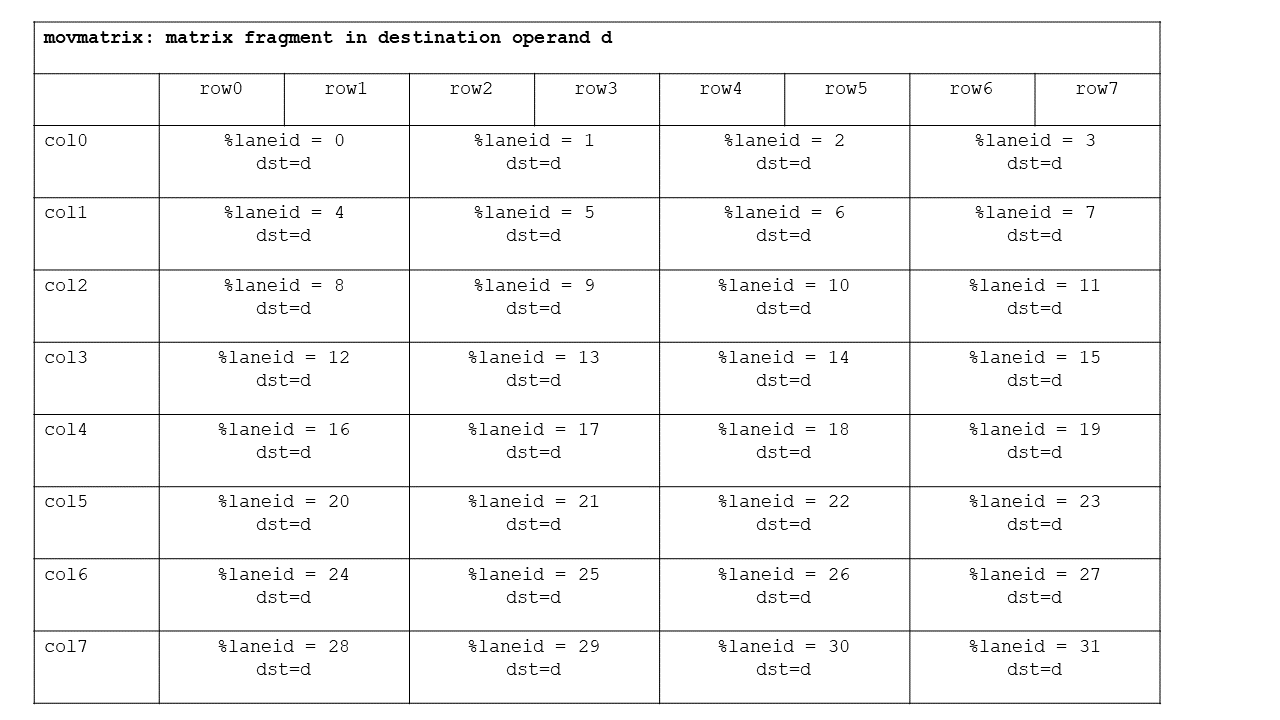
Figure 82 movmatrix result matrix fragment layout
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_75 or higher.
Examples
.reg .b32 d, a;
movmatrix.sync.aligned.m8n8.trans.b16 d, a;
9.7.13.5. Matrix multiply-accumulate operation using mma.sp instruction with sparse matrix A
This section describes warp-level mma.sp instruction with sparse matrix A. This variant of the
mma operation can be used when A is a structured sparse matrix with 50% zeros in each row
distributed in a shape-specific granularity. For an MxNxK sparse mma.sp operation, the
MxK matrix A is packed into MxK/2 elements. For each K-wide row of matrix A, 50% elements
are zeros and the remaining K/2 non-zero elements are packed in the operand representing
matrix A. The mapping of these K/2 elements to the corresponding K-wide row is provided explicitly
as metadata.
9.7.13.5.1. Sparse matrix storage
Granularity of sparse matrix A is defined as the ratio of the number of non-zero elements in a
sub-chunk of the matrix row to the total number of elements in that sub-chunk where the size of the
sub-chunk is shape-specific. For example, in a 16x16 matrix A, sparsity is expected to be at 2:4
granularity, i.e. each 4-element vector (i.e. a sub-chunk of 4 consecutive elements) of a matrix row
contains 2 zeros. Index of each non-zero element in a sub-chunk is stored in the metadata
operand. In a group of four consecutive threads, one or more threads store the metadata for the
whole group depending upon the matrix shape. These threads are specified using an additional
sparsity selector operand.
Figure 83 shows an example of a 16x16 matrix A represented in sparse format and sparsity selector indicating which thread in a group of four consecutive threads stores the metadata.
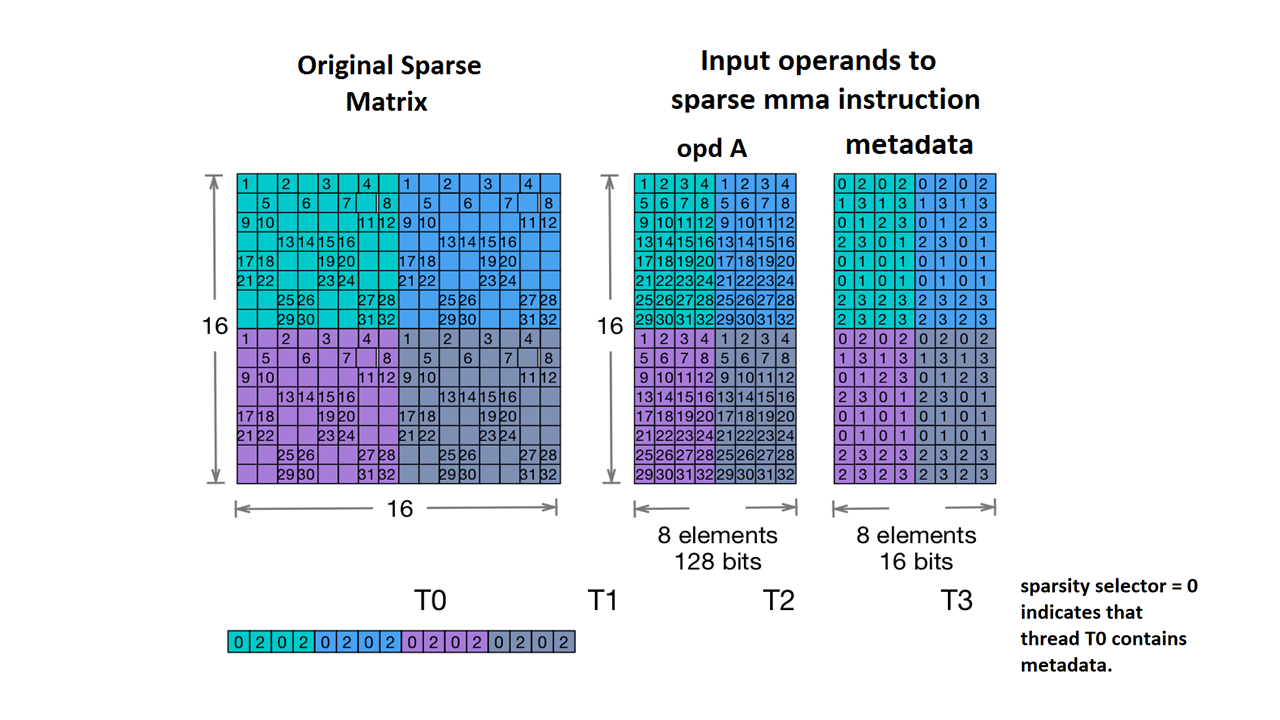
Figure 83 Sparse MMA storage example
Granularities for different matrix shapes and data types are described below.
Sparse mma.sp with half-precision and .bf16 type
For the .m16n8k16 and .m16n8k32mma.sp operations, matrix A is structured sparse at a
granularity of 2:4. In other words, each chunk of four adjacent elements in a row of matrix A has
two zeros and two non-zero elements. Only the two non-zero elements are stored in the operand
representing matrix A and their positions in the four-wide chunk in matrix A are indicated by two
2-bit indices in the metadata operand.
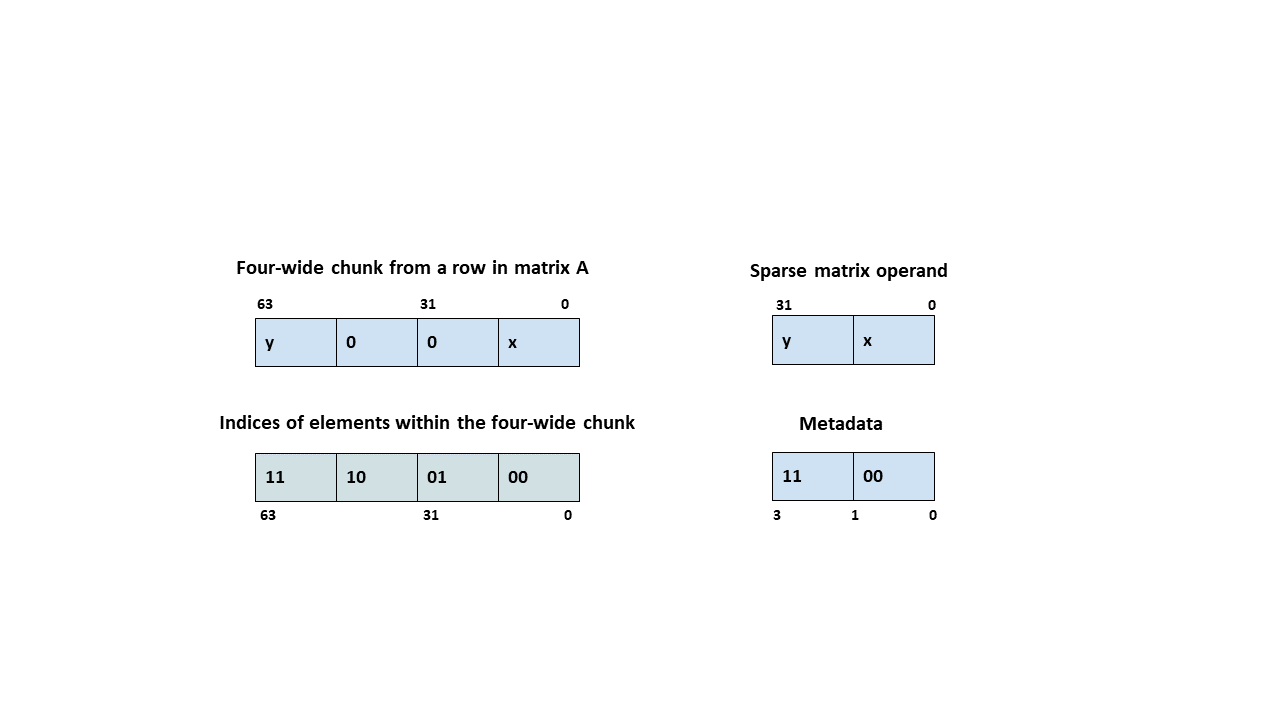
Figure 84 Sparse MMA metadata example for .f16/.bf16 type.
The sparsity selector indicates the threads which contribute metadata as listed below:
m16n8k16: One thread within a group of four consecutive threads contributes the metadata for the entire group. This thread is indicated by a value in {0, 1, 2, 3}.m16n8k32: A thread-pair within a group of four consecutive threads contributes the sparsity metadata. Hence, the sparsity selector must be either 0 (threads T0, T1) or 1 (threads T2, T3); any other value results in an undefined behavior.
Sparse mma.sp with .tf32 type
When matrix A has .tf32 elements, matrix A is structured sparse at a granularity of 1:2. In
other words, each chunk of two adjacent elements in a row of matrix A has one zero and one non-zero
element. Only the non-zero elements are stored in the operand for matrix A and their positions in a
two-wide chunk in matrix A are indicated by the 4-bit index in the metadata. 0b1110 and
0b0100 are the only meaningful index values; any other values result in an undefined behavior.
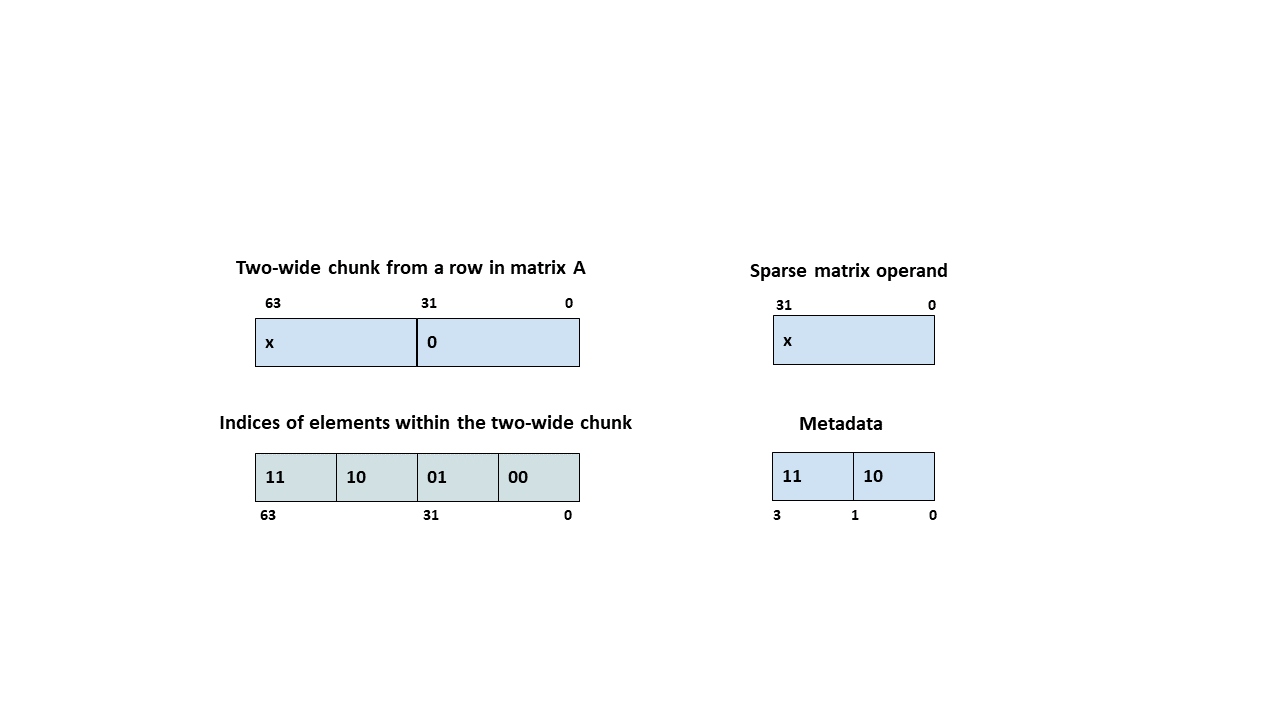
Figure 85 Sparse MMA metadata example for .tf32 type.
The sparsity selector indicates the threads which contribute metadata as listed below:
m16n8k8: One thread within a group of four consecutive threads contributes the metadata for the entire group. This thread is indicated by a value in {0, 1, 2, 3}.m16n8k16: A thread-pair within a group of four consecutive threads contributes the sparsity metadata. Hence, the sparsity selector must be either 0 (threads T0, T1) or 1 (threads T2, T3); any other value results in an undefined behavior.
Sparse mma.sp with integer type
When matrices A and B have .u8/.s8 elements, matrix A is structured sparse at a granularity
of 2:4. In other words, each chunk of four adjacent elements in a row of matrix A have two zeroes
and two non-zero elements. Only the two non-zero elements are stored in sparse matrix and their
positions in the four-wide chunk are indicated by two 2-bit indices in the metadata.
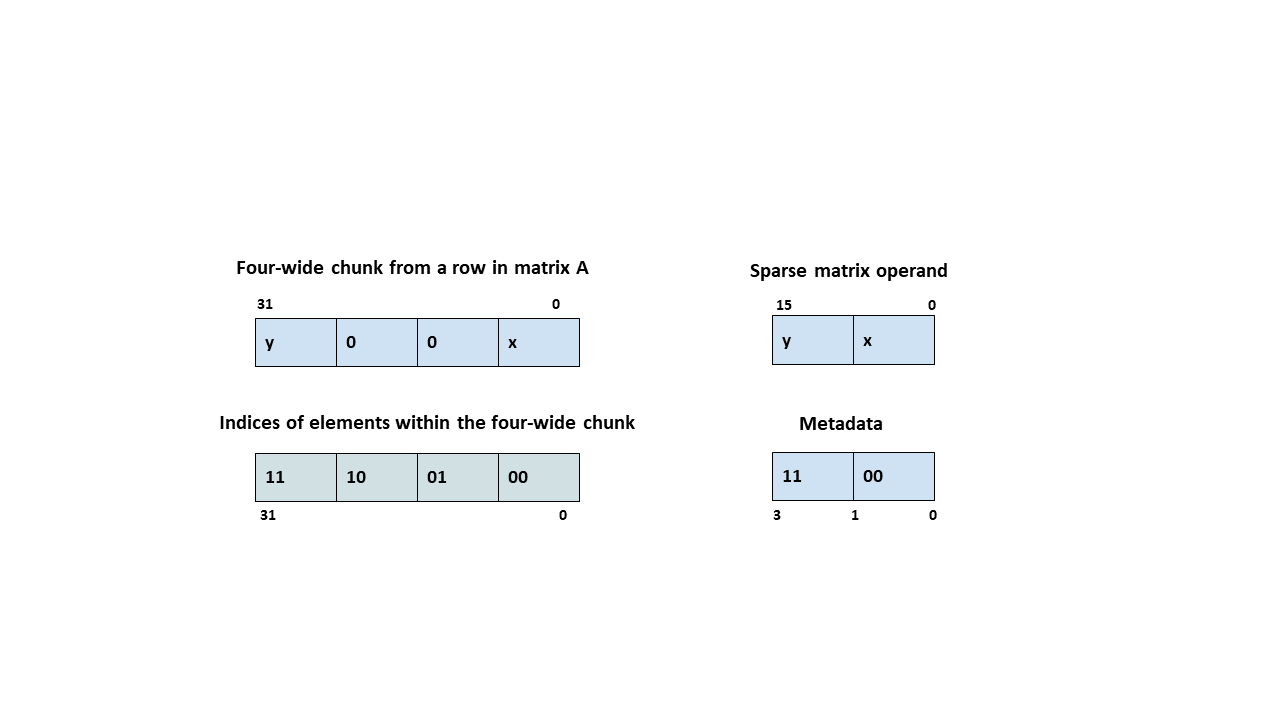
Figure 86 Sparse MMA metadata example for .u8/.s8 type.
when matrices A and B have .u4/.s4 elements, matrix A is pair-wise structured sparse at a
granularity of 4:8. In other words, each chunk of eight adjacent elements in a row of matrix A has
four zeroes and four non-zero values. Further, the zero and non-zero values are clustered in
sub-chunks of two elements each within the eight-wide chunk. i.e., each two-wide sub-chunk within
the eight-wide chunk must be all zeroes or all non-zeros. Only the four non-zero values are stored
in sparse matrix and the positions of the two two-wide sub-chunks with non-zero values in the
eight-wide chunk of a row of matrix A are indicated by two 2-bit indices in the metadata.
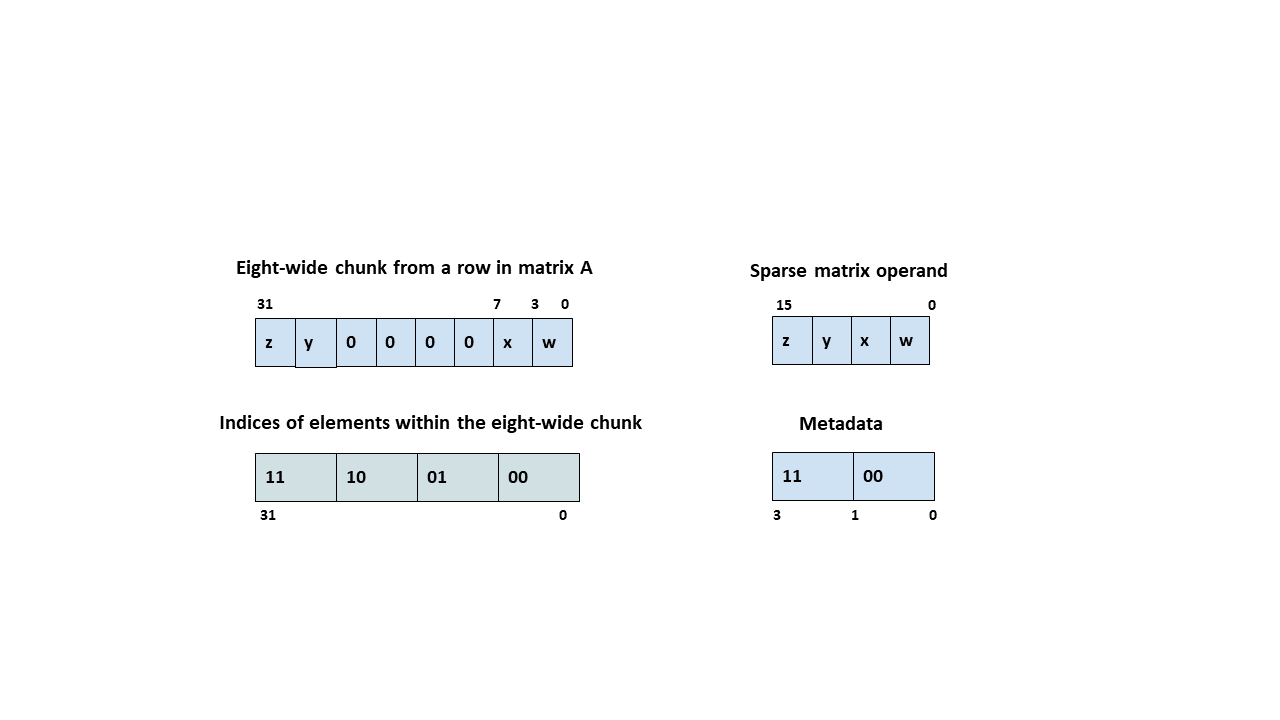
Figure 87 Sparse MMA metadata example for .u4/.s4 type.
The sparsity selector indicates the threads which contribute metadata as listed below:
m16n8k32with.u8/.s8type andm16n8k64with.u4/.s4type: A thread-pair within a group of four consecutive threads contributes the sparsity metadata. Hence, the sparsity selector must be either 0 (threads T0, T1) or 1 (threads T2, T3); any other value results in an undefined behavior.m16n8k64with.u8/.s8type andm16n8k128with.u4/.s4type: All threads within a group of four consecutive threads contribute the sparsity metadata. Hence, the sparsity selector in this case must be 0. Any other value of sparsity selector results in an undefined behavior.
Sparse mma.sp with .e4m3/.e5m2 type
When matrices A and B have .e4m3/.e5m2 elements, matrix A is structured sparse at a granularity
of 2:4. In other words, each chunk of four adjacent elements in a row of matrix A have two zeroes and
two non-zero elements. Only the two non-zero elements are stored in sparse matrix and their positions
in the four-wide chunk are indicated by two 2-bit indices in the metadata. 0b0100, 0b1000,
0b1001, 0b1100, 0b1101, 0b1110 are the meaningful values of indices; any other values
result in an undefined behavior.
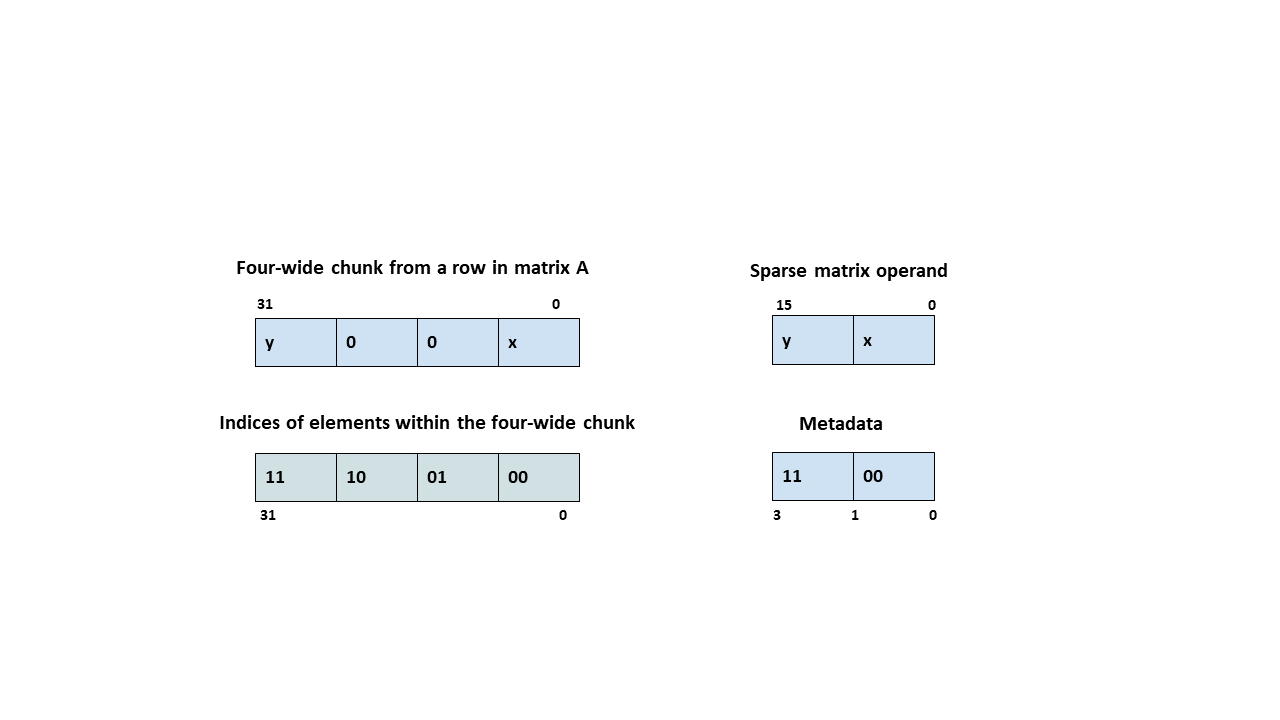
Figure 88 Sparse MMA metadata example for .e4m3/.e5m2 type.
The sparsity selector indicates the threads which contribute metadata as listed below:
m16n8k64: All threads within a group of four consecutive threads contribute the sparsity metadata. Hence, the sparsity selector in this case must be 0. Any other value of sparsity selector results in an undefined behavior.
9.7.13.5.2. Matrix fragments for multiply-accumulate operation with sparse matrix A
In this section we describe how the contents of thread registers are associated with fragments of various matrices and the sparsity metadata. The following conventions are used throughout this section:
For matrix A, only the layout of a fragment is described in terms of register vector sizes and their association with the matrix data.
For matrix B, when the combination of matrix dimension and the supported data type is not already covered in Matrix multiply-accumulate operation using mma instruction, a pictorial representation of matrix fragments is provided.
For matrices C and D, since the matrix dimension - data type combination is the same for all supported shapes, and is already covered in Matrix multiply-accumulate operation using mma instruction, the pictorial representations of matrix fragments are not included in this section.
For the metadata operand, pictorial representations of the association between indices of the elements of matrix A and the contents of the metadata operand are included.
Tk: [m..n]present in cell[x][y..z]indicates that bitsmthroughn(withmbeing higher) in the metadata operand of thread with%laneid=kcontains the indices of the non-zero elements from the chunk[x][y]..[x][z]of matrix A.
9.7.13.5.2.1. Matrix Fragments for sparse mma.m16n8k16 with .f16 and .bf16 types
A warp executing sparse mma.m16n8k16 with .f16 / .bf16 floating point type will compute
an MMA operation of shape .m16n8k16.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.f16/.bf16A vector expression containing two
.b32registers, with each register containing two non-zero.f16/.bf16elements out of 4 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 89.
Figure 89 Sparse MMA .m16n8k16 fragment layout for matrix A with
.f16/.bf16type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 and a1 groupID + 8 for a2 and a3 col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 4 lastcol = firstcol + 3
Matrix fragments for multiplicand B and accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k16 with floating point type for
.f16/.b16formats.Metadata: A
.b32register containing 16 2-bit vectors each storing the index of a non-zero element of a 4-wide chunk of matrix A as shown in Figure 90.
Figure 90 Sparse MMA .m16n8k16 metadata layout for
.f16/.bf16type.
9.7.13.5.2.2. Matrix Fragments for sparse mma.m16n8k32 with .f16 and .bf16 types
A warp executing sparse mma.m16n8k32 with .f16 / .bf16 floating point type will compute
an MMA operation of shape .m16n8k32.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.f16/.bf16A vector expression containing four
.b32registers, with each register containing two non-zero.f16/.bf16elements out of 4 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 91.
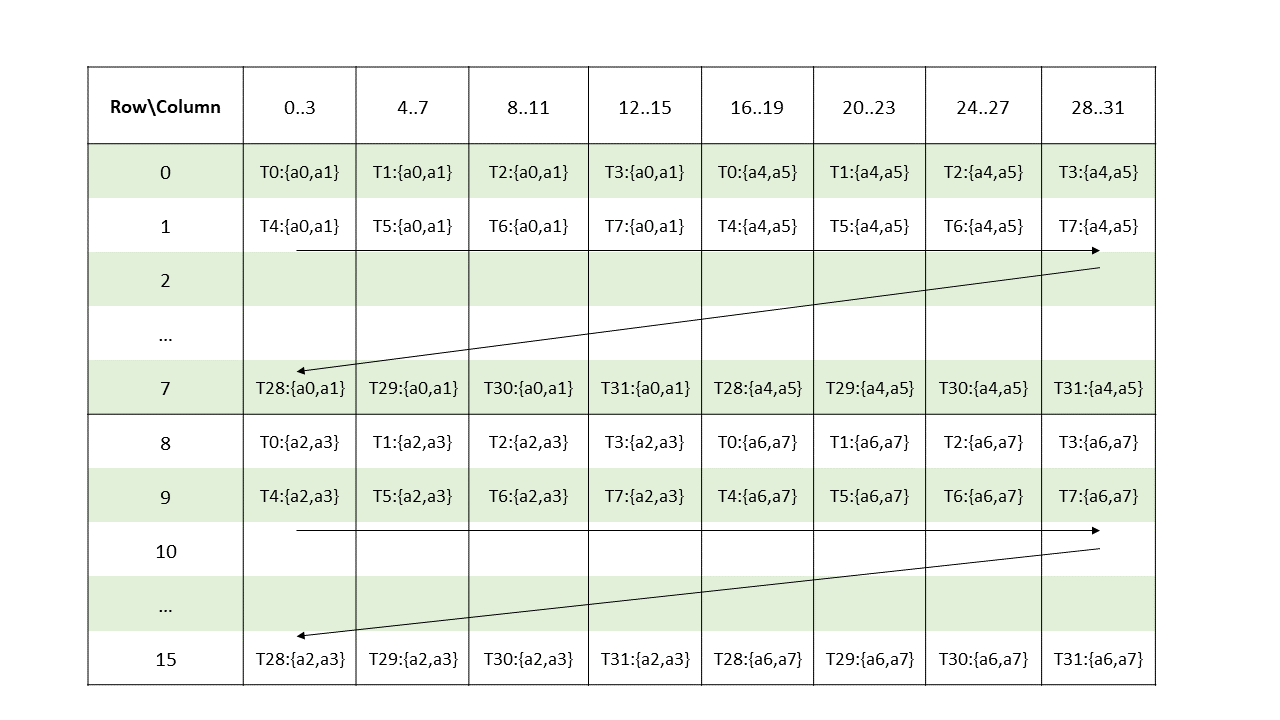
Figure 91 Sparse MMA .m16n8k32 fragment layout for matrix A with
.f16/.bf16type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 2 || 4 <= i < 6 groupID + 8 Otherwise col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 4 For ai where i < 4 (threadID_in_group * 4) + 16 for ai where i >= 4 lastcol = firstcol + 3
Multiplicand B:
.atype
Fragment
Elements (low to high)
.f16/.bf16A vector expression containing four
.b32registers, each containing two.f16/.bf16elements from matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 92.
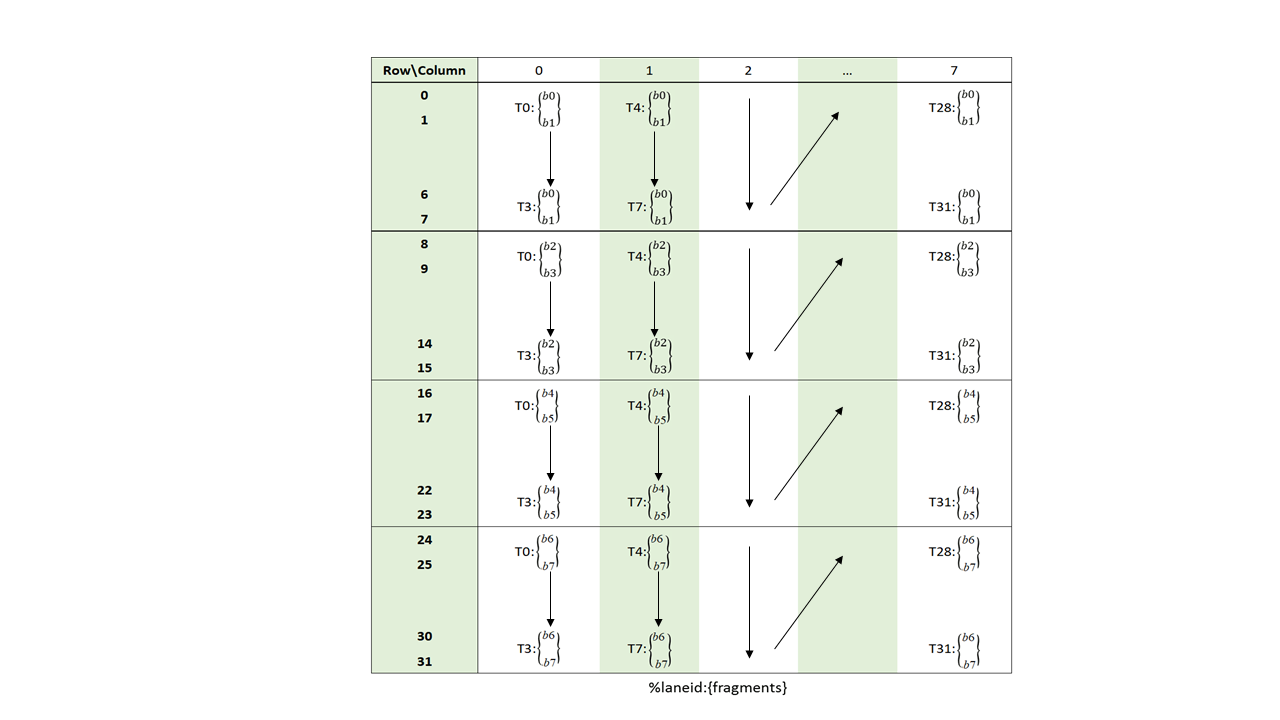
Figure 92 Sparse MMA .m16n8k32 fragment layout for matrix B with
.f16/.bf16type.Matrix fragments for accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k16 with floating point type for
.f16/.b16formats.Metadata: A
.b32register containing 16 2-bit vectors with each pair of 2-bit vectors storing the indices of two non-zero element from a 4-wide chunk of matrix A as shown in Figure 93.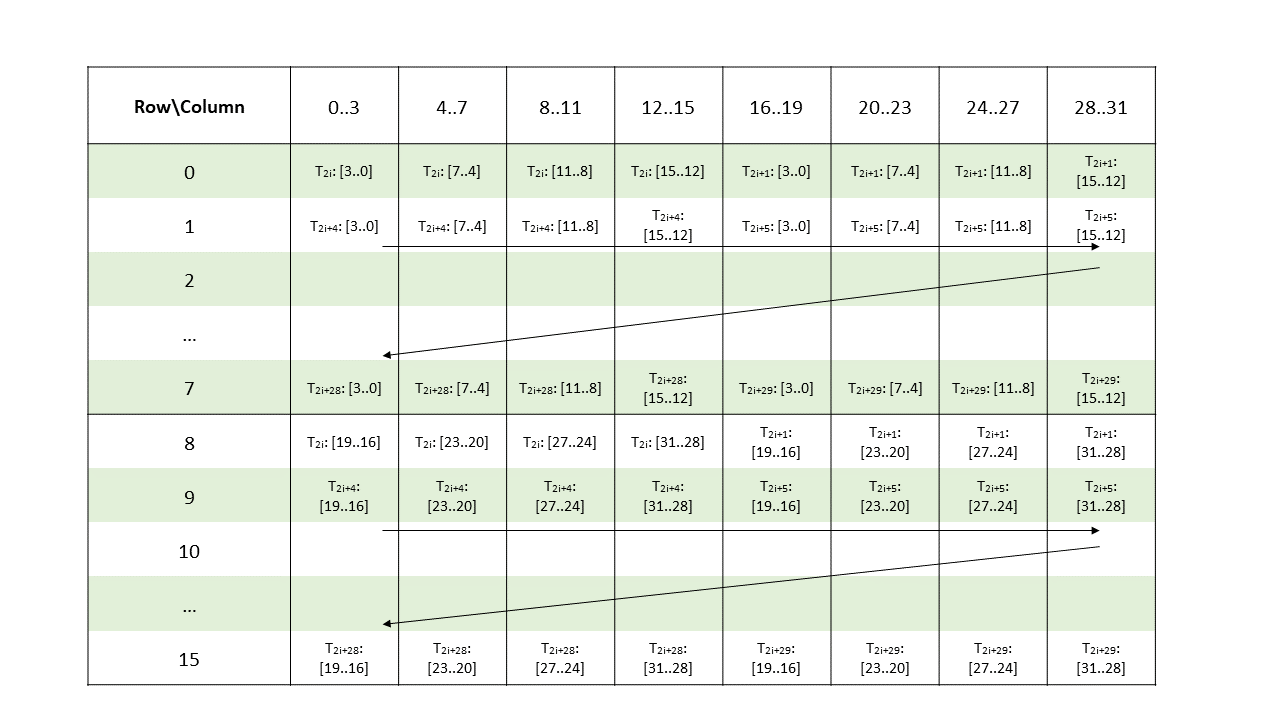
Figure 93 Sparse MMA .m16n8k32 metadata layout for
.f16/.bf16type.
9.7.13.5.2.3. Matrix Fragments for sparse mma.m16n8k16 with .tf32 floating point type
A warp executing sparse mma.m16n8k16 with .tf32 floating point type will compute an MMA
operation of shape .m16n8k16.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.tf32A vector expression containing four
.b32registers, with each register containing one non-zero.tf32element out of 2 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 94.
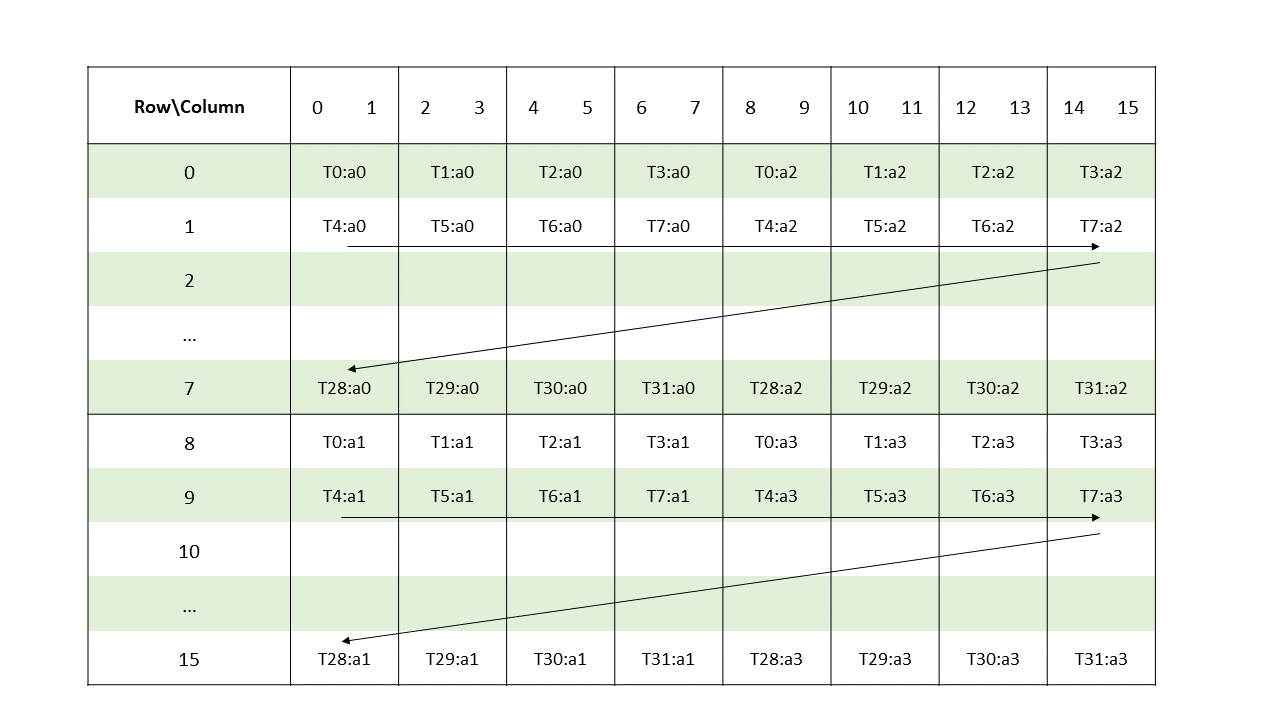
Figure 94 Sparse MMA .m16n8k16 fragment layout for matrix A with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 and a2 groupID + 8 for a1 and a3 col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 2 for a0 and a1 (threadID_in_group * 2) + 8 for a2 and a3 lastcol = firstcol + 1
Multiplicand B:
.atype
Fragment
Elements (low to high)
.tf32A vector expression containing four
.b32registers, each containing four.tf32elements from matrix B.b0, b1, b2, b3
The layout of the fragments held by different threads is shown in Figure 95.

Figure 95 Sparse MMA .m16n8k16 fragment layout for matrix B with
.tf32type.Matrix fragments for accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k16 with floating point type.
Metadata: A
.b32register containing 8 4-bit vectors each storing the index of a non-zero element of a 2-wide chunk of matrix A as shown in Figure 96.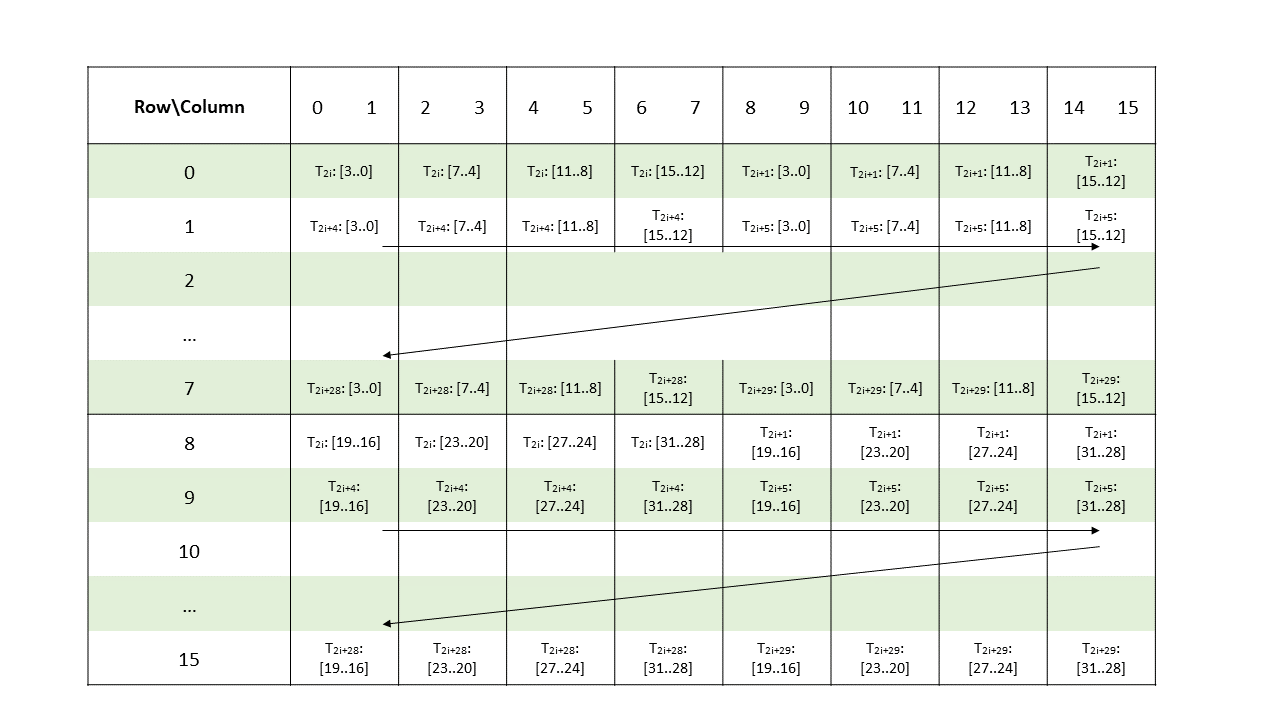
Figure 96 Sparse MMA .m16n8k16 metadata layout for
.tf32type.
9.7.13.5.2.4. Matrix Fragments for sparse mma.m16n8k8 with .tf32 floating point type
A warp executing sparse mma.m16n8k8 with .tf32 floating point type will compute an MMA
operation of shape .m16n8k8.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.tf32A vector expression containing two
.b32registers, each containing one non-zero.tf32element out of 2 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 97.
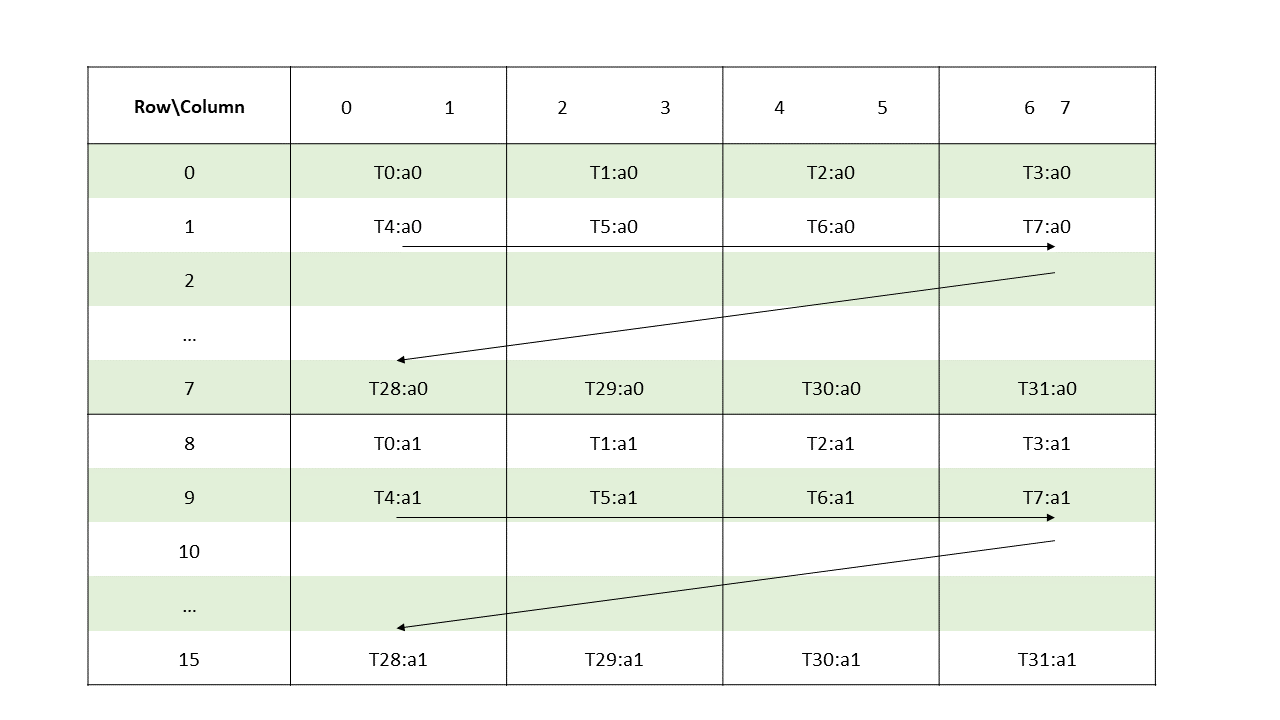
Figure 97 Sparse MMA .m16n8k8 fragment layout for matrix A with
.tf32type.The row and column of a matrix fragment can be computed as:
groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for a0 groupID + 8 for a1 col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 2 lastcol = firstcol + 1
Matrix fragments for multiplicand B and accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k8 for
.tf32format.Metadata: A
.b32register containing 8 4-bit vectors each storing the index of a non-zero element of a 2-wide chunk of matrix A as shown in Figure 98.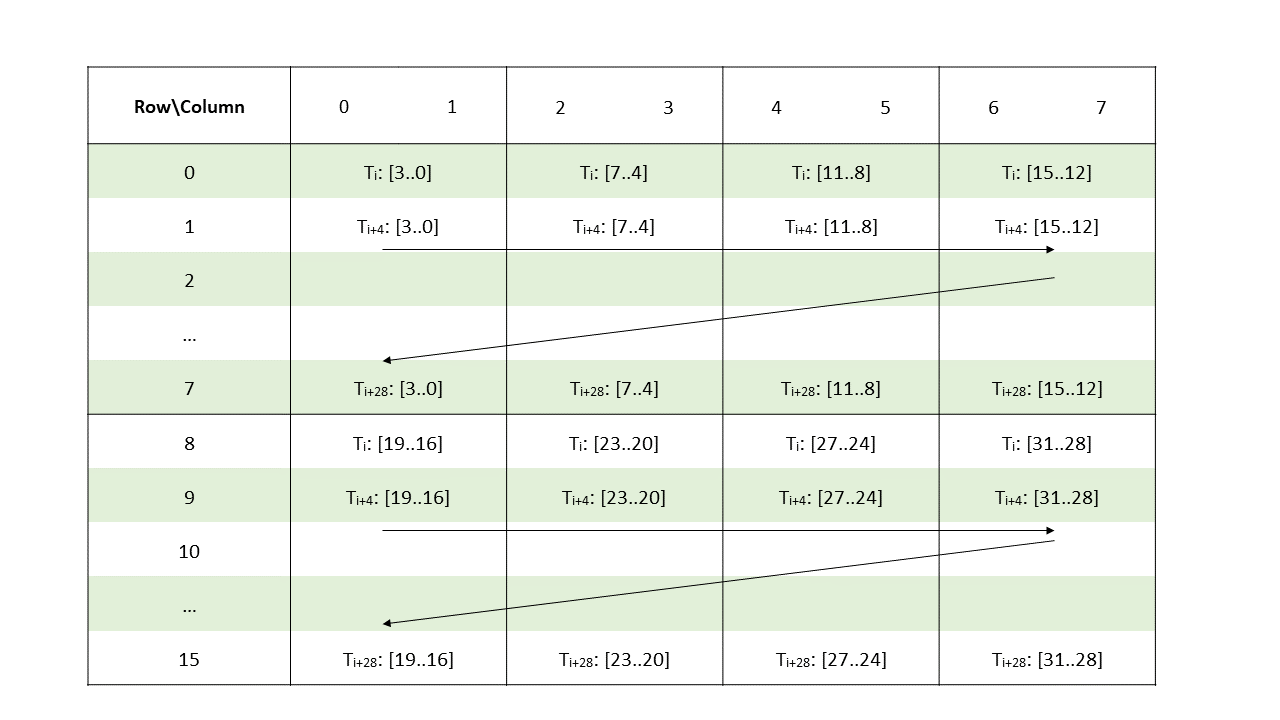
Figure 98 Sparse MMA .m16n8k8 metadata layout for
.tf32type.
9.7.13.5.2.5. Matrix Fragments for sparse mma.m16n8k32 with .u8/.s8 integer type
A warp executing sparse mma.m16n8k32 with .u8 / .s8 integer type will compute an MMA
operation of shape .m16n8k32.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.u8/.s8A vector expression containing two
.b32registers, with each register containing four non-zero.u8/.s8elements out of 8 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 99.
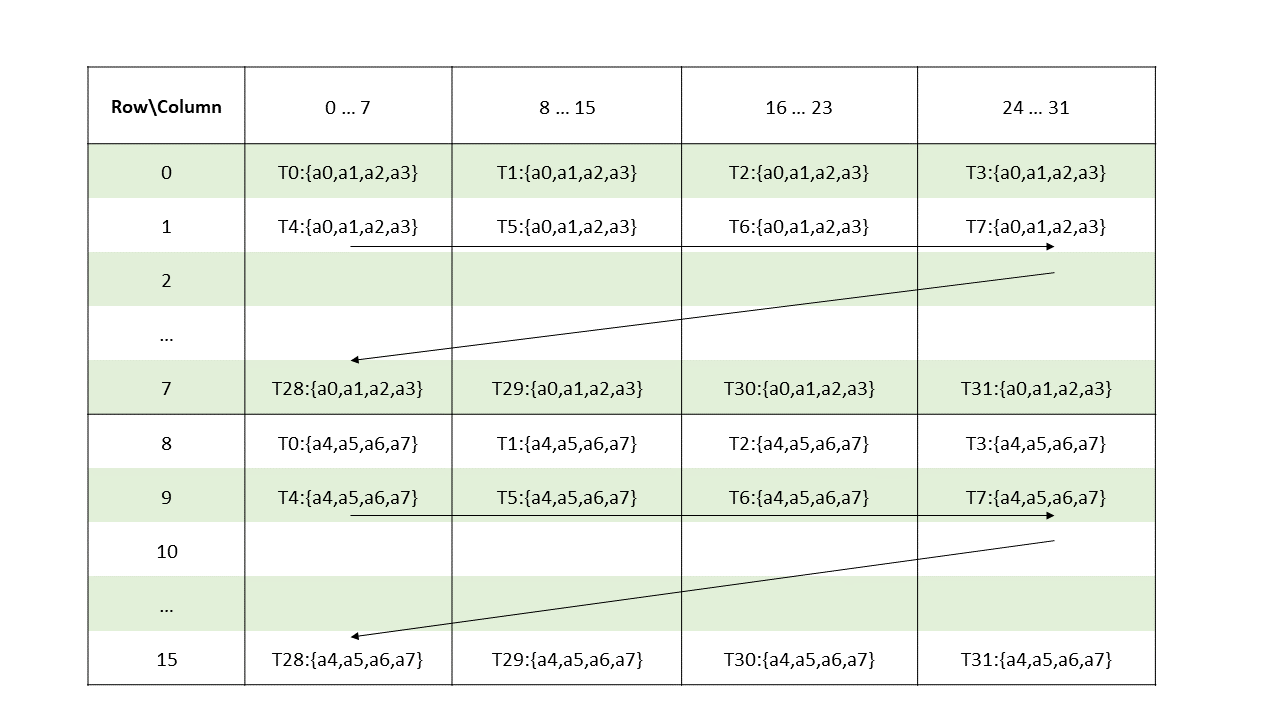
Figure 99 Sparse MMA .m16n8k32 fragment layout for matrix A with
.u8/.s8type.groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 4 groupID + 8 Otherwise col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 8 lastcol = firstcol + 7
Matrix fragments for multiplicand B and accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k32.
Metadata: A
.b32register containing 16 2-bit vectors with each pair of 2-bit vectors storing the indices of two non-zero elements from a 4-wide chunk of matrix A as shown in Figure 100.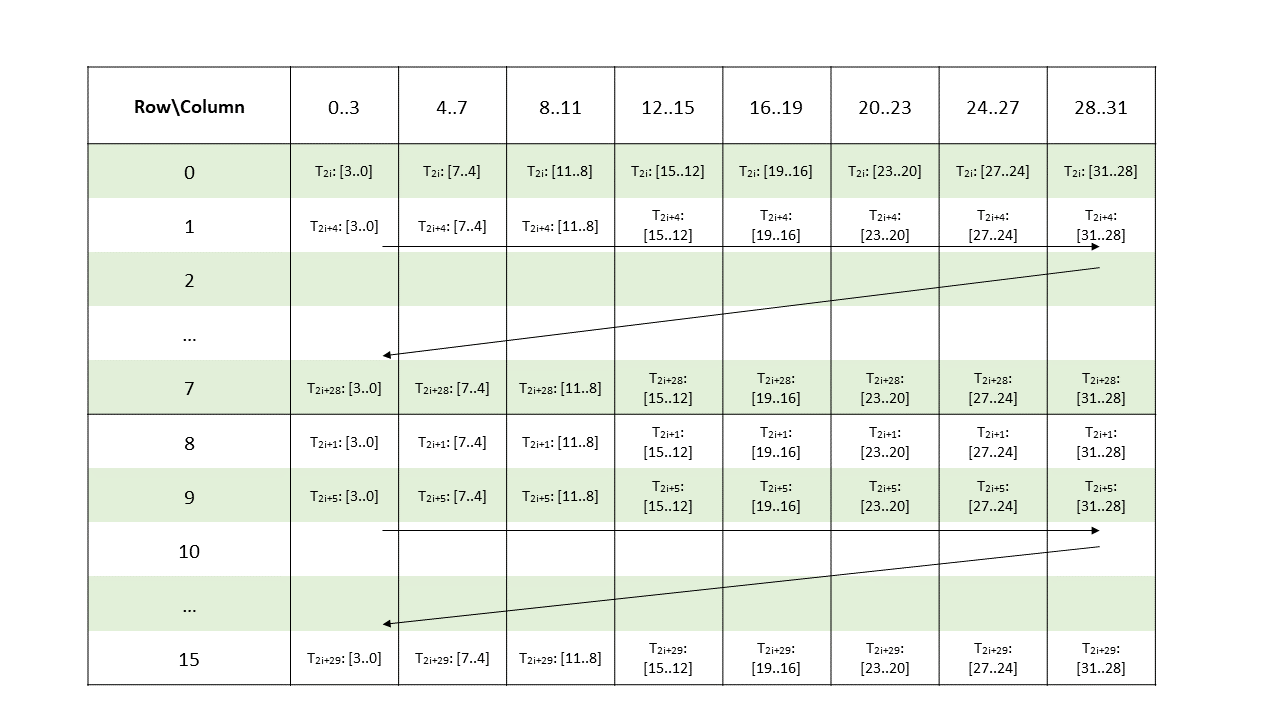
Figure 100 Sparse MMA .m16n8k32 metadata layout for
.u8/.s8type.
9.7.13.5.2.6. Matrix Fragments for sparse mma.m16n8k64 with .u8/.s8/.e4m3/.e5m2 type
A warp executing sparse mma.m16n8k64 with .u8 / .s8/ .e4m3/ .e5m2 type will compute an MMA
operation of shape .m16n8k64.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.u8/.s8A vector expression containing four
.b32registers, with each register containing four non-zero.u8/.s8elements out of 8 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
.e4m3/.e5m2A vector expression containing four
.b32registers, with each register containing four non-zero.e4m3/.e5m2elements out of 8 consecutive elements from matrix A.The layout of the fragments held by different threads is shown in Figure 101 and Figure 102.
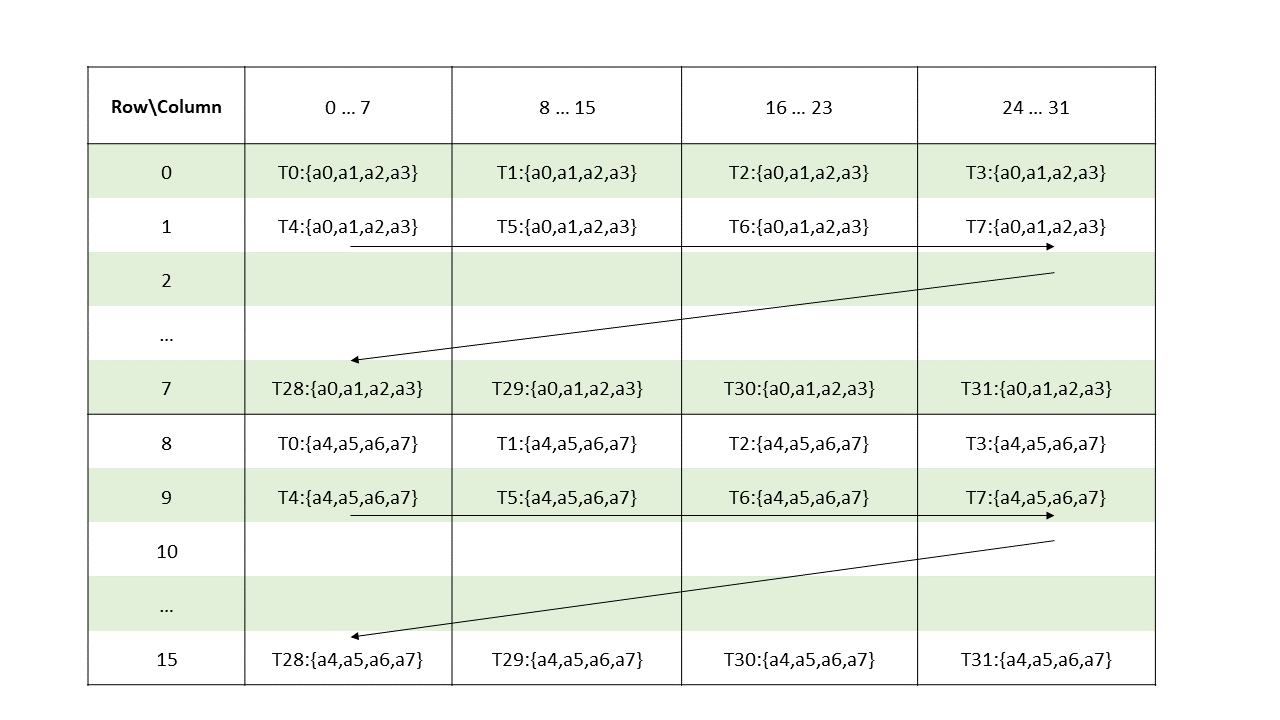
Figure 101 Sparse MMA .m16n8k64 fragment layout for columns 0–31 of matrix A with
.u8/.s8/.e4m3/.e5m2type.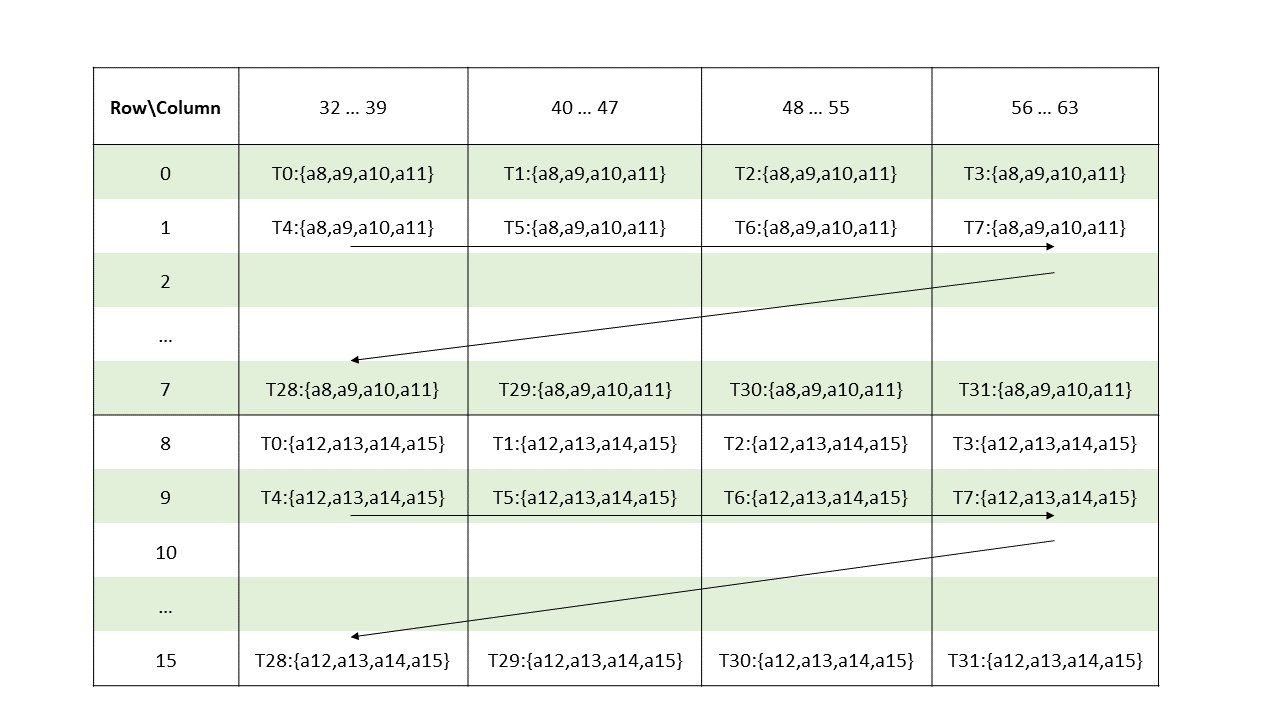
Figure 102 Sparse MMA .m16n8k64 fragment layout for columns 32–63 of matrix A with
.u8/.s8/.e4m3/.e5m2type.groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 4 || 8 <= i < 12 groupID + 8 Otherwise col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 8 For ai where i < 8 (threadID_in_group * 8) + 32 For ai where i >= 8 lastcol = firstcol + 7
Multiplicand B:
.btype
Fragment
Elements (low to high)
.u8/.s8A vector expression containing four
.b32registers, each containing four.u8/.s8elements from matrix B.b0, b1, b2, b3, …, b15
.e4m3/.e5m2A vector expression containing four
.b32registers, each containing four.e4m3/.e5m2elements from matrix B.The layout of the fragments held by different threads is shown in Figure 103, Figure 104, Figure 105 and Figure 106.
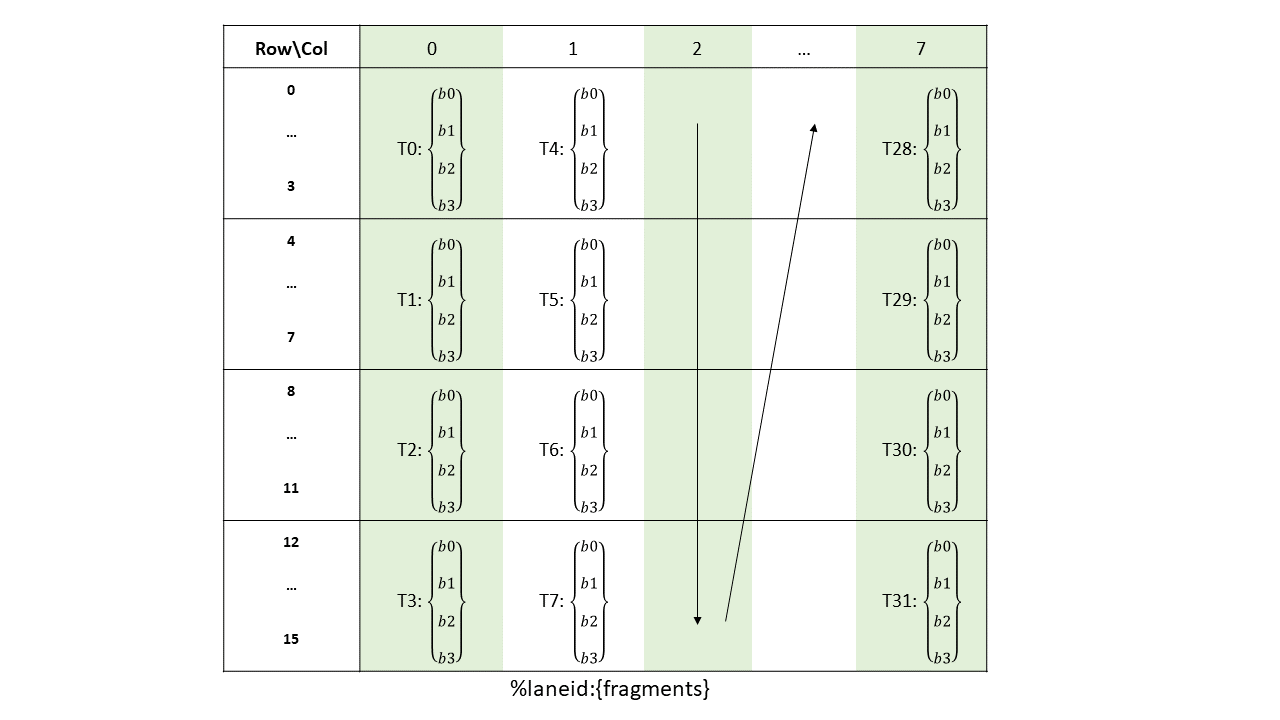
Figure 103 Sparse MMA .m16n8k64 fragment layout for rows 0–15 of matrix B with
.u8/.s8/.e4m3/.e5m2type.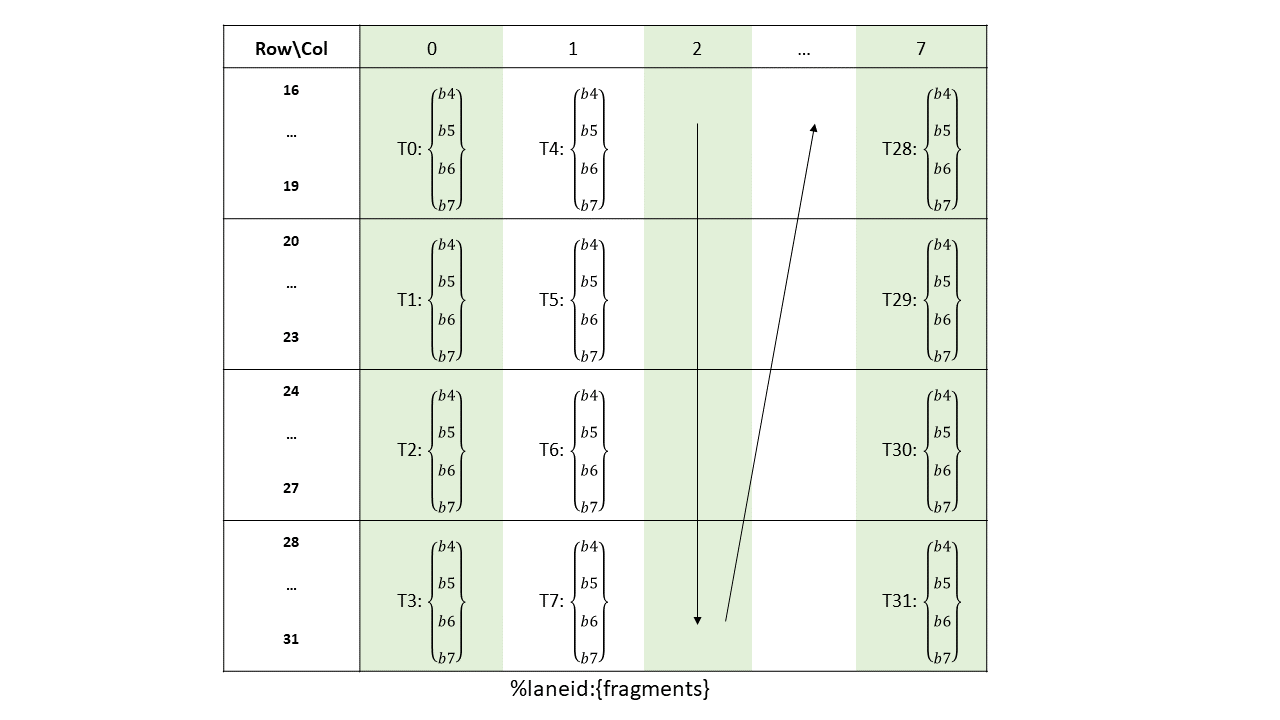
Figure 104 Sparse MMA .m16n8k64 fragment layout for rows 16–31 of matrix B with
.u8/.s8/.e4m3/.e5m2type.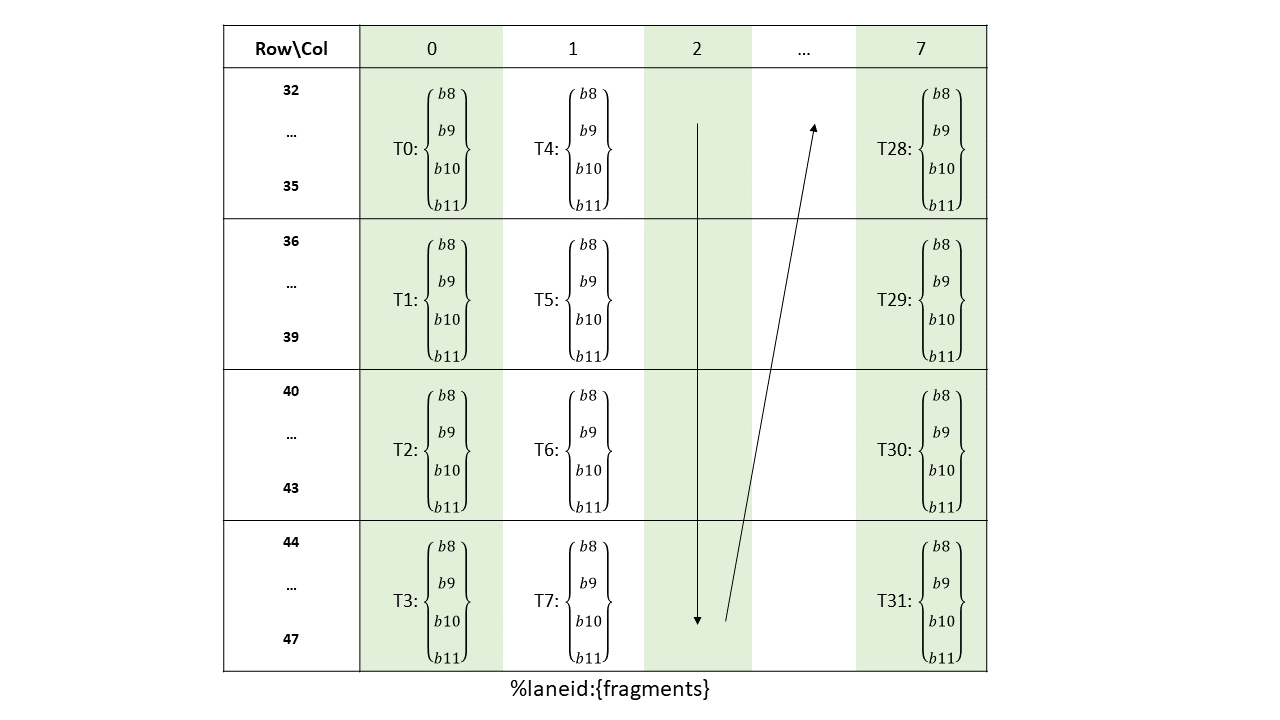
Figure 105 Sparse MMA .m16n8k64 fragment layout for rows 32–47 of matrix B with
.u8/.s8/.e4m3/.e5m2type.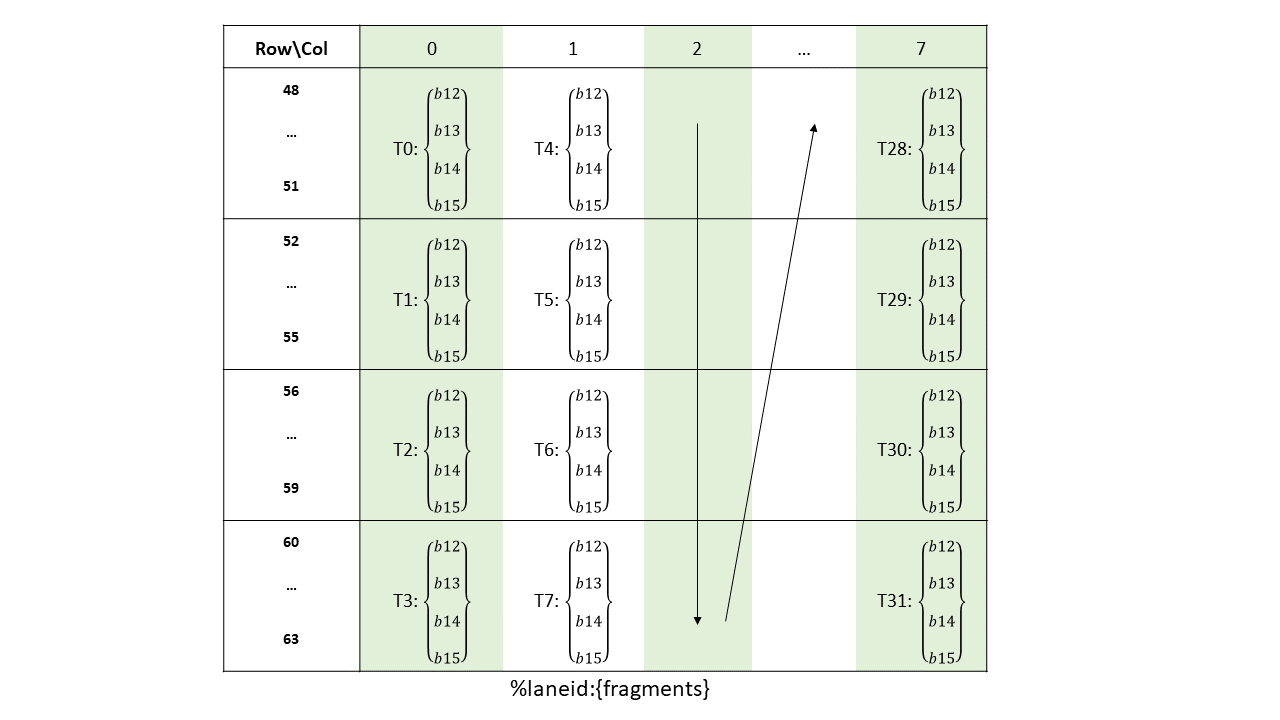
Figure 106 Sparse MMA .m16n8k64 fragment layout for rows 48–63 of matrix B with
.u8/.s8/.e4m3/.e5m2type.Matrix fragments for accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k16 with integer type.
Metadata: A
.b32register containing 16 2-bit vectors with each pair of 2-bit vectors storing the indices of two non-zero elements from a 4-wide chunk of matrix A as shown in Figure 107 and Figure 108.
9.7.13.5.2.7. Matrix Fragments for sparse mma.m16n8k64 with .u4/.s4 integer type
A warp executing sparse mma.m16n8k64 with .u4 / .s4 integer type will compute an MMA
operation of shape .m16n8k64.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.u4/.s4A vector expression containing two
.b32registers, with each register containing eight non-zero.u4/.s4elements out of 16 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 109.
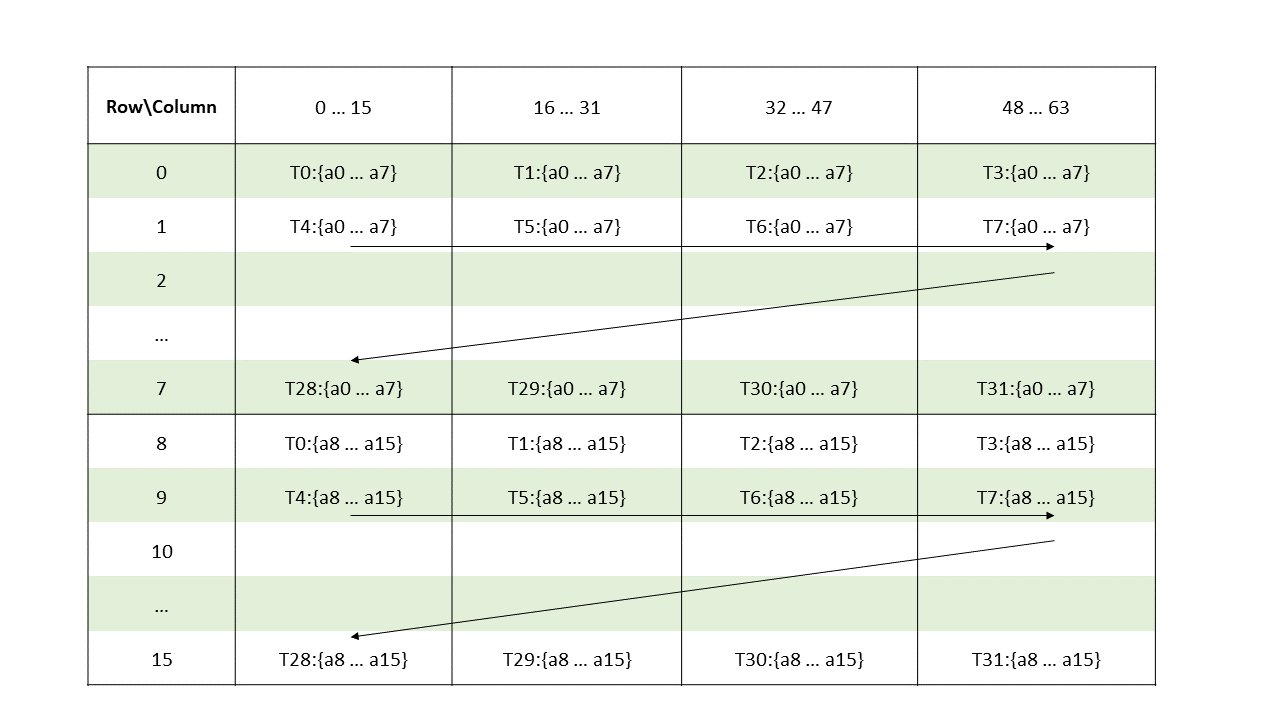
Figure 109 Sparse MMA .m16n8k64 fragment layout for matrix A with
.u4/.s4type.groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 8 groupID + 8 Otherwise col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 16 lastcol = firstcol + 15
Matrix fragments for multiplicand B and accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k64.
Metadata: A
.b32register containing 16 2-bit vectors with each pair of 2-bit vectors storing the indices of four non-zero elements from a 8-wide chunk of matrix A as shown in Figure 110.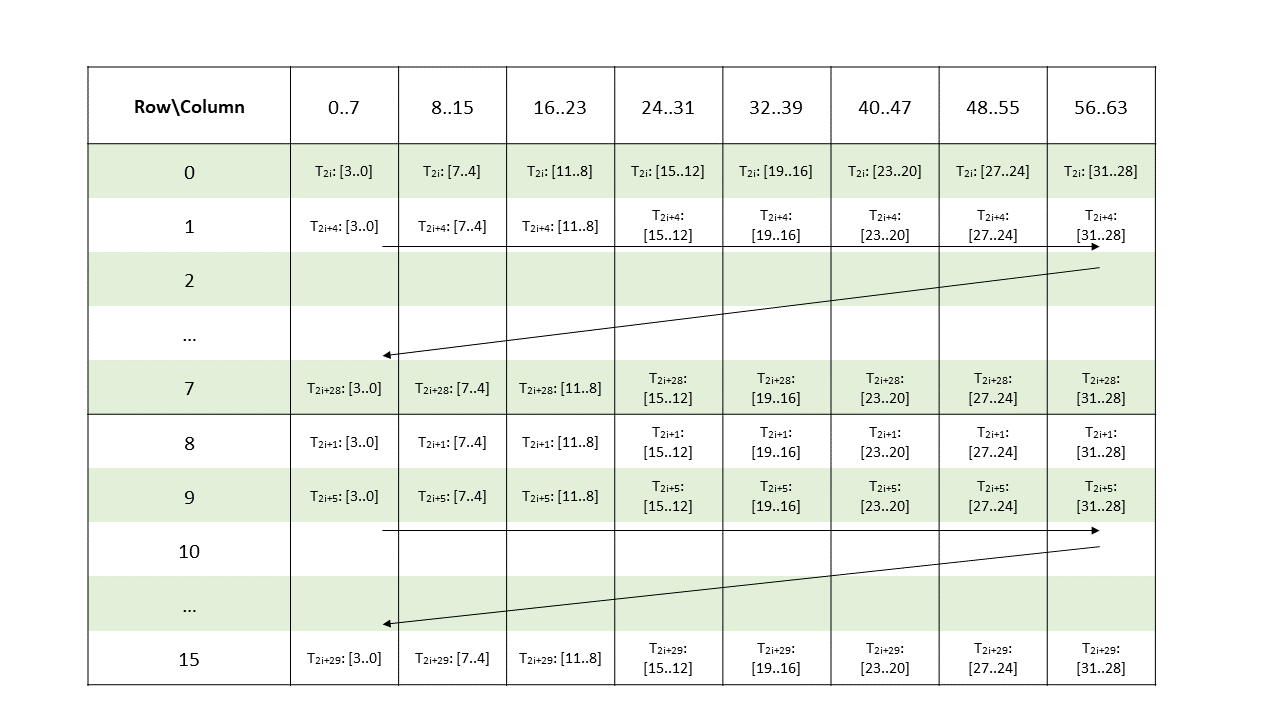
Figure 110 Sparse MMA .m16n8k64 metadata layout for
.u4/.s4type.
9.7.13.5.2.8. Matrix Fragments for sparse mma.m16n8k128 with .u4/.s4 integer type
A warp executing sparse mma.m16n8k128 with .u4 / .s4 integer type will compute an MMA
operation of shape .m16n8k128.
Elements of the matrix are distributed across the threads in a warp so each thread of the warp holds a fragment of the matrix.
Multiplicand A:
.atype
Fragment
Elements
.u4/.s4A vector expression containing four
.b32registers, with each register containing eight non-zero.u4/.s4elements out of 16 consecutive elements from matrix A.Mapping of the non-zero elements is as described in Sparse matrix storage.
The layout of the fragments held by different threads is shown in Figure 111 and Figure 112.
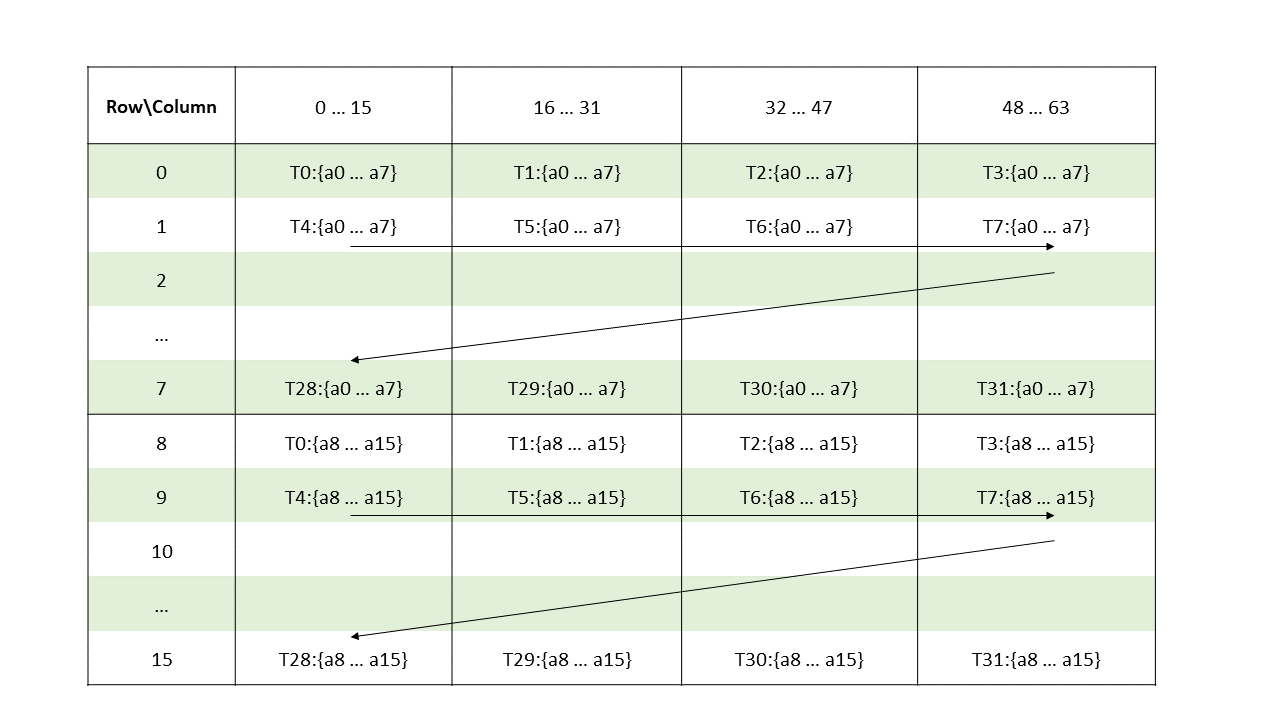
Figure 111 Sparse MMA .m16n8k128 fragment layout for columns 0–63 of matrix A with
.u4/.s4type.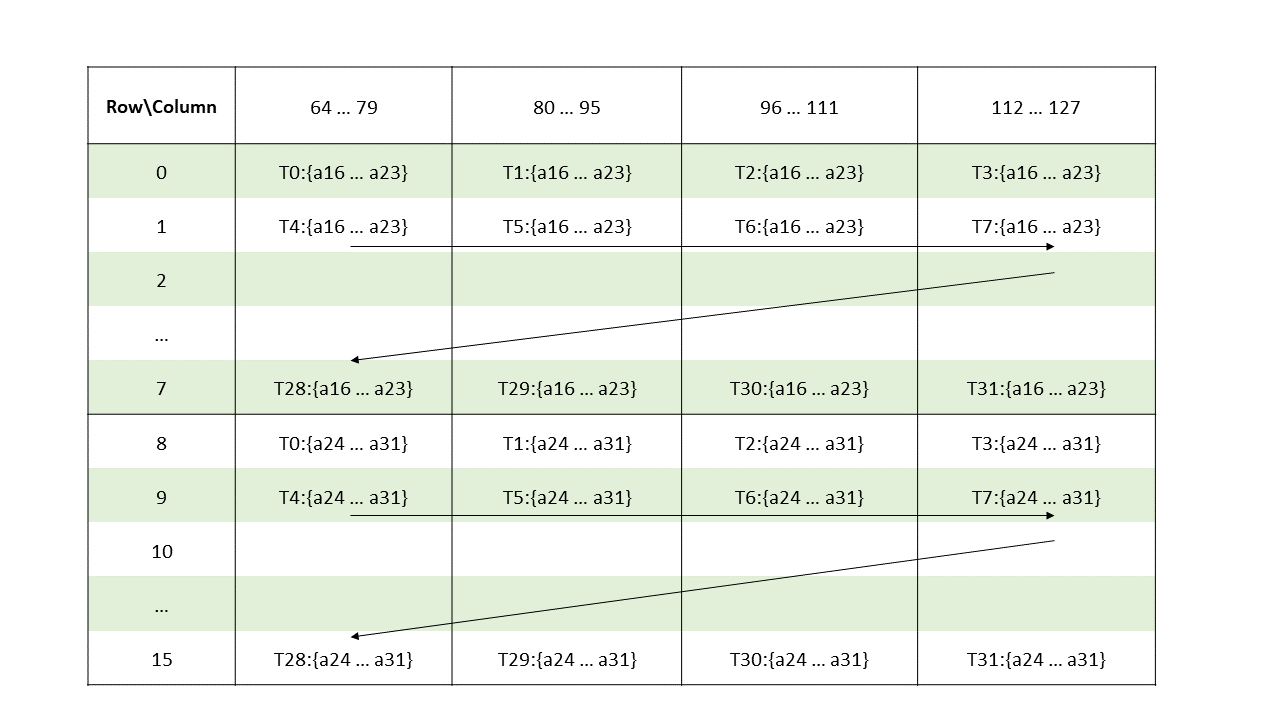
Figure 112 Sparse MMA .m16n8k128 fragment layout for columns 64–127 of matrix A with
.u4/.s4type.groupID = %laneid >> 2 threadID_in_group = %laneid % 4 row = groupID for ai where 0 <= i < 8 || 16 <= i < 24 groupID + 8 Otherwise col = [firstcol ... lastcol] // As per the mapping of non-zero elements // as described in Sparse matrix storage Where firstcol = threadID_in_group * 16 For ai where i < 16 (threadID_in_group * 16) + 64 For ai where i >= 16 lastcol = firstcol + 15
Multiplicand B:
.atype
Fragment
Elements (low to high)
.u4/.s4A vector expression containing four
.b32registers, each containing eight.u4/.s4elements from matrix B.b0, b1, b2, b3, …, b31
The layout of the fragments held by different threads is shown in Figure 113, Figure 114, Figure 115, Figure 116.
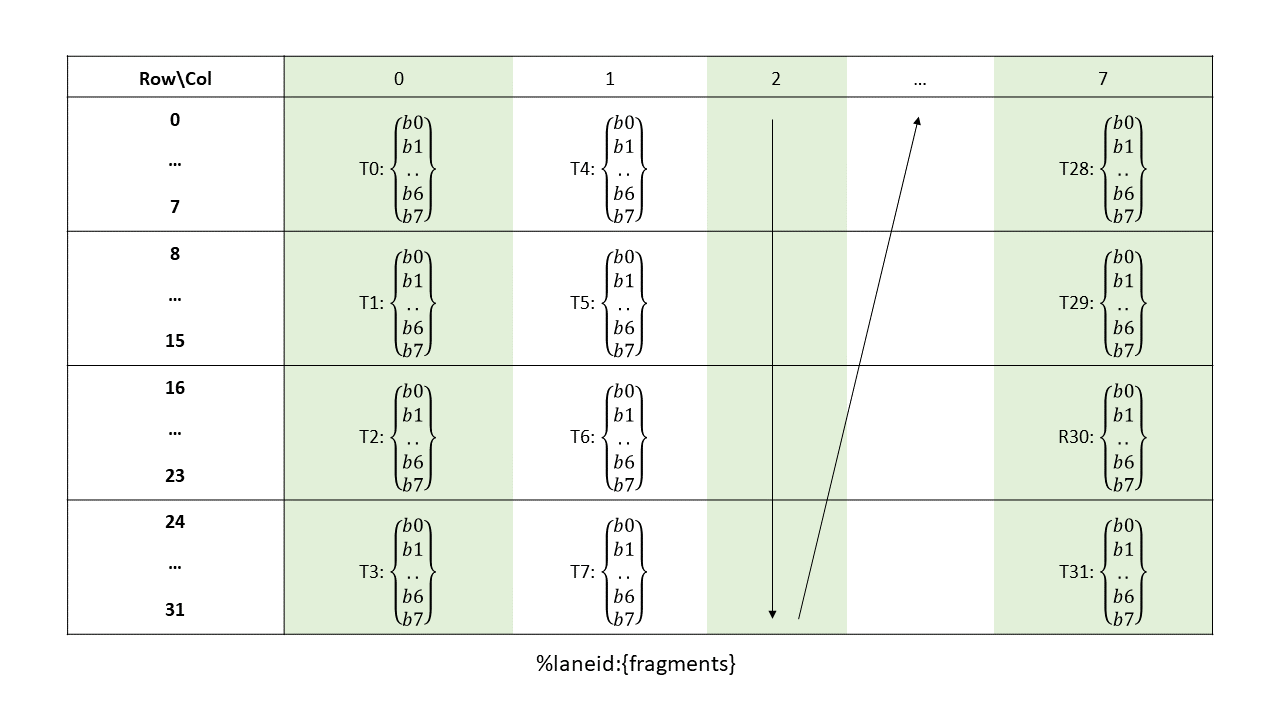
Figure 113 Sparse MMA .m16n8k128 fragment layout for rows 0–31 of matrix B with
.u4/.s4type.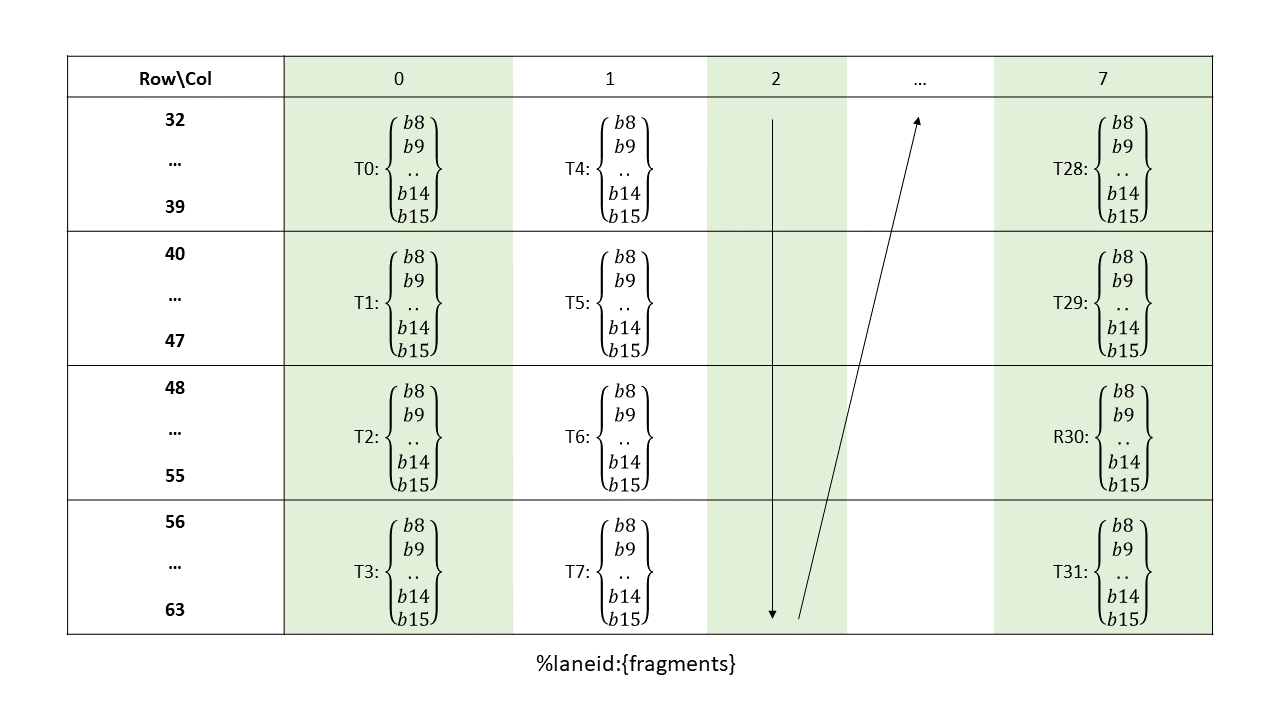
Figure 114 Sparse MMA .m16n8k128 fragment layout for rows 31–63 of matrix B with
.u4/.s4type.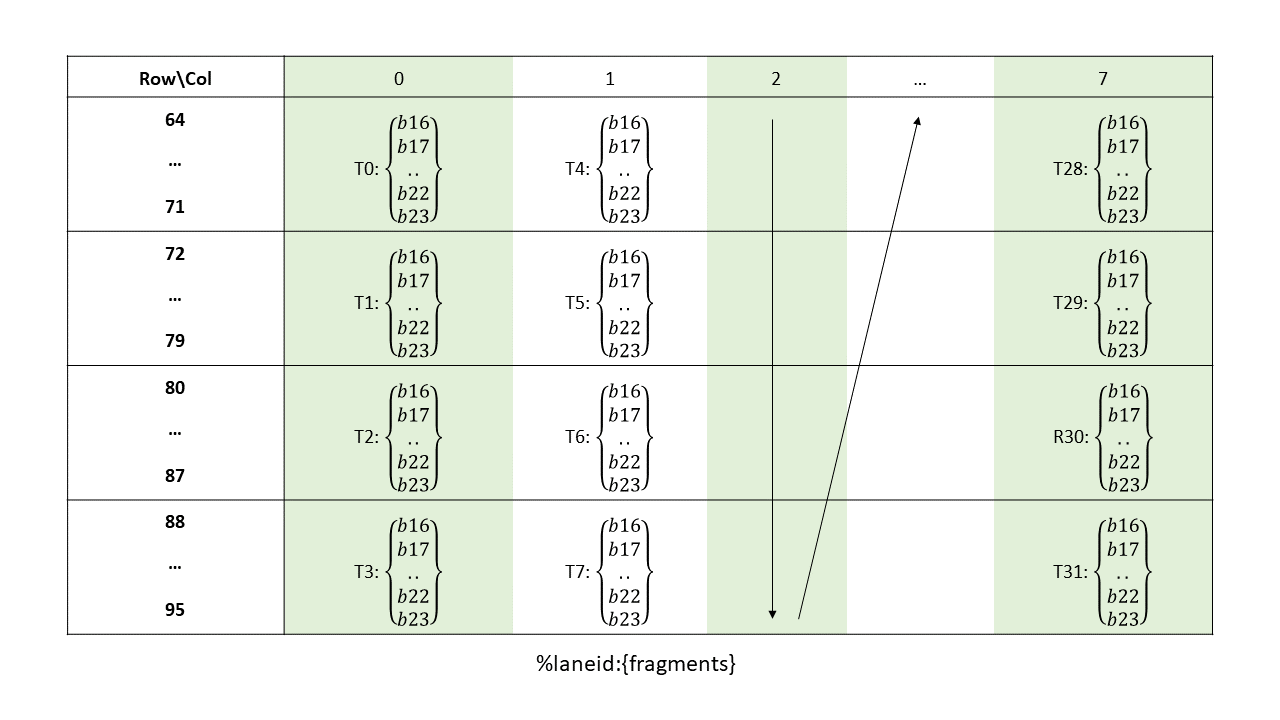
Figure 115 Sparse MMA .m16n8k128 fragment layout for rows 64–95 of matrix B with
.u4/.s4type.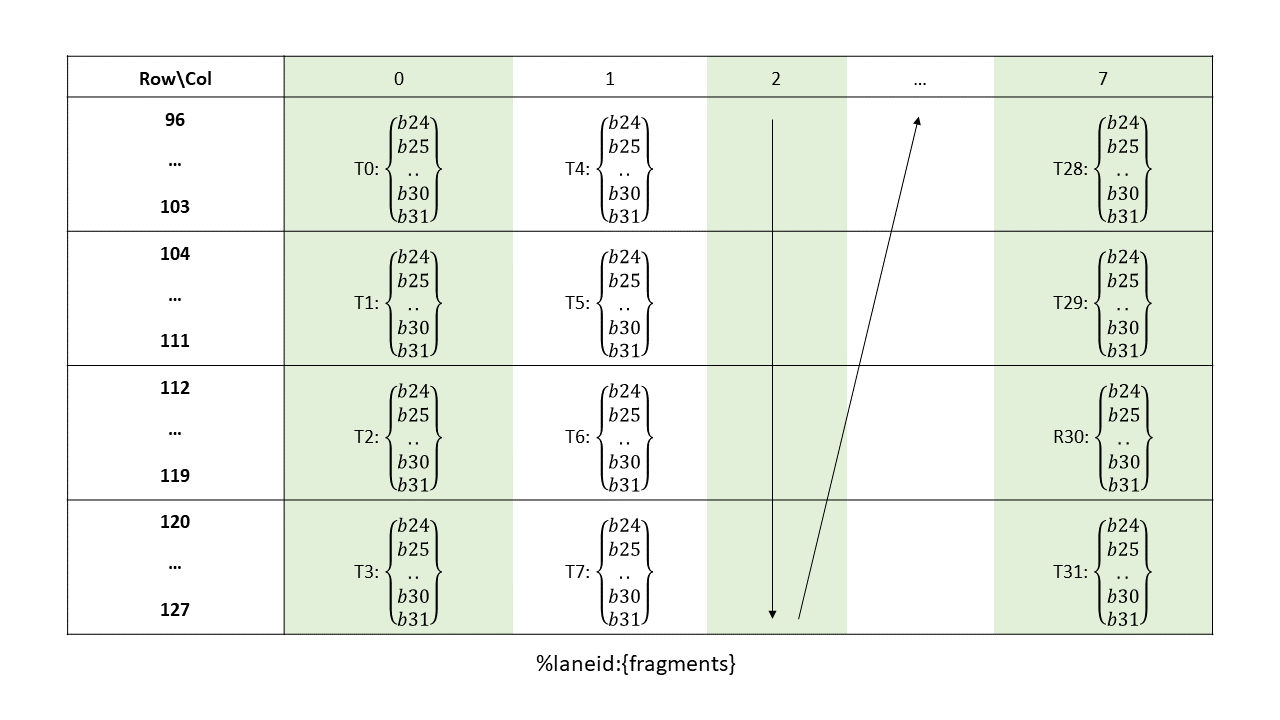
Figure 116 Sparse MMA .m16n8k128 fragment layout for rows 96–127 of matrix B with
.u4/.s4type.Matrix fragments for accumulators C and D are the same as in case of Matrix Fragments for mma.m16n8k64.
Metadata: A
.b32register containing 16 2-bit vectors with each pair of 2-bit vectors storing the indices of four non-zero elements from a 8-wide chunk of matrix A as shown in Figure 117 and Figure 118.
9.7.13.5.3. Multiply-and-Accumulate Instruction: mma.sp
mma.sp
Perform matrix multiply-and-accumulate operation with sparse matrix A
Syntax
Half precision floating point type:
mma.sp.sync.aligned.m16n8k16.row.col.dtype.f16.f16.ctype d, a, b, c, e, f;
mma.sp.sync.aligned.m16n8k32.row.col.dtype.f16.f16.ctype d, a, b, c, e, f;
.ctype = {.f16, .f32};
.dtype = {.f16, .f32};
Alternate floating point type :
mma.sp.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32 d, a, b, c, e, f;
mma.sp.sync.aligned.m16n8k32.row.col.f32.bf16.bf16.f32 d, a, b, c, e, f;
mma.sp.sync.aligned.m16n8k8.row.col.f32.tf32.tf32.f32 d, a, b, c, e, f;
mma.sp.sync.aligned.m16n8k16.row.col.f32.tf32.tf32.f32 d, a, b, c, e, f;
mma.sp.sync.aligned.m16n8k64.row.col.f32.f8type.f8type.f32 d, a, b, c, e, f;
.f8type = {.e4m3, .e5m2};
Integer type:
mma.sp.sync.aligned.shape.row.col{.satfinite}.s32.atype.btype.s32 d, a, b, c, e, f;
.shape = {.m16n8k32, .m16n8k64}
.atype = {.u8, .s8};
.btype = {.u8, .s8};
mma.sp.sync.aligned.shape.row.col{.satfinite}.s32.atype.btype.s32 d, a, b, c, e, f;
.shape = {.m16n8k64, .m16n8k128}
.atype = {.u4, .s4};
.btype = {.u4, .s4};
Description
Perform a MxNxK matrix multiply and accumulate operation, D = A*B+C, where the A matrix is
MxK, the B matrix is KxN, and the C and D matrices are MxN.
A warp executing mma.sp.sync instruction compute a single matrix mutliply and accumulate
operation.
Operands a and b represent two multiplicand matrices A and B, while c and d
represent the accumulator and destination matrices, distributed across the threads in warp. Matrix A
is structured sparse as described in Sparse matrix storage Operands e and f represent sparsity
metadata and sparsity selector respectively. Operand e is a 32-bit integer and operand f is
a 32-bit integer constant with values in the range 0..3
The registers in each thread hold a fragment of matrix as described in Matrix fragments for multiply-accumulate operation with sparse matrix A.
The qualifiers .dtype, .atype, .btype and .ctype indicate the data-type of the
elements in the matrices D, A, B and C respectively. In case of shapes .m16n8k16 and
.m16n8k32, .dtype must be the same as .ctype
- Precision and rounding :
.f16floating point operations :Element-wise multiplication of matrix A and B is performed with at least single precision. When
.ctypeor.dtypeis.f32, accumulation of the intermediate values is performed with at least single precision. When both.ctypeand.dtypeare specified as.f16, the accumulation is performed with at least half precision.The accumulation order, rounding and handling of subnormal inputs are unspecified.
.e4m3and.e5m2floating point operations :Element-wise multiplication of matrix A and B is performed with specified precision. Accumulation of the intermediate values is performed with at least single precision.
The accumulation order, rounding, and handling of subnormal inputs are unspecified.
.bf16and.tf32floating point operations :Element-wise multiplication of matrix A and B is performed with specified precision. Accumulation of the intermediate values is performed with at least single precision.
The accumulation order, rounding, and handling of subnormal inputs are unspecified.
Integer operations :
The integer
mma.spoperation is performed with.s32accumulators. The.satfinitequalifier indicates that on overflow, the accumulated value is limited to the range MIN_INT32..MAX_INT32 (where the bounds are defined as the minimum negative signed 32-bit integer and the maximum positive signed 32-bit integer respectively).If
.satfiniteis not specified, the accumulated value is wrapped instead.
The mandatory .sync qualifier indicates that mma.sp instruction causes the executing thread
to wait until all threads in the warp execute the same mma.sp instruction before resuming
execution.
The mandatory .aligned qualifier indicates that all threads in the warp must execute the same
mma.sp instruction. In conditionally executed code, a mma.sp instruction should only be used
if it is known that all threads in the warp evaluate the condition identically, otherwise behavior
is undefined.
The behavior of mma.sp instruction is undefined if all threads in the same warp do not use the
same qualifiers, or if any thread in the warp has exited.
PTX ISA Notes
Introduced in PTX ISA version 7.1.
Support for .e4m3 and .e5m2 alternate floating point type mma operation introduced in
PTX ISA version 8.4.
Target ISA Notes
Requires sm_80 or higher.
.e4m3 and .e5m2 alternate floating point type mma operation requires sm_89 or higher.
Examples of half precision floating point type
// f16 elements in C and D matrix
.reg .f16x2 %Ra<2> %Rb<2> %Rc<2> %Rd<2>
.reg .b32 %Re;
mma.sp.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16
{%Rd0, %Rd1},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1}, %Re, 0x1;
Examples of alternate floating point type
.reg .b32 %Ra<2>, %Rb<2>;
.reg .f32 %Rc<4>, %Rd<4>;
.reg .b32 %Re;
mma.sp.sync.aligned.m16n8k8.row.col.f32.tf32.tf32.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x1;
.reg .b32 %Ra<2>, %Rb<2>;
.reg .f32 %Rc<4>, %Rd<4>;
.reg .b32 %Re;
mma.sp.sync.aligned.m16n8k16.row.col.f32.bf16.bf16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x1;
.reg .b32 %Ra<4>, %Rb<4>;
.reg .f32 %Rc<4>, %Rd<4>;
.reg .b32 %Re;
mma.sp.sync.aligned.m16n8k32.row.col.f32.bf16.bf16.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1, %Rb2, %Rb3},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x1;
.reg .b32 %Ra<4>, %Rb<4>;
.reg .f32 %Rc<4>, %Rd<4>;
.reg .b32 %Re;
mma.sp.sync.aligned.m16n8k64.row.col.f32.e5m2.e4m3.f32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1, %Rb2, %Rb3},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0;
Examples of integer type
.reg .b32 %Ra<4>, %Rb<4>, %Rc<4>, %Rd<4>;
.reg .u32 %Re;
// u8 elements in A and B matrix
mma.sp.sync.aligned.m16n8k32.row.col.satfinite.s32.u8.u8.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x1;
// s8 elements in A and B matrix
mma.sp.sync.aligned.m16n8k64.row.col.satfinite.s32.s8.s8.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1, %Rb2, %Rb3},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x0;
// u4 elements in A and B matrix
mma.sp.sync.aligned.m16n8k64.row.col.s32.s4.s4.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1},
{%Rb0, %Rb1},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x1;
// u4 elements in A and B matrix
mma.sp.sync.aligned.m16n8k128.row.col.satfinite.s32.u4.u4.s32
{%Rd0, %Rd1, %Rd2, %Rd3},
{%Ra0, %Ra1, %Ra2, %Ra3},
{%Rb0, %Rb1, %Rb2, %Rb3},
{%Rc0, %Rc1, %Rc2, %Rc3}, %Re, 0x0;
9.7.14. Asynchronous Warpgroup Level Matrix Multiply-Accumulate Instructions
The warpgroup level matrix multiply and accumulate operation has either of the following forms,
where matrix D is called accumulator:
D = A * B + DD = A * B, where the input from accumulator D is disabled.
The wgmma instructions perform warpgroup level matrix multiply-and-accumulate operation by
having all threads in a warpgroup collectively perform the following actions:
Load matrices A, B and D into registers or into shared memory.
Perform the following
fenceoperations:wgmma.fenceoperations to indicate that the register/shared-memory across the warpgroup have been written into.fence.proxy.asyncoperation to make the generic proxy operations visible to the async proxy.
Issue the asynchronous matrix multiply and accumulate operations using the
wgmma.mma_asyncoperation on the input matrices. Thewgmma.mma_asyncoperation is performed in the async proxy.Create a wgmma-group and commit all the prior outstanding
wgmma.mma_asyncoperations into the group, by usingwgmma.commit_groupoperation.Wait for the completion of the required wgmma-group.
Once the wgmma-group completes, all the
wgmma.mma_asyncoperations have been performed and completed.
9.7.14.1. Warpgroup
A warpgroup is a set of four contiguous warps such that the warp-rank of the first warp is a multiple of 4.
warp-rank of a warp is defined as:
(%tid.x + %tid.y * %ntid.x + %tid.z * %ntid.x * %ntid.y) / 32
9.7.14.2. Matrix Shape
The matrix multiply and accumulate operations support a limited set of shapes for the operand
matrices A, B and D. The shapes of all three matrix operands are collectively described by the tuple
MxNxK, where A is an MxK matrix, B is a KxN matrix, while D is a MxN matrix.
The following matrix shapes are supported for the specified types for the wgmma.mma_async
operation:
Multiplicand Data type |
Sparsity |
Shape |
|---|---|---|
Floating-point - |
Dense |
|
Alternate floating-point
format - |
||
Alternate floating-point
format - |
Sparse |
|
Alternate floating-point
format - |
Dense |
|
Alternate floating-point
format - |
Dense |
|
Floating point - |
Sparse |
|
Altername floating-point
format - |
||
Integer - |
Dense |
|
Alternate floating-point
format - |
Sparse |
|
Integer - |
Sparse |
|
Single-bit - |
Dense |
|
9.7.14.3. Matrix Data-types
The matrix multiply and accumulate operation is supported separately on integer, floating-point, sub-byte integer and single bit data-types. All operands must contain the same basic type kind, i.e., integer or floating-point.
For floating-point matrix multiply and accumulate operation, different matrix operands may have different precision, as described later.
For integer matrix multiply and accumulate operation, both multiplicand matrices (A and B) must have elements of the same data-type, e.g. both signed integer or both unsigned integer.
Data-type |
Multiplicands (A or B) |
Accumulator (D) |
|---|---|---|
Integer |
both |
|
Floating Point |
|
|
Alternate floating Point |
|
|
Alternate floating Point |
|
|
Alternate floating Point |
|
|
Single-bit integer |
|
|
9.7.14.4. Async Proxy
The wgmma.mma_async operations are performed in the asynchronous proxy (or async proxy).
Accessing the same memory location across multiple proxies needs a cross-proxy fence. For the async
proxy, fence.proxy.async should be used to synchronize memory between generic proxy and the
async proxy.
The completion of a wgmma.mma_async operation is followed by an implicit generic-async proxy
fence. So the result of the asynchronous operation is made visible to the generic proxy as soon as
its completion is observed. wgmma.commit_group and wgmma.wait_group operations must be used
to wait for the completion of the wgmma.mma_async instructions.
9.7.14.5. Asynchronous Warpgroup Level Matrix Multiply-Accumulate Operation using wgmma.mma_async instruction
This section describes warpgroup level wgmma.mma_async instruction and the organization of
various matrices involved in this instruction.
9.7.14.5.2. Asynchronous Multiply-and-Accumulate Instruction: wgmma.mma_async
wgmma.mma_async
Perform matrix multiply-and-accumulate operation across warpgroup
Syntax
Half precision floating point type:
wgmma.mma_async.sync.aligned.shape.dtype.f16.f16 d, a-desc, b-desc, scale-d, imm-scale-a, imme-scale-b, imm-trans-a, imm-trans-b;
wgmma.mma_async.sync.aligned.shape.dtype.f16.f16 d, a, b-desc, scale-d, imm-scale-a, imme-scale-b, imm-trans-b;
.shape = {.m64n8k16, .m64n16k16, .m64n24k16, .m64n32k16,
.m64n40k16, .m64n48k16, .m64n56k16, .m64n64k16,
.m64n72k16, .m64n80k16, .m64n88k16, .m64n96k16,
.m64n104k16, .m64n112k16, .m64n120k16, .m64n128k16,
.m64n136k16, .m64n144k16, .m64n152k16, .m64n160k16,
.m64n168k16, .m648176k16, .m64n184k16, .m64n192k16,
.m64n200k16, .m64n208k16, .m64n216k16, .m64n224k16,
.m64n232k16, .m64n240k16, .m64n248k16, .m64n256k16};
.dtype = {.f16, .f32};
Alternate floating point type :
.bf16 floating point type:
wgmma.mma_async.sync.aligned.shape.dtype.bf16.bf16 d, a-desc, b-desc, scale-d, imm-scale-a, imme-scale-b, imm-trans-a, imm-trans-b;
wgmma.mma_async.sync.aligned.shape.dtype.bf16.bf16 d, a, b-desc, scale-d, imm-scale-a, imme-scale-b, imm-trans-b;
.shape = {.m64n8k16, .m64n16k16, .m64n24k16, .m64n32k16,
.m64n40k16, .m64n48k16, .m64n56k16, .m64n64k16,
.m64n72k16, .m64n80k16, .m64n88k16, .m64n96k16,
.m64n104k16, .m64n112k16, .m64n120k16, .m64n128k16,
.m64n136k16, .m64n144k16, .m64n152k16, .m64n160k16,
.m64n168k16, .m648176k16, .m64n184k16, .m64n192k16,
.m64n200k16, .m64n208k16, .m64n216k16, .m64n224k16,
.m64n232k16, .m64n240k16, .m64n248k16, .m64n256k16};
.dtype = {.f32};
.tf32 floating point type:
wgmma.mma_async.sync.aligned.shape.dtype.tf32.tf32 d, a-desc, b-desc, scale-d, imm-scale-a, imme-scale-b;
wgmma.mma_async.sync.aligned.shape.dtype.tf32.tf32 d, a, b-desc, scale-d, imm-scale-a, imme-scale-b;
.shape = {.m64n8k8, .m64n16k8, .m64n24k8, .m64n32k8,
.m64n40k8, .m64n48k8, .m64n56k8, .m64n64k8,
.m64n72k8, .m64n80k8, .m64n88k8, .m64n96k8,
.m64n104k8, .m64n112k8, .m64n120k8, .m64n128k8,
.m64n136k8, .m64n144k8, .m64n152k8, .m64n160k8,
.m64n168k8, .m648176k8, .m64n184k8, .m64n192k8,
.m64n200k8, .m64n208k8, .m64n216k8, .m64n224k8,
.m64n232k8, .m64n240k8, .m64n248k8, .m64n256k8};
.dtype = {.f32};
FP8 floating point type
wgmma.mma_async.sync.aligned.shape.dtype.atype.btype d, a-desc, b-desc, scale-d, imm-scale-a, imme-scale-b;
wgmma.mma_async.sync.aligned.shape.dtype.atype.btype d, a, b-desc, scale-d, imm-scale-a, imme-scale-b;
.shape = {.m64n8k32, .m64n16k32, .m64n24k32, .m64n32k32,
.m64n40k32, .m64n48k32, .m64n56k32, .m64n64k32,
.m64n72k32, .m64n80k32, .m64n88k32, .m64n96k32,
.m64n104k32, .m64n112k32, .m64n120k32, .m64n128k32,
.m64n136k32, .m64n144k32, .m64n152k32, .m64n160k32,
.m64n168k32, .m648176k32, .m64n184k32, .m64n192k32,
.m64n200k32, .m64n208k32, .m64n216k32, .m64n224k32,
.m64n232k32, .m64n240k32, .m64n248k32, .m64n256k32};
.atype = {.e4m3, .e5m2};
.btype = {.e4m3, .e5m2};
.dtype = {.f16, .f32};
Integer type:
wgmma.mma_async.sync.aligned.shape{.satfinite}.s32.atype.btype d, a-desc, b-desc, scale-d;
wgmma.mma_async.sync.aligned.shape{.satfinite}.s32.atype.btype d, a, b-desc, scale-d;
.shape = {.m64n8k32, .m64n16k32, .m64n24k32, .m64n32k32,
.m64n48k32, .m64n64k32, .m64n80k32, .m64n96k32,
.m64n112k32, .m64n128k32, .m64n144k32, .m64n160k32,
.m648176k32, .m64n192k32, .m64n208k32, .m64n224k32};
.atype = {.s8, .u8};
.btype = {.s8, .u8};
Single bit:
wgmma.mma_async.sync.aligned.shape.s32.b1.b1.op.popc d, a-desc, b-desc, scale-d;
wgmma.mma_async.sync.aligned.shape.s32.b1.b1.op.popc d, a, b-desc, scale-d;
.shape = {.m64n8k256, .m64n16k256, .m64n24k256, .m64n32k256,
.m64n48k256, .m64n64k256, .m64n80k256, .m64n96k256,
.m64n112k256, .m64n128k256, .m64n144k256, .m64n160k256,
.m64n176k256, .m64n192k256, .m64n208k256, .m64n224k256,
.m64n240k256, .m64n256k256};
.op = {.and};
Description
Instruction wgmma.mma_async issues a MxNxK matrix multiply and accumulate operation, D =
A*B+D, where the A matrix is MxK, the B matrix is KxN, and the D matrix is MxN.
The operation of the form D = A*B is issued when the input predicate argument scale-d is
false.
wgmma.fence instruction must be used to fence the register accesses of wgmma.mma_async
instruction from their prior accesses. Otherwise, the behavior is undefined.
wgmma.commit_group and wgmma.wait_group operations must be used to wait for the completion
of the asynchronous matrix multiply and accumulate operations before the results are accessed.
Register operand d represents the accumulator matrix as well as the destination matrix,
distributed across the participating threads. Register operand a represents the multiplicand
matrix A in register distributed across the participating threads. The 64-bit register operands
a-desc and b-desc are the matrix descriptors which represent the multiplicand matrices A and
B in shared memory respectively. The format of the matrix descriptor is described in Matrix
Descriptor Format.
Matrices A and B are stored in row-major and column-major format respectively. For certain floating
point variants, the input matrices A and B can be transposed by specifying the value 1 for the
immediate integer arguments imm-trans-a and imm-trans-b respectively. A value of 0 can be
used to avoid the transpose operation. The valid values of imm-trans-a and imm-trans-b are 0
and 1. The transpose operation is only supported for the wgmma.mma_async variants with .f16/
.bf16 types on matrices accessed from shared memory using matrix descriptors.
For the floating point variants of the wgmma.mma_async operation, each element of the input
matrices A and B can be negated by specifying the value -1 for operands imm-scale-a and
imm-scale-b respectively. A value of 1 can be used to avoid the negate operation. The valid
values of imm-scale-a and imm-scale-b are -1 and 1.
The qualifiers .dtype, .atype and .btype indicate the data type of the elements in
matrices D, A and B respectively. .atype and .btype must be the same for all floating point
wgmma.mma_async variants except for the FP8 floating point variants. The sizes of individual
data elements of matrices A and B in alternate floating point variants of the wgmma.mma_async
operation are as follows:
Matrices A and B have 8-bit data elements when
.atype/.btypeis.e4m3/.e5m2.Matrices A and B have 16-bit data elements when
.atype/.btypeis.bf16.Matrices A and B have 32-bit data elements when
.atype/.btypeis.tf32.
Precision and rounding:
Floating point operations:
Element-wise multiplication of matrix A and B is performed with at least single precision. When
.dtypeis.f32, accumulation of the intermediate values is performed with at least single precision. When.dtypeis.f16, the accumulation is performed with at least half precision.The accumulation order, rounding and handling of subnormal inputs are unspecified.
.bf16and.tf32floating point operations:Element-wise multiplication of matrix A and B is performed with specified precision.
wgmma.mma_asyncoperation involving type.tf32will truncate lower 13 bits of the 32-bit input data before multiplication is issued. Accumulation of the intermediate values is performed with at least single precision.The accumulation order, rounding, and handling of subnormal inputs are unspecified.
Integer operations:
The integer
wgmma.mma_asyncoperation is performed with.s32accumulators. The.satfinitequalifier indicates that on overflow, the accumulated value is limited to the range MIN_INT32..MAX_INT32 (where the bounds are defined as the minimum negative signed 32-bit integer and the maximum positive signed 32-bit integer respectively).If
.satfiniteis not specified, the accumulated value is wrapped instead.
The mandatory .sync qualifier indicates that wgmma.mma_async instruction causes the
executing thread to wait until all threads in the warp execute the same wgmma.mma_async
instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same wgmma.mma_async instruction. In conditionally executed code, a wgmma.mma_async
instruction should only be used if it is known that all threads in the warpgroup evaluate the
condition identically, otherwise behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Support for .u8.s8 and .s8.u8 as .atype.btype introduced in PTX ISA version 8.4.
Target ISA Notes
Requires sm_90a.
Examples of half precision floating point type
.reg .f16x2 f16a<40>, f16d<40>;
.reg .f32 f32d<40>;
.reg .b64 descA, descB;
.reg .pred scaleD;
wgmma.mma_async.sync.aligned.m64n8k16.f32.f16.f16
{f32d0, f32d1, f32d2, f32d3},
{f16a0, f16a1, f16a2, f16a3},
descB,
1, -1, -1, 1;
wgmma.mma_async.sync.aligned.m64n72k16.f16.f16.f16
{f16d0, f16d1, f16d2, f16d3, f16d4, f16d5, f16d6, f16d7, f16d8,
f16d9, f16d10, f16d11, f16d12, f16d13, f16d14, f16d15, f16d16, f16d17},
descA,
descB,
scaleD, -1, 1, 1, 0;
Examples of alternate floating point type
.reg .f32 f32d<40>;
.reg .b32 bf16a<40>
.reg .b64 descA, descB;
wgmma.mma_async.sync.aligned.m64n120k16.f32.bf16.bf16
{f32d0, f32d1, f32d2, f32d3, f32d4, f32d5, f32d6, f32d7, f32d8, f32d9,
f32d10, f32d11, f32d12, f32d13, f32d14, f32d15, f32d16, f32d17, f32d18, f32d19,
f32d20, f32d21, f32d22, f32d23, f32d24, f32d25, f32d26, f32d27, f32d28, f32d29,
f32d30, f32d31, f32d32, f32d33, f32d34, f32d35, f32d36, f32d37, f32d38, f32d39,
f32d40, f32d41, f32d42, f32d43, f32d44, f32d45, f32d46, f32d47, f32d48, f32d49,
f32d50, f32d51, f32d52, f32d53, f32d54, f32d55, f32d56, f32d57, f32d58, f32d59},
{bf16a0, bf16a1, bf16a2, bf16a3},
descB,
scaleD, -1, -1, 0;
.reg .f32 f32d<40>;
.reg .b64 descA, descB;
wgmma.mma_async.sync.aligned.m64n16k8.f32.tf32.tf32
{f32d0, f32d1, f32d2, f32d3, f32d4, f32d5, f32d6, f32d7},
descA,
descB,
0, -1, -1;
.reg .b32 f16d<8>, f16a<8>;
.reg .f32 f32d<8>;
.reg .b64 descA, descB;
wgmma.mma_async.sync.aligned.m64n8k32.f16.e4m3.e5m2
{f16d0, f16d1},
descA,
descB,
scaleD, -1, 1;
wgmma.mma_async.sync.aligned.m64n8k32.f32.e5m2.e4m3
{f32d0, f32d1, f32d2, f32d3},
{f16a0, f16a1, f16a2, f16a3},
descB,
1, -1, -1;
Examples of integer type
.reg .s32 s32d<8>, s32a<8>;
.reg .u32 u32a<8>;
.reg .pred scaleD;
.reg .b64 descA, descB;
wgmma.mma_async.sync.aligned.m64n8k32.s32.s8.s8.satfinite
{s32d0, s32d1, s32d2, s32d3},
{s32a0, s32a1, s32a2, s32a3},
descB,
1;
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.u8
{s32d0, s32d1, s32d2, s32d3},
descA,
descB,
scaleD;
wgmma.mma_async.sync.aligned.m64n8k32.s32.s8.u8.satfinite
{s32d0, s32d1, s32d2, s32d3},
{s32a0, s32a1, s32a2, s32a3},
descB,
scaleD;
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.s8
{s32d0, s32d1, s32d2, s32d3},
descA,
descB,
scaleD;
Examples of single bit type
.reg .s32 s32d<4>;
.reg .b32 b32a<4>;
.reg .pred scaleD;
.reg .b64 descA, descB;
wgmma.mma_async.sync.aligned.m64n8k256.s32.b1.b1.and.popc
{s32d0, s32d1, s32d2, s32d3},
{b32a0, b32a1, b32a2, b32a3},
descB,
scaleD;
9.7.14.6. Asynchronous Warpgroup Level Multiply-and-Accumulate Operation using wgmma.mma_async.sp instruction
This section describes warp-level wgmma.mma_async.sp instruction with sparse matrix A. This
variant of the wgmma.mma_async operation can be used when A is a structured sparse matrix with
50% zeros in each row distributed in a shape-specific granularity. For an MxNxK sparse
wgmma.mma_async.sp operation, the MxK matrix A is packed into MxK/2 elements. For each
K-wide row of matrix A, 50% elements are zeros and the remaining K/2 non-zero elements are
packed in the operand representing matrix A. The mapping of these K/2 elements to the
corresponding K-wide row is provided explicitly as metadata.
9.7.14.6.1. Sparse matrix storage
Granularity of sparse matrix A is defined as the ratio of the number of non-zero elements in a
sub-chunk of the matrix row to the total number of elements in that sub-chunk where the size of the
sub-chunk is shape-specific. For example, in a 64x32 matrix A used in floating point
wgmma.mma_async operations, sparsity is expected to be at 2:4 granularity, i.e. each 4-element
vector (i.e. a sub-chunk of 4 consecutive elements) of a matrix row contains 2 zeros. Index of each
non-zero element in a sub-chunk is stored in the metadata operand. In a group of four consecutive
threads, one or more threads store the metadata for the whole group depending upon the matrix
shape. These threads are specified using an additional sparsity selector operand.
Matrix A and its corresponding input operand to the sparse wgmma is similar to the diagram shown in Figure 83, with an appropriate matrix size.
Granularities for different matrix shapes and data types are described below.
Sparse wgmma.mma_async.sp with half-precision and .bf16 type
For .f16 and .bf16 types, for all supported 64xNx32 shapes, matrix A is structured
sparse at a granularity of 2:4. In other words, each chunk of four adjacent elements in a row of
matrix A have two zeroes and two non-zero elements. Only the two non-zero elements are stored in
matrix A and their positions in the four-wide chunk in Matrix A are indicated by two 2-bits indices
in the metadata operand.

Figure 145 Sparse WGMMA metadata example for .f16/.bf16 type.
The sparsity selector indicates a thread-pair within a group of four consecutive threads which contributes the sparsity metadata. Hence, the sparsity selector must be either 0 (threads T0, T1) or 1 (threads T2, T3); any other value results in an undefined behavior.
Sparse wgmma.mma_async.sp with .tf32 type
For .tf32 type, for all supported 64xNx16 shapes, matrix A is structured sparse at a
granularity of 1:2. In other words, each chunk of two adjacent elements in a row of matrix A have
one zero and one non-zero element. Only the non-zero element is stored in operand for matrix A and
the 4-bit index in the metadata indicates the position of the non-zero element in the two-wide
chunk. 0b1110 and 0b0100 are the only meaningful values of the index, the remaining values result in
an undefined behavior.

Figure 146 Sparse WGMMA metadata example for .tf32 type.
The sparsity selector indicates a thread-pair within a group of four consecutive threads which contributes the sparsity metadata. Hence, the sparsity selector must be either 0 (threads T0, T1) or 1 (threads T2, T3); any other value results in an undefined behavior.
Sparse wgmma.mma_async.sp with .e4m3 and .e5m2 floating point type
For .e4m3 and .e5m2 types, for all supported 64xNx64 shapes, matrix A is structured
sparse at a granularity of 2:4. In other words, each chunk of four adjacent elements in a row of
matrix A have two zeroes and two non-zero elements. Only the two non-zero elements are stored in
matrix A and their positions in the four-wide chunk in Matrix A are indicated by two 2-bits indices
in the metadata operand.

Figure 147 Sparse WGMMA metadata example for .e4m3/.e5m2 type.
All threads contribute the sparsity metadata and the sparsity selector must be 0; any other value results in an undefined behavior.
Sparse wgmma.mma_async.sp with integer type
For the integer type, for all supported 64xNx64 shapes, matrix A is structured sparse at a
granularity of 2:4. In other words, each chunk of four adjacent elements in a row of matrix A have
two zeroes and two non-zero elements. Only the two non-zero elements are stored in matrix A and two
2-bit indices in the metadata indicate the position of these two non-zero elements in the four-wide
chunk.

Figure 148 Sparse WGMMA metadata example for .u8/.s8 type.
All threads contribute the sparsity metadata and the sparsity selector must be 0; any other value results in an undefined behavior.
9.7.14.6.2. Matrix fragments for warpgroup-level multiply-accumulate operation with sparse matrix A
In this section we describe how the contents of thread registers are associated with fragments of A matrix and the sparsity metadata.
Each warp in the warpgroup provides sparsity information for 16 rows of matrix A. The following table shows the assignment of warps to rows of matrix A:
Warp |
Sparsity information for rows of matrix A |
|---|---|
|
48-63 |
|
32-47 |
|
16-31 |
|
0-15 |
The following conventions are used throughout this section:
For matrix A, only the layout of a fragment is described in terms of register vector sizes and their association with the matrix data.
For matrix D, since the matrix dimension - data type combination is the same for all supported shapes, and is already covered in Matrix multiply-accumulate operation using wgmma instruction, the pictorial representations of matrix fragments are not included in this section.
For the metadata operand, pictorial representations of the association between indices of the elements of matrix A and the contents of the metadata operand are included.
Tk: [m..n]present in cell[x][y..z]indicates that bitsmthroughn(withmbeing higher) in the metadata operand of thread with%laneid=kcontains the indices of the non-zero elements from the chunk[x][y]..[x][z]of matrix A.
9.7.14.6.2.1. Matrix Fragments for sparse wgmma.mma_async.m64nNk32
A warpgroup executing sparse wgmma.mma_async.m64nNk32 will compute an MMA operation of shape
.m64nNk32 where N is a valid n dimension as listed in Matrix shape.
Elements of the matrix are distributed across the threads in a warpgroup so each thread of the warpgroup holds a fragment of the matrix.
Multiplicand A, from shared memory is documented in Shared Memory Layout for wgmma.mma_async.m64nNk32.
Multiplicand A, from registers:
.atype
Fragments
Elements
.f16/.bf16A vector expression containing four.b32registers, with each register containing twonon-zero.f16/.bf16elements out of 4consecutive elements from matrix A.Non-zero elements:a0, a1, a2, a3, a4, a5, a6, a7The layout of the fragments held by different threads is shown in Figure 149.

Figure 149 Sparse WGMMA .m64nNk32 fragment layout for matrix A with
.f16/.bf16type.Accumulator D:
Matrix fragments for accumulator D are the same as in case of Matrix Fragments for wgmma.m64nNk32 with floating point type for the same
.dtypeformat.Multiplicand B:
Shared memory layout for Matrix B is documented in Shared Memory Layout for wgmma.mma_async.m64nNk32.
Metadata operand is a
.b32register containing 16 2-bit vectors each storing the index of a non-zero element of a 4-wide chunk of matrix A.Figure 150 shows the mapping of the metadata bits to the elements of matrix A for a warp. In this figure, variable
irepresents the value of the sparsity selector operand.
Figure 150 Sparse WGMMA .m64nNk32 metadata layout for
.f16/.bf16type.
9.7.14.6.2.2. Matrix Fragments for sparse wgmma.mma_async.m64nNk16
A warpgroup executing sparse wgmma.mma_async.m64nNk16 will compute an MMA operation of shape
.m64nNk16 where N is a valid n dimension as listed in Matrix shape.
Elements of the matrix are distributed across the threads in a warpgroup so each thread of the warpgroup holds a fragment of the matrix.
Multiplicand A, from shared memory is documented in Shared Memory Layout for wgmma.mma_async.m64nNk16.
Multiplicand A, from registers:
.atype
Fragments
Elements
.tf32A vector expression containing four.b32registers, containing four non-zero.tf32elements out of eight consecutive elementsfrom matrix A.Non-zero elements:a0, a1, a2, a3Mapping of the non-zeroelements is as described inThe layout of the fragments held by different threads is shown in Figure 151.
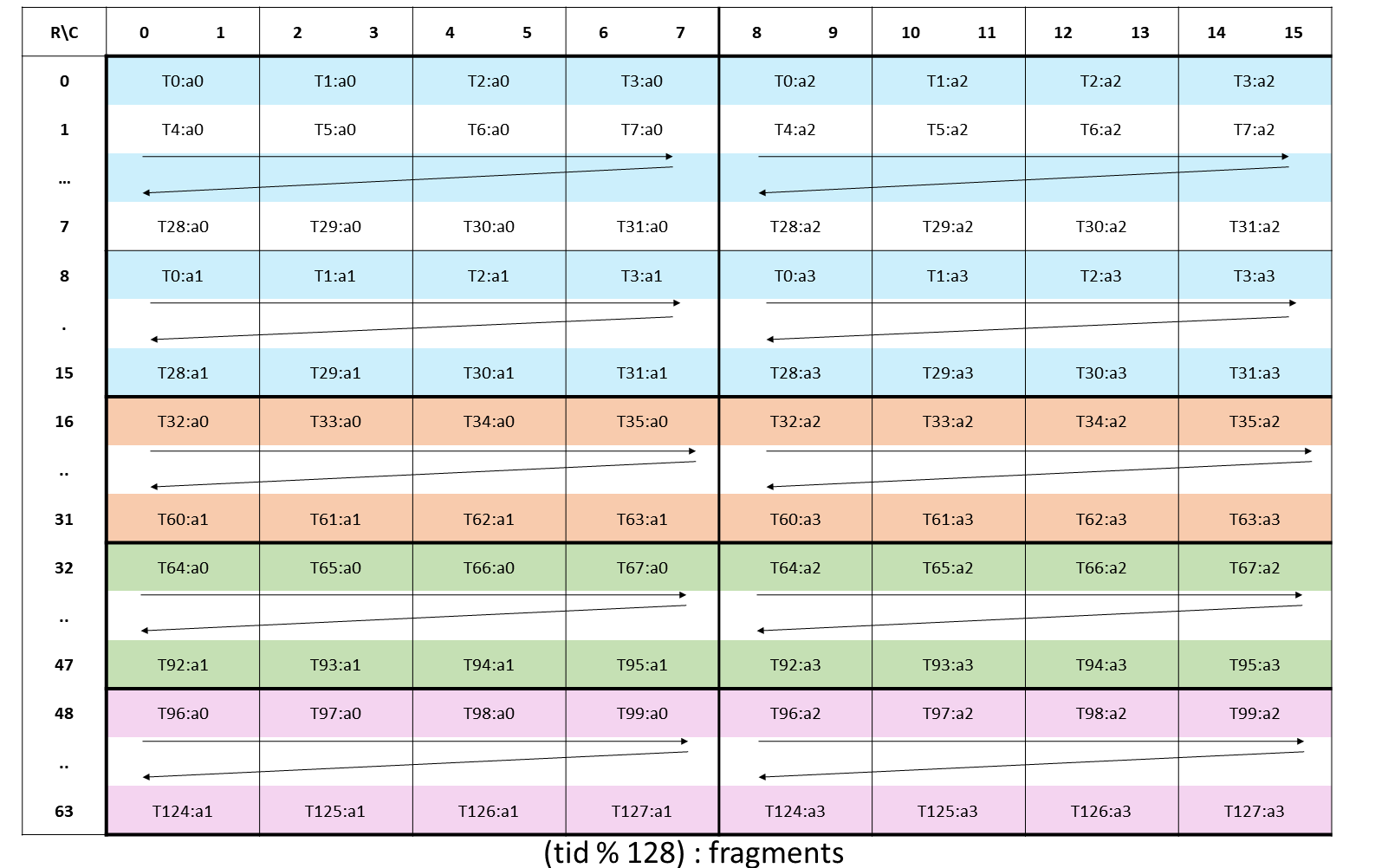
Figure 151 Sparse WGMMA .m64nNk16 fragment layout for matrix A with
.tf32type.Accumulator D:
Matrix fragments for accumulator D are the same as in case of Matrix Fragments for wgmma.m64nNk8 with floating point type for the same
.dtypeformat.Multiplicand B:
Shared memory layout for Matrix B is documented in Shared Memory Layout for wgmma.mma_async.m64nNk16.
Metadata operand is a
.b32register containing eight 4-bit vectors each storing the index of a non-zero element of a 2-wide chunk of matrix A.Figure 152 shows the mapping of the metadata bits to the elements of matrix A for a warp. In this figure, variable
irepresents the value of the sparsity selector operand.
Figure 152 Sparse WGMMA .m64nNk16 metadata layout for
.tf32type.
9.7.14.6.2.3. Matrix Fragments for sparse wgmma.mma_async.m64nNk64
A warpgroup executing sparse wgmma.mma_async.m64nNk64 will compute an MMA operation of shape
.m64nNk64 where N is a valid n dimension as listed in Matrix shape.
Elements of the matrix are distributed across the threads in a warpgroup so each thread of the warpgroup holds a fragment of the matrix.
Multiplicand A, from shared memory is documented in Shared Memory Layout for wgmma.mma_async.m64nNk64.
Multiplicand A, from registers:
.atype
Fragments
Elements
.e4m3/.e5m2A vector expression containing four.b32registers, with each register containing fournon-zero.e4m3/.e5m2elements out ofeight consecutive elements from matrix A.Non-zero elements:a0, a1, a2, … , a15Mapping of the non-zeroelements is as described in.s8/.u8A vector expression containing four.b32registers, with each register containing fournon-zero.s8/.u8elements out ofeight consecutive elements from matrix A.The layout of the fragments held by different threads is shown in Figure 153.
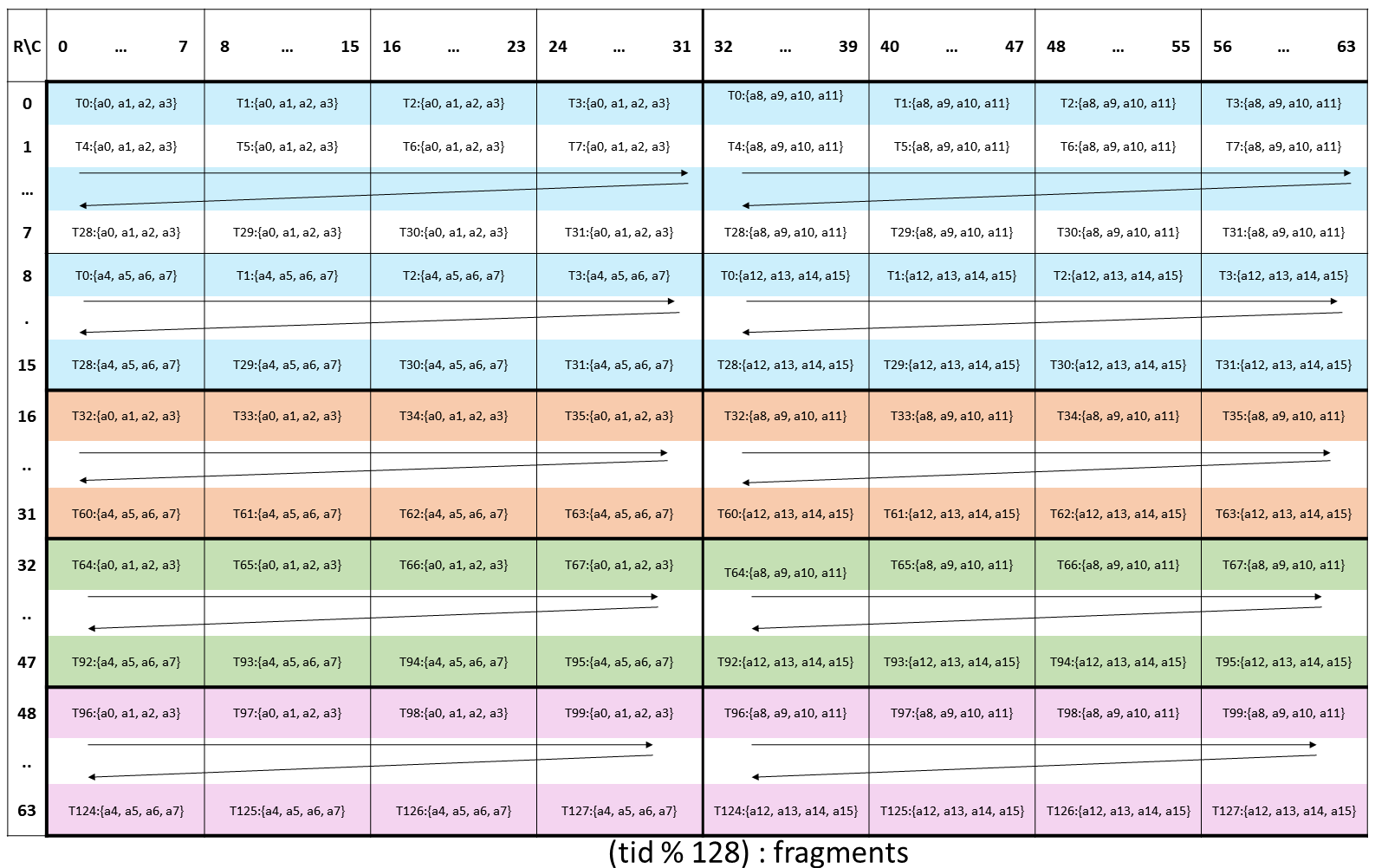
Figure 153 Sparse WGMMA .m64nNk64 fragment layout for matrix A with
.e4m3/.e5m2/.s8/.u8type.Accumulator D:
Matrix fragments for accumulator D are the same as in case of Matrix Fragments for wgmma.m64nNk32 with floating point type for the same
.dtypeformat.Multiplicand B:
Shared memory layout for Matrix B is documented in Shared Memory Layout for wgmma.mma_async.m64nNk64.
Metadata operand is a
.b32register containing 16 4-bit vectors each storing the indices of two non-zero elements of a 4-wide chunk of matrix A.Figure 154 shows the mapping of the metadata bits to the elements of columns 0–31 of matrix A.
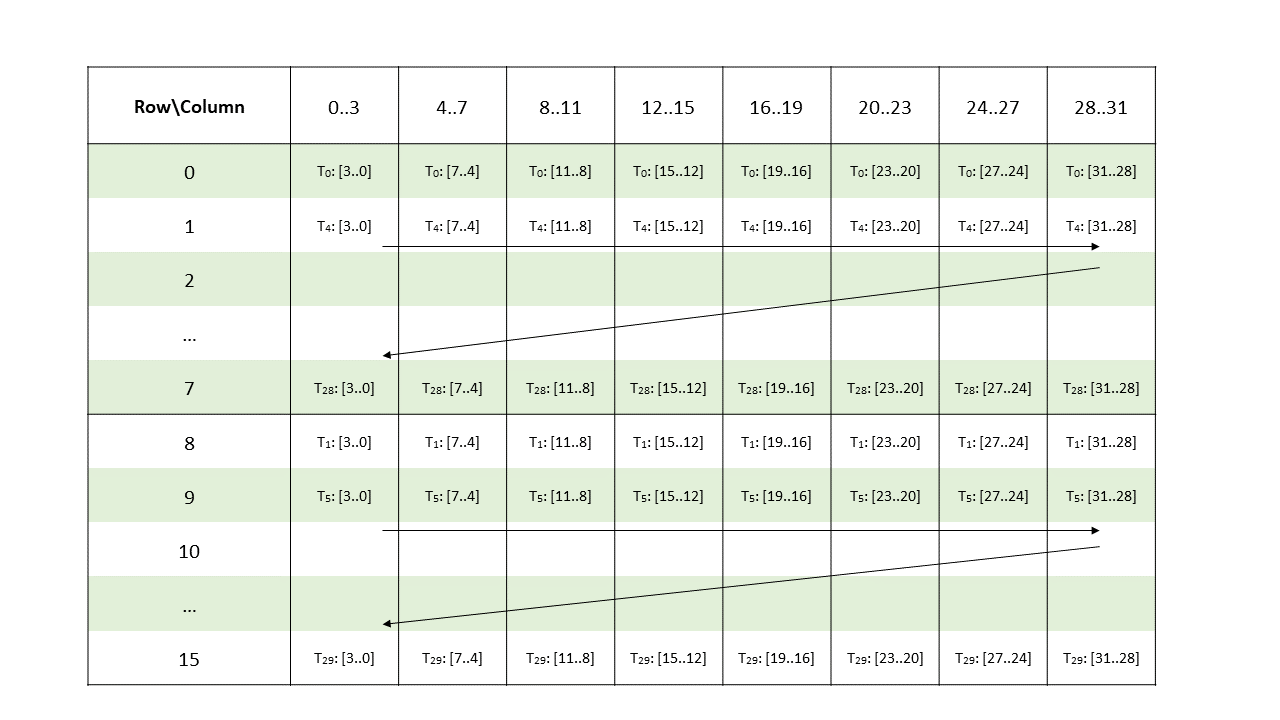
Figure 154 Sparse WGMMA .m64nNk64 metadata layout for
.e4m3/.e5m2/.s8/.u8type for columns 0–31Figure 155 shows the mapping of the metadata bits to the elements of columns 32–63 of matrix A.
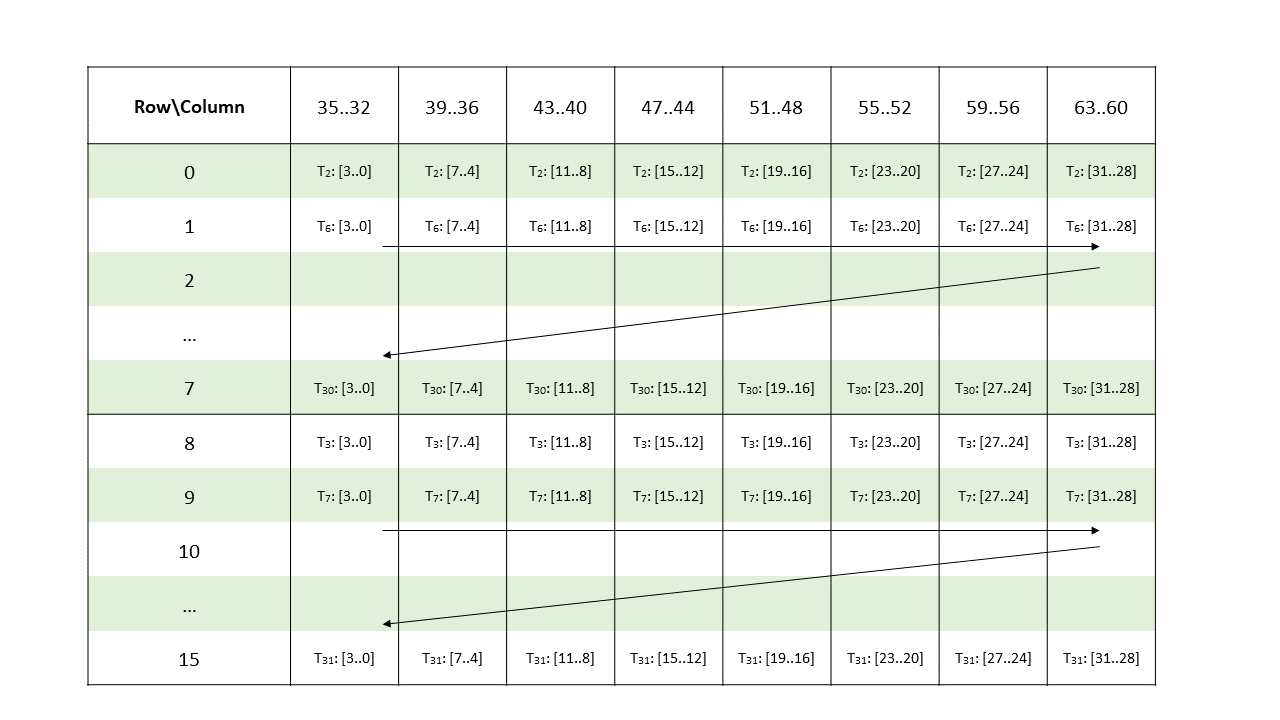
Figure 155 Sparse WGMMA .m64nNk64 metadata layout for
.e4m3/.e5m2/.s8/.u8type for columns 32–63
9.7.14.6.4. Asynchronous Multiply-and-Accumulate Instruction: wgmma.mma_async.sp
wgmma.mma_async.sp
Perform matrix multiply-and-accumulate operation with sparse matrix A across warpgroup
Syntax
Half precision floating point type:
wgmma.mma_async.sp.sync.aligned.shape.dtype.f16.f16 d, a-desc, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b, imm-trans-a, imm-trans-b;
wgmma.mma_async.sp.sync.aligned.shape.dtype.f16.f16 d, a, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b, imm-trans-b;
.shape = {.m64n8k32, .m64n16k32, .m64n24k32, .m64n32k32,
.m64n40k32, .m64n48k32, .m64n56k32, .m64n64k32,
.m64n72k32, .m64n80k32, .m64n88k32, .m64n96k32,
.m64n104k32, .m64n112k32, .m64n120k32, .m64n128k32,
.m64n136k32, .m64n144k32, .m64n152k32, .m64n160k32,
.m64n168k32, .m648176k32, .m64n184k32, .m64n192k32,
.m64n200k32, .m64n208k32, .m64n216k32, .m64n224k32,
.m64n232k32, .m64n240k32, .m64n248k32, .m64n256k32};
.dtype = {.f16, .f32};
Alternate floating point type :
.bf16 floating point type:
wgmma.mma_async.sp.sync.aligned.shape.dtype.bf16.bf16 d, a-desc, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b, imm-trans-a, imm-trans-b;
wgmma.mma_async.sp.sync.aligned.shape.dtype.bf16.bf16 d, a, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imme-scale-b, imm-trans-b;
.shape = {.m64n8k32, .m64n16k32, .m64n24k32, .m64n32k32,
.m64n40k32, .m64n48k32, .m64n56k32, .m64n64k32,
.m64n72k32, .m64n80k32, .m64n88k32, .m64n96k32,
.m64n104k32, .m64n112k32, .m64n120k32, .m64n128k32,
.m64n136k32, .m64n144k32, .m64n152k32, .m64n160k32,
.m64n168k32, .m648176k32, .m64n184k32, .m64n192k32,
.m64n200k32, .m64n208k32, .m64n216k32, .m64n224k32,
.m64n232k32, .m64n240k32, .m64n248k32, .m64n256k32};
.dtype = {.f32};
.tf32 floating point type:
wgmma.mma_async.sp.sync.aligned.shape.dtype.tf32.tf32 d, a-desc, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b;
wgmma.mma_async.sp.sync.aligned.shape.dtype.tf32.tf32 d, a, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b;
.shape = {.m64n8k16, .m64n16k16, .m64n24k16, .m64n32k16,
.m64n40k16, .m64n48k16, .m64n56k16, .m64n64k16,
.m64n72k16, .m64n80k16, .m64n88k16, .m64n96k16,
.m64n104k16, .m64n112k16, .m64n120k16, .m64n128k16,
.m64n136k16, .m64n144k16, .m64n152k16, .m64n160k16,
.m64n168k16, .m648176k16, .m64n184k16, .m64n192k16,
.m64n200k16, .m64n208k16, .m64n216k16, .m64n224k16,
.m64n232k16, .m64n240k16, .m64n248k16, .m64n256k16};
.dtype = {.f32};
FP8 floating point type
wgmma.mma_async.sp.sync.aligned.shape.dtype.atype.btype d, a-desc, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b;
wgmma.mma_async.sp.sync.aligned.shape.dtype.atype.btype d, a, b-desc, sp-meta, sp-sel, scale-d, imm-scale-a, imm-scale-b;
.shape = {.m64n8k64, .m64n16k64, .m64n24k64, .m64n32k64,
.m64n40k64, .m64n48k64, .m64n56k64, .m64n64k64,
.m64n72k64, .m64n80k64, .m64n88k64, .m64n96k64,
.m64n104k64, .m64n112k64, .m64n120k64, .m64n128k64,
.m64n136k64, .m64n144k64, .m64n152k64, .m64n160k64,
.m64n168k64, .m648176k64, .m64n184k64, .m64n192k64,
.m64n200k64, .m64n208k64, .m64n216k64, .m64n224k64,
.m64n232k64, .m64n240k64, .m64n248k64, .m64n256k64};
.atype = {.e4m3, .e5m2};
.btype = {.e4m3, .e5m2};
.dtype = {.f16, .f32};
Integer type:
wgmma.mma_async.sp.sync.aligned.shape{.satfinite}.s32.atype.btype d, a-desc, b-desc, sp-meta, sp-sel, scale-d;
wgmma.mma_async.sp.sync.aligned.shape{.satfinite}.s32.atype.btype d, a, b-desc, sp-meta, sp-sel, scale-d;
.shape = {.m64n8k64, .m64n16k64, .m64n24k64, .m64n32k64,
.m64n48k64, .m64n64k64, .m64n80k64, .m64n96k64,
.m64n112k64, .m64n128k64, .m64n144k64, .m64n160k64,
.m648176k64, .m64n192k64, .m64n208k64, .m64n224k64,
.m64n240k64, .m64n256k64};
.atype = {.s8, .u8};
.btype = {.s8, .u8};
Description
Instruction wgmma.mma_async issues a MxNxK matrix multiply and accumulate operation, D =
A*B+D, where the A matrix is MxK, the B matrix is KxN, and the D matrix is MxN.
The matrix A is stored in the packed format Mx(K/2) as described in Matrix multiply-accumulate operation using wgmma.mma_async.sp instruction with sparse matrix A.
The operation of the form D = A*B is issued when the input predicate argument scale-d is
false.
wgmma.fence instruction must be used to fence the register accesses of wgmma.mma_async
instruction from their prior accesses. Otherwise, the behavior is undefined.
wgmma.commit_group and wgmma.wait_group operations must be used to wait for the completion
of the asynchronous matrix multiply and accumulate operations before the results are accessed.
Register operand d represents the accumulator matrix as well as the destination matrix,
distributed across the participating threads. Register operand a represents the multiplicand
matrix A in register distributed across the participating threads. The 64-bit register operands
a-desc and b-desc are the matrix descriptors which represent the multiplicand matrices A and
B in shared memory respectively. The format of the matrix descriptor is described in Matrix
Descriptor Format. Matrix A is
structured sparse as described in Sparse matrix storage. Operands sp-meta and sp-sel
represent sparsity metadata and sparsity selector respectively. Operand sp-meta is a 32-bit
integer and operand sp-sel is a 32-bit integer constant with values in the range 0..3.
The valid values of sp-meta and sp-sel for each shape is specified in Matrix
multiply-accumulate operation using wgmma.mma_async.sp instruction with sparse matrix A and are summarized here :
Matrix shape |
|
Valid values of |
Valid values of |
|---|---|---|---|
|
|
0b1110 , 0b0100 |
0 (threads T0, T1) or 1 (threads T2, T3) |
|
|
0b00, 0b01, 0b10, 0b11 |
0 (threads T0, T1) or 1 (threads T2, T3) |
|
|
0b00, 0b01, 0b10, 0b11 |
0 (all threads contribute) |
Matrices A and B are stored in row-major and column-major format respectively. For certain floating
point variants, the input matrices A and B can be transposed by specifying the value 1 for the
immediate integer arguments imm-trans-a and imm-trans-b respectively. A value of 0 can be
used to avoid the transpose operation. The valid values of imm-trans-a and imm-trans-b are 0
and 1. The transpose operation is only supported for the wgmma.mma_async variants with .f16/
.bf16 types on matrices accessed from shared memory using matrix descriptors.
For the floating point variants of the wgmma.mma_async operation, each element of the input
matrices A and B can be negated by specifying the value -1 for operands imm-scale-a and
imm-scale-b respectively. A value of 1 can be used to avoid the negate operation. The valid
values of imm-scale-a and imm-scale-b are -1 and 1.
The qualifiers .dtype, .atype and .btype indicate the data type of the elements in
matrices D, A and B respectively. .atype and .btype must be the same for all floating point
wgmma.mma_async variants except for the FP8 floating point variants. The sizes of individual
data elements of matrices A and B in alternate floating point variants of the wgmma.mma_async
operation are as follows:
Matrices A and B have 8-bit data elements when
.atype/.btypeis.e4m3/.e5m2.Matrices A and B have 16-bit data elements when
.atype/.btypeis.bf16.Matrices A and B have 32-bit data elements when
.atype/.btypeis.tf32.
Precision and rounding:
Floating point operations:
Element-wise multiplication of matrix A and B is performed with at least single precision. When
.dtypeis.f32, accumulation of the intermediate values is performed with at least single precision. When.dtypeis.f16, the accumulation is performed with at least half precision.The accumulation order, rounding and handling of subnormal inputs are unspecified.
.bf16and.tf32floating point operations:Element-wise multiplication of matrix A and B is performed with specified precision.
wgmma.mma_asyncoperation involving type.tf32will truncate lower 13 bits of the 32-bit input data before multiplication is issued. Accumulation of the intermediate values is performed with at least single precision.The accumulation order, rounding, and handling of subnormal inputs are unspecified.
Integer operations:
The integer
wgmma.mma_asyncoperation is performed with.s32accumulators. The.satfinitequalifier indicates that on overflow, the accumulated value is limited to the range MIN_INT32..MAX_INT32 (where the bounds are defined as the minimum negative signed 32-bit integer and the maximum positive signed 32-bit integer respectively).If
.satfiniteis not specified, the accumulated value is wrapped instead.
The mandatory .sync qualifier indicates that wgmma.mma_async instruction causes the
executing thread to wait until all threads in the warp execute the same wgmma.mma_async
instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same wgmma.mma_async instruction. In conditionally executed code, a wgmma.mma_async
instruction should only be used if it is known that all threads in the warpgroup evaluate the
condition identically, otherwise behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.2.
Support for .u8.s8 and .s8.u8 as .atype.btype introduced in PTX ISA version 8.4.
Target ISA Notes
Requires sm_90a.
Examples of integer type
wgmma.fence.sync.aligned;
wgmma.mma_async.sp.sync.aligned.m64n8k64.s32.u8.u8 {s32d0, s32d1, s32d2, s32d3},
descA, descB, spMeta, 0, scaleD;
wgmma.mma_async.sp.sync.aligned.m64n8k64.s32.s8.u8 {s32d0, s32d1, s32d2, s32d3},
descA, descB, spMeta, 0, scaleD;
wgmma.commit_group.sync.aligned;
wgmma.wait_group.sync.aligned 0;
9.7.14.7. Asynchronous wgmma Proxy Operations
This section describes warpgroup level wgmma.fence, wgmma.commit_group and wgmma.wait_group instructions.
9.7.14.7.1. Asynchronous Multiply-and-Accumulate Instruction: wgmma.fence
wgmma.fence
Enforce an ordering of register accesses between wgmma.mma_async and other operations.
Syntax
wgmma.fence.sync.aligned;
Description
wgmma.fence instruction establishes an ordering between prior accesses to any warpgroup
registers and subsequent accesses to the same registers by a wgmma.mma_async instruction. Only
the accumulator register and the input registers containing the fragments of matrix A require this
ordering.
The wgmma.fence instruction must be issued by all warps of the warpgroup at the following
locations:
Before the first
wgmma.mma_asyncoperation in a warpgroup.Between a register access by a thread in the warpgroup and any
wgmma.mma_asyncinstruction that accesses the same registers, either as accumulator or input register containing fragments of matrix A, except when these are accumulator register accesses across multiplewgmma.mma_asyncinstructions of the same shape. In the latter case, an ordering guarantee is provided by default.
Otherwise, the behavior is undefined.
An async proxy fence must be used to establish an ordering between prior writes to shared memory
matrices and subsequent reads of the same matrices in a wgmma.mma_async instruction.
The mandatory .sync qualifier indicates that wgmma.fence instruction causes the executing
thread to wait until all threads in the warp execute the same wgmma.fence instruction before
resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same wgmma.fence instruction. In conditionally executed code, an wgmma.fence instruction
should only be used if it is known that all threads in the warpgroup evaluate the condition
identically, otherwise the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90a.
Examples
// Example 1, first use example:
wgmma.fence.sync.aligned; // Establishes an ordering w.r.t. prior accesses to the registers s32d<0-3>
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.u8 {s32d0, s32d1, s32d2, s32d3},
descA, descB, scaleD;
wgmma.commit_group.sync.aligned;
wgmma.wait_group.sync.aligned 0;
// Example 2, use-case with the input value updated in between:
wgmma.fence.sync.aligned;
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.u8 {s32d0, s32d1, s32d2, s32d3},
descA, descB, scaleD;
...
mov.b32 s32d0, new_val;
wgmma.fence.sync.aligned;
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.u8 {s32d4, s32d5, s32d6, s32d7},
{s32d0, s32d1, s32d2, s32d3},
descB, scaleD;
wgmma.commit_group.sync.aligned;
wgmma.wait_group.sync.aligned 0;
9.7.14.7.2. Asynchronous Multiply-and-Accumulate Instruction: wgmma.commit_group
wgmma.commit_group
Commits all prior uncommitted wgmma.mma_async operations into a wgmma-group.
Syntax
wgmma.commit_group.sync.aligned;
Description
wgmma.commit_group instruction creates a new wgmma-group per warpgroup and batches all prior
wgmma.mma_async instructions initiated by the executing warp but not committed to any
wgmma-group into the new wgmma-group. If there are no uncommitted wgmma.mma_async instructions
then wgmma.commit_group results in an empty wgmma-group.
An executing thread can wait for the completion of all wgmma.mma_async operations in a
wgmma-group by using wgmma.wait_group.
The mandatory .sync qualifier indicates that wgmma.commit_group instruction causes the
executing thread to wait until all threads in the warp execute the same wgmma.commit_group
instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same wgmma.commit_group instruction. In conditionally executed code, an wgmma.commit_group
instruction should only be used if it is known that all threads in the warpgroup evaluate the
condition identically, otherwise the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90a.
Examples
wgmma.commit_group.sync.aligned;
9.7.14.7.3. Asynchronous Multiply-and-Accumulate Instruction: wgmma.wait_group
wgmma.wait_group
Signal the completion of a preceding warpgroup operation.
Syntax
wgmma.wait_group.sync.aligned N;
Description
wgmma.wait_group instruction will cause the executing thread to wait until only N or fewer of
the most recent wgmma-groups are pending and all the prior wgmma-groups committed by the executing
threads are complete. For example, when N is 0, the executing thread waits on all the prior
wgmma-groups to complete. Operand N is an integer constant.
Accessing the accumulator register or the input register containing the fragments of matrix A of a
wgmma.mma_async instruction without first performing a wgmma.wait_group instruction that
waits on a wgmma-group including that wgmma.mma_async instruction is undefined behavior.
The mandatory .sync qualifier indicates that wgmma.wait_group instruction causes the
executing thread to wait until all threads in the warp execute the same wgmma.wait_group
instruction before resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same wgmma.wait_group instruction. In conditionally executed code, an wgmma.wait_group
instruction should only be used if it is known that all threads in the warpgroup evaluate the
condition identically, otherwise the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90a.
Examples
wgmma.fence.sync.aligned;
wgmma.mma_async.sync.aligned.m64n8k32.s32.u8.u8 {s32d0, s32d1, s32d2, s32d3},
descA, descB, scaleD;
wgmma.commit_group.sync.aligned;
wgmma.mma_async.sync.aligned.m64n8k16.f32.f16.f16 {f32d0, f32d1, f32d2, f32d3},
{f16a0, f16a1, f16a2, f16a3},
descB, 1, -1, -1, 1;
wgmma.commit_group.sync.aligned;
wgmma.wait_group.sync.aligned 0;
9.7.15. Stack Manipulation Instructions
The stack manipulation instructions can be used to dynamically allocate and deallocate memory on the stack frame of the current function.
The stack manipulation instrucitons are:
stacksavestackrestorealloca
9.7.15.1. Stack Manipulation Instructions: stacksave
stacksave
Save the value of stack pointer into a register.
Syntax
stacksave.type d;
.type = { .u32, .u64 };
Description
Copies the current value of stack pointer into the destination register d. Pointer returned by
stacksave can be used in a subsequent stackrestore instruction to restore the stack
pointer. If d is modified prior to use in stackrestore instruction, it may corrupt data in
the stack.
Destination operand d has the same type as the instruction type.
Semantics
d = stackptr;
PTX ISA Notes
Introduced in PTX ISA version 7.3.
- Preview Feature:
stacksaveis a preview feature in PTX ISA version 7.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
stacksave requires sm_52 or higher.
Examples
.reg .u32 rd;
stacksave.u32 rd;
.reg .u64 rd1;
stacksave.u64 rd1;
9.7.15.2. Stack Manipulation Instructions: stackrestore
stackrestore
Update the stack pointer with a new value.
Syntax
stackrestore.type a;
.type = { .u32, .u64 };
Description
Sets the current stack pointer to source register a.
When stackrestore is used with operand a written by a prior stacksave instruction, it
will effectively restore the state of stack as it was before stacksave was executed. Note that
if stackrestore is used with an arbitrary value of a, it may cause corruption of stack
pointer. This implies that the correct use of this feature requires that stackrestore.type a is
used after stacksave.type a without redefining the value of a between them.
Operand a has the same type as the instruction type.
Semantics
stackptr = a;
PTX ISA Notes
Introduced in PTX ISA version 7.3.
- Preview Feature:
stackrestoreis a preview feature in PTX ISA version 7.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
stackrestore requires sm_52 or higher.
Examples
.reg .u32 ra;
stacksave.u32 ra;
// Code that may modify stack pointer
...
stackrestore.u32 ra;
9.7.15.3. Stack Manipulation Instructions: alloca
alloca
Dynamically allocate memory on stack.
Syntax
alloca.type ptr, size{, immAlign};
.type = { .u32, .u64 };
Description
The alloca instruction dynamically allocates memory on the stack frame of the current function
and updates the stack pointer accordingly. The returned pointer ptr points to local memory and
can be used in the address operand of ld.local and st.local instructions.
If sufficient memory is unavailable for allocation on the stack, then execution of alloca may
result in stack overflow. In such cases, attempting to access the allocated memory with ptr will
result in undefined program behavior.
The memory allocated by alloca is deallocated in the following ways:
It is automatically deallocated when the function exits.
It can be explicitly deallocated using
stacksaveandstackrestoreinstructions:stacksavecan be used to save the value of stack pointer before executingalloca, andstackrestorecan be used afterallocato restore stack pointer to the original value which was previously saved withstacksave. Note that accessing deallocated memory after executingstackrestoreresults in undefined behavior.
size is an unsigned value which specifies the amount of memory in number of bytes to be
allocated on stack. size = 0 may not lead to a valid memory allocation.
Both ptr and size have the same type as the instruction type.
immAlign is a 32-bit value which specifies the alignment requirement in number of bytes for the
memory allocated by alloca. It is an integer constant, must be a power of 2 and must not exceed
2^23. immAlign is an optional argument with default value being 8 which is the minimum
guaranteed alignment.
Semantics
alloca.type ptr, size, immAlign:
a = max(immAlign, frame_align); // frame_align is the minimum guaranteed alignment
// Allocate size bytes of stack memory with alignment a and update the stack pointer.
// Since the stack grows down, the updated stack pointer contains a lower address.
stackptr = alloc_stack_mem(size, a);
// Return the new value of stack pointer as ptr. Since ptr is the lowest address of the memory
// allocated by alloca, the memory can be accessed using ptr up to (ptr + size of allocated memory).
stacksave ptr;
PTX ISA Notes
Introduced in PTX ISA version 7.3.
- Preview Feature:
allocais a preview feature in PTX ISA version 7.3. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.
Target ISA Notes
alloca requires sm_52 or higher.
Examples
.reg .u32 ra, stackptr, ptr, size;
stacksave.u32 stackptr; // Save the current stack pointer
alloca ptr, size, 8; // Allocate stack memory
st.local.u32 [ptr], ra; // Use the allocated stack memory
stackrestore.u32 stackptr; // Deallocate memory by restoring the stack pointer
9.7.16. Video Instructions
All video instructions operate on 32-bit register operands. However, the video instructions may be classified as either scalar or SIMD based on whether their core operation applies to one or multiple values.
The video instructions are:
vadd,vadd2,vadd4vsub,vsub2,vsub4vmadvavrg2,vavrg4vabsdiff,vabsdiff2,vabsdiff4vmin,vmin2,vmin4vmax,vmax2,vmax4vshlvshrvset,vset2,vset4
9.7.16.1. Scalar Video Instructions
All scalar video instructions operate on 32-bit register operands. The scalar video instructions are:
vaddvsubvabsdiffvminvmaxvshlvshrvmadvset
The scalar video instructions execute the following stages:
Extract and sign- or zero-extend byte, half-word, or word values from its source operands, to produce signed 33-bit input values.
Perform a scalar arithmetic operation to produce a signed 34-bit result.
Optionally clamp the result to the range of the destination type.
Optionally perform one of the following:
apply a second operation to the intermediate result and a third operand, or
truncate the intermediate result to a byte or half-word value and merge into a specified position in the third operand to produce the final result.
The general format of scalar video instructions is as follows:
// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.btype{.sat} d, a{.asel}, b{.bsel};
vop.dtype.atype.btype{.sat}.secop d, a{.asel}, b{.bsel}, c;
// 32-bit scalar operation, with optional data merge
vop.dtype.atype.btype{.sat} d.dsel, a{.asel}, b{.bsel}, c;
.dtype = .atype = .btype = { .u32, .s32 };
.dsel = .asel = .bsel = { .b0, .b1, .b2, .b3, .h0, .h1 };
.secop = { .add, .min, .max };
The source and destination operands are all 32-bit registers. The type of each operand (.u32 or
.s32) is specified in the instruction type; all combinations of dtype, atype, and
btype are valid. Using the atype/btype and asel/bsel specifiers, the input values are
extracted and sign- or zero-extended internally to .s33 values. The primary operation is then
performed to produce an .s34 intermediate result. The sign of the intermediate result depends on
dtype.
The intermediate result is optionally clamped to the range of the destination type (signed or unsigned), taking into account the subword destination size in the case of optional data merging.
.s33 optSaturate( .s34 tmp, Bool sat, Bool sign, Modifier dsel ) {
if ( !sat ) return tmp;
switch ( dsel ) {
case .b0, .b1, .b2, .b3:
if ( sign ) return CLAMP( tmp, S8_MAX, S8_MIN );
else return CLAMP( tmp, U8_MAX, U8_MIN );
case .h0, .h1:
if ( sign ) return CLAMP( tmp, S16_MAX, S16_MIN );
else return CLAMP( tmp, U16_MAX, U16_MIN );
default:
if ( sign ) return CLAMP( tmp, S32_MAX, S32_MIN );
else return CLAMP( tmp, U32_MAX, U32_MIN );
}
}
This intermediate result is then optionally combined with the third source operand using a secondary
arithmetic operation or subword data merge, as shown in the following pseudocode. The sign of the
third operand is based on dtype.
.s33 optSecOp(Modifier secop, .s33 tmp, .s33 c) {
switch ( secop ) {
.add: return tmp + c;
.min: return MIN(tmp, c);
.max return MAX(tmp, c);
default: return tmp;
}
}
.s33 optMerge( Modifier dsel, .s33 tmp, .s33 c ) {
switch ( dsel ) {
case .h0: return ((tmp & 0xffff) | (0xffff0000 & c);
case .h1: return ((tmp & 0xffff) << 16) | (0x0000ffff & c);
case .b0: return ((tmp & 0xff) | (0xffffff00 & c);
case .b1: return ((tmp & 0xff) << 8) | (0xffff00ff & c);
case .b2: return ((tmp & 0xff) << 16) | (0xff00ffff & c);
case .b3: return ((tmp & 0xff) << 24) | (0x00ffffff & c);
default: return tmp;
}
}
The lower 32-bits are then written to the destination operand.
9.7.16.1.1. Scalar Video Instructions: vadd, vsub, vabsdiff, vmin, vmax
vadd, vsub
Integer byte/half-word/word addition/subtraction.
vabsdiff
Integer byte/half-word/word absolute value of difference.
vmin, vmax
Integer byte/half-word/word minimum/maximum.
Syntax
// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.btype{.sat} d, a{.asel}, b{.bsel};
vop.dtype.atype.btype{.sat}.op2 d, a{.asel}, b{.bsel}, c;
// 32-bit scalar operation, with optional data merge
vop.dtype.atype.btype{.sat} d.dsel, a{.asel}, b{.bsel}, c;
vop = { vadd, vsub, vabsdiff, vmin, vmax };
.dtype = .atype = .btype = { .u32, .s32 };
.dsel = .asel = .bsel = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2 = { .add, .min, .max };
Description
Perform scalar arithmetic operation with optional saturate, and optional secondary arithmetic operation or subword data merge.
Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );
switch ( vop ) {
case vadd: tmp = ta + tb;
case vsub: tmp = ta - tb;
case vabsdiff: tmp = | ta - tb |;
case vmin: tmp = MIN( ta, tb );
case vmax: tmp = MAX( ta, tb );
}
// saturate, taking into account destination type and merge operations
tmp = optSaturate( tmp, sat, isSigned(dtype), dsel );
d = optSecondaryOp( op2, tmp, c ); // optional secondary operation
d = optMerge( dsel, tmp, c ); // optional merge with c operand
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
vadd, vsub, vabsdiff, vmin, vmax require sm_20 or higher.
Examples
vadd.s32.u32.s32.sat r1, r2.b0, r3.h0;
vsub.s32.s32.u32.sat r1, r2.h1, r3.h1;
vabsdiff.s32.s32.s32.sat r1.h0, r2.b0, r3.b2, c;
vmin.s32.s32.s32.sat.add r1, r2, r3, c;
9.7.16.1.2. Scalar Video Instructions: vshl, vshr
vshl, vshr
Integer byte/half-word/word left/right shift.
Syntax
// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.u32{.sat}.mode d, a{.asel}, b{.bsel};
vop.dtype.atype.u32{.sat}.mode.op2 d, a{.asel}, b{.bsel}, c;
// 32-bit scalar operation, with optional data merge
vop.dtype.atype.u32{.sat}.mode d.dsel, a{.asel}, b{.bsel}, c;
vop = { vshl, vshr };
.dtype = .atype = { .u32, .s32 };
.mode = { .clamp, .wrap };
.dsel = .asel = .bsel = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2 = { .add, .min, .max };
Description
vshlShift
aleft by unsigned amount inbwith optional saturate, and optional secondary arithmetic operation or subword data merge. Left shift fills with zero.vshrShift
aright by unsigned amount inbwith optional saturate, and optional secondary arithmetic operation or subword data merge. Signed shift fills with the sign bit, unsigned shift fills with zero.
Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a,atype, asel );
tb = partSelectSignExtend( b, .u32, bsel );
if ( mode == .clamp && tb > 32 ) tb = 32;
if ( mode == .wrap ) tb = tb & 0x1f;
switch ( vop ){
case vshl: tmp = ta << tb;
case vshr: tmp = ta >> tb;
}
// saturate, taking into account destination type and merge operations
tmp = optSaturate( tmp, sat, isSigned(dtype), dsel );
d = optSecondaryOp( op2, tmp, c ); // optional secondary operation
d = optMerge( dsel, tmp, c ); // optional merge with c operand
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
vshl, vshr require sm_20 or higher.
Examples
vshl.s32.u32.u32.clamp r1, r2, r3;
vshr.u32.u32.u32.wrap r1, r2, r3.h1;
9.7.16.1.3. Scalar Video Instructions: vmad
vmad
Integer byte/half-word/word multiply-accumulate.
Syntax
// 32-bit scalar operation
vmad.dtype.atype.btype{.sat}{.scale} d, {-}a{.asel}, {-}b{.bsel},
{-}c;
vmad.dtype.atype.btype.po{.sat}{.scale} d, a{.asel}, b{.bsel}, c;
.dtype = .atype = .btype = { .u32, .s32 };
.asel = .bsel = { .b0, .b1, .b2, .b3, .h0, .h1 };
.scale = { .shr7, .shr15 };
Description
Calculate (a*b) + c, with optional operand negates, plus one mode, and scaling.
The source operands support optional negation with some restrictions. Although PTX syntax allows
separate negation of the a and b operands, internally this is represented as negation of the
product (a*b). That is, (a*b) is negated if and only if exactly one of a or b is
negated. PTX allows negation of either (a*b) or c.
The plus one mode (.po) computes (a*b) + c + 1, which is used in computing averages. Source
operands may not be negated in .po mode.
The intermediate result of (a*b) is unsigned if atype and btype are unsigned and the product
(a*b) is not negated; otherwise, the intermediate result is signed. Input c has the same
sign as the intermediate result.
The final result is unsigned if the intermediate result is unsigned and c is not negated.
Depending on the sign of the a and b operands, and the operand negates, the following
combinations of operands are supported for VMAD:
(u32 * u32) + u32 // intermediate unsigned; final unsigned
-(u32 * u32) + s32 // intermediate signed; final signed
(u32 * u32) - u32 // intermediate unsigned; final signed
(u32 * s32) + s32 // intermediate signed; final signed
-(u32 * s32) + s32 // intermediate signed; final signed
(u32 * s32) - s32 // intermediate signed; final signed
(s32 * u32) + s32 // intermediate signed; final signed
-(s32 * u32) + s32 // intermediate signed; final signed
(s32 * u32) - s32 // intermediate signed; final signed
(s32 * s32) + s32 // intermediate signed; final signed
-(s32 * s32) + s32 // intermediate signed; final signed
(s32 * s32) - s32 // intermediate signed; final signed
The intermediate result is optionally scaled via right-shift; this result is sign-extended if the final result is signed, and zero-extended otherwise.
The final result is optionally saturated to the appropriate 32-bit range based on the type (signed or unsigned) of the final result.
Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );
signedFinal = isSigned(atype) || isSigned(btype) ||
(a.negate ^ b.negate) || c.negate;
tmp[127:0] = ta * tb;
lsb = 0;
if ( .po ) { lsb = 1; } else
if ( a.negate ^ b.negate ) { tmp = ~tmp; lsb = 1; } else
if ( c.negate ) { c = ~c; lsb = 1; }
c128[127:0] = (signedFinal) sext32( c ) : zext ( c );
tmp = tmp + c128 + lsb;
switch( scale ) {
case .shr7: result = (tmp >> 7) & 0xffffffffffffffff;
case .shr15: result = (tmp >> 15) & 0xffffffffffffffff;
}
if ( .sat ) {
if (signedFinal) result = CLAMP(result, S32_MAX, S32_MIN);
else result = CLAMP(result, U32_MAX, U32_MIN);
}
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
vmad requires sm_20 or higher.
Examples
vmad.s32.s32.u32.sat r0, r1, r2, -r3;
vmad.u32.u32.u32.shr15 r0, r1.h0, r2.h0, r3;
9.7.16.1.4. Scalar Video Instructions: vset
vset
Integer byte/half-word/word comparison.
Syntax
// 32-bit scalar operation, with optional secondary operation
vset.atype.btype.cmp d, a{.asel}, b{.bsel};
vset.atype.btype.cmp.op2 d, a{.asel}, b{.bsel}, c;
// 32-bit scalar operation, with optional data merge
vset.atype.btype.cmp d.dsel, a{.asel}, b{.bsel}, c;
.atype = .btype = { .u32, .s32 };
.cmp = { .eq, .ne, .lt, .le, .gt, .ge };
.dsel = .asel = .bsel = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2 = { .add, .min, .max };
Description
Compare input values using specified comparison, with optional secondary arithmetic operation or subword data merge.
The intermediate result of the comparison is always unsigned, and therefore destination d and
operand c are also unsigned.
Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );
tmp = compare( ta, tb, cmp ) ? 1 : 0;
d = optSecondaryOp( op2, tmp, c ); // optional secondary operation
d = optMerge( dsel, tmp, c ); // optional merge with c operand
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
vset requires sm_20 or higher.
Examples
vset.s32.u32.lt r1, r2, r3;
vset.u32.u32.ne r1, r2, r3.h1;
9.7.16.2. SIMD Video Instructions
The SIMD video instructions operate on pairs of 16-bit values and quads of 8-bit values.
The SIMD video instructions are:
vadd2,vadd4vsub2,vsub4vavrg2,vavrg4vabsdiff2,vabsdiff4vmin2,vmin4vmax2,vmax4vset2,vset4
PTX includes SIMD video instructions for operation on pairs of 16-bit values and quads of 8-bit values. The SIMD video instructions execute the following stages:
Form input vectors by extracting and sign- or zero-extending byte or half-word values from the source operands, to form pairs of signed 17-bit values.
Perform a SIMD arithmetic operation on the input pairs.
Optionally clamp the result to the appropriate signed or unsigned range, as determinted by the destination type.
Optionally perform one of the following:
perform a second SIMD merge operation, or
apply a scalar accumulate operation to reduce the intermediate SIMD results to a single scalar.
The general format of dual half-word SIMD video instructions is as follows:
// 2-way SIMD operation, with second SIMD merge or accumulate
vop2.dtype.atype.btype{.sat}{.add} d{.mask}, a{.asel}, b{.bsel}, c;
.dtype = .atype = .btype = { .u32, .s32 };
.mask = { .h0, .h1, .h10 };
.asel = .bsel = { .hxy, where x,y are from { 0, 1, 2, 3 } };
The general format of quad byte SIMD video instructions is as follows:
// 4-way SIMD operation, with second SIMD merge or accumulate
vop4.dtype.atype.btype{.sat}{.add} d{.mask}, a{.asel}, b{.bsel}, c;
.dtype = .atype = .btype = { .u32, .s32 };
.mask = { .b0,
.b1, .b10
.b2, .b20, .b21, .b210,
.b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };
The source and destination operands are all 32-bit registers. The type of each operand (.u32 or
.s32) is specified in the instruction type; all combinations of dtype, atype, and
btype are valid. Using the atype/btype and asel/bsel specifiers, the input values are
extracted and sign- or zero-extended internally to .s33 values. The primary operation is then
performed to produce an .s34 intermediate result. The sign of the intermediate result depends on
dtype.
The intermediate result is optionally clamped to the range of the destination type (signed or unsigned), taking into account the subword destination size in the case of optional data merging.
9.7.16.2.1. SIMD Video Instructions: vadd2, vsub2, vavrg2, vabsdiff2, vmin2, vmax2
vadd2, vsub2
Integer dual half-word SIMD addition/subtraction.
vavrg2
Integer dual half-word SIMD average.
vabsdiff2
Integer dual half-word SIMD absolute value of difference.
vmin2, vmax2
Integer dual half-word SIMD minimum/maximum.
Syntax
// SIMD instruction with secondary SIMD merge operation
vop2.dtype.atype.btype{.sat} d{.mask}, a{.asel}, b{.bsel}, c;
// SIMD instruction with secondary accumulate operation
vop2.dtype.atype.btype.add d{.mask}, a{.asel}, b{.bsel}, c;
vop2 = { vadd2, vsub2, vavrg2, vabsdiff2, vmin2, vmax2 };
.dtype = .atype = .btype = { .u32, .s32 };
.mask = { .h0, .h1, .h10 }; // defaults to .h10
.asel = .bsel = { .hxy, where x,y are from { 0, 1, 2, 3 } };
.asel defaults to .h10
.bsel defaults to .h32
Description
Two-way SIMD parallel arithmetic operation with secondary operation.
Elements of each dual half-word source to the operation are selected from any of the four half-words
in the two source operands a and b using the asel and bsel modifiers.
The selected half-words are then operated on in parallel.
The results are optionally clamped to the appropriate range determined by the destination type (signed or unsigned). Saturation cannot be used with the secondary accumulate operation.
For instructions with a secondary SIMD merge operation:
For half-word positions indicated in mask, the selected half-word results are copied into destination
d. For all other positions, the corresponding half-word from source operandcis copied tod.
For instructions with a secondary accumulate operation:
For half-word positions indicated in mask, the selected half-word results are added to operand
c, producing a result ind.
Semantics
// extract pairs of half-words and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_2( a, b, .asel, .atype );
Vb = extractAndSignExt_2( a, b, .bsel, .btype );
Vc = extractAndSignExt_2( c );
for (i=0; i<2; i++) {
switch ( vop2 ) {
case vadd2: t[i] = Va[i] + Vb[i];
case vsub2: t[i] = Va[i] - Vb[i];
case vavrg2: if ( ( Va[i] + Vb[i] ) >= 0 ) {
t[i] = ( Va[i] + Vb[i] + 1 ) >> 1;
} else {
t[i] = ( Va[i] + Vb[i] ) >> 1;
}
case vabsdiff2: t[i] = | Va[i] - Vb[i] |;
case vmin2: t[i] = MIN( Va[i], Vb[i] );
case vmax2: t[i] = MAX( Va[i], Vb[i] );
}
if (.sat) {
if ( .dtype == .s32 ) t[i] = CLAMP( t[i], S16_MAX, S16_MIN );
else t[i] = CLAMP( t[i], U16_MAX, U16_MIN );
}
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
d = c;
for (i=0; i<2; i++) { d += mask[i] ? t[i] : 0; }
} else {
d = 0;
for (i=0; i<2; i++) { d |= mask[i] ? t[i] : Vc[i]; }
}
PTX ISA Notes
Introduced in PTX ISA version 3.0.
Target ISA Notes
vadd2, vsub2, varvg2, vabsdiff2, vmin2, vmax2 require sm_30 or higher.
Examples
vadd2.s32.s32.u32.sat r1, r2, r3, r1;
vsub2.s32.s32.s32.sat r1.h0, r2.h10, r3.h32, r1;
vmin2.s32.u32.u32.add r1.h10, r2.h00, r3.h22, r1;
9.7.16.2.2. SIMD Video Instructions: vset2
vset2
Integer dual half-word SIMD comparison.
Syntax
// SIMD instruction with secondary SIMD merge operation
vset2.atype.btype.cmp d{.mask}, a{.asel}, b{.bsel}, c;
// SIMD instruction with secondary accumulate operation
vset2.atype.btype.cmp.add d{.mask}, a{.asel}, b{.bsel}, c;
.atype = .btype = { .u32, .s32 };
.cmp = { .eq, .ne, .lt, .le, .gt, .ge };
.mask = { .h0, .h1, .h10 }; // defaults to .h10
.asel = .bsel = { .hxy, where x,y are from { 0, 1, 2, 3 } };
.asel defaults to .h10
.bsel defaults to .h32
Description
Two-way SIMD parallel comparison with secondary operation.
Elements of each dual half-word source to the operation are selected from any of the four half-words
in the two source operands a and b using the asel and bsel modifiers.
The selected half-words are then compared in parallel.
The intermediate result of the comparison is always unsigned, and therefore the half-words of
destination d and operand c are also unsigned.
For instructions with a secondary SIMD merge operation:
For half-word positions indicated in mask, the selected half-word results are copied into destination
d. For all other positions, the corresponding half-word from source operandbis copied tod.
For instructions with a secondary accumulate operation:
For half-word positions indicated in mask, the selected half-word results are added to operand
c, producingaresult ind.
Semantics
// extract pairs of half-words and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_2( a, b, .asel, .atype );
Vb = extractAndSignExt_2( a, b, .bsel, .btype );
Vc = extractAndSignExt_2( c );
for (i=0; i<2; i++) {
t[i] = compare( Va[i], Vb[i], .cmp ) ? 1 : 0;
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
d = c;
for (i=0; i<2; i++) { d += mask[i] ? t[i] : 0; }
} else {
d = 0;
for (i=0; i<2; i++) { d |= mask[i] ? t[i] : Vc[i]; }
}
PTX ISA Notes
Introduced in PTX ISA version 3.0.
Target ISA Notes
vset2 requires sm_30 or higher.
Examples
vset2.s32.u32.lt r1, r2, r3, r0;
vset2.u32.u32.ne.add r1, r2, r3, r0;
9.7.16.2.3. SIMD Video Instructions: vadd4, vsub4, vavrg4, vabsdiff4, vmin4, vmax4
vadd4, vsub4
Integer quad byte SIMD addition/subtraction.
vavrg4
Integer quad byte SIMD average.
vabsdiff4
Integer quad byte SIMD absolute value of difference.
vmin4, vmax4
Integer quad byte SIMD minimum/maximum.
Syntax
// SIMD instruction with secondary SIMD merge operation
vop4.dtype.atype.btype{.sat} d{.mask}, a{.asel}, b{.bsel}, c;
// SIMD instruction with secondary accumulate operation
vop4.dtype.atype.btype.add d{.mask}, a{.asel}, b{.bsel}, c;
vop4 = { vadd4, vsub4, vavrg4, vabsdiff4, vmin4, vmax4 };
.dtype = .atype = .btype = { .u32, .s32 };
.mask = { .b0,
.b1, .b10
.b2, .b20, .b21, .b210,
.b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
defaults to .b3210
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };
.asel defaults to .b3210
.bsel defaults to .b7654
Description
Four-way SIMD parallel arithmetic operation with secondary operation.
Elements of each quad byte source to the operation are selected from any of the eight bytes in the
two source operands a and b using the asel and bsel modifiers.
The selected bytes are then operated on in parallel.
The results are optionally clamped to the appropriate range determined by the destination type (signed or unsigned). Saturation cannot be used with the secondary accumulate operation.
For instructions with a secondary SIMD merge operation:
For byte positions indicated in mask, the selected byte results are copied into destination
d. For all other positions, the corresponding byte from source operandcis copied tod.
For instructions with a secondary accumulate operation:
For byte positions indicated in mask, the selected byte results are added to operand
c, producing a result ind.
Semantics
// extract quads of bytes and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_4( a, b, .asel, .atype );
Vb = extractAndSignExt_4( a, b, .bsel, .btype );
Vc = extractAndSignExt_4( c );
for (i=0; i<4; i++) {
switch ( vop4 ) {
case vadd4: t[i] = Va[i] + Vb[i];
case vsub4: t[i] = Va[i] - Vb[i];
case vavrg4: if ( ( Va[i] + Vb[i] ) >= 0 ) {
t[i] = ( Va[i] + Vb[i] + 1 ) >> 1;
} else {
t[i] = ( Va[i] + Vb[i] ) >> 1;
}
case vabsdiff4: t[i] = | Va[i] - Vb[i] |;
case vmin4: t[i] = MIN( Va[i], Vb[i] );
case vmax4: t[i] = MAX( Va[i], Vb[i] );
}
if (.sat) {
if ( .dtype == .s32 ) t[i] = CLAMP( t[i], S8_MAX, S8_MIN );
else t[i] = CLAMP( t[i], U8_MAX, U8_MIN );
}
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
d = c;
for (i=0; i<4; i++) { d += mask[i] ? t[i] : 0; }
} else {
d = 0;
for (i=0; i<4; i++) { d |= mask[i] ? t[i] : Vc[i]; }
}
PTX ISA Notes
Introduced in PTX ISA version 3.0.
Target ISA Notes
vadd4, vsub4, varvg4, vabsdiff4, vmin4, vmax4 require sm_30 or higher.
Examples
vadd4.s32.s32.u32.sat r1, r2, r3, r1;
vsub4.s32.s32.s32.sat r1.b0, r2.b3210, r3.b7654, r1;
vmin4.s32.u32.u32.add r1.b00, r2.b0000, r3.b2222, r1;
9.7.16.2.4. SIMD Video Instructions: vset4
vset4
Integer quad byte SIMD comparison.
Syntax
// SIMD instruction with secondary SIMD merge operation
vset4.atype.btype.cmp d{.mask}, a{.asel}, b{.bsel}, c;
// SIMD instruction with secondary accumulate operation
vset4.atype.btype.cmp.add d{.mask}, a{.asel}, b{.bsel}, c;
.atype = .btype = { .u32, .s32 };
.cmp = { .eq, .ne, .lt, .le, .gt, .ge };
.mask = { .b0,
.b1, .b10
.b2, .b20, .b21, .b210,
.b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
defaults to .b3210
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };
.asel defaults to .b3210
.bsel defaults to .b7654
Description
Four-way SIMD parallel comparison with secondary operation.
Elements of each quad byte source to the operation are selected from any of the eight bytes in the
two source operands a and b using the asel and bsel modifiers.
The selected bytes are then compared in parallel.
The intermediate result of the comparison is always unsigned, and therefore the bytes of destination
d and operand c are also unsigned.
For instructions with a secondary SIMD merge operation:
For byte positions indicated in mask, the selected byte results are copied into destination
d. For all other positions, the corresponding byte from source operandbis copied tod.
For instructions with a secondary accumulate operation:
For byte positions indicated in mask, the selected byte results are added to operand
c, producing a result ind.
Semantics
// extract quads of bytes and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_4( a, b, .asel, .atype );
Vb = extractAndSignExt_4( a, b, .bsel, .btype );
Vc = extractAndSignExt_4( c );
for (i=0; i<4; i++) {
t[i] = compare( Va[i], Vb[i], cmp ) ? 1 : 0;
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
d = c;
for (i=0; i<4; i++) { d += mask[i] ? t[i] : 0; }
} else {
d = 0;
for (i=0; i<4; i++) { d |= mask[i] ? t[i] : Vc[i]; }
}
PTX ISA Notes
Introduced in PTX ISA version 3.0.
Target ISA Notes
vset4 requires sm_30 or higher.
Examples
vset4.s32.u32.lt r1, r2, r3, r0;
vset4.u32.u32.ne.max r1, r2, r3, r0;
9.7.17. Miscellaneous Instructions
The Miscellaneous instructions are:
brkptnanosleeppmeventtrapsetmaxnreg
9.7.17.1. Miscellaneous Instructions: brkpt
brkpt
Breakpoint.
Syntax
brkpt;
Description
Suspends execution.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
brkpt requires sm_11 or higher.
Examples
brkpt;
@p brkpt;
9.7.17.2. Miscellaneous Instructions: nanosleep
nanosleep
Suspend the thread for an approximate delay given in nanoseconds.
Syntax
nanosleep.u32 t;
Description
Suspends the thread for a sleep duration approximately close to the delay t, specified in
nanoseconds. t may be a register or an immediate value.
The sleep duration is approximated, but guaranteed to be in the interval [0, 2*t]. The maximum
sleep duration is 1 millisecond. The implementation may reduce the sleep duration for individual
threads within a warp such that all sleeping threads in the warp wake up together.
PTX ISA Notes
nanosleep introduced in PTX ISA 6.3.
Target ISA Notes
nanosleep requires sm_70 or higher.
Examples
.reg .b32 r;
.reg .pred p;
nanosleep.u32 r;
nanosleep.u32 42;
@p nanosleep.u32 r;
9.7.17.3. Miscellaneous Instructions: pmevent
pmevent
Trigger one or more Performance Monitor events.
Syntax
pmevent a; // trigger a single performance monitor event
pmevent.mask a; // trigger one or more performance monitor events
Description
Triggers one or more of a fixed number of performance monitor events, with event index or mask
specified by immediate operand a.
pmevent (without modifier .mask) triggers a single performance monitor event indexed by
immediate operand a, in the range 0..15.
pmevent.mask triggers one or more of the performance monitor events. Each bit in the 16-bit
immediate operand a controls an event.
Programmatic performance moniter events may be combined with other hardware events using Boolean functions to increment one of the four performance counters. The relationship between events and counters is programmed via API calls from the host.
Notes
Currently, there are sixteen performance monitor events, numbered 0 through 15.
PTX ISA Notes
pmevent introduced in PTX ISA version 1.4.
pmevent.mask introduced in PTX ISA version 3.0.
Target ISA Notes
pmevent supported on all target architectures.
pmevent.mask requires sm_20 or higher.
Examples
pmevent 1;
@p pmevent 7;
@q pmevent.mask 0xff;
9.7.17.4. Miscellaneous Instructions: trap
trap
Perform trap operation.
Syntax
trap;
Description
Abort execution and generate an interrupt to the host CPU.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
trap;
@p trap;
9.7.17.5. Miscellaneous Instructions: setmaxnreg
setmaxnreg
Hint to change the number of registers owned by the warp.
Syntax
setmaxnreg.action.sync.aligned.u32 imm-reg-count;
.action = { .inc, .dec };
Description
setmaxnreg provides a hint to the system to update the maximum number of per-thread registers
owned by the executing warp to the value specified by the imm-reg-count operand.
Qualifier .dec is used to release extra registers such that the absolute per-thread maximum
register count is reduced from its current value to imm-reg-count. Qualifier .inc is used to
request additional registers such that the absolute per-thread maximum register count is increased
from its current value to imm-reg-count.
A pool of available registers is maintained per-CTA. Register adjustments requested by the
setmaxnreg instructions are handled by supplying extra registers from this pool to the
requesting warp or by releasing extra registers from the requesting warp to this pool, depending
upon the value of the .action qualifier.
The setmaxnreg.inc instruction blocks the execution until enough registers are available in the
CTA’s register pool. After the instruction setmaxnreg.inc obtains new registers from the CTA
pool, the initial contents of the new registers are undefined. The new registers must be initialized
before they are used.
The same setmaxnreg instruction must be executed by all warps in a warpgroup. After executing a
setmaxnreg instruction, all warps in the warpgroup must synchronize explicitly before
executing subsequent setmaxnreg instructions. If a setmaxnreg instruction is not executed by all
warps in the warpgroup, then the behavior is undefined.
Operand imm-reg-count is an integer constant. The value of imm-reg-count must be in the
range 24 to 256 (both inclusive) and must be a multiple of 8.
Changes to the register file of the warp always happen at the tail-end of the register file.
The setmaxnreg instruction requires that the kernel has been launched with a valid value of
maximum number of per-thread registers specified via the appropriate compilation via the appropriate
compile-time option or the appropriate performance tuning directive. Otherwise, the setmaxnreg
instruction may have no effect.
When qualifier .dec is specified, the maximum number of per-thread registers owned by the warp
prior to the execution of setmaxnreg instruction should be greater than or equal to the
imm-reg-count. Otherwise, the behaviour is undefined.
When qualifier .inc is specified, the maximum number of per-thread registers owned by the warp
prior to the execution of setmaxnreg instruction should be less than or equal to the
imm-reg-count. Otherwise, the behaviour is undefined.
The mandatory .sync qualifier indicates that setmaxnreg instruction causes the executing
thread to wait until all threads in the warp execute the same setmaxnreg instruction before
resuming execution.
The mandatory .aligned qualifier indicates that all threads in the warpgroup must execute the
same setmaxnreg instruction. In conditionally executed code, setmaxnreg instruction should
only be used if it is known that all threads in warpgroup evaluate the condition identically,
otherwise the behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_90a.
Examples
setmaxnreg.dec.sync.aligned.u32 64;
setmaxnreg.inc.sync.aligned.u32 192;
10. Special Registers
PTX includes a number of predefined, read-only variables, which are
visible as special registers and accessed through mov or cvt
instructions.
The special registers are:
%tid%ntid%laneid%warpid%nwarpid%ctaid%nctaid%smid%nsmid%gridid%is_explicit_cluster%clusterid%nclusterid%cluster_ctaid%cluster_nctaid%cluster_ctarank%cluster_nctarank%lanemask_eq,%lanemask_le,%lanemask_lt,%lanemask_ge,%lanemask_gt%clock,%clock_hi,%clock64%pm0, ..., %pm7%pm0_64, ..., %pm7_64%envreg0, ..., %envreg31%globaltimer,%globaltimer_lo,%globaltimer_hi%reserved_smem_offset_begin,%reserved_smem_offset_end,%reserved_smem_offset_cap,%reserved_smem_offset<2>%total_smem_size%aggr_smem_size%dynamic_smem_size%current_graph_exec
10.1. Special Registers: %tid
%tid
Thread identifier within a CTA.
Syntax (predefined)
.sreg .v4 .u32 %tid; // thread id vector
.sreg .u32 %tid.x, %tid.y, %tid.z; // thread id components
Description
A predefined, read-only, per-thread special register initialized with the thread identifier within
the CTA. The %tid special register contains a 1D, 2D, or 3D vector to match the CTA shape; the
%tid value in unused dimensions is 0. The fourth element is unused and always returns
zero. The number of threads in each dimension are specified by the predefined special register
%ntid.
Every thread in the CTA has a unique %tid.
%tid component values range from 0 through %ntid-1 in each CTA dimension.
%tid.y == %tid.z == 0 in 1D CTAs. %tid.z == 0 in 2D CTAs.
It is guaranteed that:
0 <= %tid.x < %ntid.x
0 <= %tid.y < %ntid.y
0 <= %tid.z < %ntid.z
PTX ISA Notes
Introduced in PTX ISA version 1.0 with type .v4.u16.
Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit
mov and cvt instructions may be used to read the lower 16-bits of each component of
%tid.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r1,%tid.x; // move tid.x to %rh
// legacy code accessing 16-bit components of %tid
mov.u16 %rh,%tid.x;
cvt.u32.u16 %r2,%tid.z; // zero-extend tid.z to %r2
10.2. Special Registers: %ntid
%ntid
Number of thread IDs per CTA.
Syntax (predefined)
.sreg .v4 .u32 %ntid; // CTA shape vector
.sreg .u32 %ntid.x, %ntid.y, %ntid.z; // CTA dimensions
Description
A predefined, read-only special register initialized with the number of thread ids in each CTA
dimension. The %ntid special register contains a 3D CTA shape vector that holds the CTA
dimensions. CTA dimensions are non-zero; the fourth element is unused and always returns zero. The
total number of threads in a CTA is (%ntid.x * %ntid.y * %ntid.z).
%ntid.y == %ntid.z == 1 in 1D CTAs.
%ntid.z ==1 in 2D CTAs.
Maximum values of %ntid.{x,y,z} are as follows:
.target architecture |
%ntid.x |
%ntid.y |
%ntid.z |
|---|---|---|---|
|
512 |
512 |
64 |
|
1024 |
1024 |
64 |
PTX ISA Notes
Introduced in PTX ISA version 1.0 with type .v4.u16.
Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit
mov and cvt instructions may be used to read the lower 16-bits of each component of
%ntid.
Target ISA Notes
Supported on all target architectures.
Examples
// compute unified thread id for 2D CTA
mov.u32 %r0,%tid.x;
mov.u32 %h1,%tid.y;
mov.u32 %h2,%ntid.x;
mad.u32 %r0,%h1,%h2,%r0;
mov.u16 %rh,%ntid.x; // legacy code
10.3. Special Registers: %laneid
%laneid
Lane Identifier.
Syntax (predefined)
.sreg .u32 %laneid;
Description
A predefined, read-only special register that returns the thread’s lane within the warp. The lane
identifier ranges from zero to WARP_SZ-1.
PTX ISA Notes
Introduced in PTX ISA version 1.3.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r, %laneid;
10.4. Special Registers: %warpid
%warpid
Warp identifier.
Syntax (predefined)
.sreg .u32 %warpid;
Description
A predefined, read-only special register that returns the thread’s warp identifier. The warp identifier provides a unique warp number within a CTA but not across CTAs within a grid. The warp identifier will be the same for all threads within a single warp.
Note that %warpid is volatile and returns the location of a thread at the moment when read, but
its value may change during execution, e.g., due to rescheduling of threads following
preemption. For this reason, %ctaid and %tid should be used to compute a virtual warp index
if such a value is needed in kernel code; %warpid is intended mainly to enable profiling and
diagnostic code to sample and log information such as work place mapping and load distribution.
PTX ISA Notes
Introduced in PTX ISA version 1.3.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r, %warpid;
10.5. Special Registers: %nwarpid
%nwarpid
Number of warp identifiers.
Syntax (predefined)
.sreg .u32 %nwarpid;
Description
A predefined, read-only special register that returns the maximum number of warp identifiers.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%nwarpid requires sm_20 or higher.
Examples
mov.u32 %r, %nwarpid;
10.6. Special Registers: %ctaid
%ctaid
CTA identifier within a grid.
Syntax (predefined)
.sreg .v4 .u32 %ctaid; // CTA id vector
.sreg .u32 %ctaid.x, %ctaid.y, %ctaid.z; // CTA id components
Description
A predefined, read-only special register initialized with the CTA identifier within the CTA
grid. The %ctaid special register contains a 1D, 2D, or 3D vector, depending on the shape and
rank of the CTA grid. The fourth element is unused and always returns zero.
It is guaranteed that:
0 <= %ctaid.x < %nctaid.x
0 <= %ctaid.y < %nctaid.y
0 <= %ctaid.z < %nctaid.z
PTX ISA Notes
Introduced in PTX ISA version 1.0 with type .v4.u16.
Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit
mov and cvt instructions may be used to read the lower 16-bits of each component of
%ctaid.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r0,%ctaid.x;
mov.u16 %rh,%ctaid.y; // legacy code
10.7. Special Registers: %nctaid
%nctaid
Number of CTA ids per grid.
Syntax (predefined)
.sreg .v4 .u32 %nctaid // Grid shape vector
.sreg .u32 %nctaid.x,%nctaid.y,%nctaid.z; // Grid dimensions
Description
A predefined, read-only special register initialized with the number of CTAs in each grid
dimension. The %nctaid special register contains a 3D grid shape vector, with each element
having a value of at least 1. The fourth element is unused and always returns zero.
Maximum values of %nctaid.{x,y,z} are as follows:
.target architecture |
%nctaid.x |
%nctaid.y |
%nctaid.z |
|---|---|---|---|
|
65535 |
65535 |
65535 |
|
231 -1 |
65535 |
65535 |
PTX ISA Notes
Introduced in PTX ISA version 1.0 with type .v4.u16.
Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit
mov and cvt instructions may be used to read the lower 16-bits of each component of
%nctaid.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r0,%nctaid.x;
mov.u16 %rh,%nctaid.x; // legacy code
10.8. Special Registers: %smid
%smid
SM identifier.
Syntax (predefined)
.sreg .u32 %smid;
Description
A predefined, read-only special register that returns the processor (SM) identifier on which a
particular thread is executing. The SM identifier ranges from 0 to %nsmid-1. The SM
identifier numbering is not guaranteed to be contiguous.
Notes
Note that %smid is volatile and returns the location of a thread at the moment when read, but
its value may change during execution, e.g. due to rescheduling of threads following
preemption. %smid is intended mainly to enable profiling and diagnostic code to sample and log
information such as work place mapping and load distribution.
PTX ISA Notes
Introduced in PTX ISA version 1.3.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u32 %r, %smid;
10.9. Special Registers: %nsmid
%nsmid
Number of SM identifiers.
Syntax (predefined)
.sreg .u32 %nsmid;
Description
A predefined, read-only special register that returns the maximum number of SM identifiers. The SM
identifier numbering is not guaranteed to be contiguous, so %nsmid may be larger than the
physical number of SMs in the device.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%nsmid requires sm_20 or higher.
Examples
mov.u32 %r, %nsmid;
10.10. Special Registers: %gridid
%gridid
Grid identifier.
Syntax (predefined)
.sreg .u64 %gridid;
Description
A predefined, read-only special register initialized with the per-grid temporal grid identifier. The
%gridid is used by debuggers to distinguish CTAs and clusters within concurrent (small) grids.
During execution, repeated launches of programs may occur, where each launch starts a grid-of-CTAs. This variable provides the temporal grid launch number for this context.
For sm_1x targets, %gridid is limited to the range [0..216-1]. For sm_20,
%gridid is limited to the range [0..232-1]. sm_30 supports the entire 64-bit range.
PTX ISA Notes
Introduced in PTX ISA version 1.0 as type .u16.
Redefined as type .u32 in PTX ISA version 1.3.
Redefined as type .u64 in PTX ISA version 3.0.
For compatibility with legacy PTX code, 16-bit and 32-bit mov and cvt instructions may be
used to read the lower 16-bits or 32-bits of each component of %gridid.
Target ISA Notes
Supported on all target architectures.
Examples
mov.u64 %s, %gridid; // 64-bit read of %gridid
mov.u32 %r, %gridid; // legacy code with 32-bit %gridid
10.11. Special Registers: %is_explicit_cluster
%is_explicit_cluster
Checks if user has explicitly specified cluster launch.
Syntax (predefined)
.sreg .pred %is_explicit_cluster;
Description
A predefined, read-only special register initialized with the predicate value of whether the cluster launch is explicitly specified by user.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .pred p;
mov.pred p, %is_explicit_cluster;
10.12. Special Registers: %clusterid
%clusterid
Cluster identifier within a grid.
Syntax (predefined)
.sreg .v4 .u32 %clusterid;
.sreg .u32 %clusterid.x, %clusterid.y, %clusterid.z;
Description
A predefined, read-only special register initialized with the cluster identifier in a grid in each dimension. Each cluster in a grid has a unique identifier.
The %clusterid special register contains a 1D, 2D, or 3D vector, depending upon the shape and
rank of the cluster. The fourth element is unused and always returns zero.
It is guaranteed that:
0 <= %clusterid.x < %nclusterid.x
0 <= %clusterid.y < %nclusterid.y
0 <= %clusterid.z < %nclusterid.z
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r<2>;
.reg .v4 .b32 %rx;
mov.u32 %r0, %clusterid.x;
mov.u32 %r1, %clusterid.z;
mov.v4.u32 %rx, %clusterid;
10.13. Special Registers: %nclusterid
%nclusterid
Number of cluster identifiers per grid.
Syntax (predefined)
.sreg .v4 .u32 %nclusterid;
.sreg .u32 %nclusterid.x, %nclusterid.y, %nclusterid.z;
Description
A predefined, read-only special register initialized with the number of clusters in each grid dimension.
The %nclusterid special register contains a 3D grid shape vector that holds the grid dimensions
in terms of clusters. The fourth element is unused and always returns zero.
Refer to the Cuda Programming Guide for details on the maximum values of %nclusterid.{x,y,z}.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r<2>;
.reg .v4 .b32 %rx;
mov.u32 %r0, %nclusterid.x;
mov.u32 %r1, %nclusterid.z;
mov.v4.u32 %rx, %nclusterid;
10.14. Special Registers: %cluster_ctaid
%cluster_ctaid
CTA identifier within a cluster.
Syntax (predefined)
.sreg .v4 .u32 %cluster_ctaid;
.sreg .u32 %cluster_ctaid.x, %cluster_ctaid.y, %cluster_ctaid.z;
Description
A predefined, read-only special register initialized with the CTA identifier in a cluster in each dimension. Each CTA in a cluster has a unique CTA identifier.
The %cluster_ctaid special register contains a 1D, 2D, or 3D vector, depending upon the shape of
the cluster. The fourth element is unused and always returns zero.
It is guaranteed that:
0 <= %cluster_ctaid.x < %cluster_nctaid.x
0 <= %cluster_ctaid.y < %cluster_nctaid.y
0 <= %cluster_ctaid.z < %cluster_nctaid.z
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r<2>;
.reg .v4 .b32 %rx;
mov.u32 %r0, %cluster_ctaid.x;
mov.u32 %r1, %cluster_ctaid.z;
mov.v4.u32 %rx, %cluster_ctaid;
10.15. Special Registers: %cluster_nctaid
%cluster_nctaid
Number of CTA identifiers per cluster.
Syntax (predefined)
.sreg .v4 .u32 %cluster_nctaid;
.sreg .u32 %cluster_nctaid.x, %cluster_nctaid.y, %cluster_nctaid.z;
Description
A predefined, read-only special register initialized with the number of CTAs in a cluster in each dimension.
The %cluster_nctaid special register contains a 3D grid shape vector that holds the cluster
dimensions in terms of CTAs. The fourth element is unused and always returns zero.
Refer to the Cuda Programming Guide for details on the maximum values of
%cluster_nctaid.{x,y,z}.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r<2>;
.reg .v4 .b32 %rx;
mov.u32 %r0, %cluster_nctaid.x;
mov.u32 %r1, %cluster_nctaid.z;
mov.v4.u32 %rx, %cluster_nctaid;
10.16. Special Registers: %cluster_ctarank
%cluster_ctarank
CTA identifier in a cluster across all dimensions.
Syntax (predefined)
.sreg .u32 %cluster_ctarank;
Description
A predefined, read-only special register initialized with the CTA rank within a cluster across all dimensions.
It is guaranteed that:
0 <= %cluster_ctarank < %cluster_nctarank
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r;
mov.u32 %r, %cluster_ctarank;
10.17. Special Registers: %cluster_nctarank
%cluster_nctarank
Number of CTA identifiers in a cluster across all dimensions.
Syntax (predefined)
.sreg .u32 %cluster_nctarank;
Description
A predefined, read-only special register initialized with the nunber of CTAs within a cluster across all dimensions.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.reg .b32 %r;
mov.u32 %r, %cluster_nctarank;
10.18. Special Registers: %lanemask_eq
%lanemask_eq
32-bit mask with bit set in position equal to the thread’s lane number in the warp.
Syntax (predefined)
.sreg .u32 %lanemask_eq;
Description
A predefined, read-only special register initialized with a 32-bit mask with a bit set in the position equal to the thread’s lane number in the warp.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%lanemask_eq requires sm_20 or higher.
Examples
mov.u32 %r, %lanemask_eq;
10.19. Special Registers: %lanemask_le
%lanemask_le
32-bit mask with bits set in positions less than or equal to the thread’s lane number in the warp.
Syntax (predefined)
.sreg .u32 %lanemask_le;
Description
A predefined, read-only special register initialized with a 32-bit mask with bits set in positions less than or equal to the thread’s lane number in the warp.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%lanemask_le requires sm_20 or higher.
Examples
mov.u32 %r, %lanemask_le
10.20. Special Registers: %lanemask_lt
%lanemask_lt
32-bit mask with bits set in positions less than the thread’s lane number in the warp.
Syntax (predefined)
.sreg .u32 %lanemask_lt;
Description
A predefined, read-only special register initialized with a 32-bit mask with bits set in positions less than the thread’s lane number in the warp.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%lanemask_lt requires sm_20 or higher.
Examples
mov.u32 %r, %lanemask_lt;
10.21. Special Registers: %lanemask_ge
%lanemask_ge
32-bit mask with bits set in positions greater than or equal to the thread’s lane number in the warp.
Syntax (predefined)
.sreg .u32 %lanemask_ge;
Description
A predefined, read-only special register initialized with a 32-bit mask with bits set in positions greater than or equal to the thread’s lane number in the warp.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%lanemask_ge requires sm_20 or higher.
Examples
mov.u32 %r, %lanemask_ge;
10.22. Special Registers: %lanemask_gt
%lanemask_gt
32-bit mask with bits set in positions greater than the thread’s lane number in the warp.
Syntax (predefined)
.sreg .u32 %lanemask_gt;
Description
A predefined, read-only special register initialized with a 32-bit mask with bits set in positions greater than the thread’s lane number in the warp.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%lanemask_gt requires sm_20 or higher.
Examples
mov.u32 %r, %lanemask_gt;
10.23. Special Registers: %clock, %clock_hi
%clock, %clock_hi
%clockA predefined, read-only 32-bit unsigned cycle counter.
%clock_hiThe upper 32-bits of
%clock64special register.
Syntax (predefined)
.sreg .u32 %clock;
.sreg .u32 %clock_hi;
Description
Special register %clock and %clock_hi are unsigned 32-bit read-only cycle counters that wrap
silently.
PTX ISA Notes
%clock introduced in PTX ISA version 1.0.
%clock_hi introduced in PTX ISA version 5.0.
Target ISA Notes
%clock supported on all target architectures.
%clock_hi requires sm_20 or higher.
Examples
mov.u32 r1,%clock;
mov.u32 r2, %clock_hi;
10.24. Special Registers: %clock64
%clock64
A predefined, read-only 64-bit unsigned cycle counter.
Syntax (predefined)
.sreg .u64 %clock64;
Description
Special register %clock64 is an unsigned 64-bit read-only cycle counter that wraps silently.
Notes
The lower 32-bits of %clock64 are identical to %clock.
The upper 32-bits of %clock64 are identical to %clock_hi.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
%clock64 requires sm_20 or higher.
Examples
mov.u64 r1,%clock64;
10.25. Special Registers: %pm0..%pm7
%pm0..%pm7
Performance monitoring counters.
Syntax (predefined)
.sreg .u32 %pm<8>;
Description
Special registers %pm0..%pm7 are unsigned 32-bit read-only performance monitor counters. Their
behavior is currently undefined.
PTX ISA Notes
%pm0..%pm3 introduced in PTX ISA version 1.3.
%pm4..%pm7 introduced in PTX ISA version 3.0.
Target ISA Notes
%pm0..%pm3 supported on all target architectures.
%pm4..%pm7 require sm_20 or higher.
Examples
mov.u32 r1,%pm0;
mov.u32 r1,%pm7;
10.26. Special Registers: %pm0_64..%pm7_64
%pm0_64..%pm7_64
64 bit Performance monitoring counters.
Syntax (predefined)
.sreg .u64 %pm0_64;
.sreg .u64 %pm1_64;
.sreg .u64 %pm2_64;
.sreg .u64 %pm3_64;
.sreg .u64 %pm4_64;
.sreg .u64 %pm5_64;
.sreg .u64 %pm6_64;
.sreg .u64 %pm7_64;
Description
Special registers %pm0_64..%pm7_64 are unsigned 64-bit read-only performance monitor
counters. Their behavior is currently undefined.
Notes
The lower 32bits of %pm0_64..%pm7_64 are identical to %pm0..%pm7.
PTX ISA Notes
%pm0_64..%pm7_64 introduced in PTX ISA version 4.0.
Target ISA Notes
%pm0_64..%pm7_64 require sm_50 or higher.
Examples
mov.u32 r1,%pm0_64;
mov.u32 r1,%pm7_64;
10.27. Special Registers: %envreg<32>
%envreg<32>
Driver-defined read-only registers.
Syntax (predefined)
.sreg .b32 %envreg<32>;
Description
A set of 32 pre-defined read-only registers used to capture execution environment of PTX program outside of PTX virtual machine. These registers are initialized by the driver prior to kernel launch and can contain cta-wide or grid-wide values.
Precise semantics of these registers is defined in the driver documentation.
PTX ISA Notes
Introduced in PTX ISA version 2.1.
Target ISA Notes
Supported on all target architectures.
Examples
mov.b32 %r1,%envreg0; // move envreg0 to %r1
10.28. Special Registers: %globaltimer, %globaltimer_lo, %globaltimer_hi
%globaltimer, %globaltimer_lo, %globaltimer_hi
%globaltimerA predefined, 64-bit global nanosecond timer.
%globaltimer_loThe lower 32-bits of %globaltimer.
%globaltimer_hiThe upper 32-bits of %globaltimer.
Syntax (predefined)
.sreg .u64 %globaltimer;
.sreg .u32 %globaltimer_lo, %globaltimer_hi;
Description
Special registers intended for use by NVIDIA tools. The behavior is target-specific and may change or be removed in future GPUs. When JIT-compiled to other targets, the value of these registers is unspecified.
PTX ISA Notes
Introduced in PTX ISA version 3.1.
Target ISA Notes
Requires target sm_30 or higher.
Examples
mov.u64 r1,%globaltimer;
10.29. Special Registers: %reserved_smem_offset_begin, %reserved_smem_offset_end, %reserved_smem_offset_cap, %reserved_smem_offset_<2>
%reserved_smem_offset_begin, %reserved_smem_offset_end, %reserved_smem_offset_cap, %reserved_smem_offset_<2>
%reserved_smem_offset_beginStart of the reserved shared memory region.
%reserved_smem_offset_endEnd of the reserved shared memory region.
%reserved_smem_offset_capTotal size of the reserved shared memory region.
%reserved_smem_offset_<2>Offsets in the reserved shared memory region.
Syntax (predefined)
.sreg .b32 %reserved_smem_offset_begin;
.sreg .b32 %reserved_smem_offset_end;
.sreg .b32 %reserved_smem_offset_cap;
.sreg .b32 %reserved_smem_offset_<2>;
Description
These are predefined, read-only special registers containing information about the shared memory region which is reserved for the NVIDIA system software use. This region of shared memory is not available to users, and accessing this region from user code results in undefined behavior. Refer to CUDA Programming Guide for details.
PTX ISA Notes
Introduced in PTX ISA version 7.6.
Target ISA Notes
Require sm_80 or higher.
Examples
.reg .b32 %reg_begin, %reg_end, %reg_cap, %reg_offset0, %reg_offset1;
mov.b32 %reg_begin, %reserved_smem_offset_begin;
mov.b32 %reg_end, %reserved_smem_offset_end;
mov.b32 %reg_cap, %reserved_smem_offset_cap;
mov.b32 %reg_offset0, %reserved_smem_offset_0;
mov.b32 %reg_offset1, %reserved_smem_offset_1;
10.30. Special Registers: %total_smem_size
%total_smem_size
Total size of shared memory used by a CTA of a kernel.
Syntax (predefined)
.sreg .u32 %total_smem_size;
Description
A predefined, read-only special register initialized with total size of shared memory allocated (statically and dynamically, excluding the shared memory reserved for the NVIDIA system software use) for the CTA of a kernel at launch time.
Size is returned in multiples of shared memory allocation unit size supported by target architecture.
Allocation unit values are as follows:
Target architecture |
Shared memory allocation unit size |
|---|---|
|
128 bytes |
|
256 bytes |
|
128 bytes |
PTX ISA Notes
Introduced in PTX ISA version 4.1.
Target ISA Notes
Requires sm_20 or higher.
Examples
mov.u32 %r, %total_smem_size;
10.31. Special Registers: %aggr_smem_size
%aggr_smem_size
Total size of shared memory used by a CTA of a kernel.
Syntax (predefined)
.sreg .u32 %aggr_smem_size;
Description
A predefined, read-only special register initialized with total aggregated size of shared memory consisting of the size of user shared memory allocated (statically and dynamically) at launch time and the size of shared memory region which is reserved for the NVIDIA system software use.
PTX ISA Notes
Introduced in PTX ISA version 8.1.
Target ISA Notes
Requires sm_90 or higher.
Examples
mov.u32 %r, %aggr_smem_size;
10.32. Special Registers: %dynamic_smem_size
%dynamic_smem_size
Size of shared memory allocated dynamically at kernel launch.
Syntax (predefined)
.sreg .u32 %dynamic_smem_size;
Description
Size of shared memory allocated dynamically at kernel launch.
A predefined, read-only special register initialized with size of shared memory allocated dynamically for the CTA of a kernel at launch time.
PTX ISA Notes
Introduced in PTX ISA version 4.1.
Target ISA Notes
Requires sm_20 or higher.
Examples
mov.u32 %r, %dynamic_smem_size;
10.33. Special Registers: %current_graph_exec
%current_graph_exec
An Identifier for currently executing CUDA device graph.
Syntax (predefined)
.sreg .u64 %current_graph_exec;
Description
A predefined, read-only special register initialized with the identifier referring to the CUDA device graph being currently executed. This register is 0 if the executing kernel is not part of a CUDA device graph.
Refer to the CUDA Programming Guide for more details on CUDA device graphs.
PTX ISA Notes
Introduced in PTX ISA version 8.0.
Target ISA Notes
Requires sm_50 or higher.
Examples
mov.u64 r1, %current_graph_exec;
11. Directives
11.1. PTX Module Directives
The following directives declare the PTX ISA version of the code in the module, the target architecture for which the code was generated, and the size of addresses within the PTX module.
.version.target.address_size
11.1.1. PTX Module Directives: .version
.version
PTX ISA version number.
Syntax
.version major.minor // major, minor are integers
Description
Specifies the PTX language version number.
The major number is incremented when there are incompatible changes to the PTX language, such as changes to the syntax or semantics. The version major number is used by the PTX compiler to ensure correct execution of legacy PTX code.
The minor number is incremented when new features are added to PTX.
Semantics
Indicates that this module must be compiled with tools that support an equal or greater version number.
Each PTX module must begin with a .version directive, and no other .version directive is
allowed anywhere else within the module.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
.version 3.1
.version 3.0
.version 2.3
11.1.2. PTX Module Directives: .target
.target
Architecture and Platform target.
Syntax
.target stringlist // comma separated list of target specifiers
string = { sm_90a, sm_90, // sm_9x target architectures
sm_80, sm_86, sm_87, sm_89, // sm_8x target architectures
sm_70, sm_72, sm_75, // sm_7x target architectures
sm_60, sm_61, sm_62, // sm_6x target architectures
sm_50, sm_52, sm_53, // sm_5x target architectures
sm_30, sm_32, sm_35, sm_37, // sm_3x target architectures
sm_20, // sm_2x target architectures
sm_10, sm_11, sm_12, sm_13, // sm_1x target architectures
texmode_unified, texmode_independent, // texturing mode
debug, // platform option
map_f64_to_f32 }; // platform option
Description
Specifies the set of features in the target architecture for which the current PTX code was generated. In general, generations of SM architectures follow an onion layer model, where each generation adds new features and retains all features of previous generations. The onion layer model allows the PTX code generated for a given target to be run on later generation devices.
Target architectures with suffix “a”, such as sm_90a, include architecture-accelerated
features that are supported on the specified architecture only, hence such targets do not follow the
onion layer model. Therefore, PTX code generated for such targets cannot be run on later generation
devices. Architecture-accelerated features can only be used with targets that support these
features.
Semantics
Each PTX module must begin with a .version directive, immediately followed by a .target
directive containing a target architecture and optional platform options. A .target directive
specifies a single target architecture, but subsequent .target directives can be used to change
the set of target features allowed during parsing. A program with multiple .target directives
will compile and run only on devices that support all features of the highest-numbered architecture
listed in the program.
PTX features are checked against the specified target architecture, and an error is generated if an unsupported feature is used. The following table summarizes the features in PTX that vary according to target architecture.
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Adds support for |
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Adds support for |
|
Baseline feature set for |
|
Baseline feature set for |
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Adds support for integer multiplicand and accumulator matrices in Adds support for |
|
Adds support for sub-byte integer and single-bit multiplicant matrices in Adds support for Adds support for Adds support for |
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Adds support for |
|
Baseline feature set for |
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Baseline feature set for |
|
Adds support for arithmetic, comparsion and texture instructions for |
Target |
Description |
|---|---|
|
Baseline feature set for |
|
Adds 64-bit Adds Adds |
|
Adds support for CUDA Dynamic Parallelism. |
|
Baseline feature set for |
Target |
Description |
|---|---|
|
Baseline feature set for |
Target |
Description |
|---|---|
|
Baseline feature set for Requires |
|
Adds 64-bit Requires |
|
Adds Requires |
|
Adds double-precision support, including expanded rounding modifiers. Disallows use of |
The texturing mode is specified for an entire module and cannot be changed within the module.
The .target debug option declares that the PTX file contains DWARF debug information, and
subsequent compilation of PTX will retain information needed for source-level debugging. If the
debug option is declared, an error message is generated if no DWARF information is found in the
file. The debug option requires PTX ISA version 3.0 or later.
map_f64_to_f32 indicates that all double-precision instructions map to single-precision
regardless of the target architecture. This enables high-level language compilers to compile
programs containing type double to target device that do not support double-precision
operations. Note that .f64 storage remains as 64-bits, with only half being used by instructions
converted from .f64 to .f32.
Notes
Targets of the form compute_xx are also accepted as synonyms for sm_xx targets.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target strings sm_10 and sm_11 introduced in PTX ISA version 1.0.
Target strings sm_12 and sm_13 introduced in PTX ISA version 1.2.
Texturing mode introduced in PTX ISA version 1.5.
Target string sm_20 introduced in PTX ISA version 2.0.
Target string sm_30 introduced in PTX ISA version 3.0.
Platform option debug introduced in PTX ISA version 3.0.
Target string sm_35 introduced in PTX ISA version 3.1.
Target strings sm_32 and sm_50 introduced in PTX ISA version 4.0.
Target strings sm_37 and sm_52 introduced in PTX ISA version 4.1.
Target string sm_53 introduced in PTX ISA version 4.2.
Target string sm_60, sm_61, sm_62 introduced in PTX ISA version 5.0.
Target string sm_70 introduced in PTX ISA version 6.0.
Target string sm_72 introduced in PTX ISA version 6.1.
Target string sm_75 introduced in PTX ISA version 6.3.
Target string sm_80 introduced in PTX ISA version 7.0.
Target string sm_86 introduced in PTX ISA version 7.1.
Target string sm_87 introduced in PTX ISA version 7.4.
Target string sm_89 introduced in PTX ISA version 7.8.
Target string sm_90 introduced in PTX ISA version 7.8.
Target string sm_90a introduced in PTX ISA version 8.0.
Target ISA Notes
The .target directive is supported on all target architectures.
Examples
.target sm_10 // baseline target architecture
.target sm_13 // supports double-precision
.target sm_20, texmode_independent
.target sm_90 // baseline target architecture
.target sm_90a // PTX using arch accelerated features
11.1.3. PTX Module Directives: .address_size
.address_size
Address size used throughout PTX module.
Syntax
.address_size address-size
address-size = { 32, 64 };
Description
Specifies the address size assumed throughout the module by the PTX code and the binary DWARF information in PTX.
Redefinition of this directive within a module is not allowed. In the presence of separate compilation all modules must specify (or default to) the same address size.
The .address_size directive is optional, but it must immediately follow the .targetdirective if present within a module.
Semantics
If the .address_size directive is omitted, the address size defaults to 32.
PTX ISA Notes
Introduced in PTX ISA version 2.3.
Target ISA Notes
Supported on all target architectures.
Examples
// example directives
.address_size 32 // addresses are 32 bit
.address_size 64 // addresses are 64 bit
// example of directive placement within a module
.version 2.3
.target sm_20
.address_size 64
...
.entry foo () {
...
}
11.2. Specifying Kernel Entry Points and Functions
The following directives specify kernel entry points and functions.
.entry.func
11.2.1. Kernel and Function Directives: .entry
.entry
Kernel entry point and body, with optional parameters.
Syntax
.entry kernel-name ( param-list ) kernel-body
.entry kernel-name kernel-body
Description
Defines a kernel entry point name, parameters, and body for the kernel function.
Parameters are passed via .param space memory and are listed within an optional parenthesized
parameter list. Parameters may be referenced by name within the kernel body and loaded into
registers using ld.param{::entry} instructions.
In addition to normal parameters, opaque .texref, .samplerref, and .surfref variables
may be passed as parameters. These parameters can only be referenced by name within texture and
surface load, store, and query instructions and cannot be accessed via ld.param instructions.
The shape and size of the CTA executing the kernel are available in special registers.
Semantics
Specify the entry point for a kernel program.
At kernel launch, the kernel dimensions and properties are established and made available via
special registers, e.g., %ntid, %nctaid, etc.
PTX ISA Notes
For PTX ISA version 1.4 and later, parameter variables are declared in the kernel parameter list. For PTX ISA versions 1.0 through 1.3, parameter variables are declared in the kernel body.
The maximum memory size supported by PTX for normal (non-opaque type) parameters is 32764 bytes. Depending upon the PTX ISA version, the parameter size limit varies. The following table shows the allowed parameter size for a PTX ISA version:
PTX ISA Version |
Maximum parameter size (In bytes) |
|---|---|
PTX ISA version 8.1 and above |
32764 |
PTX ISA version 1.5 and above |
4352 |
PTX ISA version 1.4 and above |
256 |
The CUDA and OpenCL drivers support the following limits for parameter memory:
Driver |
Parameter memory size |
|---|---|
CUDA |
256 bytes for |
OpenCL |
32764 bytes for |
Target ISA Notes
Supported on all target architectures.
Examples
.entry cta_fft
.entry filter ( .param .b32 x, .param .b32 y, .param .b32 z )
{
.reg .b32 %r<99>;
ld.param.b32 %r1, [x];
ld.param.b32 %r2, [y];
ld.param.b32 %r3, [z];
...
}
.entry prefix_sum ( .param .align 4 .s32 pitch[8000] )
{
.reg .s32 %t;
ld.param::entry.s32 %t, [pitch];
...
}
11.2.2. Kernel and Function Directives: .func
.func
Function definition.
Syntax
.func {.attribute(attr-list)} fname {.noreturn} function-body
.func {.attribute(attr-list)} fname (param-list) {.noreturn} function-body
.func {.attribute(attr-list)} (ret-param) fname (param-list) function-body
Description
Defines a function, including input and return parameters and optional function body.
An optional .noreturn directive indicates that the function does not return to the caller
function. .noreturn directive cannot be specified on functions which have return parameters. See
the description of .noreturn directive in Performance-Tuning Directives: .noreturn.
An optional .attribute directive specifies additional information associated with the
function. See the description of Variable and Function Attribute Directive: .attribute for allowed attributes.
A .func definition with no body provides a function prototype.
The parameter lists define locally-scoped variables in the function body. Parameters must be base
types in either the register or parameter state space. Parameters in register state space may be
referenced directly within instructions in the function body. Parameters in .param space are
accessed using ld.param{::func} and st.param{::func} instructions in the body. Parameter
passing is call-by-value.
The last parameter in the parameter list may be a .param array of type .b8 with no size
specified. It is used to pass an arbitrary number of parameters to the function packed into a single
array object.
When calling a function with such an unsized last argument, the last argument may be omitted from
the call instruction if no parameter is passed through it. Accesses to this array parameter must
be within the bounds of the array. The result of an access is undefined if no array was passed, or
if the access was outside the bounds of the actual array being passed.
Semantics
The PTX syntax hides all details of the underlying calling convention and ABI.
The implementation of parameter passing is left to the optimizing translator, which may use a combination of registers and stack locations to pass parameters.
Release Notes
For PTX ISA version 1.x code, parameters must be in the register state space, there is no stack, and recursion is illegal.
PTX ISA versions 2.0 and later with target sm_20 or higher allow parameters in the .param
state space, implements an ABI with stack, and supports recursion.
PTX ISA versions 2.0 and later with target sm_20 or higher support at most one return value.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Support for unsized array parameter introduced in PTX ISA version 6.0.
Support for .noreturn directive introduced in PTX ISA version 6.4.
Support for .attribute directive introduced in PTX ISA version 8.0.
Target ISA Notes
Functions without unsized array parameter supported on all target architectures.
Unsized array parameter requires sm_30 or higher.
.noreturn directive requires sm_30 or higher.
.attribute directive requires sm_90 or higher.
Examples
.func (.reg .b32 rval) foo (.reg .b32 N, .reg .f64 dbl)
{
.reg .b32 localVar;
... use N, dbl;
other code;
mov.b32 rval,result;
ret;
}
...
call (fooval), foo, (val0, val1); // return value in fooval
...
.func foo (.reg .b32 N, .reg .f64 dbl) .noreturn
{
.reg .b32 localVar;
... use N, dbl;
other code;
mov.b32 rval, result;
ret;
}
...
call foo, (val0, val1);
...
.func (.param .u32 rval) bar(.param .u32 N, .param .align 4 .b8 numbers[])
{
.reg .b32 input0, input1;
ld.param.b32 input0, [numbers + 0];
ld.param.b32 input1, [numbers + 4];
...
other code;
ret;
}
...
.param .u32 N;
.param .align 4 .b8 numbers[8];
st.param.u32 [N], 2;
st.param.b32 [numbers + 0], 5;
st.param.b32 [numbers + 4], 10;
call (rval), bar, (N, numbers);
...
11.2.3. Kernel and Function Directives: .alias
.alias
Define an alias to existing function symbol.
Syntax
.alias fAlias, fAliasee;
Description
.alias is a module scope directive that defines identifier fAlias to be an alias to function
specified by fAliasee.
Both fAlias and fAliasee are non-entry function symbols.
Identifier fAlias is a function declaration without body.
Identifier fAliasee is a function symbol which must be defined in the same module as .alias
declaration. Function fAliasee cannot have .weak linkage.
Prototype of fAlias and fAliasee must match.
Program can use either fAlias or fAlisee identifiers to reference function defined with
fAliasee.
PTX ISA Notes
.alias directive introduced in PTX ISA 6.3.
Target ISA Notes
.alias directive requires sm_30 or higher.
Examples
.visible .func foo(.param .u32 p) {
...
}
.visible .func bar(.param .u32 p);
.alias bar, foo;
.entry test()
{
.param .u32 p;
...
call foo, (p); // call foo directly
...
.param .u32 p;
call bar, (p); // call foo through alias
}
.entry filter ( .param .b32 x, .param .b32 y, .param .b32 z )
{
.reg .b32 %r1, %r2, %r3;
ld.param.b32 %r1, [x];
ld.param.b32 %r2, [y];
ld.param.b32 %r3, [z];
...
}
11.3. Control Flow Directives
PTX provides directives for specifying potential targets for brx.idx and call
instructions. See the descriptions of brx.idx and call for more information.
.branchtargets.calltargets.callprototype
11.3.1. Control Flow Directives: .branchtargets
.branchtargets
Declare a list of potential branch targets.
Syntax
Label: .branchtargets list-of-labels ;
Description
Declares a list of potential branch targets for a subsequent brx.idx, and associates the list
with the label at the start of the line.
All control flow labels in the list must occur within the same function as the declaration.
The list of labels may use the compact, shorthand syntax for enumerating a range of labels having a common prefix, similar to the syntax described in Parameterized Variable Names.
PTX ISA Notes
Introduced in PTX ISA version 2.1.
Target ISA Notes
Requires sm_20 or higher.
Examples
.function foo () {
.reg .u32 %r0;
...
L1:
...
L2:
...
L3:
...
ts: .branchtargets L1, L2, L3;
@p brx.idx %r0, ts;
...
.function bar() {
.reg .u32 %r0;
...
N0:
...
N1:
...
N2:
...
N3:
...
N4:
...
ts: .branchtargets N<5>;
@p brx.idx %r0, ts;
...
11.3.2. Control Flow Directives: .calltargets
.calltargets
Declare a list of potential call targets.
Syntax
Label: .calltargets list-of-functions ;
Description
Declares a list of potential call targets for a subsequent indirect call, and associates the list with the label at the start of the line.
All functions named in the list must be declared prior to the .calltargets directive, and all
functions must have the same type signature.
PTX ISA Notes
Introduced in PTX ISA version 2.1.
Target ISA Notes
Requires sm_20 or higher.
Examples
calltgt: .calltargets fastsin, fastcos;
...
@p call (%f1), %r0, (%x), calltgt;
...
11.3.3. Control Flow Directives: .callprototype
.callprototype
Declare a prototype for use in an indirect call.
Syntax
// no input or return parameters
label: .callprototype _ .noreturn;
// input params, no return params
label: .callprototype _ (param-list) .noreturn;
// no input params, // return params
label: .callprototype (ret-param) _ ;
// input, return parameters
label: .callprototype (ret-param) _ (param-list);
Description
Defines a prototype with no specific function name, and associates the prototype with a label. The prototype may then be used in indirect call instructions where there is incomplete knowledge of the possible call targets.
Parameters may have either base types in the register or parameter state spaces, or array types in
parameter state space. The sink symbol '_' may be used to avoid dummy parameter names.
An optional .noreturn directive indicates that the function does not return to the caller
function. .noreturn directive cannot be specified on functions which have return parameters. See
the description of .noreturn directive in Performance-Tuning Directives: .noreturn.
PTX ISA Notes
Introduced in PTX ISA version 2.1.
Support for .noreturn directive introduced in PTX ISA version 6.4.
Target ISA Notes
Requires sm_20 or higher.
.noreturn directive requires sm_30 or higher.
Examples
Fproto1: .callprototype _ ;
Fproto2: .callprototype _ (.param .f32 _);
Fproto3: .callprototype (.param .u32 _) _ ;
Fproto4: .callprototype (.param .u32 _) _ (.param .f32 _);
...
@p call (%val), %r0, (%f1), Fproto4;
...
// example of array parameter
Fproto5: .callprototype _ (.param .b8 _[12]);
Fproto6: .callprototype _ (.param .f32 _) .noreturn;
...
@p call %r0, (%f1), Fproto6;
...
11.4. Performance-Tuning Directives
To provide a mechanism for low-level performance tuning, PTX supports the following directives, which pass information to the backend optimizing compiler.
.maxnreg.maxntid.reqntid.minnctapersm.maxnctapersm(deprecated).pragma
The .maxnreg directive specifies the maximum number of registers to be allocated to a single
thread; the .maxntid directive specifies the maximum number of threads in a thread block (CTA);
the .reqntid directive specifies the required number of threads in a thread block (CTA); and the
.minnctapersm directive specifies a minimum number of thread blocks to be scheduled on a single
multiprocessor (SM). These can be used, for example, to throttle the resource requirements (e.g.,
registers) to increase total thread count and provide a greater opportunity to hide memory
latency. The .minnctapersm directive can be used together with either the .maxntid or
.reqntid directive to trade-off registers-per-thread against multiprocessor utilization without
needed to directly specify a maximum number of registers. This may achieve better performance when
compiling PTX for multiple devices having different numbers of registers per SM.
Currently, the .maxnreg, .maxntid, .reqntid, and .minnctapersm directives may be
applied per-entry and must appear between an .entry directive and its body. The directives take
precedence over any module-level constraints passed to the optimizing backend. A warning message is
generated if the directives’ constraints are inconsistent or cannot be met for the specified target
device.
A general .pragma directive is supported for passing information to the PTX backend. The
directive passes a list of strings to the backend, and the strings have no semantics within the PTX
virtual machine model. The interpretation of .pragma values is determined by the backend
implementation and is beyond the scope of the PTX ISA. Note that .pragma directives may appear
at module (file) scope, at entry-scope, or as statements within a kernel or device function body.
11.4.1. Performance-Tuning Directives: .maxnreg
.maxnreg
Maximum number of registers that can be allocated per thread.
Syntax
.maxnreg n
Description
Declare the maximum number of registers per thread in a CTA.
Semantics
The compiler guarantees that this limit will not be exceeded. The actual number of registers used
may be less; for example, the backend may be able to compile to fewer registers, or the maximum
number of registers may be further constrained by .maxntid and .maxctapersm.
PTX ISA Notes
Introduced in PTX ISA version 1.3.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo .maxnreg 16 { ... } // max regs per thread = 16
11.4.2. Performance-Tuning Directives: .maxntid
.maxntid
Maximum number of threads in the thread block (CTA).
Syntax
.maxntid nx
.maxntid nx, ny
.maxntid nx, ny, nz
Description
Declare the maximum number of threads in the thread block (CTA). This maximum is specified by giving the maximum extent of each dimension of the 1D, 2D, or 3D CTA. The maximum number of threads is the product of the maximum extent in each dimension.
Semantics
The maximum number of threads in the thread block, computed as the product of the maximum extent specified for each dimension, is guaranteed not to be exceeded in any invocation of the kernel in which this directive appears. Exceeding the maximum number of threads results in a runtime error or kernel launch failure.
Note that this directive guarantees that the total number of threads does not exceed the maximum, but does not guarantee that the limit in any particular dimension is not exceeded.
PTX ISA Notes
Introduced in PTX ISA version 1.3.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo .maxntid 256 { ... } // max threads = 256
.entry bar .maxntid 16,16,4 { ... } // max threads = 1024
11.4.3. Performance-Tuning Directives: .reqntid
.reqntid
Number of threads in the thread block (CTA).
Syntax
.reqntid nx
.reqntid nx, ny
.reqntid nx, ny, nz
Description
Declare the number of threads in the thread block (CTA) by specifying the extent of each dimension of the 1D, 2D, or 3D CTA. The total number of threads is the product of the number of threads in each dimension.
Semantics
The size of each CTA dimension specified in any invocation of the kernel is required to be equal to that specified in this directive. Specifying a different CTA dimension at launch will result in a runtime error or kernel launch failure.
Notes
The .reqntid directive cannot be used in conjunction with the .maxntid directive.
PTX ISA Notes
Introduced in PTX ISA version 2.1.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo .reqntid 256 { ... } // num threads = 256
.entry bar .reqntid 16,16,4 { ... } // num threads = 1024
11.4.4. Performance-Tuning Directives: .minnctapersm
.minnctapersm
Minimum number of CTAs per SM.
Syntax
.minnctapersm ncta
Description
Declare the minimum number of CTAs from the kernel’s grid to be mapped to a single multiprocessor (SM).
Notes
Optimizations based on .minnctapersm need either .maxntid or .reqntid to be specified as
well.
If the total number of threads on a single SM resulting from .minnctapersm and .maxntid /
.reqntid exceed maximum number of threads supported by an SM then directive .minnctapersm
will be ignored.
In PTX ISA version 2.1 or higher, a warning is generated if .minnctapersm is specified without
specifying either .maxntid or .reqntid.
PTX ISA Notes
Introduced in PTX ISA version 2.0 as a replacement for .maxnctapersm.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo .maxntid 256 .minnctapersm 4 { ... }
11.4.5. Performance-Tuning Directives: .maxnctapersm (deprecated)
.maxnctapersm
Maximum number of CTAs per SM.
Syntax
.maxnctapersm ncta
Description
Declare the maximum number of CTAs from the kernel’s grid that may be mapped to a single multiprocessor (SM).
Notes
Optimizations based on .maxnctapersm generally need .maxntid to be specified as well. The
optimizing backend compiler uses .maxntid and .maxnctapersm to compute an upper-bound on
per-thread register usage so that the specified number of CTAs can be mapped to a single
multiprocessor. However, if the number of registers used by the backend is sufficiently lower than
this bound, additional CTAs may be mapped to a single multiprocessor. For this reason,
.maxnctapersm has been renamed to .minnctapersm in PTX ISA version 2.0.
PTX ISA Notes
Introduced in PTX ISA version 1.3. Deprecated in PTX ISA version 2.0.
Target ISA Notes
Supported on all target architectures.
Examples
.entry foo .maxntid 256 .maxnctapersm 4 { ... }
11.4.6. Performance-Tuning Directives: .noreturn
.noreturn
Indicate that the function does not return to its caller function.
Syntax
.noreturn
Description
Indicate that the function does not return to its caller function.
Semantics
An optional .noreturn directive indicates that the function does not return to caller
function. .noreturn directive can only be specified on device functions and must appear between
a .func directive and its body.
The directive cannot be specified on functions which have return parameters.
If a function with .noreturn directive returns to the caller function at runtime, then the
behavior is undefined.
PTX ISA Notes
Introduced in PTX ISA version 6.4.
Target ISA Notes
Requires sm_30 or higher.
Examples
.func foo .noreturn { ... }
11.4.7. Performance-Tuning Directives: .pragma
.pragma
Pass directives to PTX backend compiler.
Syntax
.pragma list-of-strings ;
Description
Pass module-scoped, entry-scoped, or statement-level directives to the PTX backend compiler.
The .pragma directive may occur at module-scope, at entry-scope, or at statement-level.
Semantics
The interpretation of .pragma directive strings is implementation-specific and has no impact on
PTX semantics. See Descriptions of .pragma Strings for
descriptions of the pragma strings defined in ptxas.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
Supported on all target architectures.
Examples
.pragma "nounroll"; // disable unrolling in backend
// disable unrolling for current kernel
.entry foo .pragma "nounroll"; { ... }
11.5. Debugging Directives
DWARF-format debug information is passed through PTX modules using the following directives:
@@DWARF.section.file.loc
The .section directive was introduced in PTX ISA version 2.0 and replaces the @@DWARF
syntax. The @@DWARF syntax was deprecated in PTX ISA version 2.0 but is supported for legacy PTX
ISA version 1.x code.
Beginning with PTX ISA version 3.0, PTX files containing DWARF debug information should include the
.target debug platform option. This forward declaration directs PTX compilation to retain
mappings for source-level debugging.
11.5.1. Debugging Directives: @@dwarf
@@dwarf
DWARF-format information.
Syntax
@@DWARF dwarf-string
dwarf-string may have one of the
.byte byte-list // comma-separated hexadecimal byte values
.4byte int32-list // comma-separated hexadecimal integers in range [0..2^32-1]
.quad int64-list // comma-separated hexadecimal integers in range [0..2^64-1]
.4byte label
.quad label
PTX ISA Notes
Introduced in PTX ISA version 1.2. Deprecated as of PTX ISA version 2.0, replaced by .section
directive.
Target ISA Notes
Supported on all target architectures.
Examples
@@DWARF .section .debug_pubnames, "", @progbits
@@DWARF .byte 0x2b, 0x00, 0x00, 0x00, 0x02, 0x00
@@DWARF .4byte .debug_info
@@DWARF .4byte 0x000006b5, 0x00000364, 0x61395a5f, 0x5f736f63
@@DWARF .4byte 0x6e69616d, 0x63613031, 0x6150736f, 0x736d6172
@@DWARF .byte 0x00, 0x00, 0x00, 0x00, 0x00
11.5.2. Debugging Directives: .section
.section
PTX section definition.
Syntax
.section section_name { dwarf-lines }
dwarf-lines have the following formats:
.b8 byte-list // comma-separated list of integers
// in range [-128..255]
.b16 int16-list // comma-separated list of integers
// in range [-2^15..2^16-1]
.b32 int32-list // comma-separated list of integers
// in range [-2^31..2^32-1]
label: // Define label inside the debug section
.b64 int64-list // comma-separated list of integers
// in range [-2^63..2^64-1]
.b32 label
.b64 label
.b32 label+imm // a sum of label address plus a constant integer byte
// offset(signed, 32bit)
.b64 label+imm // a sum of label address plus a constant integer byte
// offset(signed, 64bit)
.b32 label1-label2 // a difference in label addresses between labels in
// the same dwarf section (32bit)
.b64 label3-label4 // a difference in label addresses between labels in
// the same dwarf section (64bit)
PTX ISA Notes
Introduced in PTX ISA version 2.0, replaces @@DWARF syntax.
label+imm expression introduced in PTX ISA version 3.2.
Support for .b16 integers in dwarf-lines introduced in PTX ISA version 6.0.
Support for defining label inside the DWARF section is introduced in PTX ISA version 7.2.
label1-label2 expression introduced in PTX ISA version 7.5.
Negative numbers in dwarf lines introduced in PTX ISA version 7.5.
Target ISA Notes
Supported on all target architectures.
Examples
.section .debug_pubnames
{
.b32 LpubNames_end0-LpubNames_begin0
LpubNames_begin0:
.b8 0x2b, 0x00, 0x00, 0x00, 0x02, 0x00
.b32 .debug_info
info_label1:
.b32 0x000006b5, 0x00000364, 0x61395a5f, 0x5f736f63
.b32 0x6e69616d, 0x63613031, 0x6150736f, 0x736d6172
.b8 0x00, 0x00, 0x00, 0x00, 0x00
LpubNames_end0:
}
.section .debug_info
{
.b32 11430
.b8 2, 0
.b32 .debug_abbrev
.b8 8, 1, 108, 103, 101, 110, 102, 101, 58, 32, 69, 68, 71, 32, 52, 46, 49
.b8 0
.b32 3, 37, 176, -99
.b32 info_label1
.b32 .debug_loc+0x4
.b8 -11, 11, 112, 97
.b32 info_label1+12
.b64 -1
.b16 -5, -65535
}
11.5.3. Debugging Directives: .file
.file
Source file name.
Syntax
.file file_index "filename" {, timestamp, file_size}
Description
Associates a source filename with an integer index. .loc directives reference source files by
index.
.file directive allows optionally specifying an unsigned number representing time of last
modification and an unsigned integer representing size in bytes of source file. timestamp and
file_size value can be 0 to indicate this information is not available.
timestamp value is in format of C and C++ data type time_t.
file_size is an unsigned 64-bit integer.
The .file directive is allowed only in the outermost scope, i.e., at the same level as kernel
and device function declarations.
Semantics
If timestamp and file size are not specified, they default to 0.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Timestamp and file size introduced in PTX ISA version 3.2.
Target ISA Notes
Supported on all target architectures.
Examples
.file 1 "example.cu"
.file 2 "kernel.cu"
.file 1 “kernel.cu”, 1339013327, 64118
11.5.4. Debugging Directives: .loc
.loc
Source file location.
Syntax
.loc file_index line_number column_position
.loc file_index line_number column_position,function_name label {+ immediate }, inlined_at file_index2 line_number2 column_position2
Description
Declares the source file location (source file, line number, and column position) to be associated
with lexically subsequent PTX instructions. .loc refers to file_index which is defined by a
.file directive.
To indicate PTX instructions that are generated from a function that got inlined, additional
attribute .inlined_at can be specified as part of the .loc directive. .inlined_at
attribute specifies source location at which the specified function is inlined. file_index2,
line_number2, and column_position2 specify the location at which function is inlined. Source
location specified as part of .inlined_at directive must lexically precede as source location in
.loc directive.
The function_name attribute specifies an offset in the DWARF section named
.debug_str. Offset is specified as label expression or label + immediate expression
where label is defined in .debug_str section. DWARF section .debug_str contains ASCII
null-terminated strings that specify the name of the function that is inlined.
Note that a PTX instruction may have a single associated source location, determined by the nearest lexically preceding .loc directive, or no associated source location if there is no preceding .loc directive. Labels in PTX inherit the location of the closest lexically following instruction. A label with no following PTX instruction has no associated source location.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
function_name and inlined_at attributes are introduced in PTX ISA version 7.2.
Target ISA Notes
Supported on all target architectures.
Examples
.loc 2 4237 0
L1: // line 4237, col 0 of file #2,
// inherited from mov
mov.u32 %r1,%r2; // line 4237, col 0 of file #2
add.u32 %r2,%r1,%r3; // line 4237, col 0 of file #2
...
L2: // line 4239, col 5 of file #2,
// inherited from sub
.loc 2 4239 5
sub.u32 %r2,%r1,%r3; // line 4239, col 5 of file #2
.loc 1 21 3
.loc 1 9 3, function_name info_string0, inlined_at 1 21 3
ld.global.u32 %r1, [gg]; // Function at line 9
setp.lt.s32 %p1, %r1, 8; // inlined at line 21
.loc 1 27 3
.loc 1 10 5, function_name info_string1, inlined_at 1 27 3
.loc 1 15 3, function_name .debug_str+16, inlined_at 1 10 5
setp.ne.s32 %p2, %r1, 18;
@%p2 bra BB2_3;
.section .debug_str {
info_string0:
.b8 95 // _
.b8 90 // z
.b8 51 // 3
.b8 102 // f
.b8 111 // o
.b8 111 // o
.b8 118 // v
.b8 0
info_string1:
.b8 95 // _
.b8 90 // z
.b8 51 // 3
.b8 98 // b
.b8 97 // a
.b8 114 // r
.b8 118 // v
.b8 0
.b8 95 // _
.b8 90 // z
.b8 51 // 3
.b8 99 // c
.b8 97 // a
.b8 114 // r
.b8 118 // v
.b8 0
}
11.6. Linking Directives
.extern.visible.weak
11.6.1. Linking Directives: .extern
.extern
External symbol declaration.
Syntax
.extern identifier
Description
Declares identifier to be defined external to the current module. The module defining such
identifier must define it as .weak or .visible only once in a single object file. Extern
declaration of symbol may appear multiple times and references to that get resolved against the
single definition of that symbol.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
.extern .global .b32 foo; // foo is defined in another module
11.6.2. Linking Directives: .visible
.visible
Visible (externally) symbol declaration.
Syntax
.visible identifier
Description
Declares identifier to be globally visible. Unlike C, where identifiers are globally visible unless
declared static, PTX identifiers are visible only within the current module unless declared
.visible outside the current.
PTX ISA Notes
Introduced in PTX ISA version 1.0.
Target ISA Notes
Supported on all target architectures.
Examples
.visible .global .b32 foo; // foo will be externally visible
11.6.3. Linking Directives: .weak
.weak
Visible (externally) symbol declaration.
Syntax
.weak identifier
Description
Declares identifier to be globally visible but weak. Weak symbols are similar to globally visible symbols, except during linking, weak symbols are only chosen after globally visible symbols during symbol resolution. Unlike globally visible symbols, multiple object files may declare the same weak symbol, and references to a symbol get resolved against a weak symbol only if no global symbols have the same name.
PTX ISA Notes
Introduced in PTX ISA version 3.1.
Target ISA Notes
Supported on all target architectures.
Examples
.weak .func (.reg .b32 val) foo; // foo will be externally visible
11.6.4. Linking Directives: .common
.common
Visible (externally) symbol declaration.
Syntax
.common identifier
Description
Declares identifier to be globally visible but “common”.
Common symbols are similar to globally visible symbols. However multiple object files may declare the same common symbol and they may have different types and sizes and references to a symbol get resolved against a common symbol with the largest size.
Only one object file can initialize a common symbol and that must have the largest size among all other definitions of that common symbol from different object files.
.common linking directive can be used only on variables with .global storage. It cannot be
used on function symbols or on symbols with opaque type.
PTX ISA Notes
Introduced in PTX ISA version 5.0.
Target ISA Notes
.common directive requires sm_20 or higher.
Examples
.common .global .u32 gbl;
11.7. Cluster Dimension Directives
The following directives specify information about clusters:
.reqnctapercluster.explicitcluster.maxclusterrank
The .reqnctapercluster directive specifies the number of CTAs in the cluster. The
.explicitcluster directive specifies that the kernel should be launched with explicit cluster
details. The .maxclusterrank directive specifies the maximum number of CTAs in the cluster.
The cluster dimension directives can be applied only on kernel functions.
11.7.1. Cluster Dimension Directives: .reqnctapercluster
.reqnctapercluster
Declare the number of CTAs in the cluster.
Syntax
.reqnctapercluster nx
.reqnctapercluster nx, ny
.reqnctapercluster nx, ny, nz
Description
Set the number of thread blocks (CTAs) in the cluster by specifying the extent of each dimension of
the 1D, 2D, or 3D cluster. The total number of CTAs is the product of the number of CTAs in each
dimension. For kernels with .reqnctapercluster directive specified, runtime will use the
specified values for configuring the launch if the same are not specified at launch time.
Semantics
If cluster dimension is explicitly specified at launch time, it should be equal to the values specified in this directive. Specifying a different cluster dimension at launch will result in a runtime error or kernel launch failure.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.entry foo .reqnctapercluster 2 { . . . }
.entry bar .reqnctapercluster 2, 2, 1 { . . . }
.entry ker .reqnctapercluster 3, 2 { . . . }
11.7.2. Cluster Dimension Directives: .explicitcluster
.explicitcluster
Declare that Kernel must be launched with cluster dimensions explicitly specified.
Syntax
.explicitcluster
Description
Declares that this Kernel should be launched with cluster dimension explicitly specified.
Semantics
Kernels with .explicitcluster directive must be launched with cluster dimension explicitly
specified (either at launch time or via .reqnctapercluster), otherwise program will fail with
runtime error or kernel launch failure.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.entry foo .explicitcluster { . . . }
11.7.3. Cluster Dimension Directives: .maxclusterrank
.maxclusterrank
Declare the maximum number of CTAs that can be part of the cluster.
Syntax
.maxclusterrank n
Description
Declare the maximum number of thread blocks (CTAs) allowed to be part of the cluster.
Semantics
Product of the number of CTAs in each cluster dimension specified in any invocation of the kernel is required to be less or equal to that specified in this directive. Otherwise invocation will result in a runtime error or kernel launch failure.
The .maxclusterrank directive cannot be used in conjunction with the .reqnctapercluster directive.
PTX ISA Notes
Introduced in PTX ISA version 7.8.
Target ISA Notes
Requires sm_90 or higher.
Examples
.entry foo ..maxclusterrank 8 { . . . }
12. Release Notes
This section describes the history of change in the PTX ISA and implementation. The first section describes ISA and implementation changes in the current release of PTX ISA version 8.4, and the remaining sections provide a record of changes in previous releases of PTX ISA versions back to PTX ISA version 2.0.
Table 32 shows the PTX release history.
PTX ISA Version |
CUDA Release |
Supported Targets |
|---|---|---|
PTX ISA 1.0 |
CUDA 1.0 |
|
PTX ISA 1.1 |
CUDA 1.1 |
|
PTX ISA 1.2 |
CUDA 2.0 |
|
PTX ISA 1.3 |
CUDA 2.1 |
|
PTX ISA 1.4 |
CUDA 2.2 |
|
PTX ISA 1.5 |
driver r190 |
|
PTX ISA 2.0 |
CUDA 3.0, driver r195 |
|
PTX ISA 2.1 |
CUDA 3.1, driver r256 |
|
PTX ISA 2.2 |
CUDA 3.2, driver r260 |
|
PTX ISA 2.3 |
CUDA 4.0, driver r270 |
|
PTX ISA 3.0 |
CUDA 4.1, driver r285 |
|
CUDA 4.2, driver r295 |
|
|
PTX ISA 3.1 |
CUDA 5.0, driver r302 |
|
PTX ISA 3.2 |
CUDA 5.5, driver r319 |
|
PTX ISA 4.0 |
CUDA 6.0, driver r331 |
|
PTX ISA 4.1 |
CUDA 6.5, driver r340 |
|
PTX ISA 4.2 |
CUDA 7.0, driver r346 |
|
PTX ISA 4.3 |
CUDA 7.5, driver r352 |
|
PTX ISA 5.0 |
CUDA 8.0, driver r361 |
|
PTX ISA 6.0 |
CUDA 9.0, driver r384 |
|
PTX ISA 6.1 |
CUDA 9.1, driver r387 |
|
PTX ISA 6.2 |
CUDA 9.2, driver r396 |
|
PTX ISA 6.3 |
CUDA 10.0, driver r400 |
|
PTX ISA 6.4 |
CUDA 10.1, driver r418 |
|
PTX ISA 6.5 |
CUDA 10.2, driver r440 |
|
PTX ISA 7.0 |
CUDA 11.0, driver r445 |
|
PTX ISA 7.1 |
CUDA 11.1, driver r455 |
|
PTX ISA 7.2 |
CUDA 11.2, driver r460 |
|
PTX ISA 7.3 |
CUDA 11.3, driver r465 |
|
PTX ISA 7.4 |
CUDA 11.4, driver r470 |
|
PTX ISA 7.5 |
CUDA 11.5, driver r495 |
|
PTX ISA 7.6 |
CUDA 11.6, driver r510 |
|
PTX ISA 7.7 |
CUDA 11.7, driver r515 |
|
PTX ISA 7.8 |
CUDA 11.8, driver r520 |
|
PTX ISA 8.0 |
CUDA 12.0, driver r525 |
|
PTX ISA 8.1 |
CUDA 12.1, driver r530 |
|
PTX ISA 8.2 |
CUDA 12.2, driver r535 |
|
PTX ISA 8.3 |
CUDA 12.3, driver r545 |
|
PTX ISA 8.4 |
CUDA 12.4, driver r550 |
|
12.1. Changes in PTX ISA Version 8.4
New Features
PTX ISA version 8.4 introduces the following new features:
Extends
ld,standatominstructions with.b128type to support.sysscope.Extends integer
wgmma.mma_asyncinstruction to support.u8.s8and.s8.u8as.atypeand.btyperespectively.Extends
mma,mma.spinstructions to support FP8 types.e4m3and.e5m2.
Semantic Changes and Clarifications
None.
12.2. Changes in PTX ISA Version 8.3
New Features
PTX ISA version 8.3 introduces the following new features:
Adds support for pragma
used_bytes_maskthat is used to specify mask for used bytes for a load operation.Extends
isspacep,cvta.to,ldandstinstructions to accept::entryand::funcsub-qualifiers with.paramstate space qualifier.Adds support for
.b128type on instructionsld,ld.global.nc,ldu,st,movandatom.Add support for instructions
tensormap.replace,tensormap.cp_fenceproxyand support for qualifier.to_proxykind::from_proxykindon instructionfence.proxyto support modifyingtensor-map.
Semantic Changes and Clarifications
None.
12.3. Changes in PTX ISA Version 8.2
New Features
PTX ISA version 8.2 introduces the following new features:
Adds support for
.mmioqualifier onldandstinstructions.Extends
lop3instruction to allow predicate destination.Extends
multimem.ld_reduceinstruction to support.acc::f32qualifer to allow.f32precision of the intermediate accumulation.Extends the asynchronous warpgroup-level matrix multiply-and-accumulate operation
wgmma.mma_asyncto support.spmodifier that allows matrix multiply-accumulate operation when input matrix A is sparse.
Semantic Changes and Clarifications
The .multicast::cluster qualifier on cp.async.bulk and cp.async.bulk.tensor instructions
is optimized for target architecture sm_90a and may have substantially reduced performance on
other targets and hence .multicast::cluster is advised to be used with sm_90a.
12.4. Changes in PTX ISA Version 8.1
New Features
PTX ISA version 8.1 introduces the following new features:
Adds support for
st.asyncandred.asyncinstructions for asynchronous store and asynchronous reduction operations respectively on shared memory.Adds support for
.oobmodifier on half-precisionfmainstruction.Adds support for
.satfinitesaturation modifer oncvtinstruction for.f16,.bf16and.tf32formats.Extends support for
cvtwith.e4m3/.e5m2tosm_89.Extends
atomandredinstructions to support vector types.Adds support for special register
%aggr_smem_size.Extends
suredinstruction with 64-bitmin/maxoperations.Adds support for increased kernel parameter size of 32764 bytes.
Adds support for multimem addresses in memory consistency model.
Adds support for
multimem.ld_reduce,multimem.standmultimem.redinstructions to perform memory operations on multimem addresses.
Semantic Changes and Clarifications
None.
12.5. Changes in PTX ISA Version 8.0
New Features
PTX ISA version 8.0 introduces the following new features:
Adds support for target
sm_90athat supports specialized accelerated features.Adds support for asynchronous warpgroup-level matrix multiply-and-accumulate operation
wgmma.Extends the asynchronous copy operations with bulk operations that operate on large data, including tensor data.
Introduces packed integer types
.u16x2and.s16x2.Extends integer arithmetic instruction
addto allow packed integer types.u16x2and.s16x2.Extends integer arithmetic instructions
minandmaxto allow packed integer types.u16x2and.s16x2, as well as saturation modifier.reluon.s16x2and.s32types.Adds support for special register
%current_graph_execthat identifies the currently executing CUDA device graph.Adds support for
elect.syncinstruction.Adds support for
.unifiedattribute on functions and variables.Adds support for
setmaxnreginstruction.Adds support for
.semqualifier onbarrier.clusterinstruction.Extends the
fenceinstruction to allow opcode-specific synchronizaion usingop_restrictqualifier.Adds support for
.clusterscope onmbarrier.arrive,mbarrier.arrive_drop,mbarrier.test_waitandmbarrier.try_waitoperations.Adds support for transaction count operations on
mbarrierobjects, specified with.expect_txand.complete_txqualifiers.
Semantic Changes and Clarifications
None.
12.6. Changes in PTX ISA Version 7.8
New Features
PTX ISA version 7.8 introduces the following new features:
Adds support for
sm_89target architecture.Adds support for
sm_90target architecture.Extends
barandbarrierinstructions to accept optional scope qualifier.cta.Extends
.sharedstate space qualifier with optional sub-qualifier::cta.Adds support for
movmatrixinstruction which transposes a matrix in registers across a warp.Adds support for
stmatrixinstruction which stores one or more matrices to shared memory.Extends the
.f64floating point typemmaoperation with shapes.m16n8k4,.m16n8k8, and.m16n8k16.Extends
add,sub,mul,set,setp,cvt,tanh,ex2,atomandredinstructions withbf16alternate floating point data format.Adds support for new alternate floating-point data formats
.e4m3and.e5m2.Extends
cvtinstruction to convert.e4m3and.e5m2alternate floating point data formats.Adds support for
griddepcontrolinstruction as a communication mechanism to control the execution of dependent grids.Extends
mbarrierinstruction to allow a new phase completion check operation try_wait.Adds support for new thread scope
.clusterwhich is a set of Cooperative Thread Arrays (CTAs).Extends
fence/membar,ld,st,atom, andredinstructions to accept.clusterscope.Adds support for extended visibility of shared state space to all threads within a cluster.
Extends
.sharedstate space qualifier with::clustersub-qualifier for cluster-level visibility of shared memory.Extends
isspacep,cvta,ld,st,atom, andredinstructions to accept::clustersub-qualifier with.sharedstate space qualifier.Adds support for
mapainstruction to map a shared memory address to the corresponding address in a different CTA within the cluster.Adds support for
getctarankinstruction to query the rank of the CTA that contains a given address.Adds support for new barrier synchronization instruction
barrier.cluster.Extends the memory consistency model to include the new cluster scope.
Adds support for special registers related to cluster information:
%is_explicit_cluster,%clusterid,%nclusterid,%cluster_ctaid,%cluster_nctaid,%cluster_ctarank,%cluster_nctarank.Adds support for cluster dimension directives
.reqnctapercluster,.explicitcluster, and.maxclusterrank.
Semantic Changes and Clarifications
None.
12.7. Changes in PTX ISA Version 7.7
New Features
PTX ISA version 7.7 introduces the following new features:
Extends
isspacepandcvtainstructions to include the.paramstate space for kernel function parameters.
Semantic Changes and Clarifications
None.
12.8. Changes in PTX ISA Version 7.6
New Features
PTX ISA version 7.6 introduces the following new features:
Support for
szextinstruction which performs sign-extension or zero-extension on a specified value.Support for
bmskinstruction which creates a bitmask of the specified width starting at the specified bit position.Support for special registers
%reserved_smem_offset_begin,%reserved_smem_offset_end,%reserved_smem_offset_cap,%reserved_smem_offset<2>.
Semantic Changes and Clarifications
None.
12.9. Changes in PTX ISA Version 7.5
New Features
PTX ISA version 7.5 introduces the following new features:
Debug information enhancements to support label difference and negative values in the
.sectiondebugging directive.Support for
ignore-srcoperand oncp.asyncinstruction.Extensions to the memory consistency model to introduce the following new concepts:
A memory proxy as an abstract label for different methods of memory access.
Virtual aliases as distinct memory addresses accessing the same physical memory location.
Support for new
fence.proxyandmembar.proxyinstructions to allow synchronization of memory accesses performed via virtual aliases.
Semantic Changes and Clarifications
None.
12.10. Changes in PTX ISA Version 7.4
New Features
PTX ISA version 7.4 introduces the following new features:
Support for
sm_87target architecture.Support for
.level::eviction_priorityqualifier which allows specifying cache eviction priority hints onld,ld.global.nc,st, andprefetchinstructions.Support for
.level::prefetch_sizequalifier which allows specifying data prefetch hints onldandcp.asyncinstructions.Support for
createpolicyinstruction which allows construction of different types of cache eviction policies.Support for
.level::cache_hintqualifier which allows the use of cache eviction policies withld,ld.global.nc,st,atom,redandcp.asyncinstructions.Support for
applypriorityanddiscardoperations on cached data.
Semantic Changes and Clarifications
None.
12.11. Changes in PTX ISA Version 7.3
New Features
PTX ISA version 7.3 introduces the following new features:
Extends
mask()operator used in initializers to also support integer constant expression.Adds support for stack manpulation instructions that allow manipulating stack using
stacksaveandstackrestoreinstructions and allocation of per-thread stack usingallocainstruction.
Semantic Changes and Clarifications
The unimplemented version of alloca from the older PTX ISA specification has been replaced with
new stack manipulation instructions in PTX ISA version 7.3.
12.12. Changes in PTX ISA Version 7.2
New Features
PTX ISA version 7.2 introduces the following new features:
Enhances
.locdirective to represent inline function information.Adds support to define labels inside the debug sections.
Extends
minandmaxinstructions to support.xorsignand.absmodifiers.
Semantic Changes and Clarifications
None.
12.13. Changes in PTX ISA Version 7.1
New Features
PTX ISA version 7.1 introduces the following new features:
Support for
sm_86target architecture.Adds a new operator,
mask(), to extract a specific byte from variable’s address used in initializers.Extends
texandtld4instructions to return an optional predicate that indicates if data at specified coordinates is resident in memory.Extends single-bit
wmmaandmmainstructions to support.andoperation.Extends
mmainstruction to support.spmodifier that allows matrix multiply-accumulate operation when input matrix A is sparse.Extends
mbarrier.test_waitinstruction to test the completion of specific phase parity.
Semantic Changes and Clarifications
None.
12.14. Changes in PTX ISA Version 7.0
New Features
PTX ISA version 7.0 introduces the following new features:
Support for
sm_80target architecture.Adds support for asynchronous copy instructions that allow copying of data asynchronously from one state space to another.
Adds support for
mbarrierinstructions that allow creation of mbarrier objects in memory and use of these objects to synchronize threads and asynchronous copy operations initiated by threads.Adds support for
redux.syncinstruction which allows reduction operation across threads in a warp.Adds support for new alternate floating-point data formats
.bf16and.tf32.Extends
wmmainstruction to support.f64type with shape.m8n8k4.Extends
wmmainstruction to support.bf16data format.Extends
wmmainstruction to support.tf32data format with shape.m16n16k8.Extends
mmainstruction to support.f64type with shape.m8n8k4.Extends
mmainstruction to support.bf16and.tf32data formats with shape.m16n8k8.Extends
mmainstruction to support new shapes.m8n8k128,.m16n8k4,.m16n8k16,.m16n8k32,.m16n8k64,.m16n8k128and.m16n8k256.Extends
absandneginstructions to support.bf16and.bf16x2data formats.Extends
minandmaxinstructions to support.NaNmodifier and.f16,.f16x2,.bf16and.bf16x2data formats.Extends
fmainstruction to support.relusaturation mode and.bf16and.bf16x2data formats.Extends
cvtinstruction to support.relusaturation mode and.f16,.f16x2,.bf16,.bf16x2and.tf32destination formats.Adds support for
tanhinstruction that computes hyperbolic-tangent.Extends
ex2instruction to support.f16and.f16x2types.
Semantic Changes and Clarifications
None.
12.15. Changes in PTX ISA Version 6.5
New Features
PTX ISA version 6.5 introduces the following new features:
Adds support for integer destination types for half precision comparison instruction
set.Extends
absinstruction to support.f16and.f16x2types.Adds support for
cvt.packinstruction which allows converting two integer values and packing the results together.Adds new shapes
.m16n8k8,.m8n8k16and.m8n8k32on themmainstruction.Adds support for
ldmatrixinstruction which loads one or more matrices from shared memory formmainstruction.
Removed Features
PTX ISA version 6.5 removes the following features:
Support for
.satfinitequalifier on floating pointwmma.mmainstruction has been removed. This support was deprecated since PTX ISA version 6.4.
Semantic Changes and Clarifications
None.
12.16. Changes in PTX ISA Version 6.4
New Features
PTX ISA version 6.4 introduces the following new features:
Adds support for
.noreturndirective which can be used to indicate a function does not return to it’s caller function.Adds support for
mmainstruction which allows performing matrix multiply-and-accumulate operation.
Deprecated Features
PTX ISA version 6.4 deprecates the following features:
Support for
.satfinitequalifier on floating pointwmma.mmainstruction.
Removed Features
PTX ISA version 6.4 removes the following features:
Support for
shflandvoteinstructions without the.syncqualifier has been removed for.targetsm_70and higher. This support was deprecated since PTX ISA version 6.0 as documented in PTX ISA version 6.2.
Semantic Changes and Clarifications
Clarified that resolving references of a
.weaksymbol considers only.weakor.visiblesymbols with the same name and does not consider local symbols with the same name.Clarified that in
cvtinstruction, modifier.ftzcan only be specified when either.atypeor.dtypeis.f32.
12.17. Changes in PTX ISA Version 6.3
New Features
PTX ISA version 6.3 introduces the following new features:
Support for
sm_75target architecture.Adds support for a new instruction
nanosleepthat suspends a thread for a specified duration.Adds support for
.aliasdirective which allows definining alias to function symbol.Extends
atominstruction to perform.f16addition operation and.cas.b16operation.Extends
redinstruction to perform.f16addition operation.The
wmmainstructions are extended to support multiplicand matrices of type.s8,.u8,.s4,.u4,.b1and accumulator matrices of type.s32.
Semantic Changes and Clarifications
Introduced the mandatory
.alignedqualifier for allwmmainstructions.Specified the alignment required for the base address and stride parameters passed to
wmma.loadandwmma.store.Clarified that layout of fragment returned by
wmmaoperation is architecture dependent and passingwmmafragments around functions compiled for different link compatible SM architectures may not work as expected.Clarified that atomicity for
{atom/red}.f16x2}operations is guranteed separately for each of the two.f16elements but not guranteed to be atomic as single 32-bit access.
12.18. Changes in PTX ISA Version 6.2
New Features
PTX ISA version 6.2 introduces the following new features:
A new instruction
activemaskfor querying active threads in a warp.Extends atomic and reduction instructions to perform
.f16x2addition operation with mandatory.noftzqualifier.
Deprecated Features
PTX ISA version 6.2 deprecates the following features:
The use of
shflandvoteinstructions without the.syncis deprecated retrospectively from PTX ISA version 6.0, which introduced thesm_70architecture that implements Independent Thread Scheduling.
Semantic Changes and Clarifications
Clarified that
wmmainstructions can be used in conditionally executed code only if it is known that all threads in the warp evaluate the condition identically, otherwise behavior is undefined.In the memory consistency model, the definition of morally strong operations was updated to exclude fences from the requirement of complete overlap since fences do not access memory.
12.19. Changes in PTX ISA Version 6.1
New Features
PTX ISA version 6.1 introduces the following new features:
Support for
sm_72target architecture.Support for new matrix shapes
32x8x16and8x32x16inwmmainstruction.
Semantic Changes and Clarifications
None.
12.20. Changes in PTX ISA Version 6.0
New Features
PTX ISA version 6.0 introduces the following new features:
Support for
sm_70target architecture.Specifies the memory consistency model for programs running on
sm_70and later architectures.Various extensions to memory instructions to specify memory synchronization semantics and scopes at which such synchronization can be observed.
New instruction
wmmafor matrix operations which allows loading matrices from memory, performing multiply-and-accumulate on them and storing result in memory.Support for new
barrierinstruction.Extends
neginstruction to support.f16and.f16x2types.A new instruction
fnswhich allows finding n-th set bit in integer.A new instruction
bar.warp.syncwhich allows synchronizing threads in warp.Extends
voteandshflinstructions with.syncmodifier which waits for specified threads before executing thevoteandshfloperation respectively.A new instruction
match.syncwhich allows broadcasting and comparing a value across threads in warp.A new instruction
brx.idxwhich allows branching to a label indexed from list of potential targets.Support for unsized array parameter for
.funcwhich can be used to implement variadic functions.Support for
.b16integer type in dwarf-lines.Support for taking address of device function return parameters using
movinstruction.
Semantic Changes and Clarifications
Semantics of
barinstruction were updated to indicate that executing thread waits for other non-exited threads from it’s warp.Support for indirect branch introduced in PTX 2.1 which was unimplemented has been removed from the spec.
Support for taking address of labels, using labels in initializers which was unimplemented has been removed from the spec.
Support for variadic functions which was unimplemented has been removed from the spec.
12.21. Changes in PTX ISA Version 5.0
New Features
PTX ISA version 5.0 introduces the following new features:
Support for
sm_60,sm_61,sm_62target architecture.Extends atomic and reduction instructions to perform double-precision add operation.
Extends atomic and reduction instructions to specify
scopemodifier.A new
.commondirective to permit linking multiple object files containing declarations of the same symbol with different size.A new
dp4ainstruction which allows 4-way dot product with accumulate operation.A new
dp2ainstruction which allows 2-way dot product with accumulate operation.Support for special register
%clock_hi.
Semantic Changes and Clarifications
Semantics of cache modifiers on ld and st instructions were clarified to reflect cache
operations are treated as performance hint only and do not change memory consistency behavior of the
program.
Semantics of volatile operations on ld and st instructions were clarified to reflect how
volatile operations are handled by optimizing compiler.
12.22. Changes in PTX ISA Version 4.3
New Features
PTX ISA version 4.3 introduces the following new features:
A new
lop3instruction which allows arbitrary logical operation on 3 inputs.Adds support for 64-bit computations in extended precision arithmetic instructions.
Extends
tex.gradinstruction to supportcubeandacubegeometries.Extends
tld4instruction to supporta2d,cubeandacubegeometries.Extends
texandtld4instructions to support optional operands for offset vector and depth compare.Extends
txqinstruction to support querying texture fields from specific LOD.
Semantic Changes and Clarifications
None.
12.23. Changes in PTX ISA Version 4.2
New Features
PTX ISA version 4.2 introduces the following new features:
Support for
sm_53target architecture.Support for arithmetic, comparsion and texture instructions for
.f16and.f16x2types.Support for
memory_layoutfield for surfaces andsuqinstruction support for querying this field.
Semantic Changes and Clarifications
Semantics for parameter passing under ABI were updated to indicate ld.param and st.param
instructions used for argument passing cannot be predicated.
Semantics of {atom/red}.add.f32 were updated to indicate subnormal inputs and results are
flushed to sign-preserving zero for atomic operations on global memory; whereas atomic operations on
shared memory preserve subnormal inputs and results and don’t flush them to zero.
12.24. Changes in PTX ISA Version 4.1
New Features
PTX ISA version 4.1 introduces the following new features:
Support for
sm_37andsm_52target architectures.Support for new fields
array_size,num_mipmap_levelsandnum_samplesfor Textures, and thetxqinstruction support for querying these fields.Support for new field
array_sizefor Surfaces, and thesuqinstruction support for querying this field.Support for special registers
%total_smem_sizeand%dynamic_smem_size.
Semantic Changes and Clarifications
None.
12.25. Changes in PTX ISA Version 4.0
New Features
PTX ISA version 4.0 introduces the following new features:
Support for
sm_32andsm_50target architectures.Support for 64bit performance counter special registers
%pm0_64,..,%pm7_64.A new
istypepinstruction.A new instruction,
rsqrt.approx.ftz.f64has been added to compute a fast approximation of the square root reciprocal of a value.Support for a new directive
.attributefor specifying special attributes of a variable.Support for
.managedvariable attribute.
Semantic Changes and Clarifications
The vote instruction semantics were updated to clearly indicate that an inactive thread in a
warp contributes a 0 for its entry when participating in vote.ballot.b32.
12.26. Changes in PTX ISA Version 3.2
New Features
PTX ISA version 3.2 introduces the following new features:
The texture instruction supports reads from multi-sample and multisample array textures.
Extends
.sectiondebugging directive to include label + immediate expressions.Extends
.filedirective to include timestamp and file size information.
Semantic Changes and Clarifications
The vavrg2 and vavrg4 instruction semantics were updated to indicate that instruction adds 1
only if Va[i] + Vb[i] is non-negative, and that the addition result is shifted by 1 (rather than
being divided by 2).
12.27. Changes in PTX ISA Version 3.1
New Features
PTX ISA version 3.1 introduces the following new features:
Support for
sm_35target architecture.Support for CUDA Dynamic Parallelism, which enables a kernel to create and synchronize new work.
ld.global.ncfor loading read-only global data though the non-coherent texture cache.A new funnel shift instruction,
shf.Extends atomic and reduction instructions to perform 64-bit
{and, or, xor}operations, and 64-bit integer{min, max}operations.Adds support for
mipmaps.Adds support for indirect access to textures and surfaces.
Extends support for generic addressing to include the
.conststate space, and adds a new operator,generic(), to form a generic address for.globalor.constvariables used in initializers.A new
.weakdirective to permit linking multiple object files containing declarations of the same symbol.
Semantic Changes and Clarifications
PTX 3.1 redefines the default addressing for global variables in initializers, from generic
addresses to offsets in the global state space. Legacy PTX code is treated as having an implicit
generic() operator for each global variable used in an initializer. PTX 3.1 code should either
include explicit generic() operators in initializers, use cvta.global to form generic
addresses at runtime, or load from the non-generic address using ld.global.
Instruction mad.f32 requires a rounding modifier for sm_20 and higher targets. However for
PTX ISA version 3.0 and earlier, ptxas does not enforce this requirement and mad.f32 silently
defaults to mad.rn.f32. For PTX ISA version 3.1, ptxas generates a warning and defaults to
mad.rn.f32, and in subsequent releases ptxas will enforce the requirement for PTX ISA version
3.2 and later.
12.28. Changes in PTX ISA Version 3.0
New Features
PTX ISA version 3.0 introduces the following new features:
Support for
sm_30target architectures.SIMD video instructions.
A new warp shuffle instruction.
Instructions
mad.ccandmadcfor efficient, extended-precision integer multiplication.Surface instructions with 3D and array geometries.
The texture instruction supports reads from cubemap and cubemap array textures.
Platform option
.targetdebug to declare that a PTX module containsDWARFdebug information.pmevent.mask, for triggering multiple performance monitor events.Performance monitor counter special registers
%pm4..%pm7.
Semantic Changes and Clarifications
Special register %gridid has been extended from 32-bits to 64-bits.
PTX ISA version 3.0 deprecates module-scoped .reg and .local variables when compiling to the
Application Binary Interface (ABI). When compiling without use of the ABI, module-scoped .reg
and .local variables are supported as before. When compiling legacy PTX code (ISA versions prior
to 3.0) containing module-scoped .reg or .local variables, the compiler silently disables
use of the ABI.
The shfl instruction semantics were updated to clearly indicate that value of source operand
a is unpredictable for inactive and predicated-off threads within the warp.
PTX modules no longer allow duplicate .version directives. This feature was unimplemented, so
there is no semantic change.
Unimplemented instructions suld.p and sust.p.{u32,s32,f32} have been removed.
12.29. Changes in PTX ISA Version 2.3
New Features
PTX 2.3 adds support for texture arrays. The texture array feature supports access to an array of 1D or 2D textures, where an integer indexes into the array of textures, and then one or two single-precision floating point coordinates are used to address within the selected 1D or 2D texture.
PTX 2.3 adds a new directive, .address_size, for specifying the size of addresses.
Variables in .const and .global state spaces are initialized to zero by default.
Semantic Changes and Clarifications
The semantics of the .maxntid directive have been updated to match the current
implementation. Specifically, .maxntid only guarantees that the total number of threads in a
thread block does not exceed the maximum. Previously, the semantics indicated that the maximum was
enforced separately in each dimension, which is not the case.
Bit field extract and insert instructions BFE and BFI now indicate that the len and pos
operands are restricted to the value range 0..255.
Unimplemented instructions {atom,red}.{min,max}.f32 have been removed.
12.30. Changes in PTX ISA Version 2.2
New Features
PTX 2.2 adds a new directive for specifying kernel parameter attributes; specifically, there is a new directives for specifying that a kernel parameter is a pointer, for specifying to which state space the parameter points, and for optionally specifying the alignment of the memory to which the parameter points.
PTX 2.2 adds a new field named force_unnormalized_coords to the .samplerref opaque
type. This field is used in the independent texturing mode to override the normalized_coords
field in the texture header. This field is needed to support languages such as OpenCL, which
represent the property of normalized/unnormalized coordinates in the sampler header rather than in
the texture header.
PTX 2.2 deprecates explicit constant banks and supports a large, flat address space for the
.const state space. Legacy PTX that uses explicit constant banks is still supported.
PTX 2.2 adds a new tld4 instruction for loading a component (r, g, b, or a) from
the four texels compising the bilinear interpolation footprint of a given texture location. This
instruction may be used to compute higher-precision bilerp results in software, or for performing
higher-bandwidth texture loads.
Semantic Changes and Clarifications
None.
12.31. Changes in PTX ISA Version 2.1
New Features
The underlying, stack-based ABI is supported in PTX ISA version 2.1 for sm_2x targets.
Support for indirect calls has been implemented for sm_2x targets.
New directives, .branchtargets and .calltargets, have been added for specifying potential
targets for indirect branches and indirect function calls. A .callprototype directive has been
added for declaring the type signatures for indirect function calls.
The names of .global and .const variables can now be specified in variable initializers to
represent their addresses.
A set of thirty-two driver-specific execution environment special registers has been added. These
are named %envreg0..%envreg31.
Textures and surfaces have new fields for channel data type and channel order, and the txq and
suq instructions support queries for these fields.
Directive .minnctapersm has replaced the .maxnctapersm directive.
Directive .reqntid has been added to allow specification of exact CTA dimensions.
A new instruction, rcp.approx.ftz.f64, has been added to compute a fast, gross approximate
reciprocal.
Semantic Changes and Clarifications
A warning is emitted if .minnctapersm is specified without also specifying .maxntid.
12.32. Changes in PTX ISA Version 2.0
New Features
Floating Point Extensions
This section describes the floating-point changes in PTX ISA version 2.0 for sm_20 targets. The
goal is to achieve IEEE 754 compliance wherever possible, while maximizing backward compatibility
with legacy PTX ISA version 1.x code and sm_1x targets.
The changes from PTX ISA version 1.x are as follows:
Single-precision instructions support subnormal numbers by default for
sm_20targets. The.ftzmodifier may be used to enforce backward compatibility withsm_1x.Single-precision
add,sub, andmulnow support.rmand.rprounding modifiers forsm_20targets.A single-precision fused multiply-add (fma) instruction has been added, with support for IEEE 754 compliant rounding modifiers and support for subnormal numbers. The
fma.f32instruction also supports.ftzand.satmodifiers.fma.f32requiressm_20. Themad.f32instruction has been extended with rounding modifiers so that it’s synonymous withfma.f32forsm_20targets. Bothfma.f32andmad.f32require a rounding modifier forsm_20targets.The
mad.f32instruction without rounding is retained so that compilers can generate code forsm_1xtargets. When code compiled forsm_1xis executed onsm_20devices,mad.f32maps tofma.rn.f32.Single- and double-precision
div,rcp, andsqrtwith IEEE 754 compliant rounding have been added. These are indicated by the use of a rounding modifier and requiresm_20.Instructions
testpandcopysignhave been added.
New Instructions
A load uniform instruction, ldu, has been added.
Surface instructions support additional .clamp modifiers, .clamp and .zero.
Instruction sust now supports formatted surface stores.
A count leading zeros instruction, clz, has been added.
A find leading non-sign bit instruction, bfind, has been added.
A bit reversal instruction, brev, has been added.
Bit field extract and insert instructions, bfe and bfi, have been added.
A population count instruction, popc, has been added.
A vote ballot instruction, vote.ballot.b32, has been added.
Instructions {atom,red}.add.f32 have been implemented.
Instructions {atom,red}.shared have been extended to handle 64-bit data types for sm_20
targets.
A system-level membar instruction, membar.sys, has been added.
The bar instruction has been extended as follows:
A
bar.arriveinstruction has been added.Instructions
bar.red.popc.u32andbar.red.{and,or}.predhave been added.barnow supports optional thread count and register operands.
Scalar video instructions (includes prmt) have been added.
Instruction isspacep for querying whether a generic address falls within a specified state space
window has been added.
Instruction cvta for converting global, local, and shared addresses to generic address and
vice-versa has been added.
Other New Features
Instructions ld, ldu, st, prefetch, prefetchu, isspacep, cvta, atom,
and red now support generic addressing.
New special registers %nwarpid, %nsmid, %clock64, %lanemask_{eq,le,lt,ge,gt} have
been added.
Cache operations have been added to instructions ld, st, suld, and sust, e.g., for
prefetching to specified level of memory hierarchy. Instructions prefetch and prefetchu
have also been added.
The .maxnctapersm directive was deprecated and replaced with .minnctapersm to better match
its behavior and usage.
A new directive, .section, has been added to replace the @@DWARF syntax for passing
DWARF-format debugging information through PTX.
A new directive, .pragma nounroll, has been added to allow users to disable loop unrolling.
Semantic Changes and Clarifications
The errata in cvt.ftz for PTX ISA versions 1.4 and earlier, where single-precision subnormal
inputs and results were not flushed to zero if either source or destination type size was 64-bits,
has been fixed. In PTX ISA version 1.5 and later, cvt.ftz (and cvt for .target sm_1x,
where .ftz is implied) instructions flush single-precision subnormal inputs and results to
sign-preserving zero for all combinations of floating-point instruction types. To maintain
compatibility with legacy PTX code, if .version is 1.4 or earlier, single-precision subnormal inputs
and results are flushed to sign-preserving zero only when neither source nor destination type size
is 64-bits.
Components of special registers %tid, %ntid, %ctaid, and %nctaid have been extended
from 16-bits to 32-bits. These registers now have type .v4.u32.
The number of samplers available in independent texturing mode was incorrectly listed as thirty-two in PTX ISA version 1.5; the correct number is sixteen.
14. Descriptions of .pragma Strings
This section describes the .pragma strings defined by ptxas.
14.1. Pragma Strings: “nounroll”
“nounroll”
Disable loop unrolling in optimizing the backend compiler.
Syntax
.pragma "nounroll";
Description
The "nounroll" pragma is a directive to disable loop unrolling in the optimizing backend
compiler.
The "nounroll" pragma is allowed at module, entry-function, and statement levels, with the
following meanings:
- module scope
disables unrolling for all loops in module, including loops preceding the
.pragma.- entry-function scope
disables unrolling for all loops in the entry function body.
- statement-level pragma
disables unrolling of the loop for which the current block is the loop header.
Note that in order to have the desired effect at statement level, the "nounroll" directive must
appear before any instruction statements in the loop header basic block for the desired loop. The
loop header block is defined as the block that dominates all blocks in the loop body and is the
target of the loop backedge. Statement-level "nounroll" directives appearing outside of loop
header blocks are silently ignored.
PTX ISA Notes
Introduced in PTX ISA version 2.0.
Target ISA Notes
Requires sm_20 or higher. Ignored for sm_1x targets.
Examples
.entry foo (...)
.pragma "nounroll"; // do not unroll any loop in this function
{
...
}
.func bar (...)
{
...
L1_head:
.pragma "nounroll"; // do not unroll this loop
...
@p bra L1_end;
L1_body:
...
L1_continue:
bra L1_head;
L1_end:
...
}
14.2. Pragma Strings: “used_bytes_mask”
“used_bytes_mask”
Mask for indicating used bytes in data of ld operation.
Syntax
.pragma "used_bytes_mask mask";
Description
The "used_bytes_mask" pragma is a directive that specifies used bytes in a load
operation based on the mask provided.
"used_bytes_mask" pragma needs to be specified prior to a load instruction for which
information about bytes used from the load operation is needed.
Pragma is ignored if instruction following it is not a load instruction.
For a load instruction without this pragma, all bytes from the load operation are assumed to be used.
Operand mask is a 32-bit integer with set bits indicating the used bytes in data of
load operation.
Semantics
Each bit in mask operand corresponds to a byte data where each set bit represents the used byte.
Most-significant bit corresponds to most-significant byte of data.
// For 4 bytes load with only lower 3 bytes used
.pragma "used_bytes_mask 0x7";
ld.global.u32 %r0, [gbl]; // Higher 1 byte from %r0 is unused
// For vector load of 16 bytes with lower 12 bytes used
.pragma "used_bytes_mask 0xfff";
ld.global.v4.u32 {%r0, %r1, %r2, %r3}, [gbl]; // %r3 unused
PTX ISA Notes
Introduced in PTX ISA version 8.3.
Target ISA Notes
Requires sm_50 or higher.
Examples
.pragma "used_bytes_mask 0xfff";
ld.global.v4.u32 {%r0, %r1, %r2, %r3}, [gbl]; // Only lower 12 bytes used
15. Notices
15.1. Notice
This document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.
NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice.
Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.
NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgement, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.
NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk.
NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.
No license, either expressed or implied, is granted under any NVIDIA patent right, copyright, or other NVIDIA intellectual property right under this document. Information published by NVIDIA regarding third-party products or services does not constitute a license from NVIDIA to use such products or services or a warranty or endorsement thereof. Use of such information may require a license from a third party under the patents or other intellectual property rights of the third party, or a license from NVIDIA under the patents or other intellectual property rights of NVIDIA.
Reproduction of information in this document is permissible only if approved in advance by NVIDIA in writing, reproduced without alteration and in full compliance with all applicable export laws and regulations, and accompanied by all associated conditions, limitations, and notices.
THIS DOCUMENT AND ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, “MATERIALS”) ARE BEING PROVIDED “AS IS.” NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE. TO THE EXTENT NOT PROHIBITED BY LAW, IN NO EVENT WILL NVIDIA BE LIABLE FOR ANY DAMAGES, INCLUDING WITHOUT LIMITATION ANY DIRECT, INDIRECT, SPECIAL, INCIDENTAL, PUNITIVE, OR CONSEQUENTIAL DAMAGES, HOWEVER CAUSED AND REGARDLESS OF THE THEORY OF LIABILITY, ARISING OUT OF ANY USE OF THIS DOCUMENT, EVEN IF NVIDIA HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. Notwithstanding any damages that customer might incur for any reason whatsoever, NVIDIA’s aggregate and cumulative liability towards customer for the products described herein shall be limited in accordance with the Terms of Sale for the product.
15.2. OpenCL
OpenCL is a trademark of Apple Inc. used under license to the Khronos Group Inc.
15.3. Trademarks
NVIDIA and the NVIDIA logo are trademarks or registered trademarks of NVIDIA Corporation in the U.S. and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.
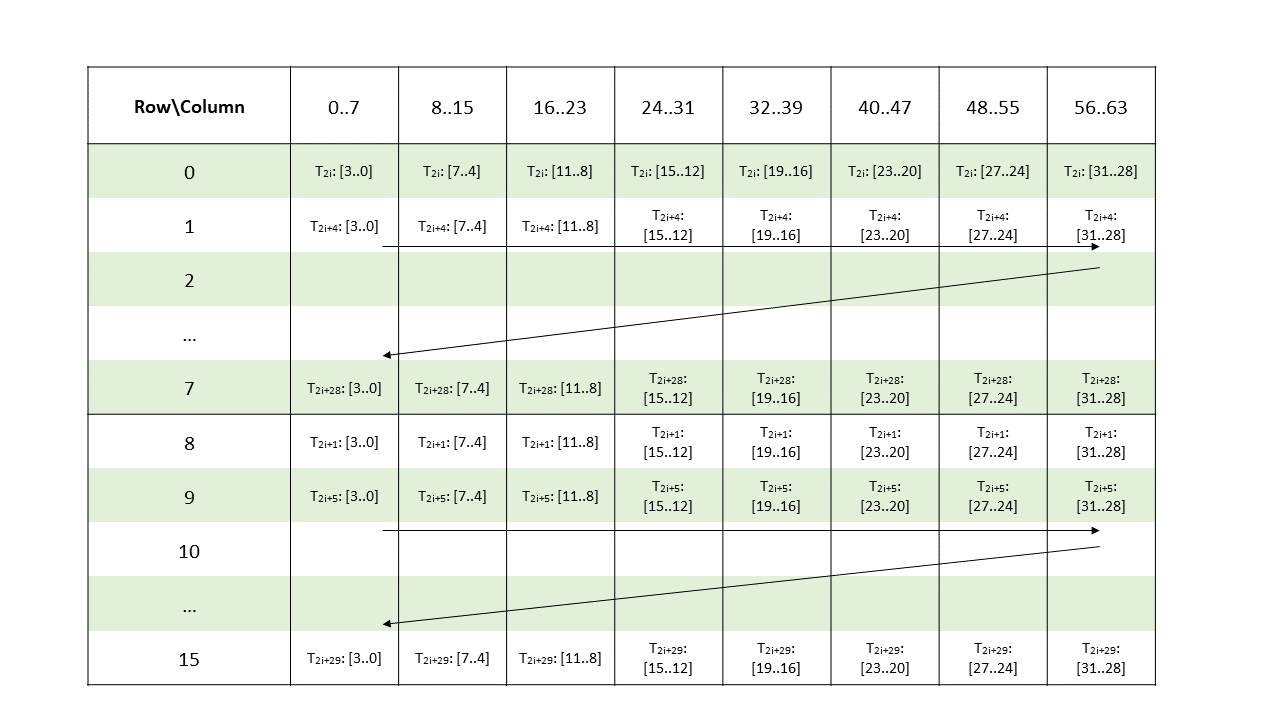
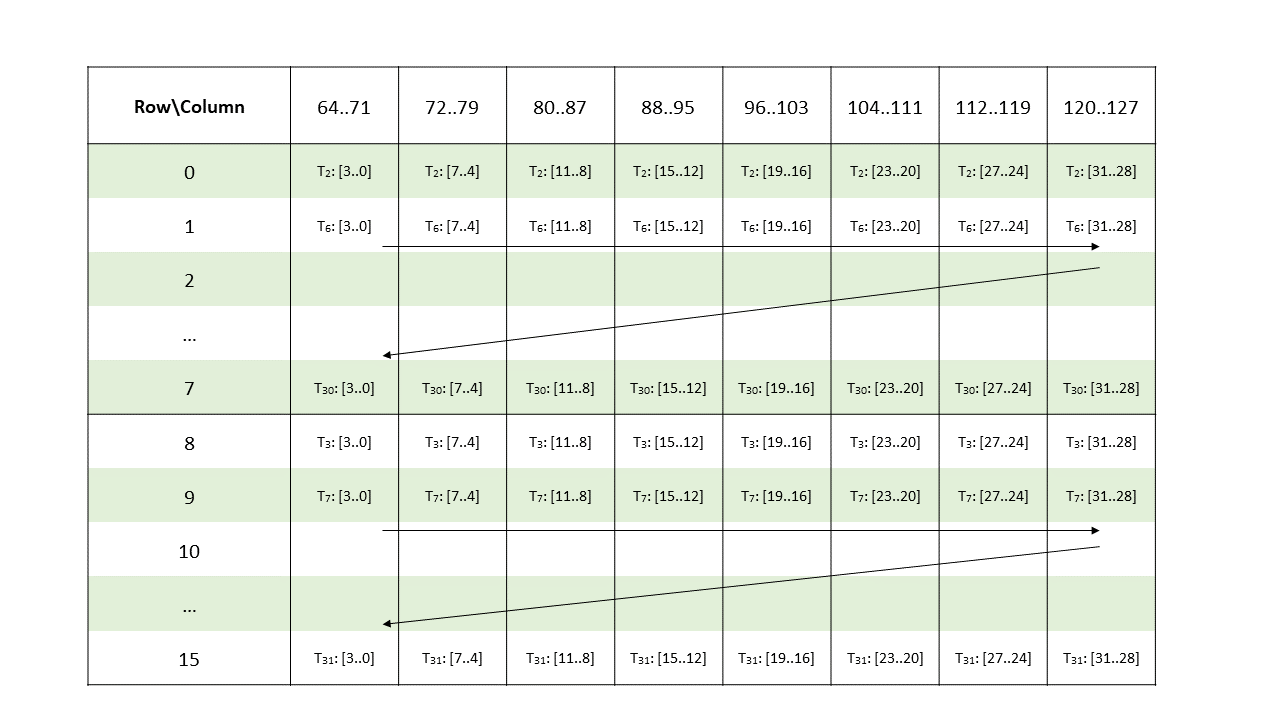
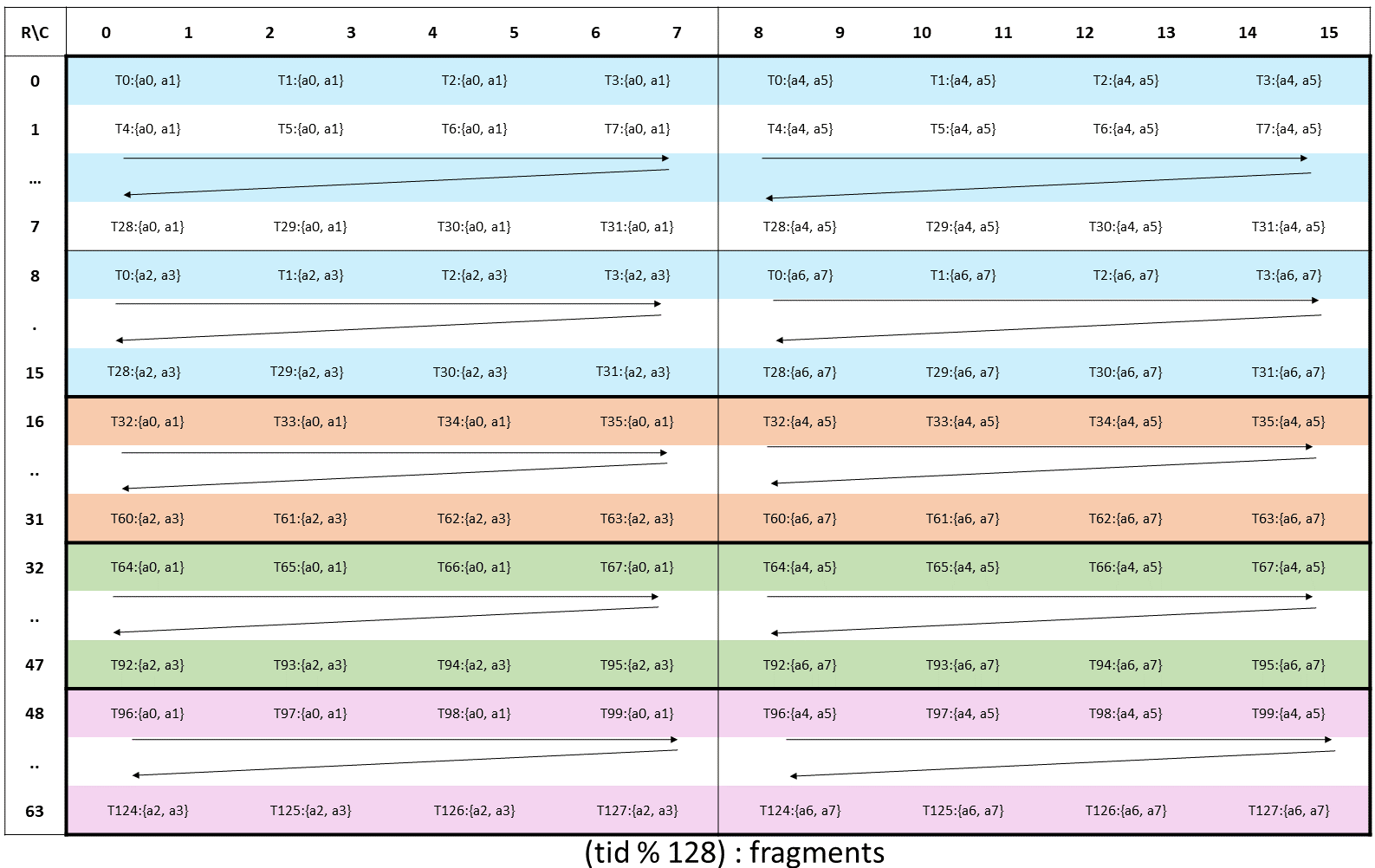
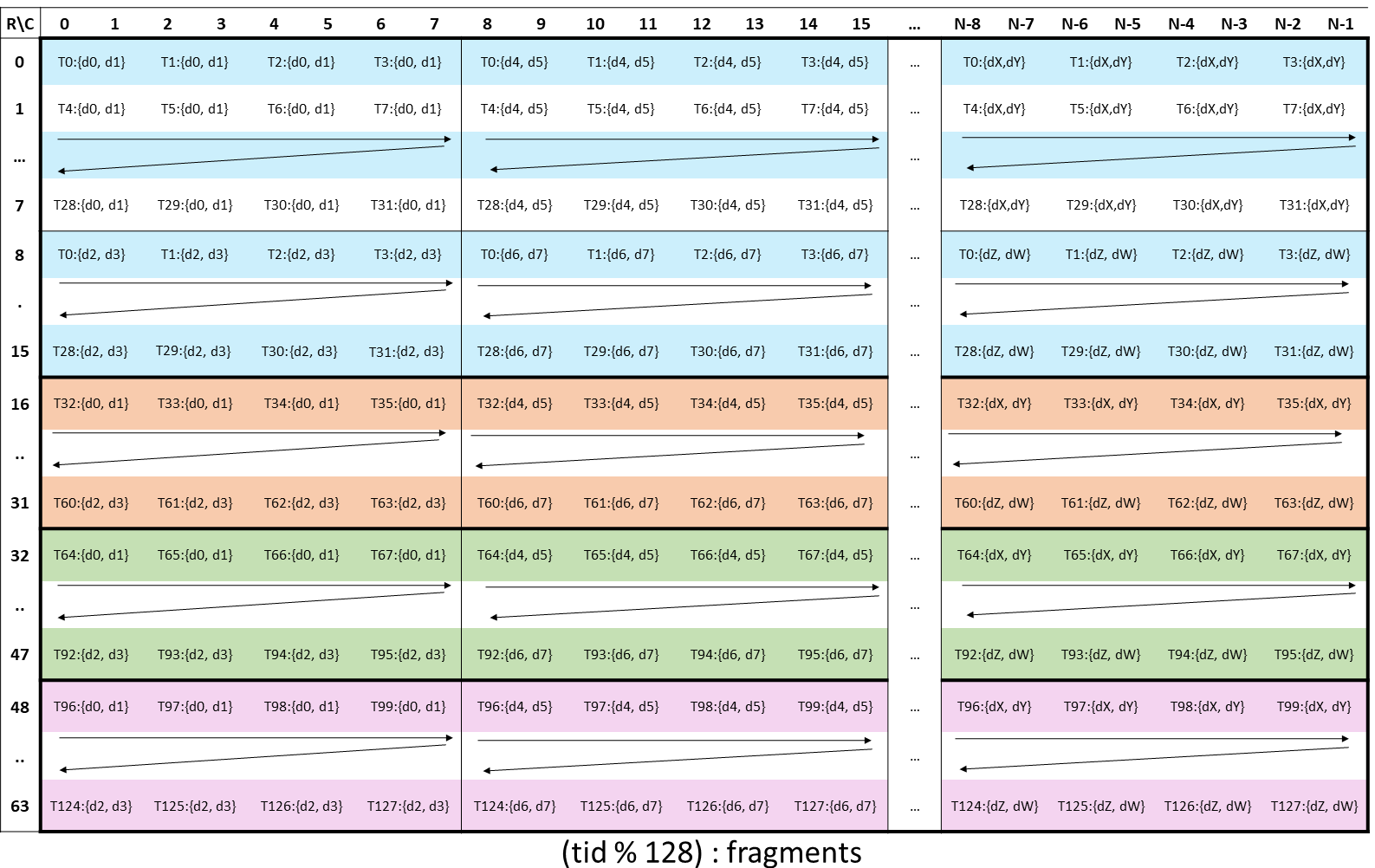

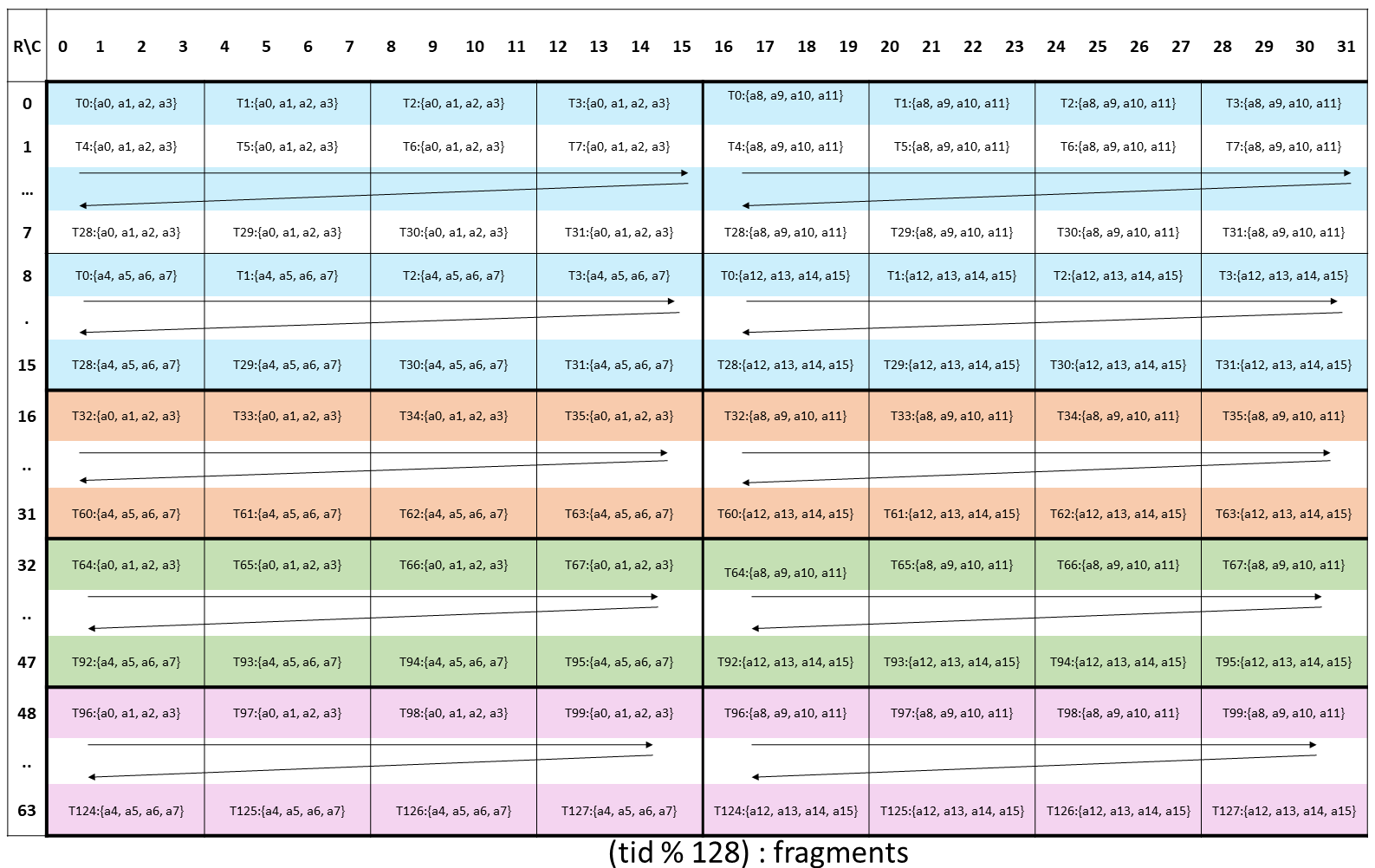
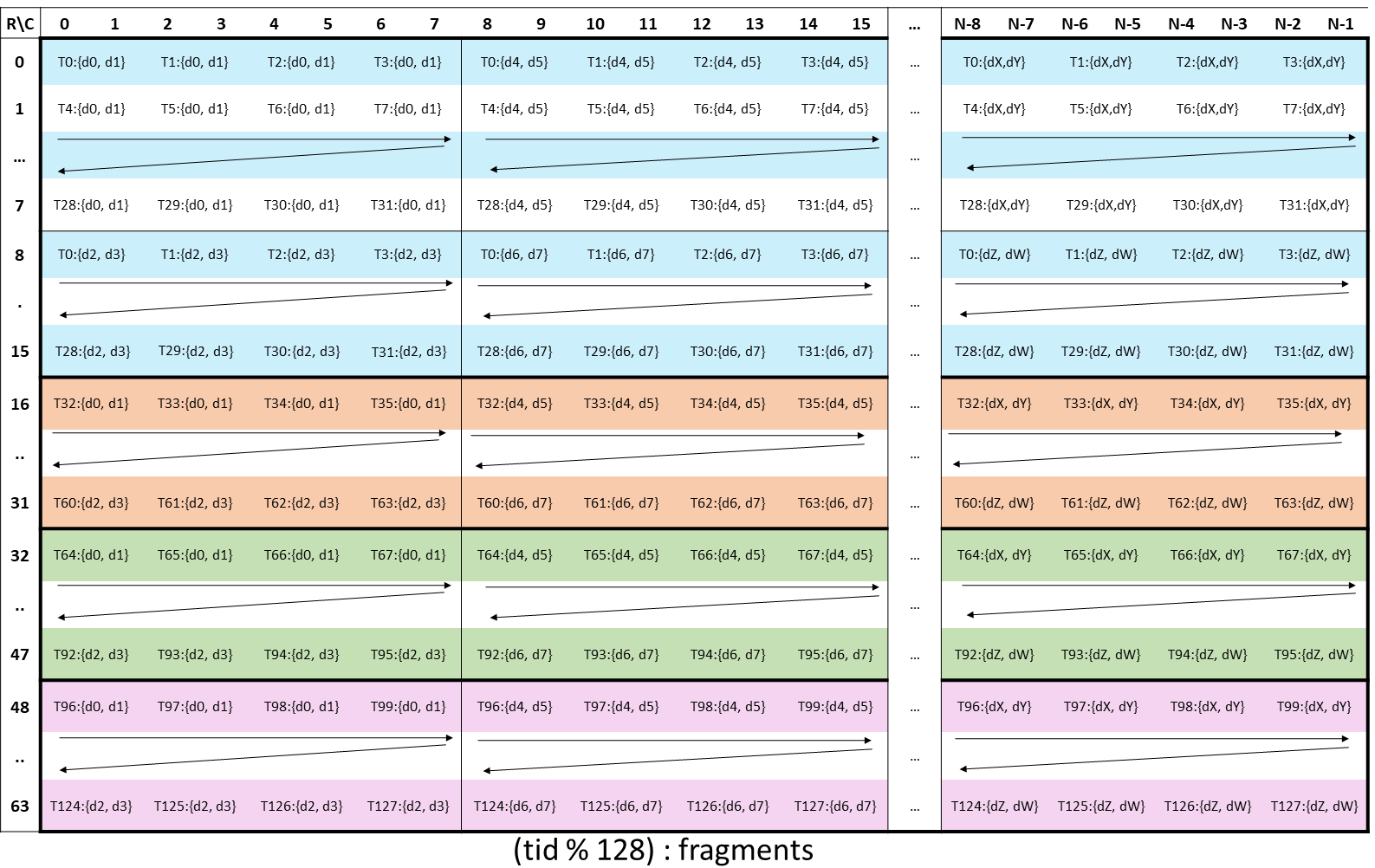


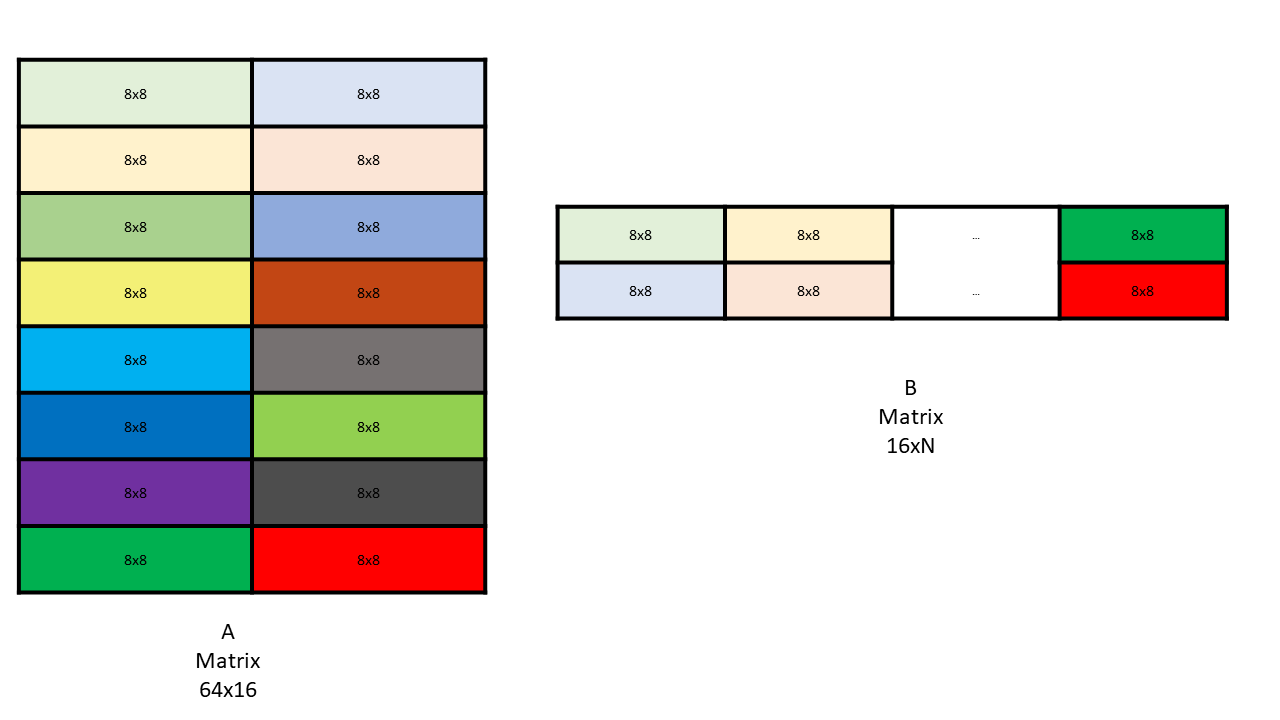
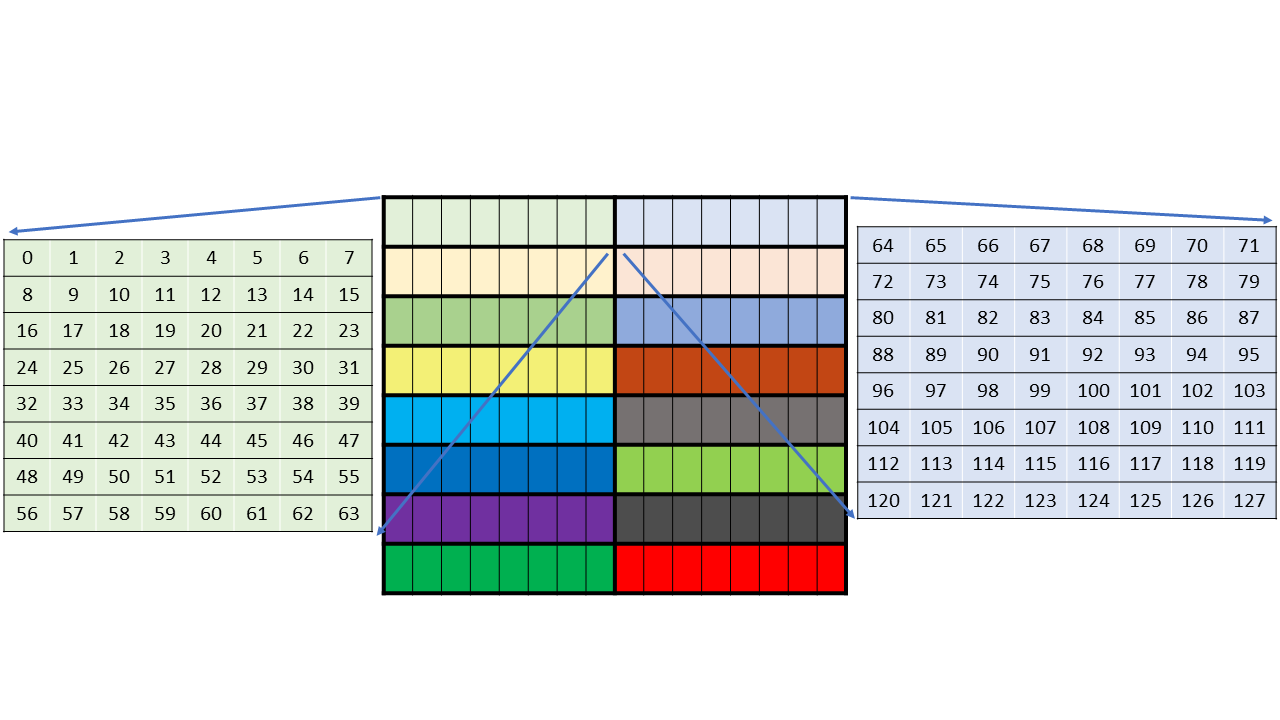
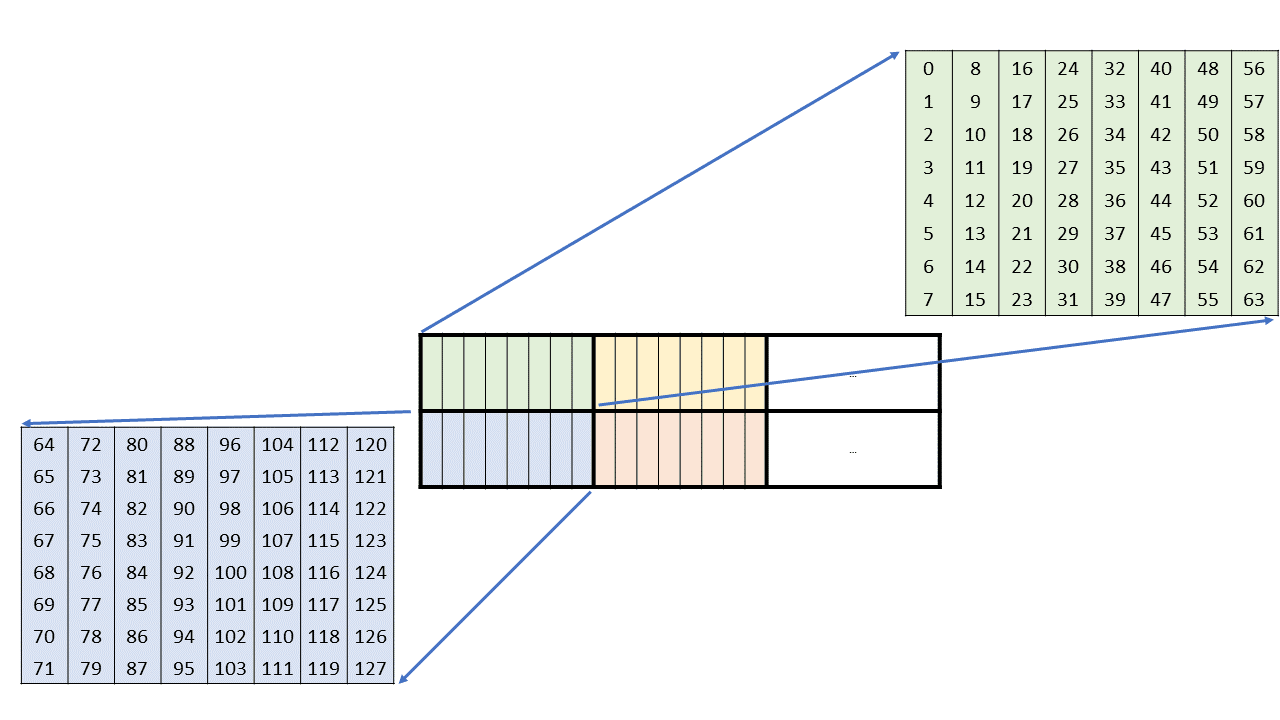
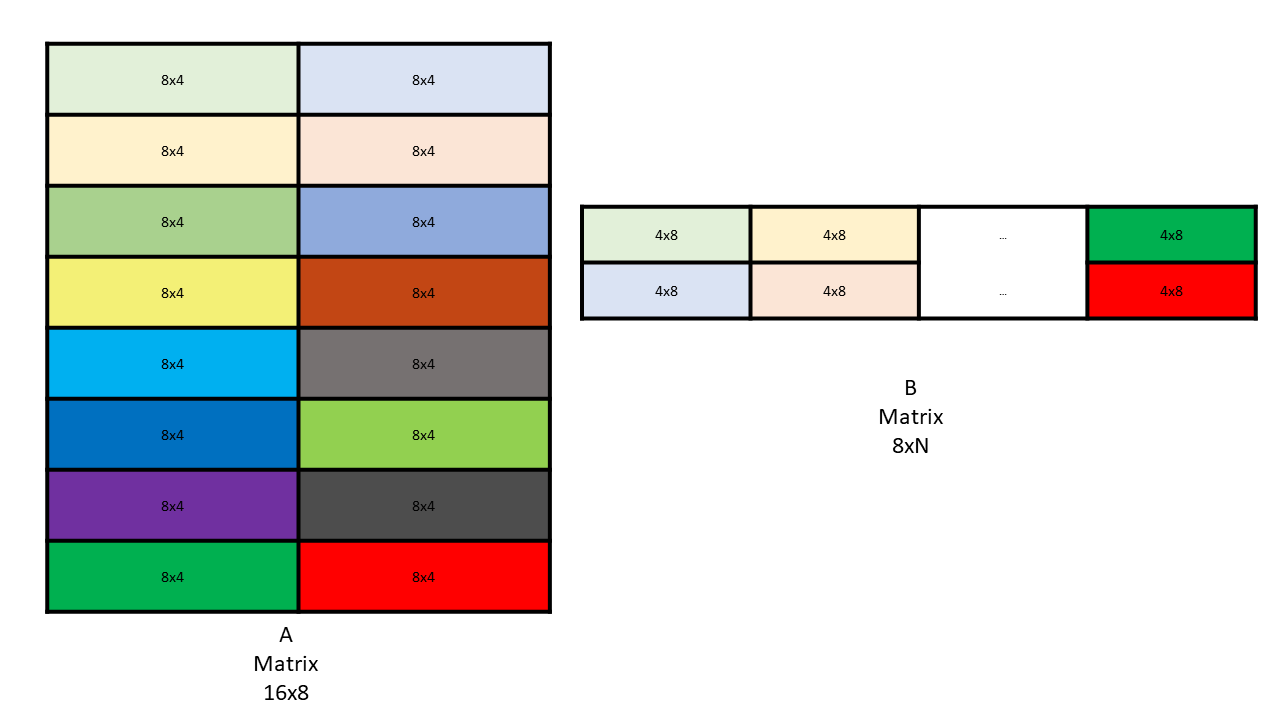
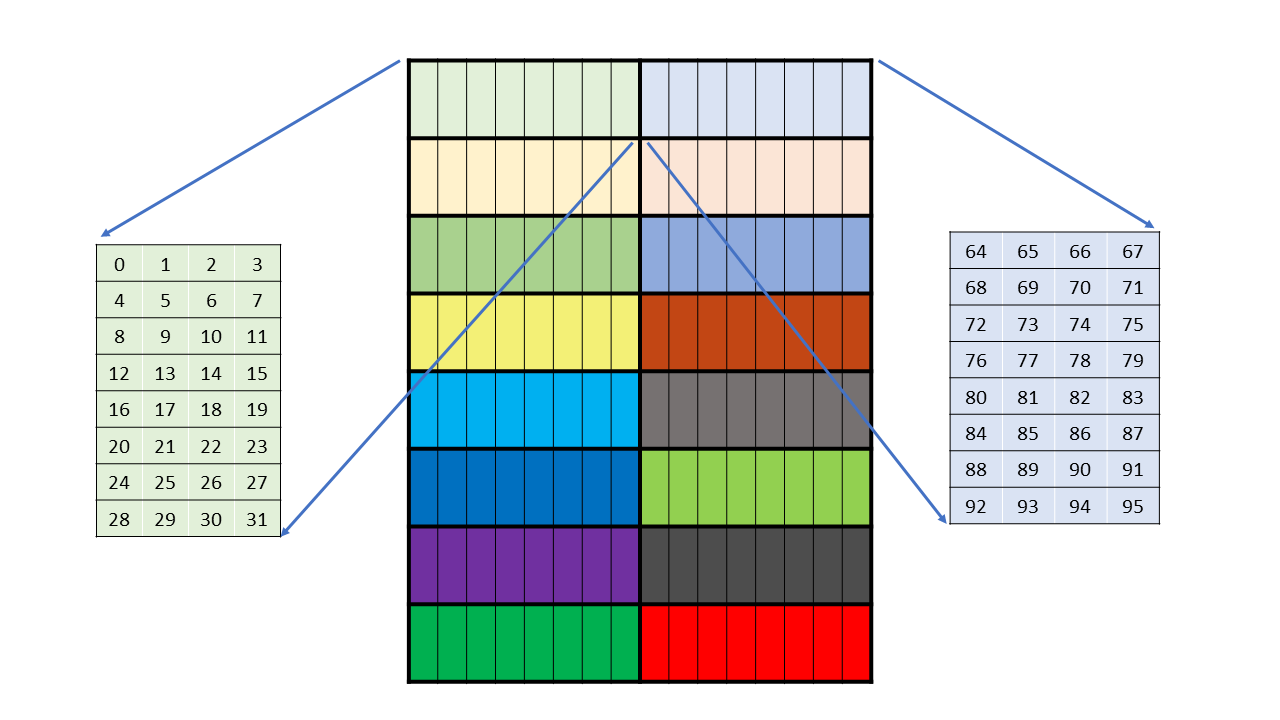
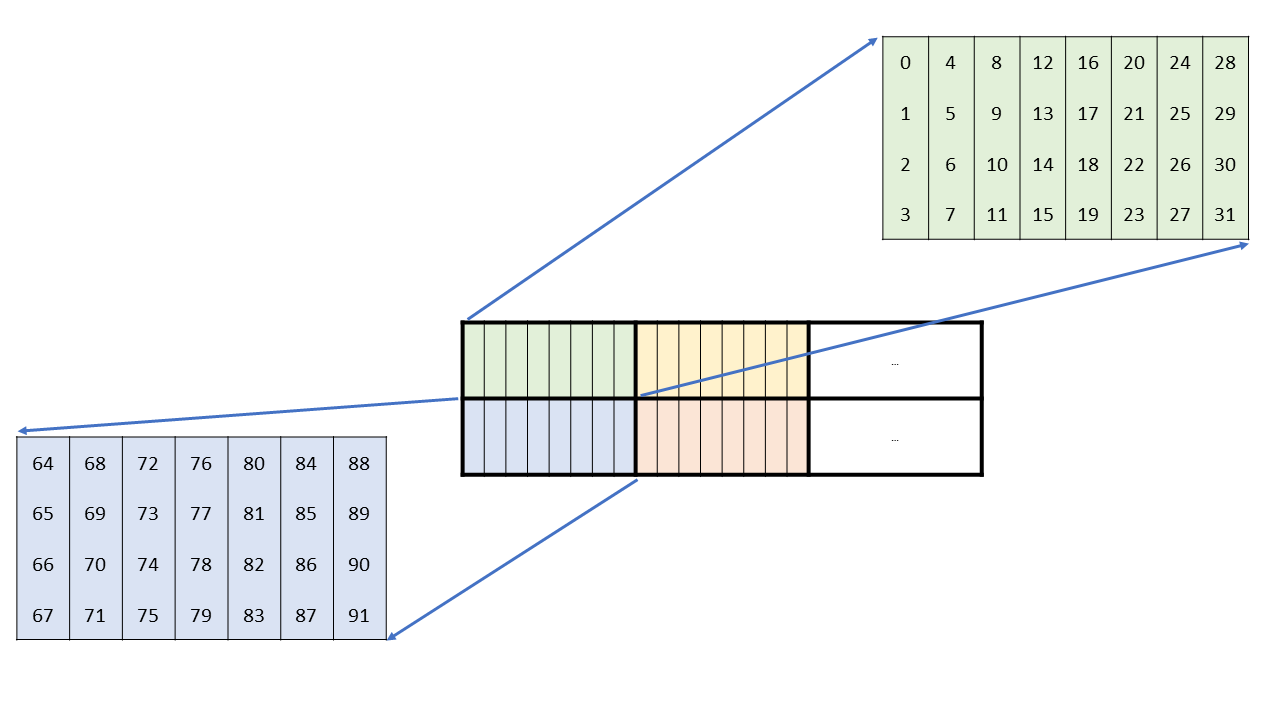
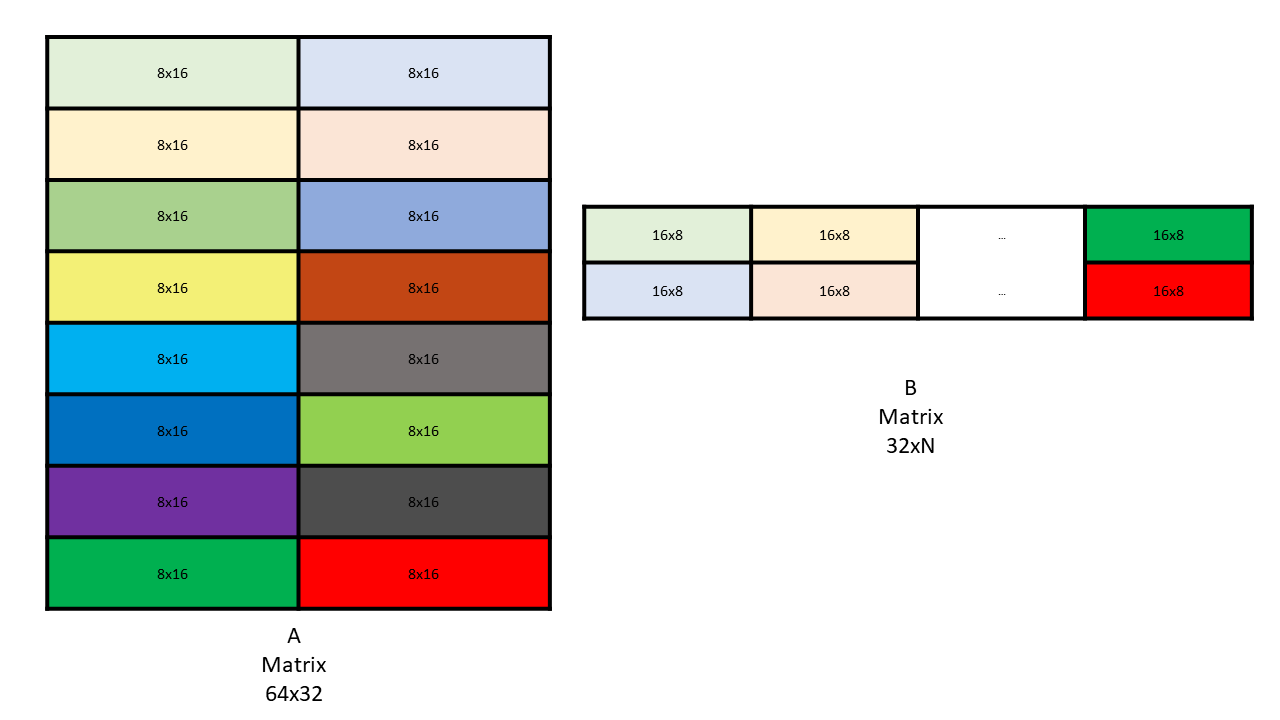
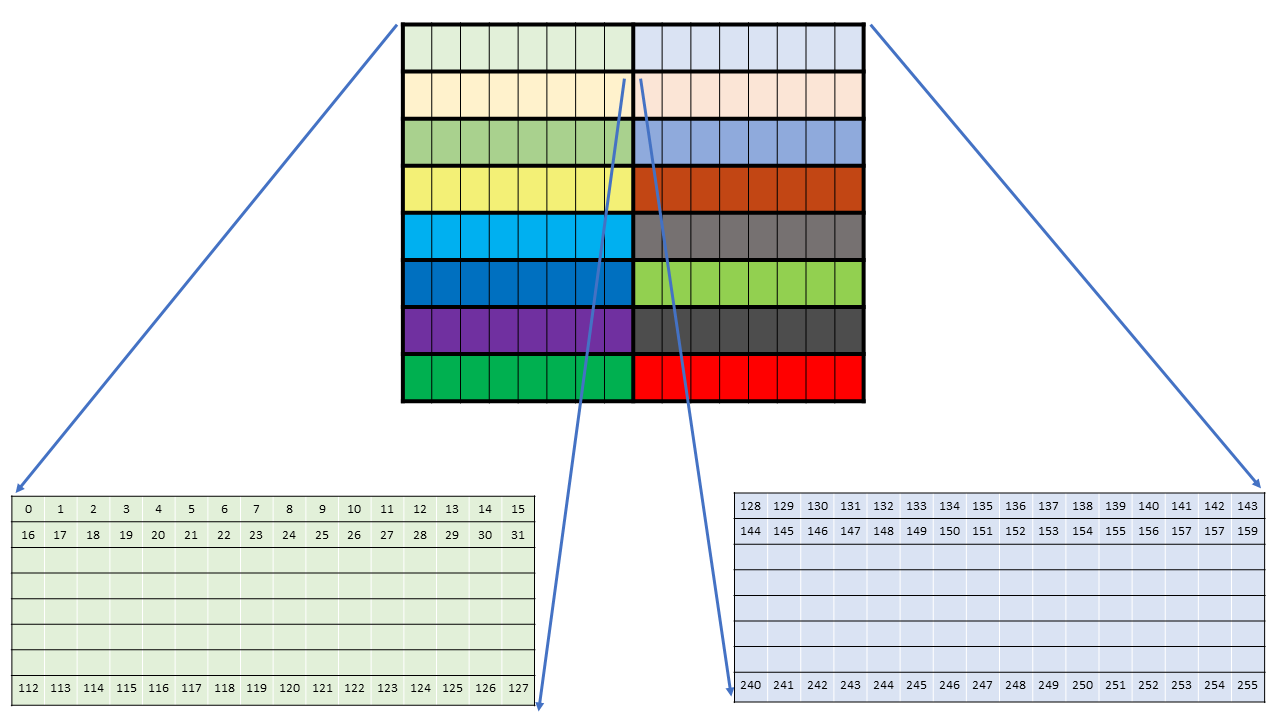
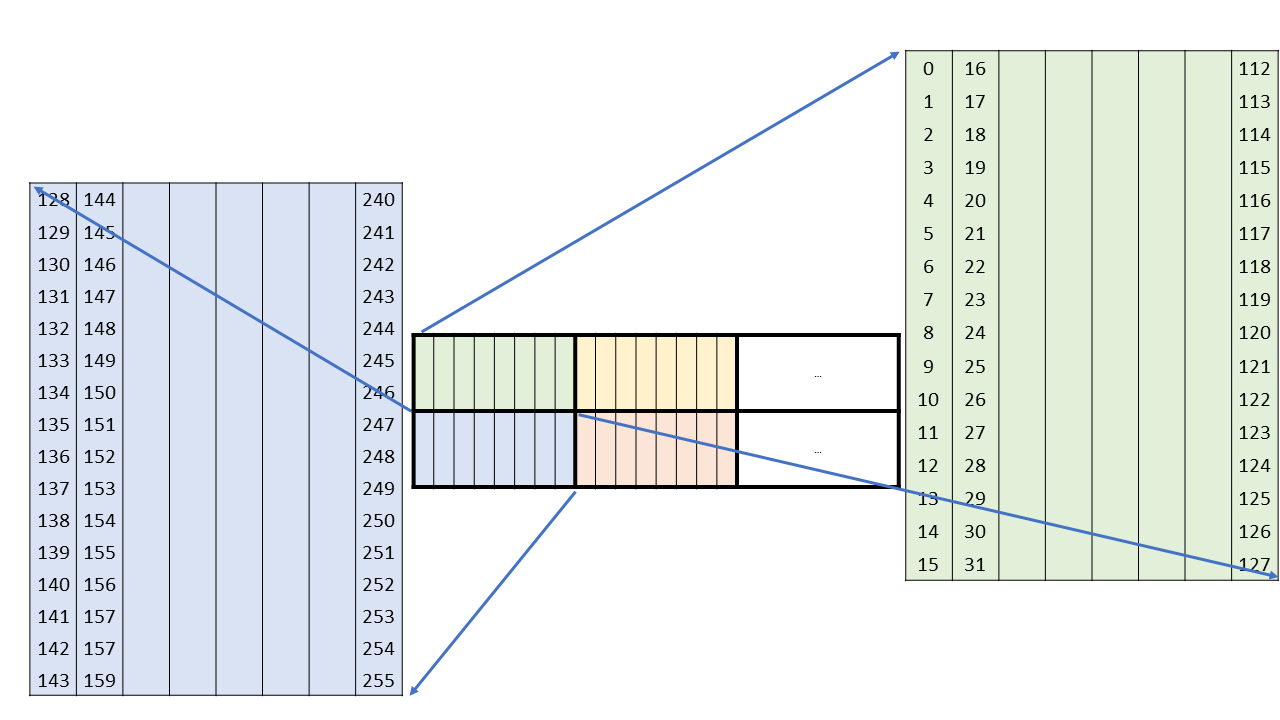
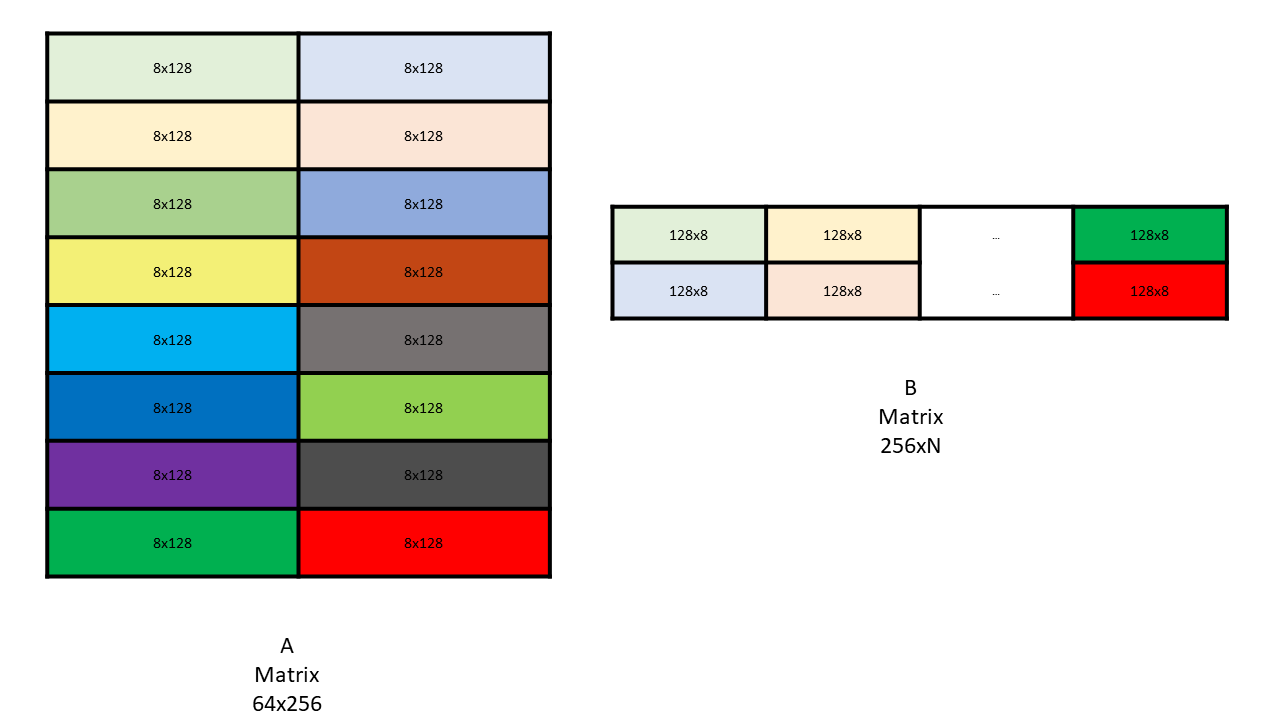
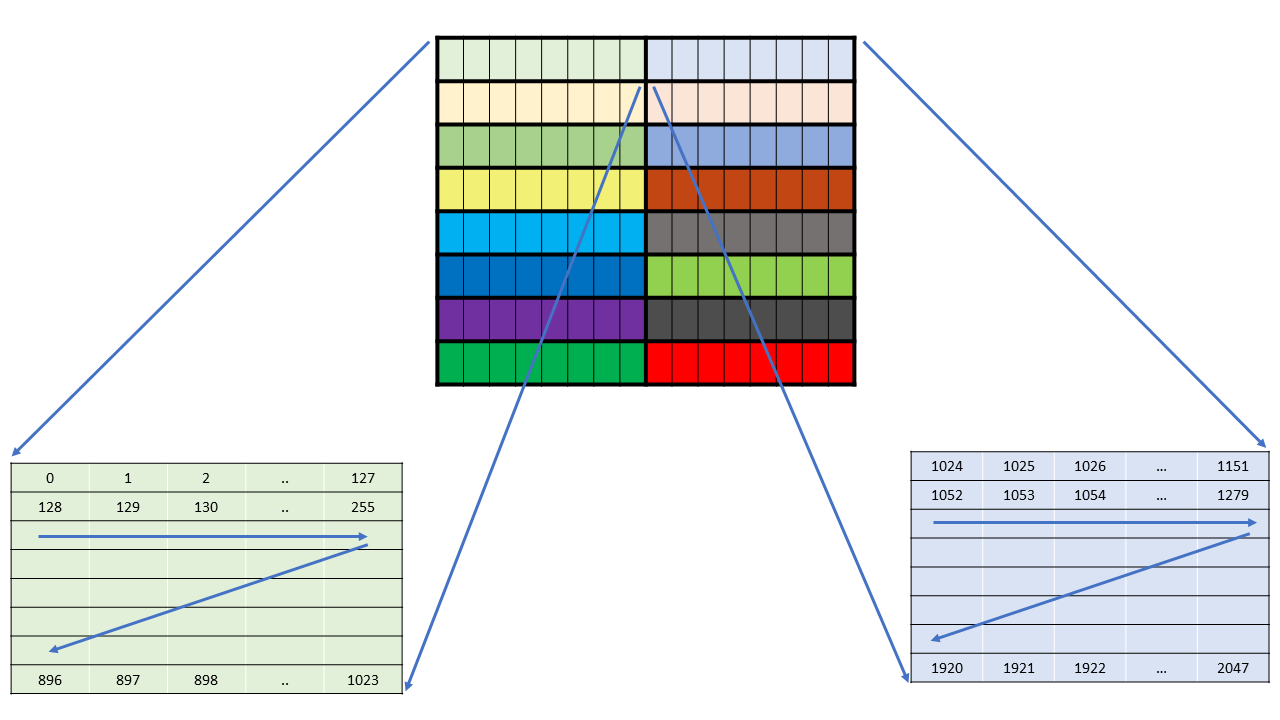
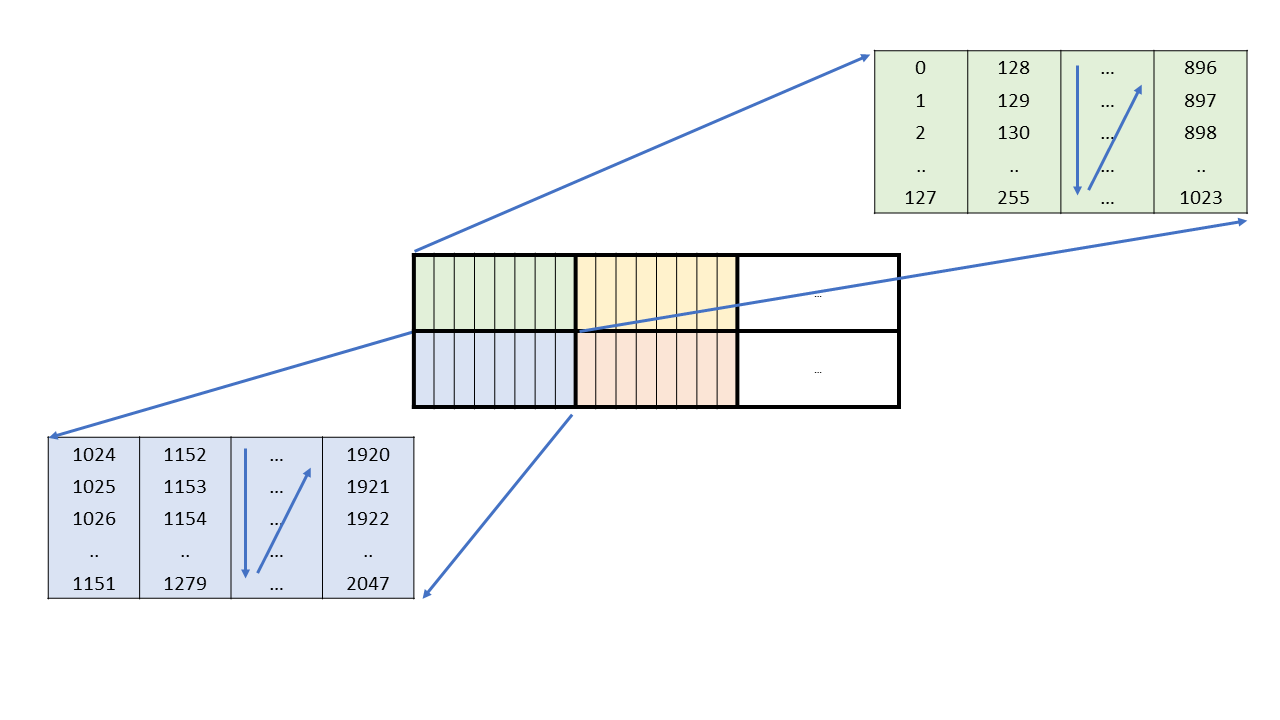
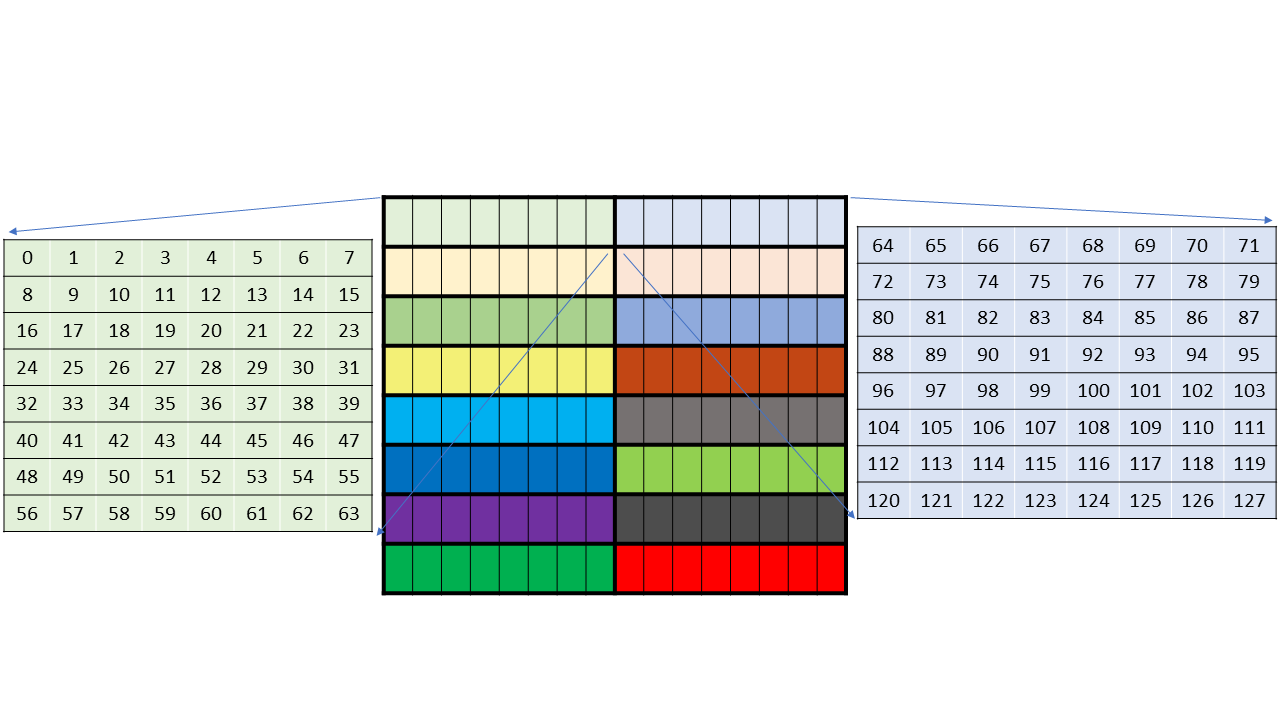
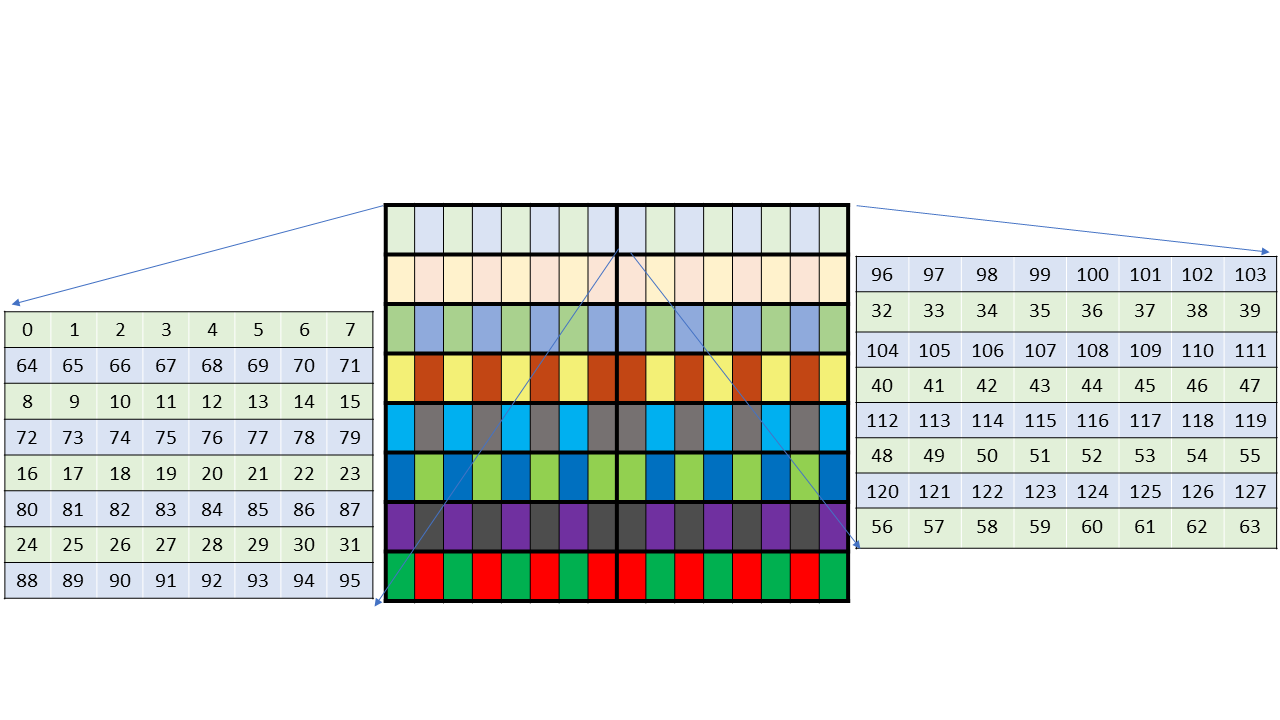
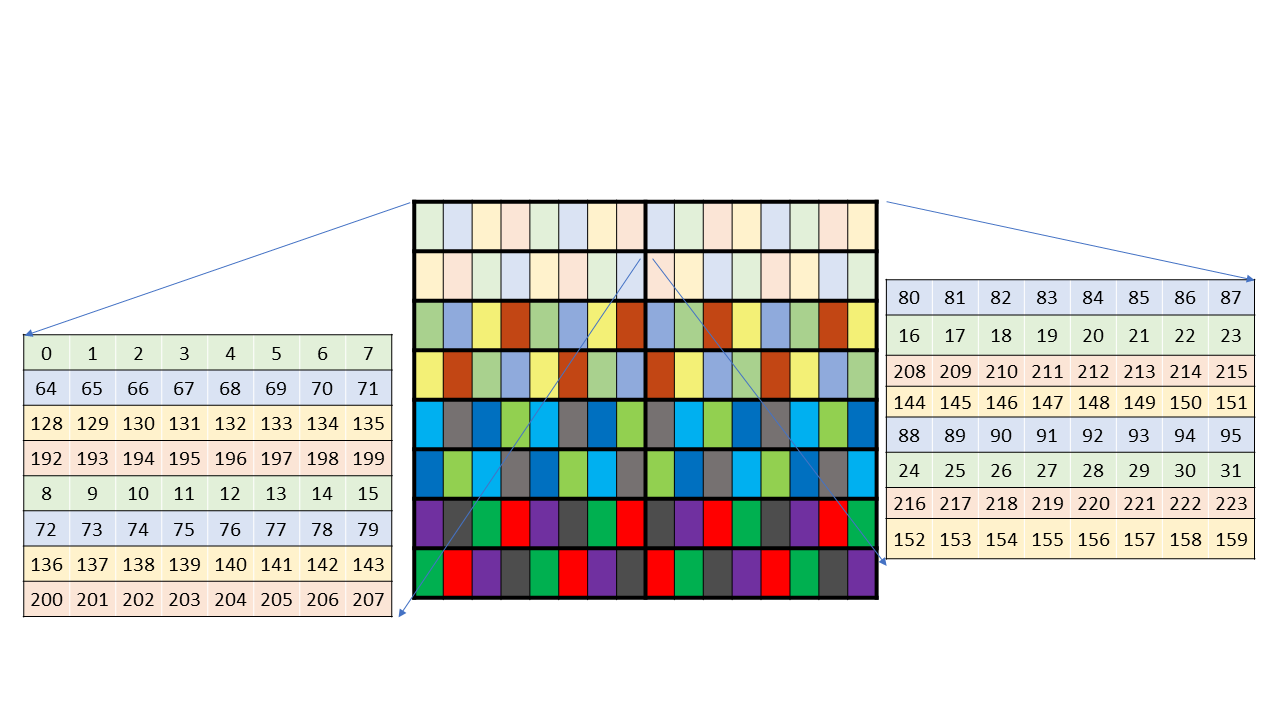
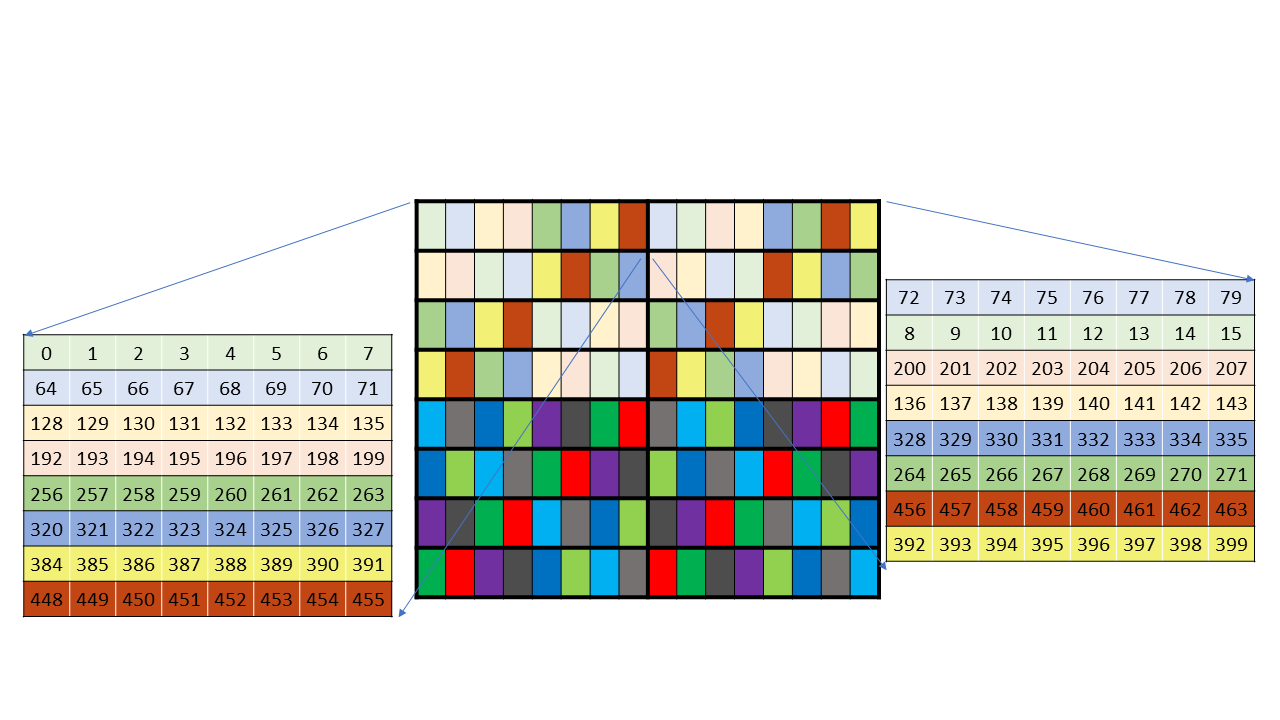
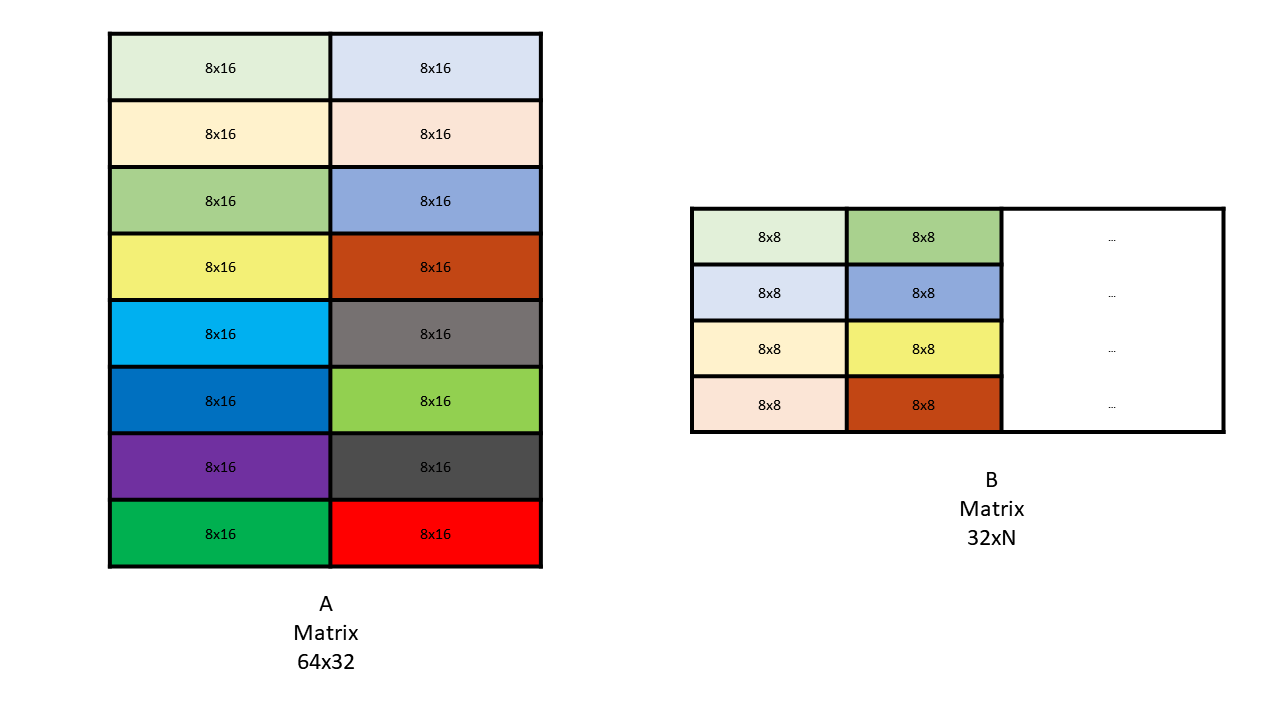
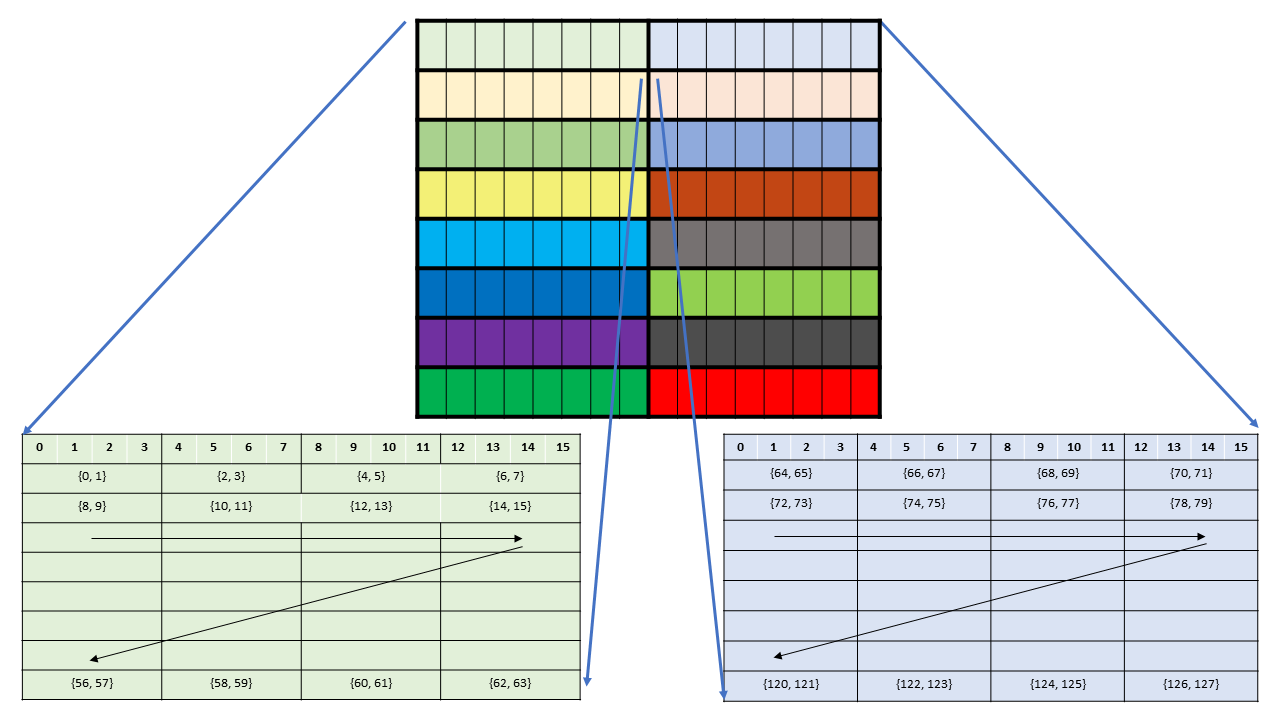
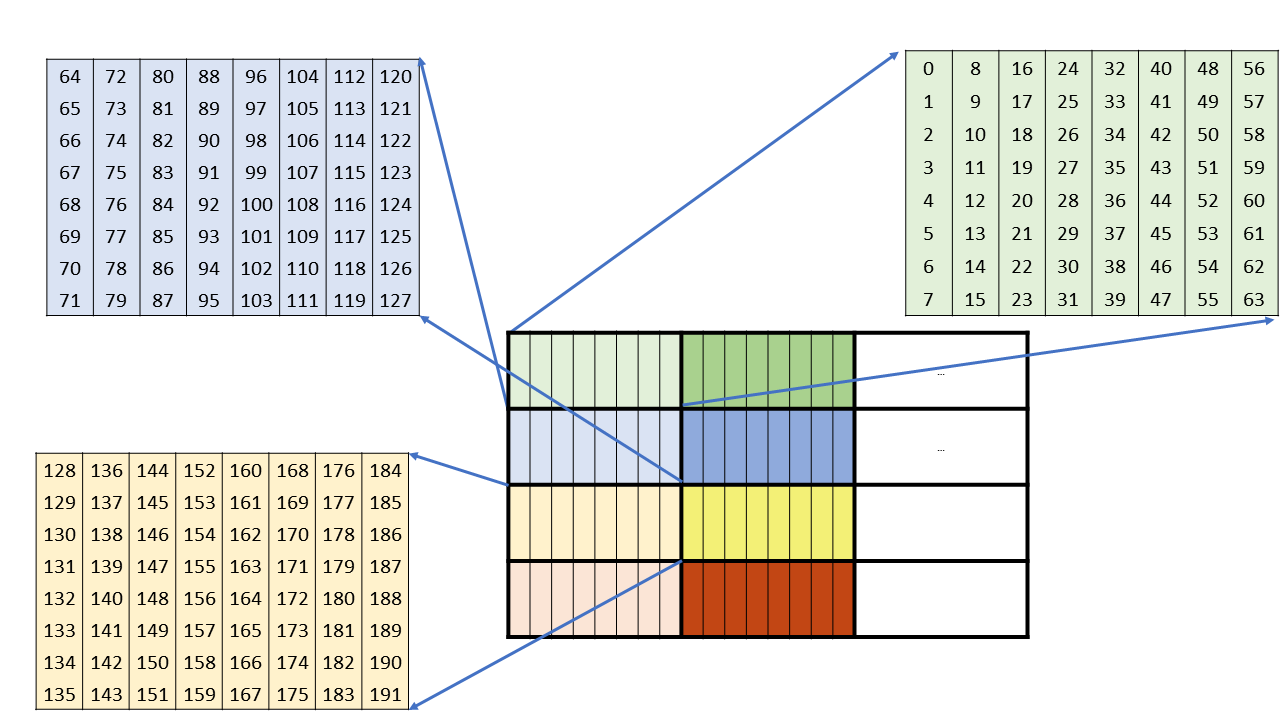
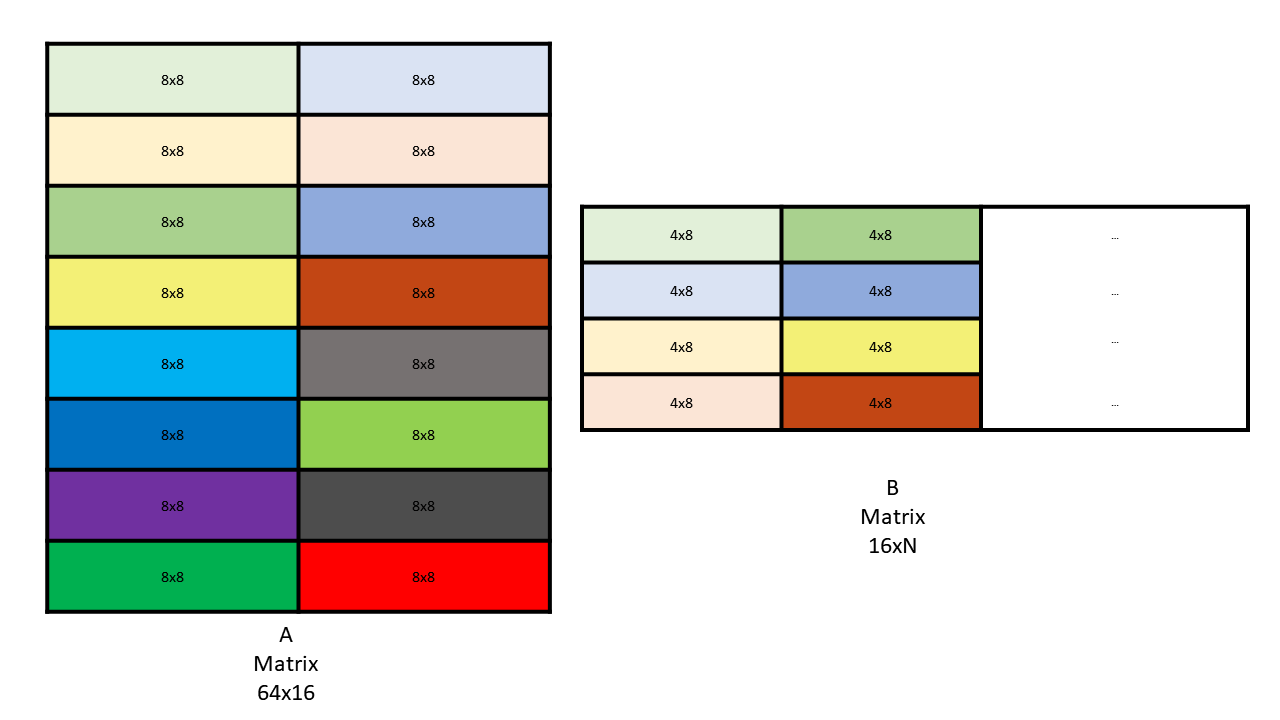
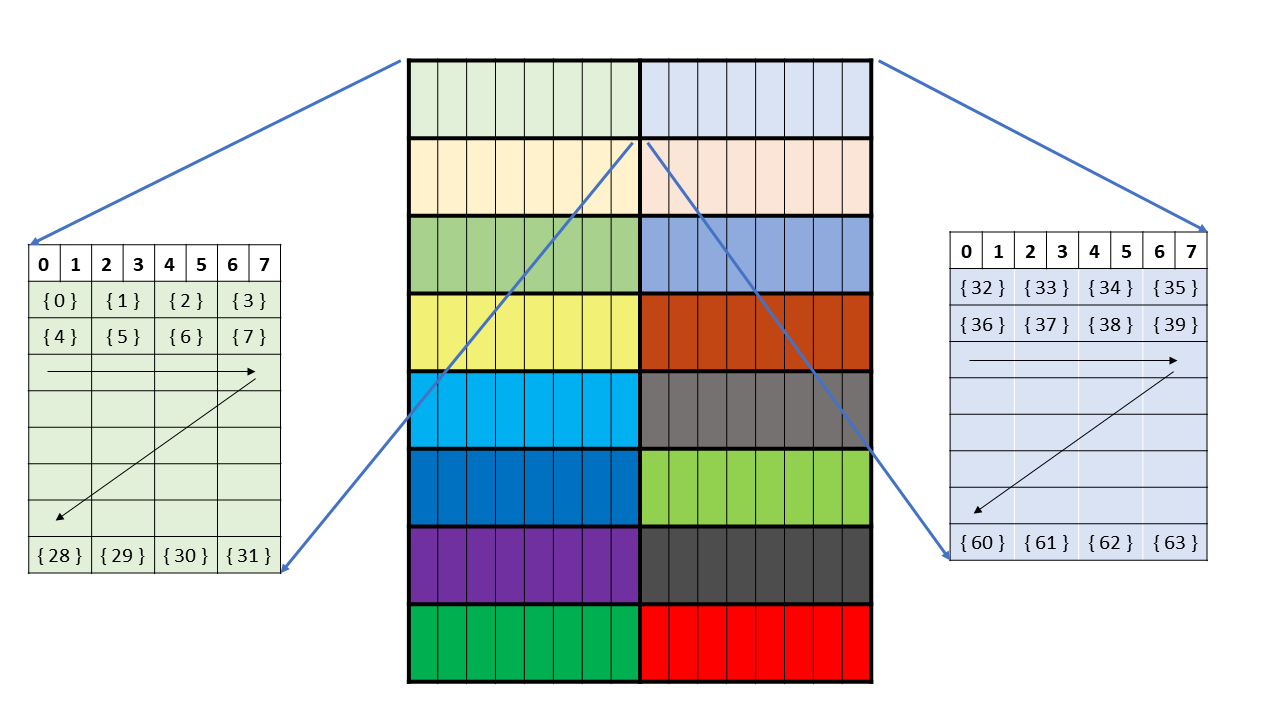
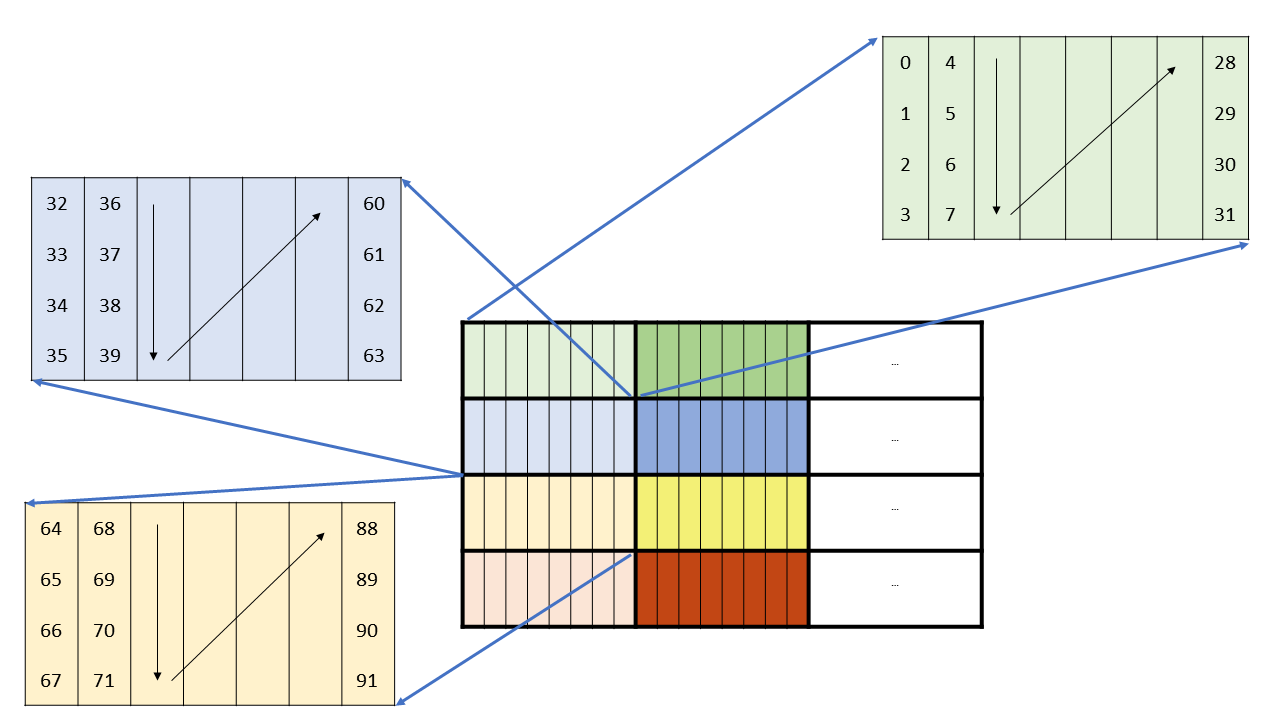
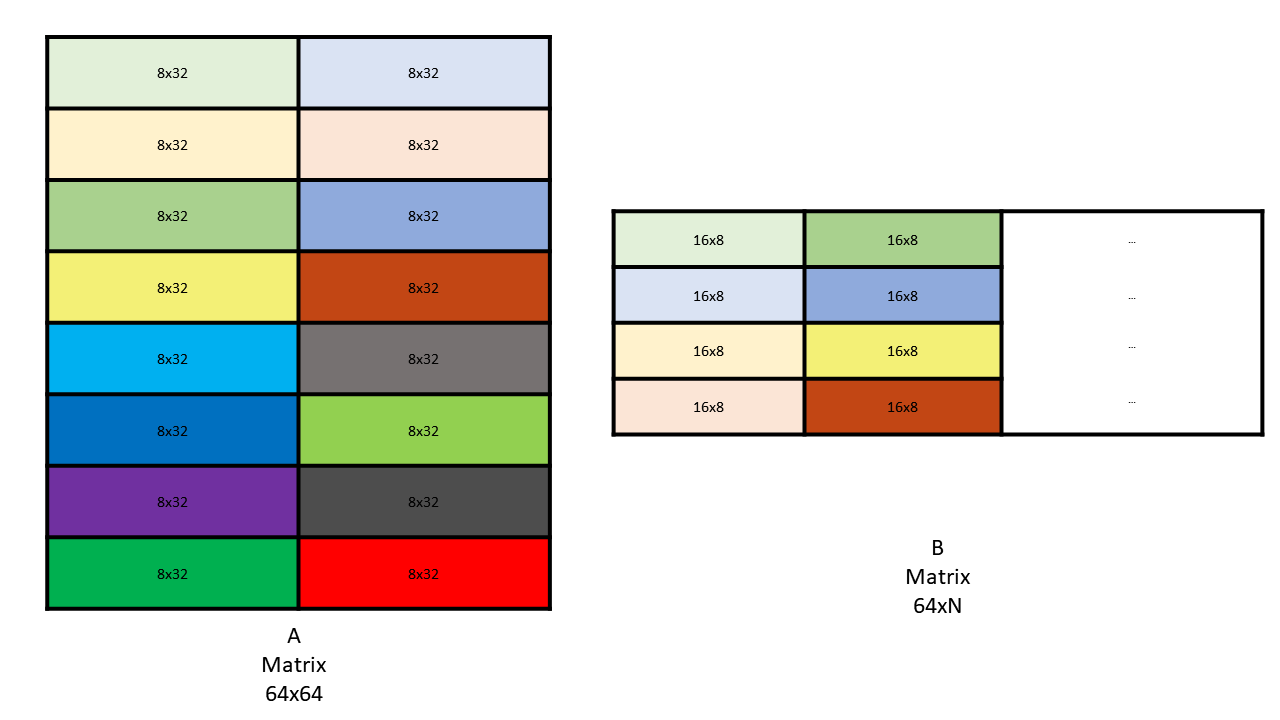
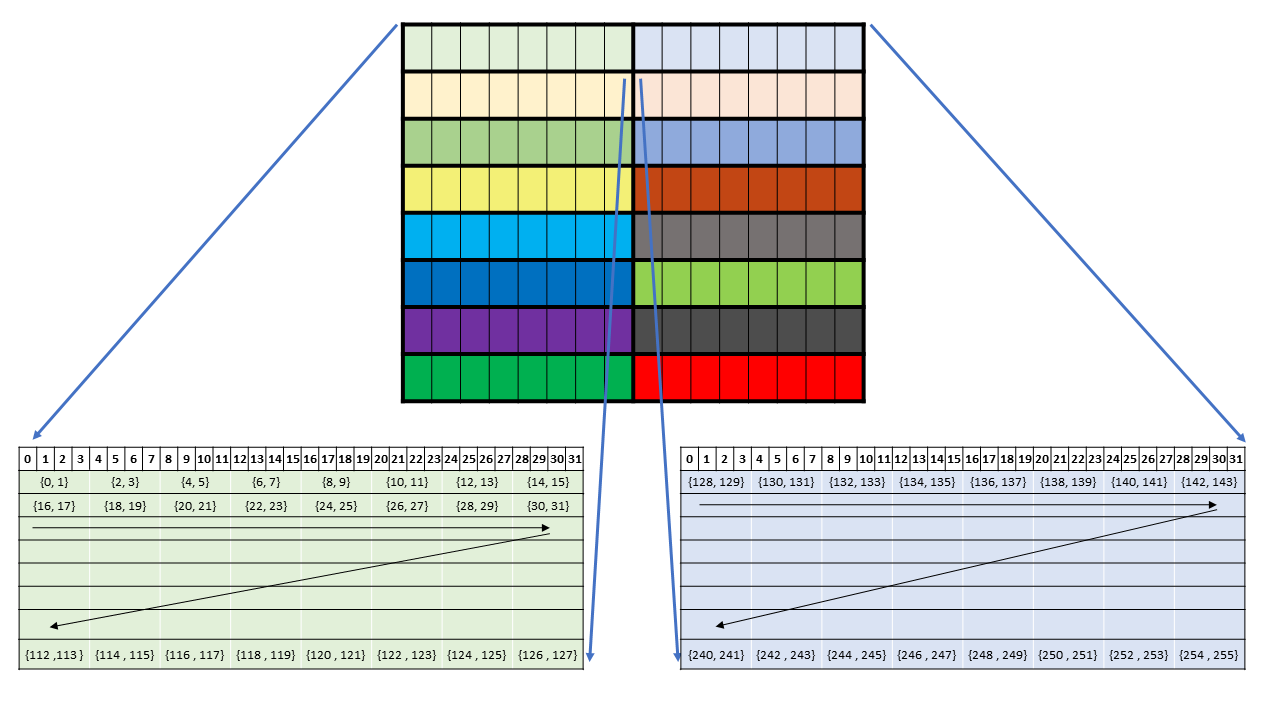
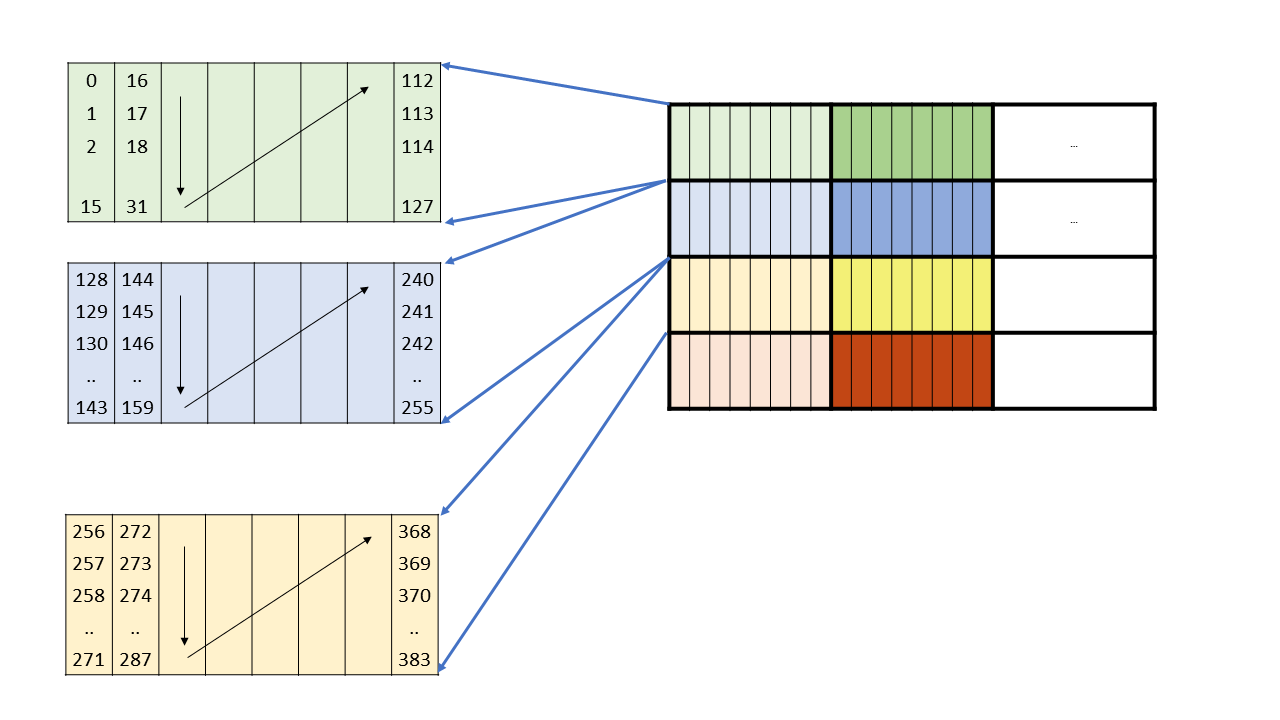
4.2. Comments
Comments in PTX follow C/C++ syntax, using non-nested
/*and*/for comments that may span multiple lines, and using//to begin a comment that extends up to the next newline character, which terminates the current line. Comments cannot occur within character constants, string literals, or within other comments.Comments in PTX are treated as whitespace.