K-Means Clustering Algorithm

Learning Outcomes

This example teaches how to implement k-means clustering algorithm using NumPy and is based on the k-means example in cuPyNumeric.

In this example, you will learn: * how to compute pairwise distances using newaxis * how to “bin” data using the bincount * how to locate data using where and argmin * how to use boolean mask to select data * how to compute norm of an n-dimensional array * how to determine if two NumPy arrays don’t have the same values using not_equal. * how to plot clusters using matplotlib

Background

To learn more about the clustering algorithm, see this material.

Implementation

import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from typing import Tuple

For reproducibility, use a seed to generate a default random number generator

# seed the random number generator for deterministic runs
random_seed: int = 42
rng = np.random.default_rng(random_seed)

def initialize(n_elements: int, n_dims: int, n_centroids: int) -> Tuple[np.ndarray, np.ndarray]:
    """
    Randomly initalize data and centroids of the clusters.

    n_elements: int
        Number of elements/observations that need to be clusters
    n_dims: int
        Dimension of the elements/observations
    n_centroids: int
        Number of clusters

    Returns:
        A Tuple with observations and centroids
    """
    data = rng.random((n_elements, n_dims))
    centroids = rng.random((n_centroids, n_dims))
    return data, centroids

def calculate_distances(data: np.ndarray, centroids: np.ndarray, data_magnitude_squared: np.ndarray) -> np.ndarray:
    """
    Return pairwise distance between the data and centroids.

    data: np.ndarray
        Observations that need to be clustered
    centroids: np.ndarray
        The center of the clusters
    data_magnitude_squared: np.ndarray
        Square of magnitude of observations (|y|^2)

    Returns: np.ndarray

    """
    centroid_dots = np.square(np.linalg.norm(centroids, ord=2, axis=1))
    pairwise_distances = (
        data_magnitude_squared[:, np.newaxis] + centroid_dots[np.newaxis, :]
    )
    # ||x-y||^2 = ||x||^2 + ||y||^2 - 2 x . y
    # pairwise_distances has ||x||^2 + ||y||^2, so beta = 1
    # The gemm calculates x.y for all x and y, so alpha = -2.0
    pairwise_distances -= 2.0 * np.dot(data, centroids.T)
    return pairwise_distances

def relabel(pairwise_distances: np.ndarray) -> np.ndarray:
    return np.argmin(pairwise_distances, axis=1)

def find_centroids(
    centroids: np.ndarray,
    data: np.ndarray,
    labels: np.ndarray,
    pairwise_distances: np.ndarray,
    zero_point: np.ndarray,
    n_centroids: int
) -> np.ndarray:
    """Find centroids following the algorithm in the reference mentioned earlier
    centroids: np.ndarray
        The center of the clusters
    data: np.ndarray
        Observations that need to be clustered
    labels: np.ndarray
        The clusters the data belong to
    pairwise_distances: np.ndarray
        Pairwise distance between each data point and centroid
    zero_point: np.ndarray

    n_centroids: np.ndarray
        Number of clusters
    """
    # Get the number of points associated with each centroid
    counts = np.bincount(labels, minlength=n_centroids)
    # Build label masks for each centroid and sum across all the
    # points assocated with each new centroid
    distance_sum = 0.0
    for idx in range(n_centroids):
        # Boolean mask indicating where the points are for this center
        centroid_mask = labels == idx
        centroids[idx, :] = np.sum(
            np.where(centroid_mask[..., np.newaxis], data, zero_point), axis=0
        )
        distance_sum += np.sum(
            np.where(centroid_mask, pairwise_distances[:, idx], 0.0)
        )
    # To avoid introducing divide by zero errors
    # If a centroid has no weight, we'll do no normalization
    # This will keep its coordinates defined.
    counts = np.maximum(counts, np.ones((1,), dtype=np.uint64))
    centroids /= counts[:, np.newaxis]
    return distance_sum

def run_kmeans(
    n_centroids: int,
    n_dims: int,
    n_iters: int,
    n_elements: int,
    n_iter_check: int
) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
    """
    Generate observations and cluster them into requested number of clusters.
    n_centroids: int
        Number of clusters
    n_dims: int
        Dimension of the elements/observations
    n_iters: int
        Maximum number of iterations
    n_elements: int
        Number of elements/observations that need to be clusters
    n_iter_check: int
        Determines how often we check for convergence.
    """
    print("Running kmeans...")
    print("Number of data points: " + str(n_elements))
    print("Number of dimensions: " + str(n_dims))
    print("Number of centroids: " + str(n_centroids))
    print("Max iterations: " + str(n_iters))

    data, centroids = initialize(n_elements, n_dims, n_centroids)

    data_magnitude_squared = np.square(np.linalg.norm(data, ord=2, axis=1))
    zero_point = np.zeros((1, data.shape[1]), dtype=data.dtype)

    labels = None
    iteration = 0
    prior_distance_sum = None
    # We run for max iterations or until we converge
    # We only test convergence every n_iter_check iterations
    while iteration < n_iters:
        pairwise_distances = calculate_distances(data, centroids, data_magnitude_squared)

        new_labels = relabel(pairwise_distances)

        distance_sum = find_centroids(
            centroids,
            data,
            new_labels,
            pairwise_distances,
            zero_point,
            n_centroids,
        )

        if iteration > 0 and iteration % n_iter_check == 0:
            changes = np.not_equal(labels, new_labels)
            total_changes = np.sum(changes)
            delta = distance_sum / prior_distance_sum
            if delta > 1 - 0.000001:
                break

        prior_distance_sum = distance_sum
        labels = new_labels
        iteration += 1

    return data, labels, centroids

Lets run the kmeans algorithm using a set of inputs

n_centroids: int = 5
n_dims: int = 2
n_elements: int = 256
n_iter_check: int = 10
n_iters: int = 100

data, labels, centroids = run_kmeans(n_centroids, n_dims, n_iters, n_elements, n_iter_check)

Running kmeans...
Number of data points: 256
Number of dimensions: 2
Number of centroids: 5
Max iterations: 100

Generate a color map to differentiate the clusters

label_color_map = {0: 'blue', 1: 'black', 2: 'red', 3: 'magenta', 4:'yellow', 5: 'green', 6:'gray'}

# make sure we have unique color for each cluster (total number of clusters specified by n_centroids)
assert len(label_color_map.items()) >= n_centroids

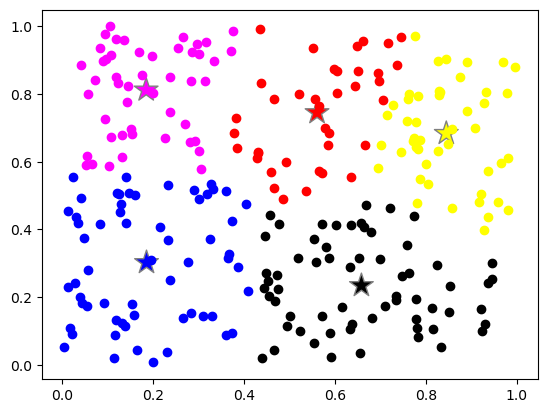
Plot the clusters. Each color represents a cluster

# lets plot the data colored by the cluster they belong to
for label_value, label_color in label_color_map.items():
    index = (labels == label_value)
    plt.plot(data[index, 0], data[index, 1], 'o', color=label_color)

# lets plot the centroid of the clusters
plt.scatter(centroids[:, 0], centroids[:, 1], s = 320, marker='*', c=list(label_color_map.values())[0:n_centroids], edgecolors='gray');

plt.show()

Exercise: Change the number of clusters and number of observations and see how the clusters change