CUDA C++ Best Practices Guide
1. Overview
The CUDA C++ Best Practices Guide provides practical guidelines for writing high-performance CUDA applications. It covers optimization strategies across memory usage, parallel execution, and instruction-level efficiency. The guide helps developers identify performance bottlenecks, leverage GPU architecture effectively, and apply profiling tools to fine-tune applications. It’s an essential resource for maximizing throughput and achieving scalable, efficient CUDA programs.
2. Preface
This Best Practices Guide is a manual to help developers obtain the best performance from NVIDIA® CUDA® GPUs. It presents established parallelization and optimization techniques and explains coding metaphors and idioms that can greatly simplify programming for CUDA-capable GPU architectures.
While the contents can be used as a reference manual, you should be aware that some topics are revisited in different contexts as various programming and configuration topics are explored. As a result, it is recommended that first-time readers proceed through the guide sequentially. This approach will greatly improve your understanding of effective programming practices and enable you to better use the guide for reference later.
2.1. Who Should Read This Guide?
The discussions in this guide all use the C++ programming language, so you should be comfortable reading C++ code.
This guide refers to and relies on several other documents that you should have at your disposal for reference, all of which are available at no cost from the CUDA website https://docs.nvidia.com/cuda/. The following documents are especially important resources:
CUDA Installation Guide
CUDA C++ Programming Guide
CUDA Toolkit Reference Manual
In particular, the optimization section of this guide assumes that you have already successfully downloaded and installed the CUDA Toolkit (if not, please refer to the relevant CUDA Installation Guide for your platform) and that you have a basic familiarity with the CUDA C++ programming language and environment (if not, please refer to the CUDA C++ Programming Guide).
2.2. Assess, Parallelize, Optimize, Deploy
This guide introduces the Assess, Parallelize, Optimize, Deploy(APOD) design cycle for applications with the goal of helping application developers to rapidly identify the portions of their code that would most readily benefit from GPU acceleration, rapidly realize that benefit, and begin leveraging the resulting speedups in production as early as possible.
APOD is a cyclical process: initial speedups can be achieved, tested, and deployed with only minimal initial investment of time, at which point the cycle can begin again by identifying further optimization opportunities, seeing additional speedups, and then deploying the even faster versions of the application into production.
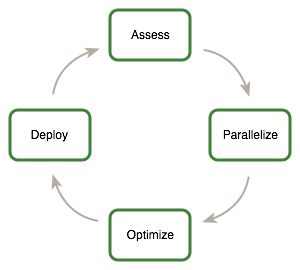
2.2.1. Assess
For an existing project, the first step is to assess the application to locate the parts of the code that are responsible for the bulk of the execution time. Armed with this knowledge, the developer can evaluate these bottlenecks for parallelization and start to investigate GPU acceleration.
By understanding the end-user’s requirements and constraints and by applying Amdahl’s and Gustafson’s laws, the developer can determine the upper bound of performance improvement from acceleration of the identified portions of the application.
2.2.2. Parallelize
Having identified the hotspots and having done the basic exercises to set goals and expectations, the developer needs to parallelize the code. Depending on the original code, this can be as simple as calling into an existing GPU-optimized library such as cuBLAS, cuFFT, or Thrust, or it could be as simple as adding a few preprocessor directives as hints to a parallelizing compiler.
On the other hand, some applications’ designs will require some amount of refactoring to expose their inherent parallelism. As even CPU architectures will require exposing parallelism in order to improve or simply maintain the performance of sequential applications, the CUDA family of parallel programming languages (CUDA C++, CUDA Fortran, etc.) aims to make the expression of this parallelism as simple as possible, while simultaneously enabling operation on CUDA-capable GPUs designed for maximum parallel throughput.
2.2.3. Optimize
After each round of application parallelization is complete, the developer can move to optimizing the implementation to improve performance. Since there are many possible optimizations that can be considered, having a good understanding of the needs of the application can help to make the process as smooth as possible. However, as with APOD as a whole, program optimization is an iterative process (identify an opportunity for optimization, apply and test the optimization, verify the speedup achieved, and repeat), meaning that it is not necessary for a programmer to spend large amounts of time memorizing the bulk of all possible optimization strategies prior to seeing good speedups. Instead, strategies can be applied incrementally as they are learned.
Optimizations can be applied at various levels, from overlapping data transfers with computation all the way down to fine-tuning floating-point operation sequences. The available profiling tools are invaluable for guiding this process, as they can help suggest a next-best course of action for the developer’s optimization efforts and provide references into the relevant portions of the optimization section of this guide.
2.2.4. Deploy
Having completed the GPU acceleration of one or more components of the application it is possible to compare the outcome with the original expectation. Recall that the initial assess step allowed the developer to determine an upper bound for the potential speedup attainable by accelerating given hotspots.
Before tackling other hotspots to improve the total speedup, the developer should consider taking the partially parallelized implementation and carry it through to production. This is important for a number of reasons; for example, it allows the user to profit from their investment as early as possible (the speedup may be partial but is still valuable), and it minimizes risk for the developer and the user by providing an evolutionary rather than revolutionary set of changes to the application.
2.3. Recommendations and Best Practices
Throughout this guide, specific recommendations are made regarding the design and implementation of CUDA C++ code. These recommendations are categorized by priority, which is a blend of the effect of the recommendation and its scope. Actions that present substantial improvements for most CUDA applications have the highest priority, while small optimizations that affect only very specific situations are given a lower priority.
Before implementing lower priority recommendations, it is good practice to make sure all higher priority recommendations that are relevant have already been applied. This approach will tend to provide the best results for the time invested and will avoid the trap of premature optimization.
The criteria of benefit and scope for establishing priority will vary depending on the nature of the program. In this guide, they represent a typical case. Your code might reflect different priority factors. Regardless of this possibility, it is good practice to verify that no higher-priority recommendations have been overlooked before undertaking lower-priority items.
Note
Code samples throughout the guide omit error checking for conciseness. Production code should, however, systematically check the error code returned by each API call and check for failures in kernel launches by calling cudaGetLastError().
2.4. Assessing Your Application
From supercomputers to mobile phones, modern processors increasingly rely on parallelism to provide performance. The core computational unit, which includes control, arithmetic, registers and typically some cache, is replicated some number of times and connected to memory via a network. As a result, all modern processors require parallel code in order to achieve good utilization of their computational power.
While processors are evolving to expose more fine-grained parallelism to the programmer, many existing applications have evolved either as serial codes or as coarse-grained parallel codes (for example, where the data is decomposed into regions processed in parallel, with sub-regions shared using MPI). In order to profit from any modern processor architecture, GPUs included, the first steps are to assess the application to identify the hotspots, determine whether they can be parallelized, and understand the relevant workloads both now and in the future.
3. Heterogeneous Computing
CUDA programming involves running code on two different platforms concurrently: a host system with one or more CPUs and one or more CUDA-enabled NVIDIA GPU devices.
While NVIDIA GPUs are frequently associated with graphics, they are also powerful arithmetic engines capable of running thousands of lightweight threads in parallel. This capability makes them well suited to computations that can leverage parallel execution.
However, the device is based on a distinctly different design from the host system, and it’s important to understand those differences and how they determine the performance of CUDA applications in order to use CUDA effectively.
3.1. Differences between Host and Device
The primary differences are in threading model and in separate physical memories:
- Threading resources
-
Execution pipelines on host systems can support a limited number of concurrent threads. For example, servers that have two 32 core processors can run only 64 threads concurrently (or small multiple of that if the CPUs support simultaneous multithreading). By comparison, the smallest executable unit of parallelism on a CUDA device comprises 32 threads (termed a warp of threads). Modern NVIDIA GPUs can support up to 2048 active threads concurrently per multiprocessor (see Features and Specifications of the CUDA C++ Programming Guide) On GPUs with 80 multiprocessors, this leads to more than 160,000 concurrently active threads.
- Threads
-
Threads on a CPU are generally heavyweight entities. The operating system must swap threads on and off CPU execution channels to provide multithreading capability. Context switches (when two threads are swapped) are therefore slow and expensive. By comparison, threads on GPUs are extremely lightweight. In a typical system, thousands of threads are queued up for work (in warps of 32 threads each). If the GPU must wait on one warp of threads, it simply begins executing work on another. Because separate registers are allocated to all active threads, no swapping of registers or other state need occur when switching among GPU threads. Resources stay allocated to each thread until it completes its execution. In short, CPU cores are designed to minimize latency for a small number of threads at a time each, whereas GPUs are designed to handle a large number of concurrent, lightweight threads in order to maximize throughput.
- RAM
-
The host system and the device each have their own distinct attached physical memories 1. As the host and device memories are separated, items in the host memory must occasionally be communicated between device memory and host memory as described in What Runs on a CUDA-Enabled Device?.
These are the primary hardware differences between CPU hosts and GPU devices with respect to parallel programming. Other differences are discussed as they arise elsewhere in this document. Applications composed with these differences in mind can treat the host and device together as a cohesive heterogeneous system wherein each processing unit is leveraged to do the kind of work it does best: sequential work on the host and parallel work on the device.
3.2. What Runs on a CUDA-Enabled Device?
The following issues should be considered when determining what parts of an application to run on the device:
The device is ideally suited for computations that can be run on numerous data elements simultaneously in parallel. This typically involves arithmetic on large data sets (such as matrices) where the same operation can be performed across thousands, if not millions, of elements at the same time. This is a requirement for good performance on CUDA: the software must use a large number (generally thousands or tens of thousands) of concurrent threads. The support for running numerous threads in parallel derives from CUDA’s use of a lightweight threading model described above.
-
To use CUDA, data values must be transferred from the host to the device. These transfers are costly in terms of performance and should be minimized. (See Data Transfer Between Host and Device.) This cost has several ramifications:
-
The complexity of operations should justify the cost of moving data to and from the device. Code that transfers data for brief use by a small number of threads will see little or no performance benefit. The ideal scenario is one in which many threads perform a substantial amount of work.
For example, transferring two matrices to the device to perform a matrix addition and then transferring the results back to the host will not realize much performance benefit. The issue here is the number of operations performed per data element transferred. For the preceding procedure, assuming matrices of size NxN, there are N2 operations (additions) and 3N2 elements transferred, so the ratio of operations to elements transferred is 1:3 or O(1). Performance benefits can be more readily achieved when this ratio is higher. For example, a matrix multiplication of the same matrices requires N3 operations (multiply-add), so the ratio of operations to elements transferred is O(N), in which case the larger the matrix the greater the performance benefit. The types of operations are an additional factor, as additions have different complexity profiles than, for example, trigonometric functions. It is important to include the overhead of transferring data to and from the device in determining whether operations should be performed on the host or on the device.
Data should be kept on the device as long as possible. Because transfers should be minimized, programs that run multiple kernels on the same data should favor leaving the data on the device between kernel calls, rather than transferring intermediate results to the host and then sending them back to the device for subsequent calculations. So, in the previous example, had the two matrices to be added already been on the device as a result of some previous calculation, or if the results of the addition would be used in some subsequent calculation, the matrix addition should be performed locally on the device. This approach should be used even if one of the steps in a sequence of calculations could be performed faster on the host. Even a relatively slow kernel may be advantageous if it avoids one or more transfers between host and device memory. Data Transfer Between Host and Device provides further details, including the measurements of bandwidth between the host and the device versus within the device proper.
-
For best performance, there should be some coherence in memory access by adjacent threads running on the device. Certain memory access patterns enable the hardware to coalesce groups of reads or writes of multiple data items into one operation. Data that cannot be laid out so as to enable coalescing, or that doesn’t have enough locality to use the L1 or texture caches effectively, will tend to see lesser speedups when used in computations on GPUs. A noteworthy exception to this are completely random memory access patterns. In general, they should be avoided, because compared to peak capabilities any architecture processes these memory access patterns at a low efficiency. However, compared to cache based architectures, like CPUs, latency hiding architectures, like GPUs, tend to cope better with completely random memory access patterns.
- 1
-
On Systems on a Chip with integrated GPUs, such as NVIDIA® Tegra®, host and device memory are physically the same, but there is still a logical distinction between host and device memory. See the Application Note on CUDA for Tegra for details.
4. Application Profiling
4.1. Profile
Many codes accomplish a significant portion of the work with a relatively small amount of code. Using a profiler, the developer can identify such hotspots and start to compile a list of candidates for parallelization.
4.1.1. Creating the Profile
There are many possible approaches to profiling the code, but in all cases the objective is the same: to identify the function or functions in which the application is spending most of its execution time.
Note
High Priority: To maximize developer productivity, profile the application to determine hotspots and bottlenecks.
The most important consideration with any profiling activity is to ensure that the workload is realistic - i.e., that information gained from the test and decisions based upon that information are relevant to real data. Using unrealistic workloads can lead to sub-optimal results and wasted effort both by causing developers to optimize for unrealistic problem sizes and by causing developers to concentrate on the wrong functions.
There are a number of tools that can be used to generate the profile. The following example is based on gprof, which is an open-source profiler for Linux platforms from the GNU Binutils collection.
$ gcc -O2 -g -pg myprog.c
$ gprof ./a.out > profile.txt
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls ms/call ms/call name
33.34 0.02 0.02 7208 0.00 0.00 genTimeStep
16.67 0.03 0.01 240 0.04 0.12 calcStats
16.67 0.04 0.01 8 1.25 1.25 calcSummaryData
16.67 0.05 0.01 7 1.43 1.43 write
16.67 0.06 0.01 mcount
0.00 0.06 0.00 236 0.00 0.00 tzset
0.00 0.06 0.00 192 0.00 0.00 tolower
0.00 0.06 0.00 47 0.00 0.00 strlen
0.00 0.06 0.00 45 0.00 0.00 strchr
0.00 0.06 0.00 1 0.00 50.00 main
0.00 0.06 0.00 1 0.00 0.00 memcpy
0.00 0.06 0.00 1 0.00 10.11 print
0.00 0.06 0.00 1 0.00 0.00 profil
0.00 0.06 0.00 1 0.00 50.00 report
4.1.2. Identifying Hotspots
In the example above, we can clearly see that the function genTimeStep() takes one-third of the total running time of the application. This should be our first candidate function for parallelization. Understanding Scaling discusses the potential benefit we might expect from such parallelization.
It is worth noting that several of the other functions in the above example also take up a significant portion of the overall running time, such as calcStats() and calcSummaryData(). Parallelizing these functions as well should increase our speedup potential. However, since APOD is a cyclical process, we might opt to parallelize these functions in a subsequent APOD pass, thereby limiting the scope of our work in any given pass to a smaller set of incremental changes.
4.1.3. Understanding Scaling
The amount of performance benefit an application will realize by running on CUDA depends entirely on the extent to which it can be parallelized. Code that cannot be sufficiently parallelized should run on the host, unless doing so would result in excessive transfers between the host and the device.
Note
High Priority: To get the maximum benefit from CUDA, focus first on finding ways to parallelize sequential code.
By understanding how applications can scale it is possible to set expectations and plan an incremental parallelization strategy. Strong Scaling and Amdahl’s Law describes strong scaling, which allows us to set an upper bound for the speedup with a fixed problem size. Weak Scaling and Gustafson’s Law describes weak scaling, where the speedup is attained by growing the problem size. In many applications, a combination of strong and weak scaling is desirable.
4.1.3.1. Strong Scaling and Amdahl’s Law
Strong scaling is a measure of how, for a fixed overall problem size, the time to solution decreases as more processors are added to a system. An application that exhibits linear strong scaling has a speedup equal to the number of processors used.
Strong scaling is usually equated with Amdahl’s Law, which specifies the maximum speedup that can be expected by parallelizing portions of a serial program. Essentially, it states that the maximum speedup S of a program is:
\(S = \frac{1}{(1 - P) + \frac{P}{N}}\)
Here P is the fraction of the total serial execution time taken by the portion of code that can be parallelized and N is the number of processors over which the parallel portion of the code runs.
The larger N is(that is, the greater the number of processors), the smaller the P/N fraction. It can be simpler to view N as a very large number, which essentially transforms the equation into \(S = 1/(1 - P)\). Now, if 3/4 of the running time of a sequential program is parallelized, the maximum speedup over serial code is 1 / (1 - 3/4) = 4.
In reality, most applications do not exhibit perfectly linear strong scaling, even if they do exhibit some degree of strong scaling. For most purposes, the key point is that the larger the parallelizable portion P is, the greater the potential speedup. Conversely, if P is a small number (meaning that the application is not substantially parallelizable), increasing the number of processors N does little to improve performance. Therefore, to get the largest speedup for a fixed problem size, it is worthwhile to spend effort on increasing P, maximizing the amount of code that can be parallelized.
4.1.3.2. Weak Scaling and Gustafson’s Law
Weak scaling is a measure of how the time to solution changes as more processors are added to a system with a fixed problem size per processor; i.e., where the overall problem size increases as the number of processors is increased.
Weak scaling is often equated with Gustafson’s Law, which states that in practice, the problem size scales with the number of processors. Because of this, the maximum speedup S of a program is:
\(S = N + (1 - P)(1 - N)\)
Here P is the fraction of the total serial execution time taken by the portion of code that can be parallelized and N is the number of processors over which the parallel portion of the code runs.
Another way of looking at Gustafson’s Law is that it is not the problem size that remains constant as we scale up the system but rather the execution time. Note that Gustafson’s Law assumes that the ratio of serial to parallel execution remains constant, reflecting additional cost in setting up and handling the larger problem.
4.1.3.3. Applying Strong and Weak Scaling
Understanding which type of scaling is most applicable to an application is an important part of estimating speedup. For some applications the problem size will remain constant and hence only strong scaling is applicable. An example would be modeling how two molecules interact with each other, where the molecule sizes are fixed.
For other applications, the problem size will grow to fill the available processors. Examples include modeling fluids or structures as meshes or grids and some Monte Carlo simulations, where increasing the problem size provides increased accuracy.
Having understood the application profile, the developer should understand how the problem size would change if the computational performance changes and then apply either Amdahl’s or Gustafson’s Law to determine an upper bound for the speedup.
5. Parallelizing Your Application
Having identified the hotspots and having done the basic exercises to set goals and expectations, the developer needs to parallelize the code. Depending on the original code, this can be as simple as calling into an existing GPU-optimized library such as cuBLAS, cuFFT, or Thrust, or it could be as simple as adding a few preprocessor directives as hints to a parallelizing compiler.
On the other hand, some applications’ designs will require some amount of refactoring to expose their inherent parallelism. As even CPU architectures require exposing this parallelism in order to improve or simply maintain the performance of sequential applications, the CUDA family of parallel programming languages (CUDA C++, CUDA Fortran, etc.) aims to make the expression of this parallelism as simple as possible, while simultaneously enabling operation on CUDA-capable GPUs designed for maximum parallel throughput.
6. Getting Started
There are several key strategies for parallelizing sequential code. While the details of how to apply these strategies to a particular application is a complex and problem-specific topic, the general themes listed here apply regardless of whether we are parallelizing code to run on for multicore CPUs or for use on CUDA GPUs.
6.1. Parallel Libraries
The most straightforward approach to parallelizing an application is to leverage existing libraries that take advantage of parallel architectures on our behalf. The CUDA Toolkit includes a number of such libraries that have been fine-tuned for NVIDIA CUDA GPUs, such as cuBLAS, cuFFT, and so on.
The key here is that libraries are most useful when they match well with the needs of the application. Applications already using other BLAS libraries can often quite easily switch to cuBLAS, for example, whereas applications that do little to no linear algebra will have little use for cuBLAS. The same goes for other CUDA Toolkit libraries: cuFFT has an interface similar to that of FFTW, etc.
Also of note is the Thrust library, which is a parallel C++ template library similar to the C++ Standard Template Library. Thrust provides a rich collection of data parallel primitives such as scan, sort, and reduce, which can be composed together to implement complex algorithms with concise, readable source code. By describing your computation in terms of these high-level abstractions you provide Thrust with the freedom to select the most efficient implementation automatically. As a result, Thrust can be utilized in rapid prototyping of CUDA applications, where programmer productivity matters most, as well as in production, where robustness and absolute performance are crucial.
6.2. Parallelizing Compilers
Another common approach to parallelization of sequential codes is to make use of parallelizing compilers. Often this means the use of directives-based approaches, where the programmer uses a pragma or other similar notation to provide hints to the compiler about where parallelism can be found without needing to modify or adapt the underlying code itself. By exposing parallelism to the compiler, directives allow the compiler to do the detailed work of mapping the computation onto the parallel architecture.
The OpenACC standard provides a set of compiler directives to specify loops and regions of code in standard C, C++ and Fortran that should be offloaded from a host CPU to an attached accelerator such as a CUDA GPU. The details of managing the accelerator device are handled implicitly by an OpenACC-enabled compiler and runtime.
See http://www.openacc.org/ for details.
6.3. Coding to Expose Parallelism
For applications that need additional functionality or performance beyond what existing parallel libraries or parallelizing compilers can provide, parallel programming languages such as CUDA C++ that integrate seamlessly with existing sequential code are essential.
Once we have located a hotspot in our application’s profile assessment and determined that custom code is the best approach, we can use CUDA C++ to expose the parallelism in that portion of our code as a CUDA kernel. We can then launch this kernel onto the GPU and retrieve the results without requiring major rewrites to the rest of our application.
This approach is most straightforward when the majority of the total running time of our application is spent in a few relatively isolated portions of the code. More difficult to parallelize are applications with a very flat profile - i.e., applications where the time spent is spread out relatively evenly across a wide portion of the code base. For the latter variety of application, some degree of code refactoring to expose the inherent parallelism in the application might be necessary, but keep in mind that this refactoring work will tend to benefit all future architectures, CPU and GPU alike, so it is well worth the effort should it become necessary.
7. Getting the Right Answer
Obtaining the right answer is clearly the principal goal of all computation. On parallel systems, it is possible to run into difficulties not typically found in traditional serial-oriented programming. These include threading issues, unexpected values due to the way floating-point values are computed, and challenges arising from differences in the way CPU and GPU processors operate. This chapter examines issues that can affect the correctness of returned data and points to appropriate solutions.
7.1. Verification
7.1.1. Reference Comparison
A key aspect of correctness verification for modifications to any existing program is to establish some mechanism whereby previous known-good reference outputs from representative inputs can be compared to new results. After each change is made, ensure that the results match using whatever criteria apply to the particular algorithm. Some will expect bitwise identical results, which is not always possible, especially where floating-point arithmetic is concerned; see Numerical Accuracy and Precision regarding numerical accuracy. For other algorithms, implementations may be considered correct if they match the reference within some small epsilon.
Note that the process used for validating numerical results can easily be extended to validate performance results as well. We want to ensure that each change we make is correct and that it improves performance (and by how much). Checking these things frequently as an integral part of our cyclical APOD process will help ensure that we achieve the desired results as rapidly as possible.
7.1.2. Unit Testing
A useful counterpart to the reference comparisons described above is to structure the code itself in such a way that is readily verifiable at the unit level. For example, we can write our CUDA kernels as a collection of many short __device__ functions rather than one large monolithic __global__ function; each device function can be tested independently before hooking them all together.
For example, many kernels have complex addressing logic for accessing memory in addition to their actual computation. If we validate our addressing logic separately prior to introducing the bulk of the computation, then this will simplify any later debugging efforts. (Note that the CUDA compiler considers any device code that does not contribute to a write to global memory as dead code subject to elimination, so we must at least write something out to global memory as a result of our addressing logic in order to successfully apply this strategy.)
Going a step further, if most functions are defined as __host__ __device__ rather than just __device__ functions, then these functions can be tested on both the CPU and the GPU, thereby increasing our confidence that the function is correct and that there will not be any unexpected differences in the results. If there are differences, then those differences will be seen early and can be understood in the context of a simple function.
As a useful side effect, this strategy will allow us a means to reduce code duplication should we wish to include both CPU and GPU execution paths in our application: if the bulk of the work of our CUDA kernels is done in __host__ __device__ functions, we can easily call those functions from both the host code and the device code without duplication.
7.2. Debugging
CUDA-GDB is a port of the GNU Debugger that runs on Linux and Mac; see: https://developer.nvidia.com/cuda-gdb.
The NVIDIA Nsight Visual Studio Edition is available as a free plugin for Microsoft Visual Studio; see: https://developer.nvidia.com/nsight-visual-studio-edition.
Several third-party debuggers support CUDA debugging as well; see: https://developer.nvidia.com/debugging-solutions for more details.
7.3. Numerical Accuracy and Precision
Incorrect or unexpected results arise principally from issues of floating-point accuracy due to the way floating-point values are computed and stored. The following sections explain the principal items of interest. Other peculiarities of floating-point arithmetic are presented in Features and Technical Specifications of the CUDA C++ Programming Guide as well as in a whitepaper and accompanying webinar on floating-point precision and performance available from https://developer.nvidia.com/content/precision-performance-floating-point-and-ieee-754-compliance-nvidia-gpus.
7.3.1. Single vs. Double Precision
Devices of CUDA Compute Capability 1.3 and higher provide native support for double-precision floating-point values (that is, values 64 bits wide). Results obtained using double-precision arithmetic will frequently differ from the same operation performed via single-precision arithmetic due to the greater precision of the former and due to rounding issues. Therefore, it is important to be sure to compare values of like precision and to express the results within a certain tolerance rather than expecting them to be exact.
7.3.2. Floating Point Math Is Not Associative
Each floating-point arithmetic operation involves a certain amount of rounding. Consequently, the order in which arithmetic operations are performed is important. If A, B, and C are floating-point values, (A+B)+C is not guaranteed to equal A+(B+C) as it is in symbolic math. When you parallelize computations, you potentially change the order of operations and therefore the parallel results might not match sequential results. This limitation is not specific to CUDA, but an inherent part of parallel computation on floating-point values.
7.3.3. IEEE 754 Compliance
All CUDA compute devices follow the IEEE 754 standard for binary floating-point representation, with some small exceptions. These exceptions, which are detailed in Features and Technical Specifications of the CUDA C++ Programming Guide, can lead to results that differ from IEEE 754 values computed on the host system.
One of the key differences is the fused multiply-add (FMA) instruction, which combines multiply-add operations into a single instruction execution. Its result will often differ slightly from results obtained by doing the two operations separately.
7.3.4. x86 80-bit Computations
x86 processors can use an 80-bit double extended precision math when performing floating-point calculations. The results of these calculations can frequently differ from pure 64-bit operations performed on the CUDA device. To get a closer match between values, set the x86 host processor to use regular double or single precision (64 bits and 32 bits, respectively). This is done with the FLDCW x86 assembly instruction or the equivalent operating system API.
8. Optimizing CUDA Applications
After each round of application parallelization is complete, the developer can move to optimizing the implementation to improve performance. Since there are many possible optimizations that can be considered, having a good understanding of the needs of the application can help to make the process as smooth as possible. However, as with APOD as a whole, program optimization is an iterative process (identify an opportunity for optimization, apply and test the optimization, verify the speedup achieved, and repeat), meaning that it is not necessary for a programmer to spend large amounts of time memorizing the bulk of all possible optimization strategies prior to seeing good speedups. Instead, strategies can be applied incrementally as they are learned.
Optimizations can be applied at various levels, from overlapping data transfers with computation all the way down to fine-tuning floating-point operation sequences. The available profiling tools are invaluable for guiding this process, as they can help suggest a next-best course of action for the developer’s optimization efforts and provide references into the relevant portions of the optimization section of this guide.
9. Performance Metrics
When attempting to optimize CUDA code, it pays to know how to measure performance accurately and to understand the role that bandwidth plays in performance measurement. This chapter discusses how to correctly measure performance using CPU timers and CUDA events. It then explores how bandwidth affects performance metrics and how to mitigate some of the challenges it poses.
9.1. Timing
CUDA calls and kernel executions can be timed using either CPU or GPU timers. This section examines the functionality, advantages, and pitfalls of both approaches.
9.1.1. Using CPU Timers
Any CPU timer can be used to measure the elapsed time of a CUDA call or kernel execution. The details of various CPU timing approaches are outside the scope of this document, but developers should always be aware of the resolution their timing calls provide.
When using CPU timers, it is critical to remember that many CUDA API functions are asynchronous; that is, they return control back to the calling CPU thread prior to completing their work. All kernel launches are asynchronous, as are memory-copy functions with the Async suffix on their names. Therefore, to accurately measure the elapsed time for a particular call or sequence of CUDA calls, it is necessary to synchronize the CPU thread with the GPU by calling cudaDeviceSynchronize() immediately before starting and stopping the CPU timer. cudaDeviceSynchronize()blocks the calling CPU thread until all CUDA calls previously issued by the thread are completed.
Although it is also possible to synchronize the CPU thread with a particular stream or event on the GPU, these synchronization functions are not suitable for timing code in streams other than the default stream. cudaStreamSynchronize() blocks the CPU thread until all CUDA calls previously issued into the given stream have completed. cudaEventSynchronize() blocks until a given event in a particular stream has been recorded by the GPU. Because the driver may interleave execution of CUDA calls from other non-default streams, calls in other streams may be included in the timing.
Because the default stream, stream 0, exhibits serializing behavior for work on the device (an operation in the default stream can begin only after all preceding calls in any stream have completed; and no subsequent operation in any stream can begin until it finishes), these functions can be used reliably for timing in the default stream.
Be aware that CPU-to-GPU synchronization points such as those mentioned in this section imply a stall in the GPU’s processing pipeline and should thus be used sparingly to minimize their performance impact.
9.1.2. Using CUDA GPU Timers
The CUDA event API provides calls that create and destroy events, record events (including a timestamp), and convert timestamp differences into a floating-point value in milliseconds. How to time code using CUDA events illustrates their use.
How to time code using CUDA events
cudaEvent_t start, stop;
float time;
cudaEventCreate(&start);
cudaEventCreate(&stop);
cudaEventRecord( start, 0 );
kernel<<<grid,threads>>> ( d_odata, d_idata, size_x, size_y,
NUM_REPS);
cudaEventRecord( stop, 0 );
cudaEventSynchronize( stop );
cudaEventElapsedTime( &time, start, stop );
cudaEventDestroy( start );
cudaEventDestroy( stop );
Here cudaEventRecord() is used to place the start and stop events into the default stream, stream 0. The device will record a timestamp for the event when it reaches that event in the stream. The cudaEventElapsedTime() function returns the time elapsed between the recording of the start and stop events. This value is expressed in milliseconds and has a resolution of approximately half a microsecond. Like the other calls in this listing, their specific operation, parameters, and return values are described in the CUDA Toolkit Reference Manual. Note that the timings are measured on the GPU clock, so the timing resolution is operating-system-independent.
9.2. Bandwidth
Bandwidth - the rate at which data can be transferred - is one of the most important gating factors for performance. Almost all changes to code should be made in the context of how they affect bandwidth. As described in Memory Optimizations of this guide, bandwidth can be dramatically affected by the choice of memory in which data is stored, how the data is laid out and the order in which it is accessed, as well as other factors.
To measure performance accurately, it is useful to calculate theoretical and effective bandwidth. When the latter is much lower than the former, design or implementation details are likely to reduce bandwidth, and it should be the primary goal of subsequent optimization efforts to increase it.
Note
High Priority: Use the effective bandwidth of your computation as a metric when measuring performance and optimization benefits.
9.2.1. Theoretical Bandwidth Calculation
Theoretical bandwidth can be calculated using hardware specifications available in the product literature. For example, the NVIDIA Tesla V100 uses HBM2 (double data rate) RAM with a memory clock rate of 877 MHz and a 4096-bit-wide memory interface.
Using these data items, the peak theoretical memory bandwidth of the NVIDIA Tesla V100 is 898 GB/s:
\(\left. \left( 0.877 \times 10^{9} \right. \times (4096/8) \times 2 \right) \div 10^{9} = 898\text{GB/s}\)
In this calculation, the memory clock rate is converted in to Hz, multiplied by the interface width (divided by 8, to convert bits to bytes) and multiplied by 2 due to the double data rate. Finally, this product is divided by 109 to convert the result to GB/s.
Note
Some calculations use 10243 instead of 109 for the final calculation. In such a case, the bandwidth would be 836.4 GiB/s. It is important to use the same divisor when calculating theoretical and effective bandwidth so that the comparison is valid.
Note
On GPUs with GDDR memory with ECC enabled the available DRAM is reduced by 6.25% to allow for the storage of ECC bits. Fetching ECC bits for each memory transaction also reduced the effective bandwidth by approximately 20% compared to the same GPU with ECC disabled, though the exact impact of ECC on bandwidth can be higher and depends on the memory access pattern. HBM2 memories, on the other hand, provide dedicated ECC resources, allowing overhead-free ECC protection.2
9.2.2. Effective Bandwidth Calculation
Effective bandwidth is calculated by timing specific program activities and by knowing how data is accessed by the program. To do so, use this equation:
\(\text{Effective\ bandwidth} = \left( {\left( B_{r} + B_{w} \right) \div 10^{9}} \right) \div \text{time}\)
Here, the effective bandwidth is in units of GB/s, Br is the number of bytes read per kernel, Bw is the number of bytes written per kernel, and time is given in seconds.
For example, to compute the effective bandwidth of a 2048 x 2048 matrix copy, the following formula could be used:
\(\text{Effective\ bandwidth} = \left( {\left( 2048^{2} \times 4 \times 2 \right) \div 10^{9}} \right) \div \text{time}\)
The number of elements is multiplied by the size of each element (4 bytes for a float), multiplied by 2 (because of the read and write), divided by 109 (or 1,0243) to obtain GB of memory transferred. This number is divided by the time in seconds to obtain GB/s.
9.2.3. Throughput Reported by Visual Profiler
For devices with compute capability of 2.0 or greater, the Visual Profiler can be used to collect several different memory throughput measures. The following throughput metrics can be displayed in the Details or Detail Graphs view:
Requested Global Load Throughput
Requested Global Store Throughput
Global Load Throughput
Global Store Throughput
DRAM Read Throughput
DRAM Write Throughput
The Requested Global Load Throughput and Requested Global Store Throughput values indicate the global memory throughput requested by the kernel and therefore correspond to the effective bandwidth obtained by the calculation shown under Effective Bandwidth Calculation.
Because the minimum memory transaction size is larger than most word sizes, the actual memory throughput required for a kernel can include the transfer of data not used by the kernel. For global memory accesses, this actual throughput is reported by the Global Load Throughput and Global Store Throughput values.
It’s important to note that both numbers are useful. The actual memory throughput shows how close the code is to the hardware limit, and a comparison of the effective or requested bandwidth to the actual bandwidth presents a good estimate of how much bandwidth is wasted by suboptimal coalescing of memory accesses (see Coalesced Access to Global Memory). For global memory accesses, this comparison of requested memory bandwidth to actual memory bandwidth is reported by the Global Memory Load Efficiency and Global Memory Store Efficiency metrics.
- 2
-
As an exception, scattered writes to HBM2 see some overhead from ECC but much less than the overhead with similar access patterns on ECC-protected GDDR5 memory.
10. Memory Optimizations
Memory optimizations are the most important area for performance. The goal is to maximize the use of the hardware by maximizing bandwidth. Bandwidth is best served by using as much fast memory and as little slow-access memory as possible. This chapter discusses the various kinds of memory on the host and device and how best to set up data items to use the memory effectively.
10.1. Data Transfer Between Host and Device
The peak theoretical bandwidth between the device memory and the GPU is much higher (898 GB/s on the NVIDIA Tesla V100, for example) than the peak theoretical bandwidth between host memory and device memory (16 GB/s on the PCIe x16 Gen3). Hence, for best overall application performance, it is important to minimize data transfer between the host and the device, even if that means running kernels on the GPU that do not demonstrate any speedup compared with running them on the host CPU.
Note
High Priority: Minimize data transfer between the host and the device, even if it means running some kernels on the device that do not show performance gains when compared with running them on the host CPU.
Intermediate data structures should be created in device memory, operated on by the device, and destroyed without ever being mapped by the host or copied to host memory.
Also, because of the overhead associated with each transfer, batching many small transfers into one larger transfer performs significantly better than making each transfer separately, even if doing so requires packing non-contiguous regions of memory into a contiguous buffer and then unpacking after the transfer.
Finally, higher bandwidth between the host and the device is achieved when using page-locked (or pinned) memory, as discussed in the CUDA C++ Programming Guide and the Pinned Memory section of this document.
10.1.1. Pinned Memory
Page-locked or pinned memory transfers attain the highest bandwidth between the host and the device. On PCIe x16 Gen3 cards, for example, pinned memory can attain roughly 12 GB/s transfer rates.
Pinned memory is allocated using the cudaHostAlloc() functions in the Runtime API. The bandwidthTest CUDA Sample shows how to use these functions as well as how to measure memory transfer performance.
For regions of system memory that have already been pre-allocated, cudaHostRegister() can be used to pin the memory on-the-fly without the need to allocate a separate buffer and copy the data into it.
Pinned memory should not be overused. Excessive use can reduce overall system performance because pinned memory is a scarce resource, but how much is too much is difficult to know in advance. Furthermore, the pinning of system memory is a heavyweight operation compared to most normal system memory allocations, so as with all optimizations, test the application and the systems it runs on for optimal performance parameters.
10.1.2. Asynchronous and Overlapping Transfers with Computation
Data transfers between the host and the device using cudaMemcpy() are blocking transfers; that is, control is returned to the host thread only after the data transfer is complete. The cudaMemcpyAsync() function is a non-blocking variant of cudaMemcpy() in which control is returned immediately to the host thread. In contrast with cudaMemcpy(), the asynchronous transfer version requires pinned host memory (see Pinned Memory), and it contains an additional argument, a stream ID. A stream is simply a sequence of operations that are performed in order on the device. Operations in different streams can be interleaved and in some cases overlapped - a property that can be used to hide data transfers between the host and the device.
Asynchronous transfers enable overlap of data transfers with computation in two different ways. On all CUDA-enabled devices, it is possible to overlap host computation with asynchronous data transfers and with device computations. For example, Asynchronous and Overlapping Transfers with Computation demonstrates how host computation in the routine cpuFunction() is performed while data is transferred to the device and a kernel using the device is executed.
Overlapping computation and data transfers
cudaMemcpyAsync(a_d, a_h, size, cudaMemcpyHostToDevice, 0);
kernel<<<grid, block>>>(a_d);
cpuFunction();
The last argument to the cudaMemcpyAsync() function is the stream ID, which in this case uses the default stream, stream 0. The kernel also uses the default stream, and it will not begin execution until the memory copy completes; therefore, no explicit synchronization is needed. Because the memory copy and the kernel both return control to the host immediately, the host function cpuFunction() overlaps their execution.
In Asynchronous and Overlapping Transfers with Computation, the memory copy and kernel execution occur sequentially. On devices that are capable of concurrent copy and compute, it is possible to overlap kernel execution on the device with data transfers between the host and the device. Whether a device has this capability is indicated by the asyncEngineCount field of the cudaDeviceProp structure (or listed in the output of the deviceQuery CUDA Sample). On devices that have this capability, the overlap once again requires pinned host memory, and, in addition, the data transfer and kernel must use different, non-default streams (streams with non-zero stream IDs). Non-default streams are required for this overlap because memory copy, memory set functions, and kernel calls that use the default stream begin only after all preceding calls on the device (in any stream) have completed, and no operation on the device (in any stream) commences until they are finished.
Asynchronous and Overlapping Transfers with Computation illustrates the basic technique.
Concurrent copy and execute
cudaStreamCreate(&stream1);
cudaStreamCreate(&stream2);
cudaMemcpyAsync(a_d, a_h, size, cudaMemcpyHostToDevice, stream1);
kernel<<<grid, block, 0, stream2>>>(otherData_d);
In this code, two streams are created and used in the data transfer and kernel executions as specified in the last arguments of the cudaMemcpyAsync call and the kernel’s execution configuration.
Asynchronous and Overlapping Transfers with Computation demonstrates how to overlap kernel execution with asynchronous data transfer. This technique could be used when the data dependency is such that the data can be broken into chunks and transferred in multiple stages, launching multiple kernels to operate on each chunk as it arrives. Sequential copy and execute and Staged concurrent copy and execute demonstrate this. They produce equivalent results. The first segment shows the reference sequential implementation, which transfers and operates on an array of N floats (where N is assumed to be evenly divisible by nThreads).
Sequential copy and execute
cudaMemcpy(a_d, a_h, N*sizeof(float), dir);
kernel<<<N/nThreads, nThreads>>>(a_d);
Staged concurrent copy and execute shows how the transfer and kernel execution can be broken up into nStreams stages. This approach permits some overlapping of the data transfer and execution.
Staged concurrent copy and execute
size=N*sizeof(float)/nStreams;
for (i=0; i<nStreams; i++) {
offset = i*N/nStreams;
cudaMemcpyAsync(a_d+offset, a_h+offset, size, dir, stream[i]);
kernel<<<N/(nThreads*nStreams), nThreads, 0,
stream[i]>>>(a_d+offset);
}
(In Staged concurrent copy and execute, it is assumed that N is evenly divisible by nThreads*nStreams.) Because execution within
a stream occurs sequentially, none of the kernels will launch until the data transfers in their respective streams complete. Current GPUs can
simultaneously process asynchronous data transfers and execute kernels. GPUs with a single copy engine can perform one asynchronous data
transfer and execute kernels whereas GPUs with two copy engines can simultaneously perform one asynchronous data transfer from the host to
the device, one asynchronous data transfer from the device to the host, and execute kernels. The number of copy engines on a GPU is given
by the asyncEngineCount field of the cudaDeviceProp structure, which is also listed in the output of the deviceQuery CUDA
Sample. (It should be mentioned that it is not possible to overlap a blocking transfer with an asynchronous transfer, because the blocking
transfer occurs in the default stream, so it will not begin until all previous CUDA calls complete. It will not allow any other CUDA call
to begin until it has completed.) A diagram depicting the timeline of execution for the two code segments is shown
in Figure 1, and nStreams is equal to 4
for Staged concurrent copy and execute in the bottom half of the figure.
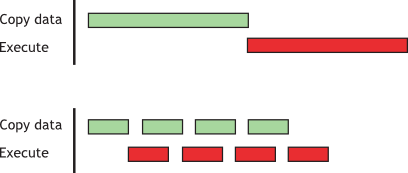
Figure 1 Timeline comparison for copy and kernel execution
- Top
-
Sequential
- Bottom
-
Concurrent
For this example, it is assumed that the data transfer and kernel execution times are comparable. In such cases, and when the execution time (tE) exceeds the transfer time (tT), a rough estimate for the overall time is tE + tT/nStreams for the staged version versus tE + tT for the sequential version. If the transfer time exceeds the execution time, a rough estimate for the overall time is tT + tE/nStreams.
10.1.3. Zero Copy
Zero copy is a feature that was added in version 2.2 of the CUDA Toolkit. It enables GPU threads to directly access host memory. For this purpose, it requires mapped pinned (non-pageable) memory. On integrated GPUs (i.e., GPUs with the integrated field of the CUDA device properties structure set to 1), mapped pinned memory is always a performance gain because it avoids superfluous copies as integrated GPU and CPU memory are physically the same. On discrete GPUs, mapped pinned memory is advantageous only in certain cases. Because the data is not cached on the GPU, mapped pinned memory should be read or written only once, and the global loads and stores that read and write the memory should be coalesced. Zero copy can be used in place of streams because kernel-originated data transfers automatically overlap kernel execution without the overhead of setting up and determining the optimal number of streams.
Note
Low Priority: Use zero-copy operations on integrated GPUs for CUDA Toolkit version 2.2 and later.
The host code in Zero-copy host code shows how zero copy is typically set up.
Zero-copy host code
float *a_h, *a_map;
...
cudaGetDeviceProperties(&prop, 0);
if (!prop.canMapHostMemory)
exit(0);
cudaSetDeviceFlags(cudaDeviceMapHost);
cudaHostAlloc(&a_h, nBytes, cudaHostAllocMapped);
cudaHostGetDevicePointer(&a_map, a_h, 0);
kernel<<<gridSize, blockSize>>>(a_map);
In this code, the canMapHostMemory field of the structure returned by cudaGetDeviceProperties() is used to check that the device
supports mapping host memory to the device’s address space. Page-locked memory mapping is enabled by calling cudaSetDeviceFlags()
with cudaDeviceMapHost. Note that cudaSetDeviceFlags() must be called prior to setting a device or making a CUDA call that
requires state (that is, essentially, before a context is created). Page-locked mapped host memory is allocated using cudaHostAlloc(),
and the pointer to the mapped device address space is obtained via the function cudaHostGetDevicePointer(). In the code
in Zero-copy host code, kernel() can reference the mapped pinned host memory using the pointer a_map in exactly the
same was as it would if a_map referred to a location in device memory.
Note
Mapped pinned host memory allows you to overlap CPU-GPU memory transfers with computation while avoiding the use of CUDA streams. But since any repeated access to such memory areas causes repeated CPU-GPU transfers, consider creating a second area in device memory to manually cache the previously read host memory data.
10.1.4. Unified Virtual Addressing
Devices of compute capability 2.0 and later support a special addressing mode called Unified Virtual Addressing (UVA) on 64-bit Linux and Windows. With UVA, the host memory and the device memories of all installed supported devices share a single virtual address space.
Prior to UVA, an application had to keep track of which pointers referred to device memory (and for which device) and which referred to host memory as a separate bit of metadata (or as hard-coded information in the program) for each pointer. Using UVA, on the other hand, the physical memory space to which a pointer points can be determined simply by inspecting the value of the pointer using cudaPointerGetAttributes().
Under UVA, pinned host memory allocated with cudaHostAlloc() will have identical host and device pointers, so it is not necessary to call cudaHostGetDevicePointer() for such allocations. Host memory allocations pinned after-the-fact via cudaHostRegister(), however, will continue to have different device pointers than their host pointers, so cudaHostGetDevicePointer() remains necessary in that case.
UVA is also a necessary precondition for enabling peer-to-peer (P2P) transfer of data directly across the PCIe bus or NVLink for supported GPUs in supported configurations, bypassing host memory.
See the CUDA C++ Programming Guide for further explanations and software requirements for UVA and P2P.
10.2. Device Memory Spaces
CUDA devices use several memory spaces, which have different characteristics that reflect their distinct usages in CUDA applications. These memory spaces include global, local, shared, texture, and registers, as shown in Figure 2.
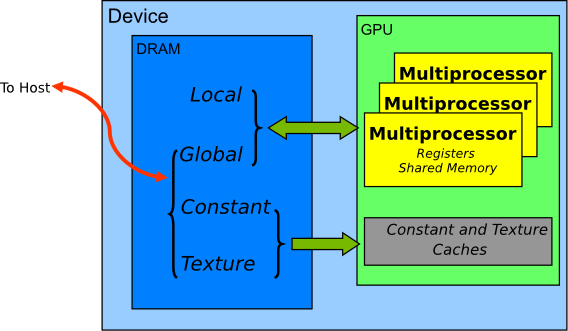
Figure 2 Memory spaces on a CUDA device
Of these different memory spaces, global memory is the most plentiful; see Features and Technical Specifications of the CUDA C++ Programming Guide for the amounts of memory available in each memory space at each compute capability level. Global, local, and texture memory have the greatest access latency, followed by constant memory, shared memory, and the register file.
The various principal traits of the memory types are shown in Table 1.
Memory |
Location on/off chip |
Cached |
Access |
Scope |
Lifetime |
|---|---|---|---|---|---|
Register |
On |
n/a |
R/W |
1 thread |
Thread |
Local |
Off |
Yes†† |
R/W |
1 thread |
Thread |
Shared |
On |
n/a |
R/W |
All threads in block |
Block |
Global |
Off |
† |
R/W |
All threads + host |
Host allocation |
Constant |
Off |
Yes |
R |
All threads + host |
Host allocation |
Texture |
Off |
Yes |
R |
All threads + host |
Host allocation |
† Cached in L1 and L2 by default on devices of compute capability 6.0 and 7.x; cached only in L2 by default on devices of lower compute capabilities, though some allow opt-in to caching in L1 as well via compilation flags. |
|||||
†† Cached in L1 and L2 by default except on devices of compute capability 5.x; devices of compute capability 5.x cache locals only in L2. |
In the case of texture access, if a texture reference is bound to a linear array in global memory, then the device code can write to the underlying array. Texture references that are bound to CUDA arrays can be written to via surface-write operations by binding a surface to the same underlying CUDA array storage). Reading from a texture while writing to its underlying global memory array in the same kernel launch should be avoided because the texture caches are read-only and are not invalidated when the associated global memory is modified.
10.2.1. Coalesced Access to Global Memory
A very important performance consideration in programming for CUDA-capable GPU architectures is the coalescing of global memory accesses. Global memory loads and stores by threads of a warp are coalesced by the device into as few as possible transactions.
Note
High Priority: Ensure global memory accesses are coalesced whenever possible.
The access requirements for coalescing depend on the compute capability of the device and are documented in the CUDA C++ Programming Guide.
For devices of compute capability 6.0 or higher, the requirements can be summarized quite easily: the concurrent accesses of the threads of a warp will coalesce into a number of transactions equal to the number of 32-byte transactions necessary to service all of the threads of the warp.
For certain devices of compute capability 5.2, L1-caching of accesses to global memory can be optionally enabled. If L1-caching is enabled on these devices, the number of required transactions is equal to the number of required 128-byte aligned segments.
Note
On devices of compute capability 6.0 or higher, L1-caching is the default, however the data access unit is 32-byte regardless of whether global loads are cached in L1 or not.
On devices with GDDR memory, accessing memory in a coalesced way is even more important when ECC is turned on. Scattered accesses increase ECC memory transfer overhead, especially when writing data to global memory.
Coalescing concepts are illustrated in the following simple examples. These examples assume compute capability 6.0 or higher and that accesses are for 4-byte words, unless otherwise noted.
10.2.1.1. A Simple Access Pattern
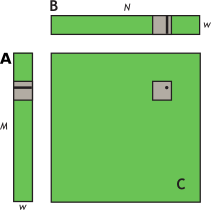
The first and simplest case of coalescing can be achieved by any CUDA-enabled device of compute capability 6.0 or higher: the k-th thread accesses the k-th word in a 32-byte aligned array. Not all threads need to participate.
For example, if the threads of a warp access adjacent 4-byte words (e.g., adjacent float values), four coalesced 32-byte
transactions will service that memory access. Such a pattern is shown in Figure 3 <coalesced-access-figure>.
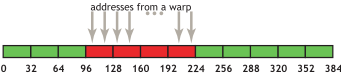
Figure 3 Coalesced access
This access pattern results in four 32-byte transactions, indicated by the red rectangles.
If from any of the four 32-byte segments only a subset of the words are requested (e.g. if several threads had accessed the same word or if some threads did not participate in the access), the full segment is fetched anyway. Furthermore, if accesses by the threads of the warp had been permuted within or accross the four segments, still only four 32-byte transactions would have been performed by a device with compute capability 6.0 or higher.
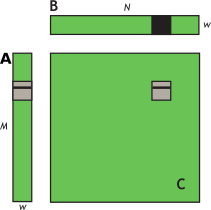
10.2.1.2. A Sequential but Misaligned Access Pattern
If sequential threads in a warp access memory that is sequential but not aligned with a 32-byte segment, five 32-byte segments will be requested, as shown in Figure 4.

Figure 4 Misaligned sequential addresses that fall within five 32-byte segments
Memory allocated through the CUDA Runtime API, such as via cudaMalloc(), is guaranteed to be aligned to at least 256 bytes. Therefore, choosing sensible thread block sizes, such as multiples of the warp size (i.e., 32 on current GPUs), facilitates memory accesses by warps that are properly aligned. (Consider what would happen to the memory addresses accessed by the second, third, and subsequent thread blocks if the thread block size was not a multiple of warp size, for example.)
10.2.1.3. Effects of Misaligned Accesses
It is easy and informative to explore the ramifications of misaligned accesses using a simple copy kernel, such as the one in A copy kernel that illustrates misaligned accesses.
A copy kernel that illustrates misaligned accesses
__global__ void offsetCopy(float *odata, float* idata, int offset)
{
int xid = blockIdx.x * blockDim.x + threadIdx.x + offset;
odata[xid] = idata[xid];
}
In A copy kernel that illustrates misaligned accesses, data is copied from the input array idata to the output array, both
of which exist in global memory. The kernel is executed within a loop in host code that varies the parameter offset from 0 to 32
(for example, Figure 4 corresponds to this misalignments).
The effective bandwidth for the copy with various offsets on an NVIDIA Tesla V100 (compute capability 7.0)
is shown in Figure 5.
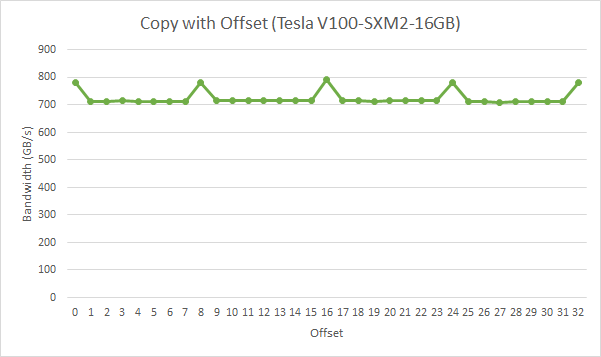
Figure 5 Performance of offsetCopy kernel
For the NVIDIA Tesla V100, global memory accesses with no offset or with offsets that are multiples of 8 words result in four 32-byte transactions. The achieved bandwidth is approximately 790 GB/s. Otherwise, five 32-byte segments are loaded per warp, and we would expect approximately 4/5th of the memory throughput achieved with no offsets.
In this particular example, the offset memory throughput achieved is, however, approximately 9/10th, because adjacent warps reuse the cache lines their neighbors fetched. So while the impact is still evident it is not as large as we might have expected. It would have been more so if adjacent warps had not exhibited such a high degree of reuse of the over-fetched cache lines.
10.2.1.4. Strided Accesses
As seen above, in the case of misaligned sequential accesses, caches help to alleviate the performance impact. It may be different with non-unit-strided accesses, however, and this is a pattern that occurs frequently when dealing with multidimensional data or matrices. For this reason, ensuring that as much as possible of the data in each cache line fetched is actually used is an important part of performance optimization of memory accesses on these devices.
To illustrate the effect of strided access on effective bandwidth, see the kernel strideCopy() in A kernel to illustrate non-unit stride data copy, which copies data with a stride of stride elements between threads from idata to odata.
A kernel to illustrate non-unit stride data copy
__global__ void strideCopy(float *odata, float* idata, int stride)
{
int xid = (blockIdx.x*blockDim.x + threadIdx.x)*stride;
odata[xid] = idata[xid];
}
Figure 6 illustrates such a situation; in this case, threads within a warp access words in memory with a stride of 2. This action leads to a load of eight L2 cache segments per warp on the Tesla V100 (compute capability 7.0).
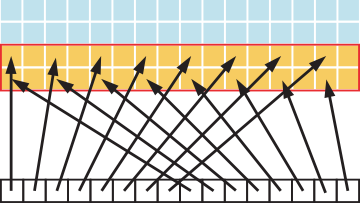
Figure 6 Adjacent threads accessing memory with a stride of 2
A stride of 2 results in a 50% of load/store efficiency since half the elements in the transaction are not used and represent wasted bandwidth. As the stride increases, the effective bandwidth decreases until the point where 32 32-byte segments are loaded for the 32 threads in a warp, as indicated in Figure 7.
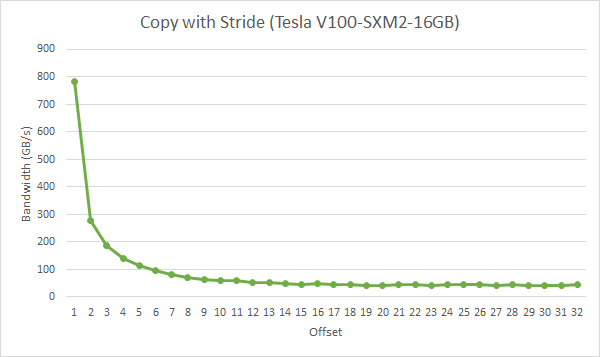
Figure 7 Performance of strideCopy kernel
As illustrated in Figure 7, non-unit-stride global memory accesses should be avoided whenever possible. One method for doing so utilizes shared memory, which is discussed in the next section.
10.2.2. L2 Cache
Starting with CUDA 11.0, devices of compute capability 8.0 and above have the capability to influence persistence of data in the L2 cache. Because L2 cache is on-chip, it potentially provides higher bandwidth and lower latency accesses to global memory.
For more details refer to the L2 Access Management section in the CUDA C++ Programming Guide.
10.2.2.1. L2 Cache Access Window
When a CUDA kernel accesses a data region in the global memory repeatedly, such data accesses can be considered to be persisting. On the other hand, if the data is only accessed once, such data accesses can be considered to be streaming. A portion of the L2 cache can be set aside for persistent accesses to a data region in global memory. If this set-aside portion is not used by persistent accesses, then streaming or normal data accesses can use it.
The L2 cache set-aside size for persisting accesses may be adjusted, within limits:
cudaGetDeviceProperties(&prop, device_id);
cudaDeviceSetLimit(cudaLimitPersistingL2CacheSize, prop.persistingL2CacheMaxSize); /* Set aside max possible size of L2 cache for persisting accesses */
Mapping of user data to L2 set-aside portion can be controlled using an access policy window on a CUDA stream or CUDA graph kernel node. The example below shows how to use the access policy window on a CUDA stream.
cudaStreamAttrValue stream_attribute; // Stream level attributes data structure
stream_attribute.accessPolicyWindow.base_ptr = reinterpret_cast<void*>(ptr); // Global Memory data pointer
stream_attribute.accessPolicyWindow.num_bytes = num_bytes; // Number of bytes for persisting accesses.
// (Must be less than cudaDeviceProp::accessPolicyMaxWindowSize)
stream_attribute.accessPolicyWindow.hitRatio = 1.0; // Hint for L2 cache hit ratio for persisting accesses in the num_bytes region
stream_attribute.accessPolicyWindow.hitProp = cudaAccessPropertyPersisting; // Type of access property on cache hit
stream_attribute.accessPolicyWindow.missProp = cudaAccessPropertyStreaming; // Type of access property on cache miss.
//Set the attributes to a CUDA stream of type cudaStream_t
cudaStreamSetAttribute(stream, cudaStreamAttributeAccessPolicyWindow, &stream_attribute);
The access policy window requires a value for hitRatio and num_bytes. Depending on the value of the num_bytes parameter and the size of L2 cache, one may need to tune the value of hitRatio to avoid thrashing of L2 cache lines.
10.2.2.2. Tuning the Access Window Hit-Ratio
The hitRatio parameter can be used to specify the fraction of accesses that receive the hitProp property. For example, if the hitRatio value is 0.6, 60% of the memory accesses in the global memory region [ptr..ptr+num_bytes) have the persisting property and 40% of the memory accesses have the streaming property. To understand the effect of hitRatio and num_bytes, we use a sliding window micro benchmark.
This microbenchmark uses a 1024 MB region in GPU global memory. First, we set aside 30 MB of the L2 cache for persisting accesses using cudaDeviceSetLimit(), as discussed above. Then, as shown in the figure below, we specify that the accesses to the first freqSize * sizeof(int) bytes of the memory region are persistent. This data will thus use the L2 set-aside portion. In our experiment, we vary the size of this persistent data region from 10 MB to 60 MB to model various scenarios where data fits in or exceeds the available L2 set-aside portion of 30 MB. Note that the NVIDIA Tesla A100 GPU has 40 MB of total L2 cache capacity. Accesses to the remaining data of the memory region (i.e., streaming data) are considered normal or streaming accesses and will thus use the remaining 10 MB of the non set-aside L2 portion (unless part of the L2 set-aside portion is unused).
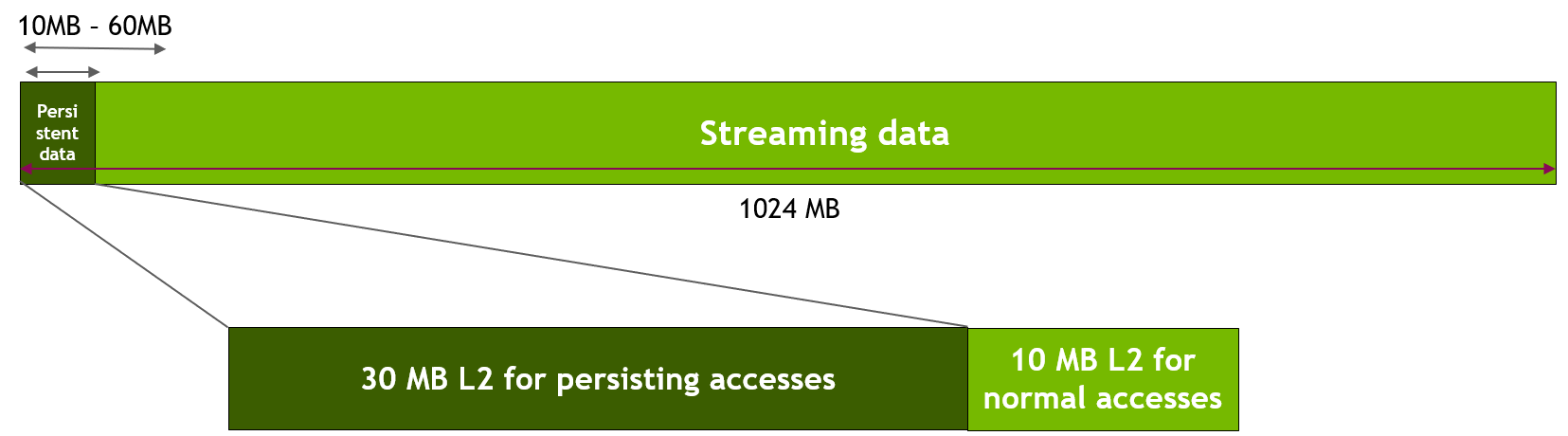
Figure 8 Mapping Persistent data accesses to set-aside L2 in sliding window experiment
Consider the following kernel code and access window parameters, as the implementation of the sliding window experiment.
__global__ void kernel(int *data_persistent, int *data_streaming, int dataSize, int freqSize) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
/*Each CUDA thread accesses one element in the persistent data section
and one element in the streaming data section.
Because the size of the persistent memory region (freqSize * sizeof(int) bytes) is much
smaller than the size of the streaming memory region (dataSize * sizeof(int) bytes), data
in the persistent region is accessed more frequently*/
data_persistent[tid % freqSize] = 2 * data_persistent[tid % freqSize];
data_streaming[tid % dataSize] = 2 * data_streaming[tid % dataSize];
}
stream_attribute.accessPolicyWindow.base_ptr = reinterpret_cast<void*>(data_persistent);
stream_attribute.accessPolicyWindow.num_bytes = freqSize * sizeof(int); //Number of bytes for persisting accesses in range 10-60 MB
stream_attribute.accessPolicyWindow.hitRatio = 1.0; //Hint for cache hit ratio. Fixed value 1.0
The performance of the above kernel is shown in the chart below. When the persistent data region fits well into the 30 MB set-aside portion of the L2 cache, a performance increase of as much as 50% is observed. However, once the size of this persistent data region exceeds the size of the L2 set-aside cache portion, approximately 10% performance drop is observed due to thrashing of L2 cache lines.
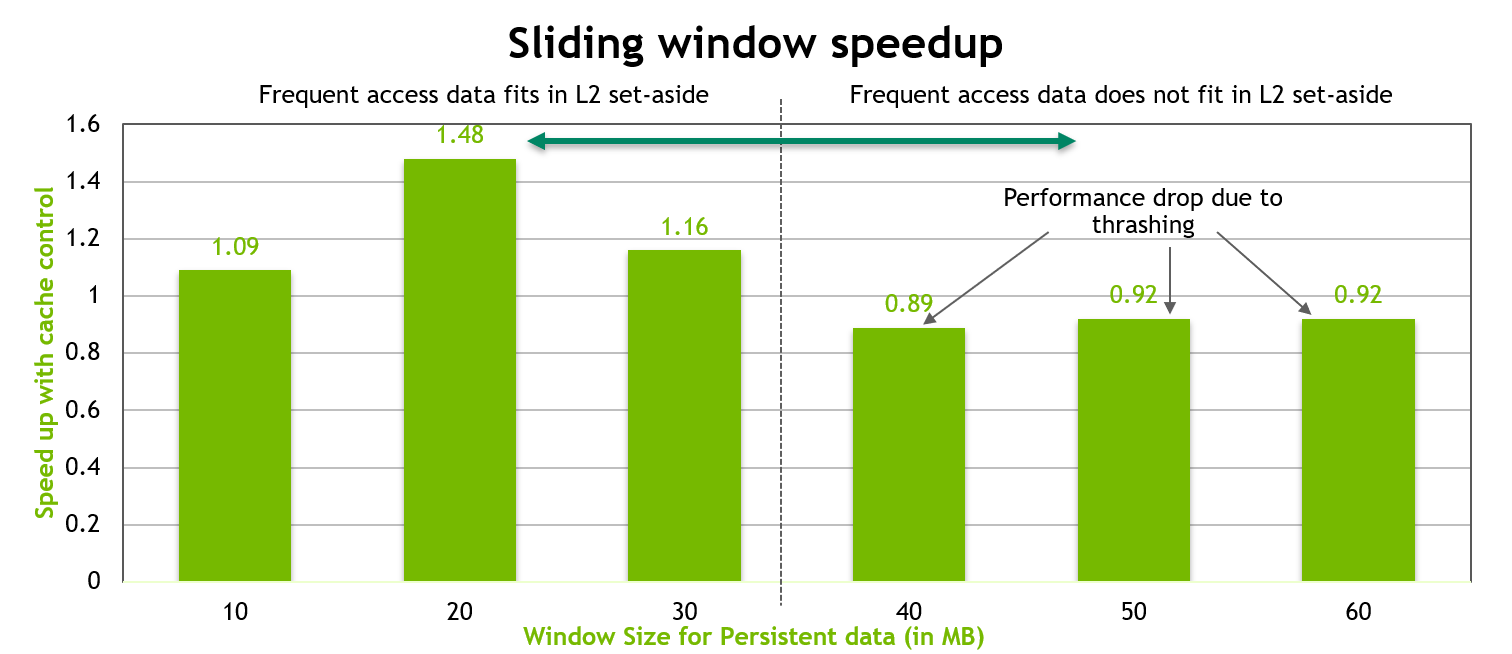
Figure 9 The performance of the sliding-window benchmark with fixed hit-ratio of 1.0
In order to optimize the performance, when the size of the persistent data is more than the size of the set-aside L2 cache portion, we tune the num_bytes and hitRatio parameters in the access window as below.
stream_attribute.accessPolicyWindow.base_ptr = reinterpret_cast<void*>(data_persistent);
stream_attribute.accessPolicyWindow.num_bytes = 20*1024*1024; //20 MB
stream_attribute.accessPolicyWindow.hitRatio = (20*1024*1024)/((float)freqSize*sizeof(int)); //Such that up to 20MB of data is resident.
We fix the num_bytes in the access window to 20 MB and tune the hitRatio such that a random 20 MB of the total persistent data is resident in the L2 set-aside cache portion. The remaining portion of this persistent data will be accessed using the streaming property. This helps in reducing cache thrashing. The results are shown in the chart below, where we see good performance regardless of whether the persistent data fits in the L2 set-aside or not.
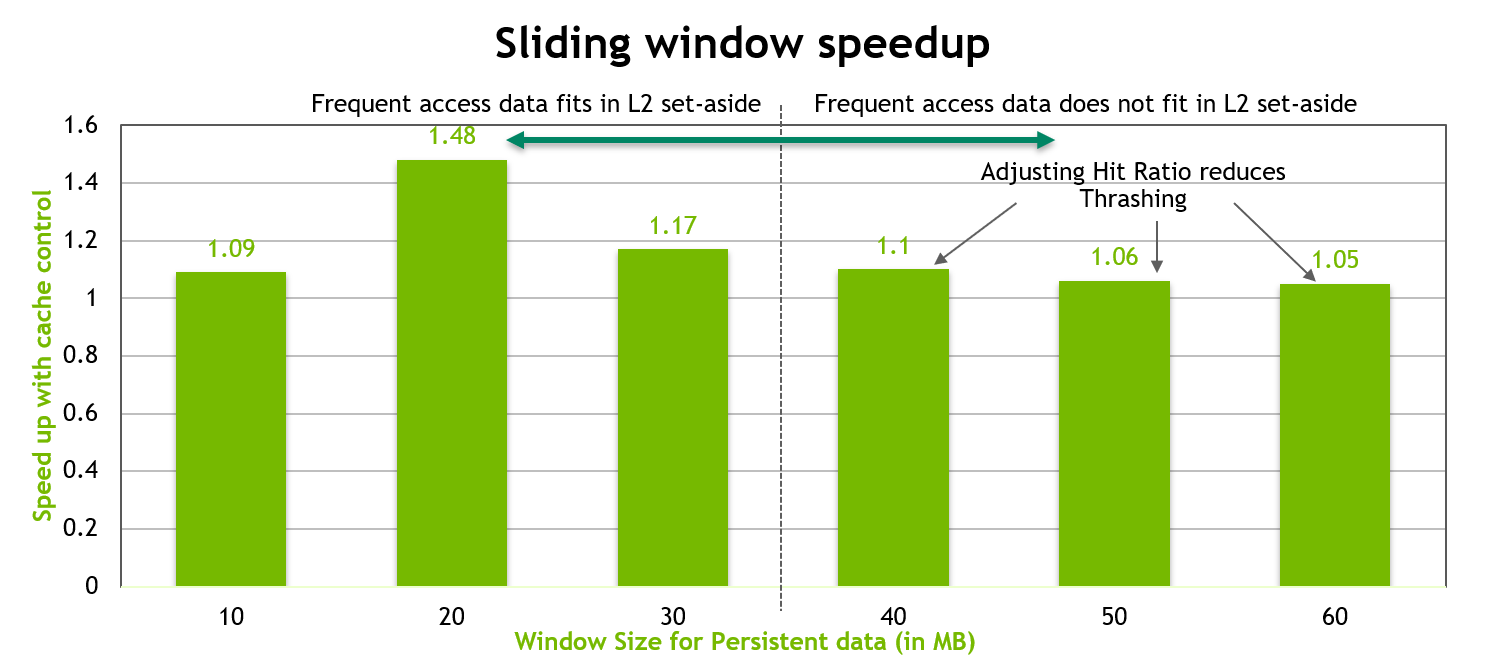
Figure 10 The performance of the sliding-window benchmark with tuned hit-ratio
10.2.4. Local Memory
Local memory is so named because its scope is local to the thread, not because of its physical location. In fact, local memory is off-chip. Hence, access to local memory is as expensive as access to global memory. In other words, the term local in the name does not imply faster access.
Local memory is used only to hold automatic variables. This is done by the nvcc compiler when it determines that there is insufficient register space to hold the variable. Automatic variables that are likely to be placed in local memory are large structures or arrays that would consume too much register space and arrays that the compiler determines may be indexed dynamically.
Inspection of the PTX assembly code (obtained by compiling with -ptx or -keep command-line options to nvcc) reveals whether a variable has been placed in local memory during the first compilation phases. If it has, it will be declared using the .local mnemonic and accessed using the ld.local and st.local mnemonics. If it has not, subsequent compilation phases might still decide otherwise, if they find the variable consumes too much register space for the targeted architecture. There is no way to check this for a specific variable, but the compiler reports total local memory usage per kernel (lmem) when run with the--ptxas-options=-v option.
10.2.5. Texture Memory
The read-only texture memory space is cached. Therefore, a texture fetch costs one device memory read only on a cache miss; otherwise, it just costs one read from the texture cache. The texture cache is optimized for 2D spatial locality, so threads of the same warp that read texture addresses that are close together will achieve best performance. Texture memory is also designed for streaming fetches with a constant latency; that is, a cache hit reduces DRAM bandwidth demand, but not fetch latency.
In certain addressing situations, reading device memory through texture fetching can be an advantageous alternative to reading device memory from global or constant memory.
10.2.5.1. Additional Texture Capabilities
If textures are fetched using tex1D(),tex2D(), or tex3D() rather than tex1Dfetch(), the hardware provides other capabilities that might be useful for some applications such as image processing, as shown in Table 4.
Feature |
Use |
Caveat |
|---|---|---|
Filtering |
Fast, low-precision interpolation between texels |
Valid only if the texture reference returns floating-point data |
Normalized texture coordinates |
Resolution-independent coding |
None |
Addressing modes |
Automatic handling of boundary cases1 |
Can be used only with normalized texture coordinates |
1 The automatic handling of boundary cases in the bottom row of Table 4 refers to how a texture coordinate is resolved when it falls outside the valid addressing range. There are two options: clamp and wrap. If x is the coordinate and N is the number of texels for a one-dimensional texture, then with clamp, x is replaced by 0 if x < 0 and by 1-1/N if 1 <x. With wrap, x is replaced by frac(x) where frac(x) = x - floor(x). Floor returns the largest integer less than or equal to x. So, in clamp mode where N = 1, an x of 1.3 is clamped to 1.0; whereas in wrap mode, it is converted to 0.3 |
Within a kernel call, the texture cache is not kept coherent with respect to global memory writes, so texture fetches from addresses that have been written via global stores in the same kernel call return undefined data. That is, a thread can safely read a memory location via texture if the location has been updated by a previous kernel call or memory copy, but not if it has been previously updated by the same thread or another thread within the same kernel call.
10.2.6. Constant Memory
There is a total of 64 KB constant memory on a device. The constant memory space is cached. As a result, a read from constant memory costs one memory read from device memory only on a cache miss; otherwise, it just costs one read from the constant cache. Accesses to different addresses by threads within a warp are serialized, thus the cost scales linearly with the number of unique addresses read by all threads within a warp. As such, the constant cache is best when threads in the same warp accesses only a few distinct locations. If all threads of a warp access the same location, then constant memory can be as fast as a register access.
10.2.7. Registers
Generally, accessing a register consumes zero extra clock cycles per instruction, but delays may occur due to register read-after-write dependencies and register memory bank conflicts.
The compiler and hardware thread scheduler will schedule instructions as optimally as possible to avoid register memory bank conflicts. An application has no direct control over these bank conflicts. In particular, there is no register-related reason to pack data into vector data types such as float4 or int4 types.
10.2.7.1. Register Pressure
Register pressure occurs when there are not enough registers available for a given task. Even though each multiprocessor contains thousands of 32-bit registers (see Features and Technical Specifications of the CUDA C++ Programming Guide), these are partitioned among concurrent threads. To prevent the compiler from allocating too many registers, use the -maxrregcount=N compiler command-line option or the launch bounds kernel definition qualifier (see Execution Configuration of the CUDA C++ Programming Guide) to control the maximum number of registers to allocated per thread.
10.3. Allocation
Device memory allocation and de-allocation via cudaMalloc() and cudaFree() are expensive operations. It is recommended to use cudaMallocAsync() and cudaFreeAsync() which are stream ordered pool allocators to manage device memory.
10.4. NUMA Best Practices
Some recent Linux distributions enable automatic NUMA balancing (or “AutoNUMA”) by default. In some instances, operations performed by automatic NUMA balancing may degrade the performance of applications running on NVIDIA GPUs. For optimal performance, users should manually tune the NUMA characteristics of their application.
The optimal NUMA tuning will depend on the characteristics and desired hardware affinities of each application and node, but in general applications computing on NVIDIA GPUs are advised to choose a policy that disables automatic NUMA balancing. For example, on IBM Newell POWER9 nodes (where the CPUs correspond to NUMA nodes 0 and 8), use:
numactl --membind=0,8
to bind memory allocations to the CPUs.
11. Execution Configuration Optimizations
One of the keys to good performance is to keep the multiprocessors on the device as busy as possible. A device in which work is poorly balanced across the multiprocessors will deliver suboptimal performance. Hence, it’s important to design your application to use threads and blocks in a way that maximizes hardware utilization and to limit practices that impede the free distribution of work. A key concept in this effort is occupancy, which is explained in the following sections.
Hardware utilization can also be improved in some cases by designing your application so that multiple, independent kernels can execute at the same time. Multiple kernels executing at the same time is known as concurrent kernel execution. Concurrent kernel execution is described below.
Another important concept is the management of system resources allocated for a particular task. How to manage this resource utilization is discussed in the final sections of this chapter.
11.1. Occupancy
Thread instructions are executed sequentially in CUDA, and, as a result, executing other warps when one warp is paused or stalled is the only way to hide latencies and keep the hardware busy. Some metric related to the number of active warps on a multiprocessor is therefore important in determining how effectively the hardware is kept busy. This metric is occupancy.
Occupancy is the ratio of the number of active warps per multiprocessor to the maximum number of possible active warps. (To determine the latter number, see the deviceQuery CUDA Sample or refer to Compute Capabilities.) Another way to view occupancy is the percentage of the hardware’s ability to process warps that is actively in use.
Higher occupancy does not always equate to higher performance-there is a point above which additional occupancy does not improve performance. However, low occupancy always interferes with the ability to hide memory latency, resulting in performance degradation.
Per thread resources required by a CUDA kernel might limit the maximum block size in an unwanted way. In order to maintain forward compatibility to future hardware and toolkits and to ensure that at least one thread block can run on an SM, developers should include the single argument __launch_bounds__(maxThreadsPerBlock) which specifies the largest block size that the kernel will be launched with. Failure to do so could lead to “too many resources requested for launch” errors. Providing the two argument version of __launch_bounds__(maxThreadsPerBlock,minBlocksPerMultiprocessor) can improve performance in some cases. The right value for minBlocksPerMultiprocessor should be determined using a detailed per kernel analysis.
11.1.1. Calculating Occupancy
One of several factors that determine occupancy is register availability. Register storage enables threads to keep local variables nearby for low-latency access. However, the set of registers (known as the register file) is a limited commodity that all threads resident on a multiprocessor must share. Registers are allocated to an entire block all at once. So, if each thread block uses many registers, the number of thread blocks that can be resident on a multiprocessor is reduced, thereby lowering the occupancy of the multiprocessor. The maximum number of registers per thread can be set manually at compilation time per-file using the -maxrregcount option or per-kernel using the __launch_bounds__ qualifier (see Register Pressure).
For purposes of calculating occupancy, the number of registers used by each thread is one of the key factors. For example, on devices of CUDA Compute Capability 7.0 each multiprocessor has 65,536 32-bit registers and can have a maximum of 2048 simultaneous threads resident (64 warps x 32 threads per warp). This means that in one of these devices, for a multiprocessor to have 100% occupancy, each thread can use at most 32 registers. However, this approach of determining how register count affects occupancy does not take into account the register allocation granularity. For example, on a device of compute capability 7.0, a kernel with 128-thread blocks using 37 registers per thread results in an occupancy of 75% with 12 active 128-thread blocks per multi-processor, whereas a kernel with 320-thread blocks using the same 37 registers per thread results in an occupancy of 63% because only four 320-thread blocks can reside on a multiprocessor. Furthermore, register allocations are rounded up to the nearest 256 registers per warp.
The number of registers available, the maximum number of simultaneous threads resident on each multiprocessor, and the register allocation granularity vary over different
compute capabilities. Because of these nuances in register allocation and the fact that a multiprocessor’s shared memory is also partitioned between resident thread blocks,
the exact relationship between register usage and occupancy can be difficult to determine. The --ptxas options=v option of nvcc details the number of registers
used per thread for each kernel. See Hardware Multithreading of the CUDA C++ Programming Guide for the register allocation formulas for devices of various compute
capabilities and Features and Technical Specifications of the CUDA C++ Programming Guide for the total number of registers available on those devices. Alternatively,
NVIDIA provides an occupancy calculator as part of Nsight Compute; refer to https://docs.nvidia.com/nsight-compute/NsightCompute/index.html#occupancy-calculator.
Figure 15 Using the CUDA Occupancy Calculator to project GPU multiprocessor occupancy
An application can also use the Occupancy API from the CUDA Runtime, e.g. cudaOccupancyMaxActiveBlocksPerMultiprocessor, to dynamically select launch configurations based on runtime parameters.
11.2. Hiding Register Dependencies
Note
Medium Priority: To hide latency arising from register dependencies, maintain sufficient numbers of active threads per multiprocessor (i.e., sufficient occupancy).
Register dependencies arise when an instruction uses a result stored in a register written by an instruction before it. The latency of most arithmetic instructions is typically 4 cycles on devices of compute capability 7.0. So threads must wait approximatly 4 cycles before using an arithmetic result. However, this latency can be completely hidden by the execution of threads in other warps. See Registers for details.
11.3. Thread and Block Heuristics
Note
Medium Priority: The number of threads per block should be a multiple of 32 threads, because this provides optimal computing efficiency and facilitates coalescing.
The dimension and size of blocks per grid and the dimension and size of threads per block are both important factors. The multidimensional aspect of these parameters allows easier mapping of multidimensional problems to CUDA and does not play a role in performance. As a result, this section discusses size but not dimension.
Latency hiding and occupancy depend on the number of active warps per multiprocessor, which is implicitly determined by the execution parameters along with resource (register and shared memory) constraints. Choosing execution parameters is a matter of striking a balance between latency hiding (occupancy) and resource utilization.
Choosing the execution configuration parameters should be done in tandem; however, there are certain heuristics that apply to each parameter individually. When choosing the first execution configuration parameter-the number of blocks per grid, or grid size - the primary concern is keeping the entire GPU busy. The number of blocks in a grid should be larger than the number of multiprocessors so that all multiprocessors have at least one block to execute. Furthermore, there should be multiple active blocks per multiprocessor so that blocks that aren’t waiting for a __syncthreads() can keep the hardware busy. This recommendation is subject to resource availability; therefore, it should be determined in the context of the second execution parameter - the number of threads per block, or block size - as well as shared memory usage. To scale to future devices, the number of blocks per kernel launch should be in the thousands.
When choosing the block size, it is important to remember that multiple concurrent blocks can reside on a multiprocessor, so occupancy is not determined by block size alone. In particular, a larger block size does not imply a higher occupancy.
As mentioned in Occupancy, higher occupancy does not always equate to better performance. For example, improving occupancy from 66 percent to 100 percent generally does not translate to a similar increase in performance. A lower occupancy kernel will have more registers available per thread than a higher occupancy kernel, which may result in less register spilling to local memory; in particular, with a high degree of exposed instruction-level parallelism (ILP) it is, in some cases, possible to fully cover latency with a low occupancy.
There are many such factors involved in selecting block size, and inevitably some experimentation is required. However, a few rules of thumb should be followed:
Threads per block should be a multiple of warp size to avoid wasting computation on under-populated warps and to facilitate coalescing.
A minimum of 64 threads per block should be used, and only if there are multiple concurrent blocks per multiprocessor.
Between 128 and 256 threads per block is a good initial range for experimentation with different block sizes.
Use several smaller thread blocks rather than one large thread block per multiprocessor if latency affects performance. This is particularly beneficial to kernels that frequently call
__syncthreads().
Note that when a thread block allocates more registers than are available on a multiprocessor, the kernel launch fails, as it will when too much shared memory or too many threads are requested.
11.5. Concurrent Kernel Execution
As described in Asynchronous and Overlapping Transfers with Computation, CUDA streams can be used to overlap kernel execution with data transfers. On devices that are capable of concurrent kernel execution, streams can also be used to execute multiple kernels simultaneously to more fully take advantage of the device’s multiprocessors. Whether a device has this capability is indicated by the concurrentKernels field of the cudaDeviceProp structure (or listed in the output of the deviceQuery CUDA Sample). Non-default streams (streams other than stream 0) are required for concurrent execution because kernel calls that use the default stream begin only after all preceding calls on the device (in any stream) have completed, and no operation on the device (in any stream) commences until they are finished.
The following example illustrates the basic technique. Because kernel1 and kernel2 are executed in different, non-default streams, a capable device can execute the kernels at the same time.
cudaStreamCreate(&stream1);
cudaStreamCreate(&stream2);
kernel1<<<grid, block, 0, stream1>>>(data_1);
kernel2<<<grid, block, 0, stream2>>>(data_2);
11.6. Multiple contexts
CUDA work occurs within a process space for a particular GPU known as a context. The context encapsulates kernel launches and memory allocations for that GPU as well as supporting constructs such as the page tables. The context is explicit in the CUDA Driver API but is entirely implicit in the CUDA Runtime API, which creates and manages contexts automatically.
With the CUDA Driver API, a CUDA application process can potentially create more than one context for a given GPU. If multiple CUDA application processes access the same GPU concurrently, this almost always implies multiple contexts, since a context is tied to a particular host process unless Multi-Process Service is in use.
While multiple contexts (and their associated resources such as global memory allocations) can be allocated concurrently on a given GPU, only one of these contexts can execute work at any given moment on that GPU; contexts sharing the same GPU are time-sliced. Creating additional contexts incurs memory overhead for per-context data and time overhead for context switching. Furthermore, the need for context switching can reduce utilization when work from several contexts could otherwise execute concurrently (see also Concurrent Kernel Execution).
Therefore, it is best to avoid multiple contexts per GPU within the same CUDA application. To assist with this, the CUDA Driver API provides methods to access and manage a special context on each GPU called the primary context. These are the same contexts used implicitly by the CUDA Runtime when there is not already a current context for a thread.
// When initializing the program/library
CUcontext ctx;
cuDevicePrimaryCtxRetain(&ctx, dev);
// When the program/library launches work
cuCtxPushCurrent(ctx);
kernel<<<...>>>(...);
cuCtxPopCurrent(&ctx);
// When the program/library is finished with the context
cuDevicePrimaryCtxRelease(dev);
Note
NVIDIA-SMI can be used to configure a GPU for exclusive process mode, which limits the number of contexts per GPU to one. This context can be current to as many threads as desired within the creating process, and cuDevicePrimaryCtxRetain will fail if a non-primary context that was created with the CUDA driver API already exists on the device.
12. Instruction Optimization
Awareness of how instructions are executed often permits low-level optimizations that can be useful, especially in code that is run frequently (the so-called hot spot in a program). Best practices suggest that this optimization be performed after all higher-level optimizations have been completed.
12.1. Arithmetic Instructions
To maximize instruction throughput the application should:
Minimize the use of arithmetic instructions with low throughput; this includes trading precision for speed when it does not affect the end result, such as using intrinsic instead of regular functions (intrinsic functions are listed in the CUDA C++ Programming Guide), single-precision instead of double-precision, or flushing denormalized numbers to zero;
Minimize divergent warps caused by control flow instructions as detailed in Control Flow Instructions
Reduce the number of instructions, for example, by optimizing out synchronization points whenever possible as described in Synchronization Instruction or by using restricted pointers as described in the CUDA C++ Programming Guide.
In this section, throughputs are given in number of operations per clock cycle per multiprocessor. For a warp size of 32, one instruction corresponds to 32 operations, so if N is the number of operations per clock cycle, the instruction throughput is N/32 instructions per clock cycle.
All throughputs are for one multiprocessor. They must be multiplied by the number of multiprocessors in the device to get throughput for the whole device.
12.1.1. Throughput of Native Arithmetic Instructions
The following table gives the throughputs of the arithmetic instructions that are natively supported in hardware for devices of various compute capabilities.
Note
This table reflects the max theoretical throughput of the mentioned operations.
In some cases, these throughputs may only be achieved via specific sequences of instructions that require special care when using a compiler.
Most rows provide a PTX instruction as an example of lower-level instruction expected to achieve the listed throughput. This PTX instruction may not be the only instructions able to perform the described operation(s).
Compute Capability |
7.5 |
8.0 |
8.6 |
8.9 |
9.0 |
10.0 |
12.0 |
|---|---|---|---|---|---|---|---|
16-bit floating-point add, multiply, multiply-add (2-way SIMD): |
64 3 |
128 4 |
64 |
128 |
64 |
||
32-bit floating-point add, multiply, multiply-add: |
64 |
128 |
|||||
64-bit floating-point add, multiply, multiply-add: |
2 |
32 |
2 |
64 |
64 |
2 |
|
32-bit approximate floating-point reciprocal, reciprocal square root, base-2 logarithm, base 2 exponential, sine, cosine: |
165 |
||||||
32-bit integer add, subtract: |
128 |
||||||
32-bit integer extended-precision add, extended-precision subtract, 3-operand addition: multiple PTX instructions |
64 |
||||||
32-bit integer multiply, multiply-add, extended-precision multiply-add: |
646 |
||||||
32-bit integer shift: |
64 |
||||||
64-bit integer add: |
32 |
64 |
|||||
32-bit integer compare, minimum, maximum: |
64 |
128 |
|||||
32-bit integer bit reverse: |
64 |
||||||
32-bit bitwise AND, OR, XOR: |
64 |
||||||
count of leading zeros, most significant non-sign bit: |
16 |
||||||
population count: |
16 |
||||||
warp shuffle 7: |
16 |
32 |
|||||
warp vote 8: |
64 |
128 |
|||||
sum of absolute difference: |
64 |
32 |
|||||
2-way SIMD absolute difference: multiple PTX instructions |
Multiple instruct. |
||||||
4-way SIMD absolute difference: |
64 9 |
32 9 |
|||||
Type conversions from 8-bit and 16-bit integer to 32-bit integer types: |
64 |
||||||
Type conversions from and to 64-bit floating-point types: |
2 |
16 |
2 |
2 |
16 |
2 |
|
Type conversion between 16-bit and 32-bit floating-point types: |
64 10 |
||||||
Type conversion between 32-bit integer and 32-bit floating-point types: |
16 |
64 11 |
|||||
DPX (32-bit and 2-way SIMD 16-bit): multiple PTX instructions |
Multiple instruct. |
64 12 |
64 13 |
||||
- 3
-
multiple instructions for __nv_bfloat16
- 4
-
64 for __nv_bfloat16
- 5
-
for reciprocal: approximate using
__fdividef(1.F, x) - 6
-
32 for extended-precision
- 7
-
assuming converged threads
- 8
-
assuming converged threads
- 9(1,2)
-
22 for signed version
- 10
-
32 for __nv_bfloat16->float, 16 for float->__half, 16 for float->__nv_bfloat16 (SM > 7.5), multiple instructions for float->__nv_bfloat16 (SM 7.5)
- 11
-
16 for float->32-bit integer type
- 12
-
multiple instructions for intrinsics with boolean predicate outputs
- 13
-
128 for intrinsics with 2 operands, multiple instructions for intrinsics with boolean predicate outputs
Other instructions and functions are implemented on top of the native instructions. The implementation may be different for devices of different compute capabilities, and the number of native instructions after compilation may fluctuate with every compiler version. For complicated functions, there can be multiple code paths depending on input. cuobjdump can be used to inspect a particular implementation in a cubin object.
The implementation of some functions are readily available on the CUDA header files (math_functions.h, device_functions.h, …).
In general, code compiled with -ftz=true (denormalized numbers are flushed to zero) tends to have higher performance than code compiled with -ftz=false. Similarly, code compiled with -prec-div=false (less precise division) tends to have higher performance code than code compiled with -prec-div=true, and code compiled with -prec-sqrt=false (less precise square root) tends to have higher performance than code compiled with -prec-sqrt=true. The nvcc user manual describes these compilation flags in more details.
Single-Precision Floating-Point Division
__fdividef(x, y) (see the CUDA C++ Programming Guide) provides faster single-precision floating-point division than the division operator.
Single-Precision Floating-Point Reciprocal Square Root
To preserve IEEE-754 semantics the compiler can optimize 1.0/sqrtf() into rsqrtf() only when both reciprocal and square root are approximate, (i.e., with -prec-div=false and -prec-sqrt=false). It is therefore recommended to invoke rsqrtf() directly where desired.
Single-Precision Floating-Point Square Root
Single-precision floating-point square root is implemented as a reciprocal square root followed by a reciprocal instead of a reciprocal square root followed by a multiplication so that it gives correct results for 0 and infinity.
Sine and Cosine
sinf(x), cosf(x), tanf(x), sincosf(x), and corresponding double-precision instructions are much more expensive and even more so if the argument x is large in magnitude.
More precisely, the argument reduction code (see the CUDA C++ Programming Guide for implementation) comprises two code paths referred to as the fast path and the slow path, respectively.
The fast path is used for arguments sufficiently small in magnitude and essentially consists of a few multiply-add operations. The slow path is used for arguments large in magnitude and consists of lengthy computations required to achieve correct results over the entire argument range.
At present, the argument reduction code for the trigonometric functions selects the fast path for arguments whose magnitude is less than 105615.0f for the single-precision functions, and less than 2147483648.0 for the double-precision functions.
As the slow path requires more registers than the fast path, an attempt has been made to reduce register pressure in the slow path by storing some intermediate variables in local memory, which may affect performance because of local memory high latency and bandwidth (see the CUDA C++ Programming Guide). At present, 28 bytes of local memory are used by single-precision functions, and 44 bytes are used by double-precision functions. However, the exact amount is subject to change.
Due to the lengthy computations and use of local memory in the slow path, the throughput of these trigonometric functions is lower by one order of magnitude when the slow path reduction is required as opposed to the fast path reduction.
Integer Arithmetic
Integer division and modulo operation are costly as they compile to up to 20 instructions. They can be replaced with bitwise operations in some cases: If n is a power of 2, (i/n) is equivalent to (i>>log2(n)) and (i%n) is equivalent to (i&(n-1)); the compiler will perform these conversions if n is literal.
__brev and __popc map to a single instruction and __brevll and __popcll to a few instructions.
__[u]mul24 are legacy intrinsic functions that no longer have any reason to be used.
Half Precision Arithmetic
In order to achieve good performance for 16-bit precision floating-point add, multiply or multiply-add, it is recommended that the half2 datatype is used for half precision and __nv_bfloat162 be used for __nv_bfloat16 precision. Vector intrinsics (for example, __hadd2, __hsub2, __hmul2, __hfma2) can then be used to do two operations in a single instruction. Using half2 or __nv_bfloat162 in place of two calls using half or __nv_bfloat16 may also help performance of other intrinsics, such as warp shuffles.
The intrinsic __halves2half2 is provided to convert two half precision values to the half2 datatype.
The intrinsic __halves2bfloat162 is provided to convert two __nv_bfloat precision values to the __nv_bfloat162 datatype.
Type Conversion
Sometimes, the compiler must insert conversion instructions, introducing additional execution cycles. This is the case for:
Functions operating on variables of type
charorshortwhose operands generally need to be converted toint,Double-precision floating-point constants (i.e., those constants defined without any type suffix) used as input to single-precision floating-point computations (as mandated by C/C++ standards).
This last case can be avoided by using single-precision floating-point constants, defined with an f suffix such as 3.141592653589793f, 1.0f, 0.5f.
12.1.2. Control Flow Instructions
Any flow control instruction (if, switch, do, for, while) can significantly impact the effective instruction throughput by causing threads of the same warp to diverge (i.e., to follow different execution paths). If this happens, the different executions paths have to be serialized, increasing the total number of instructions executed for this warp.
To obtain best performance in cases where the control flow depends on the thread ID, the controlling condition should be written so as to minimize the number of divergent warps. This is possible because the distribution of the warps across the block is deterministic as mentioned in the CUDA C++ Programming Guide. A trivial example is when the controlling condition only depends on (threadIdx / warpSize) where warpSize is the warp size. In this case, no warp diverges since the controlling condition is perfectly aligned with the warps.
Sometimes, the compiler may unroll loops or it may optimize out short if or switch blocks by using branch predication instead, as detailed below. In these cases, no warp can ever diverge. The programmer can also control loop unrolling using the #pragma unroll directive (see the CUDA C++ Programming Guide).
When using branch predication none of the instructions whose execution depends on the controlling condition gets skipped. Instead, each of them is associated with a per-thread condition code or predicate that is set to true or false based on the controlling condition and although each of these instructions gets scheduled for execution, only the instructions with a true predicate are actually executed. Instructions with a false predicate do not write results, and also do not evaluate addresses or read operands.
12.1.3. Synchronization Instruction
Throughput for __syncthreads() is 32 operations per clock cycle for devices of compute capability 6.0, 16 operations per clock cycle for devices of compute capability 7.x as well as 8.x and 64 operations per clock cycle for devices of compute capability 5.x, 6.1 and 6.2.
Note that __syncthreads() can impact performance by forcing the multiprocessor to idle as detailed in the CUDA C++ Programming Guide.
12.1.4. Division Modulo Operations
Note
Low Priority: Use shift operations to avoid expensive division and modulo calculations.
Integer division and modulo operations are particularly costly and should be avoided or replaced with bitwise operations whenever possible: If \(n\) is a power of 2, ( \(i/n\) ) is equivalent to ( \(i \gg {log2}(n)\) ) and ( \(i\% n\) ) is equivalent to ( \(i\&\left( {n - 1} \right)\) ).
The compiler will perform these conversions if n is literal. (For further information, refer to Performance Guidelines in the CUDA C++ Programming Guide).
12.1.5. Loop Counters Signed vs. Unsigned
Note
Low Medium Priority: Use signed integers rather than unsigned integers as loop counters.
In the C language standard, unsigned integer overflow semantics are well defined, whereas signed integer overflow causes undefined results. Therefore, the compiler can optimize more aggressively with signed arithmetic than it can with unsigned arithmetic. This is of particular note with loop counters: since it is common for loop counters to have values that are always positive, it may be tempting to declare the counters as unsigned. For slightly better performance, however, they should instead be declared as signed.
For example, consider the following code:
for (i = 0; i < n; i++) {
out[i] = in[offset + stride*i];
}
Here, the sub-expression stride*i could overflow a 32-bit integer, so if i is declared as unsigned, the overflow semantics prevent the compiler from using some optimizations that might otherwise have applied, such as strength reduction. If instead i is declared as signed, where the overflow semantics are undefined, the compiler has more leeway to use these optimizations.
12.1.6. Reciprocal Square Root
The reciprocal square root should always be invoked explicitly as rsqrtf() for single precision and rsqrt() for double precision. The compiler optimizes 1.0f/sqrtf(x) into rsqrtf() only when this does not violate IEEE-754 semantics.
12.1.7. Other Arithmetic Instructions
Note
Low Priority: Avoid automatic conversion of doubles to floats.
The compiler must on occasion insert conversion instructions, introducing additional execution cycles. This is the case for:
Functions operating on
charorshortwhose operands generally need to be converted to anintDouble-precision floating-point constants (defined without any type suffix) used as input to single-precision floating-point computations
The latter case can be avoided by using single-precision floating-point constants, defined with an f suffix such as 3.141592653589793f, 1.0f, 0.5f.
For single-precision code, use of the float type and the single-precision math functions are highly recommended.
It should also be noted that the CUDA math library’s complementary error function, erfcf(), is particularly fast with full single-precision accuracy.
12.1.8. Exponentiation With Small Fractional Arguments
For some fractional exponents, exponentiation can be accelerated significantly compared to the use of pow() by using square roots, cube roots, and their inverses. For those exponentiations where the exponent is not exactly representable as a floating-point number, such as 1/3, this can also provide much more accurate results, as use of pow() magnifies the initial representational error.
The formulas in the table below are valid for x >= 0, x != -0, that is, signbit(x) == 0.
Computation |
Formula |
|---|---|
x1/9 |
|
x-1/9 |
|
x1/6 |
|
x-1/6 |
|
x1/4 |
|
x-1/4 |
|
x1/3 |
|
x-1/3 |
|
x1/2 |
|
x-1/2 |
|
x2/3 |
|
x-2/3 |
|
x3/4 |
|
x-3/4 |
|
x7/6 |
|
x-7/6 |
|
x5/4 |
|
x-5/4 |
|
x4/3 |
|
x-4/3 |
|
x3/2 |
|
x-3/2 |
|
12.1.9. Math Libraries
Note
Medium Priority: Use the fast math library whenever speed trumps precision.
Two types of runtime math operations are supported. They can be distinguished by their names: some have names with prepended underscores, whereas others do not (e.g., __functionName() versus functionName()). Functions following the __functionName() naming convention map directly to the hardware level. They are faster but provide somewhat lower accuracy (e.g., __sinf(x) and __expf(x)). Functions following functionName() naming convention are slower but have higher accuracy (e.g., sinf(x) and expf(x)). The throughput of __sinf(x), __cosf(x), and__expf(x) is much greater than that of sinf(x), cosf(x), and expf(x). The latter become even more expensive (about an order of magnitude slower) if the magnitude of the argument x needs to be reduced. Moreover, in such cases, the argument-reduction code uses local memory, which can affect performance even more because of the high latency of local memory. More details are available in the CUDA C++ Programming Guide.
Note also that whenever sine and cosine of the same argument are computed, the sincos family of instructions should be used to optimize performance:
__sincosf()for single-precision fast math (see next paragraph)sincosf()for regular single-precisionsincos()for double precision
The -use_fast_math compiler option of nvcc coerces every functionName() call to the equivalent __functionName() call. It also disables single-precision denormal support and lowers the precision of single-precision division in general. This is an aggressive optimization that can both reduce numerical accuracy and alter special case handling. A more robust approach is to selectively introduce calls to fast intrinsic functions only if merited by performance gains and where altered behavior can be tolerated. Note this switch is effective only on single-precision floating point.
Note
Medium Priority: Prefer faster, more specialized math functions over slower, more general ones when possible.
For small integer powers (e.g., x2 or x3), explicit multiplication is almost certainly faster than the use of general exponentiation routines such as pow(). While compiler optimization improvements continually seek to narrow this gap, explicit multiplication (or the use of an equivalent purpose-built inline function or macro) can have a significant advantage. This advantage is increased when several powers of the same base are needed (e.g., where both x2 and x5 are calculated in close proximity), as this aids the compiler in its common sub-expression elimination (CSE) optimization.
For exponentiation using base 2 or 10, use the functions exp2() or expf2() and exp10() or expf10() rather than the functions pow() or powf(). Both pow() and powf() are heavy-weight functions in terms of register pressure and instruction count due to the numerous special cases arising in general exponentiation and the difficulty of achieving good accuracy across the entire ranges of the base and the exponent. The functions exp2(), exp2f(), exp10(), and exp10f(), on the other hand, are similar to exp() and expf() in terms of performance, and can be as much as ten times faster than their pow()/powf() equivalents.
For exponentiation with an exponent of 1/3, use the cbrt() or cbrtf() function rather than the generic exponentiation functions pow() or powf(), as the former are significantly faster than the latter. Likewise, for exponentation with an exponent of -1/3, use rcbrt() or rcbrtf().
Replace sin(π*<expr>) with sinpi(<expr>), cos(π*<expr>) with cospi(<expr>), and sincos(π*<expr>) with sincospi(<expr>). This is advantageous with regard to both accuracy and performance. As a particular example, to evaluate the sine function in degrees instead of radians, use sinpi(x/180.0). Similarly, the single-precision functions sinpif(), cospif(), and sincospif() should replace calls to sinf(), cosf(), and sincosf() when the function argument is of the form π*<expr>. (The performance advantage sinpi() has over sin() is due to simplified argument reduction; the accuracy advantage is because sinpi() multiplies by π only implicitly, effectively using an infinitely precise mathematical π rather than a single- or double-precision approximation thereof.)
12.2. Memory Instructions
Note
High Priority: Minimize the use of global memory. Prefer shared memory access where possible.
Memory instructions include any instruction that reads from or writes to shared, local, or global memory. When accessing uncached local or global memory, there are hundreds of clock cycles of memory latency.
As an example, the assignment operator in the following sample code has a high throughput, but, crucially, there is a latency of hundreds of clock cycles to read data from global memory:
__shared__ float shared[32];
__device__ float device[32];
shared[threadIdx.x] = device[threadIdx.x];
Much of this global memory latency can be hidden by the thread scheduler if there are sufficient independent arithmetic instructions that can be issued while waiting for the global memory access to complete. However, it is best to avoid accessing global memory whenever possible.
13. Control Flow
13.1. Branching and Divergence
Note
High Priority: Avoid different execution paths within the same warp.
Flow control instructions (if, switch, do, for, while) can significantly affect the instruction throughput by causing threads of the same warp to diverge; that is, to follow different execution paths. If this happens, the different execution paths must be executed separately; this increases the total number of instructions executed for this warp.
To obtain best performance in cases where the control flow depends on the thread ID, the controlling condition should be written so as to minimize the number of divergent warps.
This is possible because the distribution of the warps across the block is deterministic as mentioned in SIMT Architecture of the CUDA C++ Programming Guide. A trivial example is when the controlling condition depends only on (threadIdx / WSIZE) where WSIZE is the warp size.
In this case, no warp diverges because the controlling condition is perfectly aligned with the warps.
For branches including just a few instructions, warp divergence generally results in marginal performance losses. For example, the compiler may use predication to avoid an actual branch. Instead, all instructions are scheduled, but a per-thread condition code or predicate controls which threads execute the instructions. Threads with a false predicate do not write results, and also do not evaluate addresses or read operands.
Starting with the Volta architecture, Independent Thread Scheduling allows a warp to remain diverged outside of the data-dependent conditional block. An explicit __syncwarp() can be used to guarantee that the warp has reconverged for subsequent instructions.
13.2. Branch Predication
Note
Low Priority: Make it easy for the compiler to use branch predication in lieu of loops or control statements.
Sometimes, the compiler may unroll loops or optimize out if or switch statements by using branch predication instead. In these cases, no warp can ever diverge. The programmer can also control loop unrolling using
#pragma unroll
For more information on this pragma, refer to the CUDA C++ Programming Guide.
When using branch predication, none of the instructions whose execution depends on the controlling condition is skipped. Instead, each such instruction is associated with a per-thread condition code or predicate that is set to true or false according to the controlling condition. Although each of these instructions is scheduled for execution, only the instructions with a true predicate are actually executed. Instructions with a false predicate do not write results, and they also do not evaluate addresses or read operands.
The compiler replaces a branch instruction with predicated instructions only if the number of instructions controlled by the branch condition is less than or equal to a certain threshold.
14. Deploying CUDA Applications
Having completed the GPU acceleration of one or more components of the application it is possible to compare the outcome with the original expectation. Recall that the initial assess step allowed the developer to determine an upper bound for the potential speedup attainable by accelerating given hotspots.
Before tackling other hotspots to improve the total speedup, the developer should consider taking the partially parallelized implementation and carry it through to production. This is important for a number of reasons; for example, it allows the user to profit from their investment as early as possible (the speedup may be partial but is still valuable), and it minimizes risk for the developer and the user by providing an evolutionary rather than revolutionary set of changes to the application.
15. Understanding the Programming Environment
With each generation of NVIDIA processors, new features are added to the GPU that CUDA can leverage. Consequently, it’s important to understand the characteristics of the architecture.
Programmers should be aware of two version numbers. The first is the compute capability, and the second is the version number of the CUDA Runtime and CUDA Driver APIs.
15.1. CUDA Compute Capability
The compute capability describes the features of the hardware and reflects the set of instructions supported by the device as well as other specifications, such as the maximum number of threads per block and the number of registers per multiprocessor. Higher compute capability versions are supersets of lower (that is, earlier) versions, so they are backward compatible.
The compute capability of the GPU in the device can be queried programmatically as illustrated in the deviceQuery CUDA Sample. The output for that program is shown in Figure 16. This information is obtained by calling cudaGetDeviceProperties() and accessing the information in the structure it returns.
Figure 16 Sample CUDA configuration data reported by deviceQuery
The major and minor revision numbers of the compute capability are shown on the seventh line of Figure 16. Device 0 of this system has compute capability 7.0.
More details about the compute capabilities of various GPUs are in CUDA-Enabled GPUs and Compute Capabilities of the CUDA C++ Programming Guide. In particular, developers should note the number of multiprocessors on the device, the number of registers and the amount of memory available, and any special capabilities of the device.
15.2. Additional Hardware Data
Certain hardware features are not described by the compute capability. For example, the ability to overlap kernel execution with asynchronous data transfers between the host and the device is available on most but not all GPUs irrespective of the compute capability. In such cases, call cudaGetDeviceProperties() to determine whether the device is capable of a certain feature. For example, the asyncEngineCount field of the device property structure indicates whether overlapping kernel execution and data transfers is possible (and, if so, how many concurrent transfers are possible); likewise, the canMapHostMemory field indicates whether zero-copy data transfers can be performed.
15.3. Which Compute Capability Target
To target specific versions of NVIDIA hardware and CUDA software, use the -arch, -code, and -gencode options of nvcc. Code that uses the warp shuffle operation, for example, must be compiled with -arch=sm_30 (or higher compute capability).
See Building for Maximum Compatibility for further discussion of the flags used for building code for multiple generations of CUDA-capable device simultaneously.
15.4. CUDA Runtime
The host runtime component of the CUDA software environment can be used only by host functions. It provides functions to handle the following:
Device management
Context management
Memory management
Code module management
Execution control
Texture reference management
Interoperability with OpenGL and Direct3D
As compared to the lower-level CUDA Driver API, the CUDA Runtime greatly eases device management by providing implicit initialization, context management, and device code module management. The C++ host code generated by nvcc utilizes the CUDA Runtime, so applications that link to this code will depend on the CUDA Runtime; similarly, any code that uses the cuBLAS, cuFFT, and other CUDA Toolkit libraries will also depend on the CUDA Runtime, which is used internally by these libraries.
The functions that make up the CUDA Runtime API are explained in the CUDA Toolkit Reference Manual.
The CUDA Runtime handles kernel loading and setting up kernel parameters and launch configuration before the kernel is launched. The implicit driver version checking, code initialization, CUDA context management, CUDA module management (cubin to function mapping), kernel configuration, and parameter passing are all performed by the CUDA Runtime.
It comprises two principal parts:
A C-style function interface (
cuda_runtime_api.h).C++-style convenience wrappers (
cuda_runtime.h) built on top of the C-style functions.
For more information on the Runtime API, refer to CUDA Runtime of the CUDA C++ Programming Guide.
16. CUDA Compatibility Developer’s Guide
CUDA Toolkit is released on a monthly release cadence to deliver new features, performance improvements, and critical bug fixes. CUDA compatibility allows users to update the latest CUDA Toolkit software (including the compiler, libraries, and tools) without requiring update to the entire driver stack.
The CUDA software environment consists of three parts:
CUDA Toolkit (libraries, CUDA runtime and developer tools) - SDK for developers to build CUDA applications.
CUDA driver - User-mode driver component used to run CUDA applications (e.g. libcuda.so on Linux systems).
NVIDIA GPU device driver - Kernel-mode driver component for NVIDIA GPUs.
On Linux systems, the CUDA driver and kernel mode components are delivered together in the NVIDIA display driver package. This is shown in Figure 1.
Figure 17 Components of CUDA
The CUDA compiler (nvcc), provides a way to handle CUDA and non-CUDA code (by splitting and steering compilation), along with the CUDA runtime, is part of the CUDA compiler toolchain. The CUDA Runtime API provides developers with high-level C++ interface for simplified management of devices, kernel executions etc., While the CUDA driver API provides (CUDA Driver API) a low-level programming interface for applications to target NVIDIA hardware.
Built on top of these technologies are CUDA libraries, some of which are included in the CUDA Toolkit, while others such as cuDNN may be released independently of the CUDA Toolkit.
16.1. CUDA Toolkit Versioning
Starting with CUDA 11, the toolkit versions are based on an industry-standard semantic versioning scheme: .X.Y.Z, where:
.X stands for the major version - APIs have changed and binary compatibility is broken.
.Y stands for the minor version - Introduction of new APIs, deprecation of old APIs, and source compatibility might be broken but binary compatibility is maintained.
.Z stands for the release/patch version - new updates and patches will increment this.
Each component in the toolkit is recommended to be semantically versioned. From CUDA 11.3 NVRTC is also semantically versioned. We will note some of them later on in the document. The versions of the components in the toolkit are available in this table.
Compatibility of the CUDA platform is thus intended to address a few scenarios:
NVIDIA driver upgrades to systems with GPUs running in production for enterprises or datacenters can be complex and may need advance planning. Delays in rolling out new NVIDIA drivers could mean that users of such systems may not have access to new features available in CUDA releases. Not requiring driver updates for new CUDA releases can mean that new versions of the software can be made available faster to users.
Many software libraries and applications built on top of CUDA (e.g. math libraries or deep learning frameworks) do not have a direct dependency on the CUDA runtime, compiler or driver. In such cases, users or developers can still benefit from not having to upgrade the entire CUDA Toolkit or driver to use these libraries or frameworks.
Upgrading dependencies is error-prone and time consuming, and in some corner cases, can even change the semantics of a program. Constantly recompiling with the latest CUDA Toolkit means forcing upgrades on the end-customers of an application product. Package managers facilitate this process but unexpected issues can still arise and if a bug is found, it necessitates a repeat of the above upgrade process.
CUDA supports several compatibility choices:
First introduced in CUDA 10, the CUDA Forward Compatible Upgrade is designed to allow users to get access to new CUDA features and run applications built with new CUDA releases on systems with older installations of the NVIDIA datacenter driver.
-
First introduced in CUDA 11.1, CUDA Enhanced Compatibility provides two benefits:
By leveraging semantic versioning across components in the CUDA Toolkit, an application can be built for one CUDA minor release (for example 11.1) and work across all future minor releases within the major family (i.e. 11.x).
The CUDA runtime has relaxed the minimum driver version check and thus no longer requires a driver upgrade when moving to a new minor release.
The CUDA driver ensures backward Binary Compatibility is maintained for compiled CUDA applications. Applications compiled with CUDA toolkit versions as old as 3.2 will run on newer drivers.
16.2. Source Compatibility
We define source compatibility as a set of guarantees provided by the library, where a well-formed application built against a specific version of the library (using the SDK) will continue to build and run without errors when a newer version of the SDK is installed.
Both the CUDA driver and the CUDA runtime are not source compatible across the different SDK releases. APIs can be deprecated and removed. Therefore, an application that compiled successfully on an older version of the toolkit may require changes in order to compile against a newer version of the toolkit.
Developers are notified through deprecation and documentation mechanisms of any current or upcoming changes. This does not mean that application binaries compiled using an older toolkit will not be supported anymore. Application binaries rely on CUDA Driver API interface and even though the CUDA Driver API itself may also have changed across toolkit versions, CUDA guarantees Binary Compatibility of the CUDA Driver API interface.
16.3. Binary Compatibility
We define binary compatibility as a set of guarantees provided by the library, where an application targeting the said library will continue to work when dynamically linked against a different version of the library.
The CUDA Driver API has a versioned C-style ABI, which guarantees that applications that were running against an older driver (for example CUDA 3.2) will still run and function correctly against a modern driver (for example one shipped with CUDA 11.0). This means that even though an application source might need to be changed if it has to be recompiled against a newer CUDA Toolkit in order to use the newer features, replacing the driver components installed in a system with a newer version will always support existing applications and its functions.
The CUDA Driver API thus is binary-compatible (the OS loader can pick up a newer version and the application continues to work) but not source-compatible (rebuilding your application against a newer SDK might require source changes).
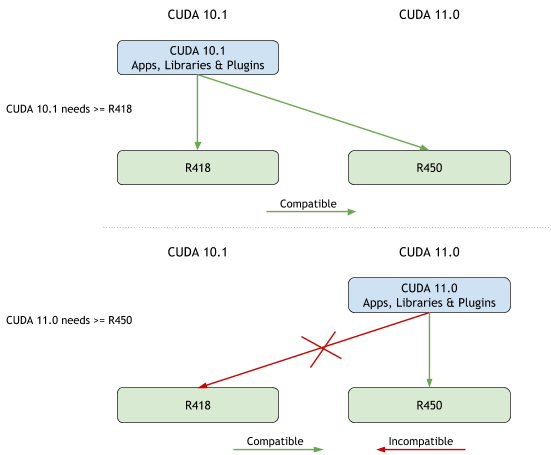
Figure 18 CUDA Toolkit and Minimum Driver Versions
Before we proceed further on this topic, it’s important for developers to understand the concept of Minimum Driver Version and how that may affect them.
Each version of the CUDA Toolkit (and runtime) requires a minimum version of the NVIDIA driver. Applications compiled against a CUDA Toolkit version will only run on systems with the specified minimum driver version for that toolkit version. Prior to CUDA 11.0, the minimum driver version for a toolkit was the same as the driver shipped with that version of the CUDA Toolkit.
So, when an application is built with CUDA 11.0, it can only run on a system with an R450 or later driver. If such an application is run on a system with the R418 driver installed, CUDA initialization will return an error as can be seen in the example below.
In this example, the deviceQuery sample is compiled with CUDA 11.1 and is run on a system with R418. In this scenario, CUDA initialization returns an error due to the minimum driver requirement.
ubuntu@:~/samples/1_Utilities/deviceQuery
$ make
/usr/local/cuda-11.1/bin/nvcc -ccbin g++ -I../../common/inc -m64 -gencode arch=compute_35,code=sm_35 -gencode arch=compute_37,code=sm_37 -gencode arch=compute_50,code=sm_50 -gencode arch=compute_52,code=sm_52 -gencode arch=compute_60,code=sm_60 -gencode arch=compute_61,code=sm_61 -gencode arch=compute_70,code=sm_70 -gencode arch=compute_75,code=sm_75 -gencode arch=compute_80,code=sm_80 -gencode arch=compute_86,code=sm_86 -gencode arch=compute_86,code=compute_86 -o deviceQuery.o -c deviceQuery.cpp
/usr/local/cuda-11.1/bin/nvcc -ccbin g++ -m64 -gencode arch=compute_35,code=sm_35 -gencode arch=compute_37,code=sm_37 -gencode arch=compute_50,code=sm_50 -gencode arch=compute_52,code=sm_52 -gencode arch=compute_60,code=sm_60 -gencode arch=compute_61,code=sm_61 -gencode arch=compute_70,code=sm_70 -gencode arch=compute_75,code=sm_75 -gencode arch=compute_80,code=sm_80 -gencode arch=compute_86,code=sm_86 -gencode arch=compute_86,code=compute_86 -o deviceQuery deviceQuery.o
$ nvidia-smi
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 418.165.02 Driver Version: 418.165.02 CUDA Version: 10.1 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla T4 On | 00000000:00:1E.0 Off | 0 |
| N/A 42C P0 28W / 70W | 0MiB / 15079MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+
$ samples/bin/x86_64/linux/release/deviceQuery
samples/bin/x86_64/linux/release/deviceQuery Starting...
CUDA Device Query (Runtime API) version (CUDART static linking)
cudaGetDeviceCount returned 3
-> initialization error
Result = FAIL
Refer to the CUDA Toolkit Release Notes for details for the minimum driver version and the version of the driver shipped with the toolkit.
16.3.1. CUDA Binary (cubin) Compatibility
A slightly related but important topic is one of application binary compatibility across GPU architectures in CUDA.
CUDA C++ provides a simple path for users familiar with the C++ programming language to easily write programs for execution by the device. Kernels can be written using the CUDA instruction set architecture, called PTX, which is described in the PTX reference manual. It is however usually more effective to use a high-level programming language such as C++. In both cases, kernels must be compiled into binary code by nvcc (called cubins) to execute on the device.
The cubins are architecture-specific. Binary compatibility for cubins is guaranteed from one compute capability minor revision to the next one, but not from one compute capability minor revision to the previous one or across major compute capability revisions. In other words, a cubin object generated for compute capability X.y will only execute on devices of compute capability X.z where z≥y.
To execute code on devices of specific compute capability, an application must load binary or PTX code that is compatible with this compute capability. For portability, that is, to be able to execute code on future GPU architectures with higher compute capability (for which no binary code can be generated yet), an application must load PTX code that will be just-in-time compiled by the NVIDIA driver for these future devices.
More information on cubins, PTX and application compatibility can be found in the CUDA C++ Programming Guide.
16.4. CUDA Compatibility Across Minor Releases
By leveraging the semantic versioning, starting with CUDA 11, components in the CUDA Toolkit will remain binary compatible across the minor versions of the toolkit. In order to maintain binary compatibility across minor versions, the CUDA runtime no longer bumps up the minimum driver version required for every minor release - this only happens when a major release is shipped.
One of the main reasons a new toolchain requires a new minimum driver is to handle the JIT compilation of PTX code and the JIT linking of binary code.
In this section, we will review the usage patterns that may require new user workflows when taking advantage of the compatibility features of the CUDA platform.
16.4.1. Existing CUDA Applications within Minor Versions of CUDA
$ nvidia-smi
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 450.80.02 Driver Version: 450.80.02 CUDA Version: 11.0 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla T4 On | 00000000:00:1E.0 Off | 0 |
| N/A 39C P8 9W / 70W | 0MiB / 15109MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+
When our CUDA 11.1 application (i.e. cudart 11.1 is statically linked) is run on the system, we see that it runs successfully even when the driver reports a 11.0 version - that is, without requiring the driver or other toolkit components to be updated on the system.
$ samples/bin/x86_64/linux/release/deviceQuery
samples/bin/x86_64/linux/release/deviceQuery Starting...
CUDA Device Query (Runtime API) version (CUDART static linking)
Detected 1 CUDA Capable device(s)
Device 0: "Tesla T4"
CUDA Driver Version / Runtime Version 11.0 / 11.1
CUDA Capability Major/Minor version number: 7.5
...<snip>...
deviceQuery, CUDA Driver = CUDART, CUDA Driver Version = 11.0, CUDA Runtime Version = 11.1, NumDevs = 1
Result = PASS
By using new CUDA versions, users can benefit from new CUDA programming model APIs, compiler optimizations and math library features.
The following sections discuss some caveats and considerations.
16.4.1.1. Handling New CUDA Features and Driver APIs
A subset of CUDA APIs don’t need a new driver and they can all be used without any driver dependencies. For example, cuMemMap APIs or any of APIs introduced prior to CUDA 11.0, such as cudaDeviceSynchronize, do not require a driver upgrade. To use other CUDA APIs introduced in a minor release (that require a new driver), one would have to implement fallbacks or fail gracefully. This situation is not different from what is available today where developers use macros to compile out features based on CUDA versions. Users should refer to the CUDA headers and documentation for new CUDA APIs introduced in a release.
When working with a feature exposed in a minor version of the toolkit, the feature might not be available at runtime if the application is running against an older CUDA driver. Users wishing to take advantage of such a feature should query its availability with a dynamic check in the code:
static bool hostRegisterFeatureSupported = false;
static bool hostRegisterIsDeviceAddress = false;
static error_t cuFooFunction(int *ptr)
{
int *dptr = null;
if (hostRegisterFeatureSupported) {
cudaHostRegister(ptr, size, flags);
if (hostRegisterIsDeviceAddress) {
qptr = ptr;
}
else {
cudaHostGetDevicePointer(&qptr, ptr, 0);
}
}
else {
// cudaMalloc();
// cudaMemcpy();
}
gemm<<<1,1>>>(dptr);
cudaDeviceSynchronize();
}
int main()
{
// rest of code here
cudaDeviceGetAttribute(
&hostRegisterFeatureSupported,
cudaDevAttrHostRegisterSupported,
0);
cudaDeviceGetAttribute(
&hostRegisterIsDeviceAddress,
cudaDevAttrCanUseHostPointerForRegisteredMem,
0);
cuFooFunction(/* malloced pointer */);
}
Alternatively the application’s interface might not work at all without a new CUDA driver and then its best to return an error right away:
#define MIN_VERSION 11010
cudaError_t foo()
{
int version = 0;
cudaGetDriverVersion(&version);
if (version < MIN_VERSION) {
return CUDA_ERROR_INSUFFICIENT_DRIVER;
}
// proceed as normal
}
A new error code is added to indicate that the functionality is missing from the driver you are running against: cudaErrorCallRequiresNewerDriver.
16.4.1.2. Using PTX
PTX defines a virtual machine and ISA for general purpose parallel thread execution. PTX programs are translated at load time to the target hardware instruction set via the JIT Compiler which is part of the CUDA driver. As PTX is compiled by the CUDA driver, new toolchains will generate PTX that is not compatible with the older CUDA driver. This is not a problem when PTX is used for future device compatibility (the most common case), but can lead to issues when used for runtime compilation.
For codes continuing to make use of PTX, in order to support compiling on an older driver, your code must be first transformed into device code via the static ptxjitcompiler library or NVRTC with the option of generating code for a specific architecture (e.g. sm_80) rather than a virtual architecture (e.g. compute_80). For this workflow, a new nvptxcompiler_static library is shipped with the CUDA Toolkit.
We can see this usage in the following example:
char* compilePTXToNVElf()
{
nvPTXCompilerHandle compiler = NULL;
nvPTXCompileResult status;
size_t elfSize, infoSize, errorSize;
char *elf, *infoLog, *errorLog;
int minorVer, majorVer;
const char* compile_options[] = { "--gpu-name=sm_80",
"--device-debug"
};
nvPTXCompilerGetVersion(&majorVer, &minorVer);
nvPTXCompilerCreate(&compiler, (size_t)strlen(ptxCode), ptxCode);
status = nvPTXCompilerCompile(compiler, 2, compile_options);
if (status != NVPTXCOMPILE_SUCCESS) {
nvPTXCompilerGetErrorLogSize(compiler, (void*)&errorSize);
if (errorSize != 0) {
errorLog = (char*)malloc(errorSize+1);
nvPTXCompilerGetErrorLog(compiler, (void*)errorLog);
printf("Error log: %s\n", errorLog);
free(errorLog);
}
exit(1);
}
nvPTXCompilerGetCompiledProgramSize(compiler, &elfSize));
elf = (char*)malloc(elfSize);
nvPTXCompilerGetCompiledProgram(compiler, (void*)elf);
nvPTXCompilerGetInfoLogSize(compiler, (void*)&infoSize);
if (infoSize != 0) {
infoLog = (char*)malloc(infoSize+1);
nvPTXCompilerGetInfoLog(compiler, (void*)infoLog);
printf("Info log: %s\n", infoLog);
free(infoLog);
}
nvPTXCompilerDestroy(&compiler);
return elf;
}
16.4.1.3. Dynamic Code Generation
NVRTC is a runtime compilation library for CUDA C++. It accepts CUDA C++ source code in character string form and creates handles that can be used to obtain the PTX. The PTX string generated by NVRTC can be loaded by cuModuleLoadData and cuModuleLoadDataEx.
Dealing with relocatable objects is not yet supported, therefore the cuLink* set of APIs in the CUDA driver will not work with enhanced compatibility. An upgraded driver matching the CUDA runtime version is currently required for those APIs.
As mentioned in the PTX section, the compilation of PTX to device code lives along with the CUDA driver, hence the generated PTX might be newer than what is supported by the driver on the deployment system. When using NVRTC, it is recommended that the resulting PTX code is first transformed to the final device code via the steps outlined by the PTX user workflow. This ensures your code is compatible. Alternatively, NVRTC can generate cubins directly starting with CUDA 11.1. Applications using the new API can load the final device code directly using driver APIs cuModuleLoadData and cuModuleLoadDataEx.
NVRTC used to support only virtual architectures through the option -arch, since it was only emitting PTX. It will now support actual architectures as well to emit SASS. The interface is augmented to retrieve either the PTX or cubin if an actual architecture is specified.
The example below shows how an existing example can be adapted to use the new features, guarded by the USE_CUBIN macro in this case:
#include <nvrtc.h>
#include <cuda.h>
#include <iostream>
void NVRTC_SAFE_CALL(nvrtcResult result) {
if (result != NVRTC_SUCCESS) {
std::cerr << "\nnvrtc error: " << nvrtcGetErrorString(result) << '\n';
std::exit(1);
}
}
void CUDA_SAFE_CALL(CUresult result) {
if (result != CUDA_SUCCESS) {
const char *msg;
cuGetErrorName(result, &msg);
std::cerr << "\ncuda error: " << msg << '\n';
std::exit(1);
}
}
const char *hello = " \n\
extern \"C\" __global__ void hello() { \n\
printf(\"hello world\\n\"); \n\
} \n";
int main()
{
nvrtcProgram prog;
NVRTC_SAFE_CALL(nvrtcCreateProgram(&prog, hello, "hello.cu", 0, NULL, NULL));
#ifdef USE_CUBIN
const char *opts[] = {"-arch=sm_70"};
#else
const char *opts[] = {"-arch=compute_70"};
#endif
nvrtcResult compileResult = nvrtcCompileProgram(prog, 1, opts);
size_t logSize;
NVRTC_SAFE_CALL(nvrtcGetProgramLogSize(prog, &logSize));
char *log = new char[logSize];
NVRTC_SAFE_CALL(nvrtcGetProgramLog(prog, log));
std::cout << log << '\n';
delete[] log;
if (compileResult != NVRTC_SUCCESS)
exit(1);
size_t codeSize;
#ifdef USE_CUBIN
NVRTC_SAFE_CALL(nvrtcGetCUBINSize(prog, &codeSize));
char *code = new char[codeSize];
NVRTC_SAFE_CALL(nvrtcGetCUBIN(prog, code));
#else
NVRTC_SAFE_CALL(nvrtcGetPTXSize(prog, &codeSize));
char *code = new char[codeSize];
NVRTC_SAFE_CALL(nvrtcGetPTX(prog, code));
#endif
NVRTC_SAFE_CALL(nvrtcDestroyProgram(&prog));
CUdevice cuDevice;
CUcontext context;
CUmodule module;
CUfunction kernel;
CUDA_SAFE_CALL(cuInit(0));
CUDA_SAFE_CALL(cuDeviceGet(&cuDevice, 0));
CUDA_SAFE_CALL(cuCtxCreate(&context, NULL, 0, cuDevice));
CUDA_SAFE_CALL(cuModuleLoadDataEx(&module, code, 0, 0, 0));
CUDA_SAFE_CALL(cuModuleGetFunction(&kernel, module, "hello"));
CUDA_SAFE_CALL(cuLaunchKernel(kernel, 1, 1, 1, 1, 1, 1, 0, NULL, NULL, 0));
CUDA_SAFE_CALL(cuCtxSynchronize());
CUDA_SAFE_CALL(cuModuleUnload(module));
CUDA_SAFE_CALL(cuCtxDestroy(context));
delete[] code;
}
16.4.1.4. Recommendations for building a minor-version compatible library
We recommend that the CUDA runtime be statically linked to minimize dependencies. Verify that your library doesn’t leak dependencies, breakages, namespaces, etc. outside your established ABI contract.
Follow semantic versioning for your library’s soname. Having a semantically versioned ABI means the interfaces need to be maintained and versioned. The library should follow semantic rules and increment the version number when a change is made that affects this ABI contract. Missing dependencies is also a binary compatibility break, hence you should provide fallbacks or guards for functionality that depends on those interfaces. Increment major versions when there are ABI breaking changes such as API deprecation and modifications. New APIs can be added in minor versions.
Conditionally use features to remain compatible against older drivers. If no new features are used (or if they are used conditionally with fallbacks provided) you’ll be able to remain compatible.
Don’t expose ABI structures that can change. A pointer to a structure with a size embedded is a better solution.
When linking with dynamic libraries from the toolkit, the library must be equal to or newer than what is needed by any one of the components involved in the linking of your application. For example, if you link against the CUDA 11.1 dynamic runtime, and use functionality from 11.1, as well as a separate shared library that was linked against the CUDA 11.2 dynamic runtime that requires 11.2 functionality, the final link step must include a CUDA 11.2 or newer dynamic runtime.
16.4.1.5. Recommendations for taking advantage of minor version compatibility in your application
Certain functionality might not be available so you should query where applicable. This is common for building applications that are GPU architecture, platform and compiler agnostic. However we now add “the underlying driver” to that mix.
As with the previous section on library building recommendations, if using the CUDA runtime, we recommend linking to the CUDA runtime statically when building your application. When using the driver APIs directly, we recommend using the new driver entry point access API (cuGetProcAddress) documented here: CUDA Driver API :: CUDA Toolkit Documentation.
When using a shared or static library, follow the release notes of said library to determine if the library supports minor version compatibility.
17. Preparing for Deployment
17.1. Testing for CUDA Availability
When deploying a CUDA application, it is often desirable to ensure that the application will continue to function properly even if the target machine does not have a CUDA-capable GPU and/or a sufficient version of the NVIDIA Driver installed. (Developers targeting a single machine with known configuration may choose to skip this section.)
Detecting a CUDA-Capable GPU
When an application will be deployed to target machines of arbitrary/unknown configuration, the application should explicitly test for the existence of a CUDA-capable GPU in order to take appropriate action when no such device is available. The cudaGetDeviceCount() function can be used to query for the number of available devices. Like all CUDA Runtime API functions, this function will fail gracefully and return cudaErrorNoDevice to the application if there is no CUDA-capable GPU or cudaErrorInsufficientDriver if there is not an appropriate version of the NVIDIA Driver installed. If cudaGetDeviceCount() reports an error, the application should fall back to an alternative code path.
A system with multiple GPUs may contain GPUs of different hardware versions and capabilities. When using multiple GPUs from the same application, it is recommended to use GPUs of the same type, rather than mixing hardware generations. The cudaChooseDevice() function can be used to select the device that most closely matches a desired set of features.
Detecting Hardware and Software Configuration
When an application depends on the availability of certain hardware or software capabilities to enable certain functionality, the CUDA API can be queried for details about the configuration of the available device and for the installed software versions.
The cudaGetDeviceProperties() function reports various features of the available devices, including the CUDA Compute Capability of the device (see also the Compute Capabilities section of the CUDA C++ Programming Guide). See Version Management for details on how to query the available CUDA software API versions.
17.2. Error Handling
All CUDA Runtime API calls return an error code of type cudaError_t; the return value will be equal to cudaSuccess if no errors have occurred. (The exceptions to this are kernel launches, which return void, and cudaGetErrorString(), which returns a character string describing the cudaError_t code that was passed into it.) The CUDA Toolkit libraries (cuBLAS, cuFFT, etc.) likewise return their own sets of error codes.
Since some CUDA API calls and all kernel launches are asynchronous with respect to the host code, errors may be reported to the host asynchronously as well; often this occurs the next time the host and device synchronize with each other, such as during a call to cudaMemcpy() or to cudaDeviceSynchronize().
Always check the error return values on all CUDA API functions, even for functions that are not expected to fail, as this will allow the application to detect and recover from errors as soon as possible should they occur. To check for errors occurring during kernel launches using the <<<...>>> syntax, which does not return any error code, the return code of cudaGetLastError() should be checked immediately after the kernel launch. Applications that do not check for CUDA API errors could at times run to completion without having noticed that the data calculated by the GPU is incomplete, invalid, or uninitialized.
Note
The CUDA Toolkit Samples provide several helper functions for error checking with the various CUDA APIs; these helper functions are located in the samples/common/inc/helper_cuda.h file in the CUDA Toolkit.
17.3. Building for Maximum Compatibility
Each generation of CUDA-capable device has an associated compute capability version that indicates the feature set supported by the device (see CUDA Compute Capability). One or more compute capability versions can be specified to the nvcc compiler while building a file; compiling for the native compute capability for the target GPU(s) of the application is important to ensure that application kernels achieve the best possible performance and are able to use the features that are available on a given generation of GPU.
When an application is built for multiple compute capabilities simultaneously (using several instances of the -gencode flag to
nvcc), the binaries for the specified compute capabilities are combined into the executable, and the CUDA Driver selects the most
appropriate binary at runtime according to the compute capability of the present device. If an appropriate native binary (cubin)
is not available, but the intermediate PTX code (which targets an abstract virtual instruction set and is used for forward-compatibility)
is available, then the kernel will be compiled Just In Time (JIT) (see Compiler JIT Cache Management Tools)
from the PTX to the native cubin for the device. If the PTX is also not available, then the kernel launch will fail.
Windows
nvcc.exe -ccbin "C:\vs2008\VC\bin"
-Xcompiler "/EHsc /W3 /nologo /O2 /Zi /MT"
-gencode=arch=compute_30,code=sm_30
-gencode=arch=compute_35,code=sm_35
-gencode=arch=compute_50,code=sm_50
-gencode=arch=compute_60,code=sm_60
-gencode=arch=compute_70,code=sm_70
-gencode=arch=compute_75,code=sm_75
-gencode=arch=compute_75,code=compute_75
--compile -o "Release\mykernel.cu.obj" "mykernel.cu"
Mac/Linux
/usr/local/cuda/bin/nvcc
-gencode=arch=compute_30,code=sm_30
-gencode=arch=compute_35,code=sm_35
-gencode=arch=compute_50,code=sm_50
-gencode=arch=compute_60,code=sm_60
-gencode=arch=compute_70,code=sm_70
-gencode=arch=compute_75,code=sm_75
-gencode=arch=compute_75,code=compute_75
-O2 -o mykernel.o -c mykernel.cu
Alternatively, the nvcc command-line option -arch=sm_XX can be used as a shorthand equivalent to the following more explicit -gencode= command-line options described above:
-gencode=arch=compute_XX,code=sm_XX
-gencode=arch=compute_XX,code=compute_XX
However, while the -arch=sm_XX command-line option does result in inclusion of a PTX back-end target by default (due to the code=compute_XX target it implies), it can only specify a single target cubin architecture at a time, and it is not possible to use multiple -arch= options on the same nvcc command line, which is why the examples above use -gencode= explicitly.
17.4. Distributing the CUDA Runtime and Libraries
CUDA applications are built against the CUDA Runtime library, which handles device, memory, and kernel management. Unlike the CUDA Driver, the CUDA Runtime guarantees neither forward nor backward binary compatibility across versions. It is therefore best to redistribute the CUDA Runtime library with the application when using dynamic linking or else to statically link against the CUDA Runtime. This will ensure that the executable will be able to run even if the user does not have the same CUDA Toolkit installed that the application was built against.
Note
When statically linking to the CUDA Runtime, multiple versions of the runtime can peacably coexist in the same application process simultaneously; for example, if an application uses one version of the CUDA Runtime, and a plugin to that application is statically linked to a different version, that is perfectly acceptable, as long as the installed NVIDIA Driver is sufficient for both.
Statically-linked CUDA Runtime
The easiest option is to statically link against the CUDA Runtime. This is the default if using nvcc to link in CUDA 5.5 and later. Static linking makes the executable slightly larger, but it ensures that the correct version of runtime library functions are included in the application binary without requiring separate redistribution of the CUDA Runtime library.
Dynamically-linked CUDA Runtime
If static linking against the CUDA Runtime is impractical for some reason, then a dynamically-linked version of the CUDA Runtime library is also available. (This was the default and only option provided in CUDA versions 5.0 and earlier.)
To use dynamic linking with the CUDA Runtime when using the nvcc from CUDA 5.5 or later to link the application, add
the --cudart=shared flag to the link command line; otherwise the statically-linked CUDA Runtime library is used by default.
After the application is dynamically linked against the CUDA Runtime, this version of the runtime library should be bundled with the application. It can be copied into the same directory as the application executable or into a subdirectory of that installation path.
Other CUDA Libraries
Although the CUDA Runtime provides the option of static linking, some libraries included in the CUDA Toolkit are available only in dynamically-linked form. As with the dynamically-linked version of the CUDA Runtime library, these libraries should be bundled with the application executable when distributing that application.
17.4.1. CUDA Toolkit Library Redistribution
The CUDA Toolkit’s End-User License Agreement (EULA) allows for redistribution of many of the CUDA libraries under certain terms and conditions. This allows applications that depend on these libraries to redistribute the exact versions of the libraries against which they were built and tested, thereby avoiding any trouble for end users who might have a different version of the CUDA Toolkit (or perhaps none at all) installed on their machines. Please refer to the EULA for details.
Note
This does not apply to the NVIDIA Driver; the end user must still download and install an NVIDIA Driver appropriate to their GPU(s) and operating system.
17.4.1.1. Which Files to Redistribute
When redistributing the dynamically-linked versions of one or more CUDA libraries, it is important to identify the exact files that need to be redistributed. The following examples use the cuBLAS library from CUDA Toolkit 5.5 as an illustration:
Linux
In a shared library on Linux, there is a string field called the SONAME that indicates the binary compatibility level of the library. The SONAME of the library against which the application was built must match the filename of the library that is redistributed with the application.
For example, in the standard CUDA Toolkit installation, the files libcublas.so and libcublas.so.5.5 are both symlinks pointing to a specific build of cuBLAS, which is named like libcublas.so.5.5.x, where x is the build number (e.g., libcublas.so.5.5.17). However, the SONAME of this library is given as “libcublas.so.5.5”:
$ objdump -p /usr/local/cuda/lib64/libcublas.so | grep SONAME
SONAME libcublas.so.5.5
Because of this, even if -lcublas (with no version number specified) is used when linking the application, the SONAME found at link time implies that “libcublas.so.5.5” is the name of the file that the dynamic loader will look for when loading the application and therefore must be the name of the file (or a symlink to the same) that is redistributed with the application.
The ldd tool is useful for identifying the exact filenames of the libraries that the application expects to find at runtime as well as the path, if any, of the copy of that library that the dynamic loader would select when loading the application given the current library search path:
$ ldd a.out | grep libcublas
libcublas.so.5.5 => /usr/local/cuda/lib64/libcublas.so.5.5
Mac
In a shared library on Mac OS X, there is a field called the install name that indicates the expected installation path and filename the library; the CUDA libraries also use this filename to indicate binary compatibility. The value of this field is propagated into an application built against the library and is used to locate the library of the correct version at runtime.
For example, if the install name of the cuBLAS library is given as @rpath/libcublas.5.5.dylib, then the library is version 5.5 and the copy of this library
redistributed with the application must be named libcublas.5.5.dylib, even though only -lcublas (with no version number specified) is used at link time.
Furthermore, this file should be installed into the @rpath of the application; see Where to Install Redistributed CUDA Libraries.
To view a library’s install name, use the otool -L command:
$ otool -L a.out
a.out:
@rpath/libcublas.5.5.dylib (...)
Windows
The binary compatibility version of the CUDA libraries on Windows is indicated as part of the filename.
For example, a 64-bit application linked to cuBLAS 5.5 will look for cublas64_55.dll at runtime, so this is the file that should be redistributed with that application, even though cublas.lib is the file that the application is linked against. For 32-bit applications, the file would be cublas32_55.dll.
To verify the exact DLL filename that the application expects to find at runtime, use the dumpbin tool from the Visual Studio command prompt:
$ dumpbin /IMPORTS a.exe
Microsoft (R) COFF/PE Dumper Version 10.00.40219.01
Copyright (C) Microsoft Corporation. All rights reserved.
Dump of file a.exe
File Type: EXECUTABLE IMAGE
Section contains the following imports:
...
cublas64_55.dll
...
17.4.1.2. Where to Install Redistributed CUDA Libraries
Once the correct library files are identified for redistribution, they must be configured for installation into a location where the application will be able to find them.
On Windows, if the CUDA Runtime or other dynamically-linked CUDA Toolkit library is placed in the same directory as the executable, Windows will locate it automatically. On Linux and Mac, the -rpath linker option should be used to instruct the executable to search its local path for these libraries before searching the system paths:
Linux/Mac
nvcc -I $(CUDA_HOME)/include
-Xlinker "-rpath '$ORIGIN'" --cudart=shared
-o myprogram myprogram.cu
Windows
nvcc.exe -ccbin "C:\vs2008\VC\bin"
-Xcompiler "/EHsc /W3 /nologo /O2 /Zi /MT" --cudart=shared
-o "Release\myprogram.exe" "myprogram.cu"
Note
It may be necessary to adjust the value of -ccbin to reflect the location of your Visual Studio installation.
To specify an alternate path where the libraries will be distributed, use linker options similar to those below:
Linux/Mac
nvcc -I $(CUDA_HOME)/include
-Xlinker "-rpath '$ORIGIN/lib'" --cudart=shared
-o myprogram myprogram.cu
Windows
nvcc.exe -ccbin "C:\vs2008\VC\bin"
-Xcompiler "/EHsc /W3 /nologo /O2 /Zi /MT /DELAY" --cudart=shared
-o "Release\myprogram.exe" "myprogram.cu"
For Linux and Mac, the -rpath option is used as before. For Windows, the /DELAY option is used; this requires that the application call SetDllDirectory() before the first call to any CUDA API function in order to specify the directory containing the CUDA DLLs.
Note
For Windows 8, SetDefaultDLLDirectories() and AddDllDirectory() should be used instead of SetDllDirectory(). Please see the MSDN documentation for these routines for more information.
18. Deployment Infrastructure Tools
18.1. Nvidia-SMI
The NVIDIA System Management Interface (nvidia-smi) is a command line utility that aids in the management and monitoring of NVIDIA GPU devices. This utility allows administrators to query GPU device state and, with the appropriate privileges, permits administrators to modify GPU device state. nvidia-smi is targeted at Tesla and certain Quadro GPUs, though limited support is also available on other NVIDIA GPUs. nvidia-smi ships with NVIDIA GPU display drivers on Linux, and with 64-bit Windows Server 2008 R2 and Windows 7. nvidia-smi can output queried information as XML or as human-readable plain text either to standard output or to a file. See the nvidia-smi documenation for details. Please note that new versions of nvidia-smi are not guaranteed to be backward-compatible with previous versions.
18.1.1. Queryable state
- ECC error counts
-
Both correctable single-bit and detectable double-bit errors are reported. Error counts are provided for both the current boot cycle and the lifetime of the GPU.
- GPU utilization
-
Current utilization rates are reported for both the compute resources of the GPU and the memory interface.
- Active compute process
-
The list of active processes running on the GPU is reported, along with the corresponding process name/ID and allocated GPU memory.
- Clocks and performance state
-
Max and current clock rates are reported for several important clock domains, as well as the current GPU performance state (pstate).
- Temperature and fan speed
-
The current GPU core temperature is reported, along with fan speeds for products with active cooling.
- Power management
-
The current board power draw and power limits are reported for products that report these measurements.
- Identification
-
Various dynamic and static information is reported, including board serial numbers, PCI device IDs, VBIOS/Inforom version numbers and product names.
18.1.2. Modifiable state
- ECC mode
-
Enable and disable ECC reporting.
- ECC reset
-
Clear single-bit and double-bit ECC error counts.
- Compute mode
-
Indicate whether compute processes can run on the GPU and whether they run exclusively or concurrently with other compute processes.
- Persistence mode
-
Indicate whether the NVIDIA driver stays loaded when no applications are connected to the GPU. It is best to enable this option in most circumstances.
- GPU reset
-
Reinitialize the GPU hardware and software state via a secondary bus reset.
18.2. NVML
The NVIDIA Management Library (NVML) is a C-based interface that provides direct access to the queries and commands exposed via nvidia-smi intended as a platform for building 3rd-party system management applications. The NVML API is shipped with the CUDA Toolkit (since version 8.0) and is also available standalone on the NVIDIA developer website as part of the GPU Deployment Kit through a single header file accompanied by PDF documentation, stub libraries, and sample applications; see https://developer.nvidia.com/gpu-deployment-kit. Each new version of NVML is backward-compatible.
An additional set of Perl and Python bindings are provided for the NVML API. These bindings expose the same features as the C-based interface and also provide backwards compatibility. The Perl bindings are provided via CPAN and the Python bindings via PyPI.
All of these products (nvidia-smi, NVML, and the NVML language bindings) are updated with each new CUDA release and provide roughly the same functionality.
See https://developer.nvidia.com/nvidia-management-library-nvml for additional information.
18.3. Cluster Management Tools
Managing your GPU cluster will help achieve maximum GPU utilization and help you and your users extract the best possible performance. Many of the industry’s most popular cluster management tools support CUDA GPUs via NVML. For a listing of some of these tools, see https://developer.nvidia.com/cluster-management.
18.4. Compiler JIT Cache Management Tools
Any PTX device code loaded by an application at runtime is compiled further to binary code by the device driver. This is called just-in-time compilation (JIT). Just-in-time compilation increases application load time but allows applications to benefit from latest compiler improvements. It is also the only way for applications to run on devices that did not exist at the time the application was compiled.
When JIT compilation of PTX device code is used, the NVIDIA driver caches the resulting binary code on disk. Some aspects of this behavior such as cache location and maximum cache size can be controlled via the use of environment variables; see Just in Time Compilation of the CUDA C++ Programming Guide.
18.5. CUDA_VISIBLE_DEVICES
It is possible to rearrange the collection of installed CUDA devices that will be visible to and enumerated by a CUDA application prior to the start of that application by way of the CUDA_VISIBLE_DEVICES environment variable.
Devices to be made visible to the application should be included as a comma-separated list in terms of the system-wide list of enumerable devices. For example, to use only devices 0 and 2 from the system-wide list of devices, set CUDA_VISIBLE_DEVICES=0,2 before launching the application. The application will then enumerate these devices as device 0 and device 1, respectively.
19. Recommendations and Best Practices
This chapter contains a summary of the recommendations for optimization that are explained in this document.
19.1. Overall Performance Optimization Strategies
Performance optimization revolves around three basic strategies:
Maximizing parallel execution
Optimizing memory usage to achieve maximum memory bandwidth
Optimizing instruction usage to achieve maximum instruction throughput
Maximizing parallel execution starts with structuring the algorithm in a way that exposes as much parallelism as possible. Once the parallelism of the algorithm has been exposed, it needs to be mapped to the hardware as efficiently as possible. This is done by carefully choosing the execution configuration of each kernel launch. The application should also maximize parallel execution at a higher level by explicitly exposing concurrent execution on the device through streams, as well as maximizing concurrent execution between the host and the device.
Optimizing memory usage starts with minimizing data transfers between the host and the device because those transfers have much lower bandwidth than internal device data transfers. Kernel access to global memory also should be minimized by maximizing the use of shared memory on the device. Sometimes, the best optimization might even be to avoid any data transfer in the first place by simply recomputing the data whenever it is needed.
The effective bandwidth can vary by an order of magnitude depending on the access pattern for each type of memory. The next step in optimizing memory usage is therefore to organize memory accesses according to the optimal memory access patterns. This optimization is especially important for global memory accesses, because latency of access costs hundreds of clock cycles. Shared memory accesses, in counterpoint, are usually worth optimizing only when there exists a high degree of bank conflicts.
As for optimizing instruction usage, the use of arithmetic instructions that have low throughput should be avoided. This suggests trading precision for speed when it does not affect the end result, such as using intrinsics instead of regular functions or single precision instead of double precision. Finally, particular attention must be paid to control flow instructions due to the SIMT (single instruction multiple thread) nature of the device.
20. nvcc Compiler Switches
20.1. nvcc
The NVIDIA nvcc compiler driver converts .cu files into C++ for the host system and CUDA assembly or binary instructions for the device. It supports a number of command-line parameters, of which the following are especially useful for optimization and related best practices:
-maxrregcount=Nspecifies the maximum number of registers kernels can use at a per-file level. See Register Pressure. (See also the__launch_bounds__qualifier discussed in Execution Configuration of the CUDA C++ Programming Guide to control the number of registers used on a per-kernel basis.)--ptxas-options=-vor-Xptxas=-vlists per-kernel register, shared, and constant memory usage.-ftz=true(denormalized numbers are flushed to zero)-prec-div=false(less precise division)-prec-sqrt=false(less precise square root)-use_fast_mathcompiler option ofnvcccoerces everyfunctionName()call to the equivalent__functionName()call. This makes the code run faster at the cost of diminished precision and accuracy. See Math Libraries.
21. Notices
21.1. Notice
This document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.
NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice.
Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.
NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgement, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.
NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk.
NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.
No license, either expressed or implied, is granted under any NVIDIA patent right, copyright, or other NVIDIA intellectual property right under this document. Information published by NVIDIA regarding third-party products or services does not constitute a license from NVIDIA to use such products or services or a warranty or endorsement thereof. Use of such information may require a license from a third party under the patents or other intellectual property rights of the third party, or a license from NVIDIA under the patents or other intellectual property rights of NVIDIA.
Reproduction of information in this document is permissible only if approved in advance by NVIDIA in writing, reproduced without alteration and in full compliance with all applicable export laws and regulations, and accompanied by all associated conditions, limitations, and notices.
THIS DOCUMENT AND ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, “MATERIALS”) ARE BEING PROVIDED “AS IS.” NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE. TO THE EXTENT NOT PROHIBITED BY LAW, IN NO EVENT WILL NVIDIA BE LIABLE FOR ANY DAMAGES, INCLUDING WITHOUT LIMITATION ANY DIRECT, INDIRECT, SPECIAL, INCIDENTAL, PUNITIVE, OR CONSEQUENTIAL DAMAGES, HOWEVER CAUSED AND REGARDLESS OF THE THEORY OF LIABILITY, ARISING OUT OF ANY USE OF THIS DOCUMENT, EVEN IF NVIDIA HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. Notwithstanding any damages that customer might incur for any reason whatsoever, NVIDIA’s aggregate and cumulative liability towards customer for the products described herein shall be limited in accordance with the Terms of Sale for the product.
21.2. OpenCL
OpenCL is a trademark of Apple Inc. used under license to the Khronos Group Inc.
21.3. Trademarks
NVIDIA and the NVIDIA logo are trademarks or registered trademarks of NVIDIA Corporation in the U.S. and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.