Core Concepts#
This section introduces the core concepts of the cuDNN backend API.
cuDNN Handle#
The cuDNN library exposes a host API but assumes that for operations using the GPU, the necessary data is directly accessible from the device.
An application using cuDNN must initialize a handle to the library context by calling cudnnCreate(). This handle is explicitly passed to every subsequent library function that operates on GPU data. Once the application finishes using cuDNN, it can release the resources associated with the library handle using cudnnDestroy(). This approach allows the user to explicitly control the library’s functioning when using multiple host threads, GPUs, and CUDA streams.
For example, an application can use cudaSetDevice (prior to creating a cuDNN handle) to associate different devices with different host threads, and in each of those host threads, create a unique cuDNN handle that directs the subsequent library calls to the device associated with it. In this case, the cuDNN library calls made with different handles would automatically run on different devices.
The device associated with a particular cuDNN context is assumed to remain unchanged between the corresponding cudnnCreate() and cudnnDestroy() calls. In order for the cuDNN library to use a different device within the same host thread, the application must set the new device to be used by calling cudaSetDevice and then create another cuDNN context, which will be associated with the new device, by calling cudnnCreate().
Tensor Core Operations#
The cuDNN v7 library introduced the acceleration of compute-intensive routines using Tensor Core hardware on supported GPU SM versions. Tensor Core operations are supported beginning with the NVIDIA Volta GPU.
Tensor Core operations accelerate matrix math operations; cuDNN uses Tensor Core operations that accumulate into FP16, FP32, and INT32 values. Setting the math mode to CUDNN_TENSOR_OP_MATH via the cudnnMathType_t enumerator indicates that the library will use Tensor Core operations. This enumerator specifies the available options to enable the Tensor Core and should be applied on a per-routine basis.
The default math mode is CUDNN_DEFAULT_MATH, which indicates that the Tensor Core operations will be avoided by the library. Because the CUDNN_TENSOR_OP_MATH mode uses the Tensor Cores, it is possible that these two modes generate slightly different numerical results due to different sequencing of the floating-point operations.
For example, the result of multiplying two matrices using Tensor Core operations is very close, but not always identical, to the result achieved using a sequence of scalar floating-point operations. For this reason, the cuDNN library requires an explicit user opt-in before enabling the use of Tensor Core operations.
However, experiments with training common deep learning models show negligible differences between using Tensor Core operations and scalar floating point paths, as measured by both the final network accuracy and the iteration count to convergence. Consequently, the cuDNN library treats both modes of operation as functionally indistinguishable and allows for the scalar paths to serve as legitimate fallbacks for cases in which the use of Tensor Core operations is unsuitable.
Kernels using Tensor Core operations are available for:
Convolutions
RNNs
Multihead Attention
For more information, refer to NVIDIA Training with Mixed Precision.
For a deep learning compiler, the following are the key guidelines:
Make sure that the convolution operation is eligible for Tensor Cores by avoiding any combinations of large padding and large filters.
Transform the inputs and filters to NHWC, pre-pad channel and batch size to be a multiple of 8.
Make sure that all user-provided tensors, workspace, and reserve space are aligned to 128-bit boundaries. Note that 1024-bit alignment may deliver better performance.
Notes on Tensor Core Precision#
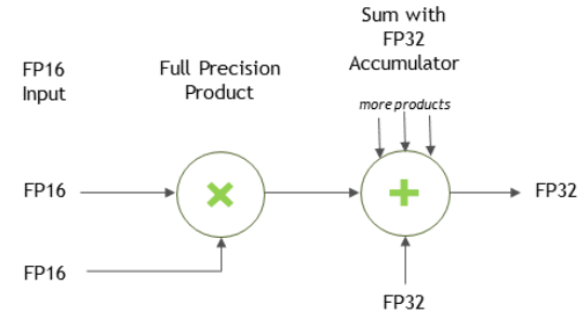
For FP16 data, Tensor Cores operate on FP16 input, output in FP16, and may accumulate in FP16 or FP32. The FP16 multiply leads to a full-precision result that is accumulated in FP32 operations with the other products in a given dot product for a matrix with m x n x k dimensions.
For an FP32 accumulation, with FP16 output, the output of the accumulator is down-converted to FP16. Generally, the accumulation type is of greater or equal precision to the output type.