Sparse Matrix Formats¶
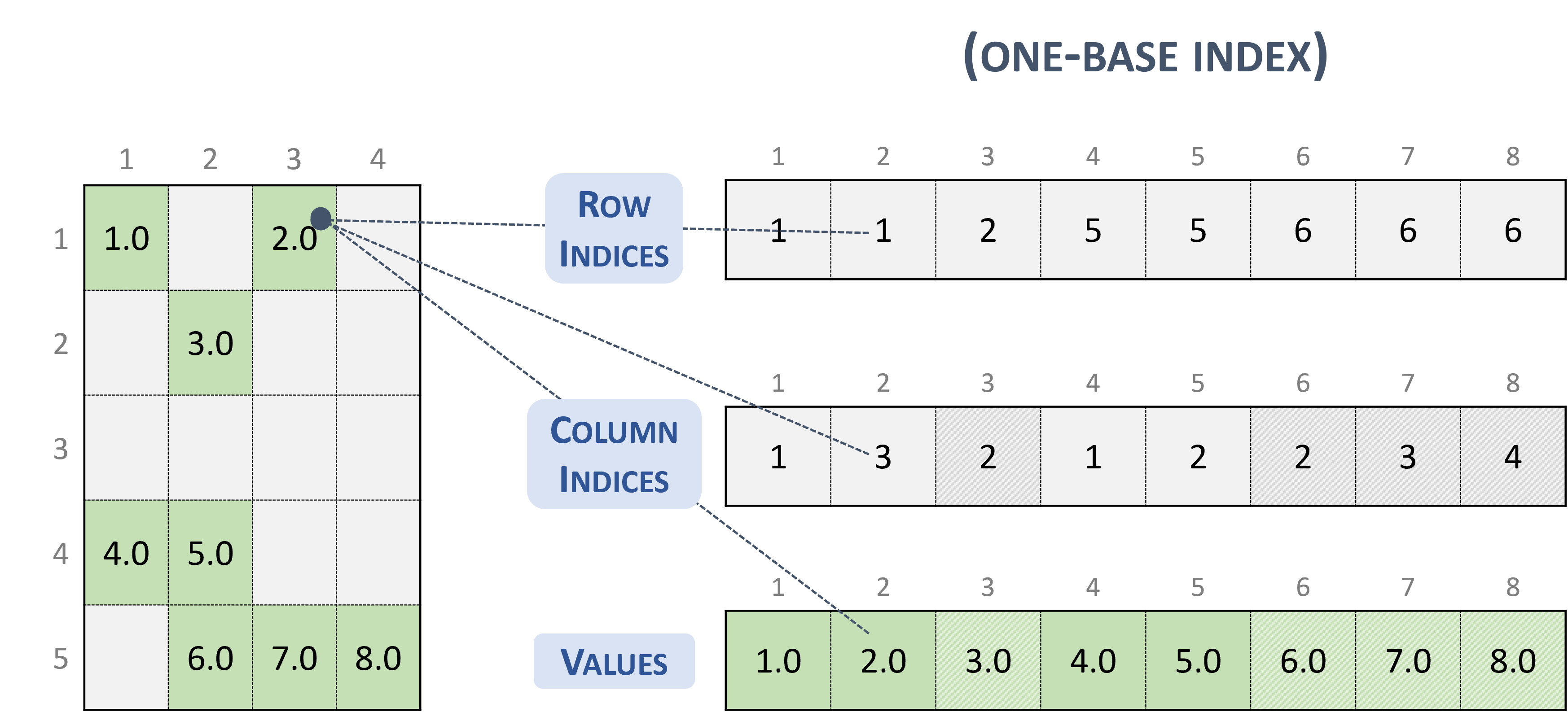
Coordinate (COO)¶
A sparse matrix stored in COO format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the row indices array of length
nnzthat contains the row indices of the corresponding elements in the values array.The pointers to the column indices array of length
nnzthat contains the column indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in row-major ordering.Each entry of the COO representation consists of a
<row, column>pair.The COO format is assumed to be sorted by row.
The following example shows a \(5 \times 4\) matrix represented in COO format.

Note
NVPL Sparse supports both sorted and unsorted column indices within a given row.
Note
If the column indices within a given row are unique, the correctness of the computation is not always ensured.
Given an entry in the COO format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
rows_indices[i] * leading_dimension + column_indices[i]
// column-major
column_indices[i] * leading_dimension + rows_indices[i]
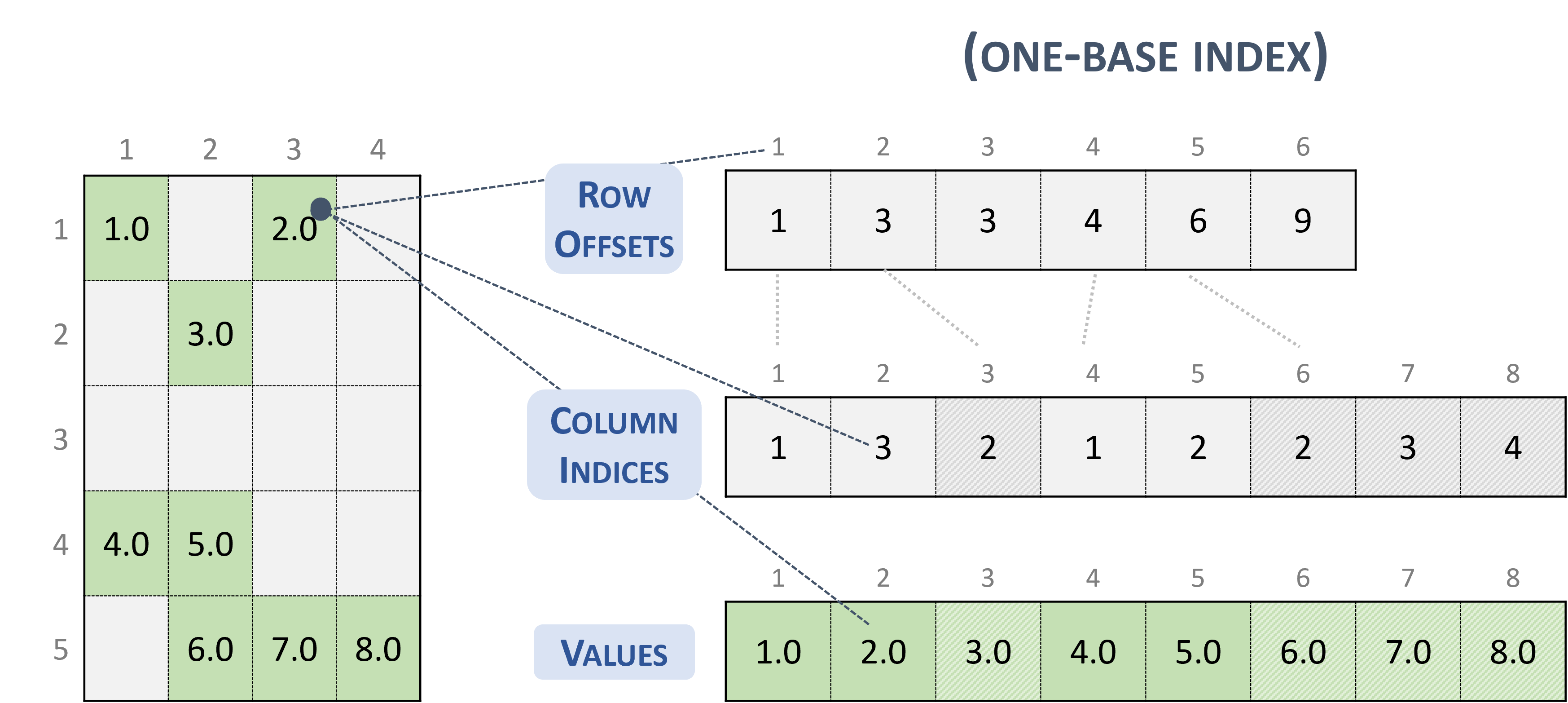
Compressed Sparse Row (CSR)¶
The CSR format is similar to COO, where the row indices are compressed and replaced by an array of offsets.
A sparse matrix stored in CSR format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the row offsets array of length number of rows + 1 that represents the starting position of each row in the columns and values arrays.
The pointers to the column indices array of length
nnzthat contains the column indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in row-major ordering.
The following example shows a \(5 \times 4\) matrix represented in CSR format.

Note
NVPL Sparse supports both sorted and unsorted column indices within a given row.
Note
If the column indices within a given row are not unique, the correctness of the computation is not always ensured.
Given an entry in the CSR format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
row * leading_dimension + column_indices[row_offsets[row] + k]
// column-major
column_indices[row_offsets[row] + k] * leading_dimension + row
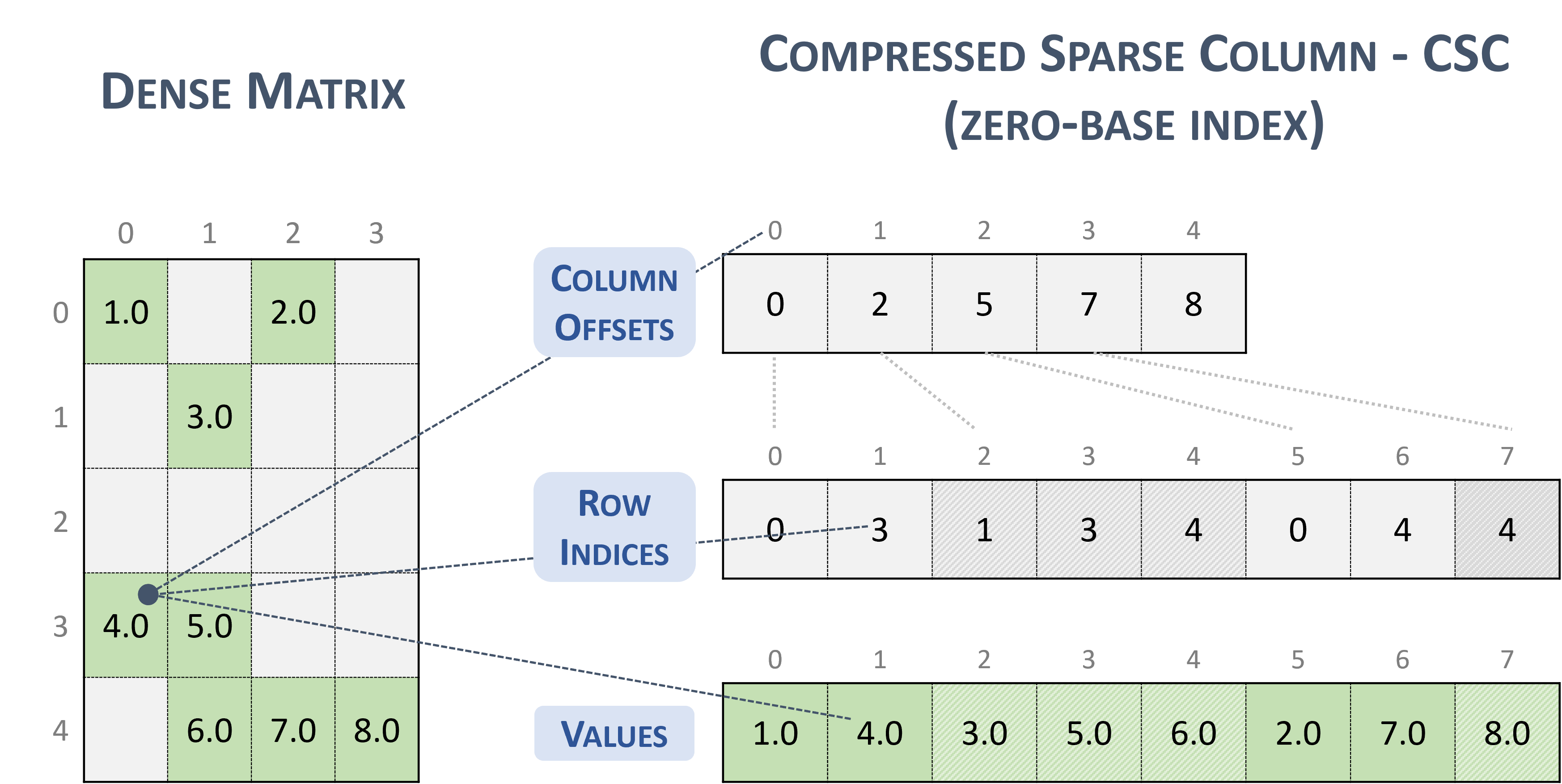
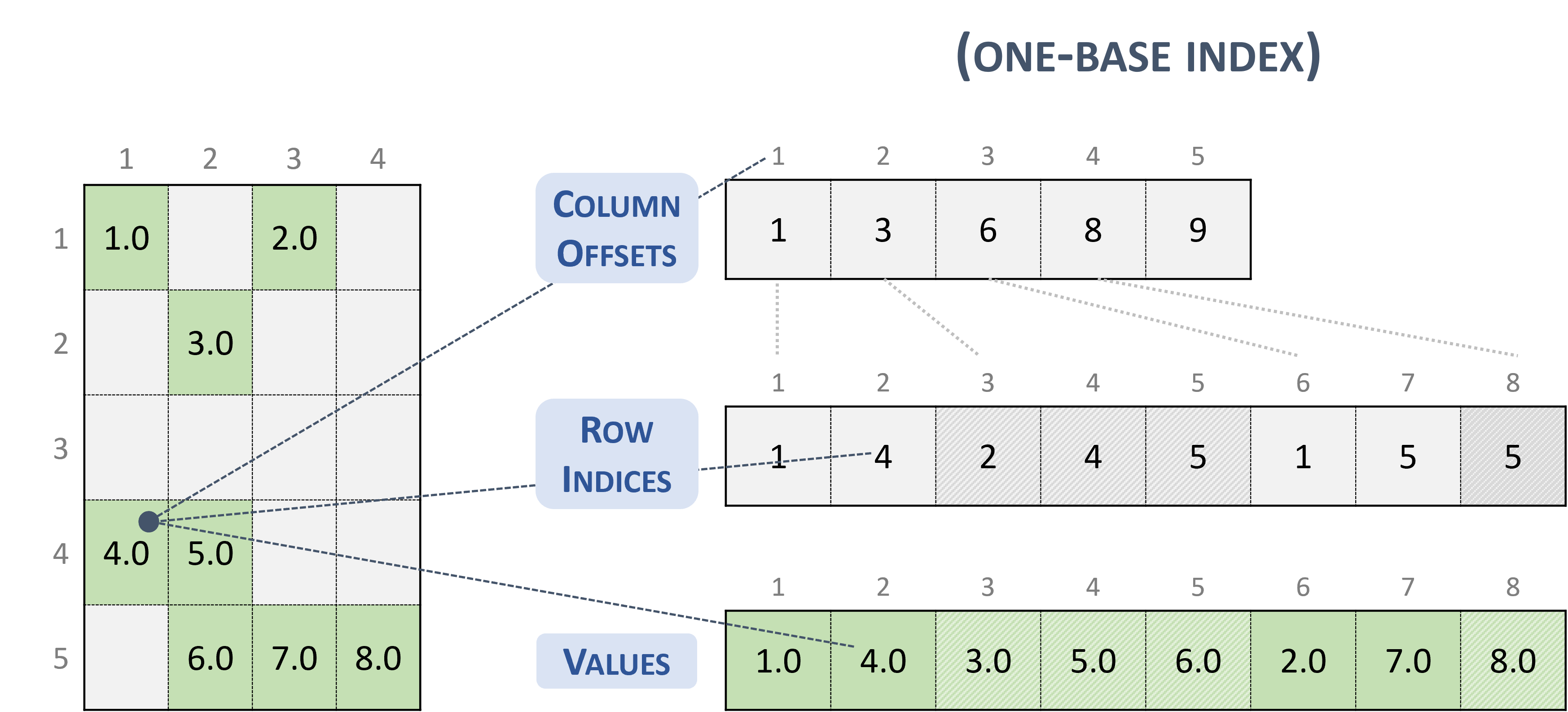
Compressed Sparse Column (CSC)¶
The CSC format is similar to COO, where the column indices are compressed and replaced by an array of offsets.
A sparse matrix stored in CSC format is represented by the following parameters.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The pointers to the column offsets array of length number of column + 1 that represents the starting position of each column in the columns and values arrays.
The pointers to the row indices array of length
nnzthat contains row indices of the corresponding elements in the values array.The pointers to the values array of length
nnzthat holds all nonzero values of the matrix in column-major ordering.
The following example shows a \(5 \times 4\) matrix represented in CSC format.
Note
The CSR format has exactly the same memory layout as its transpose in CSC format (and vice versa).
Note
NVPL Sparse supports both sorted and unsorted row indices within a given column.
Note
If the row indices within a given column are not unique, the correctness of the computation is not always ensured.
Given an entry in the CSC format (zero-base), the corresponding position in the dense matrix is computed as:
// row-major
column * leading_dimension + row_indices[column_offsets[column] + k]
// column-major
row_indices[column_offsets[column] + k] * leading_dimension + column
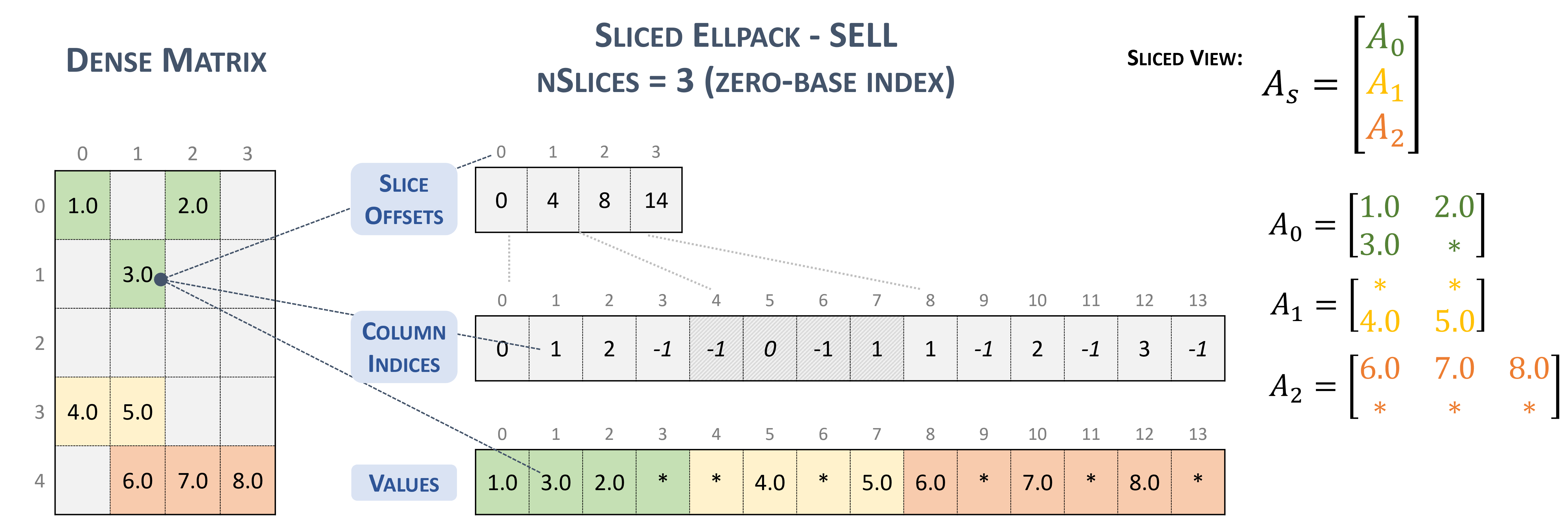
Sliced Ellpack (SELL)¶
The Sliced Ellpack format is standardized and well-known as the state of the art. This format allows to significantly improve the performance of all problems that involve low variability in the number of nonzero elements per row.
A matrix in the Sliced Ellpack format is divided into slices of an exact number of rows (\(sliceSize\)), defined by the user.
The maximum row length (i.e., the maximum non-zeros per row) is found for each slice, and every row in the slice is padded to the maximum row length.
The value -1 is used for padding.
A \(m \times n\) sparse matrix \(A\) is equivalent to a sliced sparse matrix \(A_{s}\) with \(nslices = \left \lceil{\frac{m}{sliceSize}}\right \rceil\) slice rows and \(n\) columns. To improve memory coalescing and memory utilization, each slice is stored in column-major order.
A sparse matrix stored in SELL format is represented by the following parameters.
The number of slices.
The number of rows in the matrix.
The number of columns in the matrix.
The number of non-zero elements (
nnz) in the matrix.The total number elements (
sellValuesSize), including non-zero values and padded elements.The pointer to the slice offsets of length \(nslices + 1\) that holds offsets of the slides corresponding to the columns and values arrays.
The pointer to the column indices array of length
sellValuesSizethat contains column indices of the corresponding elements in the values array. The column indices are stored in column-major layout. Value-1refers to padding.The pointer to the values array of length
sellValuesSizethat holds all non-zero values and padding in column-major layout.
The following example shows a \(5 \times 4\) matrix represented in SELL format.