Defines common types used by several components. More...
Data Structures | |
| struct | VPIPyramidalKeypointF32 |
| Stores a float32 pyramidal-based keypoint coordinate The coordinate includes the (x, y) position in an image inside a pyramid, and (octave and layer) selects a specific image on that pyramid. More... | |
| struct | VPIKeypointF32 |
| Stores a float32 keypoint coordinate The coordinate is relative to the top-left corner of an image. More... | |
| struct | VPIKeypointU32 |
| Stores a U32 keypoint coordinate The coordinate is relative to the top-left corner of an image. More... | |
| struct | VPIHomographyTransform2D |
| Stores a generic 2D homography transform. More... | |
| struct | VPIBoundingBox |
| Stores a generic 2D bounding box. More... | |
| struct | VPIAxisAlignedBoundingBoxF32 |
| Stores an axis-aligned 32-bit floating point 2D bounding box. More... | |
| struct | VPIStats |
| Stores the statistics of an image. More... | |
| struct | VPIMatches |
| Stores the matches between 2 descriptors. More... | |
| struct | VPIRectangleI |
| Stores the geometric information of a rectangle. More... | |
| struct | VPIPose |
| Estimation of a transformation from one 3D coordinate system to another with object-space error. More... | |
Macros | |
| #define | VPI_TERMINATION_CRITERIA_ITERATIONS (1u << 0) |
| Defines the termination criteria macros. More... | |
Enumerations | |
| enum | VPIInterpolationType |
| Interpolation types supported by several algorithms. More... | |
| enum | VPIBorderExtension |
| Image border extension specify how pixel values outside of the image domain should be constructed. More... | |
| enum | VPIOpticalFlowQuality |
| Defines the quality of the optical flow algorithm. More... | |
| enum | VPILockMode |
| Defines the lock modes used by memory lock functions. More... | |
| enum | VPIEventState |
| Defines the states of the event. More... | |
Detailed Description
Defines common types used by several components.
Data Structure Documentation
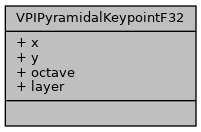
◆ VPIPyramidalKeypointF32
| struct VPIPyramidalKeypointF32 |
Stores a float32 pyramidal-based keypoint coordinate The coordinate includes the (x, y) position in an image inside a pyramid, and (octave and layer) selects a specific image on that pyramid.
Pyramids are used to approximate the scale space with one or more resolution levels, also known as octaves, where each octave may have one or more smoothing layers. One example is in the ORB algorithm, where its input is a pyramid, representing the scale space of its base image, that normally has several octaves, where each octave has a single layer. Octaves are defined as levels of dyadic-image pyramids, i.e. a VPIPyramid with scale=0.5.
 Collaboration diagram for VPIPyramidalKeypointF32:
Collaboration diagram for VPIPyramidalKeypointF32:◆ VPIKeypointF32
| struct VPIKeypointF32 |
◆ VPIKeypointU32
| struct VPIKeypointU32 |
◆ VPIHomographyTransform2D
| struct VPIHomographyTransform2D |
Stores a generic 2D homography transform.
When only scale and translation transformation is needed, these parameters must be arranged in the matrix as follows:
\[ \begin{bmatrix} s_x & 0 & p_x \\ 0 & s_y & p_y \\ 0 & 0 & 1 \end{bmatrix} \]
Scaling \((s_x,s_y)\) is relative to the center of the patch, position \((p_x,p_y)\) is relative to the top-left of the image.
In the general case, given an homogeneous 2D point \(P(x,y,1)\) and the matrix \(M^{3x3}\), the Euclidean 2D point \(O(x,y)\) is defined as
\begin{align} T &= M \cdot P \\ O &= (T_x/T_z, T_y/T_z) \end{align}
 Collaboration diagram for VPIHomographyTransform2D:
Collaboration diagram for VPIHomographyTransform2D:| Data Fields | ||
|---|---|---|
| float | mat3[3][3] | 3x3 homogeneous matrix that defines the homography. |
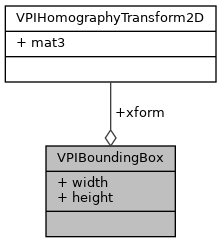
◆ VPIBoundingBox
| struct VPIBoundingBox |
Stores a generic 2D bounding box.
Although this structure can store a 2D bounding box transformed by any homography, sometimes it stores an axis-aligned bounding box. To retrieve it, do the following:
 Collaboration diagram for VPIBoundingBox:
Collaboration diagram for VPIBoundingBox:| Data Fields | ||
|---|---|---|
| VPIHomographyTransform2D | xform | Defines the bounding box top left corner and its homography. |
| float | width | Bounding box width. |
| float | height | Bounding box height. |
◆ VPIAxisAlignedBoundingBoxF32
| struct VPIAxisAlignedBoundingBoxF32 |
Stores an axis-aligned 32-bit floating point 2D bounding box.
 Collaboration diagram for VPIAxisAlignedBoundingBoxF32:
Collaboration diagram for VPIAxisAlignedBoundingBoxF32:◆ VPIStats
| struct VPIStats |
◆ VPIMatches
| struct VPIMatches |
 Collaboration diagram for VPIMatches:
Collaboration diagram for VPIMatches:| Data Fields | ||
|---|---|---|
| int | refIndex[VPI_MAX_MATCHES_PER_DESCRIPTOR] | Match reference index. |
| float | distance[VPI_MAX_MATCHES_PER_DESCRIPTOR] | Distance between query and reference descriptor. |
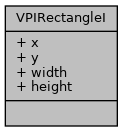
◆ VPIRectangleI
| struct VPIRectangleI |
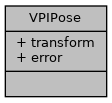
◆ VPIPose
| struct VPIPose |
Estimation of a transformation from one 3D coordinate system to another with object-space error.
 Collaboration diagram for VPIPose:
Collaboration diagram for VPIPose:Macro Definition Documentation
◆ VPI_TERMINATION_CRITERIA_ITERATIONS
| #define VPI_TERMINATION_CRITERIA_ITERATIONS (1u << 0) |
#include <vpi/Types.h>
Defines the termination criteria macros.
Termination based on maximum number of iterations.
Enumeration Type Documentation
◆ VPIInterpolationType
| enum VPIInterpolationType |
#include <vpi/Interpolation.h>
Interpolation types supported by several algorithms.
Definition at line 69 of file Interpolation.h.
◆ VPIBorderExtension
| enum VPIBorderExtension |
#include <vpi/Types.h>
Image border extension specify how pixel values outside of the image domain should be constructed.
◆ VPIOpticalFlowQuality
#include <vpi/Types.h>
Defines the quality of the optical flow algorithm.
| Enumerator | |
|---|---|
| VPI_OPTICAL_FLOW_QUALITY_LOW | Fast but low quality optical flow implementation. |
| VPI_OPTICAL_FLOW_QUALITY_MEDIUM | Speed and quality in between of VPI_OPTICAL_FLOW_QUALITY_LOW and VPI_OPTICAL_FLOW_QUALITY_HIGH. |
| VPI_OPTICAL_FLOW_QUALITY_HIGH | Slow but high quality optical flow implementation. |
◆ VPILockMode
| enum VPILockMode |
#include <vpi/Types.h>
Defines the lock modes used by memory lock functions.
◆ VPIEventState
| enum VPIEventState |
#include <vpi/Types.h>
Defines the states of the event.
| Enumerator | |
|---|---|
| VPI_EVENT_STATE_NOT_SIGNALED | Event is not signaled yet. |
| VPI_EVENT_STATE_SIGNALED | Event has been signaled. |