Accuracy Considerations#

Reduced Precision Formats#

The choice of floating-point precision can significantly impact both performance and accuracy. In addition to a standard single-precision floating-point (FP32), TensorRT supports three reduced precision formats: TensorFloat-32 (TF32), half-precision floating-point (FP16), and Brain Floating Point (BF16).

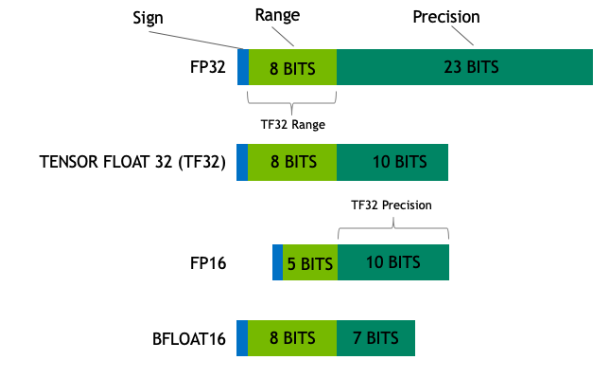
TF32, enabled by default in TensorRT, uses an 8-bit exponent and a 10-bit mantissa, combining the dynamic range of FP32 with the computational efficiency of FP16. FP16, with a 5-bit exponent and a 10-bit mantissa, offers significant speed and memory efficiency benefits but may exhibit reduced precision due to its limited precision and range. BF16, featuring an 8-bit exponent and a 7-bit mantissa, provides a larger dynamic range than FP16 but with lower precision. The larger exponent makes BF16 suitable for scenarios where overflow is a concern, but precision can be reduced. Each format offers unique trade-offs, and the choice depends on the specific task requirements, such as the need for speed, memory efficiency, or numerical accuracy.

Reduced Precision Formats

Impact of ULP on Large-Magnitude Values#

ULP, “Unit in the Last Place,” measures precision in floating-point arithmetic. It represents the smallest difference between two distinct floating-point numbers. ULP quantifies the gap between consecutive representable numbers in a given floating-point format. The size of this gap varies depending on the magnitude of the numbers being represented.

For large-magnitude values, the ULP can become quite large. This means that the difference between two consecutive floating-point numbers becomes significant. High ULP can lead to substantial rounding errors when numerical computations involve large-magnitude values. These errors accumulate and can cause numerical instability, ultimately degrading the accuracy of the computations.

In some models, the magnitude of the data increases as it passes through the network layers, especially in the absence of normalization layers. For instance, cascaded convolutional layers without normalization can amplify magnitudes, challenging reduced precision formats to maintain accuracy.

FP16 Overflow#

FP16 has a narrower range of representable values than FP32, TF32, and BF16, making it more susceptible to overflow. FP16’s 5-bit exponent limits its maximum value to 65,504, whereas FP32, TF32, and BF16 use an 8-bit exponent, offering a broader range. Overflow in FP16 results in Inf (infinity) values, which can propagate errors and lead to NaN (not-a-number) values, severely degrading model accuracy.

For example, the IReduceLayer is prone to overflows due to accumulating all values along a certain axis (except for min-reduce and max-reduce).

Sensitive Calculations#

Certain model calculations are highly sensitive to precision changes. Using reduced precision formats for these calculations can cause significant accuracy loss due to their reduced precision.

For example, Sigmoid or Softmax amplify small numerical differences due to their exponential component.

Mitigation Strategies#

To mitigate accuracy loss when using reduced precision during inference, consider the following strategies:

Mixed Precision Inference

Combine FP16, BF16, TF32, and FP32 operations. Perform critical, precision-sensitive calculations in FP32 and use reduced precision for less sensitive operations to gain performance benefits. Linear operations are particularly good candidates for reduced precision because, besides the reduced bandwidth, their compute is accelerated by the Tensor Cores. This can be achieved by adding ICastLayer in a strongly typed mode or setting layer precision constraints in a weakly typed mode. For more information, refer to the Strongly Typed Networks and Reduced Precision in Weakly-Typed Networks sections.

Control Computation Precision

In addition to setting a layer’s input/output precisions, it is sometimes possible to control the internal computation precision. For more information, refer to the Control of Computational Precision section.

Magnitude Adjustment

Scale the input data to prevent the accuracy loss associated with high-magnitude data.

Quantized Formats#

TensorRT supports several quantized formats for compressing deep learning models:

  • INT8: An 8-bit integer type with a range of [-128, 127].

  • INT4: A 4-bit integer type with a range of [-8, 7].

  • FP8: A floating point type (1-bit sign, 4-bit exponent, 3-bit mantissa) with a range [-448, 448].

  • FP4: A floating point type (1-bit sign, 2-bit exponent, 1-bit mantissa) with a range [-6, 6].

For more information, refer to the Types and Precisions section.

Uniform and Non-Uniform Distributions in Quantized Types#

Integer formats, such as INT8 and INT4, use uniform quantization, which means the range of values is divided into equal-sized intervals. This method is simple and efficient but might not optimally capture the distribution of weights and activations.

Floating point formats such as FP8E4M3 and FP4E2M1 have non-uniform distributions with more values concentrated near 0, which better aligns with the typical distribution of neural network weights and activations.

Quantization Errors#

Quantization introduces two sources of error that can significantly impact the accuracy of deep learning models: rounding errors and clamping errors.

Rounding Errors occur when continuous values are approximated to the nearest quantized value, causing a loss of information. TensorRT uses the round-to-nearest-even method, which rounds to the nearest even value in case of ties, helping reduce bias in the quantization process.

Clamping Errors occur when values exceed the quantization range and are clipped to the nearest boundary, causing a loss of dynamic range. There is a tradeoff between the clamping error and the rounding error, and this is expressed in the scale selection: Setting a scale that allows fewer values to be clipped means a higher rounding error.

On this page