Working with Quantized Types#

Introduction to Quantization#

TensorRT enables high-performance inference by supporting quantization, a technique that reduces model size and accelerates computation by representing floating-point values with lower-precision data types. Beyond raw performance, quantization is crucial for reducing memory footprint and improving energy efficiency, making it ideal for deployment on resource-constrained edge devices and for achieving greater cost-efficiency in large-scale data center deployments.

TensorRT employs a symmetric quantization scheme, where both activations and weights are mapped to quantized values centered around zero. This approach simplifies the transformation between quantized and floating-point representations, typically involving only a scaling factor. Supported quantized data types in TensorRT include:

INT8 (signed 8-bit integer)
INT4 (signed 4-bit integer, weight-only quantization)
FP8E4M3 (FP8, 8-bit floating point with 4 exponent and 3 mantissa bits)
FP4E2M1 (FP4, 4-bit floating point with 2 exponent and 1 mantissa bit)

These low-precision formats allow TensorRT to deliver efficient inference while maintaining accuracy, making it suitable for deployment on resource-constrained environments and high-throughput applications.

Quantization Workflows#

TensorRT supports both post-training quantization (PTQ) and quantization-aware training (QAT) workflows, enabling users to optimize models for low precision data types. The quantization process uses per-tensor, per-channel, or block-wise scaling, depending on the layer and data type, to best preserve model accuracy during conversion.

PTQ involves quantizing a pre-trained model without retraining. This method requires running the model with a representative “calibration data” set to compute quantization parameters for activations offline. PTQ is highly practical when retraining is infeasible due to resource limitations or data privacy concerns. However, it’s important to note that PTQ can lead to accuracy degradation, especially for complex models or sensitive layers.

QAT simulates quantization during the training process by quantizing weights and activation layers. This allows the training process to actively compensate for the effects of quantization and dequantization operations, generally leading to superior accuracy recovery compared to PTQ. While QAT can achieve high accuracy at lower precisions, it is more time-consuming, requires access to the entire (labeled) training dataset, and demands more computational resources.

The TensorRT Model Optimizer is a Python toolkit designed to facilitate the creation of quantization-aware training (QAT) models that are fully compatible with TensorRT’s optimization and deployment workflows. In addition, the toolkit provides a post-training quantization (PTQ) recipe that enables users to perform PTQ on models developed in both PyTorch and ONNX formats, streamlining the quantization process across different frameworks.

Explicit vs Implicit Quantization#

Note

Implicit quantization is deprecated. Users are strongly advised to transition to explicit quantization, typically by utilizing the TensorRT Model Optimizer to create models with explicit quantization.

Quantized networks can be processed in two (mutually exclusive) ways: using either implicit or explicit quantization. The main difference between the two processing modes is whether you require explicit control over quantization or let the TensorRT builder choose which operations and tensors to quantize (implicit). The sections below provide more details. Implicit quantization is only supported when quantizing for INT8. It can only be used together with weak typing, which is also deprecated.

TensorRT uses explicit quantization mode when a network has QuantizeLayer and DequantizeLayer layers (Q/DQ, for short). It is called explicit quantization because Q/DQ layers are used to control quantization and dequantization in the network. TensorRT uses implicit quantization mode when there are no QuantizeLayer or DequantizeLayer layers in the network, and INT8 and weak typing are enabled in the builder configuration. Only INT8 is supported in implicit quantization mode.

In implicitly quantized networks, each activation tensor that has an associated scale assigned by the calibration process or assigned by the API function setDynamicRange is considered for quantization.

When processing implicitly quantized networks, TensorRT treats the model as a floating-point model when applying the graph optimizations and uses INT8 opportunistically to optimize layer execution time. If a layer runs faster in INT8 and has assigned quantization scales on its data inputs and outputs, then a kernel with INT8 precision is assigned to that layer. Otherwise, a high-precision floating-point (FP32, FP16, or BF16) kernel is assigned. Implicit quantization is deprecated and its usage is discouraged.

In explicitly quantized networks, the quantization and dequantization operations are represented explicitly by IQuantizeLayer (C++, Python) and IDequantizeLayer (C++, Python) nodes in the graph - these will henceforth be referred to as Q/DQ nodes. By contrast with implicit quantization, the explicit form specifies exactly where conversion to and from a quantized type is performed, and the optimizer will perform only conversions to and from quantized types that are dictated by the semantics of the model.

ONNX uses an explicitly quantized representation: when a model in PyTorch or TensorFlow is exported to ONNX, each fake-quantization operation in the framework’s graph is exported as Q, followed by DQ. Since TensorRT preserves the semantics of these layers, users can expect accuracy that is very close to that seen in the deep learning framework. While optimizations preserve the arithmetic semantics of quantization and dequantization operators, they may change the order of floating-point operations in the model, so results will not be bitwise identical.

Explicit quantization offers significant advantages, as summarized in the table below:

Broader Data Type Support: It supports a wider range of quantized data types, including INT8, FP8, INT4, and FP4.
Direct User Control: Q/DQ nodes provide precise control over where conversions to and from quantized types are performed.
Preservation of Model Semantics: Ensures that the optimizer performs only conversions dictated by the model’s inherent semantics, leading to accuracy very close to that observed in the original framework.
Compatibility with ONNX Export: Performing QAT or PTQ in a deep learning framework and then exporting to ONNX naturally results in an explicitly quantized model, as ONNX represents fake-quantization operations as Q/DQ pairs.

Implicit quantization and weak typing are intrinsically linked. Implicit quantization, an opportunistic approach where the TensorRT builder automatically determines which operations and tensors to quantize, requires the use of weak typing in the builder configuration. Weak typing allows TensorRT to make flexible, on-the-fly decisions about precision, as type conversions to and from INT8 relied solely on the builder’s internal heuristics rather than explicit QuantizeLayer and DequantizeLayer layers. However, both implicit quantization and weak typing are now deprecated, as they offer less control and narrower data type support compared to the explicit quantization workflow.

It is important for developers to understand that for models with Q/DQ nodes, external calibration tables should not be provided, as TensorRT does not permit loading a calibration table if Q/DQ nodes are already present in the model. This implies that for explicit models, calibration is performed before ONNX export (for example, during PTQ/QAT with Model Optimizer), with the resulting scales embedded directly into the Q/DQ nodes.

While explicit quantization is the recommended future-proof approach, it is worth noting that for some networks, initial explicit quantization might exhibit higher latency compared to implicit quantization. However, the Model Optimizer team is actively working with the TensorRT team to minimize this gap across various models.

Implicit vs Explicit Quantization#
	Implicit Quantization (Deprecated)	Explicit Quantization
Supported quantized data-types	INT8	INT8, FP8, INT4, FP4
User control over precision	Global builder flags and per-layer precision APIs.	Encoded directly in the model.
API	Model + Scales (dynamic range API) Model + Calibration data	Model with Q/DQ layers.

Quantization Granularities#

Quantization granularity refers to how quantization scale factors are applied across a model’s tensors. Selecting the appropriate granularity is a direct lever for balancing the benefits of quantization (such as memory reduction) with its potential drawbacks (accuracy loss). The more granular the approach, the higher the potential accuracy, but also the higher the computational and memory overhead associated with managing multiple scaling factors. There are three supported quantization scale granularities in TensorRT:

Per-tensor quantization: a single scale value (scalar) is used to scale the entire tensor.
Per-channel quantization: a scale tensor is broadcast along the given axis - for convolutional neural networks, this is typically the channel axis.
Block quantization: the tensor is divided into fixed-size 1-dimensional blocks along a single dimension. A scale factor is defined for each block.

When using per-channel quantization with Convolutions, the quantization axis must be the output-channel axis. For example, when the weights of 2D convolution are described using KCRS notation, K is the output-channel axis, and the weights quantization can be described as:

For each k in K:
    For each c in C:
        For each r in R:
            For each s in S:
                output[k,c,r,s] := clamp(round(input[k,c,r,s] / scale[k]))

The scale is a vector of coefficients and must have the same size as the quantization axis.

Dequantization is performed similarly except for the pointwise operation that is defined as:

output[k,c,r,s] := input[k,c,r,s] * scale[k]

Block Quantization

In block quantization, elements are grouped into 1D blocks, with all elements in a block sharing a common scale factor. Block quantization is supported for inputs of up to 3 dimensions.

INT4 block quantization supports weight-only quantization (WoQ).

FP4 block quantization supports both weights and activations. To minimize the quantization error, it is recommended to use Dynamic Quantization for activations.

When using block quantization, the scale tensor dimensions equal the data tensor dimensions except for one dimension over which blocking is performed (the blocking axis). For example, given a 2-D RS weights input, R (dimension 0) as the blocking axis and B as the block size, the scale in the blocking axis is repeated according to the block size and can be described like this:

For each r in R:
    For each s in S:
        output[r,s] = clamp(round(input[r,s] / scale[r//B, s]))

The scale is a 2D array of coefficients with dimensions (R//B, S).

Dequantization is performed similarly, except for the pointwise operation that is defined as:

output[r,s] = input[r,s] * scale[r//B, s]

Quantized Types Rounding Modes#

TensorRT primarily employs the round-to-nearest-even method (also known as “banker’s rounding”), which rounds to the nearest even value in cases of ties (for example, 2.5 rounds to 2, 3.5 rounds to 4). This method helps reduce systematic bias in the quantization process, preventing a consistent upward or downward drift that could occur with other rounding strategies.

Backend: GPU Compute Kernel Quantization (FP32 to INT8/FP8): round-to-nearest-with-ties-to-even Weights Quantization (FP32 to INT8/FP8/INT4/FP4)
- Explicit Quantization: round-to-nearest-with-ties-to-even (INT8, FP8, INT4, FP4)
- Implicit Quantization: round-to-nearest-with-ties-to-positive-infinity (INT8 only)
Backend: DLA Compute Kernel Quantization (FP32 to INT8/FP8): round-to-nearest-with-ties-to-even Weights Quantization (FP32 to INT8/FP8/INT4/FP4)
- Explicit Quantization: N/A
- Implicit Quantization: round-to-nearest-with-ties-to-even (INT8 only)

For more information about rounding modes, refer to Rounding.

Dynamic Quantization#

Dynamic Quantization is a form of quantization in which the scales are computed during inference according to the input data. It produces two outputs: quantized data and scales. TensorRT supports Dynamic Quantization only with block quantization granularity.

Dynamic Quantization has two main benefits:

Accuracy: With dynamic quantization, a scale is selected to map only the dynamic range of a single block to the quantized type. Since the dynamic range of a single block is often much smaller than the dynamic range of the entire tensor, the quantization error is reduced. This is mostly significant for sub-byte quantized types due to the small range of values representable in these data types.
Reduced PTQ overhead: Since the scales are automatically computed during inference, the user is not required to calibrate the scales according to sample data.

For each block, the scale is computed by:

${scale}=max_{i\in \left\{ 0...blockSize-1 \right\}}\left( \frac{abs\left( x_{i} \right)}{qTypeMax} \right)$

Where:

${qTypeMax}$ is the maximum value in the quantized type (for example, 6 for FP4E2M1).

MX-Compliant Dynamic Quantization#

Dynamic quantization according to the OCP Microscaling Formats (MX) Specification v1.0. The MX-Compilant recipe performs block quantization, quantizing across 32 high-precision elements to produce 32 quantized output values and one E8M0 scaling factor.

TensorRT currently supports MX-compliant Dynamic Quantization only for the FP8E4M3 vector format, referred to as MXFP8.

The scale computation for a single block is defined as:

$scale_{E8M0}=round\_up\_to\_e8m0\left( max_{i\in \left\{ 0...blockSize-1 \right\}}\left( \frac{abs\left( x_{i} \right)}{qTypeMax} \right) \right)$

Where:

$E8M0$ is an 8-bit exponent-only floating point type, as described in Supported Types.
$round_up_to_e8m0$ is the computed scale rounded towards the smallest power of two that is larger than or equal to it.
$qTypeMax$ is the maximum value representable in the quantized type used for data.

The scale computation is repeated for each block, computing a total of $\frac{inputVolume}{blockSize}$ block scales.

Dynamic Double Quantization#

A variant of Dynamic Quantization, in which the computed scales are also quantized. Putting together the scale computation and scale quantization for a single block:

$scale_{quantized}=quantize\left( max_{i\in \left\{ 0...blockSize-1 \right\}}\left( \frac{abs\left( x_{i} \right)}{qTypeMax} \right), scale=globalSf \right)$

Where:

$globalSf$ is an offline-calibrated per-tensor quantization scale (scalar).

TensorRT currently supports Dynamic Double Quantization only for the NVFP4 vector format (FP4E2M1 data, FP8E4M3 scales, block size of 16).

Using $qTypeMax=6$ and the FP8 range of [-448,448], the quantized scale can be written as:

$scale_{fp8}=castToFp8\left( \frac{max_{i\in \left\{ 0...blockSize-1 \right\}}\left( ^{abs\left( x_{i} \right)} \right)}{6^{\ast }globalSf} \right)$

The quantized data is computed using block quantization and the computed scales.

To dequantize data that was quantized using Dynamic Double Quantization, two consecutive Dequantize operations must occur (hence, double quantization): the first to dequantize the scales using per-tensor quantization, and the second to dequantize the data.

$data_{DQ}=dequantize\left( data_{Q},dequantize\left( scale_{Q},scale=globalSf \right) \right)$

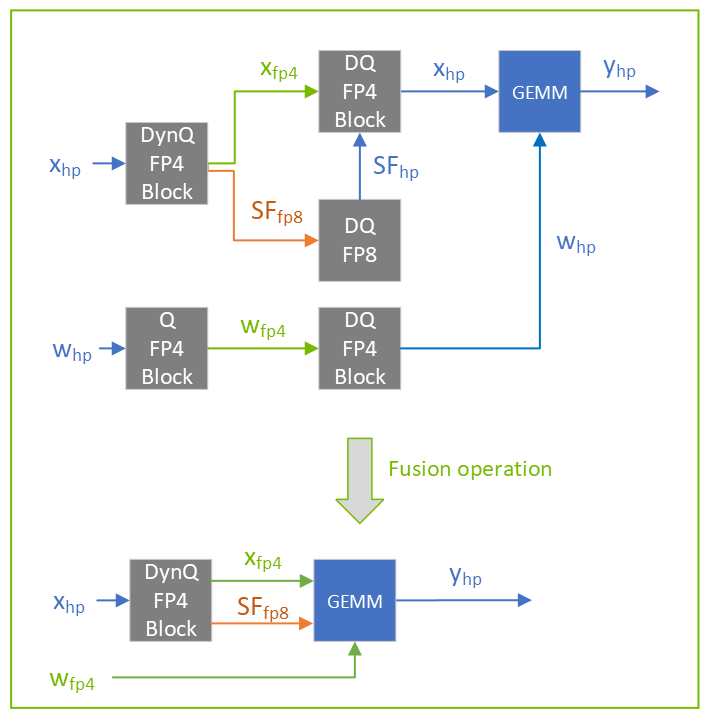
An example showing the fusion of Dynamic Double Quantization with GEMM; where: ``hp`` is high precision and ``sf`` is scale factors

Quantization Schemes#

INT8

INT8 quantization and dequantization operations are defined as follows:

$x_{q}=quantize\left(x, s \right)=roundWithTiesToEven(clip(\frac{x}{s}, -128,127))$

${x}=dequantize\left(x_{q}, s\right)=x_{q}\ast s$

Where:

${x}$ is a high-precision floating point value to be quantized.
$x_{q}$ is a quantized INT8 value in range [-128,127].
${s}$ is the quantization scale expressed using a 16-bit or 32-bit floating point scalar.
${roundWithTiesToEven}$ is described here.

When using implicit quantization, TensorRT computes the weight scale according to the following formula:

${s}=\frac{max(abs(\mathrm{x}_{min}^{ch}),abs(\mathrm{x}_{max}^{ch}))}{127}$

Where ${x}_{min}^{ch}$ and ${x}_{max}^{ch}$ are floating point minimum and maximum values for channel ${ch}$ of the weights tensor.

FP8

FP8 quantization and dequantization operations are defined as follows:

$x_{q}=quantize\left(x, s \right)=castToFp8(clip(\frac{x}{s}, -448,448))$

${x}=dequantize\left(x_{q}, s\right)=x_{q}\ast s$

Where:

${x}$ is a high-precision floating point value to be quantized.
$x_{q}$ is a quantized FP8E4M3 value in the range [-448, 448].
${s}$ is the quantization scale expressed using a 16-bit or 32-bit floating point scalar.
${castToFp8}$ rounds to the nearest value representable in FP8E4M3, ties are rounded to an even number, as described here.

MXFP8

MXFP8 is a dynamic per-block quantization scheme. The output type is FP8E4M3, the scale type is E8M0, and the block size is 32. The quantization and dequantization formulas are identical to the FP8 quantization scheme.

When quantizing activations, Dynamic Quantization is required.

INT4

INT4 quantization and dequantization operations are defined as follows:

$x_{q}=quantize\left(x, s \right)=roundWithTiesToEven(clip(\frac{x}{s}, -8,7))$

${x}=dequantize\left(x_{q}, s\right)=x_{q}\ast s$

Where:

${x}$ is a high-precision floating point value to be quantized.
$x_{q}$ is a quantized INT4 value in the range [-8, 7].
${s}$ is the block’s quantization scale expressed using a 16-bit or 32-bit floating point.
${roundWithTiesToEven}$ is described here.

INT4 quantization requires per-block scales. The supported block sizes are {64, 128}. The block dimension should be one of the last two dimensions.

TensorRT only supports INT4 for weight quantization (Q/DQ Layer-Placement Recommendations).

NVFP4

NVFP4 quantization requires per-block scales. The only supported block size is 16. The block dimension should be one of the last two dimensions.

$x_{q}=quantize\left(x, s \right)=castToFp4(clip(\frac{x}{s}, -6,6))$

${x}=dequantize\left(x_{q}, s\right)=x_{q}\ast s$

Where:

${x}$ is a high-precision floating point value to be quantized.
$x_{q}$ is a quantized FP4 value in the range [-6, 6].
${s}$ is the block’s quantization scale expressed using a 16-bit or 32-bit floating point.
${castToFp4}$ rounds to the nearest value representable in FP4E2M1, ties are rounded to an even number, as described here.

When quantizing activations, Dynamic Quantization is required.

Quantization Schemes and Precision#
Quantization Schemes	INT8	FP8	MXFP8	INT4	NVFP4
Representation	8-bit signed 2’s complement	S1E4M3 floating point	S1E4M3 floating point	4-bit signed 2’s complement	S1E2M1 floating point
Weight quantization	Per-tensor/per-axis	Per-tensor/per-axis	Per-block (block size = 32)	Per-block (block sizes = `{64, 128}`)	Per-block (block size = 16)
Activation quantization	Per-tensor	Per-tensor	Dynamic, per-block (block size = 32)	No	Dynamic, per-block (block size = 16)
Implicit quantization	Yes	No	No	No	No
Explicit quantization	Yes	Yes	Yes	Yes	Yes
Scale data type	FP32, FP16, BF16	FP32, FP16, BF16	E8MO	FP32, FP16, BF16	FP32, FP16, BF16

Explicit Quantization#

When TensorRT detects the presence of Q/DQ layers in a network, it builds an engine using explicit quantization processing logic. The rest of this section describes in more detail how explicit quantization operates.

Explicit Quantization may be used with either Strong Typing or Weak Typing ( precision-control build flags are not required and should not be specified), but since weak typing is deprecated, users are encouraged to always use strong typing.

Quantized Weights#

Weights of Q/DQ models may be specified using a high-precision data type (FP32, FP16, or BF16) or a low-precision quantized type (INT8, FP8, INT4, FP4). When TensorRT builds an engine, high-precision weights are quantized using the IQuantizeLayer scale, which operates on the weights. The quantized (low-precision) weights are stored in the engine plan file. When using pre-quantized weights, an IDequantizeLayer is required between the weights and the linear operator using the weights.

INT4 and FP4 quantized weights are stored by packing two elements per byte. The first element is stored in the 4 least significant bits, and the second is stored in the 4 most significant bits, as illustrated in the diagram below.

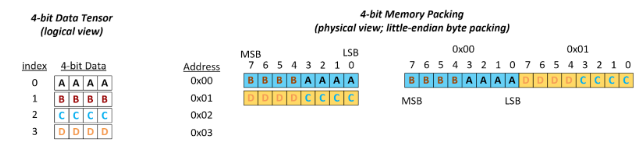
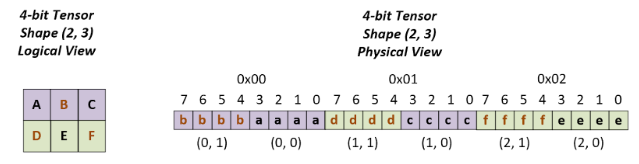
The diagram below shows an example of packing a (2, 3) 4-bit tensor.

ONNX Support#

When a model trained in PyTorch or TensorFlow using Quantization Aware Training (QAT) is exported to ONNX, each fake-quantization operation in the framework’s graph is exported as a pair of QuantizeLinear and DequantizeLinear ONNX operators. When TensorRT imports ONNX models, the ONNX QuantizeLinear operator is imported as an IQuantizeLayer instance, and the ONNX DequantizeLinear operator is imported as an IDequantizeLayer instance.

ONNX introduced support for QuantizeLinear and DequantizeLinear in opset 10, and a quantization-axis attribute was added in opset 13 (required for per-channel quantization). PyTorch 1.8 introduced support for exporting PyTorch models to ONNX using opset 13.

ONNX opset 19 added four FP8 formats, of which TensorRT supports E4M3FN (also referred to as tensor (float8e4m3fn) in the ONNX operator schema). The latest Pytorch version (Pytorch 2.0) does not support FP8 formats, nor does it support export to ONNX using opset 19. To bridge the gap, TransformerEngine exports its FP quantization functions as custom ONNX Q/DQ operators that belong to the “trt” domain (TRT_FP8 QuantizeLinear and TRT_FP8 DequantizeLinear). TensorRT can parse both the custom operators and standard opset 19 Q/DQ operators; however, it is noted that opset 19 is not fully supported by TensorRT. Other tools like ONNX Runtime cannot parse the custom operators. ONNX opset 21 added support for INT4 data type and block quantization. ONNX opset 23 added support for FP4E2M1 type.

Warning

The ONNX GEMM operator is an example that can be quantized per channel. PyTorch torch.nn.Linear layers are exported as an ONNX GEMM operator with (K, C) weights layout and the transB GEMM attribute enabled (this transposes the weights before performing the GEMM operation). TensorFlow, on the other hand, pre-transposes the weights (C, K) before ONNX export:

PyTorch: $y=xW^{T}$
TensorFlow: $y=xW$

TensorRT, therefore, transposes pyTorch weights. TensorRT quantizes the weights before they are transposed, so GEMM layers originating from ONNX QAT models that were exported from PyTorch use dimension 0 for per-channel quantization (axis K = 0), while models originating from TensorFlow use dimension 1 (axis K = 1).

TensorRT does not support pre-quantized ONNX models that use INT8/FP8 quantized operators. Specifically, the following ONNX quantized operators are not supported and generate an import error if they are encountered when TensorRT imports the ONNX model:

QLinearConv and QLinearMatmul
ConvInteger and MatmulInteger

TensorRT Processing of Q/DQ Networks#

When TensorRT optimizes a network in Q/DQ mode, the optimization process is limited to optimizations that do not change the arithmetic correctness of the network. Bit-level accuracy is rarely possible since the order of floating-point operations can produce different results (for example, rewriting ${a}\ast s+b\ast s$ as $\left(a+b \right)\ast s$ is a valid optimization). Allowing these differences is fundamental to backend optimization in general, and this also applies to converting a graph with Q/DQ layers to use quantized operations.

Q/DQ layers control the compute and data precision of a network. An IQuantizeLayer instance converts a high-precision floating-point tensor to a quantized tensor by employing quantization, and an IDequantizeLayer instance converts a quantized tensor to a high-precision floating-point tensor using dequantization. TensorRT expects a Q/DQ layer pair on each input of quantizable layers. Quantizable layers are deep-learning layers that can be converted to quantized layers by fusing with IQuantizeLayer and IDequantizeLayer instances. When TensorRT performs these fusions, it replaces the quantizable layers with quantized layers that operate on quantized data using compute operations suitable for quantized types.

For the diagrams used in this chapter, green designates low precision (quantized), and blue designates high precision. Arrows represent network activation tensors, and squares represent network layers.

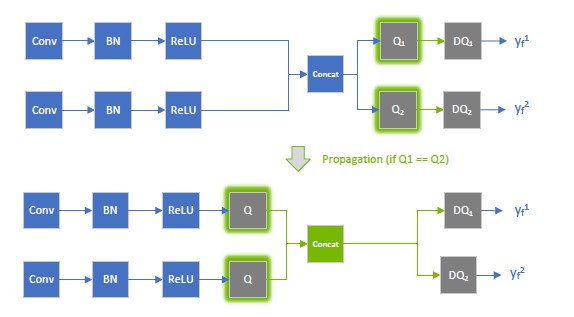
During network optimization, TensorRT moves Q/DQ layers in Q/DQ propagation. The goal in propagation is to maximize the proportion of the graph that can be processed at low precision. Thus, TensorRT propagates Q nodes backward (quantization happens as early as possible) and DQ nodes forward (so dequantization happens as late as possible). Q-layers can swap places with layers that commute with Quantization, and DQ-layers can swap places with layers that commute with Dequantization.

A layer ${Op}$ commutes with quantization if ${Q}\left(Op\left(x \right) \right)=={Op}\left(Q\left(x \right) \right)$

Similarly, a layer ${Op}$ commutes with dequantization if ${Op}\left(DQ\left(x \right) \right)=={DQ}\left(Op\left(x \right) \right)$

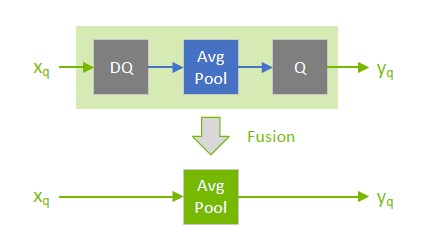
The following diagram illustrates DQ forward propagation and Q backward propagation. These are legal rewrites of the model because Max Pooling has an INT8 implementation and commutes with DQ and Q.

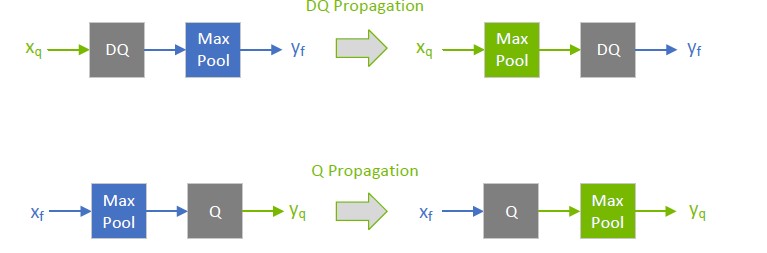
An illustration depicting a DQ forward-propagation and Q backward-propagation

To understand Max Pooling commutation, let us look at the output of the maximum-pooling operation applied to some arbitrary input. Max Pooling is applied to groups of input coefficients and outputs the coefficient with the maximum value. For group i composed of coefficients $\left\{x_{0}..x_{m} \right\}$:

$output_{i}:=max\left( \left\{ x_{0},x_{1},...x_{m} \right\} \right)=max\left( \left\{max\left( \left\{ max\left( \left\{ x_{0},x_{1} \right\} \right),x_{2} \right\} \right),...x_{3} \right\} \right)$

It is, therefore, enough to look at two arbitrary coefficients without loss of generality (WLOG):

$x_{j}=max\left( \left\{ x_{j},x_{k} \right\} \right)for\: x_{j}\ge x_{k}$

For the quantization function ${Q}\left( a,scale,x_{max},x_{min} \right):=truncate\left( round\left( \frac{a}{scale} \right),x_{max},x_{min}\right) scale> 0$, note that (without providing proof and using simplified notation): ${Q}\left( x_{j},scale \right)\ge {Q}\left( x_{k},scale \right)for x_{j}\ge x_{k}$

Therefore: ${max}\left( \left\{ {Q}\left( x_{j},scale \right),{Q}\left( x_{k},scale \right) \right\} \right)={Q}\left( x_{j},scale \right) for x_{j}\ge x_{k}$

However, by definition: ${Q}\left( max\left( \left\{ x_{j},x_{k} \right\} \right),scale \right)={Q}\left( x_{j},scale \right) for x_{j}\ge x_{k}$

Function ${max}$ commutes with quantization, and so does Max Pooling.

Similarly, for dequantization, function ${DQ}\left( a,scale \right):=a\ast scale$ with ${scale}> 0$ it can be shown that: ${max}\left( \left\{ {DQ}\left(x_{j},scale \right),{DQ}\left( x_{k},scale \right) \right\} \right)={DQ}\left( x_{j},scale \right)={DQ}\left( {max}\left( \left\{ x_{j},x_{k} \right\} \right),scale \right) for x_{j}\ge x_{k}$

There is a distinction between how quantizable layers and commuting layers are processed. Both layers can be computed in INT8/FP8, but quantizable layers also fuse with a DQ input and a Q output layer. For example, an AveragePooling layer (quantizable) does not commute with either Q or DQ, so it is quantized using Q/DQ fusion, as illustrated in the first diagram. This is in contrast to how Max Pooling (commuting) is quantized.

Weight-Only Quantization#

Weight-only quantization (WoQ) is an optimization useful when memory bandwidth limits the performance of GEMM operations or when GPU memory is scarce. In WoQ, GEMM weights are quantized to INT4 precision while the GEMM input data and compute operation remain high precision. TensorRT’s WoQ kernels read the 4-bit weights from memory and dequantize them before performing the dot product in high precision.

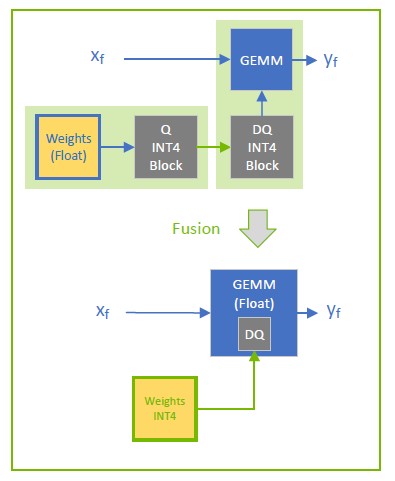
WoQ is available only for INT4 block quantization with GEMM layers. The GEMM data input is specified in high-precision (FP32, FP16, BF16), and the weights are quantized using Q/DQ as usual. TensorRT creates an engine with INT4 weights and a high-precision GEMM operation. The engine reads the low-precision weights and dequantizes them before performing the GEMM operation in high-precision.

Q/DQ Layer-Placement Recommendations#

The placement of Q/DQ layers in a network affects performance and accuracy. Aggressive quantization can lead to degradation in model accuracy because of the error introduced by quantization. But quantization also enables latency reductions. Listed here are some recommendations for placing Q/DQ layers in your network.

Note that older devices may not have low-precision kernel implementations for all layers, and you may encounter a could not find any implementation error while building your engine. To resolve this, remove the Q/DQ nodes, which quantize the failing layers.

Quantize all inputs of weighted operations (Convolution, Transposed Convolution, and GEMM). Quantizing the weights and activations reduces bandwidth requirements and enables INT8 computation to accelerate bandwidth-limited and compute-limited layers.

Two examples of how TensorRT fuses convolutional layers. On the left, only the input is quantized. On the right, both the input and output are quantized.

By default, do not quantize the outputs of weighted operations. It is sometimes useful to preserve the higher-precision dequantized output. For example, if the linear operation is followed by an activation function (SiLU, in the following diagram), it requires higher precision input to produce acceptable accuracy.

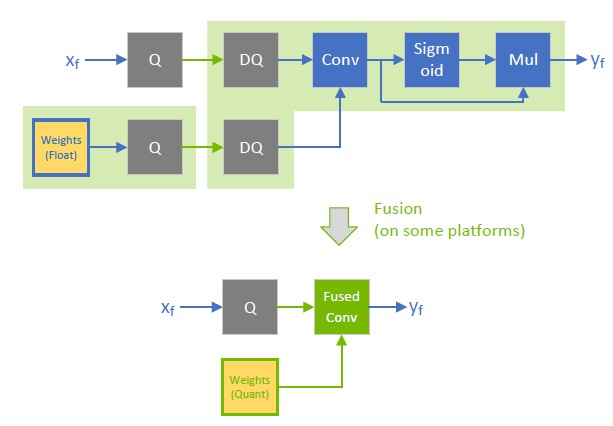
Do not simulate batch normalization and ReLU fusions in the training framework because TensorRT optimizations guarantee the preservation of these operations’ arithmetic semantics.

Quantize the residual input in skip connections. TensorRT can fuse element-wise addition following weighted layers, which is useful for models with skip connections like ResNet and EfficientNet. The precision of the first input to the element-wise addition layer determines the fusion output’s precision.

For example, in the following diagram, the precision of $x_{f^{}}^{1}$ is a floating point, so the output of the fused convolution is limited to the floating point, and the trailing Q-layer cannot be fused with the convolution.

$The precision of :math:`x_{f^{}}^{1}` is a floating point, so the output of the fused convolution is limited to the floating point, and the trailing Q-layer cannot be fused with the convolution.$

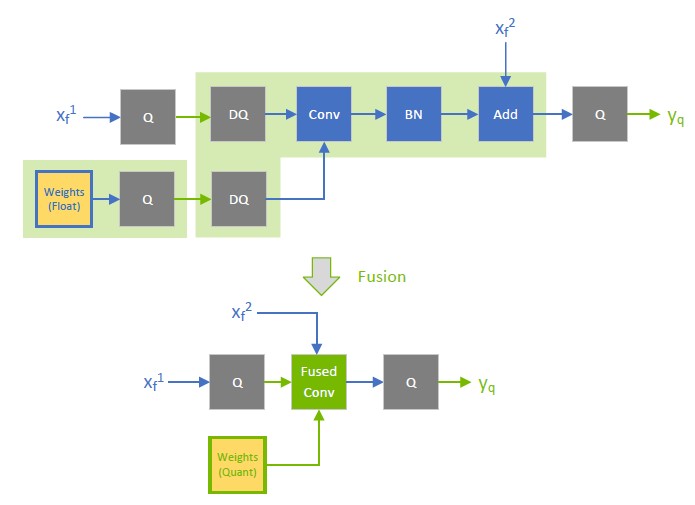
In contrast, when $x_{f^{}}^{1}$ is quantized to INT8, as depicted in the following diagram, the output of the fused convolution is also INT8, and the trailing Q-layer is fused with the convolution.

$When :math:`x_{f^{}}^{1}` is quantized to INT8, the output of the fused convolution is also INT8, and the trailing Q-layer is fused with the convolution.$

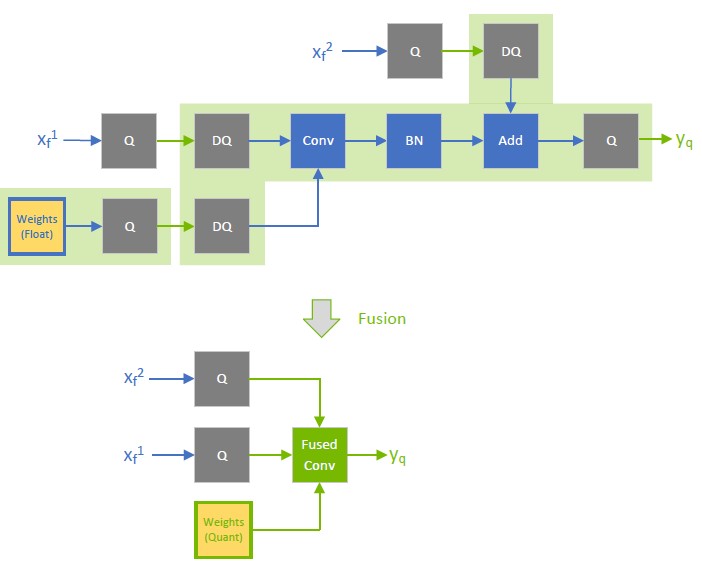
For extra performance, try quantizing layers that do not commute with Q/DQ. Currently, non-weighted layers with INT8 inputs also require INT8 outputs, so quantize both inputs and outputs.

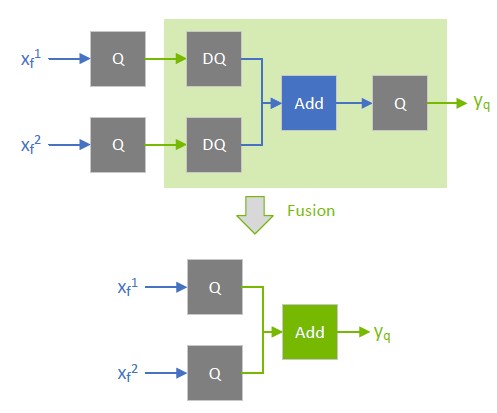
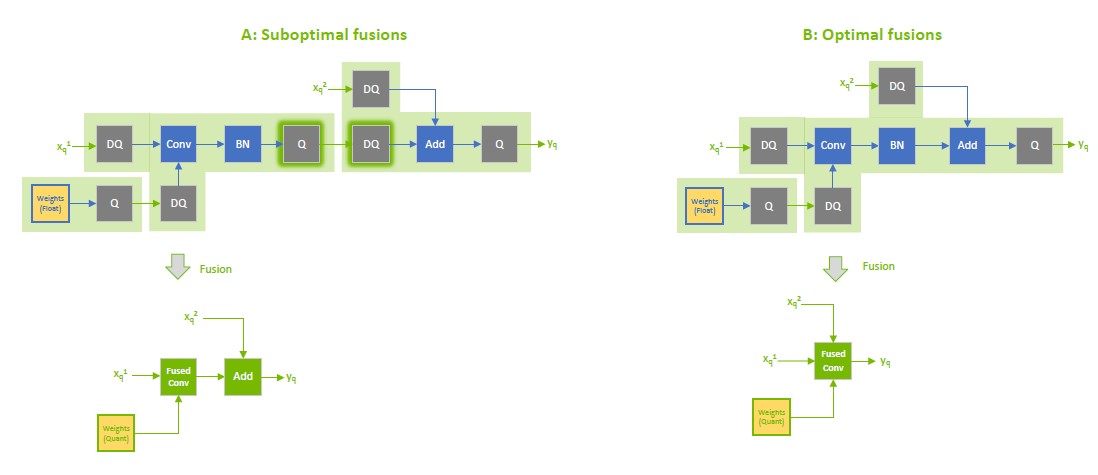
Performance can decrease if TensorRT cannot fuse the operations with the surrounding Q/DQ layers, so be conservative when adding Q/DQ nodes and experiment with accuracy and TensorRT performance in mind.

The following figure shows suboptimal fusions (the highlighted light green background rectangles) that can result from extra Q/DQ operations. The convolution is fused separately from the element-wise addition because Q/DQ pairs surround each other.

An example of suboptimal quantization fusions: contrast the suboptimal fusion in A and the optimal fusion in B. The extra pair of Q/DQ operations (highlighted with a glowing green border) forces the separation of the convolution from the element-wise addition.

Use per-tensor quantization for activations and per-channel quantization for weights. This configuration has been demonstrated empirically to lead to the best quantization accuracy.

You can further optimize engine latency by enabling FP16. TensorRT attempts to use FP16 instead of FP32 whenever possible (this is not currently supported for all layer types).

Q/DQ Limitations#

A few Q/DQ graph-rewrite optimizations that TensorRT performs compare the values of quantization scales between two or more Q/DQ layers and only perform the graph-rewrite if the compared quantization scales are equal. When a refittable TensorRT engine is refitted, the scales of Q/DQ nodes can be assigned new values. During the refitting operation of Q/DQ engines, TensorRT checks if Q/DQ layers that participated in scale-dependent optimizations are assigned new values that break the rewrite optimizations and throw an exception if true.

Q/DQ Interaction with Plugins#

Plugins extend TensorRT’s capabilities by allowing the replacement of a group of layers with a custom and proprietary implementation. You can decide what functionality to include in the plugin and what to leave for TensorRT to handle.

The same applies to a TensorRT network with Q/DQ layers. When a plugin consumes quantized inputs (INT8/FP8) and generates quantized outputs, the input DQ and output Q nodes must be included in the plugin and removed from the network.

Consider a simple case of a sequential graph consisting of a single INT8 plugin (aptly named MyInt8Plugin) sandwiched between two convolution layers (ignoring weights quantization):

${Input}> {Q}\rightarrow {DQ}> {Conv}> {Q}\rightarrow {DQ\_i}> {MyInt8Plugin}> {Q\_o}\rightarrow {DQ}> {Conv}> {Output}$

The $>$ arrows indicate activation tensors with FP32 precision, and the $\rightarrow$ arrows indicate INT8 precision.

When TensorRT optimizes this graph, it fuses the layers to the following graph (square brackets indicate TensorRT fusions):

${Input}> {Q}\rightarrow \left[{DQ}\rightarrow {Conv}\rightarrow {Q}\right]\rightarrow {DQ\_i}> {MyInt8Plugin}> {Q\_o}\rightarrow \left[{DQ}\rightarrow {Conv}\right]> {Output}$

In the graph above, the plugin consumes and generates FP32 inputs and outputs. Since the plugin MyInt8Plugin uses INT8 precision, the subsequent procedure involves the manual integration of $DQ\_i$ and $Q\_o$ with the MyInt8Plugin, followed by invoking the setOutputType(kINT8) method for this particular plugin layer; TensorRT will see a network like this:

${Input}> {Q}\rightarrow {DQ}> {Conv}> {Q}\rightarrow {MyInt8Plugin}\rightarrow {DQ}> {Conv}> {Output}$

Which it will fuse to:

${Input}> {Q}\rightarrow \left[{DQ}\rightarrow {Conv}\rightarrow {Q}\right]> {MyInt8Plugin}\rightarrow \left[{DQ}\rightarrow {Conv}\right]> {Output}$

When “manually fusing” $DQ\_i$, you take the input quantization scale and give it to your plugin so it will know how to dequantize (if needed) the input. The same applies to using the scale from $Q\_o$ to quantize your plugin’s output.

QAT Networks Using TensorFlow#

You can use the TensorRT Model Optimizer to perform QAT in TensorFlow 2 Keras models following NVIDIA’s QAT recipe. This leads to optimal model acceleration with TensorRT on NVIDIA GPUs and hardware accelerators.

TensorFlow 1 does not support per-channel quantization (PCQ), which is recommended for weights to preserve the model’s accuracy.

QAT Networks Using PyTorch#

PyTorch 1.8.0+ supports ONNX QuantizeLinear and DequantizeLinear support per channel scales.

You can use the TensorRT Model Optimizer to calibrate INT8, perform QAT and PTQ for the various precisions that TensorRT supports, and export to ONNX.

Implicit Quantization#

This section covers features only available in implicit quantization, which is limited to INT8. Implicit quantization is deprecated and its use is discouraged.

Setting Dynamic Range#

The dynamic range API is only applicable to INT8 quantization.

TensorRT provides APIs to directly set the dynamic range (which must be represented by the quantized tensor) to support implicit quantization where these values have been calculated outside TensorRT.

The API allows setting the dynamic range for a tensor using minimum and maximum values. Since TensorRT currently supports only symmetric range, the scale is calculated using max(abs(min_float), abs(max_float)). Note that when abs(min_float) != abs(max_float), TensorRT uses a larger dynamic range than configured, which may increase the rounding error.

You can set the dynamic range for a tensor as follows:

C++

tensor->setDynamicRange(min_float, max_float);

Python

tensor.dynamic_range = (min_float, max_float)

sampleINT8API illustrates the use of these APIs in C++.

Post-Training Quantization Using Calibration#

Note

This section describes deprecated APIs. It is recommended to use explicit quantization.

Calibration is only applicable to INT8 quantization.

In post-training quantization, TensorRT computes a scale value for each tensor in the network. This process, called calibration, requires you to supply representative input data on which TensorRT runs the network to collect statistics for each activation tensor.

The amount of input data required is application-dependent, but experiments indicate that about 500 images are sufficient for calibrating ImageNet classification networks.

Given the statistics for an activation tensor, deciding on the best scale value is not an exact science - it requires balancing two sources of error in the quantized representation: discretization error (which increases as the range represented by each quantized value becomes larger) and truncation error (where values are clamped to the limits of the representable range.) Thus, TensorRT provides multiple calibrators that calculate the scale differently. Older calibrators also performed layer fusion for GPU to optimize away unneeded Tensors before calibration. This can be problematic when using DLA, where fusion patterns may be different and can be overridden using the kCALIBRATE_BEFORE_FUSION quantization flag.

Calibration batch size can also affect the truncation error for IInt8EntropyCalibrator2 and IInt8EntropyCalibrator. For example, calibrating using multiple small batches of calibration data may result in reduced histogram resolution and poor scale value. For each calibration step, TensorRT updates the histogram distribution for each activation tensor. Suppose it encounters a value in the activation tensor larger than the current histogram max. In that case, the histogram range is increased by a power of two to accommodate the new maximum value. This approach works well unless the histogram reallocates in the last calibration step, resulting in a final histogram with half the empty bins. Such a histogram can produce poor calibration scales. This also makes calibration susceptible to the order of calibration batches; a different order can increase the histogram size at different points, producing slightly different calibration scales. To avoid this issue, calibrate with as large a single batch as possible and ensure that calibration batches are well randomized and have a similar distribution.

IInt8EntropyCalibrator2: Entropy calibration chooses the tensor’s scale factor to optimize the quantized tensor’s information-theoretic content and usually suppresses outliers in the distribution. This is the current and recommended entropy calibrator and is required for DLA. Calibration happens before Layer fusion by default. Calibration batch size may impact the final result. It is recommended for CNN-based networks.
IInt8MinMaxCalibrator: This calibrator uses the entire range of the activation distribution to determine the scale factor. It works better for NLP tasks. Calibration happens before Layer fusion by default. This is recommended for networks such as NVIDIA BERT (an optimized version of Google’s official implementation).
IInt8EntropyCalibrator: This is the original entropy calibrator. It is less complicated than the LegacyCalibrator and typically produces better results. The calibration batch size may impact the final result. By default, calibration happens after Layer fusion.
IInt8LegacyCalibrator: This calibrator is for compatibility with TensorRT 2.0 EA. It requires user parameterization and is a fallback option if the other calibrators yield poor results. Calibration happens after Layer fusion by default. You can customize this calibrator to implement percentile max. For example, 99.99% percentile max is observed to have the best accuracy for NVIDIA BERT and NeMo ASR model QuartzNet.

When building an INT8 engine, the builder performs the following steps:

Build a 32-bit engine, run it on the calibration set, and record a histogram for each tensor of the distribution of activation values.
Build from the histograms a calibration table providing a scale value for each tensor.
Build the INT8 engine from the calibration table and the network definition.

Calibration can be slow; therefore, the output of step 2 (the calibration table) can be cached and reused. This is useful when building the same network multiple times on a given platform and is supported by all calibrators.

Before running calibration, TensorRT queries the calibrator implementation to see if it has access to a cached table. If so, it proceeds directly to step 3. Cached data is passed as a pointer and length.

The calibration cache data is portable across different devices as long as the calibration happens before layer fusion. Specifically, the calibration cache is portable when using the IInt8EntropyCalibrator2 or IInt8MinMaxCalibrator calibrators or when QuantizationFlag::kCALIBRATE_BEFORE_FUSION is set. For example, this can simplify the workflow by building the calibration table on a machine with a discrete GPU and then reusing it on an embedded platform. Fusions are not guaranteed the same across platforms or devices, so calibrating after layer fusion may not result in a portable calibration cache. The calibration cache is, in general, not portable across TensorRT releases.

TensorRT uses symmetric quantization with a quantization scale calculated using the maximum absolute values found in the weight tensor. For convolution, deconvolution, and fully connected weights, scales are per-channel.

Note

When the builder is configured to use INT8 I/O, TensorRT still expects calibration data to be in FP32. You can create FP32 calibration data by casting INT8 I/O to FP32 precision. Also, FP32 cast calibration data should be in the range [-128.0F, 127.0F] and converted to INT8 data without any precision loss.

INT8 calibration can be used along with the dynamic range APIs. Setting the dynamic range manually overrides the dynamic range generated from INT8 calibration.

Note

Calibration is deterministic - that is, if you provide TensorRT with the same input to calibration in the same order on the same device, the scales generated will be the same across different runs. The data in the calibration cache will be bitwise identical when generated using the same device with the same batch size when provided with identical calibration inputs. The exact data in the calibration cache is not guaranteed to be bitwise identical when generated using different devices, batch sizes, or calibration inputs.

INT8 Calibration Using C++#

To provide calibration data to TensorRT, the IInt8Calibrator interface must be implemented.

Steps to use the calibrator with the builder:

Determine the input batch size.
1. Query the calibrator interface for the batch size.
2. Call getBatchSize() to retrieve the expected input batch size.
Provide input batches.
1. Repeatedly call getBatch() to supply batches of input data.
2. Each batch must exactly match the size specified by getBatchSize().
3. When no more input data is available, getBatch() must return false to indicate completion.
Configure the builder to use the calibrator.
1. After implementing the calibrator, link it to the builder configuration:
```
config->setInt8Calibrator(calibrator.get());
```
Implement calibration cache methods.
1. Implement the following methods to handle the calibration cache:
  1. writeCalibrationCache() – stores the calibration data for reuse.
  2. readCalibrationCache() – retrieves the stored calibration data, if available.

Calibration Using Python#

The following steps illustrate creating an INT8 calibrator object using the Python API.

Import TensorRT.
```
import tensorrt as trt
```
Similar to test/validation datasets, use a set of input files as a calibration dataset. Ensure that the calibration files represent the overall inference data files. For TensorRT to use the calibration files, you must create a batchstream object. A batchstream object is used to configure the calibrator.
```
NUM_IMAGES_PER_BATCH = 5
batchstream = ImageBatchStream(NUM_IMAGES_PER_BATCH, calibration_files)
```

Create an Int8_calibrator object with input node names and batch stream.

Int8_calibrator = EntropyCalibrator(["input_node_name"], batchstream)

Set INT8 mode and INT8 calibrator.

config.set_flag(trt.BuilderFlag.INT8)
config.int8_calibrator = Int8_calibrator

Quantization Noise Reduction#

For networks with implicit quantization, TensorRT attempts to reduce quantization noise in the output by forcing some layers near the network outputs to run in FP32, even if INT8 implementations are available.

The heuristic attempts to ensure that INT8 quantization is smooth by summating multiple quantized values. Layers considered “smoothing layers” are convolution, deconvolution, a fully connected layer, or matrix multiplication before reaching the network output. For example, if a network consists of a series of (convolution + activation + shuffle) subgraphs and the network output has type FP32, the last convolution will output FP32 precision, even if INT8 is allowed and faster.

The heuristic does not apply in the following scenarios:

The network output has type INT8.
An operation on the path (inclusively) from the last smoothing layer to the output is constrained by ILayer::setOutputType or ILayer::setPrecision to output INT8.
There is no smoothing layer with a path to the output, or that path has an intervening plugin layer.
The network uses explicit quantization.