Geometry

Curves - IwCurve and IwBSplineCurve

The two primary curve classes of interest are IwBSplineCurve and its parent class IwCurve. The other curve classes (IwCrvOnSurf, IwCompositeCurve, IwOffsetCurve, IwHermiteCurve, IwIsoCurve) are for more specific uses or for internal or advanced use. The IwBSplineCurve class represents a NURBS curve. It provides a method interface for creation, modification, query, and eval of the NURBS representation. The IwCurve class contains the method interface for most of the numerical algorithms. Some common methods include:

• GetNaturalInterval() - returns the parametric domain of the curve.
• Evaluate() - evaluates the point and requested derivatives of the curve/surface.
• EvaluatePoint() - evaluates just the point of the curve/surface.

Figure 5: Curve Properties and Analysis

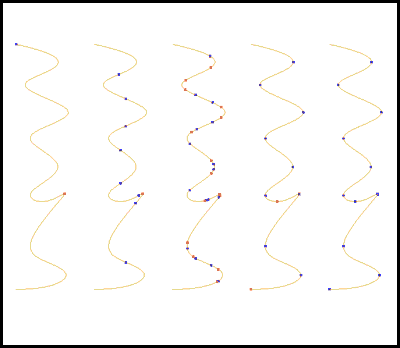
Figure 6: Curve Properties and Analysis continued

IwCurve

• point and derivative evaluation
• evaluation of geometric properties
• bounding box calculation
• creation of a mirror curve
• creation of a curve by projection to a plane
• transformation with optional scaling
• high precision curve length computation
• closure, periodicity and degeneracy testing
• tessellation using both chord height and angular tolerances
• find intersections with a plane
• find inflection points
• find minimum/maximum magnitude of 1st derivative and radius of curvature
• find 1st derivative or radius of curvature of a given magnitude
• find points where tangent is parallel to X, Y, and/or Z axis
• find points where tangent is parallel to a given vector
• find silhouette points with either parallel or perspective projection

IwBSplineCurve

• construction/modification/query/eval
• continuity calculation, removal of extra knots, conversion to 2D
• creation by joining connected curve segments
• creation of a circle segment, ellipse segment line segment, degenerate curve
• creation of mirror curve
• editing the end points of a B-Spline
• extraction of analytical information for lines and arcs
• curve offset

Surfaces - IwSurface and IwBSplineSurface

The two primary surface classes are IwBSplineSurface and its parent class IwSurface. The other surface classes (IwOffsetSurface, IwCurveBoundedSurface, IwSrfInVolume, etc) are for more specific uses or for internal or advanced use.. The IwBSplineSurface is the class which represents a NURBS surface. It provides a method interface for creation, query and editing of the NURBS representation. The IwBSplineSurface class also contains implementations for abstract IwSurface methods. The IwSurface class contains the method interface for most of the numerical algorithms.

IwSurface

• point and derivative evaluation, evaluation of geometric properties
• normal evaluation, evaluation of a normal section
• high precision surface area computation
• dropping 3D vectors into parameter space
• closed and periodic testing, singularity testing
• validation
• transformation

IwBSplineSurface

• construction using STEP format or NLib data structures
• continuity calculation
• query
• creation of planar section curves - see Figure 14
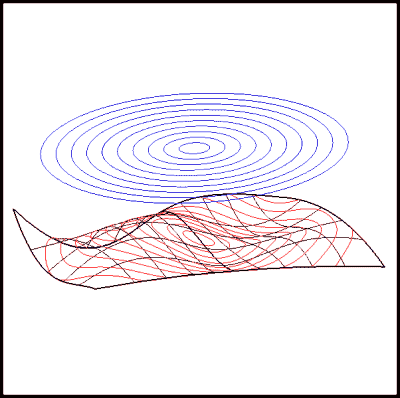
• creation of parallel projection curves - see Figure 15

Figure 14: Creation of Planar Section Curves

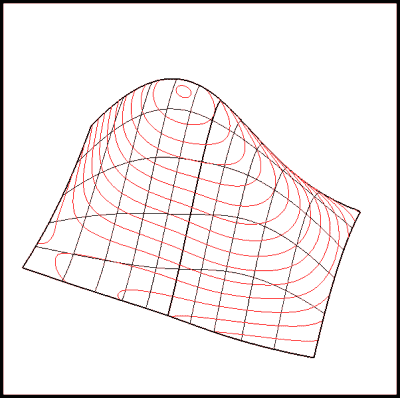
Figure 15: Creation of Curves by Parallel Projection

Trimmed Surfaces - IwFace

• IwBrep::CreateFaceFromSurface from a parametrically bounded NURBS surface.
• IwBrep::MakeFaceWithCurves from a surface and 2-D parameter space curves.
• From a surface and 3-D model space curves. Use IwBrep::MakeFaceWithCurves.
• From a surface with both 2-D and 3-D space curves. UseIwBrep::MakeFaceWithCurves.
• Creation of topological elements (vertices, edges, faces) using "Euler like" topological operators. See the tutorial on Solid Creation by Topology Tables.
• Adjustment of operational tolerances to compensate for gaps. See as an example IwEdge::SetTolerance.
• Sewing together trimmed surfaces to create shells or solids. Use IwBrep::SewFaces.

This section of the quick start is intended to help you to understand how to create trimmed surfaces such that the subsequent operations performed on them are very reliable. SMLib is designed to enable it to handle trimmed surfaces which are generated from a variety of different CAD and graphics systems. SMLib allows the creation of trimmed surfaces from either parameter space or model space curves. The operational tolerances can be adjusted to match those of the system which originally produced the trimmed surface.
An empty IwBrep is created which will eventually contain one or more trimmed surfaces. Prior to adding faces to the brep ( IwBrep::MakeFaceWithCurves )

The next major decision to make is what to use for trimming curves, 3-D model space curves or 2-D parameter space curves. In cases where only one set of trimming curves are available or one set is clearly the master representation your decision is not a difficult one. However if you have both sets of trimming curves and neither of them is the master representation, than you may have decisions to make. In this case is important to know what happens in each of your three options:

2-D Trimming Curves are used to create Trimmed Surfaces

• Approximate 3-D Curves are created using the mapping of the 2-D Curves through the surface.
• The 3-D Curves are approximated to within the IwBrep tolerance ( IwBrep::GetTolerance ) of the corresponding 2-D curves.
• The 3-D Curves are synchronized in terms of their parameter space and orientation.
• The 2-D Curves have their end points "joined" through a process which does extension and intersection.

3-D Trimming Curves are used to create Trimmed Surfaces

• 2-D curves are created using the IwSurface::DropCurve method.
• The tolerances of the corresponding edges are adjusted relative to the distance between the 3-D curve and its 2-D image.
• The 2-D Curves have their end points "joined" through a process which does extension and intersection.

Both 2-D and 3-D Curves are used to create Trimmed Surfaces

• The distance between the 3-D curve and the 3-D image of the 2-D curve is measured and an appropriate tolerance is chosen for the edge.
• The 2-D Curves have their end points "joined" through a process which does extension and intersection.

Of the three possibilities, #2 is by far the slowest and #3 is somewhat faster than #1. If you are doing primarily 2-D operations, #1 or #3 are probably a little better than #2. If you are doing primarily 3-D operations, #2 or #3 might give you some advantages. We have found that #1 seems to be the best option when we are reading and testing IGES trimmed surfaces generated by the RHINO NURBS Modeler.

Trimmed Surface Creation

Creating correctly defined trimmed surfaces is essential. There are two different ways in which trimmed surfaces may be created. First you may create a trimmed surface (IwFace) directly from a surface and its parametric domain (IwBrep::CreateFaceFromSurface). You may also create a trimmed surface from the surface and a set of oriented boundary curves. This tutorial shows how this may be done. Our tutorial demonstrates the creation of a trimmed surface from class (IwCurveBoundedSurface) which mirrors the IGES trimmed surface structure. This code is actually used in our IGES processor to create trimmed surfaces. Note that this code allows you to add a trimmed surface to an already existing brep. It is possible to put multiple trimmed surfaces in a single brep. You need to first create a brep prior to invoking this method. The following code shows how you might set up a brep prior to calling the function:

***Please refer to Example.cpp***

Trimmed Surface/Point Solver Tutorial

The following code demonstrates the use of the IwTopologySolver to solve an operation between a brep and a point. This solver allows the user to find intersections (IW_SO_INTERSECT), minimum/maximum distance between the brep and the point (IW_SO_MINIMIZE/>IW_SO_MAXIMIZE), and points were the tangent plane of the trimmed surface is perpendicular to the vector to the point (IW_SO_NORMALIZE.

See Source code for my_test_tsurface_point_extrema() in: iwtopo_test.cpp

Trimmed Surface/Curve Solver Tutorial

The following code demonstrates the use of the IwTopologySolver to solve an operation between a brep and a curve. This solver allows the user to find intersections (W_SO_INTERSECT, minimum/maximum distance between the brep and the curve (IW_SO_MINIMIZE IW_SO_MAXIMIZE), and points were the tangent plane of the trimmed surface and the tangent of the curve are perpendicular to the vector between the trimmed surface and the curve (IW_SO_NORMALIZE).

See Source code for my_test_tsurface_curve_solve() in: iwtopo_test.cp

Trimmed Surface/Trimmed Surface Solver Tutorial

The following code demonstrates the use of the IwTopologySolver to solve an operation between two breps with trimmed surfaces. This solver allows the user to find the minimum/maximum distance between two breps with trimmed surfaces(IW_SO_MINIMIZE IW_SO_MAXIMIZE, and points were the tangent planes of the trimmed surfaces of each are perpendicular to the vector between the two trimmed surface (IW_SO_NORMALIZE).

See Source code for my_test_tsurface_tsurface_solve()iwtopo_test.cpp

Planar Sectioning Example

This tutorial demonstrates how to do planar sectioning of a brep with trimmed surfaces. It creates a set of planes which span the bounding box of the brep and uses them to section the brep.

See Source code for my_test_tsurf_section() in: iwtopo_test.cpp

Point Classification Example

This tutorial demonstrates the classification of a parameter space point on a surface relative to the surface boundary. The function creates a grid of points in the parameter space of the surface and classifies them.

See Source code for my_test_tsurface_point_classify() iwtopo_test.cpp

Curve Classification Example

This tutorial demonstrates the classification of a 2D curve relative to the boundary of a trimmed surface. Please note that the method being demonstrated here also allows you to specify a 3D curve. The method will automatically choose the correct place to classify the curve based on its dimension.

See Source code for my_test_tsurface_curve_classify() in iwtopo_test.cpp

Analytical Classes

Analytic or exact representations of common curve or surface objects often provide faster results with more precision. The following classes have been implemented along with supporting methods for creation and evaluation.

• IwLine, IwEllipse, IwCircle, IwHyperbola, IwParabola
• IwPlane, IwCylinder, IwCone, IwSphere, IwTorus, IwSurfOfRevolution, IwSurfOfExtrusion

Solids - IwBrep

The IwBrep class represents a collection of IwFaces. If the collection, one or more faces, form a closed, water tight object then the object is manifold. Otherwise the object is non manifold. In either case, the object can be merged (boolean) , filleted, offset, shelled, de-featured, sliced, etc. Some of the possible operations on IwBreps are:

*****See SMLibBoolean.html, SMLibFilles.html, SMLibShell.html, etc*****

A word about m_bEditingEnabled. We have added a flag to IwBrep which enables editing. There are many of the creation and a few editing operations which require the m_bEditingEnabled flag to be turned on. An example is sewing. This flag needs to be turned off to make many of the evaluation functions work.