Polygon Modeling

In addition to using NURBS and analytic representations for geometric models, SMLib also has polygonal data structures, polygonal construction and modeling tools, polygonal refinement tools, and conversion functions. Advanced functions include polygon booleans, decimation, hole filling, ray firing, etc.
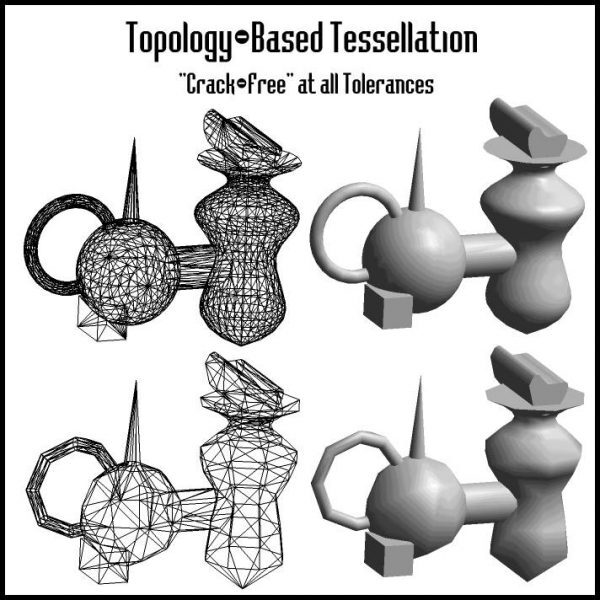
In addition to constructing polygonal breps from scratch, customers can easily create polygonal models by importing STL files or by using one of several tessellators to convert NURBS models. SMLib features topology-based tessellation to produce "Crack-Free" polygonal meshes.
Because of our attention to both NURBS and polygons, hybrid CAD systems will find SMlib particularly useful.

Advanced polygon refinement tools can be found in PolyMLib. Refer to PolyMLib manual page.

Import Polygonal Model

Refer to IwPolyBrep::ReadFromSTLFile

ReadFromSTLFile exists in SMLib. HW translators are not required for importing STIL files.

Tessellation

Refer to example
Refer to IwBrep::CreatePolyBrep

SmLib contain three tessellators each designed for different purposes.

Tessellation is the process of converting smooth curves, surfaces and faces into linear or polygonal segments.
This has many uses, primarily in graphics, where curves are represented by a large number of small line segments, and surfaces get converted into planar triangles, which are then passed to a graphics engine for display.

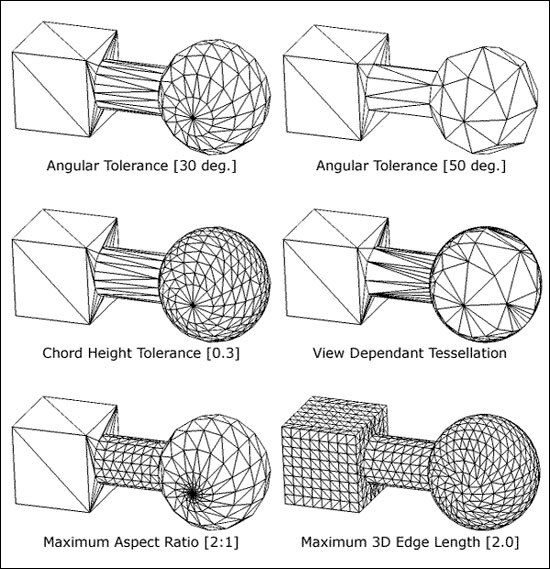
The criteria for tessellation may be selected by the user. In general they relate to curvature, (the flatter the curve, the less line segments are needed), and absolute size (very tiny curves would require less lines than very large curves of the same shape).

• Tessellation Criteria
  
  • Chord Height Tolerance
  • Angular Tolerance
  • Maximum Aspect Ratio
  • Maximum Polygon Edge Length
  • Minimum UV Polygon Edge Length

• Dynamic tessellation
  
  • Object Oriented Curve and Surface Subdivision Classes allow the user to modify the tessellation criteria during the tessellation process. For example, in a graphical application the user could adjust tessellation criteria based on distance from an "Eye Point" of the geometry being subdivided. This customizability feature enables the Tessellation Library to easily be adapted to different applications. See the view dependent tessellation example in the "Tessellation Criteria" image.
• Tessellation Output:
  
  • As a topological data structure which contains a connected set of polygons with 3D points, UV points and surface normals.
  • User Call Backs with 3D points and surface normals. You will need to subclass the IwPolygonOutputCallback class and implement the OutputPolygon method on to implement the callback.
• "Crack-free" Tessellation:
  
  • SMLib offers a significant upgrade to NLib and OpenGL tessellation, in that it ensures that there are no cracks between tessellations of faces that share a common edge. This ensures that the shaded image will not contain ugly black cracks along the joins in the shaded image. This process is complex, and may account for some lack of performance, but the results show a significant improvement over competing products.

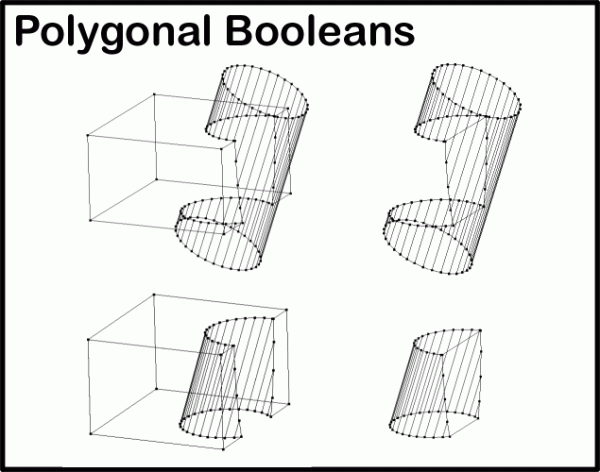
Polygon Booleans

Boolean operations like Union, Difference, Intersection can be performed on polygonal breps (IwPolyBrep).

Boolean operations are contained in the class IwPolyMerge

Decimation

Decimation is the process of removing polygons to achieve a significant data reduction with an acceptable loss of accuracy.

This allows very large models to be reduced to a size where the performance of some of these complex operations can be run in real-time.

Two decimation algorithms are available:

• a vertex removal decimation algorithm that utilizes accumulated error measurement
• an edge squeezing decimation algorithm that utilizes a fast quadric error distance to choose optimal points.

Ray Firing

The process of ray firing is useful for selection, position dependent projection, among other applications. In most cases it is very desirable for ray firing to be extremely fast so it can be performed as the mouse is dragged across an object, for example. For this reason, ray firing is generally divided into an initial setup and a faster execution that takes advantage of the knowledge that the next iteration is close to the last.