Channel Estimation for Uplink Shared Channel (PUSCH) in PyAerial#
This notebook provides researchers an example of how to prototype machine learning in PyAerial. PyAerial is the Python bindings for the Aerial SDK, NVIDIA’s L1 accelerated stack that is also integrated in the Aerial Omniverse Digital Twin (AODT). This enables researchers to develop standard-compliant approaches focusing on enhancing their link-level performance. Subsequently, the approach can be evaluated realistically in AODT, showing how the link-level performance translates to system-level KPIs.
In particular, this notebook focuses on improving the channel estimation based on the DMRS pilots in a PUSCH transmission. First, we isolate the channel estimator block from the PyAerial PUSCH pipeline. The channel estimation is on one of the first receiver blocks, as seen in the figure below:
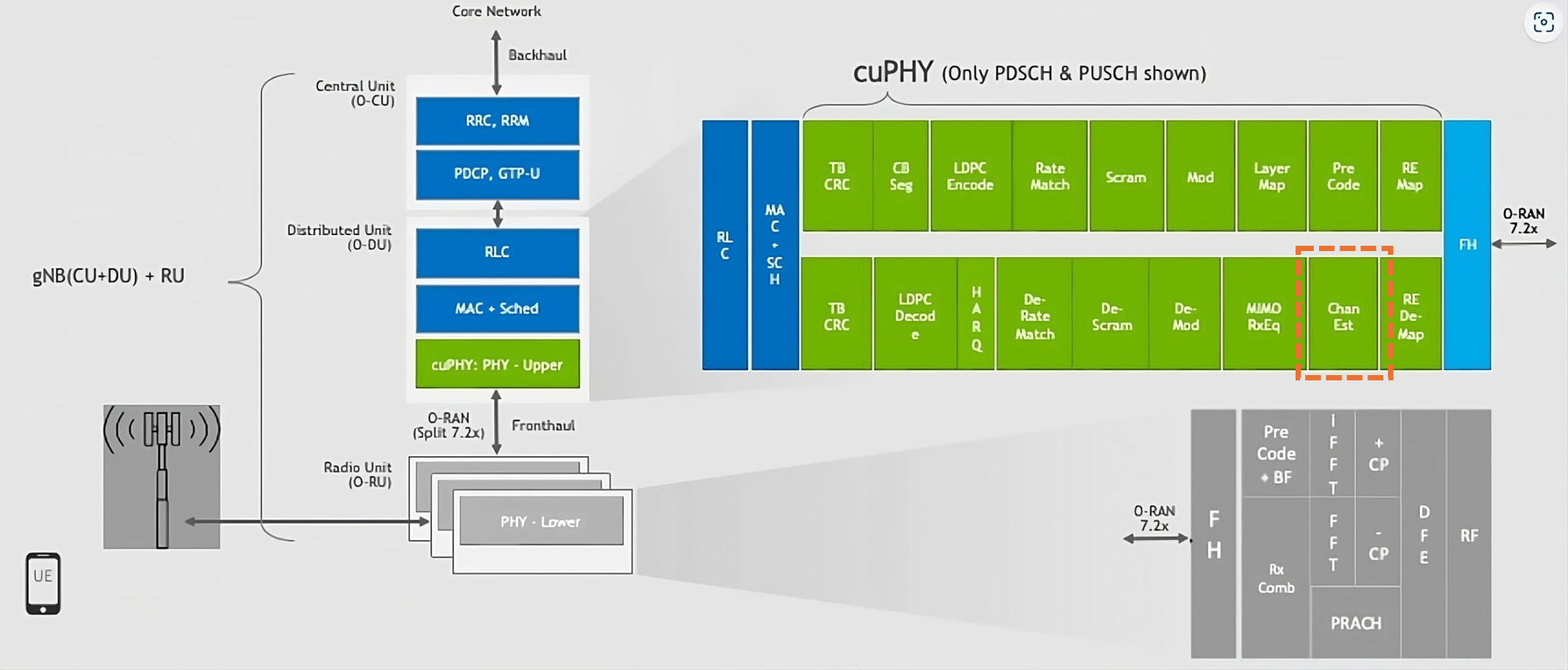
To isolate the channel estimation block, we refer to the modular PUSCH pipeline in Example PUSCH Simulation.ipynb. There, we see how to interface channel estimation downstream with resource element (RE) demapper and with the wireless channel, and upstream with other components like the MIMO Equalizer. Similar approaches can be done for other blocks in the receiver or transmitter pipelines.
This notebook uses PyTorch to train a convolutional neural network that improves and interpolates least squares (LS) channel estimates. The training uses a custom LS estimator which interfaces with a resource grid, resource mapper, and channel generator from Sionna. The trained models are then integrated and validated in PyAerial PUSCH pipeline with standard-compliant signal transmission and reception blocks running on top of Sionna channels.
*
See below how we train and test the channel estimator models.
[1]:
# Standard imports
import os
# GPU setup
GPU_IDX = 0
os.environ["CUDA_VISIBLE_DEVICES"] = str(GPU_IDX) # Select only one GPU
os.environ['TF_CPP_MIN_LOG_LEVEL'] = "3" # Silence TensorFlow.
import torch
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
# Our imports
from channel_est_models import FusedChannelEstimator, ComplexMSELoss
from channel_gen_funcs import (SionnaChannelGenerator,
PyAerialChannelEstimateGenerator,
sionna_to_pyaerial_shape)
import utils as ut
dev = torch.device(f'cuda')
torch.set_default_device(dev)
# General parameters
num_prbs = 48 # Number of PRBs in the UE allocated bandwidth
interp = 2 # Interpolation factor = comb_size (2 or 4) = 2 for DMRS
models_folder = f'saved_models_prbs={num_prbs}_interp={interp}' # Folder to save trained models
# Training parameters
train_snrs = np.arange(-10, 40.1, 10) # Train models for these SNRs.
training_ch_model = 'UMa' # Channel model ['Rayleigh', 'CDL-x', 'TDL-x', 'UMa', 'UMi'],
# where x is in ["A", "B", "C", "D", "E"] as per TR 38.901
n_iter = 500 # Number of training iterations. For best results: >20k
batch_size = 32 # Batch size = number of channels to train simultaneously
# Testing parameters
test_snrs = np.arange(-10, 40.1, 5) # Test models for these SNRs.
testing_ch_model = 'UMi' # Channel for testing
n_iter_test = 500 # Number of testing iterations
[PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')]
Training channel estimation model#
The example machine learning model uses the least squares (LS) estimates and outputs a more accurate channel estimate. In its base configuration, the DMRS has 1/2 density in frequency (i.e. one RE for every two subcarriers). Our ChannelEstimator, therefore, needs to output twice many estimates as DMRS pilots to cover all subcarriers.
Important note on training: Our approach consists of training one model per SNR. SNR-specific models can learn more accurately how to estimate the channels for SNRs close to the original SNR that was used for model training. This approach also solves the problem where low SNR channels incur in higher loss and lead to the model focusing on them and not working for the high SNR cases.
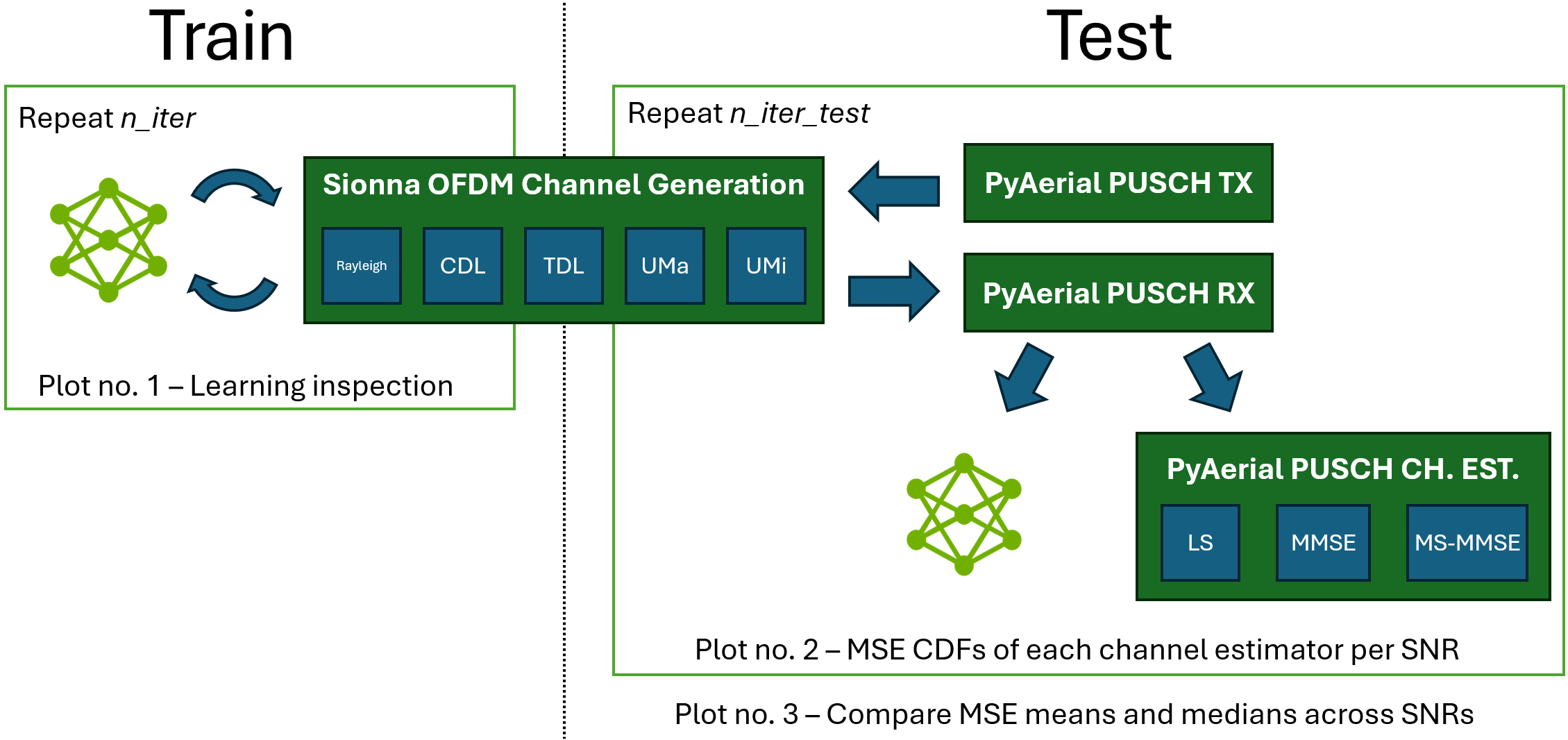
For training, the model interfaces directly with Sionna channel models. For testing, the model is integrated in PyAerial’s PUSCH pipeline and evaluated alongside other classic channel estimators, like the minimum mean squared error (MMSE) and the multi-stage MMSE (MS-MMSE). A diagram of training and testing is below:
[2]:
models_dir = ut.get_model_training_dir(models_folder, training_ch_model,
num_prbs, n_iter, batch_size)
os.makedirs(models_dir, exist_ok=True)
# Channel generator for training
train_ch_gen = SionnaChannelGenerator(num_prbs, training_ch_model, batch_size)
n_sub = num_prbs * 12 // interp # number of subcarriers with reference symbols
for snr_idx, snr in enumerate(train_snrs):
print(f'Training model for SNRs: {snr} dB')
save_model_path = ut.get_snr_model_path(models_dir, snr)
model = FusedChannelEstimator(n_sub, comb_size=interp).to(dev)
criterion = ComplexMSELoss()
optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-4)
model.train()
train_loss, mse_loss = [], []
count = []
for i in (pbar := tqdm(range(n_iter))): # trick: n_iter*(snr_idx+1), high SNR needs longer
# Sionna generate Channels
h, h_ls = train_ch_gen.gen_channel_jit(snr)
# Reshape to match exactly PyAerial's shapes
h_p = sionna_to_pyaerial_shape(h.numpy(), n_sub, interp, est_type='mmse')
h_ls_p = sionna_to_pyaerial_shape(h_ls[..., ::interp].numpy(), n_sub, interp, est_type='ls')
# Transition tensors to PyTorch
h_t, h_ls_t = torch.tensor(h_p).to(dev), torch.tensor(h_ls_p).to(dev)
inputs = torch.view_as_real(h_ls_t)
outputs = model(inputs)
h_hat = torch.view_as_complex(outputs)
loss = criterion(h_hat, h_t)
optimizer.zero_grad(); loss.backward(); optimizer.step()
train_loss += [ut.db(loss.item())]
pbar.set_description(f"Iteration {i+1}/{n_iter}")
pbar.set_postfix_str(f"Training loss: {train_loss[-1]:.1f} dB")
last_model = save_model_path
torch.save(model.state_dict(), save_model_path)
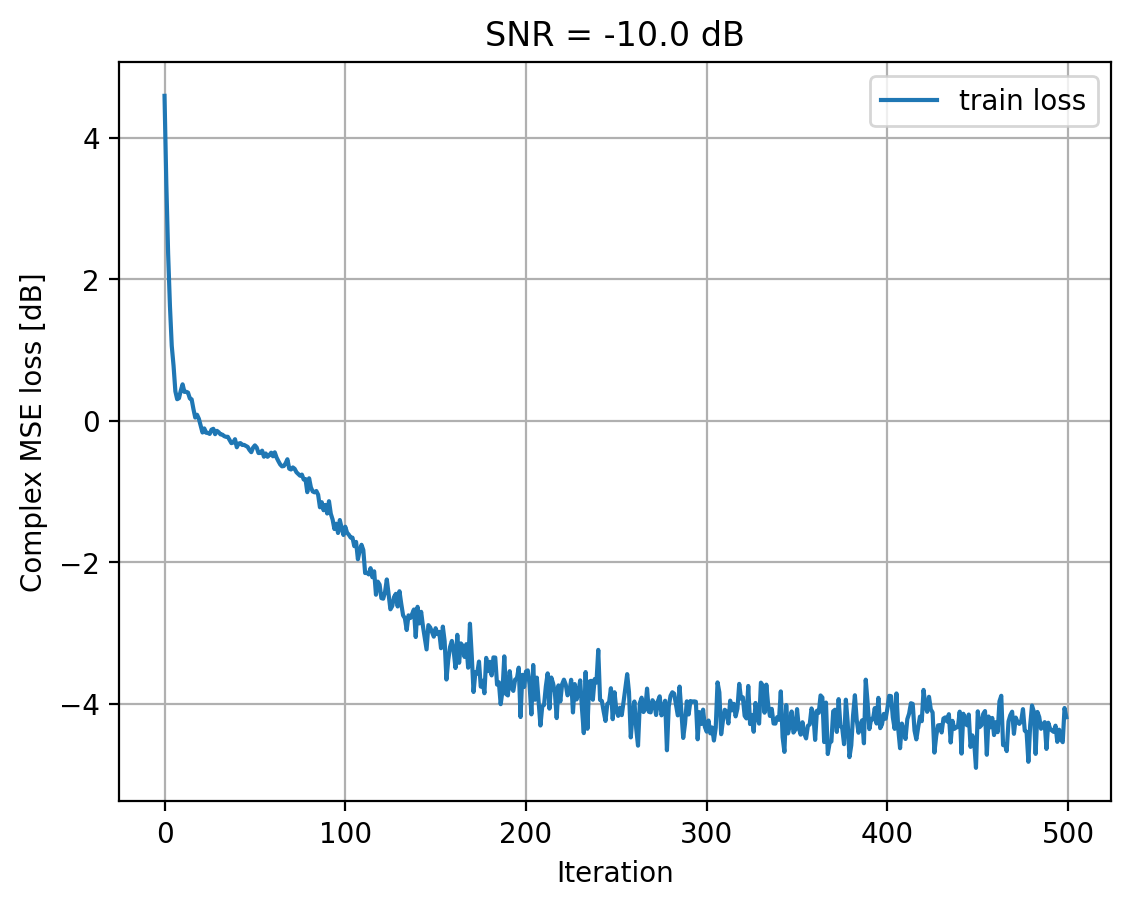
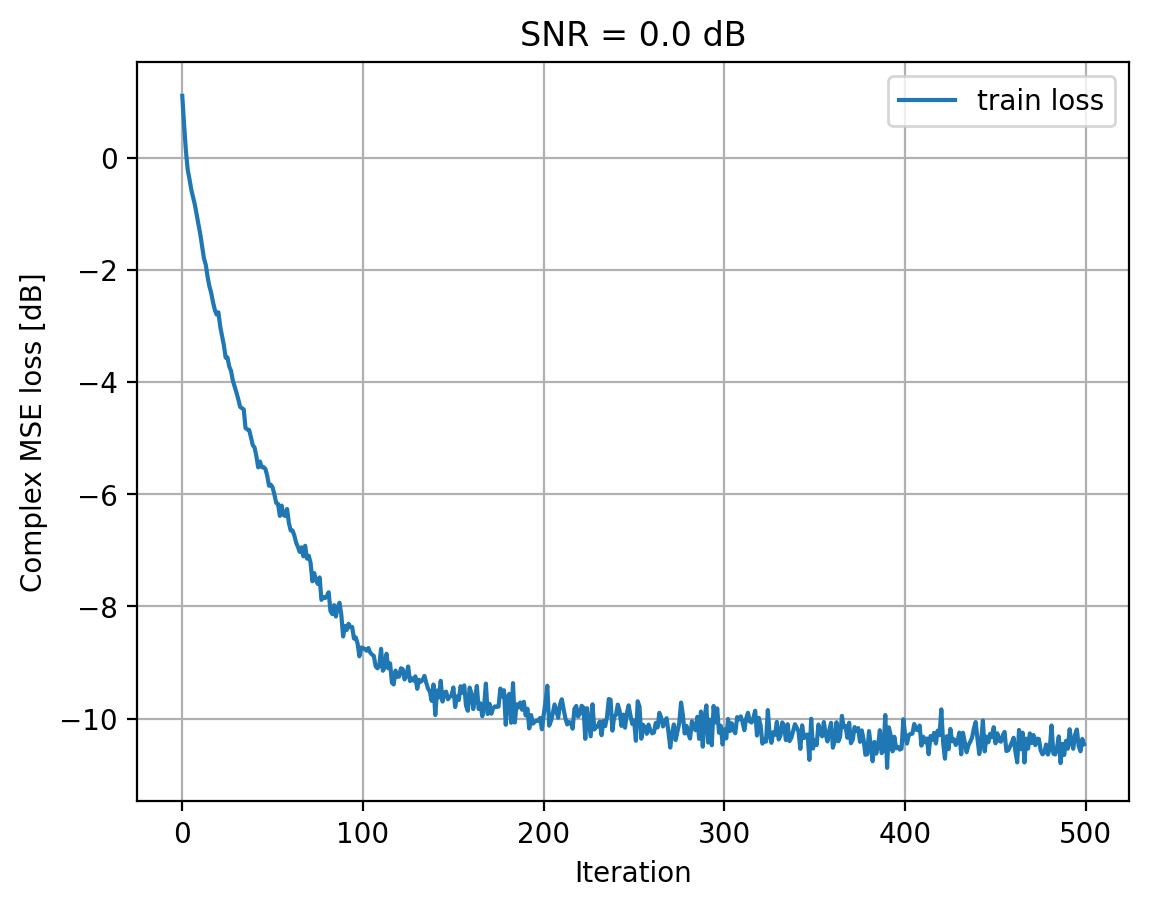
ut.plot_losses([train_loss], ['train loss'], title=f'SNR = {snr} dB')
XLA can lead to reduced numerical precision. Use with care.
Training model for SNRs: -10.0 dB
0%| | 0/500 [00:00<?, ?it/s]WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1739325981.380854 41780 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
Iteration 500/500: 100%|██████████████████████████████████████████████████████████████████████████| 500/500 [00:26<00:00, 19.16it/s, Training loss: -4.2 dB]
Training model for SNRs: 0.0 dB
Iteration 500/500: 100%|█████████████████████████████████████████████████████████████████████████| 500/500 [00:08<00:00, 60.60it/s, Training loss: -10.5 dB]
Training model for SNRs: 10.0 dB
Iteration 500/500: 100%|█████████████████████████████████████████████████████████████████████████| 500/500 [00:08<00:00, 60.17it/s, Training loss: -16.4 dB]
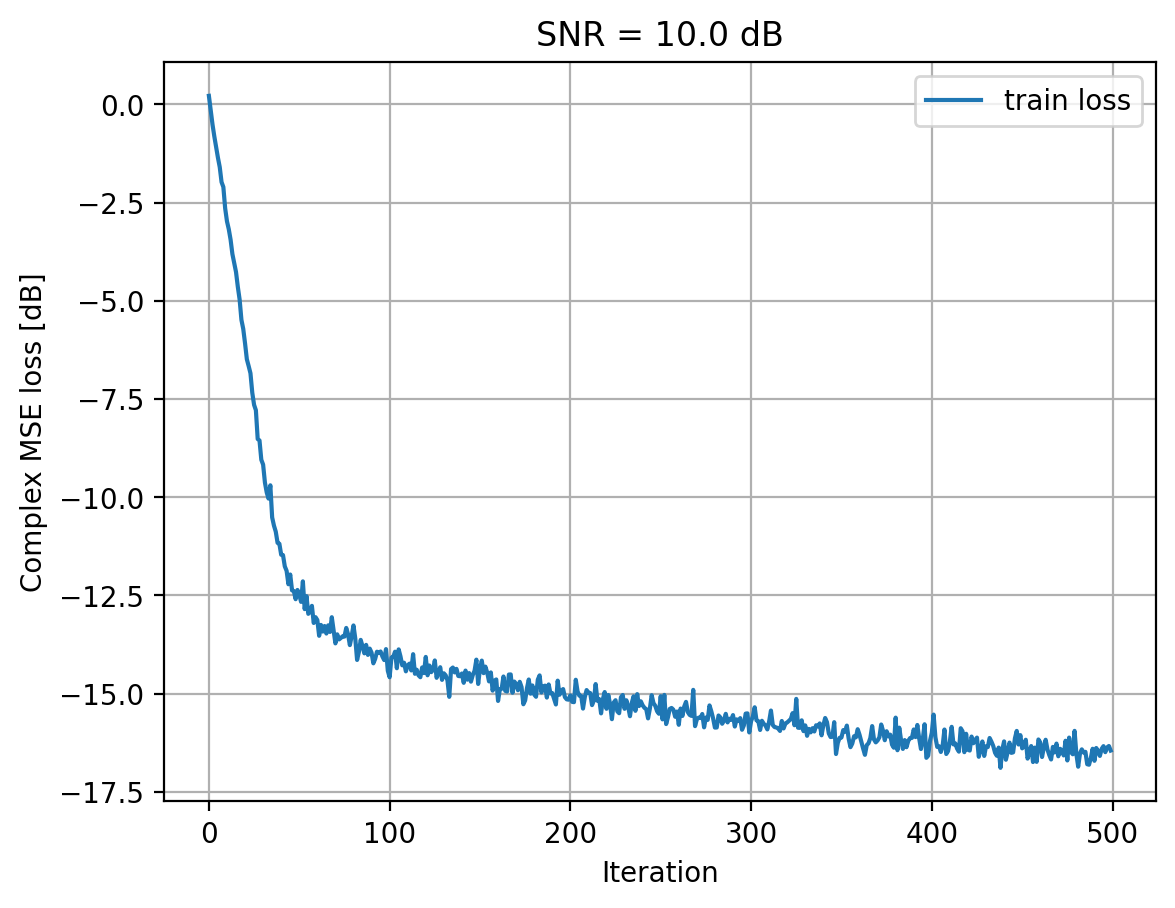
Training model for SNRs: 20.0 dB
Iteration 500/500: 100%|█████████████████████████████████████████████████████████████████████████| 500/500 [00:08<00:00, 60.47it/s, Training loss: -21.2 dB]
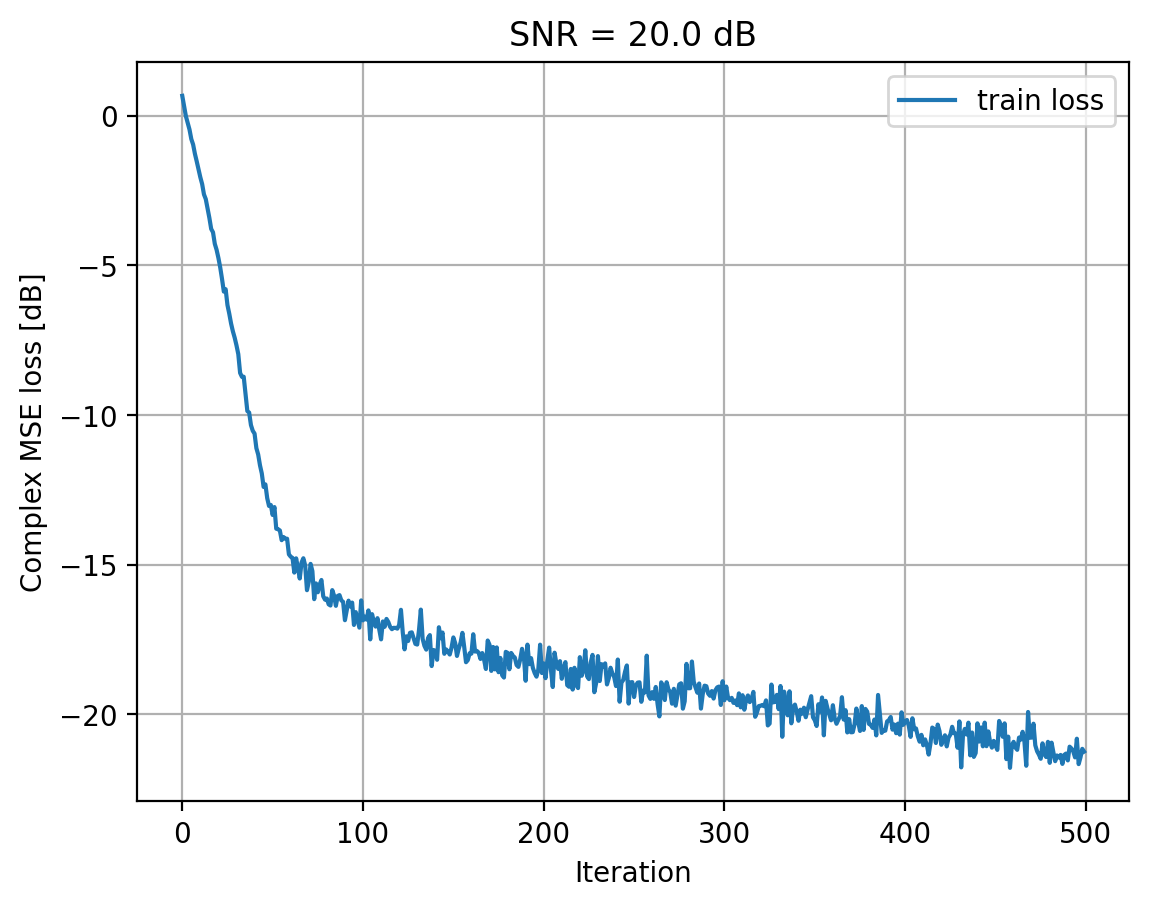
Training model for SNRs: 30.0 dB
Iteration 500/500: 100%|█████████████████████████████████████████████████████████████████████████| 500/500 [00:08<00:00, 61.92it/s, Training loss: -23.8 dB]
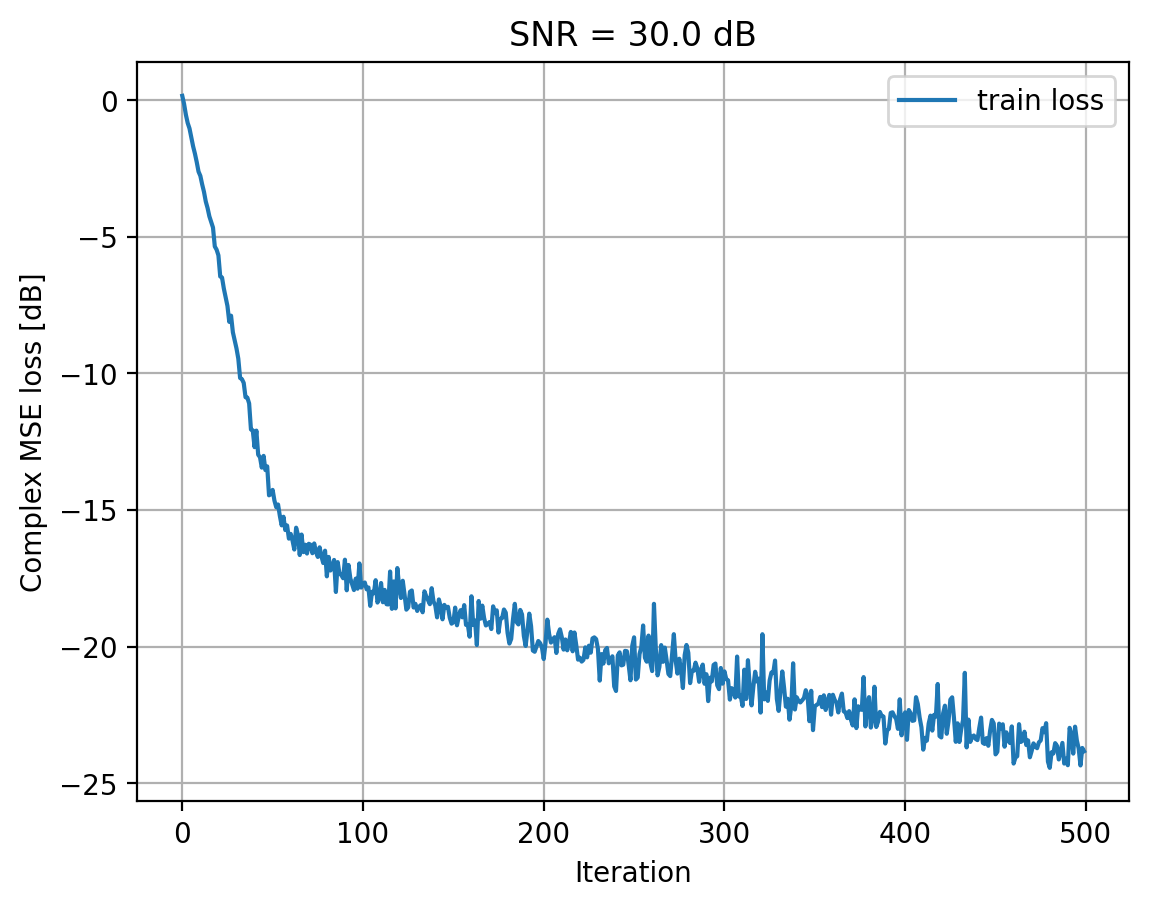
Training model for SNRs: 40.0 dB
Iteration 500/500: 100%|█████████████████████████████████████████████████████████████████████████| 500/500 [00:08<00:00, 60.73it/s, Training loss: -24.1 dB]
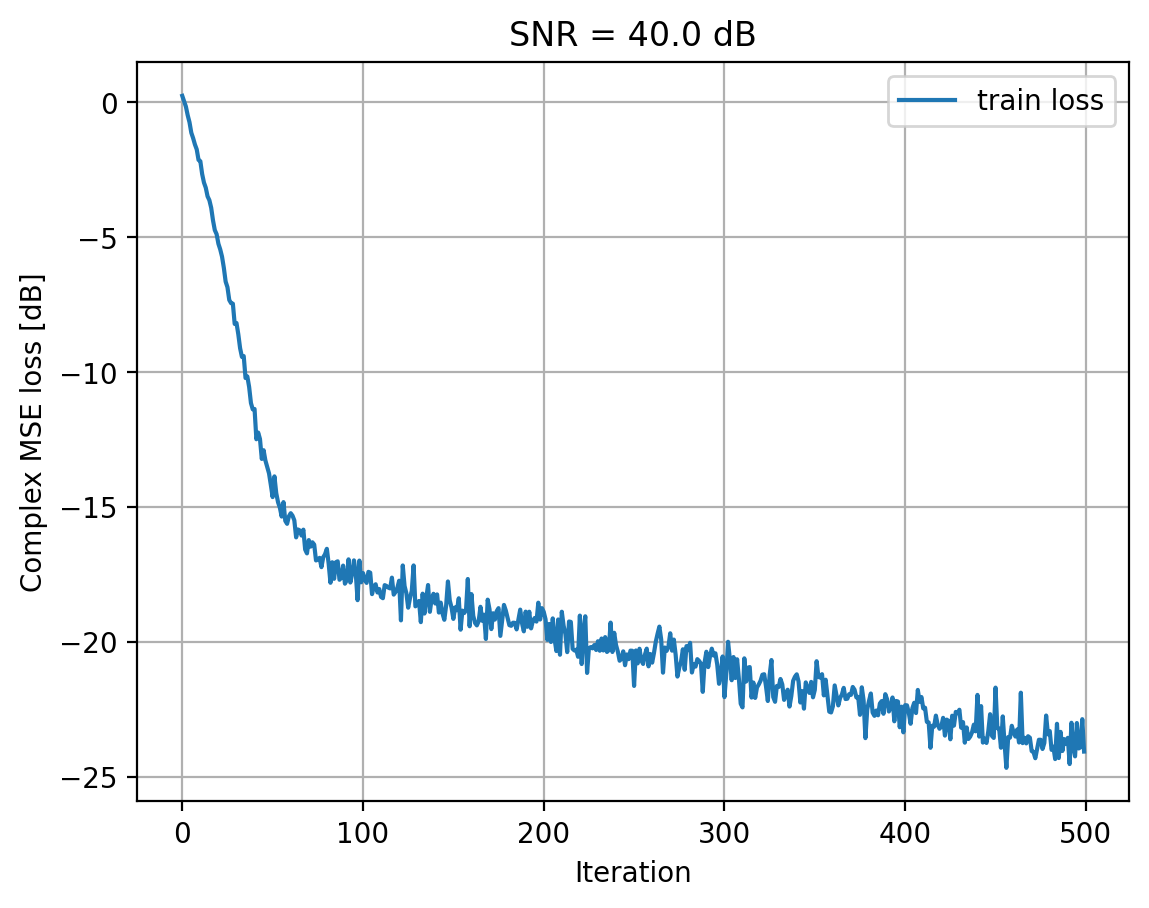
Testing channel estimation model#
The model trained above is a convolutional network, made of RESNET layers. This network consists of two separate blocks, each estimating as many subcarriers as reference signals. The subcarriers are then interleaved to compose the complete channel estimate. The diagram for this network is presented below for an example user allocated 48 PRBs:
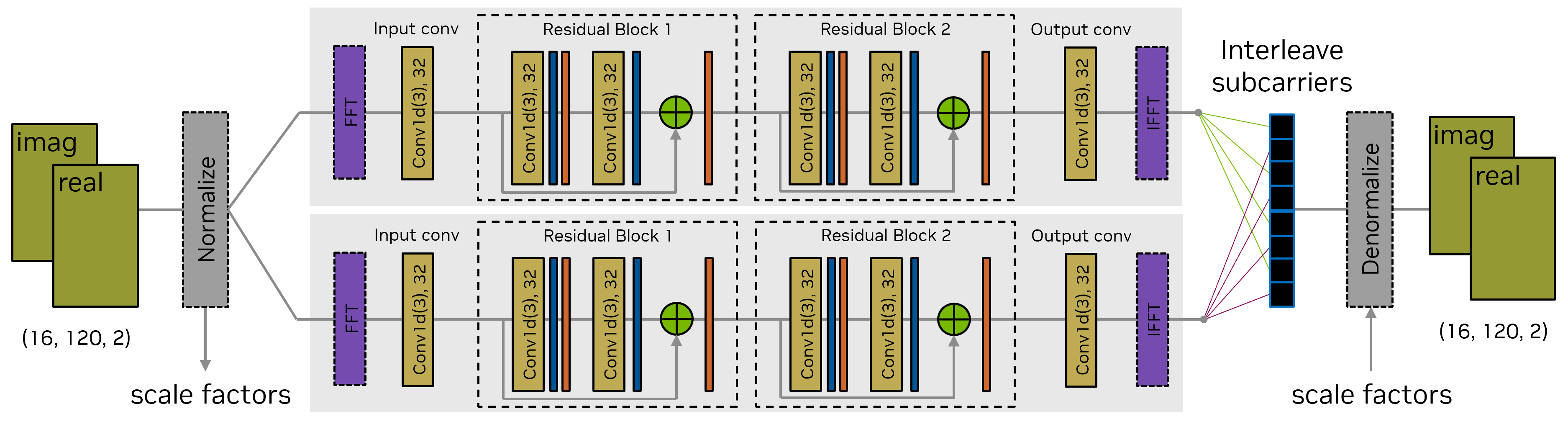
Now we evaluate this network using the LS channel estimates extracted from a PUSCH receiver, as opposed to manually extracted from the channel. The output of the network is compared with MS-MMSE.
[3]:
train_dir = ut.get_model_training_dir(models_folder, training_ch_model,
num_prbs, n_iter, batch_size)
snr_losses_ls = [] # LS from PyAerial
snr_losses_mmse = [] # MMSE from PyAerial
snr_losses_mmse2 = [] # MMSE from PyAerial (median)
snr_losses_ml = [] # ML channel estimation losses
snr_losses_ml2 = [] # ML channel estimation losses (median)
# Channel generator for testing
test_ch_gen = SionnaChannelGenerator(num_prbs, testing_ch_model, batch_size=32)
# Create PyAerial channel estimate generator by applying PyAerial components on Sionna Channels
pyaerial_ch_est_gen = PyAerialChannelEstimateGenerator(test_ch_gen)
for snr_idx, snr in enumerate(test_snrs):
print(f'Testing SNR {snr} dB')
# Select model trained on the SNR closest to the test SNR
snr_model_idx = np.argmin(abs(train_snrs - snr))
snr_model = train_snrs[snr_model_idx]
print(f'Testing model trained on SNR {snr_model}')
# Load ML model
model = FusedChannelEstimator(n_sub, comb_size=interp).to(dev)
model.load_state_dict(torch.load(ut.get_snr_model_path(train_dir, snr_model)))
criterion = ComplexMSELoss()
model.eval()
ls_loss, mmse_loss, ml_loss = [], [], []
with torch.no_grad():
for i in tqdm(range(n_iter_test), desc='Testing LS & MS-MMSE in PyAerial'):
# Internally generate channels, add noise, receive the DM-RS symbols and estimate the channel
ls, mmse, gt = pyaerial_ch_est_gen(snr)
ls = ls[:,::interp//2] # to support comb4
# Reshape to match exactly PyAerial's shapes
ls_p = sionna_to_pyaerial_shape(ls, n_sub, interp, est_type='ls')
mmse_p = sionna_to_pyaerial_shape(mmse, n_sub, interp, est_type='mmse')
gt_p = sionna_to_pyaerial_shape(gt, n_sub, interp, est_type='mmse')
# Evaluate PyAerial classic estimators
for b in range(len(ls)):
ls_loss += [ut.complex_mse_loss(ls[b], gt[b][::interp])]
mmse_loss += [ut.complex_mse_loss(mmse[b], gt[b])]
# Evaluate ML approach
h, h_ls = torch.tensor(gt_p).to(dev), torch.tensor(ls_p).to(dev)
inputs = torch.view_as_real(h_ls)
outputs = model(inputs)
h_hat = torch.view_as_complex(outputs)
ml_loss += [criterion(h_hat, h).item()]
# # Uncomment to inspect channel estimates vs ground-truth
# ut.compare_ch_ests([ls[0,:],
# mmse[0,:],
# h_hat.detach().cpu().numpy()[0,0,0,:,0],
# gt[0,:]],
# ['LS', 'MMSE', 'ML', 'GT'], title=f'SNR = {snr} dB')
# Compute means and medians of LS, LS+ML and MS-MMSE
snr_losses_ml += [ut.db(np.mean(ml_loss))]
snr_losses_ml2 += [ut.db(np.median(ml_loss))]
snr_losses_ls += [ut.db(np.mean(ls_loss))]
snr_losses_mmse += [ut.db(np.mean(mmse_loss))]
snr_losses_mmse2 += [ut.db(np.median(mmse_loss))]
print(f'Avg. ML test loss for {snr} dB SNR is {snr_losses_ml[-1]:.1f} dB')
# Plot CDFs of MSE losses
ut.plot_annotaded_cdfs([ml_loss, mmse_loss], ['LS+ML', 'MS-MMSE'],
title=f'MSE CDFs for SNR = {snr} dB')
XLA can lead to reduced numerical precision. Use with care.
Testing SNR -10.0 dB
Testing model trained on SNR -10.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:53<00:00, 9.43it/s]
Avg. ML test loss for -10.0 dB SNR is -5.5 dB
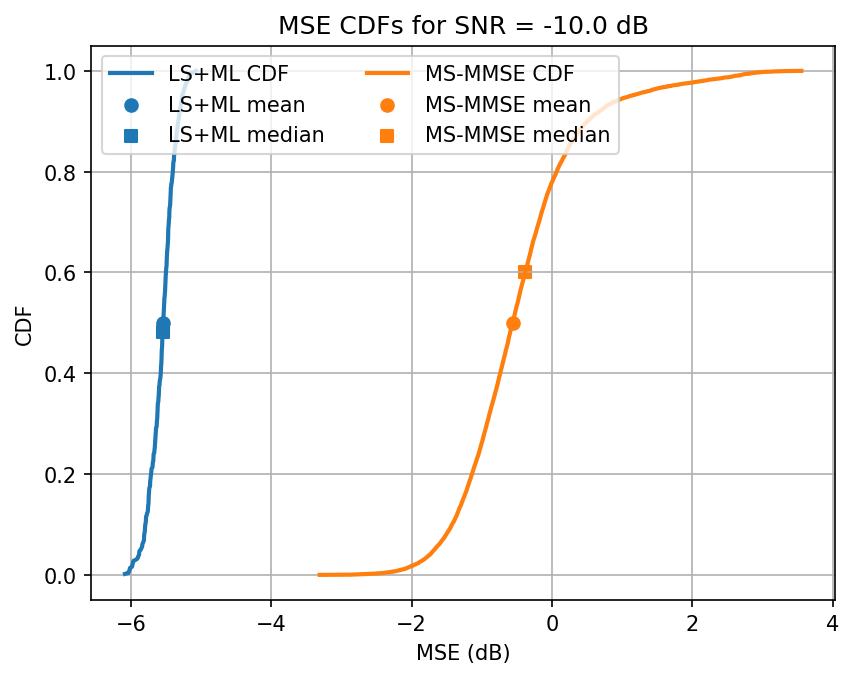
Testing SNR -5.0 dB
Testing model trained on SNR -10.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:26<00:00, 19.21it/s]
Avg. ML test loss for -5.0 dB SNR is -4.4 dB
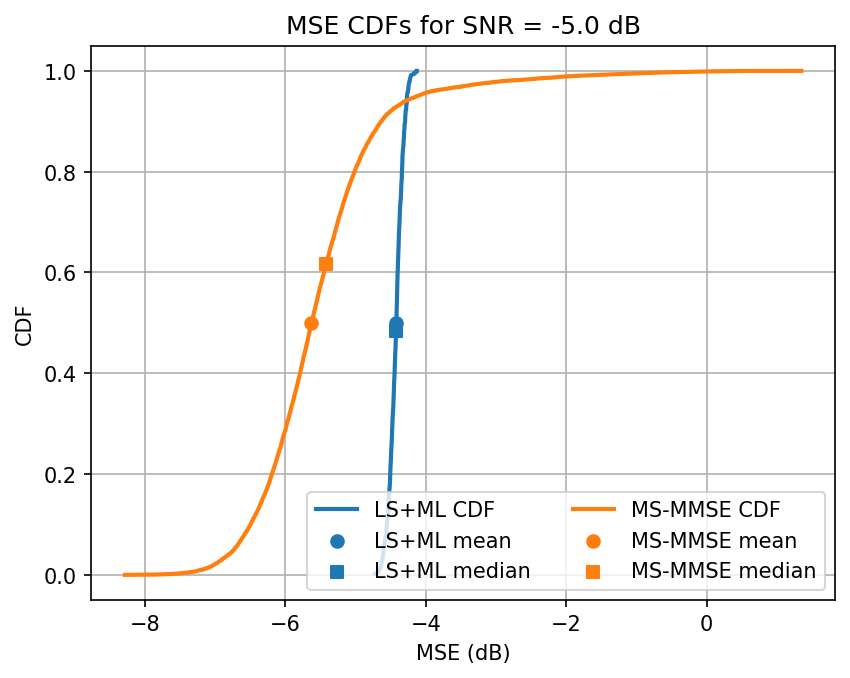
Testing SNR 0.0 dB
Testing model trained on SNR 0.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.27it/s]
Avg. ML test loss for 0.0 dB SNR is -11.5 dB
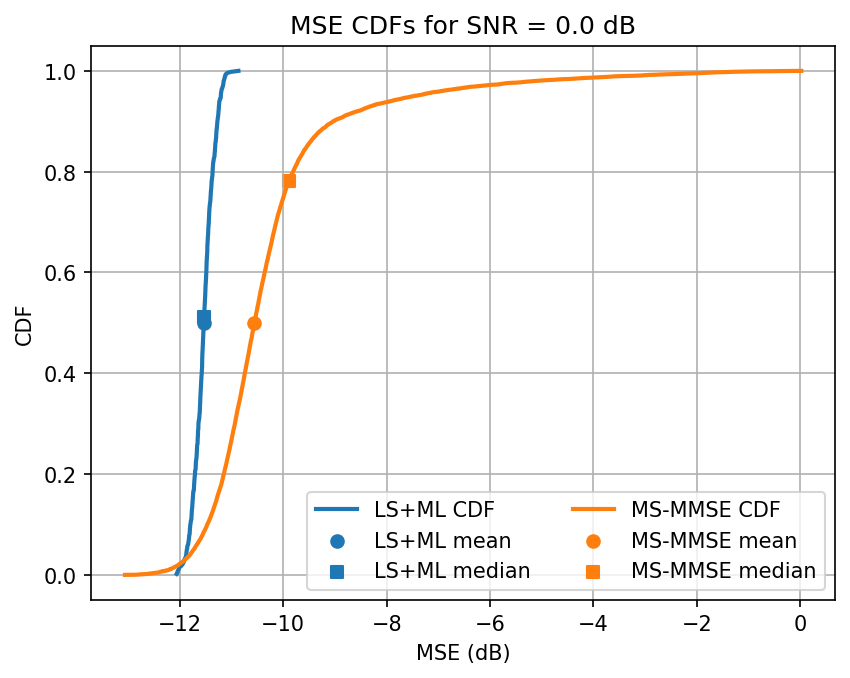
Testing SNR 5.0 dB
Testing model trained on SNR 0.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.27it/s]
Avg. ML test loss for 5.0 dB SNR is -10.2 dB
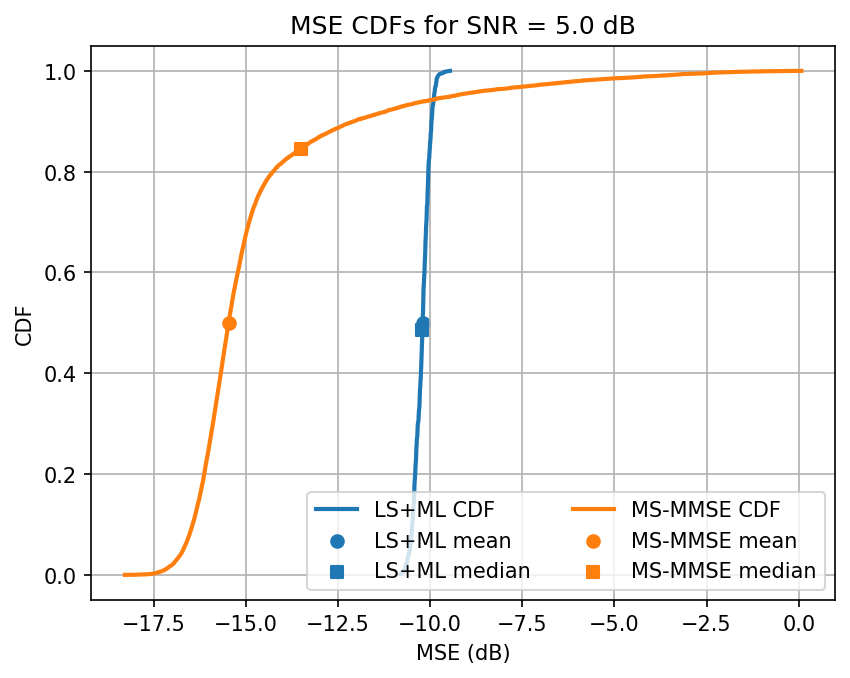
Testing SNR 10.0 dB
Testing model trained on SNR 10.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.33it/s]
Avg. ML test loss for 10.0 dB SNR is -17.7 dB
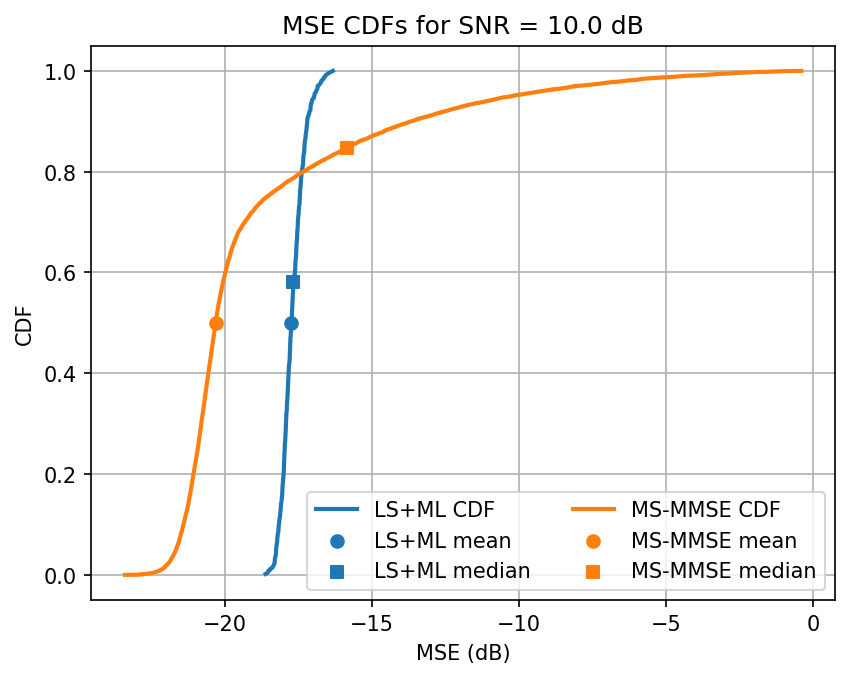
Testing SNR 15.0 dB
Testing model trained on SNR 10.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.35it/s]
Avg. ML test loss for 15.0 dB SNR is -17.8 dB
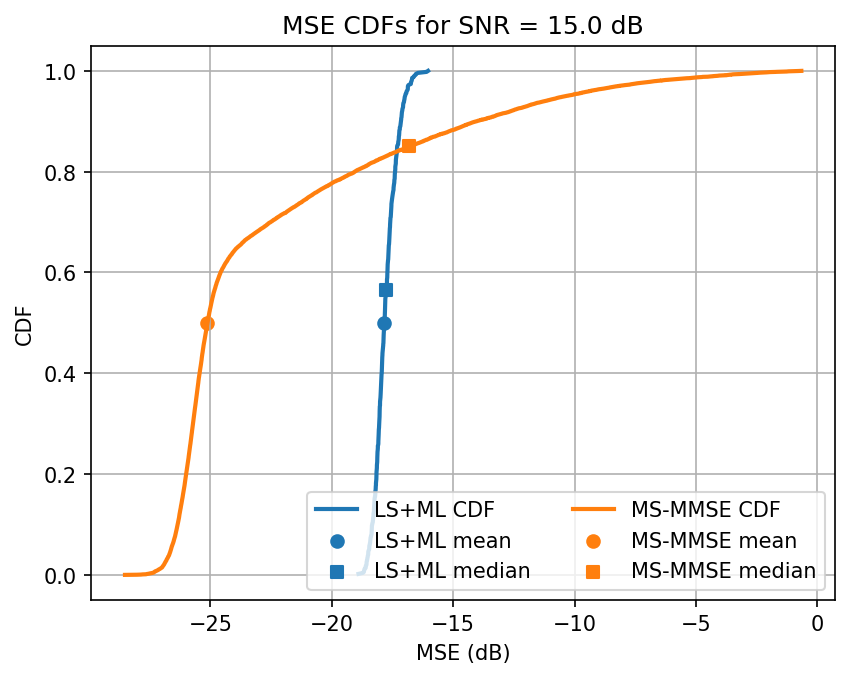
Testing SNR 20.0 dB
Testing model trained on SNR 20.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.32it/s]
Avg. ML test loss for 20.0 dB SNR is -21.3 dB
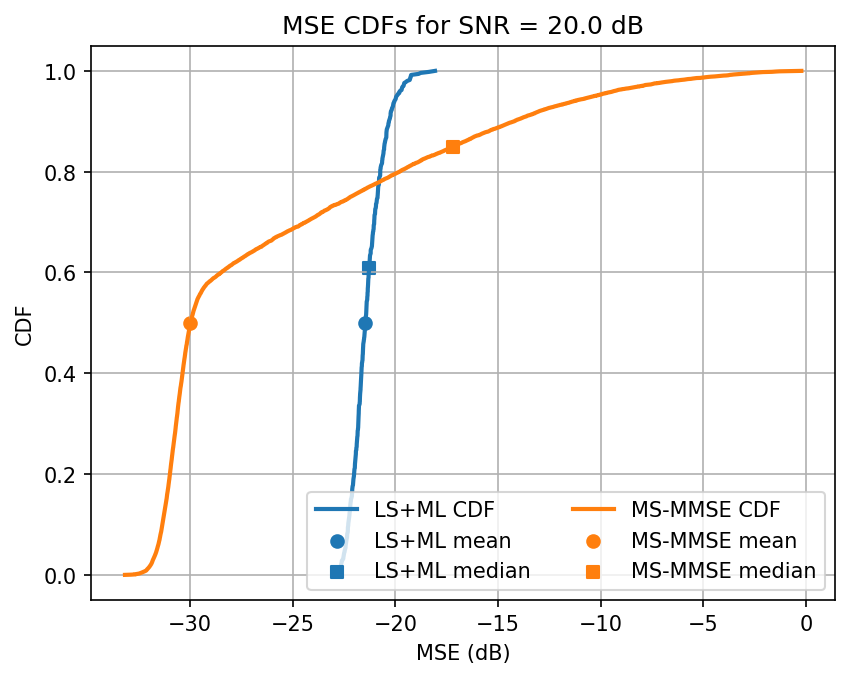
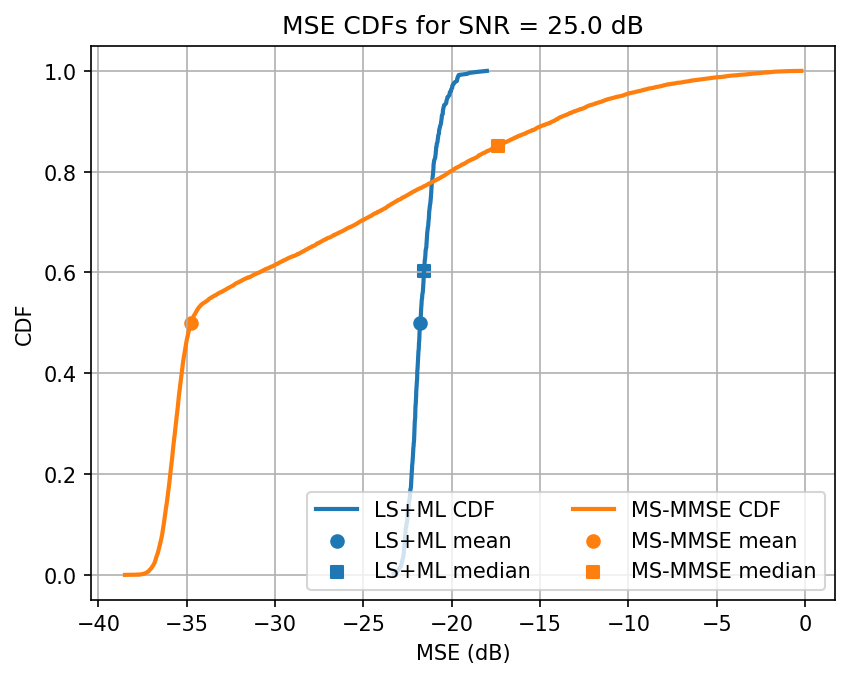
Testing SNR 25.0 dB
Testing model trained on SNR 20.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.35it/s]
Avg. ML test loss for 25.0 dB SNR is -21.6 dB
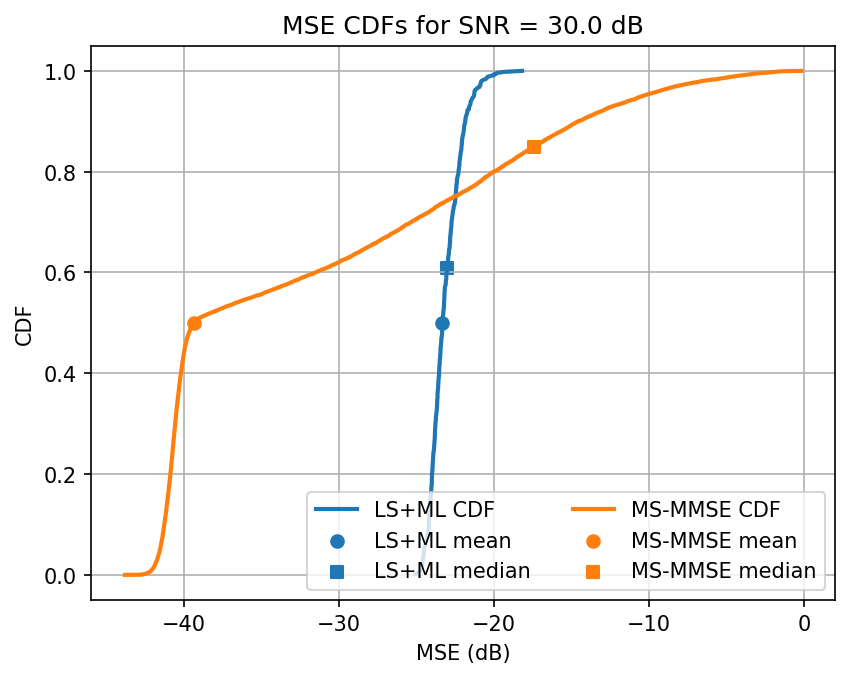
Testing SNR 30.0 dB
Testing model trained on SNR 30.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.34it/s]
Avg. ML test loss for 30.0 dB SNR is -23.0 dB
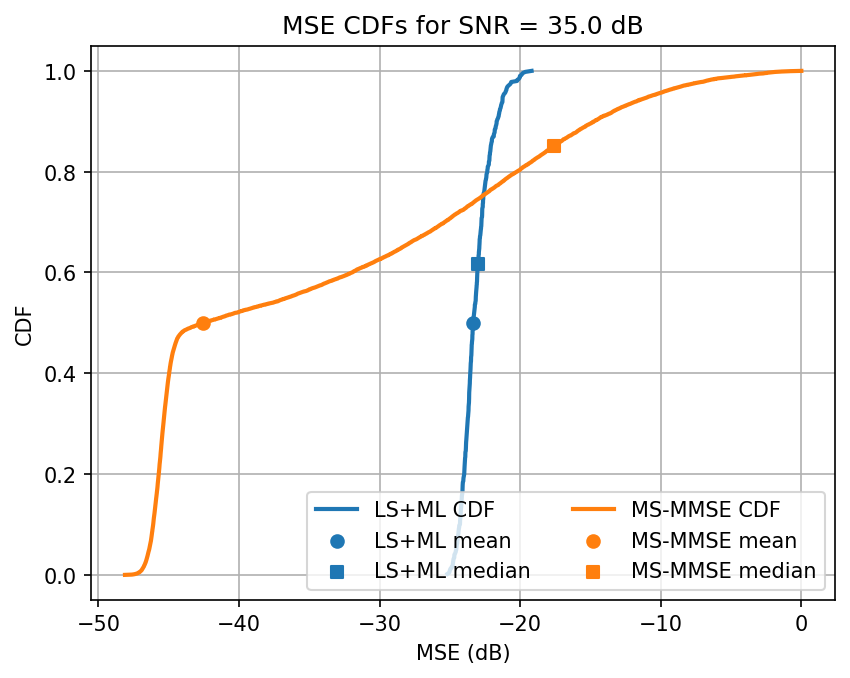
Testing SNR 35.0 dB
Testing model trained on SNR 30.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.39it/s]
Avg. ML test loss for 35.0 dB SNR is -23.0 dB
Testing SNR 40.0 dB
Testing model trained on SNR 40.0
Testing LS & MS-MMSE in PyAerial: 100%|███████████████████████████████████████████████████████████████████████████████████| 500/500 [00:25<00:00, 19.32it/s]
Avg. ML test loss for 40.0 dB SNR is -22.7 dB
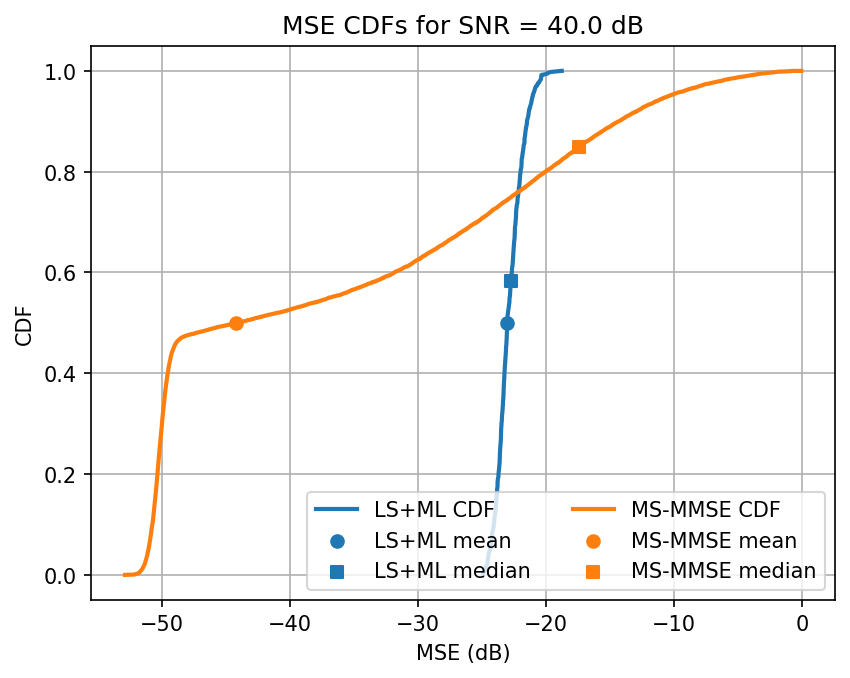
Observation: When we fine tune our training, we see the ML model outperforming the MS-MMSE approach for most SNRs. The performance decays slightly when interpolation is necessary. Additionally, the ML seems more reliable for a wider class of channels. The variance of estimates is lower for ML, on average, it’s performance saturates for high SNRs, even if the median continues to decay.
Plot comparison across SNRs#
Requirement: test_snrs must have more than one element. Read below why we would want to do this.
Model switching depending on SNR: One of the challenges in channel estimation is having it work across SNRs. Lower SNRs have higher channel estimation mean squared error (MSE), which influences more heavily the loss of these samples in machine learning models, thus leading the model learn only low-SNR channels. One way to avoid this problem is to do a model-switching approach. In model-switching, each model is trained for a single SNR and use the model that has the closest SNR to the SNR of the user.
Note that this approach requires a sufficiently good estimate of the SNR so the correct model is chosen. Usually, acquiring such an estimate is not difficult - for example, using the MMSE channel estimate should have more resolution than needed. As such, here we assume the SNR of the user is known and the closest model is selected.
If we set train_snrs = [-10, 0, 10, 20, 30, 40] and test_snrs = [-10, -5, 0, 5, 10, 15, ..., 40], then we will see that the model trained for an SNR of -10 dB is also used to estimate channels at -5 dB, and the model trained for 0 dB is also used at 5 dB, etc. This leads to a higher MSE in SNRs divisible by 5 but not 10.
[4]:
plt.figure(dpi=200)
plt.plot(test_snrs, snr_losses_ls, '-', label='LS', color='k', alpha=.7)
plt.plot(test_snrs, snr_losses_ml, '-', label='LS+ML (mean)', color='tab:orange')
plt.plot(test_snrs, snr_losses_ml2, '--', label='LS+ML (median)', color='tab:orange')
plt.plot(test_snrs, snr_losses_mmse, '-', label='MMSE (mean)', color='tab:green')
plt.plot(test_snrs, snr_losses_mmse2, '--', label='MMSE (median)', color='tab:green')
plt.xlabel('SNR [dB]')
plt.ylabel('NMSE [dB]')
plt.xlim((min(test_snrs), max(test_snrs)))
plt.legend(fontsize=7)
plt.grid()
plt.show()
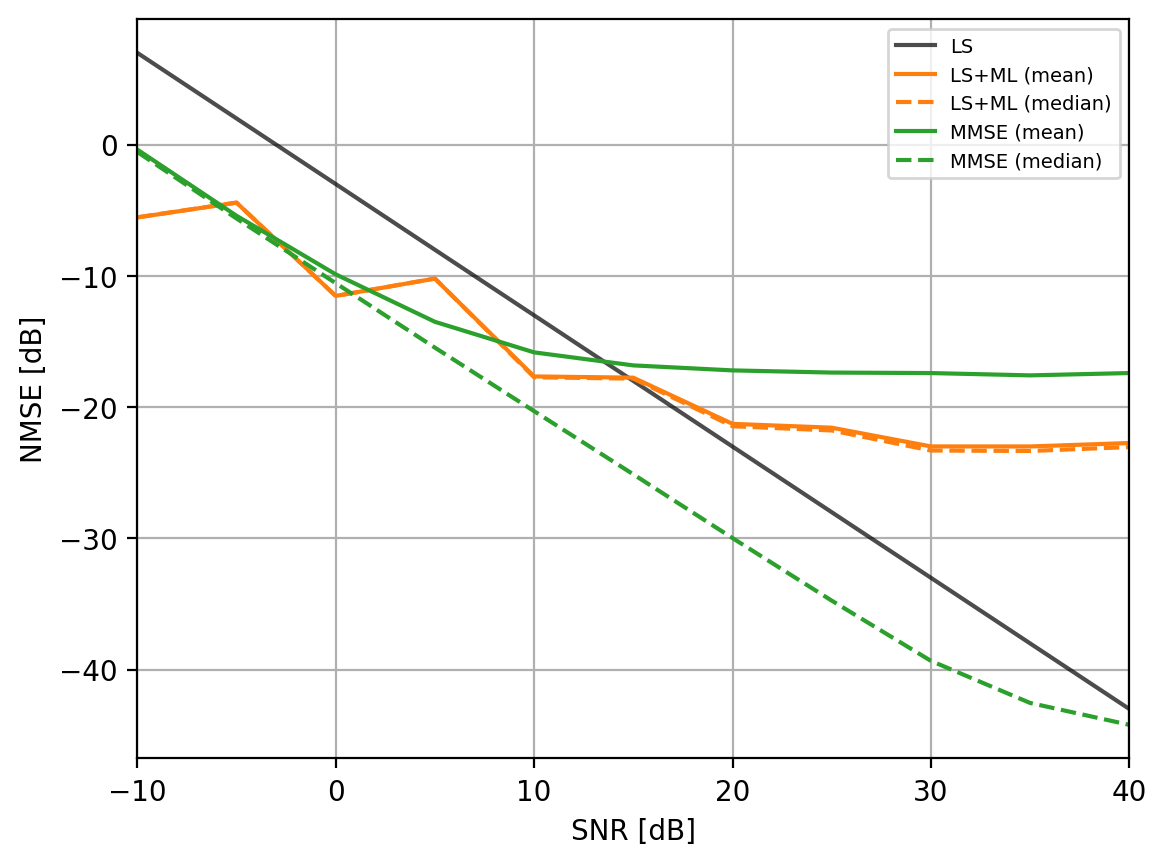
Below is an example of this plot for the case interp = 2, trained with models every 5 dB SNRs, for 20k iterations, and 48 PRBs.
Noteworthy ML gains in MSE compared to MS-MMSE median performance:
4-7 dB gain for SNRs \(\in [-10, 0]\) dB
3-4 dB gain for SNRs \(\in [ 0, 10]\) dB
1-3 dB gain for SNRs \(\in [10, 20]\) dB
Furthermore, when comparing mean performances (dashed lines), results indicate that the ML approach provides a more deterministic channel estimation, offering predictably lower errors also in high delay spread regimes. For channels at SNRs 20 dB, the benefit of ML is over 10 dB on average and it grows for higher SNRs. Note further that this approach is expected to work better for higher PRB allocations. Higher allocations allow the models to leverage more information across the band. However, performance should decrease when the interpolation factor (comb size) increases.
Considerations for Real Deployments#
For such approach to work in real deployments, it requires two additional steps we choose to omit here for simplicity:
SNR estimation: required to estimate the optimized model to perform channel estimation. Here, we consider the SNR is known and choose the closest model to that SNR.
PRB parallelization: during inference, the PRB parallelizer would split the LS estimates (e.g. 78 PRBs) into chunks that could be processed in parallel by the trained models of different sizes, and then put back together. As an example, if we trained models for {1, 4, 16} PRBs, the 78 PRB estimate would results in 4 batches for the 16 PRB model, 3 batches for the 4 PRB and 2 batches for the 1 PRB (4 * 16 + 3 * 4 + 2*1 = 64 + 12 + 2 = 78)
Assessing System-level Performance in the Aerial Omniverse Digital Twin#
This notebook can be used to generate models compatible with the machine learning example of PUSCH channel estimation in the AODT. As long as the models_folder variable is kept constant across runs, a single folder will be populated with the correct structure for multiple SNRs and PRBs. As mentioned in the AODT user guide, this folder will then need to be moved to a directory accessible by the AODT backend, and the config_est.ini file populated with the absolute path to the folder.
Benefits of using PyAerial as a bridge to AODT
AODT uses a high-performance EM solver for computing raytracing propagation simulations. Raytracing is necessary for studying ML approaches in site-specific settings, offering insight and explainability to edge-cases previously unavailable in stochastic simulations.
AODT RAN simulations use the same software running on the same hardware deployed in the real world. This unprecedented combination creates an accurate system representation, giving researchers the possibility to design new features (AI/ML powered or not) and assess their network-wide end-to-end impact.
PyAerial currently provides a Python interface only to cuPHY, the PHY layer of Aerial. As such, comparions beyond the PHY are not possible in PyAerial, and the last link-level quantity that can be computed is block error rates. The AODT, on the other hand, integrates both Aerial’s cuPHY and cuMAC, allowing researchers to measure how channel estimation impacts higher layers.
For more information about how to run this ML channel estimation in AODT, see the AODT user guide.