Sort

Overview

Sort primitive performs high-performance sorting operations on a 1D array of elements. It implements an optimized version of the bitonic sort algorithm using VPU vector instructions.

Requirements

Sort primitive has the following requirements:

1. The data type must be one of: uint16_t, int16_t, uint32_t, int32_t.

2. The number of elements to sort (Size) has specific requirements based on data type:

   • For 16-bit data types (uint16_t, int16_t), must be one of: 1024, 2048, 4096, 8192, 16384.

   • For 32-bit data types (uint32_t, int32_t), must be one of: 256, 512, 1024, 2048, 4096, 8192.

3. The Sort primitive only supports ascending sort.

4. Because we need transpose operations, the input and output buffers need to be larger than Size.

   • The size of input buffer should be (vecw + 1) * (Size / vecw) * sizeof(DataType) bytes.

   • The size of output buffer should be (Size / vecw + 1) * vecw * sizeof(DataType) bytes.

where Size = the number of elements to sort, vecw = 32 for 16-bit data, vecw = 16 for 32-bit data.

5. The input data should be contiguously stored in a 1D array with no pitch.

6. The output data will be stored in a 2D buffer with

   • Width = Size / vecw

   • Height = vecw

   • Pitch = Size / vecw + 1

where Size = the number of elements to sort, vecw = 32 for 16-bit data, vecw = 16 for 32-bit data.

Implementation Details

The Sort primitive can be broken down into two phases: even-odd merge sort and bitonic merge.

Take sort_height_16 as an example, it is used to sort 256 elements of 32-bit data type.

Intrinsics

The Sort primitive utilizes the dvsort2 intrinsic to sort two vectors.

void dvsort2(dvintx src1, dvintx src2, dvintx & dst1, dvintx & dst2);

The dvsort2 intrinsic performs a 2-way merge sort on two input vectors. For each lane in the vector, dst1 = min(src1, src2), dst2 = max(src1, src2).

The Sort primitive also uses dvint_load_perm_transp to load data with reverse order permutation. This helps to form a bitonic sequence.

dvintx dvint_load_perm_transp(agen& agen1, vshortx src);

The dvint_load_perm_transp intrinsic loads data with the permutation specified by src vector. By setting src to decreasing order (e.g. [15, 14, 13, … 1, 0]), it can load data in reverse order.

Even-Odd Merge Sort

First phase: use even-odd merge sort to sort each group of 8 vectors.

Figure 1 illustrates the sorting network for even-odd merge sort. The horizontal lines represent input elements. The vertical connections represent comparators which perform compare-and-swap operations between the connected inputs.

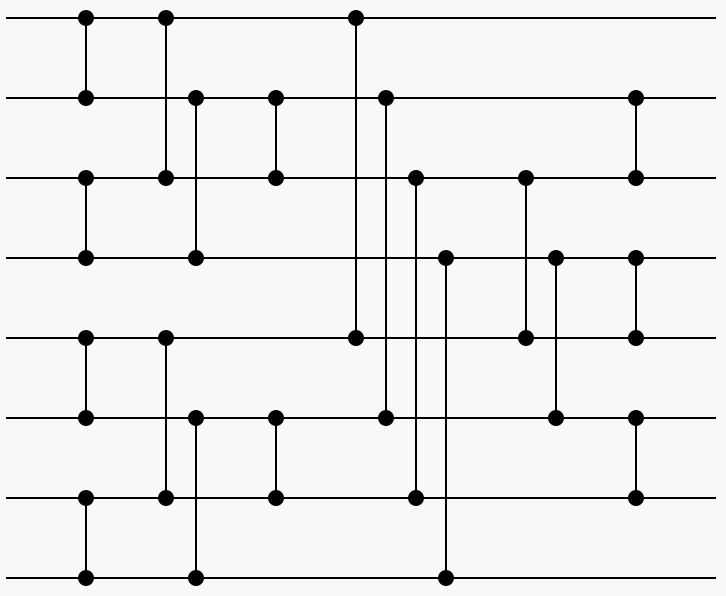
Figure 1: even-odd merge sort with eight inputs.

Even-odd merge sort is faster than bitonic sort, but its address pattern is more complex.

Due to the limited number of vector registers, only 8 vectors can be processed in one iteration.

Bitonic Merge

After even-odd merge sort, each group of 8 vectors are sorted. Note that two consecutive groups of 8 sorted vectors can form a bitonic sequence, with the second group in reverse order (see Figure 3).

Second phase: use bitonic sort to merge these two groups into one group of 16 sorted vectors.

Figure 2 illustrates the sorting network for bitonic merge. The horizontal lines represent input elements. The vertical connections represent comparators which perform compare-and-swap operations between the connected inputs. After sorting, arrows should point to the larger elements.

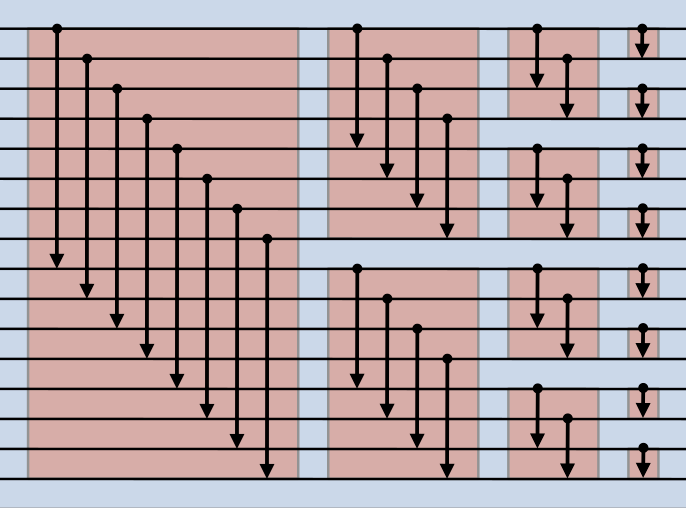
Figure 2: bitonic merge with 16 inputs.

First invoke bitonic_merge_4_way_reverse with vdist = 4 (vertical distance = 4).

• reverse means the second group of 8 vectors is read in reverse order.

• vdist = 4 means the vertical distance between two reads is 4.

In Figure 3, each row represents a vector register which contains 16 elements. The four highlighted rows show where elements in corresponding lanes (columns) are compared and swapped.

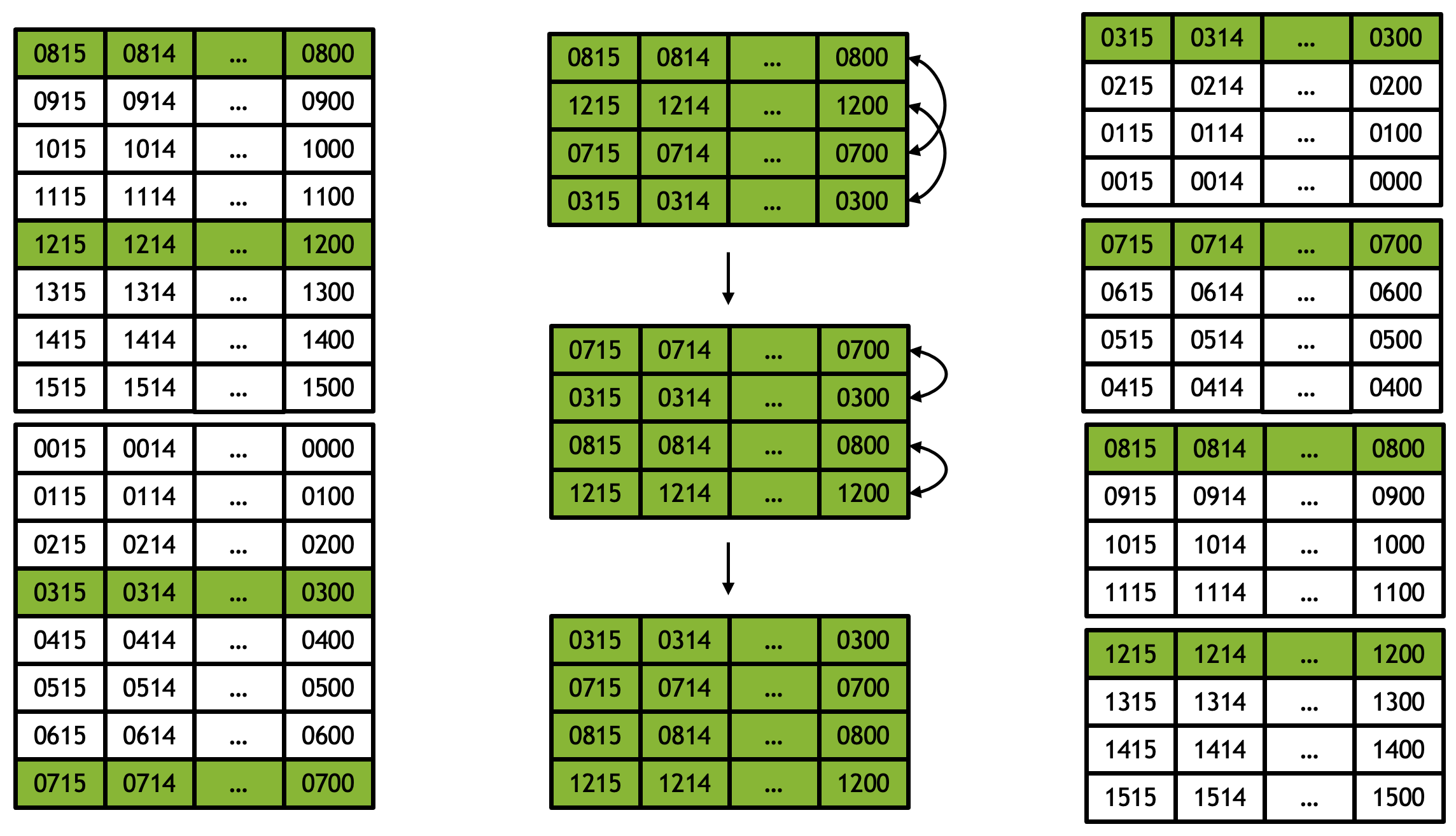
Figure 3: bitonic merge 4-way reverse with vdist = 4.

Then invoke bitonic_merge_4_way with vdist = 1.

In Figure 4, each row represents a vector register which contains 16 elements. The four highlighted rows show where elements in corresponding lanes (columns) are compared and swapped.

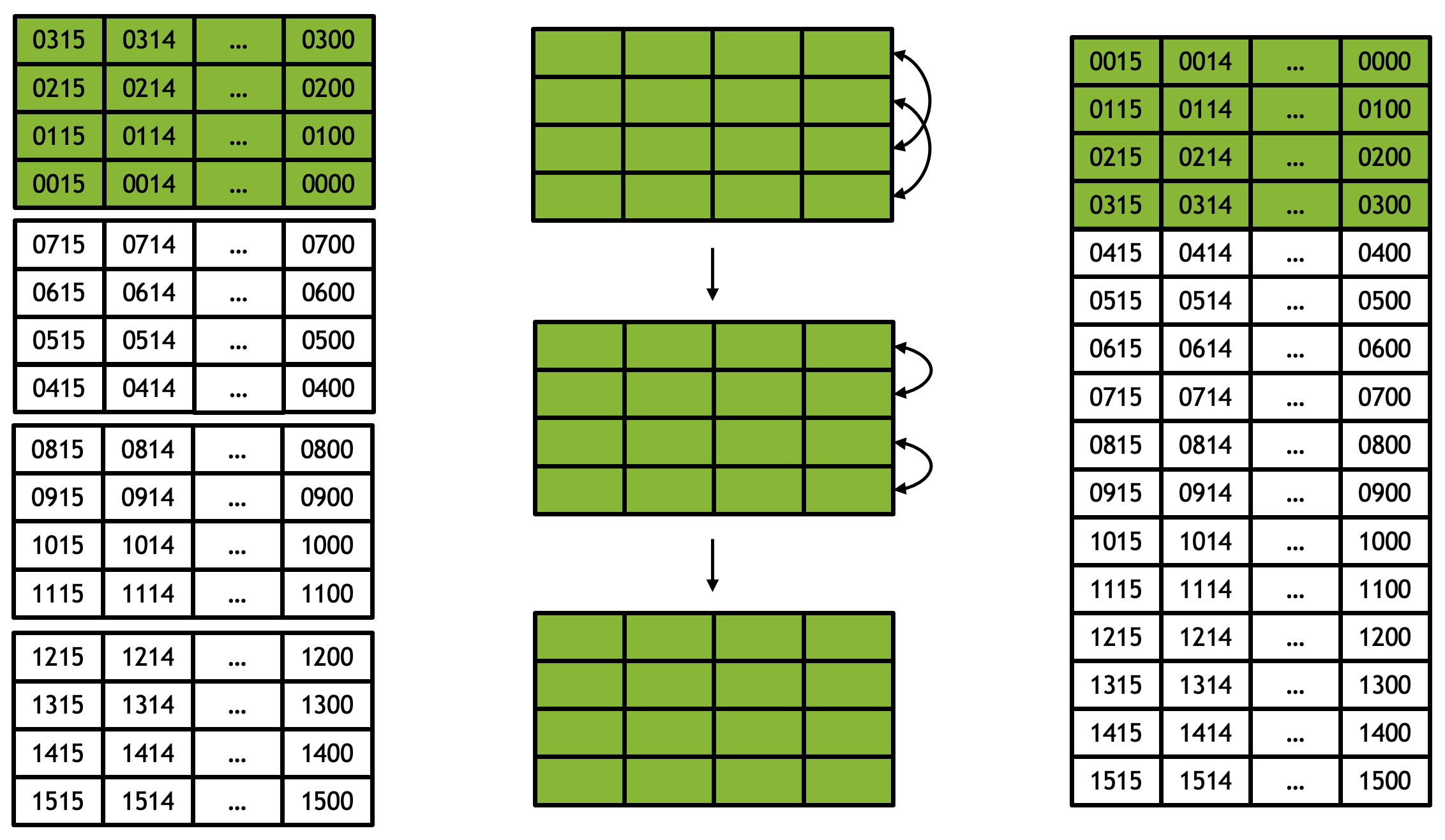
Figure 4: bitonic merge 4-way with vdist = 1.

Now two groups of 8 sorted vectors are merged into one group of 16 sorted vectors. Note that elements in the first column and the second column can form a bitonic sequence, with the second column in reverse order (see Figure 5).

Invoke bitonic_merge_tranpose_2_way_reverse with hdist = 1 (horizontal distance = 1).

• reverse means the second column is read in reverse order.

• hdist = 1 means the horizontal distance between two transpose reads is 1.

In Figure 5, each column represents a vector register which contains 16 sorted elements. The second column is read in reverse order to form a bitonic sequence with the first column. Elements in corresponding lanes (rows) are compared and swapped.

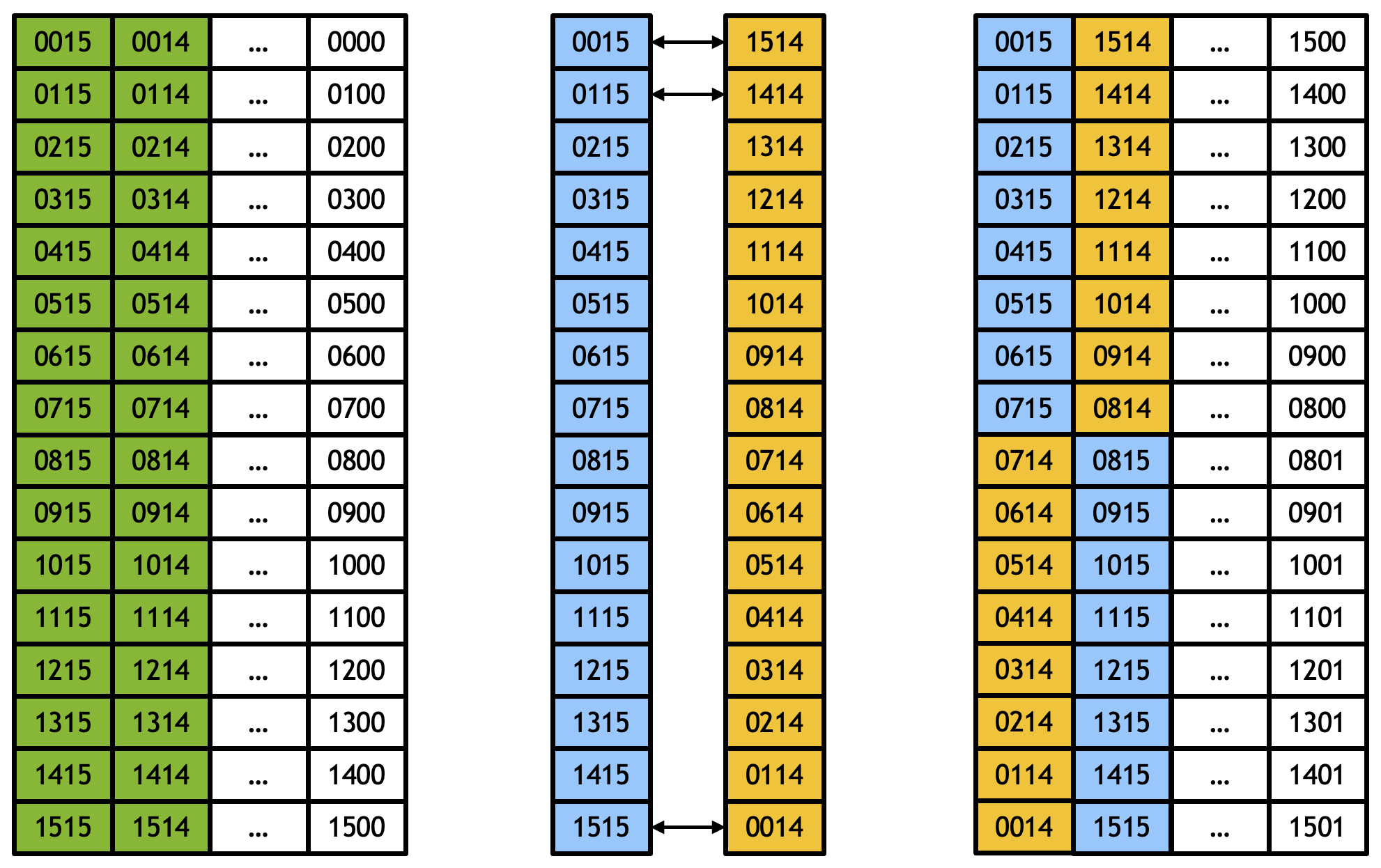
Figure 5: bitonic merge transpose 2-way reverse with hdist = 1.

Then invoke bitonic_merge_4_way to finish the merge of the first two columns. We can further do this process on the rest of data.

Memory Management

The Sort primitive uses a scratch buffer (tmp) for intermediate results during the sorting process. This scratch buffer is provided as part of the SortContext.

DataType *tmp = reinterpret_cast<DataType *>(context->scratch);

Compatibility

Requires PVA SDK 2.6.0 and later.