Heat Transfer with High Thermal Conductivity
This tutorial discusses strategies that can be employed for handling conjugate heat transfer problems with higher thermal conductivities that represent more realistic materials. The Conjugate Heat Transfer tutorial introduced how you can setup a simple conjugate heat transfer problem in Modulus. However, the thermal properties in that example do not represent realistic material properties used to manufacture a heatsink or to cool one. Usually the heatsinks are made of a highly conductive material like Aluminum/Copper, and for air cooled cases, the fluid surrounding the heatsink is air. The conductivities of these materials are orders of magnitude different. This causes sharp gradients at the interface and makes the neural network training very complex. This tutorial shows how such properties and scenarios can be handled via appropriate scaling and architecture choices.
This tutorial presents two scenarios, one where both the materials are solids but the conductivity ratio between the two is \(10^4\) and a second scenario where there is conjugate heat transfer between a solid and a fluid where the solid is copper and fluid is air. The scripts used in this problem can be found in examples/chip_2d/ directory.
The geometry of the problem is a simple composite 2D geometry with different material conductivities. The heat source is placed in inside the material of higher conductivity to replicate the actual heatsink and scenario. The objective of this case is to mimic the orders of magnitude difference between Copper \((k=385 \text{ } W/m-K)\) and Air \((k=0.0261 \text{ } W/m-K)\). Therefore, set the conductivity of the heatsink and surrounding solid to 100 and 0.01 respectively.

Fig. 149 Geometry for 2D solid-solid case
For this problem, it was observed that using the Modified Fourier Networks with Gaussian frequencies led to the best results. Also, for this problem you can predict the temperatures directly in \((^{\circ} C)\). To achieve this, rescale the network outputs according to the rough range of the target solution, which typically requires some domain knowledge of the problem. It turns out that this simple strategy not only greatly accelerates the training convergence, but also effectively improves the model performance and predictions. The code to setup this problem is shown here:
import torch
import numpy as np
from sympy import Symbol, Eq, Or, And
import modulus
from modulus.hydra import to_absolute_path, instantiate_arch, ModulusConfig
from modulus.utils.io import csv_to_dict
from modulus.solver import Solver
from modulus.domain import Domain
from modulus.geometry import Bounds
from modulus.geometry.primitives_2d import Rectangle, Line, Channel2D
from modulus.eq.pdes.navier_stokes import GradNormal
from modulus.eq.pdes.diffusion import Diffusion, DiffusionInterface
from modulus.domain.constraint import (
PointwiseBoundaryConstraint,
PointwiseInteriorConstraint,
IntegralBoundaryConstraint,
)
from modulus.models.layers import Activation
from modulus.domain.monitor import PointwiseMonitor
from modulus.domain.validator import PointwiseValidator
from modulus.utils.io.plotter import ValidatorPlotter, InferencerPlotter
from modulus.key import Key
from modulus.node import Node
from modulus.models.modified_fourier_net import ModifiedFourierNetArch
@modulus.main(config_path="conf_2d_solid_solid", config_name="config")
def run(cfg: ModulusConfig) -> None:
# add constraints to solver
# simulation params
channel_origin = (-2.5, -0.5)
channel_dim = (5.0, 1.0)
heat_sink_base_origin = (-1.0, -0.5)
heat_sink_base_dim = (1.0, 0.2)
fin_origin = heat_sink_base_origin
fin_dim = (1.0, 0.6)
total_fins = 1
box_origin = (-1.1, -0.5)
box_dim = (1.2, 1.0)
source_origin = (-0.7, -0.5)
source_dim = (0.4, 0.0)
source_length = 0.4
inlet_temp = 25.0
conductivity_I = 0.01
conductivity_II = 100.0
source_grad = 0.025
# make list of nodes to unroll graph on
d_solid_I = Diffusion(T="theta_I", D=1.0, dim=2, time=False)
d_solid_II = Diffusion(T="theta_II", D=1.0, dim=2, time=False)
interface = DiffusionInterface(
"theta_I", "theta_II", conductivity_I, conductivity_II, dim=2, time=False
)
gn_solid_I = GradNormal("theta_I", dim=2, time=False)
gn_solid_II = GradNormal("theta_II", dim=2, time=False)
solid_I_net = ModifiedFourierNetArch(
input_keys=[Key("x"), Key("y")],
output_keys=[Key("theta_I_star")],
layer_size=128,
frequencies=("gaussian", 0.2, 64),
activation_fn=Activation.TANH,
)
solid_II_net = ModifiedFourierNetArch(
input_keys=[Key("x"), Key("y")],
output_keys=[Key("theta_II_star")],
layer_size=128,
frequencies=("gaussian", 0.2, 64),
activation_fn=Activation.TANH,
)
nodes = (
d_solid_I.make_nodes()
+ d_solid_II.make_nodes()
+ interface.make_nodes()
+ gn_solid_I.make_nodes()
+ gn_solid_II.make_nodes()
+ [
Node.from_sympy(100 * Symbol("theta_I_star") + 25.0, "theta_I")
] # Normalize the outputs
+ [
Node.from_sympy(Symbol("theta_II_star") + 200.0, "theta_II")
] # Normalize the outputs
+ [solid_I_net.make_node(name="solid_I_network")]
+ [solid_II_net.make_node(name="solid_II_network")]
)
# define sympy variables to parametrize domain curves
x, y = Symbol("x"), Symbol("y")
# define geometry
# channel
channel = Channel2D(
channel_origin,
(channel_origin[0] + channel_dim[0], channel_origin[1] + channel_dim[1]),
)
# heat sink
heat_sink_base = Rectangle(
heat_sink_base_origin,
(
heat_sink_base_origin[0] + heat_sink_base_dim[0], # base of heat sink
heat_sink_base_origin[1] + heat_sink_base_dim[1],
),
)
fin_center = (fin_origin[0] + fin_dim[0] / 2, fin_origin[1] + fin_dim[1] / 2)
fin = Rectangle(
fin_origin, (fin_origin[0] + fin_dim[0], fin_origin[1] + fin_dim[1])
)
chip2d = heat_sink_base + fin
# entire geometry
geo = channel - chip2d
# low and high resultion geo away and near the heat sink
box = Rectangle(
box_origin,
(box_origin[0] + box_dim[0], box_origin[1] + box_dim[1]), # base of heat sink
)
lr_geo = geo - box
hr_geo = geo & box
lr_bounds_x = (channel_origin[0], channel_origin[0] + channel_dim[0])
lr_bounds_y = (channel_origin[1], channel_origin[1] + channel_dim[1])
hr_bounds_x = (box_origin[0], box_origin[0] + box_dim[0])
hr_bounds_y = (box_origin[1], box_origin[1] + box_dim[1])
# inlet and outlet
inlet = Line(
channel_origin, (channel_origin[0], channel_origin[1] + channel_dim[1]), -1
)
outlet = Line(
(channel_origin[0] + channel_dim[0], channel_origin[1]),
(channel_origin[0] + channel_dim[0], channel_origin[1] + channel_dim[1]),
1,
)
# make domain
domain = Domain()
# inlet
inlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=inlet,
outvar={"theta_I": inlet_temp},
lambda_weighting={"theta_I": 10.0},
batch_size=cfg.batch_size.inlet,
)
domain.add_constraint(inlet, "inlet")
# outlet
outlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=outlet,
outvar={"normal_gradient_theta_I": 0},
batch_size=cfg.batch_size.outlet,
)
domain.add_constraint(outlet, "outlet")
# channel walls insulating
def walls_criteria(invar, params):
sdf = chip2d.sdf(invar, params)
return np.less(sdf["sdf"], -1e-5)
walls = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=channel,
outvar={"normal_gradient_theta_I": 0},
batch_size=cfg.batch_size.walls,
criteria=walls_criteria,
)
domain.add_constraint(walls, "channel_walls")
# solid I interior lr
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=lr_geo,
outvar={"diffusion_theta_I": 0},
batch_size=cfg.batch_size.interior_lr,
lambda_weighting={"diffusion_theta_I": 1.0},
)
domain.add_constraint(interior, "solid_I_interior_lr")
# solid I interior hr
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=hr_geo,
outvar={"diffusion_theta_I": 0},
batch_size=cfg.batch_size.interior_hr,
lambda_weighting={"diffusion_theta_I": 1.0},
)
domain.add_constraint(interior, "solid_I_interior_hr")
# solid II interior
interiorS = PointwiseInteriorConstraint(
nodes=nodes,
geometry=chip2d,
outvar={"diffusion_theta_II": 0},
batch_size=cfg.batch_size.interiorS,
lambda_weighting={"diffusion_theta_II": 1.0},
)
domain.add_constraint(interiorS, "solid_II_interior")
# solid-solid interface
def interface_criteria(invar, params):
sdf = channel.sdf(invar, params)
return np.greater(sdf["sdf"], 0)
interface = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=chip2d,
outvar={
"diffusion_interface_dirichlet_theta_I_theta_II": 0,
"diffusion_interface_neumann_theta_I_theta_II": 0,
},
batch_size=cfg.batch_size.interface,
lambda_weighting={
"diffusion_interface_dirichlet_theta_I_theta_II": 10,
"diffusion_interface_neumann_theta_I_theta_II": 1,
},
criteria=interface_criteria,
)
domain.add_constraint(interface, name="interface")
# heat source
heat_source = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=chip2d,
outvar={"normal_gradient_theta_II": source_grad},
batch_size=cfg.batch_size.heat_source,
lambda_weighting={"normal_gradient_theta_II": 1000},
criteria=(
Eq(y, source_origin[1])
& (x >= source_origin[0])
& (x <= (source_origin[0] + source_dim[0]))
),
)
domain.add_constraint(heat_source, name="heat_source")
# chip walls
chip_walls = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=chip2d,
outvar={"normal_gradient_theta_II": 0},
batch_size=cfg.batch_size.chip_walls,
# lambda_weighting={"normal_gradient_theta_II": 1000},
criteria=(
Eq(y, source_origin[1])
& ((x < source_origin[0]) | (x > (source_origin[0] + source_dim[0])))
),
)
domain.add_constraint(chip_walls, name="chip_walls")
# add monitor
monitor = PointwiseMonitor(
chip2d.sample_boundary(10000, criteria=Eq(y, source_origin[1])),
output_names=["theta_II"],
metrics={
"peak_temp": lambda var: torch.max(var["theta_II"]),
},
nodes=nodes,
)
domain.add_monitor(monitor)
# add validation data
mapping = {"Points:0": "x", "Points:1": "y", "Temperature": "theta_I"}
openfoam_var = csv_to_dict(
to_absolute_path("openfoam/2d_solid_solid_D1.csv"), mapping
)
openfoam_var["x"] += channel_origin[0] # normalize pos
openfoam_var["y"] += channel_origin[1]
openfoam_invar_solid_I_numpy = {
key: value for key, value in openfoam_var.items() if key in ["x", "y"]
}
openfoam_outvar_solid_I_numpy = {
key: value for key, value in openfoam_var.items() if key in ["theta_I"]
}
openfoam_validator_solid_I = PointwiseValidator(
nodes=nodes,
invar=openfoam_invar_solid_I_numpy,
true_outvar=openfoam_outvar_solid_I_numpy,
plotter=ValidatorPlotter(),
)
domain.add_validator(openfoam_validator_solid_I)
mapping = {"Points:0": "x", "Points:1": "y", "Temperature": "theta_II"}
openfoam_var = csv_to_dict(
to_absolute_path("openfoam/2d_solid_solid_D2.csv"), mapping
)
openfoam_var["x"] += channel_origin[0] # normalize pos
openfoam_var["y"] += channel_origin[1]
openfoam_invar_solid_II_numpy = {
key: value for key, value in openfoam_var.items() if key in ["x", "y"]
}
openfoam_outvar_solid_II_numpy = {
key: value for key, value in openfoam_var.items() if key in ["theta_II"]
}
openfoam_validator_solid_II = PointwiseValidator(
nodes=nodes,
invar=openfoam_invar_solid_II_numpy,
true_outvar=openfoam_outvar_solid_II_numpy,
plotter=ValidatorPlotter(),
)
domain.add_validator(openfoam_validator_solid_II)
# make solver
slv = Solver(cfg, domain)
# start solver
slv.solve()
if __name__ == "__main__":
run()
You can monitor the Tensorboard plots to see the convergence of the simulation. The following table summarizes a comparison of the peak temperature achieved by the heat sink between the Commercial solver and Modulus results.
Property |
OpenFOAM (Reference) |
Modulus (Predicted) |
Peak temperature \((^{\circ} C)\) |
\(180.24\) |
\(180.28\) |
This figure visualizes the solution.
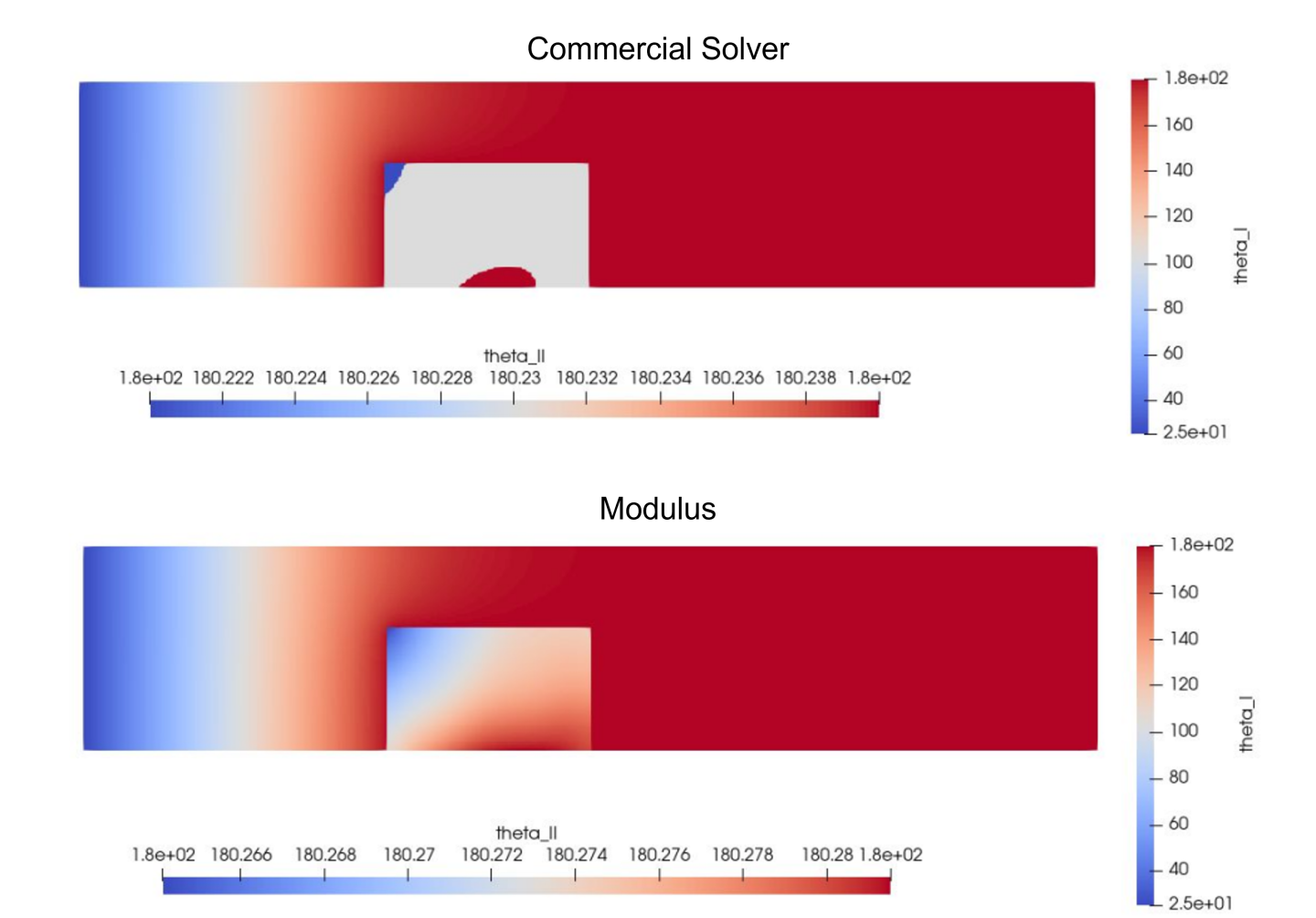
Fig. 150 Results for 2D solid-solid case
The geometry of the problem is very similar to the earlier case, except that now you have a fluid surrounding the solid chip and the dimensions of the geometry are more representative of a real heatsink geometry scales. The real properties for air and copper will also be used in this example. This example is also a good demonstrator for nondimensionalizing the properties/geometries to improve the neural network training. This figure shows the geometry and measurements for this problem.

Fig. 151 Geometry for 2D solid-fluid case
For this problem you can employ the same strategies for the heat solution that was used in the solid-solid case and use the Modified Fourier Networks with Gaussian frequencies. The flow solution and heat solution is one way coupled. Use the same multi-phase training approach that was introduced in Conjugate Heat Transfer. A similar approach with rescaling of the network outputs is taken to improve the performance of the model.
The code for solving the flow is very similar to the other examples such as Scalar Transport: 2D Advection Diffusion and Conjugate Heat Transfer.
The heat setup is also similar to the solid-solid case that was covered earlier.
See examples/chip_2d/chip_2d_solid_fluid_heat_transfer_flow.py and examples/chip_2d/chip_2d_solid_fluid_heat_transfer_heat.py for more details on the
definitions of flow/heat constraints and boundary conditions.
The figure below visualizes the thermal solution in solid and fluid. You can observe that Modulus prediction does a much better job in predicting the temperature continuity at the interface when compared to the commercial solution. We believe these differences in the solver results are due to the discretization errors and can be potentially fixed by improving the grid resolution at the interface. Modulus prediction however does not suffer from such errors and the physical constraints are respected to a better degree of accuracy.
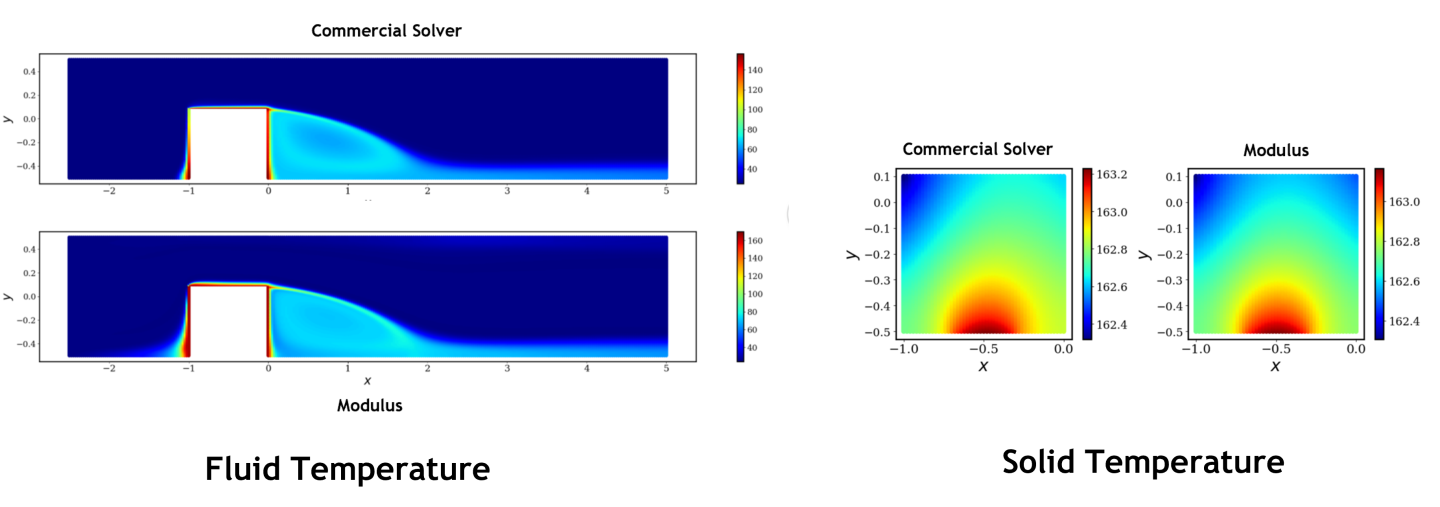
Fig. 152 Results for 2D solid-fluid case