FPGA Heat Sink with Laminar Flow
This tutorial shows how some of the features in Modulus apply for a complicated FPGA heat sink design and solve the conjugate heat transfer. In this tutorial you will learn:
How to use Fourier Networks for complicated geometries with sharp gradients
How to solve problem with symmetry using symmetry boundary conditions
How to formulate velocity field as a vector potential (Exact continuity feature)
How different features and architectures in Modulus perform on a problem with complicated geometry
This tutorial is very similar to the conjugate heat transfer problem shown in the Conjugate Heat Transfer and Parameterized 3D Heat Sink tutorials. You should review review these tutorials (especially the Conjugate Heat Transfer tutorial) for the details on the geometry generation, constraints, etc. This tutorial skips the description for these processes and instead focuses on the implementation of different features and the case study.
The geometry of the FPGA heatsink is shown in Fig. 153. This particular geometry is challenging to simulate due to the thin closely spaced fins that causes sharp gradients which are particularly difficult to learn using regular fully connected neural network (slow convergence).

Fig. 153 FPGA heat sink geometry
This section solves the conjugate heat transfer problem for the geometry above at \(Re=50\). The dimensions of the geometry, as modeled in Modulus, are summarized here:
Dimension |
Value |
Heat Sink Base (l x b x h) |
0.65 x 0.875 x 0.05 |
Fin dimension (l x b x h) |
0.65 x 0.0075 x 0.8625 |
Heat Source (l x b) |
0.25 x 0.25 |
Channel (l x b x h)` |
5.0 x 1.125 x 1.0 |
All the dimensions are scaled such that the channel height is 1 \(m\). The temperature is scaled according to \(\theta=T / 273.15-1.0\). The channel walls are treated as adiabatic and the interface boundary conditions are applied at the fluid-solid interface. Other flow and thermal parameters are described in the table below.
Property |
Fluid |
Solid |
Inlet Velocity \((m/s)\) |
1.0 |
NA |
Density \((kg/m^3)\) |
1.0 |
1.0 |
Kinematic Viscosity \((m^2/s)\) |
0.02 |
NA |
Thermal Diffusivity \((m^2/s)\) |
0.02 |
0.1 |
Thermal Conductivity \((W/m.K)\) |
1.0 |
1.0 |
Inlet Temperature \((K)\) |
273.15 |
NA |
Heat Source Temperature Gradient \((K/m)\) |
409.725 |
NA |
The case setup for this problem is very similar to the problem described in the Conjugate Heat Transfer tutorial. Like the Conjugate Heat Transfer tutorial, you have 3 separate scripts for this problem for the geometry definition, flow constraints and solver and heat constraints and solver.
All the relevant domain, flow and heat solver files for this problem using various versions of features can be found at examples/fpga/.
As described in the Theory, in Modulus, the spectral bias of the neural networks can be overcome by using the Fourier Networks. These networks have shown a significant improvement in results over the regular fully connected neural networks due to their ability to capture sharp gradients.
You do not need to make any special changes to the way the geometry and constraints definition while making changes to the neural network architectures. This also means the architecture is independent of the physics or parameterization being solved and can be applied to any other class of problems covered in the User Guide. More details about architecture configuration can be found in the Hydra configs section (Modulus Configuration).
A note on frequencies: One of the main parameters of these networks are the frequencies. In Modulus, you can choose frequencies from the spectrum you want to sample (full/axis/gaussian/diagonal) and the number of frequencies in the spectrum. The optimal number of frequencies depends on every problem and one often needs to balance the accuracy benefits and the computational expense added due to use of extra Fourier features. For the FPGA problem, choosing the default works for the laminar problem, while for the turbulent case, you increase the number of frequencies to 35.
The solver file for the parameterized FPGA flow field simulation for laminar case is shown below. The different architectures can be chosen by setting the appropriate keyword in the custom arguments defined in the config file.
# make list of nodes to unroll graph on
ns = NavierStokes(nu=nu, rho=rho, dim=3, time=False)
normal_dot_vel = NormalDotVec()
equation_nodes = ns.make_nodes() + normal_dot_vel.make_nodes()
# determine inputs outputs of the network
input_keys = [Key("x"), Key("y"), Key("z")]
if cfg.custom.exact_continuity:
c = Curl(("a", "b", "c"), ("u", "v", "w"))
equation_nodes += c.make_nodes()
output_keys = [Key("a"), Key("b"), Key("c"), Key("p")]
else:
output_keys = [Key("u"), Key("v"), Key("w"), Key("p")]
# select the network and the specific configs
if cfg.custom.arch == "FullyConnectedArch":
flow_net = FullyConnectedArch(
input_keys=input_keys,
output_keys=output_keys,
adaptive_activations=cfg.custom.adaptive_activations,
)
elif cfg.custom.arch == "FourierNetArch":
flow_net = FourierNetArch(
input_keys=input_keys,
output_keys=output_keys,
adaptive_activations=cfg.custom.adaptive_activations,
)
elif cfg.custom.arch == "SirenArch":
flow_net = SirenArch(
input_keys=input_keys,
output_keys=output_keys,
normalization={"x": (-2.5, 2.5), "y": (-2.5, 2.5), "z": (-2.5, 2.5)},
)
elif cfg.custom.arch == "ModifiedFourierNetArch":
flow_net = ModifiedFourierNetArch(
input_keys=input_keys,
output_keys=output_keys,
adaptive_activations=cfg.custom.adaptive_activations,
)
elif cfg.custom.arch == "DGMArch":
flow_net = DGMArch(
input_keys=input_keys,
output_keys=output_keys,
layer_size=128,
adaptive_activations=cfg.custom.adaptive_activations,
)
else:
sys.exit(
"Network not configured for this script. Please include the network in the script"
)
Whenever there is a symmetric geometry and the variable fields are expected to be symmetric, you can use symmetry boundary conditions about the plane or axis symmetry to minimize the computational expense of modeling the entire geometry. For the FPGA heat sink, you have such a plane of symmetry in the z-plane (Fig. 154). The symmetry boundary conditions are discussed in the Symmetry section. Simulating the FPGA problem using symmetry, you can achieve about 33% reduction in training time, compared to a training on the full domain.
For the FPGA problem where the plane of symmetry is z-plane, the boundary conditions stated in Section Symmetry can be translated to the following:
Variables which are odd functions w.r.t.
zcoordinate axis:'w'. Hence on symmetry plane'w'=0.Variables which are even functions w.r.t.
zcoordinate axis:'u', 'v'components of velocity vector and scalar quantities like'p', 'theta_s' , 'theta_f'. On a symmetry plane, set their normal derivative to \(0\). Eg.'u__z'=0.
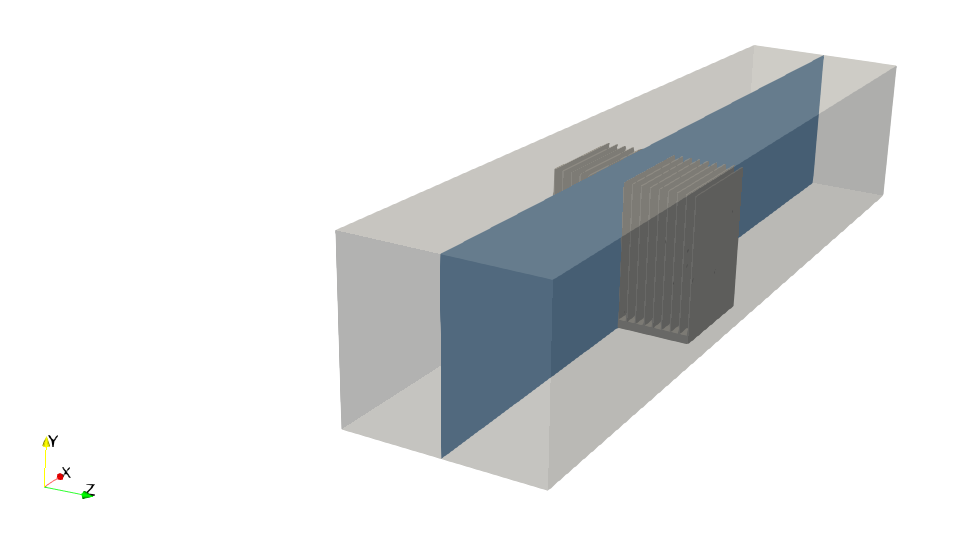
Fig. 154 FPGA plane of symmetry
Only the symmetry boundary conditions in the flow and heat
training domains are shown here. The rest of the training domain remains the same.
(Full files can be accessed at examples/fpga/laminar_symmetry/)
# symmetry channel
symmetry = PointwiseBoundaryConstraint(
nodes=flow_nodes,
geometry=geo,
outvar={"w": 0, "u__z": 0, "v__z": 0, "p__z": 0},
batch_size=cfg.batch_size.symmetry,
criteria=Eq(z, channel_origin[2] + channel_dim[2] / 2.0),
)
flow_domain.add_constraint(symmetry, "symmetry")
# symmetry bc
symmetry_fluid = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=geo,
outvar={"theta_f__z": 0},
batch_size=cfg.batch_size.symmetry_fluid,
criteria=Eq(z, channel_origin[2] + channel_dim[2] / 2.0),
)
thermal_domain.add_constraint(symmetry_fluid, "symmetry_channel_fluid")
symmetry_solid = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=fpga,
outvar={"theta_s__z": 0},
batch_size=cfg.batch_size.symmetry_solid,
criteria=Eq(z, channel_origin[2] + channel_dim[2] / 2.0),
)
thermal_domain.add_constraint(symmetry_solid, "symmetry_channel_solid")
You can define the velocity field as a vector potential such that it is divergence free and satisfies continuity automatically. You can use this formulation for any class of flow problems covered in this guide regardless of the network architecture. However, it is most effective when using fully connected networks.
The code below shows how the exact continuity is implemented by modifying the output nodes of the problem. Caution should be taken when using the exact continuity as it is memory intensive and you might have to modify the batch sizes to fit the problem in GPU memory.
# make list of nodes to unroll graph on
ns = NavierStokes(nu=nu, rho=rho, dim=3, time=False)
normal_dot_vel = NormalDotVec()
equation_nodes = ns.make_nodes() + normal_dot_vel.make_nodes()
# determine inputs outputs of the network
input_keys = [Key("x"), Key("y"), Key("z")]
if cfg.custom.exact_continuity:
c = Curl(("a", "b", "c"), ("u", "v", "w"))
equation_nodes += c.make_nodes()
output_keys = [Key("a"), Key("b"), Key("c"), Key("p")]
else:
output_keys = [Key("u"), Key("v"), Key("w"), Key("p")]
The Summary of features introduced in this tutorial table summarizes the features discussed in this chapter and their applications. The Comparison of pressure drop and peak temperatures from various runs table summarizes the important results of these features on this FPGA problem. Also, Fig. 155, provides a comparison for the loss values from different runs.
Feature |
Applicability to other problems |
Comments |
Fourier Networks |
Applicable to all class of problems |
Shown to be highly effective for problems involving sharp gradients. Modified Fourier network found to improve the performance one step further. |
Symmetry |
Applicable to all problems with a plane/axis of symmetry |
Reduces the computational domain to half leading to significant speed-up (33% reduction in training time compared to full domain). |
Exact Continuity |
Applicable to incompressible flow problems requiring solution to Navier Stokes equation |
Gives better satisfaction of the continuity equation than Velocity-pressure formulation. Found to work best with standard fully connected networks. Also improves the accuracy of results in Fourier networks. |
SiReNs |
Applicable to all class of problems |
Shown to be effective for problems with sharp gradients. However, it does not outperform the Fourier Networks in terms of accuracy. |
DGM Networks Global Adaptive, Activations and Halton Sequences, etc. |
Applicable to all class of problems |
Improves accuracy compared to regular fully connected networks. |
Case Description |
\(P_{drop}\) \((Pa)\) |
\(T_{peak}\) \((^{\circ} C)\) |
Modulus: Fully Connected Networks |
29.24 |
77.90 |
Modulus: Fully Connected Networks with Exact Continuity |
28.92 |
90.63 |
Modulus: Fourier Networks |
29.19 |
77.08 |
Modulus: Modified Fourier Networks |
29.23 |
80.96 |
Modulus: SiReNs |
29.21 |
76.54 |
Modulus: Fourier Networks with Symmetry |
29.14 |
78.56 |
Modulus: DGM Networks with Global LR annealing, Global Adaptive Activations, and Halton Sequences |
29.10 |
76.86 |
OpenFOAM Solver |
28.03 |
76.67 |
Commercial Solver |
28.38 |
84.93 |
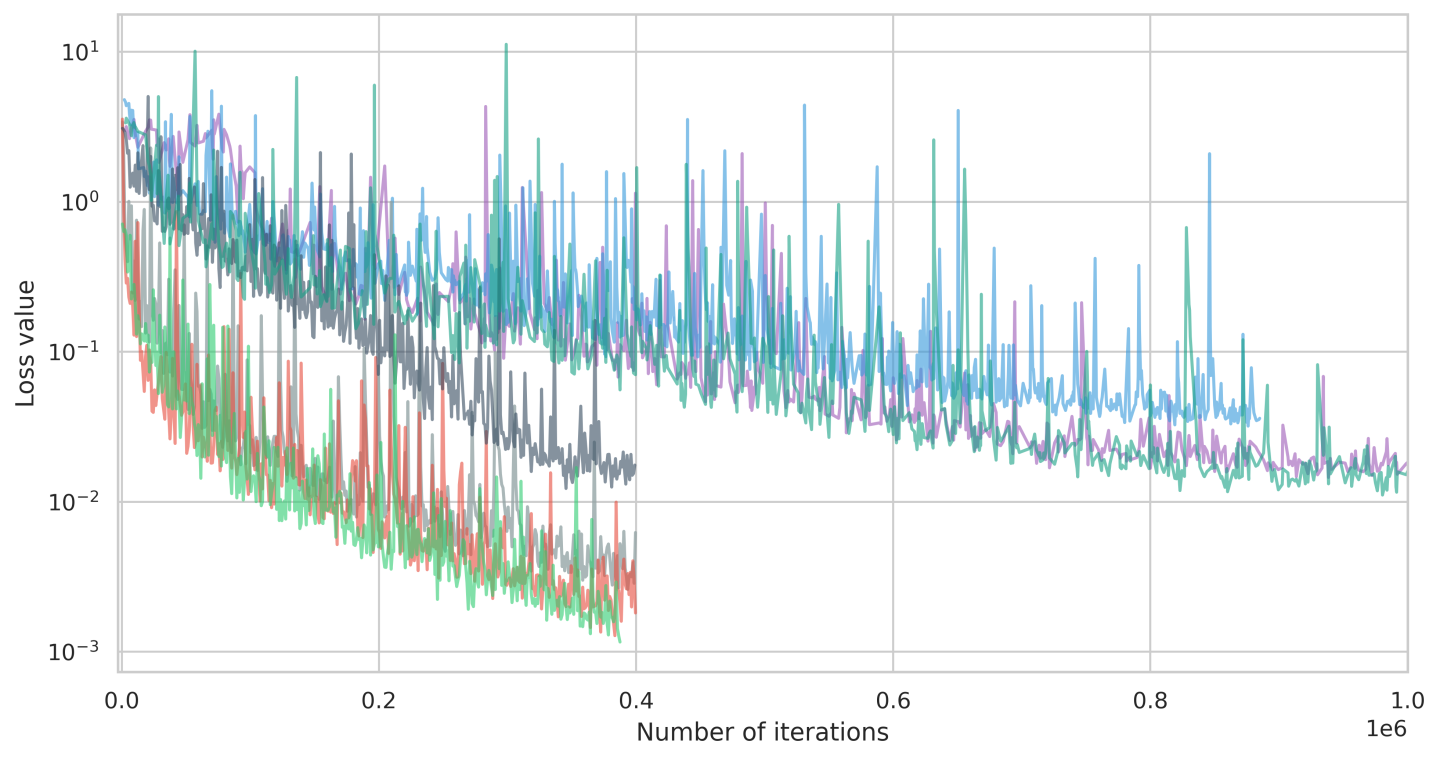
Fig. 155 Flow comparisons
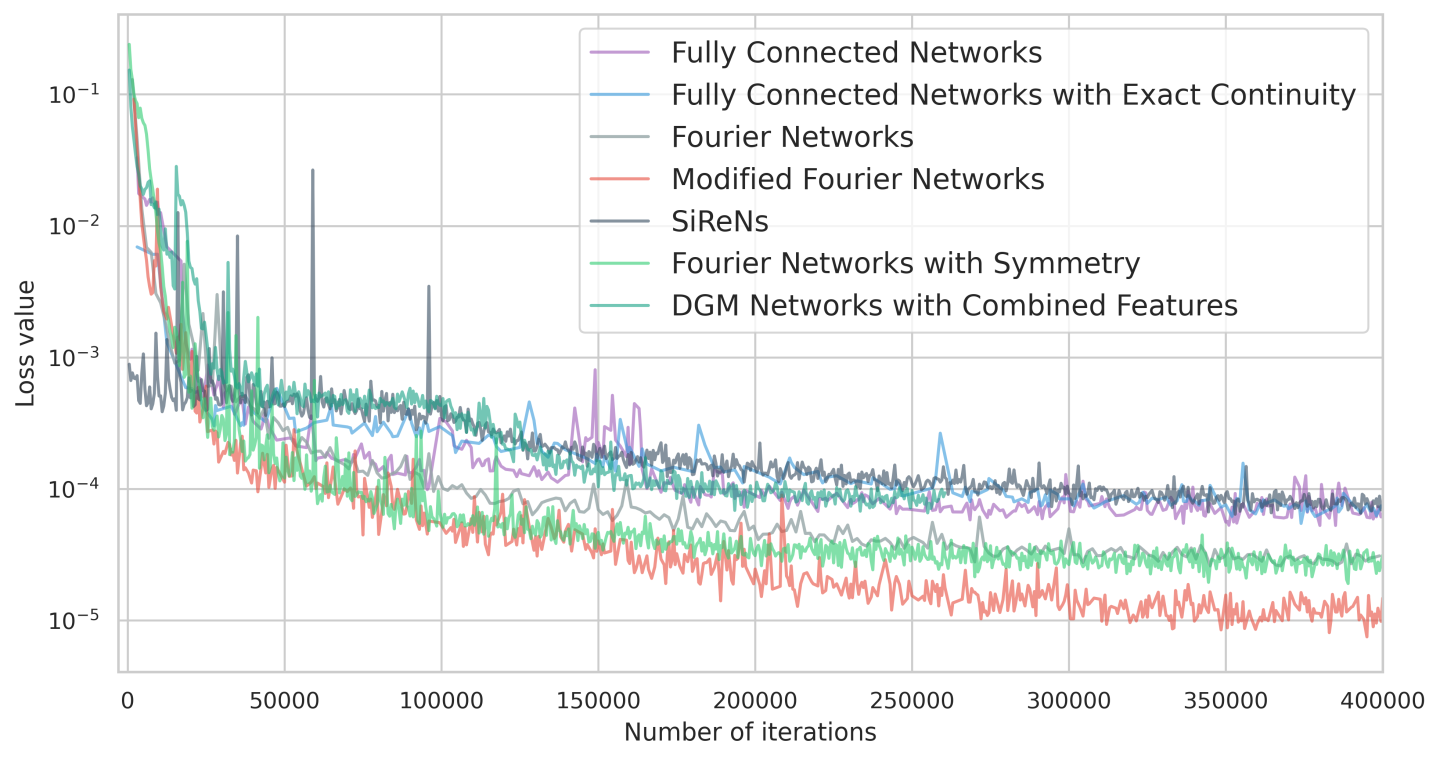
Fig. 156 Heat comparisons