Fully Developed Turbulent Channel Flow
This tutorial demonstrates the use of PINNs to solve a canonical turbulent flow in a 2D channel using two equation turbulence models and wall functions, without using any training data.
This tutorial also demonstrates how lookup tables can be created which are used in some forms of turbulence modeling using neural networks.
Solving turbulence using PINNs and Neural networks in general, is an active field of research. While making a generalizable turbulence model implementation in PINNs is an ambitious goal, with this example, the aim is to provide a few potential ideas that you can use to solve turbulent systems using two equation models and wall functions.
This chapter is in continuous development and will be updated with new methods and improvements over time.
This tutorial tests the turbulence implementation and the wall functions on a fully developed channel flow case. The flow is set between two flat plates separated by a distance 2H in y-direction and is driven by a constant negative pressure gradient in the streamwise direction. The flow in streamwise direction is periodic and flow is homogenous in the z-direction.

Fig. 134 Turbulent flow in a 2D channel
Solve the problem for a friction Reynolds number of 590. The friction Reynolds number is defined as
(196)\[Re_{\tau} = \frac{u_{\tau}H}{\nu}\]
The pressure gradient is determined from the friction velocity as
(197)\[\frac{\partial p}{\partial x} = \frac{u_{\tau}^2}{H}\]
This example implements the high Reynolds number version of the standard k epsilon model with wall functions. The goal is to solve the equations beyond a certain distance from the wall so that the viscous sublayer is not resolved. The turbulence equations for the k-epsilon model is shown here:
(198)\[\frac{\partial k}{\partial t} + U \cdot \nabla k = \nabla \cdot \left[ \left( \nu + \frac{\nu_t}{\sigma_k} \night) \nabla k \night] + P_k - \varepsilon\]
(199)\[\frac{\partial \varepsilon}{\partial t} + U \cdot \nabla \varepsilon = \nabla \cdot \left[ \left( \nu + \frac{\nu_t}{\sigma_{\varepsilon}} \night) \nabla \varepsilon \night] + (C_{\varepsilon 1}P_k - C_{\varepsilon 2} \varepsilon)\frac{\varepsilon}{k}\]
Next, this tutorial focuses on wall functions. Fig. 135 shows the wall modeling approach followed in this example. As seen in the figure, the equation loses are applied beyond a particular wall height that is chosen a priori. The points below this chosen wall height are discarded. The wall function relations that are shown in the following sections are then applied at this wall height. The wall height is chosen such that the \(y^+\) is \(~30\) which ensures that the inertial sublayer assumption is valid.
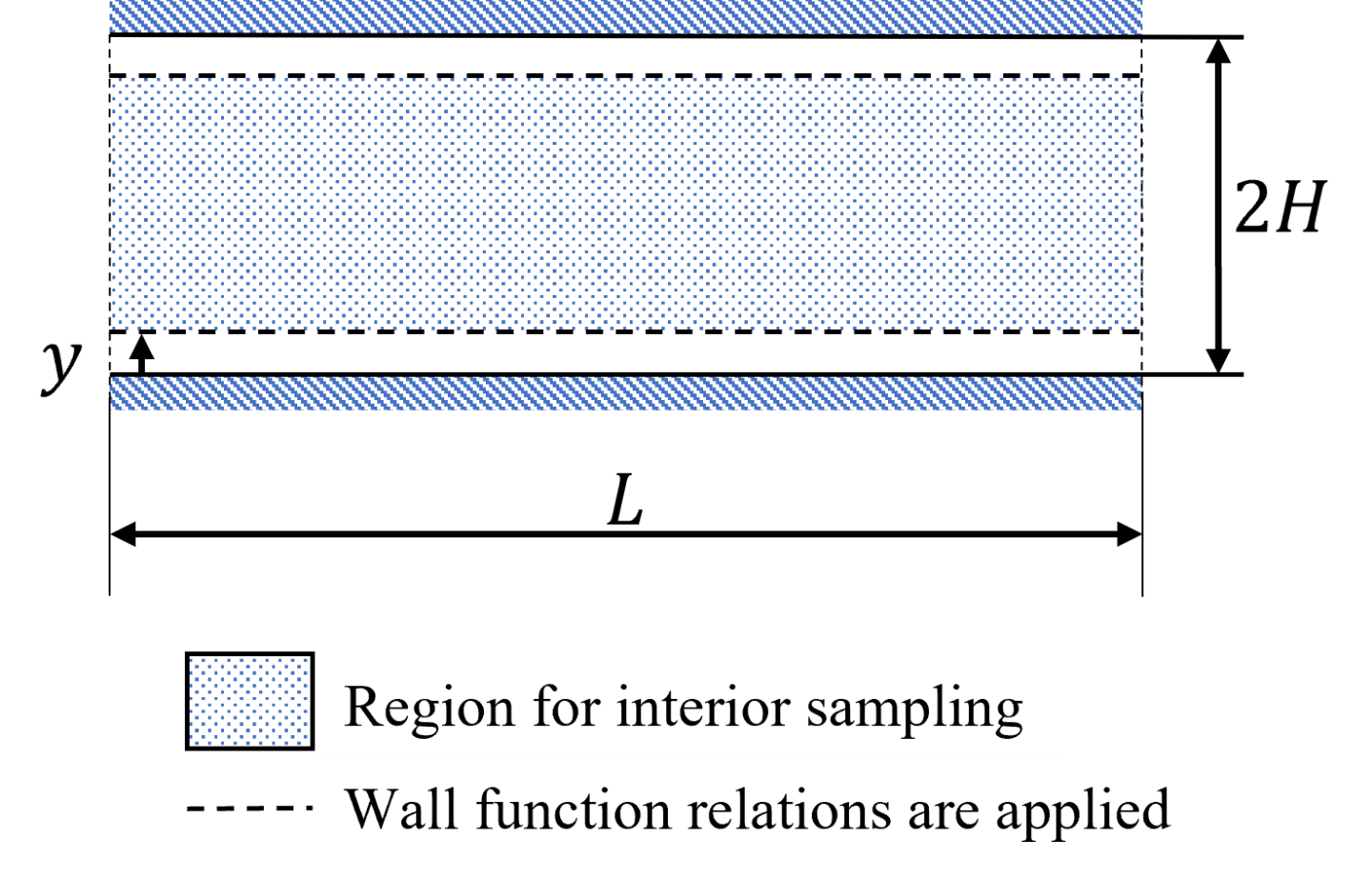
Fig. 135 Sampling for interior and wall function points
Not all of the important equations used in the formulation are presented here. For a more detailed description of the wall functions, see 1 2.
Standard Wall Functions
Assuming the closest point to the wall (\(P\)) is within the logarithmic layer, the tangential velocity can be set as
(200)\[\begin{align}
U &= \frac{u_{\tau}}{\kappa} \ln{(E y^+)}
\end{align}\]
Where, \(\kappa=0.4187\) and \(E=9.793\).
Here, since the \(U\) and \(u_{\tau}\) are related implicitly, you can use a lookup table approach to solve for \(u_{\tau}\) given \(U\) and the wall distance \(y\). This approach is similar to the one discussed here 4.
The \(k\) and \(\varepsilon\) can be set using the below relations
(201)\[\begin{split}\begin{align}
k &= \frac{u_{\tau}^2}{\sqrt{C_{\mu}}} \\
\varepsilon &= \frac{C_{\mu} ^ {3 / 4} k ^ {3 / 2}}{\kappa y}
\end{align}\end{split}\]
The total shear stress \(\tau\) is the sum of laminar and turbulent shear stresses, i.e. \(\tau=\tau_l+\tau_t\). At the wall, the laminar shear dominates and turbulent shear stress drops to zero, while in the log layer, the turbulent shear stress dominates. For setting the shear stress appropriately, it is assumed that the total shear stress at wall is equal to the turbulent shear stress in the log layer. For \(y^+\) values closer to 30, this assumption does not lead to large inaccuracies. 3 1
Therefore, the wall friction can be set using the log-law assumption and the approximation above as shown here:
(202)\[\tau_w \equiv \mu \frac{\partial U}{\partial y} \Bigg|_{w} \approx (\mu + \mu_t) \frac{\partial U}{\partial y} \Bigg|_{P} = \frac{\nho u_{\tau}U \kappa}{\ln{(E y^+)}}\]
Launder Spalding Wall Functions
The relations for Launder-Spalding wall functions formulation are similar to standard one, except now the friction velocity can directly be computed from the turbulent kinetic energy as shown below:
(203)\[\begin{split}\begin{align}
u_{\tau} &= C_{\mu} ^ {1 / 4} k ^ {1 / 2} \\
U &= \frac{C_{\mu} ^ {1 / 4} k ^ {1 / 2}}{\kappa} \ln{(E y^+)}
\end{align}\end{split}\]
With this formulation, it was found that an explicit boundary condition for \(k\) is not required as the log-law, relation for \(\varepsilon\) and \(\tau_w\) are sufficient to define all the variables at point \(P\).
(204)\[\begin{split}\begin{align}
\varepsilon &= \frac{C_{\mu} ^ {3 / 4} k ^ {3 / 2}}{\kappa y} \\
\tau_w \equiv \mu \frac{\partial U}{\partial y} \Bigg|_{w} \approx (\mu + \mu_t) \frac{\partial U}{\partial y} \Bigg|_{P} &= \frac{\nho C_{\mu} ^ {1 / 4} k ^ {1 / 2} U \kappa}{\ln{(E y^+)}}
\end{align}\end{split}\]
The python code for this problem can be found in the directory examples/turbulent_channel/.
The equations are symbolically defined using the custom PDEs (for details on setting up custom PDEs in Modulus, please see 1D Wave Equation). For these problems, the convergence behavior is greatly influenced by the initialization of the network. Therefore, this example starts by training the network to predict constant profiles for turbulent flow quantities and then slowly ramps up the equation losses while ramping down the initialization losses. To do this, a Custom Aggregator is defined.
For the Standard wall function approach, the equation (200) needs to be satisfied exactly. So, train a neural network that can lookup values of \(u_{\tau}\). This is done by solving the log law for a range of \(u\) and \(y\) values and using a Newton-Raphson method to find the zeros. Once you have the table ready, you can train a network to assimilate these values.
Now let’s walk through each of the sections one by one.
This code shows the script to generate the lookup table and assimilate the values in a neural network.
import torch
import numpy as np
from sympy import Symbol, Eq, sin, cos, Min, Max, Abs, log, exp
from scipy import optimize
import modulus
from modulus.hydra import to_absolute_path, instantiate_arch, ModulusConfig
from modulus.solver import Solver
from modulus.domain import Domain
from modulus.utils.io import csv_to_dict
from modulus.domain.constraint import (
PointwiseBoundaryConstraint,
PointwiseInteriorConstraint,
IntegralBoundaryConstraint,
PointwiseConstraint,
)
from modulus.domain.monitor import PointwiseMonitor
from modulus.domain.inferencer import PointwiseInferencer
from modulus.domain.validator import PointwiseValidator
from modulus.key import Key
from modulus.node import Node
@modulus.main(config_path="conf_u_tau_lookup", config_name="config")
def run(cfg: ModulusConfig) -> None:
u = np.linspace(1e-3, 50, num=100)
y = np.linspace(1e-3, 0.5, num=100)
U, Y = np.meshgrid(u, y)
U = np.reshape(U, (U.size,))
Y = np.reshape(Y, (Y.size,))
Re = 590
nu = 1 / Re
def f(u_tau, y, u):
return u_tau * np.log(9.793 * y * u_tau / nu) - u * 0.4187
def fprime(u_tau, y, u):
return 1 + np.log(9.793 * y * u_tau / nu)
u_tau = []
for i in range(len(U)):
u_tau_calc = optimize.newton(
f,
1.0,
fprime=fprime,
args=(Y[i], U[i]),
tol=1.48e-08,
maxiter=200,
fprime2=None,
)
u_tau.append(u_tau_calc)
# save tabulations to a csv file
results = np.concatenate(
(
np.reshape(U, (len(U), 1)),
np.reshape(Y, (len(Y), 1)),
np.reshape(u_tau, (len(u_tau), 1)),
),
axis=1,
)
np.savetxt("u_tau.csv", results, delimiter=",")
invar = {"u_in": np.reshape(U, (len(U), 1)), "y_in": np.reshape(Y, (len(Y), 1))}
outvar = {"u_tau_out": np.reshape(u_tau, (len(u_tau), 1))}
u = np.random.uniform(1e-3, 50, size=100)
y = np.random.uniform(1e-3, 0.5, size=100)
U, Y = np.meshgrid(u, y)
U = np.reshape(U, (U.size,))
Y = np.reshape(Y, (Y.size,))
u_tau_val = []
for i in range(len(U)):
u_tau_calc = optimize.newton(
f,
1.0,
fprime=fprime,
args=(Y[i], U[i]),
tol=1.48e-08,
maxiter=200,
fprime2=None,
)
u_tau_val.append(u_tau_calc)
# save tabulations to a csv file
results = np.concatenate(
(
np.reshape(U, (len(U), 1)),
np.reshape(Y, (len(Y), 1)),
np.reshape(u_tau, (len(u_tau), 1)),
),
axis=1,
)
np.savetxt("u_tau_val.csv", results, delimiter=",")
invar_val = {"u_in": np.reshape(U, (len(U), 1)), "y_in": np.reshape(Y, (len(Y), 1))}
outvar_val = {"u_tau_out": np.reshape(u_tau_val, (len(u_tau_val), 1))}
# make list of nodes to unroll graph on
u_tau_net = instantiate_arch(
input_keys=[Key("u_in"), Key("y_in")],
output_keys=[Key("u_tau_out")],
cfg=cfg.arch.fully_connected,
)
nodes = [u_tau_net.make_node(name="u_tau_network")]
# make domain
domain = Domain()
train = PointwiseConstraint.from_numpy(
nodes=nodes,
invar=invar,
outvar=outvar,
batch_size=10000,
)
domain.add_constraint(train, "LogLawLoss")
# add validation
validator = PointwiseValidator(nodes=nodes, invar=invar_val, true_outvar=outvar_val)
domain.add_validator(validator)
# make solver
slv = Solver(cfg, domain)
# start solver
slv.solve()
if __name__ == "__main__":
run()
The code below shows the definition of custom PDEs. Define separate PDEs for the initialization losses, equation losses and wall function losses. For this, use the initialization strategy that is used for CFD problems discussed here .
"""Equations related to Navier Stokes Equations
"""
from sympy import Symbol, Function, Number, log, Abs, simplify
from modulus.eq.pde import PDE
from modulus.node import Node
class kEpsilonInit(PDE):
def __init__(self, nu=1, rho=1):
# set params
nu = Number(nu)
rho = Number(rho)
# coordinates
x = Symbol("x")
y = Symbol("y")
# make input variables
input_variables = {"x": x, "y": y}
# velocity componets
u = Function("u")(*input_variables)
v = Function("v")(*input_variables)
p = Function("p")(*input_variables)
k = Function("k")(*input_variables)
ep = Function("ep")(*input_variables)
# flow initialization
C_mu = 0.09
u_avg = 21 # Approx average velocity
Re_d = (
u_avg * 1 / nu
) # Reynolds number based on centerline and channel hydraulic dia
l = 0.038 * 2 # Approx turbulent length scale
I = 0.16 * Re_d ** (
-1 / 8
) # Turbulent intensity for a fully developed pipe flow
u_init = u_avg
v_init = 0
p_init = 0
k_init = 1.5 * (u_avg * I) ** 2
ep_init = (C_mu ** (3 / 4)) * (k_init ** (3 / 2)) / l
# set equations
self.equations = {}
self.equations["u_init"] = u - u_init
self.equations["v_init"] = v - v_init
self.equations["p_init"] = p - p_init
self.equations["k_init"] = k - k_init
self.equations["ep_init"] = ep - ep_init
class kEpsilon(PDE):
def __init__(self, nu=1, rho=1):
# set params
nu = Number(nu)
rho = Number(rho)
# coordinates
x = Symbol("x")
y = Symbol("y")
# make input variables
input_variables = {"x": x, "y": y}
# velocity componets
u = Function("u")(*input_variables)
v = Function("v")(*input_variables)
p = Function("p")(*input_variables)
k = Function("k")(*input_variables)
ep = Function("ep")(*input_variables)
# Model constants
sig_k = 1.0
sig_ep = 1.3
C_ep1 = 1.44
C_ep2 = 1.92
C_mu = 0.09
E = 9.793
# Turbulent Viscosity
nu_t = C_mu * (k ** 2) / (ep + 1e-4)
# Turbulent Production Term
P_k = nu_t * (
2 * (u.diff(x)) ** 2
+ 2 * (v.diff(y)) ** 2
+ (u.diff(y)) ** 2
+ (v.diff(x)) ** 2
+ 2 * u.diff(y) * v.diff(x)
)
# set equations
self.equations = {}
self.equations["continuity"] = simplify(u.diff(x) + v.diff(y))
self.equations["momentum_x"] = simplify(
u * u.diff(x)
+ v * u.diff(y)
+ p.diff(x)
- ((nu + nu_t) * u.diff(x)).diff(x)
- ((nu + nu_t) * u.diff(y)).diff(y)
)
self.equations["momentum_y"] = simplify(
u * v.diff(x)
+ v * v.diff(y)
+ p.diff(y)
- ((nu + nu_t) * v.diff(x)).diff(x)
- ((nu + nu_t) * v.diff(y)).diff(y)
)
self.equations["k_equation"] = simplify(
u * k.diff(x)
+ v * k.diff(y)
- ((nu + nu_t / sig_k) * k.diff(x)).diff(x)
- ((nu + nu_t / sig_k) * k.diff(y)).diff(y)
- P_k
+ ep
)
self.equations["ep_equation"] = simplify(
u * ep.diff(x)
+ v * ep.diff(y)
- ((nu + nu_t / sig_ep) * ep.diff(x)).diff(x)
- ((nu + nu_t / sig_ep) * ep.diff(y)).diff(y)
- (C_ep1 * P_k - C_ep2 * ep) * ep / (k + 1e-3)
)
class kEpsilonStdWF(PDE):
def __init__(self, nu=1, rho=1):
# set params
nu = Number(nu)
rho = Number(rho)
# coordinates
x = Symbol("x")
y = Symbol("y")
# make input variables
input_variables = {"x": x, "y": y}
# velocity componets
u = Function("u")(*input_variables)
v = Function("v")(*input_variables)
k = Function("k")(*input_variables)
ep = Function("ep")(*input_variables)
# normals
normal_x = -1 * Symbol(
"normal_x"
) # Multiply by -1 to flip the direction of normal
normal_y = -1 * Symbol(
"normal_y"
) # Multiply by -1 to flip the direction of normal
# wall distance
normal_distance = Function("normal_distance")(*input_variables)
# Model constants
C_mu = 0.09
E = 9.793
C_k = -0.36
B_k = 8.15
karman_constant = 0.4187
# Turbulent Viscosity
nu_t = C_mu * (k ** 2) / (ep + 1e-4)
u_tau = Function("u_tau")(*input_variables)
y_plus = u_tau * normal_distance / nu
u_plus = log(Abs(E * y_plus)) / karman_constant
ep_true = (C_mu ** (3 / 4)) * (k ** (3 / 2)) / karman_constant / normal_distance
u_parallel_to_wall = [
u - (u * normal_x + v * normal_y) * normal_x,
v - (u * normal_x + v * normal_y) * normal_y,
]
du_parallel_to_wall_dx = [
u.diff(x) - (u.diff(x) * normal_x + v.diff(x) * normal_y) * normal_x,
v.diff(x) - (u.diff(x) * normal_x + v.diff(x) * normal_y) * normal_y,
]
du_parallel_to_wall_dy = [
u.diff(y) - (u.diff(y) * normal_x + v.diff(y) * normal_y) * normal_x,
v.diff(y) - (u.diff(y) * normal_x + v.diff(y) * normal_y) * normal_y,
]
du_dsdf = [
du_parallel_to_wall_dx[0] * normal_x + du_parallel_to_wall_dy[0] * normal_y,
du_parallel_to_wall_dx[1] * normal_x + du_parallel_to_wall_dy[1] * normal_y,
]
wall_shear_stress_true_x = (
u_tau * u_parallel_to_wall[0] * karman_constant / log(Abs(E * y_plus))
)
wall_shear_stress_true_y = (
u_tau * u_parallel_to_wall[1] * karman_constant / log(Abs(E * y_plus))
)
wall_shear_stress_x = (nu + nu_t) * du_dsdf[0]
wall_shear_stress_y = (nu + nu_t) * du_dsdf[1]
u_normal_to_wall = u * normal_x + v * normal_y
u_normal_to_wall_true = 0
u_parallel_to_wall_mag = (
u_parallel_to_wall[0] ** 2 + u_parallel_to_wall[1] ** 2
) ** 0.5
u_parallel_to_wall_true = u_plus * u_tau
# k_normal_gradient = normal_x*k.diff(x) + normal_y*k.diff(y)
# k_normal_gradient_true = 0
k_true = u_tau ** 2 / C_mu ** 0.5
# set equations
self.equations = {}
self.equations["velocity_wall_normal_wf"] = (
u_normal_to_wall - u_normal_to_wall_true
)
self.equations["velocity_wall_parallel_wf"] = (
u_parallel_to_wall_mag - u_parallel_to_wall_true
)
self.equations["k_wf"] = k - k_true
self.equations["ep_wf"] = ep - ep_true
self.equations["wall_shear_stress_x_wf"] = (
wall_shear_stress_x - wall_shear_stress_true_x
)
self.equations["wall_shear_stress_y_wf"] = (
wall_shear_stress_y - wall_shear_stress_true_y
)
Custom Aggregator
The aggregator in Modulus combines different loss terms together to form a global loss that is used by the network during optimization. The default behavior of the aggregator is to sum all the weighted losses. However, this example varies which losses are applied in the begining of the model training (initialization losses) and which ones are applied later (equations and wall function relations). For this, a \(tanh\) function is used to smoothly ramp up and ramp down the different losses. The code for the following is shown here:
# Import libraries
import torch
from torch import nn
from typing import Dict, List
# Import from Modulus
from modulus.eq.derivatives import gradient
from modulus.loss.aggregator import Aggregator
class CustomSum(Aggregator):
"""
Loss aggregation by summation
"""
def __init__(self, params, num_losses, weights=None):
super().__init__(params, num_losses, weights)
def forward(self, losses: Dict[str, torch.Tensor], step: int) -> torch.Tensor:
"""
Aggregates the losses by summation
Parameters
----------
losses : Dict[str, torch.Tensor]
A dictionary of losses
step : int
Optimizer step
Returns
-------
loss : torch.Tensor
Aggregated loss
"""
# weigh losses
losses = self.weigh_losses(losses, self.weights)
# Initialize loss
loss: torch.Tensor = torch.zeros_like(self.init_loss)
smoothness = 0.0005 # use 0.0005 to smoothen the transition over ~10k steps
step_tensor = torch.tensor(step, dtype=torch.float32)
decay_weight = (torch.tanh((20000 - step_tensor) * smoothness) + 1.0) * 0.5
# Add losses
for key in losses.keys():
if "init" not in key:
loss += (1 - decay_weight) * (losses[key])
else:
loss += decay_weight * (losses[key])
return loss
The custom aggregator is then called in the config files under the loss config group as shown here:
defaults:
- modulus_default
- arch:
- fourier
- fully_connected
- optimizer: adam
- scheduler: tf_exponential_lr
- loss: custom-aggregator
- _self_
jit: false
scheduler:
decay_rate: 0.95
decay_steps: 8000
network_dir: "network_checkpoint"
initialization_network_dir: "../u_tau_lookup/network_checkpoint/"
save_filetypes: "vtk,npz"
cuda_graphs: False
optimizer:
lr: 1e-4
training:
rec_validation_freq: 1000
rec_inference_freq: 1000
rec_monitor_freq: 1000
rec_constraint_freq: 1000
max_steps: 400000
batch_size:
wf_pt: 512
interior: 2048
inlet: 256
outlet: 256
interior_init: 2048
Once all the prerequisites are defined, you can start solving the turbulent channel flow. Notice that the config file imports the u_tau_network from a previous tutorial by setting the appropriate initialization directory. Set the optimize
parameter for that network to False so that the weights and biases from that network do not change during the training. Also, to setup the
periodicity in the domain, create symbolic nodes that transform \(x\) to \(sin(x)\) which will become the input to the neural network.
import torch
import numpy as np
from sympy import Symbol, Eq, sin, cos, Min, Max, Abs, log, exp
import modulus
from modulus.hydra import to_absolute_path, instantiate_arch, ModulusConfig
from modulus.solver import Solver
from modulus.domain import Domain
from modulus.geometry.primitives_2d import Rectangle, Line, Channel2D
from modulus.utils.sympy.functions import parabola
from modulus.utils.io import csv_to_dict
from modulus.eq.pdes.navier_stokes import NavierStokes
from modulus.domain.constraint import (
PointwiseBoundaryConstraint,
PointwiseInteriorConstraint,
IntegralBoundaryConstraint,
)
from modulus.domain.monitor import PointwiseMonitor
from modulus.domain.inferencer import PointwiseInferencer
from modulus.key import Key
from modulus.node import Node
from custom_k_ep import kEpsilonInit, kEpsilon, kEpsilonStdWF
@modulus.main(config_path="conf_re590_k_ep", config_name="config")
def run(cfg: ModulusConfig) -> None:
# simulation parameters
Re = 590
nu = 1 / Re
y_plus = 30
karman_constant = 0.4187
resolved_y_start = y_plus * nu
channel_width = (-1, 1)
channel_length = (-np.pi / 2, np.pi / 2)
inlet = Line(
(channel_length[0], channel_width[0]),
(channel_length[0], channel_width[1]),
normal=1,
)
outlet = Line(
(channel_length[1], channel_width[0]),
(channel_length[1], channel_width[1]),
normal=1,
)
geo_sdf = Channel2D(
(channel_length[0], channel_width[0]), (channel_length[1], channel_width[1])
)
# geometry where the equations are solved
geo_resolved = Channel2D(
(channel_length[0], channel_width[0] + resolved_y_start),
(channel_length[1], channel_width[1] - resolved_y_start),
)
# make list of nodes to unroll graph on
init = kEpsilonInit(nu=nu, rho=1.0)
eq = kEpsilon(nu=nu, rho=1.0)
wf = kEpsilonStdWF(nu=nu, rho=1.0)
u_tau_net = instantiate_arch(
input_keys=[Key("u_in"), Key("y_in")],
output_keys=[Key("u_tau_out")],
cfg=cfg.arch.fully_connected,
)
flow_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("u"), Key("v")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
p_net = instantiate_arch(
input_keys=[Key("x"), Key("y")],
output_keys=[Key("p")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
k_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("k_star")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
ep_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("ep_star")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
nodes = (
init.make_nodes()
+ eq.make_nodes()
+ wf.make_nodes()
+ [
Node.from_sympy(
sin(2 * np.pi * Symbol("x") / (channel_length[1] - channel_length[0])),
"x_sin",
)
]
+ [Node.from_sympy(Min(log(1 + exp(Symbol("k_star"))) + 1e-4, 20), "k")]
+ [Node.from_sympy(Min(log(1 + exp(Symbol("ep_star"))) + 1e-4, 180), "ep")]
+ [flow_net.make_node(name="flow_network")]
+ [p_net.make_node(name="p_network")]
+ [k_net.make_node(name="k_network")]
+ [ep_net.make_node(name="ep_network")]
)
nodes_u_tau = (
[Node.from_sympy(Symbol("normal_distance"), "y_in")]
+ [
Node.from_sympy(
(
(
Symbol("u")
- (
Symbol("u") * (-Symbol("normal_x"))
+ Symbol("v") * (-Symbol("normal_y"))
)
* (-Symbol("normal_x"))
)
** 2
+ (
Symbol("v")
- (
Symbol("u") * (-Symbol("normal_x"))
+ Symbol("v") * (-Symbol("normal_y"))
)
* (-Symbol("normal_y"))
)
** 2
)
** 0.5,
"u_parallel_to_wall",
)
]
+ [Node.from_sympy(Symbol("u_parallel_to_wall"), "u_in")]
+ [Node.from_sympy(Symbol("u_tau_out"), "u_tau")]
+ [u_tau_net.make_node(name="u_tau_network", optimize=False)]
)
# add constraints to solver
p_grad = 1.0
x, y = Symbol("x"), Symbol("y")
# make domain
domain = Domain()
# Point where wall funciton is applied
wf_pt = PointwiseBoundaryConstraint(
nodes=nodes + nodes_u_tau,
geometry=geo_resolved,
outvar={
"velocity_wall_normal_wf": 0,
"velocity_wall_parallel_wf": 0,
"ep_wf": 0,
"k_wf": 0,
"wall_shear_stress_x_wf": 0,
"wall_shear_stress_y_wf": 0,
},
lambda_weighting={
"velocity_wall_normal_wf": 100,
"velocity_wall_parallel_wf": 100,
"ep_wf": 1,
"k_wf": 1,
"wall_shear_stress_x_wf": 100,
"wall_shear_stress_y_wf": 100,
},
batch_size=cfg.batch_size.wf_pt,
parameterization={"normal_distance": resolved_y_start},
)
domain.add_constraint(wf_pt, "WF")
# interior
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=geo_resolved,
outvar={
"continuity": 0,
"momentum_x": 0,
"momentum_y": 0,
"k_equation": 0,
"ep_equation": 0,
},
lambda_weighting={
"continuity": 100,
"momentum_x": 1000,
"momentum_y": 1000,
"k_equation": 10,
"ep_equation": 1,
},
batch_size=cfg.batch_size.interior,
bounds={x: channel_length, y: channel_width},
)
domain.add_constraint(interior, "Interior")
# pressure pc
inlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=inlet,
outvar={"p": p_grad * (channel_length[1] - channel_length[0])},
lambda_weighting={"p": 10},
batch_size=cfg.batch_size.inlet,
)
domain.add_constraint(inlet, "Inlet")
# pressure pc
outlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=outlet,
outvar={"p": 0},
lambda_weighting={"p": 10},
batch_size=cfg.batch_size.outlet,
)
domain.add_constraint(outlet, "Outlet")
# flow initialization
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=geo_resolved,
outvar={"u_init": 0, "v_init": 0, "k_init": 0, "p_init": 0, "ep_init": 0},
batch_size=cfg.batch_size.interior_init,
bounds={x: channel_length, y: channel_width},
)
domain.add_constraint(interior, "InteriorInit")
# add inferencing and monitor
invar_wf_pt = geo_resolved.sample_boundary(1024, parameterization={"normal_distance": resolved_y_start})
u_tau_monitor = PointwiseMonitor(
invar_wf_pt,
output_names=["u_tau"],
metrics={"mean_u_tau": lambda var: torch.mean(var["u_tau"])},
nodes=nodes + nodes_u_tau,
)
domain.add_monitor(u_tau_monitor)
# add inferencer data
inference = PointwiseInferencer(
nodes=nodes,
invar=geo_resolved.sample_interior(
5000, bounds={x: channel_length, y: channel_width}
),
output_names=["u", "v", "p", "k", "ep"],
)
domain.add_inferencer(inference, "inf_interior")
inference = PointwiseInferencer(
nodes=nodes + nodes_u_tau,
invar=geo_resolved.sample_boundary(10, parameterization={"normal_distance": resolved_y_start}),
output_names=["u", "v", "p", "k", "ep", "normal_distance", "u_tau"],
)
domain.add_inferencer(inference, "inf_wf")
# make solver
slv = Solver(cfg, domain)
# start solver
slv.solve()
if __name__ == "__main__":
run()
The case setup for this problem is very similar to the earlier one, except now that you can avoid training of the lookup network as the \(u_{\tau}\) is explicitly defined using the turbulent
kinetic energy. The process to define the custom PDEs is similar as before. The custom PDEs for the Launder Spalding wall functions can be found in examples/turbulent_channel/2d/custom_k_ep_ls.py
Use the same custom aggregator you defined earlier as a similar initialization strategy will work for this problem as well. Once you have the PDEs and the aggregator defined, you can setup the script to solve the problem as shown below. There is no seperate network for the lookup table and the losses at the wall are different from the standard wall function formulation.
import torch
import numpy as np
from sympy import Symbol, Eq, sin, cos, Min, Max, Abs, log, exp
import modulus
from modulus.hydra import to_absolute_path, instantiate_arch, ModulusConfig
from modulus.solver import Solver
from modulus.domain import Domain
from modulus.geometry.primitives_2d import Rectangle, Line, Channel2D
from modulus.eq.pdes.navier_stokes import NavierStokes
from modulus.domain.constraint import (
PointwiseBoundaryConstraint,
PointwiseInteriorConstraint,
IntegralBoundaryConstraint,
)
from modulus.domain.monitor import PointwiseMonitor
from modulus.domain.inferencer import PointwiseInferencer
from modulus.key import Key
from modulus.node import Node
from custom_k_ep_ls import kEpsilonInit, kEpsilon, kEpsilonLSWF
@modulus.main(config_path="conf_re590_k_ep_LS", config_name="config")
def run(cfg: ModulusConfig) -> None:
# simulation parameters
Re = 590
nu = 1 / Re
y_plus = 30
karman_constant = 0.4187
resolved_y_start = y_plus * nu
channel_width = (-1, 1)
channel_length = (-np.pi / 2, np.pi / 2)
inlet = Line(
(channel_length[0], channel_width[0]),
(channel_length[0], channel_width[1]),
normal=1,
)
outlet = Line(
(channel_length[1], channel_width[0]),
(channel_length[1], channel_width[1]),
normal=1,
)
geo_sdf = Channel2D(
(channel_length[0], channel_width[0]), (channel_length[1], channel_width[1])
)
# geometry where the equations are solved
geo_resolved = Channel2D(
(channel_length[0], channel_width[0] + resolved_y_start),
(channel_length[1], channel_width[1] - resolved_y_start),
)
# make list of nodes to unroll graph on
init = kEpsilonInit(nu=nu, rho=1.0)
eq = kEpsilon(nu=nu, rho=1.0)
wf = kEpsilonLSWF(nu=nu, rho=1.0)
flow_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("u"), Key("v")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
p_net = instantiate_arch(
input_keys=[Key("x"), Key("y")],
output_keys=[Key("p")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
k_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("k_star")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
ep_net = instantiate_arch(
input_keys=[Key("x_sin"), Key("y")],
output_keys=[Key("ep_star")],
frequencies=("axis", [i / 2 for i in range(8)]),
frequencies_params=("axis", [i / 2 for i in range(8)]),
cfg=cfg.arch.fourier,
)
nodes = (
init.make_nodes()
+ eq.make_nodes()
+ wf.make_nodes()
+ [
Node.from_sympy(
sin(2 * np.pi * Symbol("x") / (channel_length[1] - channel_length[0])),
"x_sin",
)
]
+ [Node.from_sympy(Min(log(1 + exp(Symbol("k_star"))) + 1e-4, 20), "k")]
+ [Node.from_sympy(Min(log(1 + exp(Symbol("ep_star"))) + 1e-4, 180), "ep")]
+ [flow_net.make_node(name="flow_network")]
+ [p_net.make_node(name="p_network")]
+ [k_net.make_node(name="k_network")]
+ [ep_net.make_node(name="ep_network")]
)
# add constraints to solver
p_grad = 1.0
x, y = Symbol("x"), Symbol("y")
# make domain
domain = Domain()
# Point where wall funciton is applied
wf_pt = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=geo_resolved,
outvar={
"velocity_wall_normal_wf": 0,
"velocity_wall_parallel_wf": 0,
"ep_wf": 0,
"wall_shear_stress_x_wf": 0,
"wall_shear_stress_y_wf": 0,
},
lambda_weighting={
"velocity_wall_normal_wf": 100,
"velocity_wall_parallel_wf": 100,
"ep_wf": 1,
"wall_shear_stress_x_wf": 100,
"wall_shear_stress_y_wf": 100,
},
batch_size=cfg.batch_size.wf_pt,
parameterization={"normal_distance": resolved_y_start},
)
domain.add_constraint(wf_pt, "WF")
# interior
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=geo_resolved,
outvar={
"continuity": 0,
"momentum_x": 0,
"momentum_y": 0,
"k_equation": 0,
"ep_equation": 0,
},
lambda_weighting={
"continuity": 100,
"momentum_x": 1000,
"momentum_y": 1000,
"k_equation": 10,
"ep_equation": 1,
},
batch_size=cfg.batch_size.interior,
bounds={x: channel_length, y: channel_width},
)
domain.add_constraint(interior, "Interior")
# pressure pc
inlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=inlet,
outvar={"p": p_grad * (channel_length[1] - channel_length[0])},
lambda_weighting={"p": 10},
batch_size=cfg.batch_size.inlet,
)
domain.add_constraint(inlet, "Inlet")
# pressure pc
outlet = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=outlet,
outvar={"p": 0},
lambda_weighting={"p": 10},
batch_size=cfg.batch_size.outlet,
)
domain.add_constraint(outlet, "Outlet")
# flow initialization
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=geo_resolved,
outvar={"u_init": 0, "v_init": 0, "k_init": 0, "p_init": 0, "ep_init": 0},
batch_size=cfg.batch_size.interior_init,
bounds={x: channel_length, y: channel_width},
)
domain.add_constraint(interior, "InteriorInit")
# add inferencing and monitor
invar_wf_pt = geo_resolved.sample_boundary(
1024,
)
u_tau_monitor = PointwiseMonitor(
invar_wf_pt,
output_names=["k"],
metrics={
"mean_u_tau": lambda var: torch.mean((0.09 ** 0.25) * torch.sqrt(var["k"]))
},
nodes=nodes,
)
domain.add_monitor(u_tau_monitor)
# add inferencer data
inference = PointwiseInferencer(
nodes=nodes,
invar=geo_resolved.sample_interior(
5000, bounds={x: channel_length, y: channel_width}
),
output_names=["u", "v", "p", "k", "ep"],
)
domain.add_inferencer(inference, "inf_interior")
inference = PointwiseInferencer(
nodes=nodes,
invar=geo_resolved.sample_boundary(10, parameterization={"normal_distance": resolved_y_start}),
output_names=["u", "v", "p", "k", "ep", "normal_distance"],
)
domain.add_inferencer(inference, "inf_wf")
# make solver
slv = Solver(cfg, domain)
# start solver
slv.solve()
if __name__ == "__main__":
run()
The Modulus results are shown in the figure below along with the DNS data 3 and Solver data 5. Observe that the the nondimensionalized velocity and turbulent kinetic energy profiles match very well with the DNS and solver data. Also, the k-omega models are able to predict the friction velocity with better accuracy when compared to the k-epsilon models.
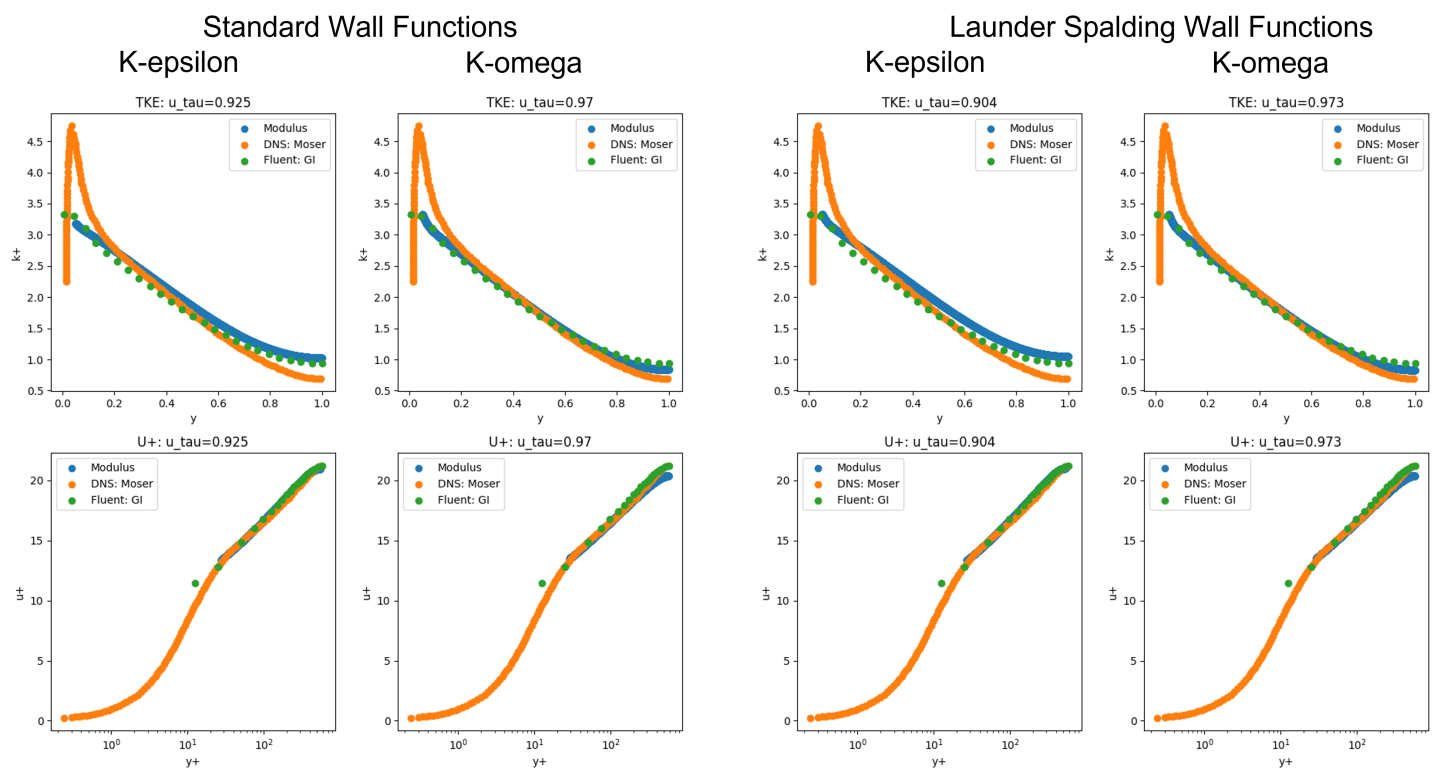
Fig. 136 Turbulent channel flow results
The scripts for generating the plots shown above as well as the scripts for k-omega models can be found the the examples directory at examples/turbulent_channel/.
References
Bredberg, Jonas. “On the wall boundary condition for turbulence models.” Chalmers University of Technology, Department of Thermo and Fluid Dynamics. Internal Report 00/4. G oteborg (2000): 8-16.
Lacasse, David, Eric Turgeon, and Dominique Pelletier. “On the judicious use of the k–ε model, wall functions and adaptivity.” International Journal of Thermal Sciences 43.10 (2004): 925-938.
Moser, Robert D., John Kim, and Nagi N. Mansour. “Direct numerical simulation of turbulent channel flow up to Re τ= 590.” Physics of fluids 11.4 (1999): 943-945.
Kalitzin, Georgi, et al. “Near-wall behavior of RANS turbulence models and implications for wall functions.” Journal of Computational Physics 204.1 (2005): 265-291.
Gianluca Iaccarino Lecture handouts: Computational Methods in Fluid Dynamics using commercial CFD codes. https://web.stanford.edu/class/me469b/handouts/turbulence.pdf