2D Seismic Wave Propagation
This tutorial extends the previous 1D wave equation example and solve a 2D seismic wave propagation problem commonly used in seismic surveying. In this tutorial, you will learn the following:
How to solve a 2D time-dependent problem in Modulus
How to define an open boundary condition using custom equations
How to present a variable velocity model as an additional network
This tutorial assumes that you have completed the Introductory Example tutorial on Lid Driven Cavity flow and have familiarized yourself with the basics of Modulus. Also, see the 1D Wave Equation tutorial for more information on defining new differential equations, and solving time-dependent problems in Modulus.
The acoustic wave equation for the square slowness, defined as \(m=1/c^2\) where \(c\) is the speed of sound (velocity) of a given physical medium with constant density, and a source \(q\) is given by:
(140)\[u_{tt} = c^2u_{xx} + c^2u_{yy} + q \quad \mbox{ in } \Omega\]
Where \(u(\mathbf{x},t)\) represents the pressure response (known as the “wavefield”) at location vector \(\mathbf{x}\) and time \(t\) in an acoustic medium. Despite its linearity, the wave equation is notoriously challenging to solve in complex media, because the dynamics of the wavefield at the interfaces of the media can be highly complex, with multiple types of waves with large range of amplitudes and frequencies interfering simultaneously.
In this tutorial, you will solve the 2D acoustic wave equation with a single Ricker Source in a layered velocity model, 1.0 \(km/s\) at the top layer and 2.0 \(km/s\) the bottom (Fig. 60). Sources in seismic surveys are positioned at a single or a few physical locations where artificial pressure is injected into the domain you want to model. In the case of land survey, it is usually dynamite blowing up at a given location, or a vibroseis (a vibrating plate generating continuous sound waves). For a marine survey, the source is an air gun sending a bubble of compressed air into the water that will expand and generate a seismic wave.
This problem, uses a domain size 2 \(km\) x 2 \(km\), and a single source is located at the center of the domain. The source signature is modelled using a Ricker wavelet, illustrated in Fig. 61, with a peak wavelet frequency of \(f_0=15 Hz\).
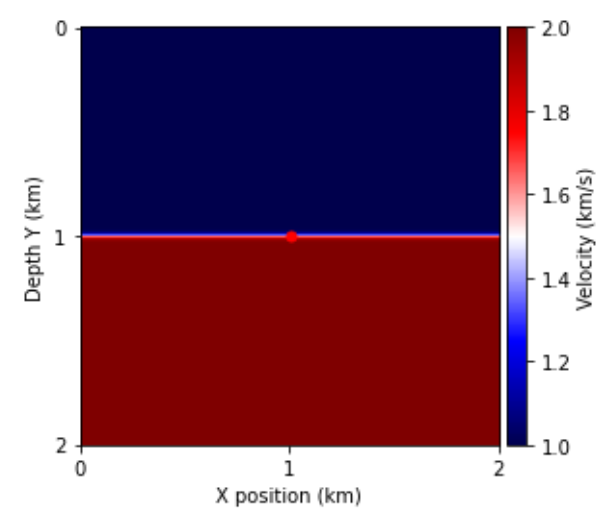
Fig. 60 Velocity model of the medium

Fig. 61 Ricker source signature
The problem uses wavefield data at time steps (150 \(ms\) - 300 \(ms\)) generated from finite difference simulations, using Devito, as constraints for the temporal boundary conditions, and train Modulus to produce wavefields at later time steps (300 \(ms\) – 1000 \(ms\)).
The setup for this problem is similar to tutorial 1D Wave Equation. So, only the main highlights of this problem is discussed here.
The full python script for this problem can be found at examples/seismic_wave/wave_2d.py
A second-order PDE requires strict BC on both the initial wavefield and its derivatives for its solution to be unique. In the field, the seismic wave propagates in every direction to an “infinite” distance. In the finite computational domain, Absorbing BC (ABC) or Perfectly Matched Layers (PML) are artificial boundary conditions that are typically applied to approximate an infinite media by damping and absorbing the waves at the edges of the domain, in order to avoid reflections from the boundary. However, a NN solver is meshless – it is not suitable to implement ABC or PML. To enable a wave to leave the computational domain and travel undisturbed through the boundaries, you can apply an open boundary condition, also called a radiation condition, which imposes the first-order PDEs at the boundaries:
(141)\[\begin{split}\begin{split}
\frac{\partial u}{\partial t} - c\frac{\partial u}{\partial x} &= 0,\quad \mbox{ at } x = 0 \\
\frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} &= 0,\quad \mbox{ at } x = dLen \\
\frac{\partial u}{\partial t} - c\frac{\partial u}{\partial y} &= 0,\quad \mbox{ at } y = 0 \\
\frac{\partial u}{\partial t} + c\frac{\partial u}{\partial y} &= 0,\quad \mbox{ at } y = dLen \\
\end{split}\end{split}\]
Previous tutorials have described how to define custom PDEs. Similarly
here you create a class OpenBoundary that inherits from PDES:
# define open boundary conditions
class OpenBoundary(PDE):
"""
Open boundary condition for wave problems
Ref: http://hplgit.github.io/wavebc/doc/pub/._wavebc_cyborg002.html
Parameters
==========
u : str
The dependent variable.
c : float, Sympy Symbol/Expr, str
Wave speed coefficient. If `c` is a str then it is
converted to Sympy Function of form 'c(x,y,z,t)'.
If 'c' is a Sympy Symbol or Expression then this
is substituted into the equation.
dim : int
Dimension of the wave equation (1, 2, or 3). Default is 2.
time : bool
If time-dependent equations or not. Default is True.
"""
name = "OpenBoundary"
def __init__(self, u="u", c="c", dim=3, time=True):
# set params
self.u = u
self.dim = dim
self.time = time
# coordinates
x, y, z = Symbol("x"), Symbol("y"), Symbol("z")
# normal
normal_x, normal_y, normal_z = (
Symbol("normal_x"),
Symbol("normal_y"),
Symbol("normal_z"),
)
# time
t = Symbol("t")
# make input variables
input_variables = {"x": x, "y": y, "z": z, "t": t}
if self.dim == 1:
input_variables.pop("y")
input_variables.pop("z")
elif self.dim == 2:
input_variables.pop("z")
if not self.time:
input_variables.pop("t")
# Scalar function
assert type(u) == str, "u needs to be string"
u = Function(u)(*input_variables)
# wave speed coefficient
if type(c) is str:
c = Function(c)(*input_variables)
elif type(c) in [float, int]:
c = Number(c)
# set equations
self.equations = {}
self.equations["open_boundary"] = (
u.diff(t)
+ normal_x * c * u.diff(x)
+ normal_y * c * u.diff(y)
+ normal_z * c * u.diff(z)
)
In the 1D Wave Equation tutorial, the velocity (\(c\)) of the physical medium is constant. In this problem, you have a velocity model that varies with locations \(x\). Use a \(tanh\) function form to represent the velocity \(c\) as a function of \(x\) and \(y\):
A \(tanh\) function was used to avoid the sharp discontinuity at the interface. Such smoothing of sharp boundaries helps the convergence of the Neural network solver.
# define target velocity model
# 2.0 km/s at the bottom and 1.0 km/s at the top using tanh function
mesh_x, mesh_y = np.meshgrid(
np.linspace(0, 2, 512), np.linspace(0, 2, 512), indexing="ij"
)
wave_speed_invar = {}
wave_speed_invar["x"] = np.expand_dims(mesh_x.flatten(), axis=-1)
wave_speed_invar["y"] = np.expand_dims(mesh_y.flatten(), axis=-1)
wave_speed_outvar = {}
wave_speed_outvar["c"] = np.tanh(80 * (wave_speed_invar["y"] - 1.0)) / 2 + 1.5
First, define the Modulus PDE and NN nodes for this problem:
# define networks and nodes
wave_net = instantiate_arch(
input_keys=[Key("x"), Key("y"), Key("t")],
output_keys=[Key("u")],
cfg=cfg.arch.fully_connected,
)
speed_net = instantiate_arch(
input_keys=[Key("x"), Key("y")],
output_keys=[Key("c")],
cfg=cfg.arch.fully_connected,
)
nodes = (
we.make_nodes(detach_names=["c"])
+ ob.make_nodes(detach_names=["c"])
+ [
wave_net.make_node(name="wave_network"),
speed_net.make_node(name="speed_network"),
]
)
The PDE nodes are created using both the OpenBoundary PDE defined above and the WaveEquation PDE defined within Modulus. Since this is a time-dependent problem, use the time=True arguments.
Here two neural network nodes are defined where wave_net is used to learn the solution to the wave equation and speed_net is used to learn the velocity model given the training data (wave_speed_invar and wave_speed_outvar) defined above.
The 2D geometry of the computational domain as well as the time range of the solution is defined:
# define geometry
dLen = 2 # km
rec = Rectangle((0, 0), (dLen, dLen))
# define sympy domain variables
x, y, t = Symbol("x"), Symbol("y"), Symbol("t")
# define time range
time_length = 1
time_range = {t: (0.15, time_length)}
A total of four different constraints is sufficient to define this problem. The first constraint is a simple supervised constraint which matches the velocity model to the training data above. The second is another supervised constraint, constraining the wavefield solution to match the numerical wavefield generated using Devito at 4 starting time steps. The third constraint ensures the WaveEquation PDE is honoured in the interior of the domain, whilst the fourth constraint ensures the OpenBoundary PDE is honoured along the boundaries of the domain:
# make domain
domain = Domain()
# add velocity constraint
velocity = PointwiseConstraint.from_numpy(
nodes=nodes, invar=wave_speed_invar, outvar=wave_speed_outvar, batch_size=1024
)
domain.add_constraint(velocity, "Velocity")
# add initial timesteps constraints
batch_size = 1024
for i, ms in enumerate(np.linspace(150, 300, 4)):
timestep_invar, timestep_outvar = read_wf_data(ms, dLen)
lambda_weighting = {}
lambda_weighting["u"] = np.full_like(timestep_invar["x"], 10.0 / batch_size)
timestep = PointwiseConstraint.from_numpy(
nodes,
timestep_invar,
timestep_outvar,
batch_size,
lambda_weighting=lambda_weighting,
)
domain.add_constraint(timestep, f"BC{i:04d}")
# add interior constraint
interior = PointwiseInteriorConstraint(
nodes=nodes,
geometry=rec,
outvar={"wave_equation": 0},
batch_size=4096,
bounds={x: (0, dLen), y: (0, dLen)},
lambda_weighting={"wave_equation": 0.0001},
parameterization=time_range,
)
domain.add_constraint(interior, "Interior")
# add open boundary constraint
edges = PointwiseBoundaryConstraint(
nodes=nodes,
geometry=rec,
outvar={"open_boundary": 0},
batch_size=1024,
lambda_weighting={"open_boundary": 0.01 * time_length},
parameterization=time_range,
)
domain.add_constraint(edges, "Edges")
# add validators
for i, ms in enumerate(np.linspace(350, 950, 13)):
val_invar, val_true_outvar = read_wf_data(ms, dLen)
validator = PointwiseValidator(
nodes=nodes,
invar=val_invar,
true_outvar=val_true_outvar,
batch_size=1024,
plotter=WavePlotter(),
)
domain.add_validator(validator, f"VAL_{i:04d}")
validator = PointwiseValidator(
nodes=nodes,
invar=wave_speed_invar,
true_outvar=wave_speed_outvar,
batch_size=1024,
plotter=WavePlotter(),
)
domain.add_validator(validator, "Velocity")
The supervised constraints are added using the PointwiseConstraint.from_numpy(...) constructor.
Finally, you can validate your results using 13 later time steps from Devito, defined within a Modulus validator as shown below.
# add validators
for i, ms in enumerate(np.linspace(350, 950, 13)):
val_invar, val_true_outvar = read_wf_data(ms, dLen)
validator = PointwiseValidator(
nodes=nodes,
invar=val_invar,
true_outvar=val_true_outvar,
batch_size=1024,
plotter=WavePlotter(),
)
domain.add_validator(validator, f"VAL_{i:04d}")
validator = PointwiseValidator(
nodes=nodes,
invar=wave_speed_invar,
true_outvar=wave_speed_outvar,
batch_size=1024,
plotter=WavePlotter(),
)
domain.add_validator(validator, "Velocity")
You can define a custom tensorboard plotter within examples/seismic_wave/wave_2d.py to add validation plots to TensorBoard, see TensorBoard in Modulus for more details on how to do this.
Now that you have defined the model, its constraints and validation data, you can form a solver to train your model. All of the hyperparameters used for the example can be found in the project’s Hydra configuration file.
slv = Solver(cfg, domain)
slv.solve()
The training results can be viewed in TensorBoard. It can be seen that the Modulus results are noticeably better than Devito, predicting the wavefield with much less boundary reflections, especially at later time steps.

Fig. 62 Comparison of Modulus results with Devito solution