Industrial Heat Sink
This tutorial uses Modulus to conduct a thermal simulation of NVIDIA’s NVSwitch heatsink. You will learn:
How to use hFTB algorithm to solve conjugate heat transfer problems
How to build a gPC based Surrogate via Transfer Learning
This tutorial assumes you have completed tutorial Moving Time Window: Taylor Green Vortex Decay as well as the tutorial Conjugate Heat Transfer on conjugate heat transfer.
This tutorial solves the conjugate heat transfer problem of NVIDIA’s NVSwitch heat sink as shown in Fig. 157. Similar to the previous FPGA problem, the heat sink is placed in a channel with inlet velocity similar to its operating conditions. This case differs from the FPGA one, because you will be using the real heat properties for atmospheric air and copper as the heat sink material. Unlike Heat Transfer with High Thermal Conductivity, a hFTB algorithm will be used to handle the large conductivity differences.

Fig. 157 NVSwitch heat sink geometry
Using real heat properties causes an issue on the interface between the solid and fluid because the conductivity is around 4 orders of magnitude different (Air: 0.0261 \(W/m.K\) and Copper: 385 \(W/m.K\)). To remedy this, Modulus has a static conjugate heat transfer approached referred to as heat transfer coefficient forward temperature backward or hFTB 1. This method works by iteratively solving for the heat transfer in the fluid and solid where they are one way coupled. Using the hFTB method, assign Robin boundary conditions on the solid interface and Dirichlet boundaries for the fluid. The simulation starts by giving an initial guess for the solid temperature and uses a hyper parameter \(h\) for the Robin boundary conditions. A description of the algorithm is shown in Fig. 158. A more complete description can be found here 1.

Fig. 158 hFTB algorithm
The case setup for this problem is similar to the FPGA and three fin examples (covered in tutorials Parameterized 3D Heat Sink and FPGA Heat Sink with Laminar Flow) however, this section shows construction of multiple train domains to implement the hFTB method.
The python script for this problem can be found at examples/limerock/limerock_hFTB.
Defining Domain
This case setup skips over several sections of the code and
only focuses on the portions related to the hFTB algorithm. You should
be familiar with how to set up the flow simulation from
previous tutorials. Geometry construction is not discussed in detail as well
and all relevant information can be found in examples/limerock/limerock_hFTB/limerock_geometry.py.
The code description begins by defining the parameters of the
simulation and importing all needed modules.
from limerock_geometry import LimeRock
# make limerock
limerock = LimeRock()
#############
# Real Params
#############
# fluid params
fluid_viscosity = 1.84e-05 # kg/m-s
fluid_density = 1.1614 # kg/m3
fluid_specific_heat = 1005 # J/(kg K)
fluid_conductivity = 0.0261 # W/(m K)
# copper params
copper_density = 8930 # kg/m3
copper_specific_heat = 385 # J/(kg K)
copper_conductivity = 385 # W/(m K)
# boundary params
inlet_velocity = 5.7 # m/s
inlet_temp = 0 # K
# source
source_term = 2127.71 # K/m
source_origin = (-0.061667, -0.15833, limerock.geo_bounds_lower[2])
source_dim = (0.1285, 0.31667, 0)
################
# Non dim params
################
length_scale = 0.0575 # m
velocity_scale = 5.7 # m/s
time_scale = length_scale / velocity_scale # s
density_scale = 1.1614 # kg/m3
mass_scale = density_scale * length_scale ** 3 # kg
pressure_scale = mass_scale / (length_scale * time_scale ** 2) # kg / (m s**2)
temp_scale = 273.15 # K
watt_scale = (mass_scale * length_scale ** 2) / (time_scale ** 3) # kg m**2 / s**3
joule_scale = (mass_scale * length_scale ** 2) / (time_scale ** 2) # kg * m**2 / s**2
##############################
# Nondimensionalization Params
##############################
# fluid params
nd_fluid_viscosity = fluid_viscosity / (
length_scale ** 2 / time_scale
) # need to divide by density to get previous viscosity
nd_fluid_density = fluid_density / density_scale
nd_fluid_specific_heat = fluid_specific_heat / (joule_scale / (mass_scale * temp_scale))
nd_fluid_conductivity = fluid_conductivity / (watt_scale / (length_scale * temp_scale))
nd_fluid_diffusivity = nd_fluid_conductivity / (
nd_fluid_specific_heat * nd_fluid_density
)
# copper params
nd_copper_density = copper_density / (mass_scale / length_scale ** 3)
nd_copper_specific_heat = copper_specific_heat / (
joule_scale / (mass_scale * temp_scale)
)
nd_copper_conductivity = copper_conductivity / (
watt_scale / (length_scale * temp_scale)
)
nd_copper_diffusivity = nd_copper_conductivity / (
nd_copper_specific_heat * nd_copper_density
)
# boundary params
nd_inlet_velocity = inlet_velocity / velocity_scale
nd_volumetric_flow = limerock.inlet_area * nd_inlet_velocity
nd_inlet_temp = inlet_temp / temp_scale
nd_source_term = source_term / (temp_scale / length_scale)
We nondimensionalize all parameters so that the scales for velocity, temperature, and pressure are roughly in the range 0-1. Such nondimensionalization trains the Neural network more efficiently.
Sequence Solver
Now setup the solver. Similar to the moving time window implementation in Tutorial Moving Time Window: Taylor Green Vortex Decay, construct a separate neural network that stores the thermal solution from the previous cycles fluid solution. We suggest that this problem is either run on \(8\) GPUs or gradient aggregation frequency is set to \(8\). Details on running with multi-GPUs and multi-nodes can be found in tutorial Performance and the details on using gradient aggregation can be found in tutorial Modulus Configuration.
Next, set up a train domain to only solve for the temperature in the fluid given a Dirichlet boundary condition on the solid. This will be the first stage of the hFTB method. After getting this initial solution for the temperature in the fluid solve for the main loop of the hFTB algorithm. Now you will solve for both the fluid and solid in a one way coupled manner. The Robin boundary conditions for the solid are coming from the previous iteration of the fluid solution.
Sometimes for visualization purposes it is beneficial to visualize the
results on a mesh. Here, this is done using the VTKUniformGrid method.
Note that the SDF was used as a mask function to filter out the temperature evaluations outside the
solid.
Multi-GPU training is currently not supported for this problem.
import torch
from torch.utils.data import DataLoader, Dataset
from torch import Tensor
import copy
import numpy as np
from sympy import Symbol, Eq, tanh, Or, And
from omegaconf import DictConfig, OmegaConf
import hydra
from hydra.utils import to_absolute_path
from typing import Dict
import modulus
from modulus.hydra import to_absolute_path, instantiate_arch, ModulusConfig
from modulus.utils.io import csv_to_dict
from modulus.solver import SequentialSolver
from modulus.domain import Domain
from modulus.geometry.primitives_3d import Box, Channel, Plane
from modulus.models.fourier_net import FourierNetArch
from modulus.models.arch import Arch
from modulus.domain.constraint import (
PointwiseBoundaryConstraint,
PointwiseInteriorConstraint,
)
from modulus.domain.monitor import PointwiseMonitor
from modulus.domain.inferencer import PointVTKInferencer
from modulus.utils.io import (
VTKUniformGrid,
)
from modulus.key import Key
from modulus.node import Node
from modulus.eq.pdes.basic import NormalDotVec, GradNormal
from modulus.eq.pdes.advection_diffusion import AdvectionDiffusion
from modulus.distributed.manager import DistributedManager
from limerock_properties import *
from flux_diffusion import (
FluxDiffusion,
FluxIntegrateDiffusion,
FluxGradNormal,
FluxRobin,
Dirichlet,
)
class hFTBArch(Arch):
def __init__(
self,
arch: Arch,
) -> None:
output_keys = arch.output_keys + [
Key(x.name + "_prev_step") for x in arch.output_keys
]
super().__init__(
input_keys=arch.input_keys,
output_keys=output_keys,
periodicity=arch.periodicity,
)
# set networks for current and prev time window
self.arch_prev_step = arch
self.arch = copy.deepcopy(arch)
for param, param_prev_step in zip(
self.arch.parameters(), self.arch_prev_step.parameters()
):
param_prev_step.requires_grad = False
def forward(self, in_vars: Dict[str, Tensor]) -> Dict[str, Tensor]:
y_prev_step = self.arch_prev_step.forward(in_vars)
y = self.arch.forward(in_vars)
for (key, b) in y_prev_step.items():
y[key + "_prev_step"] = b
return y
def move_network(self):
for param, param_prev_step in zip(
self.arch.parameters(), self.arch_prev_step.parameters()
):
param_prev_step.data = param.detach().clone().data
param_prev_step.requires_grad = False
@modulus.main(config_path="conf", config_name="conf_thermal")
def run(cfg: ModulusConfig) -> None:
if DistributedManager().distributed:
print("Multi-GPU currently not supported for this example. Exiting.")
return
# make list of nodes to unroll graph on
ad = AdvectionDiffusion(
T="theta_f", rho=nd_fluid_density, D=nd_fluid_diffusivity, dim=3, time=False
)
dif = FluxDiffusion(D=nd_copper_diffusivity)
flow_grad_norm = GradNormal("theta_f", dim=3, time=False)
solid_grad_norm = FluxGradNormal()
integrate_flux_dif = FluxIntegrateDiffusion()
robin_flux = FluxRobin(
theta_f_conductivity=nd_fluid_conductivity,
theta_s_conductivity=nd_copper_conductivity,
h=500.0,
)
dirichlet = Dirichlet(lhs="theta_f", rhs="theta_s")
flow_net = FourierNetArch(
input_keys=[Key("x"), Key("y"), Key("z")],
output_keys=[Key("u"), Key("v"), Key("w"), Key("p")],
)
f_net = FourierNetArch(
input_keys=[Key("x"), Key("y"), Key("z")], output_keys=[Key("theta_f")]
)
thermal_f_net = hFTBArch(f_net)
thermal_s_net = FourierNetArch(
input_keys=[Key("x"), Key("y"), Key("z")], output_keys=[Key("theta_s")]
)
flux_s_net = FourierNetArch(
input_keys=[Key("x"), Key("y"), Key("z")],
output_keys=[
Key("flux_theta_s_x"),
Key("flux_theta_s_y"),
Key("flux_theta_s_z"),
],
)
thermal_nodes = (
ad.make_nodes(detach_names=["u", "v", "w"])
+ dif.make_nodes()
+ flow_grad_norm.make_nodes()
+ solid_grad_norm.make_nodes()
+ integrate_flux_dif.make_nodes(
detach_names=["flux_theta_s_x", "flux_theta_s_y", "flux_theta_s_z"]
)
+ robin_flux.make_nodes(
detach_names=[
"theta_f_prev_step",
"theta_f_prev_step__x",
"theta_f_prev_step__y",
"theta_f_prev_step__z",
]
)
+ dirichlet.make_nodes(detach_names=["theta_s"])
+ [flow_net.make_node(name="flow_network", optimize=False)]
+ [
thermal_f_net.make_node(
name="thermal_fluid_network", optimize=True
)
]
+ [
thermal_s_net.make_node(
name="thermal_solid_network", optimize=True
)
]
+ [flux_s_net.make_node(name="flux_solid_network", optimize=True)]
)
# make domain for first cycle of hFTB
cycle_1_domain = Domain("cycle_1")
# add constraints to solver
x, y, z = Symbol("x"), Symbol("y"), Symbol("z")
import time as time
tic = time.time()
# inlet
inlet = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.inlet,
outvar={"theta_f": nd_inlet_temp},
batch_size=cfg.batch_size.inlet,
batch_per_epoch=50,
lambda_weighting={"theta_f": 1000.0},
)
cycle_1_domain.add_constraint(inlet, "inlet")
# outlet
outlet = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.outlet,
outvar={"normal_gradient_theta_f": 0},
batch_size=cfg.batch_size.outlet,
lambda_weighting={"normal_gradient_theta_f": 1.0},
)
cycle_1_domain.add_constraint(outlet, "outlet")
# channel walls insulating
walls = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.geo,
outvar={"normal_gradient_theta_f": 0},
batch_size=cfg.batch_size.no_slip,
criteria=Or(
Or(
Eq(y, limerock.geo_bounds_lower[1]), Eq(z, limerock.geo_bounds_lower[2])
),
Or(
Eq(y, limerock.geo_bounds_upper[1]), Eq(z, limerock.geo_bounds_upper[2])
),
),
lambda_weighting={"normal_gradient_theta_f": 1.0},
)
cycle_1_domain.add_constraint(walls, name="ChannelWalls")
# flow interior low res away from heat sink
lr_interior_f = PointwiseInteriorConstraint(
nodes=thermal_nodes,
geometry=limerock.geo,
outvar={"advection_diffusion_theta_f": 0},
batch_size=cfg.batch_size.lr_interior_f,
criteria=Or(
(x < limerock.heat_sink_bounds[0]), (x > limerock.heat_sink_bounds[1])
),
lambda_weighting={"advection_diffusion_theta_f": 1000.0},
)
cycle_1_domain.add_constraint(lr_interior_f, "lr_interior_f")
# flow interiror high res near heat sink
hr_interior_f = PointwiseInteriorConstraint(
nodes=thermal_nodes,
geometry=limerock.geo,
outvar={"advection_diffusion_theta_f": 0},
batch_size=cfg.batch_size.hr_interior_f,
lambda_weighting={"advection_diffusion_theta_f": 1000.0},
criteria=And(
(x > limerock.heat_sink_bounds[0]), (x < limerock.heat_sink_bounds[1])
),
)
cycle_1_domain.add_constraint(hr_interior_f, "hr_interior_f")
# fluid solid interface
interface = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.geo_solid,
outvar={"theta_f": 0.05},
batch_size=cfg.batch_size.interface,
criteria=z > limerock.geo_bounds_lower[2],
lambda_weighting={"theta_f": 100.0},
)
cycle_1_domain.add_constraint(interface, "interface")
# add inferencer data
vtk_obj = VTKUniformGrid(
bounds=[limerock.geo_bounds[x], limerock.geo_bounds[y], limerock.geo_bounds[z]],
npoints=[256, 128, 256],
export_map={"u": ["u", "v", "w"], "p": ["p"], "theta_f": ["theta_f"]},
)
def mask_fn(x, y, z):
sdf = limerock.geo.sdf({"x": x, "y": y, "z": z}, {})
return sdf["sdf"] < 0
grid_inferencer = PointVTKInferencer(
vtk_obj=vtk_obj,
nodes=thermal_nodes,
input_vtk_map={"x": "x", "y": "y", "z": "z"},
output_names=["u", "v", "w", "p", "theta_f"],
mask_fn=mask_fn,
mask_value=np.nan,
requires_grad=False,
batch_size=100000,
)
cycle_1_domain.add_inferencer(grid_inferencer, "grid_inferencer")
# make domain for all other cycles
cycle_n_domain = Domain("cycle_n")
# inlet
cycle_n_domain.add_constraint(inlet, "inlet")
# outlet
cycle_n_domain.add_constraint(outlet, "outlet")
# channel walls insulating
cycle_n_domain.add_constraint(walls, name="ChannelWalls")
# flow interior low res away from heat sink
cycle_n_domain.add_constraint(lr_interior_f, "lr_interior_f")
# flow interiror high res near heat sink
cycle_n_domain.add_constraint(hr_interior_f, "hr_interior_f")
# diffusion dictionaries
diff_outvar = {
"diffusion_theta_s": 0,
"compatibility_theta_s_x_y": 0,
"compatibility_theta_s_x_z": 0,
"compatibility_theta_s_y_z": 0,
"integrate_diffusion_theta_s_x": 0,
"integrate_diffusion_theta_s_y": 0,
"integrate_diffusion_theta_s_z": 0,
}
diff_lambda = {
"diffusion_theta_s": 1000000.0,
"compatibility_theta_s_x_y": 1.0,
"compatibility_theta_s_x_z": 1.0,
"compatibility_theta_s_y_z": 1.0,
"integrate_diffusion_theta_s_x": 1.0,
"integrate_diffusion_theta_s_y": 1.0,
"integrate_diffusion_theta_s_z": 1.0,
}
# solid interior
interior_s = PointwiseInteriorConstraint(
nodes=thermal_nodes,
geometry=limerock.geo_solid,
outvar=diff_outvar,
batch_size=cfg.batch_size.interior_s,
lambda_weighting=diff_lambda,
)
cycle_n_domain.add_constraint(interior_s, "interior_s")
# limerock base
sharpen_tanh = 60.0
source_func_xl = (tanh(sharpen_tanh * (x - source_origin[0])) + 1.0) / 2.0
source_func_xh = (
tanh(sharpen_tanh * ((source_origin[0] + source_dim[0]) - x)) + 1.0
) / 2.0
source_func_yl = (tanh(sharpen_tanh * (y - source_origin[1])) + 1.0) / 2.0
source_func_yh = (
tanh(sharpen_tanh * ((source_origin[1] + source_dim[1]) - y)) + 1.0
) / 2.0
gradient_normal = (
nd_source_term
* source_func_xl
* source_func_xh
* source_func_yl
* source_func_yh
)
base = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.geo_solid,
outvar={"normal_gradient_flux_theta_s": gradient_normal},
batch_size=cfg.batch_size.base,
criteria=Eq(z, limerock.geo_bounds_lower[2]),
lambda_weighting={"normal_gradient_flux_theta_s": 10.0},
)
cycle_n_domain.add_constraint(base, "base")
# fluid solid interface
interface = PointwiseBoundaryConstraint(
nodes=thermal_nodes,
geometry=limerock.geo_solid,
outvar={"dirichlet_theta_s_theta_f": 0, "robin_theta_s": 0},
batch_size=cfg.batch_size.interface,
criteria=z > limerock.geo_bounds_lower[2],
lambda_weighting={"dirichlet_theta_s_theta_f": 100.0, "robin_theta_s": 1.0},
)
cycle_n_domain.add_constraint(interface, "interface")
# add fluid inferencer data
cycle_n_domain.add_inferencer(grid_inferencer, "grid_inferencer")
# add solid inferencer data
vtk_obj = VTKUniformGrid(
bounds=[
limerock.geo_hr_bounds[x],
limerock.geo_hr_bounds[y],
limerock.geo_hr_bounds[z],
],
npoints=[128, 128, 512],
export_map={"theta_s": ["theta_s"]},
)
def mask_fn(x, y, z):
sdf = limerock.geo.sdf({"x": x, "y": y, "z": z}, {})
return sdf["sdf"] > 0
grid_inferencer = PointVTKInferencer(
vtk_obj=vtk_obj,
nodes=thermal_nodes,
input_vtk_map={"x": "x", "y": "y", "z": "z"},
output_names=["theta_s"],
mask_fn=mask_fn,
mask_value=np.nan,
requires_grad=False,
batch_size=100000,
)
cycle_n_domain.add_inferencer(grid_inferencer, "grid_inferencer_solid")
# peak temperature monitor
invar_temp = limerock.geo_solid.sample_boundary(
10000, criteria=Eq(z, limerock.geo_bounds_lower[2])
)
peak_temp_monitor = PointwiseMonitor(
invar_temp,
output_names=["theta_s"],
metrics={"peak_temp": lambda var: torch.max(var["theta_s"])},
nodes=thermal_nodes,
)
cycle_n_domain.add_monitor(peak_temp_monitor)
# make solver
slv = SequentialSolver(
cfg,
[(1, cycle_1_domain), (20, cycle_n_domain)],
custom_update_operation=thermal_f_net.move_network,
)
# start solver
slv.solve()
if __name__ == "__main__":
run()
To confirm the accuracy of the model, the results are compared for pressure drop and peak temperature with the OpenFOAM and a commercial solver results, and the results are reported in Table 14. The results show good accuracy achieved by the hFTB method. Table 15 demonstrates the impact of mesh refinement on the solution of the commercial solver where with increasing mesh density and mesh quality, the commercial solver results show convergence towards the Modulus results. A visualization of the heat sink temperature profile is shown in Fig. 159.
Property |
OpenFOAM |
Commercial Solver |
Modulus |
Pressure Drop \((Pa)\) |
\(133.96\) |
\(137.50\) |
\(150.25\) |
Peak Temperature \((^{\circ} C)\) |
\(93.41\) |
\(95.10\) |
\(97.35\) |
Number of elements |
Pressure drop (Pa) |
Peak temperature \((^{\circ} C)\) |
||||
Commercial solver |
Modulus |
% diff |
Commercial solver |
Modulus |
% diff |
|
22.4 M |
81.27 |
150.25 |
84.88 |
97.40 |
97.35 |
0.05 |
24.7 M |
111.76 |
150.25 |
34.44 |
95.50 |
97.35 |
1.94 |
26.9 M |
122.90 |
150.25 |
22.25 |
95.10 |
97.35 |
2.36 |
30.0 M |
132.80 |
150.25 |
13.14 |
|||
32.0 M |
137.50 |
150.25 |
9.27 |
|||
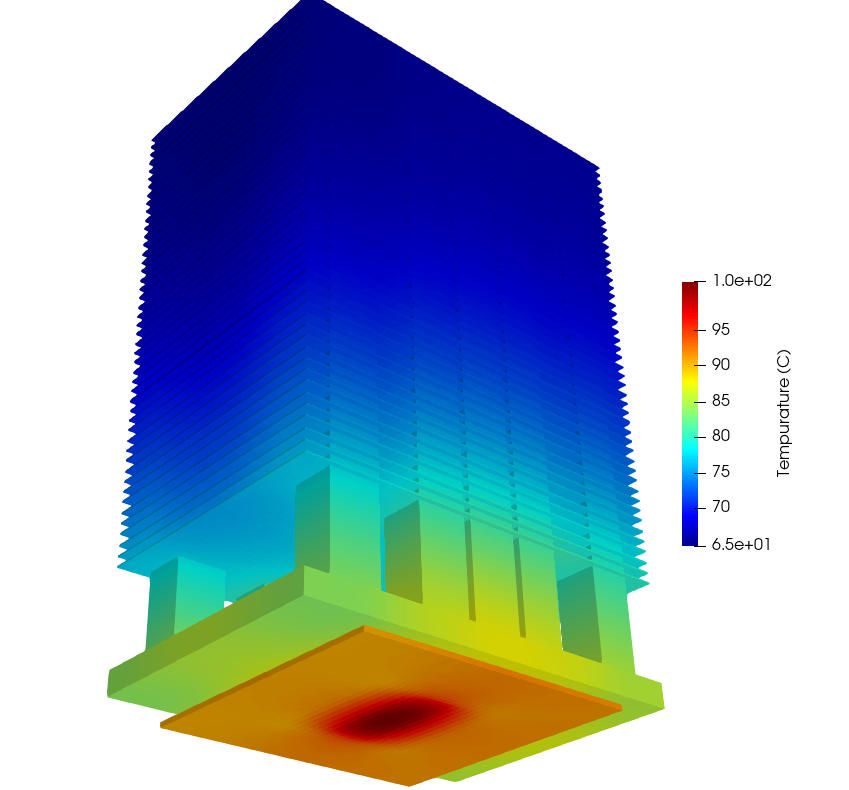
Fig. 159 NVSwitch Solid Temperature
Previously, Chapter Parameterized 3D Heat Sink showed that by parameterizing the input of the neural network, you can solve for multiple design parameters in a single run and use that parameterized network for design optimization. This section introduces another approach for parameterization and design optimization, which is based on constructing a surrogate using the solution obtained from a limited number of non-parameterized neural network models. Compared to the parameterized network approach that is limited to the CSG module, this approach can be used for parameterization of both constructive solid and STL geometries, and additionally, can offer improved accuracy specially for cases with a high-dimensional parameter space and also in cases where some or all of the design parameters are discrete. However, this approach requires training of multiple neural networks and may require multi-node resources.
This section focuses on surrogates based on the generalized Polynomial Chaos (gPC) expansions. The gPC is an efficient tool for uncertainty quantification using limited data, and in introduced in Section Generalized Polynomial Chaos. It starts off by generating the required number of realizations form the parameter space using a low discrepancy sequence such as Halton or Sobol. Next, for each realization, a separate neural network model is trained. Note that these trainings are independent from each other and therefore, this training step is embarrassingly parallel and can be done on multiple GPUs or nodes. Finally, a gPC surrogate is trained that maps the parameter space to the quantities of interest (e.g., pressure drop and peak temperature in the heat sink design optimization problem).
In order to reduce the computational cost of this approach associated with training of multiple models, transfer learning is used, that is, once a model is fully trained for a single realization, it is used for initialization of the other models, and this can significantly reduce the total time to convergence. Transfer learning has been previously introduced in Chapter STL Geometry: Blood Flow in Intracranial Aneurysm.
Here, to illustrate the gPC surrogate modeling accelerated via transfer learning, consider the NVIDIA’s NVSwitch heat sink introduced above. We introduce four geometry parameters related to fin cut angles, as shown in Fig. 160. We then construct a pressure drop surrogate. Similarly, one can also construct a surrogate for the peak temperature and use these two surrogates for design optimization of this heat sink.
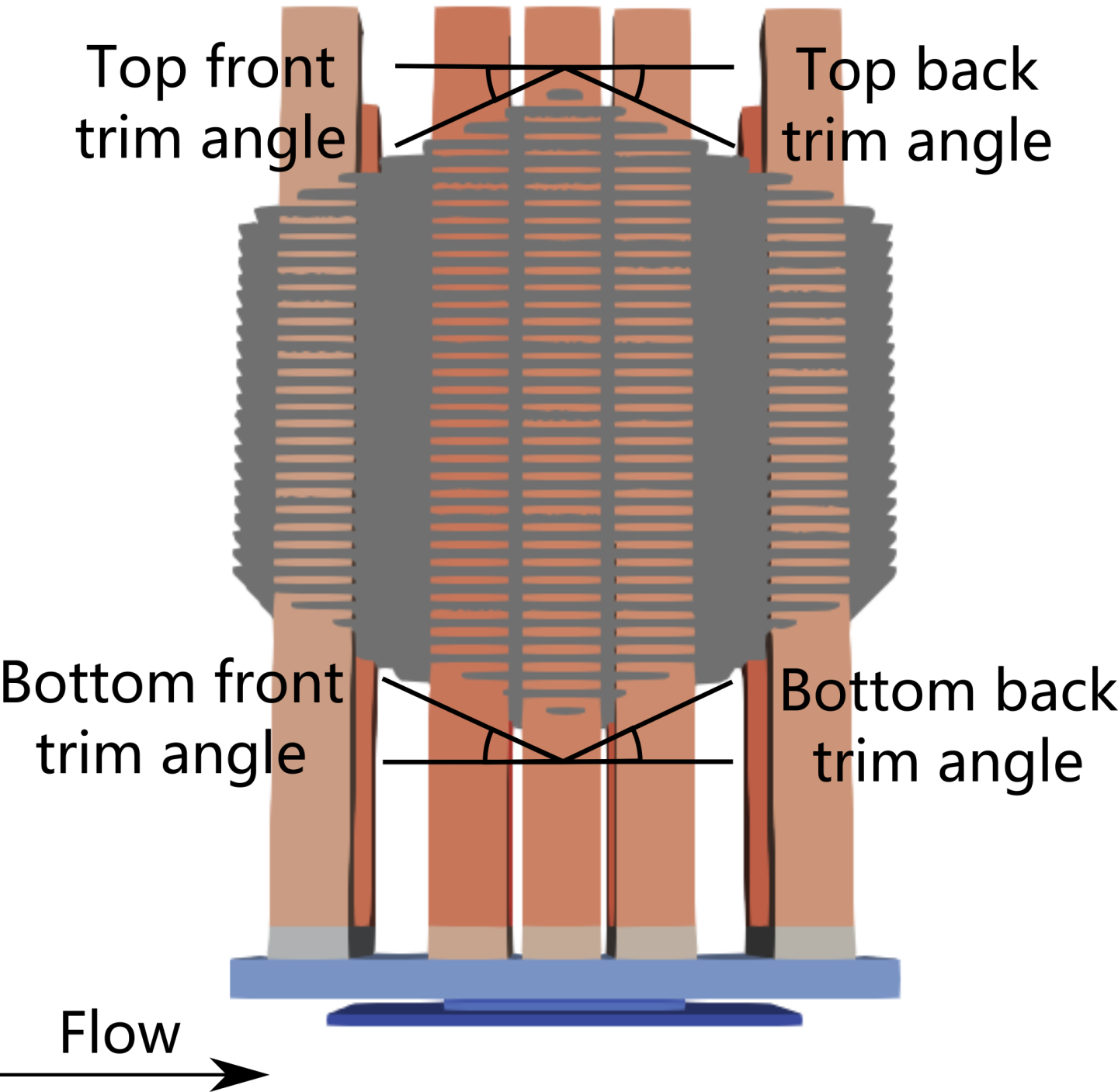
Fig. 160 NVSwitch heat sink geometry parameterization. Each parameter ranges between 0 and \(\pi/6\).
The scripts for this example are available at examples/limerock/limerock_transfer_learning.
Following Section
Generalized Polynomial Chaos, one can
generate 30 geometry realizations according to a Halton sequence by
running sample_generator.py, as follows
# import libraries
import numpy as np
import chaospy
# define parameter ranges
fin_front_top_cut_angle_ranges = (0.0, np.pi / 6.0)
fin_front_bottom_cut_angle_ranges = (0.0, np.pi / 6.0)
fin_back_top_cut_angle_ranges = (0.0, np.pi / 6.0)
fin_back_bottom_cut_angle_ranges = (0.0, np.pi / 6.0)
# generate samples
samples = chaospy.generate_samples(
order=30,
domain=np.array(
[
fin_front_top_cut_angle_ranges,
fin_front_bottom_cut_angle_ranges,
fin_back_top_cut_angle_ranges,
fin_back_bottom_cut_angle_ranges,
]
).T,
rule="halton",
)
samples = samples.T
np.random.shuffle(samples)
np.savetxt("samples.txt", samples)
Then train a separate flow network for each of these realizations
using transfer learning. To do this, update the configs for network checkpoint,
learning rate and decay rate, and the maximum training iterations in
conf/config.py. Also change the sample_id
variable in limerock_geometry.py, and then run limerock_flow.py.
This is repeated until all of the geometry realizations are covered.
These flow models are initialized using the trained network for the base
geometry (as shown in Fig. 157), and are
trained for a fraction of the total training iterations for the base
geometry, with a smaller learning rate and a faster learning rate decay,
as specified in conf/config.yaml.
This is because you only need to fine-tune these models as opposed to
training them from the scratch. Please note that, before you launch the
transfer learning runs, a flow network for the base geometry needs to be
fully trained.
Fig. 161 shows the front and back pressure results for different runs. It is evident that the pressure has converged faster in the transfer learning runs compared to the base geometry full run, and that transfer learning has reduced the total time to convergence by a factor of 5.
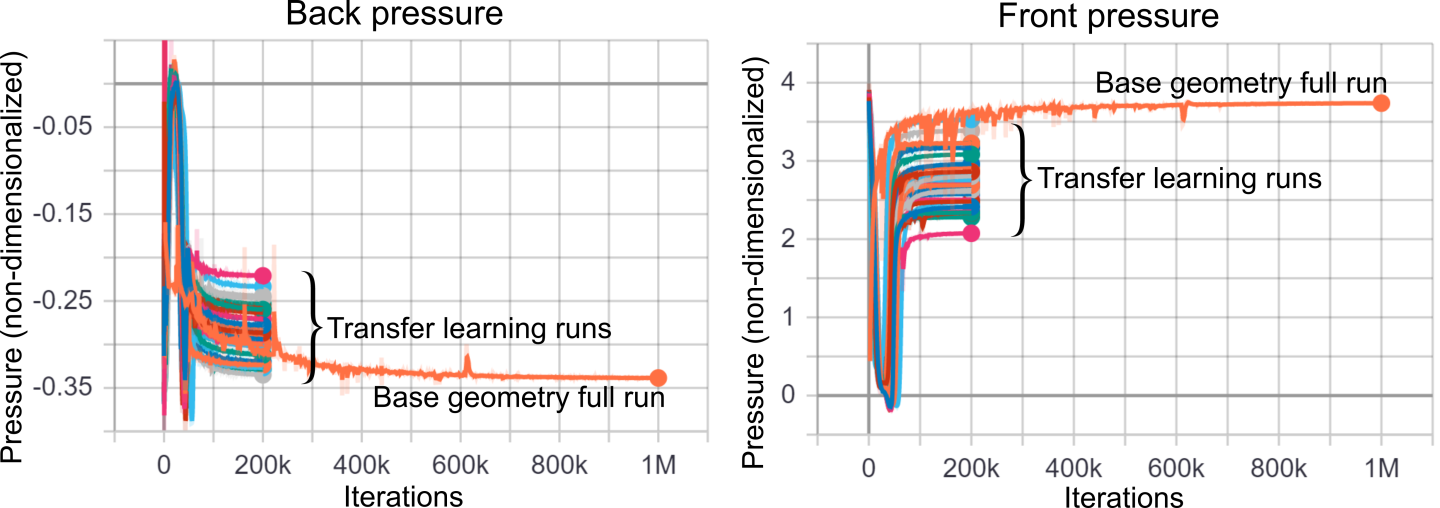
Fig. 161 NVSwitch front and back pressure convergence results for different geometries using transfer learning.
Finally, randomly divide the pressure drop data obtained from these models into training and test sets, and construct a gPC surrogate, as follows:
# import libraries
import numpy as np
import csv
import chaospy
# load data
samples = np.loadtxt("samples.txt")
num_samples = len(samples)
# read monitored values
y_vec = []
for i in range(num_samples):
front_pressure_dir = (
"./outputs/limerock_flow/tl_" + str(i) + "/monitors/front_pressure.csv"
)
back_pressure_dir = (
"./outputs/limerock_flow/tl_" + str(i) + "/monitors/back_pressure.csv"
)
with open(front_pressure_dir, "r", encoding="utf-8", errors="ignore") as scraped:
front_pressure = float(scraped.readlines()[-1].split(",")[1])
with open(back_pressure_dir, "r", encoding="utf-8", errors="ignore") as scraped:
back_pressure = float(scraped.readlines()[-1].split(",")[1])
pressure_drop = front_pressure - back_pressure
y_vec.append(pressure_drop)
y_vec = np.array(y_vec)
# Split data into training and validation
val_portion = 0.15
val_idx = np.random.choice(
np.arange(num_samples, dtype=int), int(val_portion * num_samples), replace=False
)
val_x, val_y = samples[val_idx], y_vec[val_idx]
train_x, train_y = np.delete(samples, val_idx, axis=0).T, np.delete(
y_vec, val_idx
).reshape(-1, 1)
# Construct the PCE
distribution = chaospy.J(
chaospy.Uniform(0.0, np.pi / 6),
chaospy.Uniform(0.0, np.pi / 6),
chaospy.Uniform(0.0, np.pi / 6),
chaospy.Uniform(0.0, np.pi / 6),
)
expansion = chaospy.generate_expansion(2, distribution)
poly = chaospy.fit_regression(expansion, train_x, train_y)
# PCE closed form
print("__________")
print("PCE closd form:")
print(poly)
print("__________")
# Validation
print("PCE evaluatins:")
for i in range(len(val_x)):
pred = poly(val_x[i, 0], val_x[i, 1], val_x[i, 2], val_x[i, 3])[0]
print("Sample:", val_x[i])
print("True val:", val_y[i])
print("Predicted val:", pred)
print("Relative error (%):", abs(pred - val_y[i]) / val_y[i] * 100)
print("__________")
The code for constructing this surrogate is available at limerock_pce_surrogate.py:
Fig. 162 shows the gPC surrogate
performance on the test set. The relative errors are below 1%, showing
the good accuracy of the constructed gPC pressure drop surrogate.
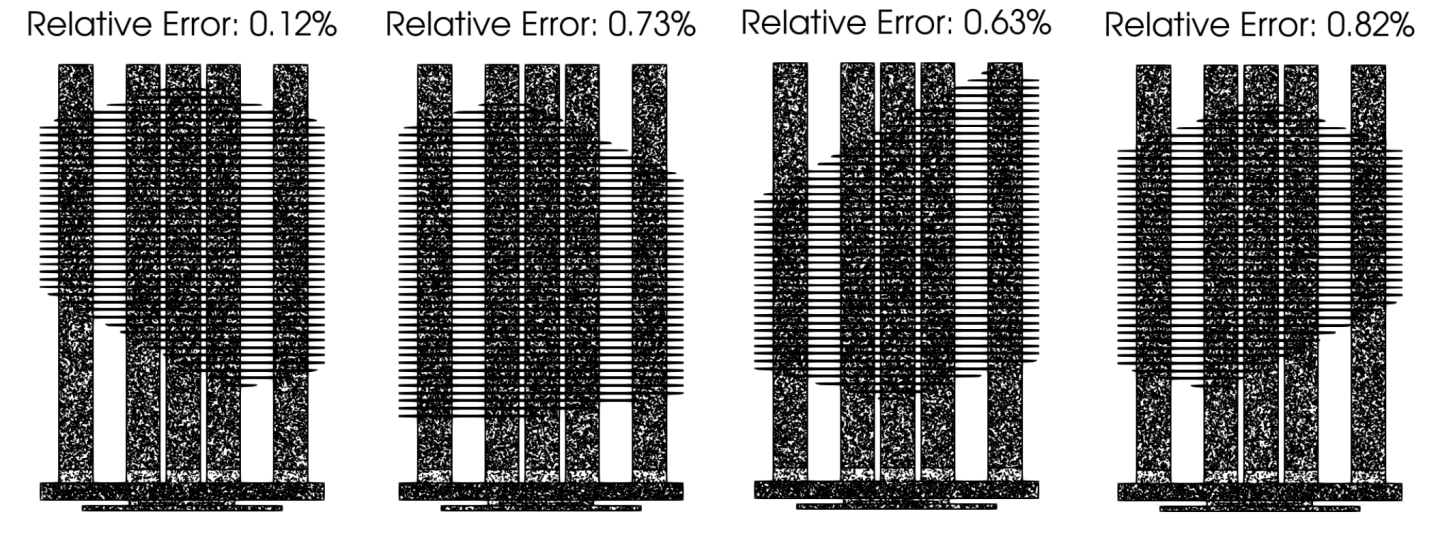
Fig. 162 The gPC pressure drop surrogate accuracy tested on four geometries
References