Computational Graph, Nodes and Architectures

Modulus contains APIs that make adding a neural network architecture or a equation to your problem very easy. Modulus relies on Pytorch’s torch.nn.Module to build these various nodes. Nodes are used to represent components that will be executed in the forward pass during the training. The nodes in Modulus can be thought as a torch.nn.Module wrapper that contains additional information regarding what the input/output variables are needed allowing Modulus to develop execution graphs for multi-objective problems. Nodes may contain models or functions such as PyTorch neural networks that are built into Modulus, user defined PyTorch networks, feature transformations and equations.

The nodes are combined in such a way that they can interact with one another easily. In other words, within a few lines of code, it is possible to create a computational graph that computes the PDE loss using the outputs of a neural network architecture and also create an architecture that uses the outputs of some equations. Modulus solves problems by setting them up like optimization problems. The optimization objectives are defined using constraints in Modulus. The different type of constraints are covered in detail in Constraints . One of the input to each of the constraints is the nodes. This is basically a list of all the Modulus nodes (architecures, equations, etc.) that are required to compute the desired output (specified in the outvar of either the constraint or the dataset) from the inputs to the constraint (specified in the invar of either the constraint or the dataset). Modulus figures out to compute the required derivatives and model gradients to prepare a computational graph and evaluate the loss. If any information is missing that prevents Modulus to compute the required outvars from the given invars, Modulus will throw a graph unroll error.

This example explores the different types of architecures and equations available within Modulus and also looks at how to customize each of these to prepare your own custom models to train.

Modulus comes with a model zoo containing several optimized architectures such as fully connected multi-layer perceptrons, Fourier feature neural networks, SiReNs, Fourier Neural Operators, DeepNeuralOperators and etc. Each of these architectures can be instantiated in your project very easily and the hyper parameters of the model can be tuned using hydra. Please refer Modulus Configuration for more information on the configurations for these various neural networks. For a deep dive into the theory and the mathematical underpinnings of these models, please refer: Architectures In Modulus. Below, you can find two different ways of using the neural network models within Modulus.

All the models in Modulus have a method called .make_nodes() that is used to generate the computational graph for the network architecture.

The architecture, its intermediate layers can be visualized by printing the model or using visualization libraries like torchviz.

Listing 6 Architecture node in Modulus

            

            
from modulus.models.fully_connected import FullyConnectedArch
from modulus.key import Key

u_net = FullyConnectedArch(
    input_keys=[Key("x")], output_keys=[Key("u")], nr_layers=3, layer_size=32
)

# visualize the network
print(u_net)

# graphically visualize the PyTorch execution graph # NOTE: Requires installing torchviz library: https://pypi.org/project/torchviz/
import torch
from torchviz import make_dot

# pass dummy data through the model
data_out = u_net({"x": (torch.rand(10, 1)),})
make_dot(data_out["u"], params=dict(u_net.named_parameters())).render("u_network", format="png")
        

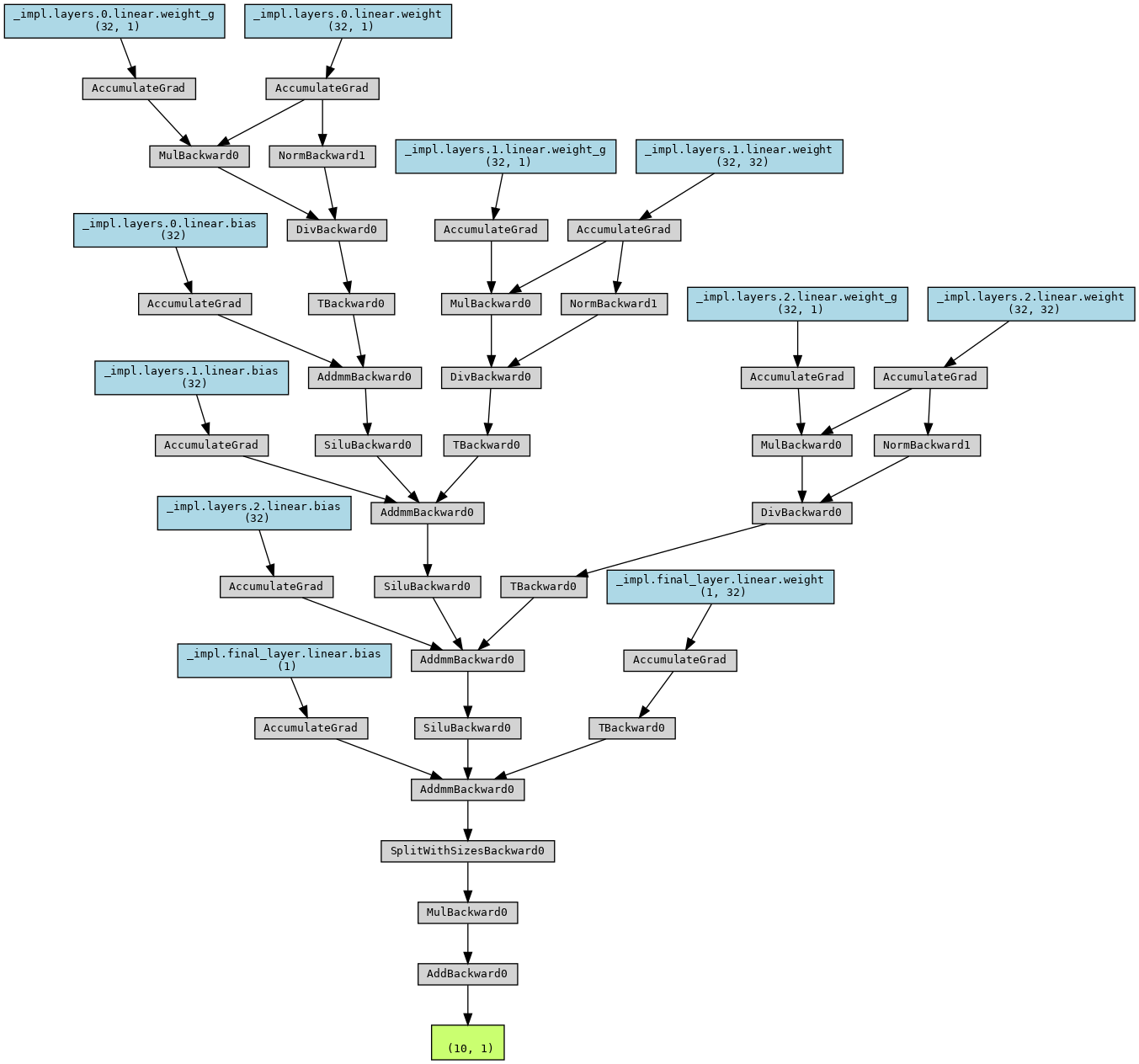
Fig. 42 Visualizing a neural network model in Modulus using Torchviz

At several places you will see the use of a Key and Node. A Key class is used for describing inputs and outputs used for graph unroll/evaluation. The most basic key is just a string that is used to represent the name of inputs or outputs of the model. A Node class represents a typical node in a graph. The node evaluates an expression to produce output given some inputs.

Modulus is a framework to develop solutions to problems in science and engineering. Since both these fields have equations at their core, Modulus has several utilities to aid defining these equations with ease. With Modulus’ symbolic library, you can define the equations using SymPy in the most natural way possible. The expressions are converted to PyTorch expressions in the backend. Modulus comes with several built-in PDEs that are customizable such that they can be applied to steady-state or transient problems in 1D/2D/3D (this is not applicable to all the PDEs). A nonexhaustive list of PDEs that are currently available in Modulus include:

• AdvectionDiffusion: Advection diffusion equation

• GradNormal: Normal gradient of a scalar

• Diffusion: Diffusion equation

• MaxwellFreqReal: Frequency domain Maxwell’s equation

• LinearElasticity: Linear elasticity equations

• LinearElasticityPlaneStress: Linear elasticity plane stress equations

• NavierStokes: Navier stokes equations for fluid flow

• ZeroEquation: Zero equation turbulence model

• WaveEquation: Wave equation

Since the PDEs are defined symbolically, they can be printed to ensure correct implementation.

Listing 7 Equations in Modulus

            

            
>>> from modulus.eq.pdes.navier_stokes import NavierStokes

>>> ns = NavierStokes(nu=0.01, rho=1, dim=2)
>>> ns.pprint()
continuity: u__x + v__y
momentum_x: u*u__x + v*u__y + p__x + u__t - 0.01*u__x__x - 0.01*u__y__y
momentum_y: u*v__x + v*v__y + p__y + v__t - 0.01*v__x__x - 0.01*v__y__y
        

The PDE class allows you to write the equations symbolically in SymPy. This allows you to quickly write your equations in the most natural way possible. Below, the code to setup a simple PDE is shown.

Listing 8 Custom equations in Modulus

            

            
from sympy import Symbol, Number, Function
from modulus.eq.pde import PDE

class CustomPDE(PDE):
    def __init__(self, f=1.0):
        # coordinates
        x = Symbol("x")

        # make input variables
        input_variables = {"x": x}

        # make u function
        u = Function("u")(*input_variables)

        # source term
        if type(f) is str:
            f = Function(f)(*input_variables)
        elif type(f) in [float, int]:
            f = Number(f)

        # set equations
        self.equations = {}
        self.equations["custom_pde"] = (
            u.diff(x, 2) - f
        )  # "custom_pde" key name will be used in constraints

eq = CustomPDE(f=1.0)
        

Modulus also allows users to create simple nodes for custom calculation. These can be generated either using SymPy or using the base Node class. Some examples of this are shown below.

Custom Nodes using torch.nn.Module

Listing 9 Custom node using torch nn.Module

            

            
>>> import torch
>>> import torch.nn as nn
>>> from torch import Tensor
>>> from typing import Dict
>>> import numpy as np
>>> from modulus.node import Node
>>> class ComputeSin(nn.Module):
...     def forward(self, in_vars: Dict[str, Tensor]) -> Dict[str, Tensor]:
...         return {"sin_x": torch.sin(in_vars["x"])}
...
>>> node = Node(['x'], ['sin_x'], ComputeSin())
>>> node.evaluate({"x": (torch.ones(10, 1))*np.pi/4,})
{'sin_x': tensor([[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071]])}
        

Custom Nodes using SymPy

Below, an example code to generate a Node using a symbolic expression is shown.

Listing 10 Custom node using sympy

            

            
>>> import torch
>>> import numpy as np
>>> from sympy import Symbol, sin
>>> from modulus.node import Node
>>> node = Node.from_sympy(sin(Symbol("x")), "sin_x")
>>> node.evaluate({"x": (torch.ones(10, 1))*np.pi/4,})
{'sin_x': tensor([[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071],
[0.7071]])}