State Vector Algorithms#

This section describes key algorithmic concepts used in quantum circuit simulations with state vector.

Gate fusion#

Gate applications account for large proportion of the computation cost in quantum simulators. We can reduce the overall memory footprint required in gate applications by fusing multiple gates into one larger gate.

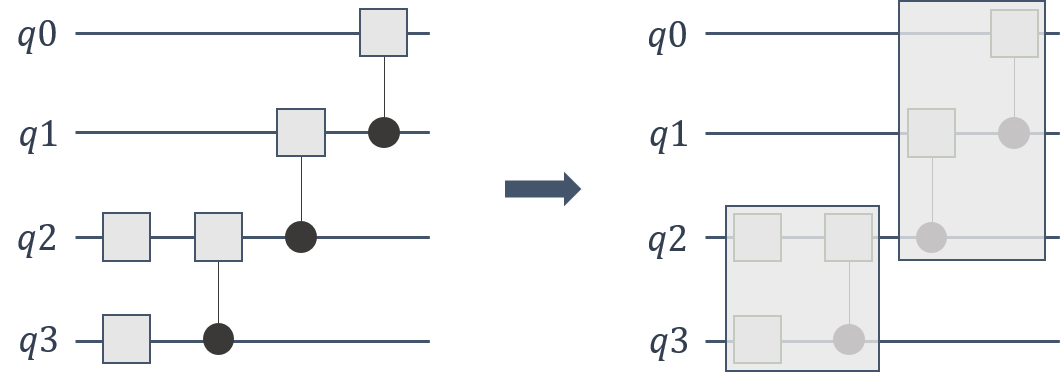
../../_images/fusion.png

cuStateVec API supports these general gate applications with multiple qubits. For detailed information, please refer to custatevecApplyMatrix().

cuStateVec Ex API provides pipelined gate application with gate fusion for improved performance. For detailed information, please refer to State Vector Updater.

Multi-GPU computation#

The memory usage in quantum circuit simulations increases exponentially with the number of qubits. To simulate more qubits, multiple GPUs are required. A typical approach is to divide the qubits into global and local ones.

For instance, a 3-qubit system with 8 state vector elements can be equally distributed to 4 GPUs as described in the following figure.

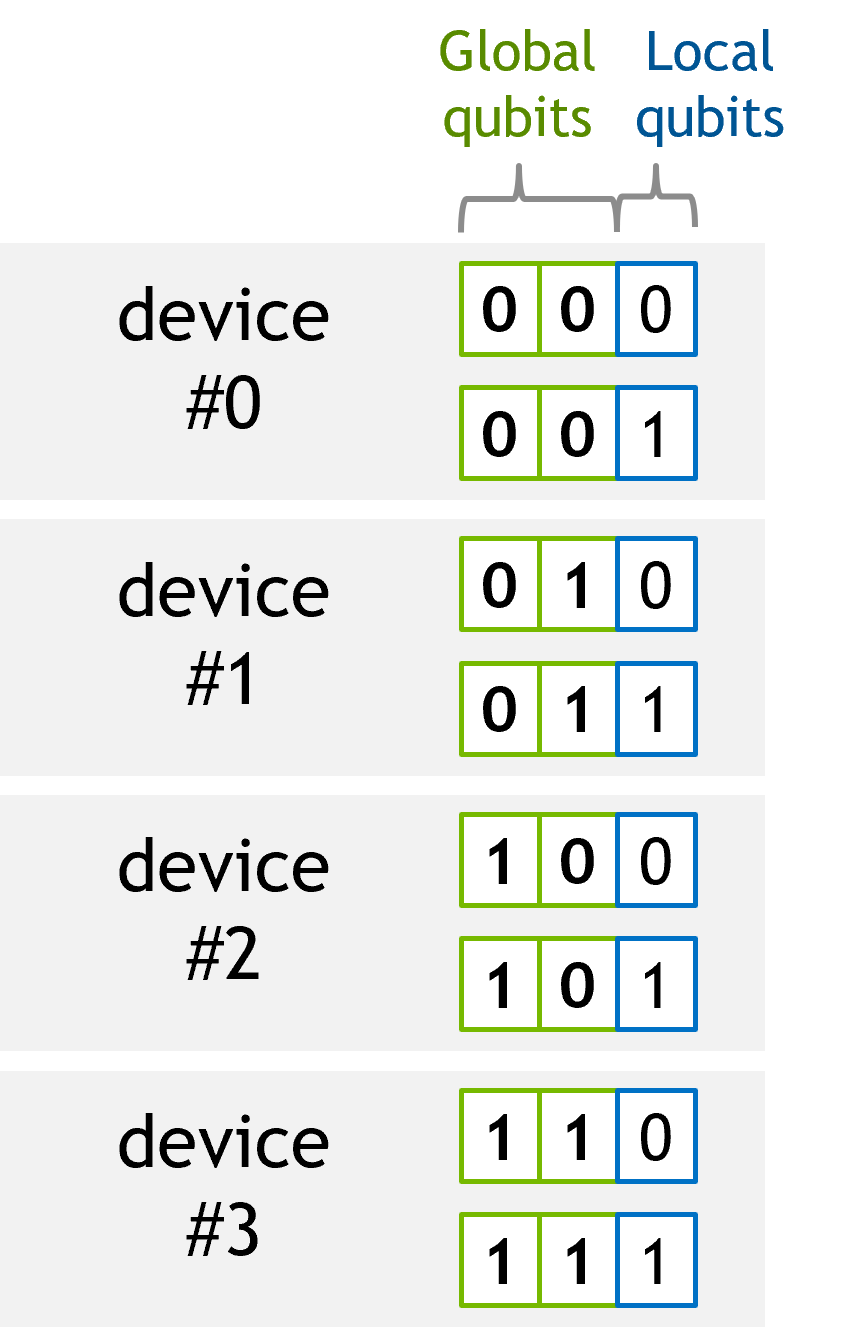
../../_images/globalQubits.png

When an index is assigned for each sub state vector, it can represent the higher-order qubits. We refer to these qubits as global qubits and other qubits as local qubits. In the example above, we have 2 global qubits and 1 local qubit.

In general, for an \(M\)-qubit system, suppose each GPU can store \(2^N\) state vector elements (for \(N\) local qubits), then \(2^{M-N}\) GPUs (that is, \(M-N\) global qubits) are required to store the entire state vector. The \(k\)-th GPU (\(k = (i_{M-1} i_{M-2} \cdots i_{N})_2\)) stores the state vector elements \(\alpha_{i_{M-1} i_{M-2} \cdots i_{N} i_{N-1} \cdots i_{0}}\) with \(i_p \in \{0, 1\}, 0 \leq p \leq N-1\).

For instance,

  • GPU #0 handles elements from \(\alpha_{0_{M-1} \cdots 0_{N+1} 0_{N} 0_{N-1} \cdots 0_{0}}\) to \(\alpha_{0_{M-1} \cdots 0_{N+1} 0_{N} 1_{N-1} \cdots 1_{0}}\),

  • GPU #1 handles elements from \(\alpha_{0_{M-1} \cdots 0_{N+1} 1_{N} 0_{N-1} \cdots 0_{0}}\) to \(\alpha_{0_{M-1} \cdots 0_{N+1} 1_{N} 1_{N-1} \cdots 1_{0}}\)

  • GPU #2 handles elements from \(\alpha_{0_{M-1} \cdots 1_{N+1} 0_{N} 0_{N-1} \cdots 0_{0}}\) to \(\alpha_{0_{M-1} \cdots 1_{N+1} 0_{N} 1_{N-1} \cdots 1_{0}}\)

  • GPU #3 handles elements from \(\alpha_{0_{M-1} \cdots 1_{N+1} 1_{N} 0_{N-1} \cdots 0_{0}}\) to \(\alpha_{0_{M-1} \cdots 1_{N+1} 1_{N} 1_{N-1} \cdots 1_{0}}\), and so on.

Here, the indices \(i_{M-1}, i_{M-2}, \cdots, i_{N}\) belong to the global qubits, and others belong to the local qubits.